小升初数学专题训练—“图形问题(五)立体图形的面积与体积(全国通用)

小升初数学几何图形专题知识训练含答案一、单选题1．甲数和乙数的比是4∶7，甲数是乙数的（）A．47B．74C．342．甲数的14和乙数的34相等，那么甲数（）乙数。

A．大于B．小于C．等于D．不能比较3．在一张长8厘米，宽6厘米的长方形纸上，剪下一个最大的正方形，这个正方形的面积是（）。

A．36平方厘米B．48平方厘米C．64平方厘米4．下面图形都是由3个边长1厘米的小正方形组成的，其中周长最长的是（）。

A．B．C．5．旋转能得到（）A．圆柱B．圆锥C．一个空心的球6．如图，图中的物体从（）看到的形状是相同的．A．正面和上面B．正面和右面C．上面和右面7．下面运用“转化”思想方法的是（）。

A．①和②B．①和③C．②和③8．下列叙述正确的是（）A．两个数的最小公倍数是它们最大公因数的倍数。

B．三角形的底和高扩大2倍，它的面积也扩大2倍。

C．相邻两个非0的自然数，其中一定有一个是合数。

9．两个完全相同的长方形（如图），将图①和图②阴影部分的面积相比，（）A．图①大B．图②大C．图①和图②相等10．下列说法中正确的有（）。

①2厘米长的线段向上平移10厘米，线段的长还是2厘米。

②8080008000这个数只读出一个“零”。

③万级包括亿万、千万、百万、十万、万五个数位。

④三位数乘两位数，积不可能是六位数。

A．2个B．3个C．4个二、填空题11．在一个宽为6厘米的长方形里恰好能画两个同样尽量大的圆(如图).圆的直径为厘米，半径为厘米；一个圆的周长为厘米，面积为平方厘米；长方形的面积是平方厘米，阴影部分的面积是平方厘米．12．一个梯形的上底是5.8厘米，下底是6.2厘米，高是2.5厘米，它的面积是平方厘米。

13．是由几个拼成的。

；；。

14．在横线上填上“平移”或“旋转”。

汽车行驶中车轮的运动是现象；推拉门被推开是现象。

15．把一个棱长为6 cm的正方体木块削成一个最大的圆柱，圆柱的体积是，再把这个圆柱削成一个最大的圆锥，这个圆锥的体积是。

小升初数学试题《空间与图形》计算体积、表面积、阴影面积一、计算题1．求下面未知角的度数。

4．求下图阴影部分的周长2．计算下面各图形的面积． （单5．求下面立体图形的表面积和体积。

（单位: 分米）6．求阴影部分的面积7．求阴影部分的面积9．计算图中阴影部分的面积二、作图题10．分别画出每个图形底边上的高13．一个长方体的纸盒如图。

请在方格中画出这个长方体纸盒的展开图三、解答题每个12．过点 A 画直线 BC 的垂线 AD ，过点 C 画直线 AB 的14．一个长方形操场，长220 米，宽90 米。

小勇沿操场的边跑了两圈，他一共跑了多少米?15．下面的图形是由七巧板中的哪几块拼成的？你试着拼一拼．16．求下面体育场的面积．17．在一块周长是80 米的正方形花坛里，用一串红围出一个最大的圆形，这个圆形的面积是多少平方米？这个花坛还剩下多少平方米的空地？18．一间会议室长8m，宽 6.5m，用边长0.5m 的正方形瓷砖给这会议室铺上地面，大约要用瓷砖多少块？19．一个长方形的长和宽都是以厘米为单位的质数，并且周长是36 cm．这个长方形的面积最大是多少平方厘米？20．一个长方体长10 厘米、宽8 厘米、高 5 厘米．把它切成两个长方体，这两个长方体的表面积的和最大是多少平方厘米？21．如图中梯形的面积是20dm2，阴影三角形的面积是多少？22．一个圆形的铁环，直径是40 厘米，做这样一个铁环需要用多长的铁条？23．（东城区）将图中的长方形，以虚线为轴旋转一周，得到的立体形的体积是多少？24．把两个长30 厘米、宽20 厘米的长方形拼成一个大长方形，大长方形的周长比原来 2 个小长方形的周长的和少多少厘米？A画出已知直线的垂线和平行线．26．一个长方体的棱长之和是60 厘米，宽是 5 厘米，高是 2 厘米，长是多少厘米？27．到圆上各点的距离相等的点只有圆心一个点．28．画一个三角形，使它的面积与五边形（如图）面积相等．29．一块梯形的草地，上底250 米，下底150米，高是180米，它的面积是多少公顷？30．一个高30 厘米、底面半径10 厘米的无盖圆柱形铁皮水桶，要用多少平方厘米的铁皮？31．中祥小区靠墙边用46m的篱笆围了一块梯形空地（见下图）种草坪。

小升初数学复习专题《立体图形》练习一、填空题1．圆锥是由两个面组成，其中一个面是平面，另一个面是。

2．正方体的棱长是2a厘米，它的表面积是平方厘米，体积是立方厘米。

3．小明家挖了一个长为6m、宽为5m、深为2m的长方体地窖，这个地窖占地m2。

4．一个圆锥的体积是4.2dm3，底面积是0.9 dm2，高是。

5．一个正方体木块的棱长是6cm，把它削成一个最大的圆柱体，圆柱体的体积是cm3，再把这个圆柱体削成一个最大的圆锥体，圆锥体的体积约是cm3．6．圆柱的侧面沿高展开后是形或形。

一个圆柱的侧面沿高展开是正方形，正方形的边长是12.56cm，圆柱的底面积是cm2。

7．圆柱有个面是大小相同的圆，有一个面是面，圆柱的两个底面是半径相等的两个圆，两个底面间的距离叫做，圆柱周围的曲面叫做面。

8．把一个底面半径6厘米、高8厘米的圆柱体，切拼成一个近似的长方体，表面积比原来增加了平方厘米。

9．如图，在直角三角形MON中，MO=2cm，NO=5cm，如果分别以MO、NO边为轴旋转一周形M成圆锥，那么以MO为轴和以NO为轴的圆锥体积之比是。

二、单选题10．下面的图形中，()是正方体的展开图。

A．B．C．D．11．把一个圆柱的侧面展开，不可能得到（）。

A．长方形B．正方形C．平行四边形D．梯形12．下列图形由（）组成。

A．圆锥和圆柱B．圆柱和球体C．圆锥和球体D．圆锥和圆台13．小强测量一个土豆的体积，在一个棱长1分米的正方体容器中装了一些水，水面距离杯口2厘米（如图）。

他把土豆浸没在水中，有部分水溢出，接着他又把土豆取出来，水面下降了3厘米，土豆的体积是（）立方厘米。

A．200B．500C．100D．30014．如图（单位：厘米），酒瓶中装有一些酒，倒进一只酒杯中，酒杯的直径是酒瓶内直径的一半，共能倒满（）杯。

A．10B．15C．20D．3015．将一个棱长是6分米的正方体木块削成一个最大的圆锥，圆锥的体积是（）立方分米。

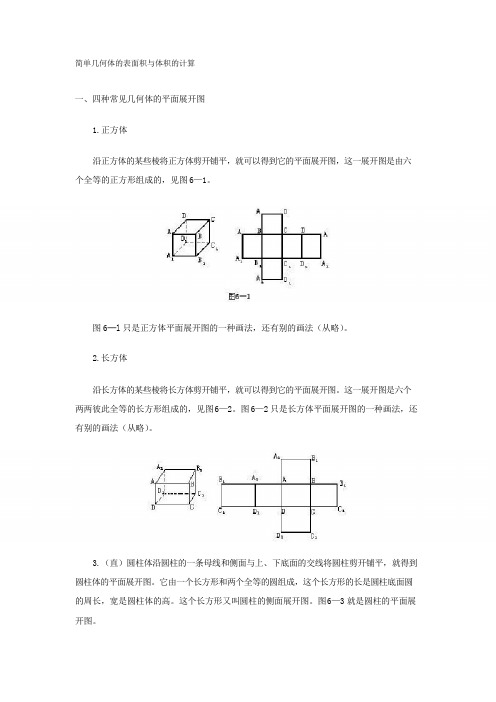
简单几何体的表面积与体积的计算一、四种常见几何体的平面展开图1.正方体沿正方体的某些棱将正方体剪开铺平，就可以得到它的平面展开图，这一展开图是由六个全等的正方形组成的，见图6—1。

图6─l只是正方体平面展开图的一种画法，还有别的画法（从略）。

2.长方体沿长方体的某些棱将长方体剪开铺平，就可以得到它的平面展开图。

这一展开图是六个两两彼此全等的长方形组成的，见图6—2。

图6—2只是长方体平面展开图的一种画法，还有别的画法（从略）。

3.（直）圆柱体沿圆柱的一条母线和侧面与上、下底面的交线将圆柱剪开铺平，就得到圆柱体的平面展开图。

它由一个长方形和两个全等的圆组成，这个长方形的长是圆柱底面圆的周长，宽是圆柱体的高。

这个长方形又叫圆柱的侧面展开图。

图6—3就是圆柱的平面展开图。

4.（直）圆锥体沿圆锥体的一条母线和侧面与下底面圆的交线将圆锥体剪开铺平，就得到圆锥的平面展开图。

它是由一个半径为圆锥体的母线长，弧长等于圆锥体底面圆的周长的扇形和一个圆组成的，这个扇形又叫圆锥的侧面展开图。

具体图形见图6—4。

二、四种常见几何体表面积与体积公式1.长方体长方体的表面积=2×（a×b+b×c+c×a）长方体的体积=a×b×c（这里a、b、c分别表示长方体的长、宽、高）。

2.正方体正方体的表面积=6×a2正方体的体积=a3（这里a为正方体的棱长）。

3.圆柱体圆柱体的侧面积=2πRh圆柱体的全面积=2πRh+2πR2=2πR（h+R）圆柱体的体积=πR2h（这里R表示圆柱体底面圆的半径，h表示圆柱的高）。

4.圆锥体圆锥体的侧面积=πRl圆锥体的全面积=πRl+πR2母线长与高）。

三、例题选讲例1图6—5中的几何体是一个正方体，图6—6是这个正方体的一个平面展开图，图6—7（a）、（b）、（c）也是这个正方体的平面展开图，但每一展开图上都有四个面上的图案没画出来，请你给补上。

通用版小升初专项复习：立体图形一、填空题1．下面图形以红色线为轴旋转后会得到圆锥吗，如果是说出圆锥的高和底面半径。

2．至少用个棱长1cm的小正方体可以拼成一个较大的正方体。

拼成这个大正方体的体积是，表面积是。

3．把一块长8dm、宽6dm、高5dm的长方体分割成两个完全相同的小长方体，则它的表面积最多增加dm2，最少增加dm2。

4．绕着一个圆锥形状的碎石堆的外边缘走一圈，要走18.84米．如果这堆碎石的高是2.4米，它的体积是立方米？5．一个底面半径是20cm、高是15cm的圆柱形铁块，可以熔铸成个底面直径是20cm、高是15cm的圆锥形铁块。

（损耗不计）6．一个圆柱的底面周长是6.28厘米，高5厘米，它的侧面积是，表面积是，体积是。

7．把一个底面直径为3厘米、高是5厘米的圆柱体沿直径切割成两个半圆柱，表面积增加了。

8．把一个棱长是3dm的正方体，切削成最大的圆柱，这个圆柱的侧面积是dm2。

9．5x＝4y，那么x∶y＝∶．二、单选题10．下面图形中，折叠后能围成正方体的是（）。

A．B．C．D．11．一个圆锥的体积是141.3cm3，与它等底等高的圆柱的体积是（）cm3。

A．47.1B．141.3C．282.6D．423.912．有一堆小麦如下图，从上面及侧面看，形状大致会是（）A．三角形，圆形B．梯形，圆形C．圆形，长方形D．圆形，三角形13．如下图，这块石头的体积约是（）cm3。

A．500B．1000C．5000D．6000 14．一个圆锥的体积是100立方厘米，底面积是50平方厘米，它的高是（）厘米。

A．2B．23C．6D．1015．奇奇将圆柱内的水倒入（）圆锥内，正好倒满。

A．B．C．D．16．学校买来420本课外书，按照人数的比分配给六年级3个班。

六（1）班42人，六（2）班50人，六（3）班48人。

六（3）班可分得（）本。

A．126B．140C．144D．15017．如图所示的展开图中是左边的正方体的展开图的是（）A．B．C．D．18．用一块长56.52cm、宽31.4cm的长方形铁皮，配上一块直径（）cm的圆形铁皮可以做成一个容积最大的水桶。

巧求周长面积几个重要的解题思想（1）平移在平面图形的计算中，常常要将一个平面图形移动到平面上的另一个位置进行计算．其中，将图形沿一个固定方向的移动叫做平移，一个图形经过平行移动不改变其形状与大小，所以图形面积是保持不变的．（2）割补这个原理的内容是几何图形经过分、合、移、补所拼凑成的新图形，它的面积不变．（3）旋转在平面图形的割补中，有时要将一个图形绕定点旋转到一个新的位置，产生一种新的图形结构，图形在转动过程中形状大小不发生改变．利用这种新的图形结构可以帮我们解决面积的计算问题．（4）对称平面图形中有许多简单漂亮的图形都是轴对称图形．轴对称图形沿对称轴折叠，轴两侧可以完全重合．也就是说，如果一个图形是轴对称图形，那么对称轴平分这个图形的面积．熟悉轴对称图形这个性质，对面积计算会有很大帮助．（5）代换在几何计算中，对有关数量进行适当的等量代换也是解决问题的已知技巧．1、如图，一个正方形被分割成24个互不重叠的小长方形，这24个小长方形的周长总和为24，原正方形的面积是。

2、如图，每个小格的边长都是1个单位长度，一只甲虫在水平方向上每爬行1个单位长度需要5秒，在竖直方向上每爬行1个单位长度需要6秒，每拐弯一次需要1秒。

它从A点爬到B点，最少需要秒。

3、 下图(单位：厘米)是两个相同的直角梯形重叠在一起，求阴影部分的面积.4、如图，一个正方形被分成4个小长方形，它们的面积分别是110平方米、15平方米、310平方米和25平方米．已知图中的阴影部分是正方形，那么它的面积是多少平方米？三角形的比例关系我们在解决直线型问题时经常会使用到三角形的比例关系．例如等积变形，一半模型等． 三角形的比例关系可以概括为以下三点： ① 等底等高的两个三角形面积相等；BA② 两个三角形高相等，面积比等于它们的底之比； ③ 两个三角形底相等，面积比等于它们的高之比．夹在一组平行线之间的等积变形，如右图ACD BCD S S ∆∆=； 反之，如果ACD BCD S S ∆∆=，则可知直线AB 平行于CD ．5、图中ABCD 是个直角梯形(∠DAB =∠ABC =90°)，以AD 为一边向外作长方形ADEF ，其面积为6.36平方厘米。

一.立体图形的表面积知识要点梳理一、立体图形的切割1 •立体图形每切割一次，增加两个面的面积。

2•立体图形每拼一次，减少两个面的面积。

二、表面积表面积：物体表面面积的总和叫做物体的表面积。

表面积通常用S表示，常用面积单位有平方千米、公顷、平方米、平方分米、平方厘米。

1 •长方体、正方体的表面积为6个面的面积和。

2. 圆柱的表面积=侧面积+ 2个底面面积。

3. 圆锥的表面积=侧面积+底面积三、立体图形的表面积计算公式考点精讲分析典例精讲考点 1 长方体与正方体的表面积【例1】一个长40 厘米，截面是正方形的长方体，如果长增加5 厘米，表面积就增加80 平方厘米，原来长方体的表面积是多少？【精析】根据题意可知，一个长方体如果长增加 5 厘米，增加的80 平方厘米是 4 个同样的长方形的面积和。

【答案】80 - 4- 5=4 （厘米）O X 4X 4 + 4X 4X 2 = 672 （平方厘米）答：原来长方体的表面积是672 平方厘米。

【归纳总结】根据长方体增加的面积，计算出长方体的宽和高，然后根据长方体的表面积计算公式解答即可。

【例2】学校新建一个游泳池，长50 米，宽20 米，深 2 米。

这个游泳池占地面积有多大？如果游泳池的四壁和底面都要贴上瓷砖，一共需要贴多少平方米的瓷砖？【精析】此题主要考查长方体底面积及表面积的计算方法在实际生活中的应用。

解答时要清楚长方体游泳池的占地面积是指长方体的底面积。

贴瓷砖的面积，就等于游泳池的表面积减去上面的面积。

【答案】占地面积：50X 20= 1000 （平方米）贴瓷砖的面积：（50 X 2+ 20 X 2）X 2+ 50 X 20= 1280 （平方米）答：这个游泳池占地面积有1000 平方米，共需要贴1280 平方米的瓷砖。

【归纳总结】这类题目解答时一般遵循下列步骤：①识别形体；②搞清问题（求表面积还是求体积、容积、求表面积涉及几个面）；③回忆公式；④正确列式；⑤计算解答。

小升初数学平面图形与立体图形综合练习1、时针和分针一昼夜的路程分别为360°和720°，因为圆的周长为2πr，所以时针和分针一昼夜的路程分别为2π×0.3×360/360°=1.884π厘米和2π×0.4×720/360°=3.768π厘米。

2、根据半圆周长公式C=πr，可得半圆的半径为2.46米，面积为πr²/2=3.783平方米。

3、根据半圆弧长公式L=πr，可得这个半圆的半径为15.7厘米，与之半径相等的圆的面积为πr²=776.7平方厘米。

4、根据半圆周长公式C=πr，可得这个半圆的半径为8.2厘米，与之半径相等的圆的面积为πr²=211.1平方厘米。

5、正方形的面积为31.4²=985.96平方厘米，每个圆的面积为π×5²=78.54平方厘米，所以可以容纳985.96/78.54=12个圆。

6、正方形的面积为12²=144平方厘米，4个圆的总面积为4×π×(12/4)²=36π平方厘米，每个圆的面积为9π平方厘米。

7、前轮每分钟滚动的路程为2×π×7.5×5=235.62厘米，每分钟前进的距离为235.62×2=471.24厘米，每分钟压路面积为2×1×471.24=942.48平方厘米。

8、养鱼池的周长为100.48米，减去圆形小岛的周长2πr=12π米，得到养鱼池的周长为88.48米，根据周长公式C=2πr，可得养鱼池的半径为14.06米，面积为πr²=623.16平方米。

9、大圆的周长是小圆周长的2倍，面积比是4:1.10、围成正方形的绳长为31.4米，所以每条边长为7.85米，正方形的面积为7.85²=61.5225平方米，围成圆形的周长为31.4米，所以半径为5厘米，圆形的面积为π×5²=78.54平方厘米，两者面积相差17.0175平方米。