高二下学期选修三第一次月考

2023-2024学年山西省高二下册第一次月考数学试题一、单选题1．已知1()2P BA =∣，3()8P AB =，则()P A 等于（）A ．316B ．1316C ．34D ．14【正确答案】C根据条件概率公式计算．【详解】由()()()P AB P BA P A =∣，可得()3()()4P AB P A P B A ==∣.故选：C.2．已知012233C 2C 2C 2C 2C 81n n n n n n n ++++⋅⋅⋅+=，则123C C C C nn n n n +++⋅⋅⋅+等于（）A ．15B ．16C ．7D ．8【正确答案】A【分析】根据二项式定理展开式的逆运算即可求得n 的值，再由由二项式系数和即得.【详解】逆用二项式定理得()01223322221281nn n nn n n n C C C C C ++++⋅⋅⋅+=+=，即433n =，所以n =4，所以12342115n n n n n C C C C +++⋅⋅⋅+=-=．故选：A.3．(x +y )(2x -y )5的展开式中x 3y 3的系数为A ．-80B ．-40C ．40D ．80【正确答案】C【详解】()()()()555222x y x y x x y y x y +-=-+-，由()52x y -展开式的通项公式()()515C 2rrrr T x y -+=-可得：当3r =时，()52x x y -展开式中33x y 的系数为()3325C 2140⨯⨯-=-；当2r =时，()52y x y -展开式中33x y 的系数为()2235C 2180⨯⨯-=，则33x y 的系数为804040-=.故选C.【名师点睛】（1）二项式定理的核心是通项公式，求解此类问题可以分两步完成：第一步根据所给出的条件(特定项)和通项公式，建立方程来确定指数(求解时要注意二项式系数中n 和r 的隐含条件，即n ，r 均为非负整数，且n ≥r ，如常数项指数为零、有理项指数为整数等)；第二步是根据所求的指数，再求所求解的项.（2）求两个多项式的积的特定项，可先化简或利用分类加法计数原理讨论求解.4．若22nx ⎫⎪⎭展开式中只有第六项的二项式系数最大，则展开式中常数项是（）A ．180B ．120C ．90D ．45【正确答案】A【分析】已知条件中只有第六项的二项式系数最大，n 应为偶数，可确定n 值，进而利用展开式即可求得常数项.【详解】如果n 为奇数，那么是中间两项的二项式系数最大；如果n 为偶数，那么是中间一项的二项式系数最大；只有第六项的二项式系数最大10n ∴=，1022x ⎫∴⎪⎭展开式的通项为：10521102r r r r T C x -+=⨯⨯令10502r-=，解得：2r =∴展开式中常数项是.22102180C ⨯=故选：A.5．有8位学生春游，其中小学生2名､初中生3名､高中生3名.现将他们排成一列，要求2名小学生相邻､3名初中生相邻，3名高中生中任意两名都不相邻，则不同的排法种数有（）A ．288种B ．144种C ．72种D ．36种【正确答案】B【分析】利用捆绑法和插空法可求得结果.【详解】第一步，先将2名小学生看成一个人，3名初中生看成一个人，然后排成一排有22A 种不同排法；第二步，将3名高中生插在这两个整体形成的3个空档中，有33A 种不同排法；第三步，排2名小学生有22A 种不同排法，排3名初中生有33A 种不同排法.根据分步计数原理，共有23232323144A A A A =种不同排法.故选：B方法点睛：本题主要考查排列的应用，属于中档题.常见排列数的求法为：（1）相邻问题采取“捆绑法”；（2）不相邻问题采取“插空法”；（3）有限制元素采取“优先法”；（4）特殊元素顺序确定问题，先让所有元素全排列，然后除以有限制元素的全排列数.6．已知(1)n x +的展开式中第4项与第8项的二项式系数相等，则奇数项的二项式系数和为（）．A ．122B ．112C ．102D ．92【正确答案】D【详解】因为(1)n x +的展开式中第4项与第8项的二项式系数相等，所以，解得，所以二项式10(1)x +中奇数项的二项式系数和为．二项式系数，二项式系数和．7．现有甲､乙､丙､丁､戊五位同学，分别带着A ､B ､C ､D ､E 五个不同的礼物参加“抽盲盒”学游戏，先将五个礼物分别放入五个相同的盒子里，每位同学再分别随机抽取一个盒子，恰有一位同学拿到自己礼物的概率为（）A ．45B ．12C ．47D ．38【正确答案】D【分析】利用排列组合知识求出每位同学再分别随机抽取一个盒子，恰有一位同学拿到自己礼物的情况个数，以及五人抽取五个礼物的总情况，两者相除即可.【详解】先从五人中抽取一人，恰好拿到自己的礼物，有15C 种情况，接下来的四人分为两种情况，一种是两两一对，两个人都拿到对方的礼物，有224222C C A 种情况，另一种是四个人都拿到另外一个人的礼物，不是两两一对，都拿到对方的情况，由3211C C 种情况，综上：共有22111425322245C C C C C A ⎛⎫⋅+= ⎪⎝⎭种情况，而五人抽五个礼物总数为55120A =种情况，故恰有一位同学拿到自己礼物的概率为4531208=.故选：D8．设5nx⎛⎝的展开式的各项系数和为M ，二项式系数和为N ，若240M N -=，则展开式中有理项共有（）A ． 1项B ．2项C ．3项D ． 4项【正确答案】C【分析】根据二项式系数和公式，结合赋值法、二项式的通项公式进行求解即可.【详解】二项式系数和为2n N =，在5nx⎛ ⎝中，令1x =，得4nM =，由()()24042240021521602164n n n n nM N n -=⇒--=⇒+-=⇒=⇒=，二项式45x⎛ ⎝的通项公式为()()34442144C 5C 51rr r r r r r r T x x ---+⎛=⋅⋅=⋅⋅-⋅ ⎝，令0,2,4r =，则344,1,22r-=-，所以展开式中有理项共有3项，故选：C9．设双曲线C ：()222210,0x y a b a b-=>>的左､右焦点分别为1F ，2F ，以2F 为圆心的圆恰好与双曲线C 的两渐近线相切，且该圆恰好经过线段2OF 的中点，则双曲线C 的离心率是（）AB C ．3D 【正确答案】A【分析】先由焦点到渐近线的距离求出半径，再利用该圆过线段2OF 的中点得到2c b =，即可求出离心率,【详解】由题意知：渐近线方程为by x a=±，由焦点2(,0)F c ，222c a b =+，以2F 为圆心的圆恰好与双曲线C 的两渐近线相切，则圆的半径r等于圆心到切线的距离，即r b ==，又该圆过线段2OF 的中点，故2cr b ==，所以离心率为ca=故答案为.310．数学对于一个国家的发展至关重要，发达国家常常把保持数学领先地位作为他们的战略需求.现某大学为提高数学系学生的数学素养，特开设了“古今数学思想”，“世界数学通史”，“几何原本”，“什么是数学”四门选修课程，要求数学系每位同学每学年至多选3门，大一到大三三学年必须将四门选修课程选完，则每位同学的不同选修方式有（）A ．60种B ．78种C ．84种D ．144种【正确答案】B【分析】先分类，再每一类中用分步乘法原理即可.【详解】由题意可知三年修完四门课程，则每位同学每年所修课程数为1,1,2或0,1,3或0,2,2若是1,1,2，则先将4门学科分成三组共11243222C C C A 种不同方式.再分配到三个学年共有33A 种不同分配方式，由乘法原理可得共有112343232236C C C A A ⋅=种，若是0,1,3，则先将4门学科分成三组共1343C C 种不同方式，再分配到三个学年共有33A 种不同分配方式，由乘法原理可得共有13343324C C A ⋅=种，若是0,2,2，则先将门学科分成三组共224222C CA 种不同方式，再分配到三个学年共有33A 种不同分配方式，由乘法原理可得共有2234232218C C A A ⋅=种所以每位同学的不同选修方式有36241878++=种，故选：B.二、多选题11．若()102100121021,R x a a x a x a x x -=++++∈ ，则（）A ．2180a =B ．10012103a a a a +++= C ．100210132a a a -+++=D ．31012231012222a a a a ++++=- 【正确答案】ABD【分析】根据二项式展开式的系数特点，结合通项公式，采用赋值法，一一求解各个选项，即得答案.【详解】由题意1021001210(21)x a a x a x a x -=++++ ，所以8282310C (2)(1)180T x x =-=，所以2180a =，故A 正确．令=1x -，则1021001210(21)x a a x a x a x -=++++ ，即为1021001210(21)||||||||x a a x a x a x +=++++ ，令1x =，得1001210||||||||3a a a a ++++= ，故B 正确；对于1021001210(21)x a a x a x a x -=++++ ，令1x =，得012101a a a a ++++= ，令=1x -，得：10012103a a a a -+-+= ，两式相加再除以2可得100210132a a a ++++= ，故C 错误.对于1021001210(21)x a a x a x a x -=++++ ，令0x =，得01a =，令12x =，得310120231002222a a a aa +++++= ，故31012231012222a a a a ++++=- ，故D 正确，故选：ABD12．为庆祝建党100周年，讴歌中华民族实现伟大复兴的奋斗历程，增进全体党员干部职工对党史知识的了解，某单位组织开展党史知识竞赛活动，以支部为单位参加比赛，某支部在5道党史题中(有3道选择题和2道填空题)，不放回地依次随机抽取2道题作答，设事件A为“第1次抽到选择题”，事件B 为“第2次抽到选择题”，则下列结论中正确的是（）A ．()35P A =B ．()310P AB =C ．()12P B A =D ．()12P B A =【正确答案】ABC【分析】根据古典概型概率的求法及条件概率，互斥事件概率求法，可以分别求得各选项.【详解】()131535C C P A ==,故A 正确；()11321154310C C P AB C C ==，故B 正确；()()()0351231P AB P P A B A ===，故C 正确；()121525C C P A ==，()11231154103C C C C P AB ==，()()()3310245P AB P B A P A ===，故D 错误.故选:ABC三、填空题13．已知事件A 和B 是互斥事件，()16P C =，()118P B C ⋂=，()()89P A B C ⋃=，则()P A C =______．【正确答案】59【分析】根据条件概率的定义以及运算性质，可得答案.【详解】解：由题意知，()()()()89P A B C P A C P B C ⋃=+=，()()()1118136P B C P B C P C ⋂===，则()()()()815939P A C P A B C P B C =⋃-=-=．故59．14．5555除以8，所得余数为_______.【正确答案】7【分析】由55561=-，运用二项式定理，结合整除的性质，即可求解.【详解】依题意，()()()()()()5512545555055154253541550555555555555561C 561C 561C 561C 561C 561=-=-+-+-++-+- 因为56能被8整除，所以5555除以8，所得的余数为.187-+=故7.15．已知()()()420122111x a a x a x -=+-+-()()343411a x a x +-+-，则3a =____.【正确答案】32对多项式进行变形得()44444112122122x x x ⎛⎫⎛⎫-=-=+- ⎪ ⎪⎝⎭⎝⎭，再研究441212x ⎛⎫+- ⎪⎝⎭展开式中的()31x -项，即可得答案.【详解】对多项式进行变形得()44444112122122x x x ⎛⎫⎛⎫-=-=+- ⎪ ⎪⎝⎭⎝⎭，∴44142((,0,1,,411)2r r rr T C r x -+-=⋅= ，当3r =时，4343342(3212a C -=⋅=.故答案为.32本题考查二项式定理求展开式指定项的系数，考查函数与方程思想、转化与化归思想，考查逻辑推理能力、运算求解能力.16．有10个相同的小球，现全部分给甲、乙、丙3人，若甲至少得1球，乙至少得2球，丙至少得3球，则他们所得的球数的不同情况有__________种．【正确答案】15【分析】依题意，首先分给甲1个球，乙2个球，丙3个球，还剩下4个球，再来分配这4个球，按照分类加法计数原理计算可得；【详解】解：有10个相同的小球，现全部分给甲、乙、丙3人，若甲至少得1球，乙至少得2球，丙至少得3球，故首先分给甲1个球，乙2个球，丙3个球，还剩下4个球，①4个球分给一人，有3种分法；②4个球分给两个人，又有两种情况，一人3个一人1个有236A =种分法；两人都是2个有3种分法；③4个球分给3个人，只有1、1、2这种情况，有3种分法，按照分类加法计数原理可得一共有363315+++=种；故15本题考查分类加法计数原理的应用，属于基础题.四、解答题17．已知{}n a 为等差数列，前n 项和为()*N n S n ∈，{}n b 是首项为2的等比数列，公比大于0，且2312b b +=，3412b a a =-，11411S b =.(1)求{}n a 和{}n b 的通项公式；(2)求数列{}n n a b 的前n 项和()*N n ∈.【正确答案】(1)32n a n =-，2nn b =(2)前n 项和110(35)2n n T n +=+-⋅【分析】（1）根据等比数列的通项公式可计算得到公比q 的值，再根据等差数列的通项公式和求和公式可列出方程组，解出首项1a 和公差d 的值，即可求得{}n a 和{}n b 的通项公式；（2）先根据第（1）题的结论得到数列{}n n a b ×的通项公式，然后运用错位相减法求出前n 项和n T ．【详解】（1）由题意，设等差数列{}n a 的公差为d ，等比数列{}n b 的公比为q ，则0q >．故22212q q +=，解得2q =，12b = ，则2231228b b q ==⨯=，33412216b b q ==⨯=，由题意，得11132811101111162a d a a d +-=⎧⎪⎨⨯+=⨯⎪⎩，解得113a d =⎧⎨=⎩．13(1)32n a n n ∴=+-=-；1222n n n b -=⨯=．（2）由（1）知，(32)2n n n a b n ⋅=-⋅．设其前n 项和为n T ，211221242(32)2n n n n T a b a b a b n ∴=++⋯+=⨯+⨯+⋯+-⋅，①23121242(35)2(32)2n n n T n n +=⨯+⨯+⋯+-⋅+-⋅，②①-②，得23112323232(32)2n n n T n +-=⨯+⨯+⨯+⋯+⋅--⋅21212(122)(32)2n n n -+=+⨯++⋯+--⋅1112212(32)212n n n -+-=+⨯--⋅-()153210n n +=-⋅-．()110352n n T n +∴=+-⋅．18．在平面直角坐标系xOy 中，抛物线方程为()220x py p =>，其顶点到焦点的距离为2.(1)求抛物线的方程；(2)若点()0,4P -，设直线():0l y kx t t =+≠与抛物线交于A 、B 两点，且直线PA 、PB 的斜率之和为0，证明：直线l 必过定点，并求出该定点．【正确答案】(1)28x y =；(2)详见解析；【分析】（1）根据题意求出抛物线的焦点坐标，可求得p 的值，进而可求得抛物线的方程；（2）设点()11,A x y 、()22,B x y ，将直线l 的方程与抛物线的方程联立，列出韦达定理，根据直线PA 、PB 的斜率之和为0求得实数t 的值，即可求得直线l 所过定点的坐标.【详解】（1）0p > ，且抛物线22x py =的顶点到焦点的距离为2，则该抛物线的焦点坐标为()0,2，22p∴=，解得4p =，因此，该抛物线的方程为28x y =；（2）设点()11,A x y 、()22,B x y ，将直线l 的方程与抛物线的方程联立28y kx tx y=+⎧⎨=⎩，消去y 并整理得2880x kx t --=，由韦达定理得128x x k +=，128x x t =-.直线PA 的斜率为2111111144488x y x k x x x ++===，同理直线PB 的斜率为22248x k x =+，由题意得()1212121212124448324108888x x x x x x k k k k k x x x x t t +++⎛⎫+=++=+=+=-= ⎪-⎝⎭，上式对任意的非零实数k 都成立，则410t -=，解得4t =，所以，直线l 的方程为4y kx =+，该直线过定点()0,4.设而不求，联立方程，利用韦达定理解题是本类题目常用思路.本题中表示出()12121212121244441088x x x x x x k k k x x x x t +++⎛⎫+=++=+=-= ⎪⎝⎭是解题关键，也是计算难点.19．已知函数()2()24ln f x x ax x =-，a R ∈.（1）当0a =时，求函数()f x 的单调区间；（2）令2()()g x f x x =+，若[1,)x ∀∈+∞，函数()g x 有两个零点，求实数a 的取值范围.【正确答案】(1)函数()f x 的单调递减区间为120,e -⎛⎫ ⎪⎝⎭，单调递增区间为12e ,-⎛⎫+∞ ⎪⎝⎭(2))+∞【分析】（1）当0a =时，()22ln f x x x =，求出()f x ¢，可得函数()f x 的单调区间；（2）依题意得，()()2224ln g x x ax x x =-+，然后求导，得()()()()44ln 2424ln 1g x x a x x a x x a x =-+-+=-+'，然后，分情况讨论即可求出实数a 的取值范围【详解】（1）函数()f x 的定义域为()0,+¥当0a =时，()22ln f x x x =()()4ln 222ln 1f x x x x x x =+=+'令()'0f x >得2ln 10x +>，解得12x e ->，令()'0f x <得2ln 10x +<，解得120x e -<<，所以函数()f x 的单调递减区间为120,e -⎛⎫ ⎪⎝⎭，单调递增区间为12e ,-⎛⎫+∞ ⎪⎝⎭（2）()()2224ln g x x ax x x =-+，()()()()44ln 2424ln 1g x x a x x a x x a x =-+-+=-+'由[)1,x ∈+∞得ln 10x +>①当1a ≤时，()'0g x ≥，函数()g x 在[)1,+∞上单调递增，所以()()1g x g ≥，即()1g x ≥，函数()g x 在[)1,+∞上没有零点.②当1a >时，()1,x a ∈时，()'0g x <，(),∈+∞x a 时，()'0g x >所以函数()g x 在()1,a 上单调递减，在(),+∞a 上单调递增因为()110g =>，()2240g a a =>所以函数()g x 在[)1,+∞有两个零点只需()()()2min 12ln 0g x g a a a ==-<解得a >综上所述，实数a 的取值范围为)+∞本题考查利用导数求单调性和单调区间的问题，解题的关键在于分情况讨论时注意数形结合，属于难题。

2022-2023学年广东省深圳技术大学附属中学高二下学期第一次月考数学试题一、单选题1．设函数在处的导数为2，则（ ）()f x 1x =0(1)(1)limx f x f x ∆→+∆-=∆A ．B ．2C ．D ．62-23【答案】B【分析】根据导数的定义即可.【详解】;()0(1)(1)lim21x f x f f x ∆→'+∆-==∆故选：B.2．某校开设A 类选修课4门,B 类选修课3门,一同学从中选1门,则该同学的不同选法共有（ ）A ．7种B ．12种C ．4种D ．3种【答案】A【分析】根据题意求出所有的可能性即可选出结果.【详解】解:由题知某校开设A 类选修课4门,B 类选修课3门,共7门,故该同学的不同选法共有7种.故选:A3．抛物线的准线方程为24y x =A ．B ．C ．D ．1x =2x ==1x -2x =-【答案】C【分析】由抛物线标准方程知p ＝2，可得抛物线准线方程．【详解】抛物线y 2＝4x 的焦点在x 轴上，且2p=4,=1，2p∴抛物线的准线方程是x ＝﹣1．故选C ．【点睛】本题考查抛物线的标准方程、抛物线的简单性质等基础知识，属于基础题．4．函数的单调递增区间是（ ）()25ln 4f x x x =--A ．B ．和5,2⎛⎫+∞ ⎪⎝⎭(),0∞-5,2⎛⎫+∞ ⎪⎝⎭C ．D ．50,2⎛⎫ ⎪⎝⎭()0,3【答案】A【分析】确定函数定义域，求出函数的导数，根据导数大于0，即可求得答案.【详解】函数的定义域为 ，()25ln 4f x x x =--(0,)+∞，当时，解得，()5252,0x f x x x x -'=-=>()250x f x x -'=>52x >故函数的单调递增区间是，()25ln 4f x x x =--5,2⎛⎫+∞ ⎪⎝⎭故选：A5．函数的零点个数为（ ）3()1216f x x x =--A ．B ．C ．D ．0123【答案】C【解析】求出函数的单调区间得到函数的极值，即得解.【详解】由题得，2()3123(2)(2)f x x x x '=-=+-令得或，令得，()0f x '>2x ><2x -()0f x '<22x -<<所以函数的单调递增区间为，减区间为.(,2),(2,)-∞-+∞(2,2)-所以函数的极大值为，极小值为，(2)0f -=(2)32f =-当时，当时，x →-∞0,y <x →+∞0,y >所以函数的零点个数为2.故选：C【点睛】方法点睛：研究函数的零点问题常用的方法有：（1）方程法（直接解方程得解）；（2）图象法（直接研究函数的性质画出函数的图象得解）；（3）方程+图象法“（令重新构造函()=0f x 数，画出两个函数的图象得解）”()()g x h x =6．已知正项数列满足，若，则数列的前项的和为（ ）{}n a 22nSn n =+11n n n b a a +={}n b n A ．B ．C ．D ．163n n -+2263n n -+69n n +263n n +【答案】C【分析】由和的关系，利用公式求出数列的通项公式，可得到数列n a n S ()()1112n n n S n a S S n -⎧=⎪=⎨-≥⎪⎩{}n a 的通项公式，利用裂项相消法求前项的和.{}n b n 【详解】，当时，，22n S n n =+1n =113a S ==当时，，当时，也满足，2n ≥221(2)(1)2(1)21n n n a S S n n n n n -⎡⎤=-=+--+-=+⎣⎦1n =∴ 数列的通项公式为，{}n a 21n a n =+，111111(21)(23)22123n n n b a a n n n n +⎛⎫===- ⎪++++⎝⎭12311111111123557792123n b b b b n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫++++=-+-+-++- ⎪ ⎪ ⎪ ⎪⎢⎥++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦111.232369nn n ⎛⎫=-= ⎪++⎝⎭故选：C7．已知上的函数满足，且，则不等式的解集为（ ）R ()f x ()13f =()2f x '<()21f x x <+A ．B ．C ．D ．(,1)-∞()3,+∞()1,+∞(2,)+∞【答案】C【分析】令，从而求导可判断导数恒成立，从而可判断函数的单调性，()()21F x f x x =--()0F x '<从而可得当时，，从而得到不等式的解集．1x >()()10F x F <=()21f x x <+【详解】解：令，()()21F x f x x =--则，()()2F x f x ''=-又的导数在上恒有，()f x ()f x 'R ()2f x '<恒成立，()()20F x f x ''∴=-<是上的减函数，()()21F x f x x ∴=--R 又，()()11210F f =--= 当时，，即，∴1x >()()10F x F <=()210f x x --<即不等式的解集为；()21f x x <+(1,)+∞故选：C ．8．若是的切线，则的取值范围为（ ）y ax b =+()ln f x x x=ab A ．B ．C ．D ．[)1,-+∞[)1,+∞(],1-∞[]1,0-【答案】A【分析】利用导数的几何意义可求得在处的切线方程，由此可用表示，得到(),ln t t t t ,a b ，设，利用导数可求得的值域，由此可得所求范围.ln 1a t b t +=-()()ln 10t g t t t +=->()g t 【详解】设切点坐标为，()(),ln 0t t t t >，，又，，()ln 1f x x '=+ ()ln 1a f t t '∴==+()ln f t t t =ln b t t at t∴=-=-，ln 1ln 1a t tb t t ++∴==--令，则，()()ln 10t g t t t +=->()2ln tg t t '=则当时，；当时，；()0,1t ∈()0g t '<()1,t ∈+∞()0g t '>在上单调递减，在上单调递增，()g t ∴()0,1()1,+∞，又当时，，，()()11g t g ∴≥=-0t →()g t ∞→+()[)1,g t ∴∈-+∞即的取值范围为.ab [)1,-+∞故选：A.二、多选题9．函数的导函数的图象如图所示，则下列说法正确的有（ ）()f x ()f x 'A ．为函数的一个零点2x =-()f x B ．为函数的一个极大值点12x =()f x C ．函数在区间上单调递增()f x 12,2⎛⎫- ⎪⎝⎭D ．是函数的最大值()1f -()f x 【答案】BC【分析】利用导函数的图象分析函数的单调性，由此可判断各选项的正误.()f x 【详解】由的导函数的图象可知，函数在、上单调递减，在、()f x ()f x '(),2-∞-1,22⎛⎫ ⎪⎝⎭12,2⎛⎫- ⎪⎝⎭上单调递增，()2,+∞故当或时，取得极小值；当时，取得极大值，故BC 正确，AD 错误.2x =-2x =()f x 12x =()f x 故选：BC.10．如图是正方体的平面展开图，则在这个正方体中（ ）A ．AB 与CD 平行B ．CD 与GH 是异面直线C ．EF 与GH 成角D ．CD 与EF 平行60︒【答案】CD【分析】根据正方体的平面展开图得到直观图，然后判断即可.【详解】该正方体的直观图如下：与是异面直线，故A 错；与相交，故B 错；因为该几何体为正方体，所以，AB CD CD GH EF CD 三角形为正三角形，直线与直线所成角为，则与所成角为，故CD 正GHD GH GD 60︒EF GH 60︒确.故选：CD.11．在流行病学中，基本传染数是指在没有外力介入，同时所有人都没有免疫力的情况下，一0R 个感染者平均传染的人数．初始感染者传染个人为第一轮传染，第一轮被传染的个人每人再0R 0R 传染个人为第二轮传染，…．假设某种传染病的基本传染数，平均感染周期为7天，初始R 04R =感染者为1人，则（ ）A ．第三轮被传染人数为16人B ．前三轮被传染人数累计为80人C ．每一轮被传染的人数组成一个等比数列D ．被传染人数累计达到1000人大约需要35天【答案】CD【分析】根据已知条件，可转化为等比数列问题，结合等比数列前项和公式，即可求解．n 【详解】由题意，设第轮感染的人数为，则数列是首项，公比的等比数列，故n n a {}n a 14a =4q =C 正确；所以，当时，，故A 错误；4nn a =3n =33464a ==前三轮被传染人数累计为，故B 错误；334(14)118514S ⨯-+=+=-当时，，当时，由，故D 正4n =444(14)1134114S ⨯-+=+=-3557n ==554(14)111365100014S ⨯-+=+=>-确.故选：CD 12．对于函数，下列说法正确的是（ ）()2ln xf x x =A ．在()f x x =12eB ．有两个不同的零点()f xC ．ff f <<D ．若在上恒成立，则()21f x k x <-()0,∞+2ek >【答案】ACD【分析】根据导函数确定的单调性极值及最值情况，就能确定ABC 的正误，对于D ，恒成立()f x 问题，可通过参变分离求最值来解决.【详解】【解】A 选项，，定义域为，，令，解得()2ln xf x x =()0,∞+()312ln x f x x -'∴=()0f x '=x当时，，函数在上单调递增，0x <<()0f x ¢>∴()f x (当，函数在上单调递减，x >()0f x '<∴()f x )+∞函数在，故A 对，∴x 12fe =B 选项，时，，，当时，如下图01x << ()0f x <()10f =max 0(2)1fe f x ==>1x >()0f x >所示：函数有且只有唯一一个零点，故B 错，∴()f x C选项，当为单调递减函数，，x>()fx f f∴<，，故C对，ln 2(2)4ff f===<f f f ∴<<D 选项，，故，由于函数在上恒成立，()21f x k x <- ()221ln 1x k f x x x +>+=()0,∞+，设，定义域为，则，2max ln 1x k x +⎛⎫∴> ⎪⎝⎭()2ln 1x g x x +=()0,∞+()32ln1x g x x --'=设，解得，单调递增，单调()0g x '=x =()0,()x g x g x '∴∈>()),0,()x g x g x '∈+∞<递减，，故，故D 对.()max 22e e g x g e ∴==-=2e k >故选：ACD.三、填空题13．函数在处的切线与直线平行，则a ＝______．()af x x x =-1x =2y x =【答案】1【分析】求导函数，利用导数的几何意义求出切线斜率，结合直线平行建立方程求解即可.【详解】因为，所以，()af x x x =-()2a f x x =1+'所以函数在处的切线斜率为，()af x x x =-1x =()11'=+f a 因为该切线与直线平行，故，解得2y x =12a +=1a =故答案为：114．函数在区间上的最大值为______．()cos sin f x x x x=-[]π,0-【答案】π【分析】利用导数，判断函数的单调性，可得结果.()f x 【详解】由，所以，()cos sin f x x x x=-()cos sin cos sin f x x x x x x x'=--=-当时，，所以，[]π,0x ∈-sin 0x ≤()sin 0f x x x =-≤则在单调递减，()f x []π,0-所以.()max ()ππf x f =-=故答案为：.π15．已知，分别为椭圆的左，右焦点，点P 为C 的上顶点，且1F 2F ()2222:10x y C a b a b +=>>，C 的方程是______．123F PF π∠=12F PF S = 【答案】22143x y +=【分析】根据椭圆的性质，即可求解.【详解】解：123F PF π∠=⇒2,a c =12122F PF S c b =⨯⨯= b =又，即，解得：，故，222a b c =+22234c c c =+21c =224,3a b ==所以C 的方程是，22143x y +=故答案为：22143x y +=16．已知函数（且）的极大值和极小值分别为，，且，()22e xf x x a =-0a >1a ≠()1f x ()2f x 12x x <则的取值范围是______．a 【答案】21,1e ⎛⎫ ⎪⎝⎭【分析】由有两个根，转化为函数和的图象有两个不同的交点，结合切()0f x '=14e y x =2ln xy a a =线以及导数求得的取值范围.a 【详解】，所以方程的两个根为，，()4e ln x f x x a a '=-4e ln 0x x a a -=1x 2x 即函数和的图象有两个不同的交点，14e y x =2ln xy a a =因为的极大值和极小值分别为，，()f x 1()f x 2()f x 故当时，，的图象在的下方，12(,)x x x ∈()0f x '<1y 2y 当、时，，的图象在的上方；1(,)x x ∈-∞2(,)x +∞()0f x '>1y 2y 易知，设过原点且与图象相切的直线斜率为，则，01a <<2y l k 4e k <设与切于点，而，所以，l 2ln x y a a =()00,ln xx a a 22ln x y a a '=002ln ln x x a ak a a x ==解得，所以，01ln x a =12ln ln 4e a k a a =⨯<因为，即，又，所以，所以．1ln e aa=2ln 4a <01a <<2ln 0a -<<21,1e a ⎛⎫∈ ⎪⎝⎭故答案为：21,1e ⎛⎫⎪⎝⎭【点睛】求解与曲线的切线有关问题，易错点是没有分清已知点是曲线上的点还是曲线外的点.两种情况下，切线都可以通过导数求得，关注点有切点和斜率两个.极值点的导数为，反之却不成立.0四、解答题17．已知函数.()2ln f x x x =-（1）求函数的单调增区间；()f x （2）求函数在上的最大值.()f x (()0,0a a⎤>⎦【答案】（1）；（2）答案见解析.⎛ ⎝【分析】（1）利用导数，直接解得的单调递增区间；'()0f x >()f x （2）分类讨论：当在上单调递增，此时；0a <<()f x (]0,a ()2max ()ln f x f a aa ==-当在上单调递增，在上单调递减，可以求出最大值.a ≥()f x ⎛ ⎝a ⎫⎪⎪⎭【详解】（1）的定义域为，，()f x ()0,∞+2112'()2x f x x x x -=-=令，得，∵，∴'()0f x >2120x x ->0x >0x <<故的单调递增区间为.()fx ⎛ ⎝（2）由（1）知，在上是增函数，在上是减函数.()fx ⎛ ⎝⎫+∞⎪⎪⎭∴当在上单调递增，此时；0a <<()f x (]0,a ()2max ()ln f x f a a a ==-当在上单调递增，在上单调递减，此时a≥()f x ⎛⎝a ⎫⎪⎪⎭.max 111ln 2222()f f x ==--=综上所述，当的最大值为；当的最大值为0a <<()f x 2max ()ln f x a a =-a ≥()f x .11ln 222f =--18．为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层．某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能源消耗费用（单位：万元）与隔热层厚度（单位：cm ）满足关系：，设为C x ()()4011035C x x x =≤≤+()f x 隔热层建造费用与20年的能源消耗费用之和．(1)求的表达式；()f x (2)隔热层修建多厚时，总费用达到最小，并求最小值．()f x 【答案】(1)800()635f x x x =++()110x ≤≤(2)当隔热层修建5cm 厚时，总费用最小，最小值为70万元．【分析】（1）根据已给模型确定函数解析式；（2）利用导数求得最小值．【详解】（1）每年能源消耗费用为，建造费用为，40()35C x x =+6x ．．()()800206635f x C x x x x ∴=+=++()110x ≤≤（2），令得或（舍．()()22400'635f x x =-+()0f x '=5x =253x =-)当时，，当时，．∴15x ≤<()0f x '<510x <≤()0f x '>在，上单调递减，在，上单调递增．()f x ∴[15)[510]当时，取得最小值（5）．∴5x =()f x f 70=当隔热层修建厚时，总费用最小，最小值为70万元．∴5cm 19．如图，在四棱锥中，底面ABCD 是边长为2的正方形，为正三角形，且侧面P ABCD -PAB 底面ABCD ，．PAB ⊥PM MD =(1)求证：平面ACM ；PB ∥(2)求平面MBC 与平面DBC 的夹角的大小．【答案】(1)证明见解析(2)30°【分析】（1）连接BD ，借助三角形中位线可证；（2）建立空间直角坐标系，利用向量法直接可求.【详解】（1）连接BD ，与AC 交于点O ，在中，因为O ，M 分别为BD ，PD 的中点，则，PBD △BP OM ∥又平面ACM ，平面ACM ，所以平面ACM .BP ⊄OM ⊂BP ∥（2）设E 是AB 的中点，连接PE ，因为为正三角形，则，PAB PE AB ⊥又因为平面底面ABCD ，平面平面，PAB ⊥PAB ⋂ABCD AB =则平面ABCD ，过点E 作EF 平行于CB ，与CD 交于点F ，PE ⊥以E 为坐标原点，建立空间直角坐标系如图所示，则，，，，，，()0,0,0E ()1,0,0B (P ()1,2,0C ()1,2,0D -12M ⎛- ⎝所以，，3,2⎛=-- ⎝ CM ()0,2,0BC = 设平面CBM 的法向量为，则，(),,n x y z =30,220,n CM x y n BC y ⎧⋅=--=⎪⎨⎪⋅==⎩ 令，则，因为平面ABCD ，则平面ABCD 的一个法向量为，1x=(n = PE ⊥()0,0,1m = 所以||cos ,n m m n n m⋅== 所以平面MBC 与平面DBC 所成角的大小为30°．20．已知数列是等差数列，且，.{}n a 12312a a a ++=816a =(1)若数列中依次取出第2项，第4项，第6项，…，第项，按原来顺序组成一个新数列{}n a 2n ，试求出数列的通项公式；{}n b {}n b (2)令，求数列的前项和.3n n n c b =⋅{}n c n n S 【答案】(1)，；4n b n =*n ∈N (2).()12133n n S n +=-⋅+【分析】(1)利用等差数列性质求出数列公差及通项公式，由求解作答.{}n a 2n n b a =(2)由(1)的结论求出，再用错位相减法计算作答.n c 【详解】（1）等差数列中，，解得，公差，{}n a 2123312a a a a =++=24a =28282a d a -==-则，因此，，()()224222n a a n d n n=+-=+-⨯=2224n a n n =⨯=依题意，，24n n b a n ==所以数列的通项公式，.{}n b 4n b n =*n ∈N（2）由(1)知，，343n n n n c b n =⋅=⋅则，()21438344343n n n S n n -=⋅+⋅+⋅⋅⋅+-⋅+⋅因此，，()2313438344343n n n S n n +=⋅+⋅+⋅⋅⋅+-⋅+⋅，()()231113243333434(13)413363143n n n n n n n S n n n +++--=+++⋅⋅⋅+-⋅-⋅=--⋅=⨯-1(42)36n n +=--⋅-所以.()12133n n S n +=-+21．点到定点的距离和它到定直线的距离之比为.P ()1,0F 4x =1:2(1)求点的轨迹方程.P (2)记点的轨迹为曲线,若过点的动直线与的另一个交点为,并且满足:原点到的距离为P C P l C Q O l ,弦长,求直线的方程.322PQ =l 【答案】(1).22143x y +=(2).32y =±【分析】(1)利用直译法即可求解轨迹方程；(2)先设出直线方程,利用弦长及点到直线的距离为两个条件即可解出直线方程.2PQ =l 32【详解】（1）设,点到定直线的距离为.由题意可得:,即(),P x y P 4x =d12PF d=,12=整理化简得:.即点的轨迹方程为.22143x y +=P 22143x y +=（2）设.当直线的斜率不存在时,由原点到的距离为,由对称性不妨设直线:()()1122,,,P x y Q x y l O l 32l .32x =所以满足,()()1122,,,P x y Q x y 2232143x x y ⎧=⎪⎪⎨⎪+=⎪⎩解得:,（舍去）.33,,22P Q ⎛⎛⎝⎝2≠当直线的斜率存在时,可设.l :l y kx m =+因为原点到的距离为,,即,O l 3232=()22491m k =+则满足,消去可得:,()()1122,,,P x y Q x y 22143y kx m x y =+⎧⎪⎨+=⎪⎩y ()2223484120k x kmx m +++-=,()()2222223442412644481914k m k m k m +-∆=-=++因为,所以恒成立.()22491m k =+22481921440m k ∆=-++>则.21122228412,3434km m x x x x k k --+=⋅=++==因为,()22491m k =+所以.2==化简得:,42560k k +=解得:,所以,直线的方程为:.0k =32m =±l 32y =±综上所述:直线的方程为:.l 32y =±【点睛】方法点睛：利用韦达定理法解决直线与圆锥曲线相交问题的基本步骤如下：（1）设直线方程，设交点坐标为；()()1122,,,x y x y （2）联立直线与圆锥曲线的方程，得到关于（或）的一元二次方程，必要时计算；x y ∆（3）列出韦达定理；（4）将所求问题或题中的关系转化为、（或、）的形式；12x x +12x x 12y y +12y y （5）代入韦达定理求解.22．已知函数.()ln 2f x x ax =-(1)讨论函数的单调性；()f x (2)若恒成立，求a 的取值范围；()0f x ≤(3)求证：.2021202020202021>【答案】(1)在上单调递增，在上单调递减()f x 10,2a ⎛⎫ ⎪⎝⎭1,2a∞⎛⎫+ ⎪⎝⎭(2)12ea ≥(3)证明见解析【分析】（1）求导数，根据导数的正负性分类讨论进行求解即可；（2）利用常变量分离法，构造新函数，结合导数的性质、函数的最值进行求解即可；（3）利用分析法，结合（2）中函数的单调性进行证明即可.ln ()x g x x =【详解】（1）.()1122ax f x a x x -'=-=当时，，所以在上单调递增；0a ≤()120ax f x x -'=>()f x ()0,∞+当时，令，解得，0a >()120ax f x x '-==12x a =当时，；10,2x a ⎛⎫∈ ⎪⎝⎭()120ax f x x -'=>当时，；1,2x a ⎛⎫∈+∞ ⎪⎝⎭()120ax f x x -'=<所以上单调递增，在上单调递减；()f x 10,2a ⎛⎫ ⎪⎝⎭1,2a∞⎛⎫+ ⎪⎝⎭（2）的定义域为，若恒成立，则恒成立，()f x (0,)+∞()0f x ≤ln 20x ax -≤即恒成立，ln 2xa x ≥令，只需，又，ln ()x g x x =max 2()a g x ≥22(ln )ln 1ln ()x x x x x g x x x '''⋅-⋅-==令得，()0g x '=e x =时，，则单调递增；(0,e)x ∈()0g x '>ln ()xg x x =时，，则单调递减；(e,)x ∈+∞()0g x '<ln ()xg x x =所以，解得：；max 12()(e)e a g x g ≥==12e a ≥（3）要证明，只需证明，即，2021202020202021>20212020ln 2020ln 2021>2021ln 20202020ln 2021>即只需证明，由（2）可知：在单调递减，所以ln 2020ln 202120202021>ln ()x g x x =(e,)x ∈+∞，(2020)(2021)g g >故得证. 从而得证.ln 2020ln 202120202021>2021202020202021>【点睛】关键点点睛：利用常变量分离法，结合构造函数法进行求解证明是解题的关键.。

贵溪市实验中学高中部2020-2021学期第二学期第一次月考高二三校生语文试卷考试时间150分钟试卷分值150分命题人：一、（24分，每小题3分）1、下列各组加点字注音正确的一项是（）A．憎恶（zèng）给(jǐ)予顶礼膜拜（mó）酝酿（liàng）B．菜畦（qí）提防（dī）戛然而止（gá）挫折（cuò）C．甑屋（zèng）惩罚（chéng）义愤填膺（yīng）谬赞（miù）D．追溯（sù) 肖像（xiào）猝然长逝（cuì）粗犷（guǎng）2．下列各组词语中，没有错别字的一组是（）A．哀声叹气光阴荏苒朔风吹撼鸦鹊无声B．贪脏枉法鬼鬼祟祟碎琼乱玉余音绕梁C．应接不遐交头接耳毕恭毕敬黄天厚土D．素不相识吃饭防噎人才荟萃厚颜无耻3.下列各句中,加点的词语运用不正确的一项是( )A.阳春三月，肉明几净，肉外野花竞相开放，姹紫嫣红．．．．、给小屋增添了许多生机。

B我想象金先生坐在平板三轮上东张西望．．．．，那情景定非常有趣。

C.学生提的问题深浅不一．．．．，金先生有问必答。

D.读汪曾棋先生的文意，真是一件大快人心．．．．的事。

4．下列各句中，标点符号使用有误的一项是（）A．我给他画了几个青头菌、牛肝菌，一根大葱，两头蒜，还有一块很大的宣威火腿。

——火腿是很少入画的。

B．种菜是细致活儿，“种菜如绣花”；认真干起来也很累人，就劳动量来说，“一亩园十亩田。

”C．除了文学院大一学生必修逻辑，金先生还开了一门“符号逻辑”，是选修课。

D．林徽因死后，有一年，金先生在北京饭店请了一次客，老朋友收到通知，都纳闷：老金为什么请客？到了之后，金先生才宣布：“今天是徽因的生日。

”5．依次填入各句横线处的词语，最恰当的一组是（）①作曲家多年积淀的质朴纯实与崇高宽阔的胸怀相，充满了纯朴的人性之美。

②他对我有很深的，以致在我提出合理的建议时也常常反对。

湖北省天门2023-2024学年度高二下学期三月月考数学试题（答案在最后）考试内容：选修一第一章——选修三第六章6.1考试时间：2024年3月31日出题人：审题人：一、单选题（共40分）1.某圆锥的侧面积为16π，其侧面展开图为一个半圆，则该圆锥的底面半径长为（）A.2B.4C. D.【答案】C 【解析】【分析】设圆锥的母线长为l ，底面半径为r ，由题意得到2ππr l =求解.【详解】设圆锥的母线长为l ，底面半径为r ，即侧面展开图的半径为l ，侧面展开图的弧长为πl .又圆锥的底面周长为2πr ，所以2ππr l =，即圆锥的母线长2l r =.所以圆锥的侧面积为2π2π16πrl r ==，解得r =故选：C.2.若直线1l ：2(1)40x m y +++=与直线2l ：320mx y +-=平行，则m 的值为（）A.2B.3- C.2或3- D.2-或3-【答案】C 【解析】【分析】依题意可得23(1)0m m ⨯-+=，求出m 的值，再检验即可.【详解】直线1l ：2(1)40x m y +++=与直线2l ：320mx y +-=平行，则23(1)0m m ⨯-+=，解得3m =-或2m =，当3m =-时，此时直线1l ：2240x y -+=与直线2l ：3320x y -+-=平行，当2m =时，此时直线1l ：2340x y ++=与直线2l ：2320x y +-=平行，故3m =-或 2.m =故选：C3.等比数列{}n a 的各项均为正数，且564718a a a a +=，则3132310log log log a a a ++⋅⋅⋅+=（）A.12B.10C.5D.32log 5【答案】B 【解析】【分析】利用等比数列的性质，结合对数的运算法则即可得解.【详解】因为{}n a 是各项均为正数的等比数列，564718a a a a +=，所以564756218a a a a a a +==，即569a a =，则11029569a a a a a a ==== 记3132310log log log S a a a =++⋅⋅⋅+，则3103931log log log S a a a =+⋅+⋅⋅+，两式相加得()()()3110329310132log log log 10log 920S a a a a a a =++⋅⋅⋅+=⨯=，所以10S =，即3132310log log log 10a a a ++⋅⋅⋅+=.故选：B.4.已知函数()()()ln 2ln 4f x x x =-+-，则()f x 的单调递增区间为（）A.()2,3 B.()3,4 C.(),3-∞ D.()3,+∞【答案】A 【解析】【分析】根据对数真数大于零可构造不等式组求得函数定义域；利用导数可求得函数单调递增区间．【详解】由2040x x ->⎧⎨->⎩得：24x <<，即()f x 的定义域为()2,4；()()()()23112424x f x x x x x -'=-=---- ，∴当()2,3x ∈时，()0f x ¢>；当()3,4x ∈时，()0f x '<；()f x \的单调递增区间为()2,3．故选：A ．5.已知函数()2xf x =，则函数()f x 的图象在点()()0,0f 处的切线方程为（）A.10x y --=B.10x y -+=C.ln 210x y ⋅--=D.ln 210x y ⋅-+=【答案】D【分析】求出函数()f x 的导数，再利用导数的几何意义求出切线方程.【详解】函数()2xf x =，求导得()2ln 2x fx '=，则(0)ln 2f '=，而(0)1f =，所以所求切线方程为1ln 2(0)y x -=⋅-，即ln 210x y ⋅-+=.故选：D6.在平面直角坐标系xOy 中，点()()1,0,2,3A B -，向量OC mOA nOB =+，且40m n --=.若P 为椭圆2217y x +=上一点，则PC 的最小值为（）A.B.C.D.【答案】A 【解析】【分析】根据给定条件，求出点C 的轨迹，再借助三角代换及点到直线距离公式求出最小值.【详解】设点(,)C x y ，由()()1,0,2,3A B -及OC mOA nOB =+，得(,)(2,3)x y m n n =-+，即23x m ny n=-+⎧⎨=⎩，而40m n --=，消去,m n 得：3120x y -+=，设椭圆2217y x +=上的点(cos ),R P θθθ∈，则点P 到直线3120x y -+=的距离d =，其中锐角ϕ由tanϕ=确定，当sin()1θϕ+=时，min d =PC d ≥ ，所以PC 的故选：A【点睛】思路点睛：求出椭圆上的点与其相离的直线上点的距离最小值，可转化为求椭圆上的点到直线距离有最小值解决.7.5人排一个5天的值日表，每天排一人值日，每人可以排多天或不排，但相邻两天不能排同一人，值日表排法的总数为（）A.120B.324C.720D.1280【分析】利用分步乘法计数原理计算即可.【详解】第一天可以排5个人中的任意一个，有5种排法；第二天可以排另外4个人中任意一个，有4种排法；第三天同上，有4种排法；第四天同上，有4种排法；第五天同上，有4种排法．根据分步乘法计数原理得所有的排法总数为544441280⨯⨯⨯⨯=．故选:D ．8.函数32()(1)f x x a x x b =+--+为R 上的奇函数，过点1,12P ⎛⎫- ⎪⎝⎭作曲线()y f x =的切线，可作切线条数为（）A.1B.2C.3D.不确定【答案】A 【解析】【分析】根据奇函数确定3()f x x x =-，求导得到导函数，设出切点，根据切线方程公式计算01x =-，计算切线得到答案.【详解】()3232()(1)(1)f x x a x x b f x x a x x b -=-+-+=-=--++--，故1a =，0b =，3()f x x x =-，2()31x f x '=-，设切点为()00,Mxy ，则2000012()311y f x x x '-=+=-，且30000()f x x x y -==，整理得到()()20001410x x x +-+=，解得01x =-，(1)2f '-=，故切线方程为22y x =+，故选：A二、多选题（共18分）9.公差为d 的等差数列{}n a ，其前n 项和为n S ，110S >，120S <，下列说法正确的有（）A.0d < B.70a > C.{}n S 中5S 最大D.49a a <【分析】利用等差数列性质结合给定条件可得60a >，670a a +<，再逐项分析判断作答.【详解】由()111116111102a a S a +==>，得60a >，又()()112126712602a a S a a +==+<，得，670a a +<，所以60a >，70a <，数列{}n a 是递减数列，其前6项为正，从第7项起均为负数，等差数列{}n a ，公差0d <，A 选项正确；70a <，B 选项错误；前6项和最大，C 选项错误；由40a >，90a <，有4949670a a a a a a -=+=+<，则49a a <，D 选项正确.故选：AD.10.已知函数()()322R x x a a f x x =-++∈的图像为曲线C ，下列说法正确的有（）A.R a ∀∈，()f x 都有两个极值点B.R a ∀∈，()f x 都有零点C.R a ∀∈，曲线C 都有对称中心D.R a ∃∈，使得曲线C 有对称轴【答案】ABC 【解析】【分析】根据函数极值的定义、零点的定义，结合函数的对称性的性质逐一判断即可.【详解】A ：()()()()3222341311x x x a f x x x x x f x '=-++⇒=-+=--，当1x >时，()()0,f x f x '>单调递增，当113x <<时，()()0,f x f x '<单调递减，当13x <时，()()0,f x f x '>单调递增，因此13x =是函数的极大值点，1x =是函数的极小值点，因此本选项正确；B ：当x →+∞时，()f x →+∞，当x →-∞时，()f x →-∞，而函数()f x 是连续不断的曲线，所以一定存在0R x ∈，使得()0f x =，因此本选项正确；C ：假设曲线C 的对称中心为(),b c ，则有()()()()()()32322222,f b x f b x c b x b x b x a b x b x b x a c ++-=⇒+-+++++---+-+=化简，得()232322b x c a b b b -=---+，因为x ∈R ，所以有322320320227b b c a b b b c a ⎧=⎪-=⎧⎪⇒⎨⎨---+=⎩⎪-=⎪⎩，因此给定a 一个实数，一定存在唯一的一个实数c 与之对应，因此假设成立，所以本选项说法正确；D ：由上可知当x →+∞时，()f x →+∞，当x →-∞时，()f x →-∞，所以该函数不可能是关于直线对称，因此本选项说法不正确，故选：ABC11.已知正方体1111ABCD A B C D -的棱长为1，下列四个结论中正确的是（）A.直线1B C 与直线1AD 所成的角为90B.直线1B C 与平面1ACD 所成角的余弦值为33C.1B D ⊥平面1ACD D.点1B 到平面1ACD 的距离为32【答案】ABC 【解析】【分析】如图建立空间直角坐标系，求出1B C 和1AD uuu r的坐标，由110AD B C ⋅= 可判断A ；证明10AC B D ⋅= ，110AD B D ⋅=，再由线面垂直的判定定理可判断C ；计算11cos ,B D B C 的值可得线面角的正弦值，再求出夹角的余弦值可判断B ；利用向量求出点A 到平面11D B C 的距离可判断D.【详解】如图以D 为原点，分别以1,,DA DC DD 所在的直线为,,x y z 轴建立空间直角坐标系，则()0,0,0D ，()1,0,0A ，()0,1,0C ，()10,0,1D ，()11,1,1B ，对于A ：()11,0,1B C =-- ，()11,0,1AD =-，因为()()()111100110B C AD ⋅=-⨯-+⨯+-⨯= ，所以11AD B C ⊥ ，即11B C AD ⊥，直线1B C 与直线1AD 所成的角为90 ，故选项A 正确；对于C ：因为()1,1,0AC =- ，()11,0,1AD =- ，()11,1,1B D =---，所以11100AC B D ⋅=-+= ，111010AD B D ⋅=+-= ，所以1AC B D ⊥ ，11AD B D ⊥uuur uuu r ，因为1AC AD A =I ，1,AC AD ⊂平面A 1，所以1B D ⊥平面1ACD ，故选项C 正确；对于B ：由选项C 知：1B D ⊥平面1ACD ，所以平面1ACD 的一个法向量()11,1,1B D =---，因为()11,0,1B C =-- ，所以111111cos ,B D B C B D B C B D B C⋅=== 即直线1B C 与平面1ACD 所成，所以直线1B C 与平面1ACD33=，故选项B 正确；对于D ：因为()11,0,1B C =-- ，平面1ACD 的一个法向量()11,1,1B D =---，所以点1B 到平面1ACD的距离为1113B D B C d B D⋅=== ，故选项D 不正确.故选：ABC.三、填空题（共15分）12.若抛物线22y px =-过点()1,2-，则该抛物线的焦点为________．【答案】()1,0-【解析】【分析】根据题意，代入求得2p =，结合抛物线的几何性质，即可求解.【详解】解：将()1,2-代入抛物线方程22y px =-，可得2p =，即24y x =-，所以抛物线24y x =-的焦点为()1,0-．故答案为：()1,0-.13.已知等比数列{}n a 的前n 项和为n S ，且满足122n n S λ+=+，则实数λ的值是_____．【答案】-2【解析】【分析】由已知推得1q ≠，继而结合等比数列的前n 项和的特点及已知即可求解.【详解】等比数列{}n a 中，由122n n S λ+=+可得122n n S λ=+，则11122a S λ==+，若公比1q =，则2211224,02S a λλλ=+==+∴=，则13323S a =≠，故1q ≠，则等比数列的前n 项和()1111111n nn a q a S qa q a a--=⋅--=-，（1q ≠），故令112λ=-，即2λ=-，故答案为：2-14.若e e e e ()cos 22x x x xf x x x ---+=+，则不等式(sin )(cos )0f x f x +>的解集是________．【答案】π3π|2π2π,44x k x k k ⎧⎫-<<+∈⎨⎬⎩⎭Z 【解析】【分析】根据奇偶性的定义和导数分析可知()f x 在[]1,1-内单调递增，且为奇函数，进而可得sin cos x x >-，利用辅助角公式结合正弦函数运算求解.【详解】取()f x 的定义域为[]1,1-，关于原点对称，且()()()e e e e e e e e ()cos cos sin 2222x x x x x x x xf x x x x x f x -----+-+-=-+-=--=-，所以()f x 为定义在[]1,1-上的奇函数，因为()e e e e e e e e ()cos sin sin cos e e cos 2222x x x x x x x xx x f x x x x x x ------+-+'=-++=+，若[]1,1x ∈-，则e 0,e cos 00,x x x ->>>，可得()()e e cos 0x xf x x -'=+>，可知()f x 在[]1,1-内单调递增，对于不等式(sin )(cos )0f x f x +>，则(sin )(cos )(cos )f x f x f x >-=-，且[][]sin 1,1,cos 1,1x x ∈--∈-，可得sin cos x x >-，整理得πsin cos 04x x x ⎛⎫+=+> ⎪⎝⎭，令π2π2ππ,4k x k k <+<+∈Z ，解得π3π2π2π,44k x k k -<<+∈Z ，所以不等式(sin )(cos )0f x f x +>的解集是π3π|2π2π,44x k x k k ⎧⎫-<<+∈⎨⎬⎩⎭Z .故答案为：π3π|2π2π,44x k x k k ⎧⎫-<<+∈⎨⎬⎩⎭Z .四、解答题（共77分）15.已知函数()ln 1f x x ax =++.（1）当1a =-时，求()f x 的最大值.（2）讨论函数()f x 的单调性.【答案】（1）0（2）答案见解析【解析】【分析】（1）利用导数求解函数最值即可.（2）含参讨论函数单调性即可.【小问1详解】当1a =-时，()ln 1f x x x =-+，由0x >，所以()111x f x x x-=-='，当01x <<时，()0f x '>，所以函数()f x 在()0,1上单调递增；当1x >时，()0f x '<，所以函数()f x 在()1,∞+上单调递减；故()()max 1ln1110f x f ==-+=；【小问2详解】定义域为(0,)+∞，()1f x a x'=+，当0a ≥时，()10f x a x+'=>，()f x 在(0,)+∞上递增；当a<0时，令()10f x a x +'=>，解得10,x a ⎛⎫∈- ⎪⎝⎭，令()10f x a x +'=<，解得1,x a ∞⎛⎫∈-+ ⎪⎝⎭.于是()f x 在10,a ⎛⎫-⎪⎝⎭上单调递增；在1,a ⎛⎫-+∞ ⎪⎝⎭上单调递减.16.如图，在底面为菱形的直四棱柱1111ABCD A B C D -中，12π,23BAD AA AB ∠===，,,E F G 分别是111,,BB CC DD 的中点．（1）求证：1A E GC ∥；（2）求平面1A EF 与平面ABCD 所成夹角的大小．【答案】（1）证明见解析（2）π6【解析】【分析】（1）建立空间直角坐标系，利用向量的坐标运算即可求解，（2）根据法向量的夹角即可求解.【小问1详解】取BC 中点H ，连接AH因为底面ABCD 为菱形，2π3BAD ∠=，所以AH AD ⊥以A 为原点，1,,AH AD AA 所在直线分别为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系，则()()()10,0,2,3,1,1,0,2,1A E G -，()()3,1,0,3,1,1C F ))13,1,1,3,1,1A E GC =--=-- 1A E GC∴ ∥1A E GC∴∥【小问2详解】设平面1A EF 的法向量为(),,n x y z =又()0,2,0EF = 所以100n A E n EF ⎧⋅=⎪⎨⋅=⎪⎩ 即3020y z y --==⎪⎩取1x =，则0,3y z ==(3n = ()10,0,2AA = 为平面ABCD 的法向量，设平面1A EF 与平面ABCD 的夹角为θ，则11233cos 222AA n AA nθ⋅===⨯ π6θ∴=∴平面1A EF 与平面ABCD 的夹角为π617.已知数列{}n a 的前n 项和n S 满足()1122n n S n +=-+．（1）求{}n a 的通项公式；（2）求数列12·1n n a n ++⎧⎫⎨⎬+⎩⎭的前n 项和n T ．【答案】（1）2nn a n =⨯（2）()2124n n T n +=+⨯-【解析】【分析】（1）由已知结合数列的和与项的递推关系即可求解；（2）先求数列121n n a n ++⎧⎫⎨⎬+⎩⎭的通项公式，然后利用错位相减求和即可求解．【小问1详解】当1n =时，112a S ==，当2n ≥时，由()1122n n S n +=-+，得()1222n n S n -=-+，则()()1112222n n n n n n a S S n n n +-=-=---=⨯，因为11212a ==⨯，所以2n n a n =⨯；【小问2详解】由（1）可知，()112·221n n n a n n +++=+⨯+，则()234132425222n n T n +=⨯+⨯+⨯+⋯++⨯，则()3452232425222n n T n +=⨯+⨯+⨯+⋯++⨯，则()234123222222n n n T n ++-=⨯+++⋯+-+⨯()()12812122212n n n -+-=+-+⨯-()22122822n n n ++=+--+⨯()2412n n +=-+⨯，所以()2124n n T n +=+⨯-．18.在平面直角坐标系xOy 中，已知椭圆2222:1x y C a b +=（0a b >>过点(2,1)P，且离心率2e =．（1）求椭圆C 的方程；（2）直线l 的斜率为12，直线l 与椭圆C 交于A 、B 两点，求PAB 的面积的最大值．【答案】（1）22182x y +=（2）2【解析】【分析】（1）利用222c e a =，可得22234a b a -=，再将点P 坐标代入方程，解方程组求得,a b 从而可得椭圆的方程；（2）设直线l 的方程为1,2y x m =+，代入椭圆方程中整理得222240x mx m ++-=，借助根的判别式可得||2m <，结合根与系数的关系可得AB ==直线的距离公式可求出点P 到直线的距离d ，再利用三角形面积公式1||2PAB S d AB =⋅ 和基本不等式进行求解，即可解决问题.【小问1详解】因为22222234c a b e a a -===，所以224a b =，①因为椭圆C 过点(2,1)P ，所以22411a b +=，②由①②解得228,2a b ==，所以椭圆的方程为22182x y +=．【小问2详解】设直线l 的方程为()()11221,,,,2y x m A x y B x y =+，联立2212182y x m x y ⎧=+⎪⎪⎨⎪+=⎪⎩，得222240x mx m ++-=，所以212122,24x x m x x m +=-=-，又直线l 与椭圆相交，所以2248160m m =-+> ，解得||2m <，则AB ==P 到直线l的距离d ==，所以221142222PAB m m S d AB +-=⋅==≤= ，当且仅当22m =，即m =时，PAB 的面积取得最大值为2．19.已知函数()2e e x x f x a x =-+，其中0a >.（1）当1a =时，求函数()f x 在0x =处的切线方程；（2）讨论函数()f x 的极值点的个数；（3）若对任意的0a >，关于x 的方程()f x m =仅有一个实数根，求实数m 的取值范围.【答案】（1）20x y -=（2）见解析（3）3ln 2,2⎡⎫-++∞⎪⎢⎣⎭【解析】【分析】（1）求导得斜率，再利用点斜式求直线方程；（2）求导，讨论判别式与0的关系得单调性即可求解极值点个数；（3）构造新函数()2ee x x g x a x m =-+-，判单调性，得到()()120,ln 2,ln 2,x x ∞∈∈+，结合()10g x <或()20g x >即可求解.【小问1详解】当1a =时，()()22e e ,2e e 1x x x x f x x f x '=-+=-+，()02f '=，()00f =，所以函数()f x 在0x =处的切线方程为()020y x -=-，即20x y -=.【小问2详解】()22e e 1x x f x a '=-+，令()0,e x f x t ='=，得2210at t -+=，则18a ∆=-.当18a ≥时，0∆≤，此时()0f x '≥，故函数()f x 在(),∞∞-+上单调递增，没有极值点；当108a <<时，0∆>，令()0f x '=，则1e 4x a =，则1211ln ln 44x x a a-+==，则当()1,x x ∞∈-时，()0f x '>，当()12,x x x ∈时，()0f x '<，当()2,x x ∞∈+时，()0f x '>，则()f x 在()()12,,,x x ∞∞-+单调递增，在()12,x x 单调递减，此时函数()f x 有两个极值点.综上所述，当18a ≥时，函数()f x 没有极值点；当108a <<时，函数()f x 有两个极值点.【小问3详解】依题意，2e e x x a x m -+=，记()2e e x x g x a x m =-+-，()()g x f x '='.（i ）由（2）知当18a ≥时，()0g x '≥，则函数()g x 在(),∞∞-+上单调递增；可知当x →-∞时，()g x ∞→-，当x →+∞时，()g x ∞→+，故当18a ≥时，函数()g x 恰有一个零点，方程()f x m =仅有一个实数根，此时R m ∈.（ii ）当108a <<时，()g x 在()1,x ∞-上单调递增，在()12,x x 上单调递减，在()2,x ∞+单调递增，()()112222122e e 12e e 10x x x x g x a g x a ''=-+==-+=，则121222e 1e 12e 2ex x x x a --==，所以()()1112111e 1ee 22x x x g x g x a x m x m ==-+-=-+--极大值，()()2222222e 1e e 22x x x g x g x a x m x m ==-+-=-+--极小值，因为当(),x g x ∞∞→-→-，当(),x g x ∞∞→+→+，故只需()10g x <或()20g x >，令()e 122x h x x =-+-，则()e 12xh x '=-+，故当(),ln 2x ∞∈-时，()0h x '>，当()ln 2,x ∞∈+时，()0h x '<，则()h x 在(),ln 2∞-单调递增，在()ln 2,∞+单调递减；又121ln ln ln4x x a -===又108a <<，故()0,1，则()()120,ln 2,ln 2,x x ∞∈∈+，所以()()12331,ln 2,,ln 222h x h x ∞⎛⎫⎛⎫∈--+∈--+ ⎪ ⎪⎝⎭⎝⎭，故3ln 22m ≥-+.综上所述，实数m 的取值范围为3ln 2,2∞⎡⎫-++⎪⎢⎣⎭.【点睛】关键点点睛：本题考查函数极值点及零点个数问题，解决问题关键是利用第二问单调性解决第三问零点问题，并利用构造函数法求函数值域。

高二(地理)下学期第一次月考本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题）两部分。

满分100分，考试用时90分钟.第Ⅰ卷（选择题，共60分）一、单项选择题（共60分，下列各题的四个备选项中,只有一个是正确的,多选、不选或错选,该题不得分，选对一题得2分）1．关于旅游资源的正确说法是（）A．人文景观包括公园和城市游乐园B．自然景观以水域风光景观为主C．旅游资源和其他资源相比最突出的特性是其永续性D．旅游资源是无价的精神文化资源而不是经济资源2．北京故宫对旅游者吸引力大的原因是（）A．具有多样性,是自然景观、人文景观和城市游憩景观的最佳结合点B．给人以情观景的享受C．具有非凡性和历史文化价值,能起到情感升华的巨大作用D．较高的美学价值和科学价值读云南省某地示意图，回答3～6题:3．在云南西双版纳林海中的傣家村落,建筑形式是当地高脚式竹楼,这表明（）A．竹楼这种文化事物受自然环境影响较小B．竹楼的材料和结构反映了当地自然环境C．竹楼记录了当地人的意识形态D．竹楼反映了早期社会制度4．图中属于人文旅游资源的是( ）A．石林B．湖泊C．雪山D．竹楼5．图中的自然景观与人文景观的共同特点是( ）A．多样性、非凡性B．季节性、地域性C．可创造性、长存性D．可变异性、可移动性6．图中的景观中没有（）A．地质地貌景观B．水文地理景观C．生物景观D．气象气候景观7．下列我国著名的旅游名胜中，位于陇海线和兰新线沿线，又符合自西向东排列的一组是( ）A．峨眉山长江三峡洛阳龙门石窟苏州园林B．敦煌莫高窟秦陵兵马俑黄河三门峡洛阳白马寺C．西安大雁塔大同云冈石窟南京中山陵东岳泰山D．西岳华山四川九寨沟湖北神农架开封宋城8．家住重庆的一位退休教师欲乘火车到庐山旅游，距离最短的乘车路线是( ）A．襄渝线一焦柳线一湘黔线一浙赣线一京九线B．成昆线一宝成线一陇海线一京九线C．川黔线一黔桂线一湘桂线一京广线一浙赣线一京九线D．川黔线一湘黔线一浙赣线一京九线9．下列说法中，正确的是( ) A．贵州的黄果树瀑布是重要的人文景观B．山东的泰山是著名的断块山构造,有很重要的地学价值C．北京故宫是自然景观和人文景观相结合的旅游资源D．曲阜孔庙、孔林、孔府具有极其重要的科学价值10．下列有关我国旅游资源的叙述，正确的是（）A．形象美是云南石林美的核心B．安徽“黄山四绝”具有重复使用性和可创性的特点C．河南嵩山以少林寺著称,因而嵩山属于人文景观D．江西庐山从成因上看是褶皱山11．“停车坐爱枫林晚,霜叶红于二月花"反映了自然景观的（）A．形象美B．色彩美C．动态美D．朦胧美12．下列景观具有动态美和听觉美的是( ）A．钱塘江大潮B．黄山云海C．云南路南石林D．武陵源群峰13．下列关于自然美和人工美的叙述，正确的是（) A．自然美和人工美都随季节变化而变化B．名人轶事和民间传说呈现出的人工美，对自然景观和人文景观起到了渲染作用C．自然景观中的人造景物只是为了欣赏D．古典园林主要是由山、水、花木和建筑四种基本要素组合而成的综合艺术品14．观赏黄山“云海”的最佳季节是( ) A．春季B．夏季C．秋季D．冬季15．清朝画家恽田云“春山如笑，夏山如怒，秋山如妆，冬山如睡，四山之意，山不言，人能言。

高二生物选修三月考试卷（前两章）（试卷分第I卷和第Ⅱ卷，满分100分,考试时间为90分钟）第I卷一、单项选择题：（50小题，每小题1分，共50分，每小题只有一个选项符合题意。

）1．下列关于染色体和质粒的叙述，正确的是（）A．染色体只存在于真核生物细胞中，质粒只存在于原核生物细胞中B．在基因工程中染色体和质粒均可以作为运载体C．染色体和质粒均与生物的遗传有关D．染色体和质粒的化学本质相同2.下列关于基因工程应用的叙述，正确的是( )A．基因治疗就是把缺陷基因诱变成正常基因B．基因诊断的基本原理是DNA分子杂交C．一种基因探针能检测水体中的各种病毒D．原核基因不能用来进行真核生物的遗传改良3.下列有关基因工程的叙述，正确的是：（）A．DNA连接酶的作用是将两个黏性末端的碱基连接起来B．目的基因导入受体细胞后，受体细胞即发生基因突变C．目的基因与运载体结合的过程发生在细胞外D．常使用的运载体有大肠杆菌、噬菌体和动植物病毒等4．基因工程是在DNA分子水平上进行设计施工的。

在基因操作的基本步骤中，不进行碱基互补配对的是（）A.人工合成目的基因B.目的基因与运载体结合C.将目的基因导入受体细胞D.目的基因的检测表达5．苏云金芽孢杆菌的抗虫基因导入棉花细胞是否已表达，其检测方法是（）A．是否有抗生素抗性 B．是否能检测到标记基因C．是否有相应的性状 D．是否能分离到目的基因6. 下列关于基因工程的叙述中，正确的是（）A．基因工程是细胞水平上的生物工程B．基因工程产生的变异属于人工诱变C．基因工程育种的优点之一是目的性强D．基因工程的产物对人类都是有益的7. 下列有关基因工程中限制内切酶的描述，错误的是（）A.一种限制性内切酶只能识别一种特定的脱氧核苷酸序列B.限制性内切酶的活性受温度的影响C.限制性内切酶能别和切割RNAD.限制性内切酶可从原核生物中提取8.依右下图有关基因工程的工具酶功能的叙述，不．正确的是（）A．切断a处的酶为限制性内切酶B．连接a处的酶为DNA连接酶C．切断b处的酶为DNA解旋酶D．作用b处的酶为限制性内切酶9.下列不可作为基因工程中的标记基因的是：（）A．抗性基因 B．发光基因C．产物具有颜色反应的基因 D．贮藏蛋白的基因10.下列关于蛋白质工程的叙述中，错误的是（）A、蛋白质工程的实现需要多学科技术的参与B、蛋白质工程创造出新的基因C、蛋白质工程是对蛋白质分子的直接改造D、蛋白质工程又称为第二代基因工程11.为了防止转基因作物的目的基因通过花粉转移到自然界中的其他植物，科学家设法将目的基因整合到受体细胞的叶绿体基因组中。

2024-2025学年新科版选修3语文下册月考试卷225考试试卷考试范围：全部知识点；考试时间：120分钟学校：______ 姓名：______ 班级：______ 考号：______总分栏一、名著阅读(共5题，共10分)1、名著导读简述《堂吉诃德》中一个令你难忘的情景。

2、请从下列两道题中任选一题作答（1）简述堂吉诃德斗风车的故事。

（2）子曰：“后生可畏，焉知来者之不如今也？四十、五十而无闻焉，斯亦不足畏也已。

”本章孔予的话有什么含义？选答第（）题3、下列各项中，对作品故事情节的叙述有误的两项是 ()E.爱斯梅拉达被冤枉刺杀弗比斯，当她被架上囚车时，卡西莫多从教堂正面滑下，冲向两个刽子手，挥拳将他们击倒，然后一手夹起爱斯梅拉达，一个箭步蹿进了教堂。

(《巴黎圣母院》)A. 爱斯梅拉达逃跑时，被修女居第尔抓住，当居第尔拿出一只小鞋时，爱斯梅拉达也拿出一只小鞋。

居第尔经过比较两只鞋，才发觉自己抓的正是自己失散多年的女儿。

(《巴黎圣母院》)B. 堂吉诃德在路上遇见一辆运载狮子的车辆，他想与狮子较量一番，便用长枪挑开笼门，但这匹体格雄壮的狮子对他的冒犯满不在乎，不但没有冲出狮笼，反而掉转身子，慢吞吞、懒洋洋地又躺下了。

堂吉诃德在管狮人的假意夸奖之下自以为得胜，并要求管狮人见到国王时，一定要把这件英勇的事迹禀报给国王。

还说：“假如陛下问这是谁的英雄事迹，你就告诉他是狮子骑士的……” (《堂吉诃德》)C. 大路上赶来了两群羊。

堂吉诃德把公羊、母羊的叫唤，当成是“萧萧马嘶、悠悠角声、咚咚鼓响”，把羊群看成是出现在他面前的左右两支军队。

这是对堂吉诃德“大战羊群”情节的描写。

他用长枪向羊群乱刺，也被牧羊人乱石打倒。

等到牧羊人走后，桑丘才把他扶了起来。

堂吉诃德对他说，自己被魔法师作弄了。

魔法师由于妒忌他胜利，便把敌对的两军变成两群羊。

(《堂吉诃德》)D. “跃马过檀溪”的是刘备，“威震逍遥津”的是张辽，“百骑劫魏营”的是甘宁，“抬榇决死战”的是许褚，“拔矢啖睛”的是关羽。

宁南中学2018-2019学年度下期第一次月考高二化学试题时间：90分钟满分100分命题人：陈小波审题人：刘学可能用到的相对原子质量：H 1 C 12 N:14 O 16 Na 23 Mg 24一、选择题：本题共20个小题，每小题2.5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.化学与生活密切相关，下列有关说法正确的是（）A.把浸泡过KMnO4溶液的硅藻土放在水果箱里可延长水果的保鲜期B.糖类、蛋白质、油脂属于天然高分子化合物C.煤经气化和液化两个物理变化过程，可变为清洁能源D.制作航天服聚酯纤维和用于光缆通信的光导纤维都是新型无机非金属材料2.下列做法不能达到除杂目的的是（）A.乙酸乙酯（乙酸）：加饱和Na2CO3溶液，荡静置后，分液B.乙醇（水）：加入新制生石灰，蒸馏C.乙酸（乙醇）：加入金属钠，蒸馏D.溴苯（溴）：加入NaOH溶液，充分振荡静置后，分液3. 下列实验操作正确的是（）4.下列有关化学键的叙述，正确的是（）A．离子化合物中一定含有离子键B．只要有化学键的断裂必然有化学反应发生C．由非金属元素组成的化合物一定是共价化合物D．含有共价键的化合物一定是共价化合物5. N A为阿伏伽德罗常数的数值，下列说法正确的是（）A.2.4gMg与H2SO4完全反应，转移的电子数为0.1NAB.2.2g重水(D218O)中含有的中子数为1.2N AC.标准状况下，11.2L苯中含有碳原子数目为3N AD.1L 1mol/L CH3COONa 溶液中含CH3COO−的数目为N A6.能正确表示下列反应的离子方程式为（）A. 将大理石溶于醋酸中：2CH3COOH＋CaCO3===2CH3COO-+Ca2＋＋CO2↑＋H2OB.氯化铝溶液中加入过量的氨水：Al3+ + 4NH3·H2O = AlO2－+ 4 NH4++2H2OC.NH4HCO3溶于过量的NaOH溶液中：HCO3-+OH-=CO32-+H2OD．向Ba(OH)2溶液中滴加稀硫酸：Ba2＋＋OH－＋H＋＋SO42-=BaSO4↓＋H2O7.下列用来表示物质变化的化学用语中，正确的是（）A.钢铁发生电化学腐蚀的正极反应式:Fe﹣2e-=Fe2+B.HS- 的水解方程式:HS-+H 2O S2-+H3O+C.CO 32-的水解方程式:CO32-+H2O HCO3-+OH-D.AlCl3溶液与Na2CO3溶液混合:2Al3++3CO32-=Al2(CO3)3↓8．常温下，在由水电离产生的H+浓度为1×10-10mol•L-1的溶液中，一定能大量共存的离子组是（）A．K+、Fe2+、Cl-、NO3- B．Na+、Ca2+、Cl-、HCO3-C．K+、NH4+、Cl-、SO42- D．K+、Na+、Cl-、SO42-9．水的电离过程为H 2O H++OH，在25 ℃时，水的离子积为K w =1×10-14，在35℃时，水的离子积为K w =2.1×10-14，下列叙述正确的是()A．c(H＋)随温度的升高而降低B．35℃时，c（H+）>c（OH—）C.35℃时水的电离程度比25 ℃时水的电离程度小D．水的电离过程是个吸热过程10.下面是用已知的盐酸滴定未知浓度的氢氧化钠的实验叙述：①实验中的锥形瓶、滴定管都需润洗。

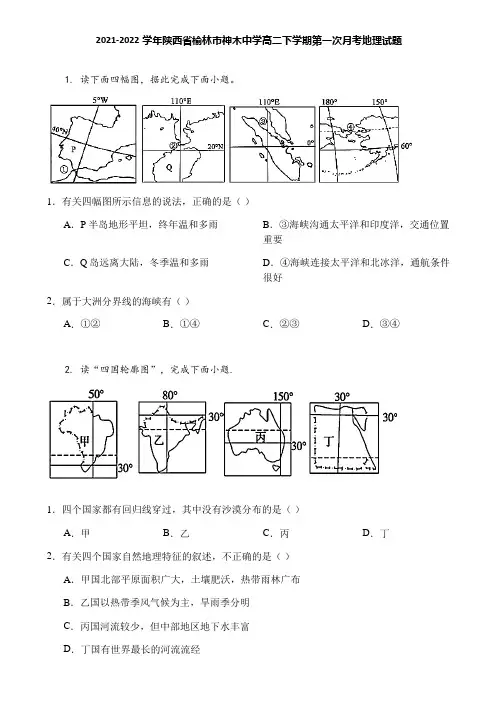
2021-2022学年陕西省榆林市神木中学高二下学期第一次月考地理试题1. 读下面四幅图，据此完成下面小题。

1．有关四幅图所示信息的说法，正确的是（）A．P半岛地形平坦，终年温和多雨B．③海峡沟通太平洋和印度洋，交通位置重要C．Q岛远离大陆，冬季温和多雨D．④海峡连接太平洋和北冰洋，通航条件很好2．属于大洲分界线的海峡有（）A．①②B．①④C．②③D．③④2. 读“四国轮廓图”，完成下面小题.1．四个国家都有回归线穿过，其中没有沙漠分布的是（）A．甲B．乙C．丙D．丁2．有关四个国家自然地理特征的叙述，不正确的是（）A．甲国北部平原面积广大，土壤肥沃，热带雨林广布B．乙国以热带季风气候为主，旱雨季分明C．丙国河流较少，但中部地区地下水丰富D．丁国有世界最长的河流流经3．有关四个国家经济特征的叙述，正确的是（）A．甲国是世界最大的咖啡和天然橡胶生产国B．乙国工业集中分布在东南沿海地区C．丙国是工矿业和农牧业发达的国家D．丁国最主要的经济支柱是长绒棉的生产和出口3. 以自然为中心的观念深深扎根于日本人心中，人们与自然无限亲近，又心怀敬畏。

顺应自然、融入自然是日本人自然观的核心。

完成下面小题。

1. 生食海鲜拉近了人与自然的距离，是日餐的突出特色。

从自然环境分析，是因为日本（）A．四面环海，海产品新鲜B．地形以山地为主C．属于雨热同期的季风气候D．河流短小、湍急2．日本人自然观中的“敬畏”，主要来自（）A．矿产资源贫乏B．气候变化多端C．多火山地震D．农业靠天吃饭3．能体现出日本人自然观的做法是（）A．节日穿着和服B．严格保护森林C．建造摩天大楼D．大量捕杀鲸鱼4. 有关美国东北部工业区的叙述，正确的是（）A．工业中心有洛杉矶、休斯敦等B．有五大湖及沿海便利的水运条件C．工业区内的“硅谷”是美国新兴的电子工D．为新兴工业区业中心5. 下图为芬兰部分地理事物分布图。

读图完成下面小题。

1．芬兰（）A．森林资源丰富，木材加工业发达B．山区水土流失严重，城镇数量少C．人口稀疏区以大牧场放牧业为主D．盛行西风，终年温和多雨2．燕麦种植北界呈图示走向，主要是由于该国（）A．东部地区河湖密布，灌溉条件好B．西部受暖流、地形影响，气温偏高C．东南部土层较深厚，耕作技术高D．西北部多晴朗天气，日照时间长6. 北半球的寒冷中心不在北极而在东西伯利亚山地的奥伊米亚康地区。

2013-2014年度第二学期阶段性检测高二生物2014.03第Ⅰ卷（选择题共60分）本卷包括30小题，每小题2分，每小题只有一个选项最符合题意。

1.将β－胡萝卜素合成途径中的相关基因导入水稻，可以使米粒中含有β－胡萝卜素，称为“金色大米”。

这种“金色大米”形成的全过程中不需要的酶是 ( )A．限制性内切酶 B．逆转录酶C．RNA聚合酶 D．DNA连接酶2.下列有关基因工程操作的叙述正确的是( )A．用同种限制酶切割运载体与目的基因可获得相同的黏性末端B．以蛋白质的氨基酸序列为依据合成的目的基因与原基因的碱基序列相同C．检测到受体细胞含有目的基因就标志着基因工程操作的成功D．用含抗生素抗性基因的质粒作为运载体是因为其抗性基因便于与外源基因连接3.下列有关质粒的叙述，正确的是( )A．质粒是广泛存在于细菌细胞中的一种颗粒状的细胞器B．质粒是细菌细胞质中能自主复制的小型环状DNA分子C．质粒只有在侵入宿主细胞后才能复制D．细菌的抗性基因一般位于拟核DNA上4.下图四种质粒含有E1和E2两种限制酶的识别位点，Ap r表示抗青霉素的抗性基因，Tc r表示抗四环素的抗性基因。

若将下图所示X－1、X－2、X－3、X－4四种质粒导入大肠杆菌，然后分别涂布在含有青霉素或四环素的两种培养基上。

在这两种培养上均能生长的大肠杆菌细胞类型是A．含X－1的细胞 B．含X－4的细胞 C．含X－3的细胞 D．含X－2的细胞5. 限制酶是一种核酸切割酶，可辨识并切割DNA分子上特定的核苷酸碱基序列。

下图为四种限制酶BamHI，EcoRI，HindⅢ以及BglⅡ的辨识序列。

箭头表示每一种限制酶的特定切割部位，其中哪两种限制酶所切割出来的DNA片段末端可以互补黏合？其正确的末端互补序列为何？A. BamHI和EcoRI；末端互补序列—AATT—B. BamHI和HindⅢ；末端互补序列—GATC—C. EcoRI和HindⅢ；末端互补序列—AATT—D. BamHI和BglII；末端互补序列—GATC—6.科学家为提高玉米中赖氨酸含量，计划将天冬氨酸激酶的第352号苏氨酸变为异亮氨酸，将二氢吡啶二羧酸合成酶中第104号的氨基酸由天冬氨酸变成异亮氨酸，就可以使玉米叶片和种子中游离赖氨酸含量分别提高5倍和2倍，下列对蛋白质的改造，操作正确的是A ．直接对原有的蛋白质进行加工改造B ．直接改造相应的mRNAC ．对相应的基因进行操作D ．重新合成新的基因7.下面的简式表示植物组织培养的大致过程，据此判断不正确的是( )①――→脱分化②――→再分化③――→④A ．若①是来自不同植物体细胞融合的杂种细胞，则④可能出现不同植物的遗传特性B ．若①是花粉，则④是单倍体植株，经染色体加倍后可得到稳定遗传的品种C ．若①是人参细胞，对②进行扩大培养可提高细胞产物人参皂甙的产量D ．若①是具有杂种优势的农作物细胞，则用③进行繁育会发生性状分离8.下列过程不需要应用植物组织培养技术的是( )A.脱毒马铃薯植株的培养B. 制造“人工种子”C.白菜－甘蓝杂种植株的培育D.八倍体小黑麦的培育9.下列关于单克隆抗体的应用的说法中，不正确的是A ．可以准确地识别抗原B ．可以用于治疗癌症C ．可以制成“生物导弹”D ．单克隆抗体的缺陷是不能大量制备10. 下列有关PCR 技术的叙述，正确的是A ．PCR 建立在对扩增的目的基因序列完全已知的基础上B ．该技术需要解旋酶和热稳定的DNA 聚合酶C ．该技术应用体内DNA 双链复制原理，也需要模板、原料、能量、酶等条件D ．该技术需要一对特异性的引物，要求一对引物的序列是互补的11.下列关于生殖细胞的发生和受精过程的叙述错误的是 （ ）A ．雄原核形成的同时，卵子完成减数第二次分裂B ．卵细胞需要经过类似于精子获能的过程C ．精子与卵黄膜相互融合，精子入卵D ．卵子是从动物的初情期开始，经过M Ⅰ和M Ⅱ两次连续分裂形成的12.试管婴儿、试管苗和克隆羊三者均属于生物工程技术的杰出成果，下面叙述正确的( )A ．都属于无性生殖能保持母本性状B ．都需要细胞工程的技术C ．都充分体现了体细胞的全能性D ．都不会发生基因重组和变异13.下列有关生物工程叙述，不正确的是 ( )A ．进行胚胎移植时，可选用右图所示时期的胚胎或卵裂球或桑椹胚B ．高等动物的胚胎发育是指从受精卵发育到幼体的过程C ．右图是胚胎发育过程中囊胚示意图，其中③为内细胞团细胞，具有发育全能性D ．进行胚胎分割时，应选择原肠胚期的胚胎进行14.下列关于干细胞的叙述中，正确的是 ( )A ．胚胎干细胞在形态上表现为体积大，细胞核小，核仁明显B ．干细胞分化形成不同组织细胞是基因选择性表达的结果C ．异体造血干细胞移植成功后，不影响患者的血型D ．肝脏干细胞分化形成肝脏细胞的过程表现了细胞的全能性15．胚胎工程的最终技术环节是A ．细胞融合B ．体外受精C ．胚胎移植D ．胚胎分割16．次级卵母细胞的第二次成熟分裂完成于A ．排卵前，在卵巢内 B. 受精前，在输卵管内17．一般情况下，下列细胞的分化程度由高到低的顺序依次是①神经细胞②受精卵③胚胎干细胞④造血干细胞A．②③④① B．③①②④ C．①④②③ D．①④③②18．植物组织培养过程中可以形成愈伤组织，下列有关愈伤组织的叙述错误的是A．愈伤组织是离体细胞经过脱分化形成的B．形成愈伤组织的培养基不需含有机分子C．愈伤组织可以形成具有生根能力的胚状结构D．愈伤组织细胞的线粒体和核糖体可能发生碱基互补配对19. 下列关于细胞全能性的说法错误的是A. 细胞具有全能性的原因是生物体细胞具有使后代细胞形成完整个体的潜能B. 植物细胞表现出全能性的必要条件是脱离母体后，给予适当的营养和外界条件C. 生物体内细胞没有表现出全能性，原因是基因表达有选择性D. 细胞全能性是受精卵大于生殖细胞大于体细胞20．某同学在进行植物组织培养过程中，发现只分裂而不分化出芽和根，最可能的原因是A．未见阳光B．培养时间不够C．培养基营养过多D．细胞分裂素和生长素配比不对21．下列选项中能正确说明生物工程技术应用的是A．植物组织培养是指离体的植物器官或细胞进行脱分化形成新个体B．细菌质粒是基因工程常用的运载体C．人工诱变、细胞工程、基因工程等都能对微生物进行定向改造D．动物细胞融合技术的最重要用途是培养具有双亲优良性状的经济动物22．下列有关细胞工程的叙述，错误的是A．在制备单克隆抗体过程中，杂交瘤细胞既可在体外培养又可在体内培养B．在植物体细胞杂交中，常用灭活的病毒诱导原生质体融合C．动物细胞培养所用的培养液中通常含有动物血清D．一株盛开菊花的不同部位的细胞，离体培养形成的愈伤组织基因可能不同23．下列关于利用胚胎工程技术繁殖优质奶羊的叙述，错误的是A．对受体母羊与供体母羊进行同期发情处理B．人工授精后的一定时间内，收集供体原肠胚用于胚胎分割C．可以用促性腺激素促进供体母羊超数排卵D．受体对移入子宫的外来胚胎基本上不发生免疫排斥反应24．某研究小组为测定药物对体外培养细胞的毒性，准备对某种动物的肝肿瘤细胞（甲）和正常肝细胞（乙）进行动物细胞培养。