角平分线性质定理及逆定理的证明
- 格式:doc
- 大小:165.50 KB
- 文档页数:2

角平分线的性质定理及其逆定理定理一、角平分线的性质定理及其逆定理1.角平分线的性质定理:角平分线上的点到这个角的两边的距离相等。
2.角平分线的逆定理:在角的内部,且到角的两边距离相等的点,在这个角的平分线上。
不难发现,定理1的条件是定理2的结论,同时它的结论又是定理2的条件,它们互为逆定理。
定理1说明了角平分线上点的纯粹性,即:只要是角平分线上的点,它到此角两边一定等距离,而无一例外;定理2反映了角平分线的完备性,即只要是到角两边距离相等的点,都一定在角平分线上,而绝不会漏掉一个。
在实际应用中,前者用来证明线段相等,后者用来证明角相等或证明点在一个角的平分线上。
用数学语言可表示如下:例题一:(1)∵OC平分∠AOB,点P在射线OC上,PD⊥OA于D,PE⊥OB于E∴PD=PE(定理1)(2)∵PD⊥OA,PE⊥OB,PD=PE∴OC平分∠AOB(定理2)例题二:如图,△ABC的ㄥB平分线BD与ㄥC的外角的平分线CE相较于点P。
求证:点P到三边AB、BC、CA所在直线的距离相等。
从P点向边AB做垂线,垂足为F,向BC边作垂线,垂足为G,向AC边作垂线,垂足为H因为BD是角ABC的角平分线所以PF=PG因为CE是角ACB的外角平分线所以PH=PG所以PF=PG=PH即,点P到三这AB,BC,CA所在直线的距离相等从P点向边AB做垂线,垂足为F,向BC边作垂线,垂足为G,向AC边作垂线,垂足为H因为BD是角ABC的角平分线所以PF=PG因为CE是角ACB的外角平分线所以PH=PG所以PF=PG=PH即,点P到三这AB,BC,CA所在直线的距离相等这题对吗?。


初二数学角的平分线的性质及其逆定理通用版【本讲主要内容】角的平分线的性质及其逆定理【知识掌握】 【知识点精析】1. 角的平分线上的点到角的两边的距离相等;2. 到角的两边的距离相等的点在角的平分线上。
以上两个定理互为逆定理,要正确加以区分,性质1是指如果一个点在一个角的平分线上,可以得出它到角的两边的距离相等; 而性质2却与它恰好相反,如果一个点到角的两边距离相等,那么它的位置一定在这个角的平分线上。
通俗地说,性质1是先知点的位置,得到它的性质;性质2先由点满足某个性质,再确定它的位置。
【解题方法指导】例1. 已知:如图所示,E 是AD 上一点,∠=∠⊥⊥BAD CAD EB AB EC AC ,,。
求证:∠=∠DBE DCE分析:欲证∠=∠DBE DCE ,只要证DBE ∆≌DCE ∆即可。
由于DE 是它们的公共边,只要证出BE=CE ,∠=∠BED CED 即可,或证出BD=CD 。
已知AE 是∠BAC 的平分线,EB AB EC AC ⊥⊥,,可得出EB EC =,由∠=∠AEB AEC ,可得∠=∠BED CED 。
至此思路已通。
证明:∵AC EC AB EB CAD BAD ⊥⊥∠=∠,,∴=EB EC (角的平分线上的点到角的两边的距离相等)∵ABE BAE BED ∠+∠=∠,∠=∠+∠CED CAE ACE (三角形的外角等于不相邻的两个内角的和)DEDE CED BED =∠=∠∴又BDE ∆∴≌)(SAS CDE ∆ DCE DBE ∠=∠∴评析:如果由两次三角形全等来解决此题,实际上是把角平分线的性质又重新证了一遍,走了一个弯路,因此可直接由角平分线的性质,得出EB=EC 。
例2. 已知:如图所示,△ABC 中,D 是BC 的中点,F AC DF E AB DE 于,于⊥⊥,BE=CF 。
求证:AD 平分∠BAC 。
B D C分析:欲证AD 平分∠BAC ,由于DE ⊥AB ,DF ⊥AC ,因此只要证明DE=DF 即可,可通过△BDE ≌△CDF 加以解决。


角平分线得性质定理及其逆定理一、基础概念学习目标:掌握角平分线得性质定理及其逆定理得证明与简单应用,掌握尺规作图做角平分线,规范证明步骤。
(1)角平分线得性质定理证明:角平分线得性质定理:角平分线上得点到这个角得两边得距离相等。
证明角平分线得性质定理时,将用到三角形全等得判定公理得推论:推论:两角及其中一角得对边对应相等得两个三角形全等。
(AAS)推导过程:已知:OC平分∠MON,P就是OC上任意一点,PA⊥OM,PB⊥ON,垂足分别为点A、点B.求证:PA=PB.证明:∵PA⊥OM,PB⊥ON∴∠PAO=∠PBO=90°∵OC平分∠MON∴∠1=∠2在△PAO与△PBO中,∴△PAO≌△PBO∴PA=PB②几何表达:(角得平分线上得点到角得两边得距离相等)如图所示,∵OP平分∠MON(∠1=∠2),PA⊥OM,PB⊥ON,∴PA=PB.(2)角平分线性质定理得逆定理:到一个角得两边距离相等得点,在这个角得平分线上。
推导过程已知:点P就是∠MON内一点,PA⊥OM于A,PB⊥ON于B,且PA=PB.求证:点P在∠MON得平分线上.证明:连结OP在Rt△PAO与Rt△PBO中,∴Rt△PAO≌Rt△PBO(HL)∴∠1=∠2∴OP平分∠MON即点P在∠MON得平分线上.②几何表达:(到角得两边得距离相等得点在角得平分线上.)如图所示,∵PA⊥OM,PB⊥ON,PA=PB∴∠1=∠2(OP平分∠MON)(3) 角平分线性质及判定得应用①为推导线段相等、角相等提供依据与思路;②实际生活中得应用.例:一个工厂,在公路西侧,到公路得距离与到河岸得距离相等,并且到河上公路桥头得距离为300米.在下图中标出工厂得位置,并说明理由.(4)角平分线得尺规作图活动三:观察与思考: 尺规作角得平分线观察下面用尺规作角得平分线得步骤(如图),思考这种作法得依据。
步骤一:以点O为圆心,以适当长为半径画弧,弧与角得两边分别交于A,B两点。



线段垂直平分线、角平分线和等腰三角形的性质知识点梳理1、 线段垂直平分线性质定理及其逆定理:定理:线段垂直平分线上的任意一点到这条线段两个端点的距离相等. 逆定理:和一条线段两个端点距离相等的点,在这条线段的直平分线上.2、 角平分线的性质定理及其逆定理:定理:在角的平分线上的点到这个角两边的距离相等.逆定理:在一个角的内部(包括顶点)且到这个角两边距离相等的点,在这个角的平分线上.D21P CABEO1、 等腰三角形的性质等边对等角:等腰三角形的两个底角相等。
三线合一:等腰三角形的顶角的平分线,底边上的中线,底边上的高的重合 证明以下推论:等腰三角形的两底角的平分线相等; 两条腰上的中线相等; 两条腰上的高相等。
等腰三角形的一腰上的高与底边的夹角等于顶角的一半4、 等腰三角形的判定:等角对等边:有两个角相等的三角形是等腰三角形 ◆ 命题、公理、定理命题:判断性的语句 陈述句,一般由题设和结论组成,写成“如果……,那么……”的形式 几个重要的公理(不需证明): (1) 两点之间线段最短;(2) 过直线外一点有且只有一条直线与已知直线平行 (3) 过一点有且只有一条直线与已知直线垂直;(4) 同位角相等,两直线平行; (5)两直线平行,同位角相等。
1、已知:如图,∠ABC ,∠ACB 的平分线交于F ,过F 作DE ∥BC ,交AB 于D ,交AC 于E 。
求证:BD +EC =DE 。
2、已知:如图所示△ABC ,∠ACB=90°,D 为BC 延长线上一点,E 是AB 上一点,EM 垂直平分BD ,M 为垂足,DE 交AC 于F ,求证:E 在AF 的垂直平分线上.3、如图,已知:CD 、CE 分别是AB 边上的高和中线,且ACE ECD DCB ∠=∠=∠。
求证:90o ACB ∠=CA4、如图,已知:在,90,30ooABC C A ∆∠=∠=中,DE 垂直平分AB ,FM 垂直平分AD ,GN 垂直平分BD 。

19.5(1)角的平分线(角平分线的性质定理及逆定理) 要点归纳1.角平分线的性质定理给我们提供了证明两条线段相等的又一个重要方法,而且在已知中有角平分线时,往往在角平分线上选择适当的点向角的两边作垂线段。
2.角平分线性质定理的逆定理是证明两个角相等的一个重要方法。
3.利用以上两个定理可以得到:三角形三个角的平分线交于一点,且这点到三角形三边的距离相等。
疑难分析例1 已知:如图,BN 平分∠ABC ,P 为BN 上一点,PD ⊥BC 于点D ,AB+BC=2BD. 求证:∠BAP 与∠BCP 互补。
例2 已知:如图,在Rt △ABC 中,AD 是斜边BC 上的高,BF 平分∠ABC ,交AC 于点F 、AD 于点E ,EG ∥BC 交AC 于点G 。
求证:AF=CG 。
BB C A D基础训练1. ∠AOB 的平分线上的一点M ,点M 到OA 的距离为1.5厘米,则点M 到OB 的距离为____;2. 如图,∠AOB=60°,CD ⊥OA 于点,CE ⊥OB 于点E ,且CD=CE ,则∠DOC 的度数为____;(第2题) (第3题) (第4题)3. 如图,在△ABC 中,∠C=90°,AD 是∠BAC 的平分线,DE ⊥AB 于点E ,且DE=3厘米,BD=5厘米,则BC=____厘米;4. 如图,CD 为△ABC 斜边上的高,∠BAC 的平分线分别交CD 、CB 于点E 、F ,FG ⊥AB ,垂足为G ,若CF=3厘米,则CE=____;OBA B A B E D G5. 如图,已知AB 、CD 相交于点E ,过点E 作∠AEC 及∠AED 的平分线PQ 与MN ,则直线MN 与PQ 的位置关系是____;(第5题) (第6题) (第7题)6. 如图,在△ABC 中,∠ACB=90°,BE 平分∠ABC ,DE ⊥AB 于点D ,如果AC=3厘米,那么AE+DE 等于( )A. 2厘米B. 3厘米C. 4厘米D. 5厘米7. 如图,已知AB=AC ,AE=AF ,BE 与CF 交于点D ,则①△ABE ≌△ACF ;②△BDF ≌△CDE ;③D 在∠BAC 的平分线上。
角平分线的定理及其逆定理在几何学中,角平分线是一条穿过一个角的中点,且与角的两条边平分的直线。
它也可以定义为一个不断变化的折线,它的关键特性是它的内部角平分线的链接。
角平分定理可以被描述为:穿过一个多边形上任意两点的直线,如果该直线将角分为两个部分,其中一部分是锐角,另一部分是钝角,则该直线与角的两条边平分。
角平分定理的逆定理可以这样表述:如果一条直线穿过一个多边形上的任意两点,并且将角分为两个部分,其中一部分由钝角构成,另一部分由锐角构成,则该直线与角的两条边不会平分。
角平分定理的形式有很多,可以有效地应用于不同的情境,也可以有助于帮助解决问题。
例如,角平分定理可以用来求解正多边形上两个点之间的距离,这对于解决建筑和绘图等应用场景是非常有用的。
角平分定理也可以用来求解圆周率π的值。
把圆分成四等份,用角平分定理就可以求出它的圆周率π的值,并且也是一种实用的应用场景。
角平分定理可以在几何构造中得到有效的应用,例如,可以使用它来构建一个正方形,也可以将正方形分割成四个角,使其分别被一条角平分线分割。
在三角形中,角平分定理也可以用来解决多项问题。
例如,如果想知道一个三角形中某个角的度数,那么可以使用角平分定理,来表达该角的度数。
另外,角平分定理也有助于解决三角形的角的余弦公式的计算问题。
在多边形的几何构造中,角平分定理也有着独特的应用,例如,可以使用角平分定理解决一个多边形内角的总和的问题,也可以利用角平分定理求解多边形的内角的度数。
角平分定理也可以在数学函数中得到应用,例如,可以使用它来解决弦长公式或圆周上任意两点间距离的求解问题,以及采用它解决抛物线等几何函数的计算问题。
综上所述,角平分定理及其逆定理在几何学中有着广泛的应用,可以帮助人们解决多种几何问题,甚至在数学函数中也有很多实用的应用场景。
24.8角平分线的性质定理及其逆定理教学设计教学设计思想通过前面的学习已经探究出角平分线上的点所具有的性质,本节学习对这个性质进行证明.让学生完成对三角形全等的判定公理的推论的证明,进而应用这个公理完成对角平分线性质定理的证明,对于平分线的性质定理的逆定理仿照上节课处理线段垂直平分线逆命题的思路,引导学生解决与定理和逆定理的有关问题.对于尺规作角平分线,要让学生明白每步做法的依据.最后通过例题的学习来巩固这些知识点.教学目标知识与技能总结角平分线的性质定理及其逆定理的证明并能灵活应用它们进行有关的计算和证明;说出用尺规作角平分线的依据;能够熟练地按照证明的格式和步骤对一些命题进行证明.过程与方法经历用尺规作角平分线的过程;经历寻找证明、作图思路的过程,进一步发展推理证明意识和能力;情感态度价值观通过观察、类比、对比、归纳等方法尝试从不同角度分析问题,形成不同的策略;愿意动手操作,并和同伴交流,形成不同意见.教学重点和难点重点是角平分线的性质定理和逆定理的证明及其应用;难点是角平分线的性质定理和逆定理的应用.解决办法:通过例题的学习,分析出解题的思路,总结出做题的方法.教学方法启发引导、小组讨论课时安排1课时教具学具准备投影仪或电脑、三角板教学过程设计(一)角平分线的性质定理我们已经探究出角平分线上的点所具有的性质,怎样对这个性质进行证明呢?角平分线的性质定理角平分线上的点到这个角的两边的距离相等.证明角平分线的性质定理时,我们将用到三角形全等判定公理的推论:推论两角及其中一角的对边对应相等的两个三角形全等(AAS).做一做证明三角形全等判定公理的推论.注:让学生独立按照证明的格式完成对“AAS”定理的证明,作为证明本节定理的依据.证明略.利用上面你已经证明的推论,可以对角平分线的性质定理给出如下的证明.已知:如下图,OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别为D,E.求证:PD=PE.证明:∴OC是∠AOB的平分线(已知),∴∠1=∠2(角平分线的定义).∵PD⊥OA,P E⊥OB(已知),∴∠PDO=∠PEO=90°(垂直的定义).在△PDO和△PEO中,∠PDO=∠PEO (已证),∠1=∠2(已证),OP=OP(公共边),∴△PDO≌△PEO (AAS).∴PD=PE(全等三角形的对应边相等).(二)角平分线性质定理的逆定理做一做1.请写出角平分线性质定理的逆命题.2.请根据逆命题的内容,画出图形,并结合图形,写出已知和求证.3.写出证明过程.注:类比“线段垂直平分线的性质定理及其逆定理”的学习过程,让学生独立完成“做一做”中提出的问题.这样,我们就得到:角平分线性质定理的逆定理到一个角的两边距离相等的点,在这个角的平分线上.(三)尺规作角的平分线观察与思考观察下面用尺规作角的平分线的步骤(如下图),思考这种作法的依据.步骤一:以点O为圆心,以适当长为半径画弧,弧与角的两边分别交于A,B两点.步骤二:分别以点A,B为圆心,以固定长(大于AB长的一半)为半径画弧,两弧交于点C步骤三:作射线OC,则OC就是∠AOB的平分线.注:独立完成用尺规作角平分线的过程,进一步培养学生的操作能力,并能说出作图过程中每步的依据.依据是“SSS”公理和全等三角形的对应角相等.(四)练习1.已知:如图,△ABC的角平分线BM,CN相交于点P.求证,点P到三条边AB,BC,CA的距离相等.2.在△A BC中,∠B=∠C,点D为BC边的中点,DE⊥AB,DF⊥AC,垂足分别是E,F.求证:点D在∠A的平分线上.1.提示:过点P分别向△ABC三边作垂线,由角平分线的性质定理及其逆定理即可证明结论.2.提示:先证△BD E≌△CDF(AAS). 再由角平分线的性质定理及其逆定理即可得到结论.(五)小结引导学生总结本节的主要知识点.(六)板书设计角平分线的性质定理及其逆定理角平分线的性质定理及其证明角平分线的性质定理的逆定理及其证明角平分线的画法练习。
角平分线的性质及其逆定理1、 如图,已知点D 是∠ABC 的平分线上一点,点P 在BD 上,PA ⊥AB ,PC ⊥BC ,垂足分别为A ,C .求证:DA= DC (性质定理)2、已知:如图,AC 平分∠BAD ,CE ⊥AB 于E ,CF ⊥AD 于F ,且BC =DC .你能说明BE 与DF 相等吗? 解:BE=DF∵CE ⊥AB, CF ⊥AD (已知)∵AC 平分∠BAD(已知)∴CE= CF ( )在Rt △CDF 和Rt △CBE 中CE= CF__________(已知)∴Rt △CDF ≌Rt △CBE ( )∴__________________( ) 3、 如图,△ABC 中,AD 为∠BAC 的平分线,DE ⊥AB ,DF ⊥AC ,E 、F 为垂足,在以下结论中:①△ADE ≌△ADF ;②△BDE ≌△CDF ;③△ABD ≌△ACD ;④AE =AF ;⑤BE =CF ; ⑥BD =CD .其中正确结论的个数是( )A .1B .2C .3D .4FD E C B AA BC D E FE F C B A D (第3题)4、如图,CD ⊥AB 于D ,BE ⊥AC 于E ,CD ,BE 交于点O ,且∠1=∠2 ,求证:OB =OCO 21DEB CA5 、 已知:如图,在四边形ABCD 中,BC >AB ,AD =DC ,BD 平分∠ABC.求证:∠A+∠C =180度1、判断:(1)如图:OP 是∠AOB 的平分线,则PE=PF ( )(2)如图 :PE ⊥OA 于E ,PF ⊥OB 于F ,则 PE=PF ( )(3)在∠AOB 的平分线上任取一点Q ,点Q 到OA 的距离等于3cm,则点Q 到OB 距离等于3cm ( )2、三角形中到三边距离相等的点是( )A .三条边的垂直平分线的交点B .三条高的交点C .三条中线的交点D .三条角平分线的交点3、如图,在△ABC 中,AD 为∠BAC 的平分线,DE ⊥AB 于E ,DF ⊥AC 于F ,△ABC 面积是28 cm 2,AB=20cm ,AC=8cm ,则DE 的长为_________ cm .4、在三角形ABC 中,∠ACB=90゜,AC=5,BC=12,AB=13,三条角平分线交于P 点,PE ⊥AB 于E,则PE=________ FO B。
角的平分线的定理和逆定理一、角的平分线的定理角的平分线的定理是几何学中的一个重要定理,它指出:如果一条直线通过一个角的顶点,并且把这个角分成两个相等的部分,那么这条直线就是这个角的平分线。
简而言之,角的平分线将一个角分为两个相等的角。
具体来说,设有一个角AOC,直线OB通过角的顶点O,并且将角AOC分成两个相等的角AOB和BOC。
那么我们可以得出结论:直线OB就是角AOC的平分线。
为了证明这个定理,我们可以使用等角的性质。
首先,根据等角的定义,我们可以得出两个角AOB和BOC相等。
其次,根据角的定义,我们可以得出AOB+BOC=BOC+COA,即AOB=COA。
因此,直线OB平分了角AOC。
角的平分线定理在解决几何问题时非常有用。
通过找到角的平分线,我们可以将一个角分成两个相等的部分,从而简化问题的求解过程。
这个定理在证明其他定理时也经常被使用。
二、角的平分线的逆定理角的平分线的逆定理是角的平分线定理的逆命题,也就是说,如果一条直线通过一个角的顶点,并且将这个角分成两个相等的部分,那么这条直线就是这个角的平分线。
具体来说,设有一个角AOC,直线OB通过角的顶点O,并且将角AOC分成两个相等的角AOB和BOC。
那么我们可以得出结论:直线OB是角AOC的平分线。
为了证明这个逆定理,我们可以使用等角的性质。
首先,根据等角的定义,我们可以得出两个角AOB和BOC相等。
其次,根据角的定义,我们可以得出AOB+BOC=BOC+COA,即AOB=COA。
因此,直线OB 平分了角AOC。
角的平分线的逆定理在解决几何问题时也非常有用。
通过已知角的两个相等的部分,我们可以确定角的平分线的位置,从而进一步求解其他相关问题。
三、应用实例下面我们通过一个实例来应用角的平分线定理和逆定理。
例题:在平面上,给定三个点A、B和C,要找到一个点P,使得角APB和角BPC相等。
解题思路:根据题目中的要求,我们需要找到一个点P,使得角APB 和角BPC相等。
A P
B F E C
角平分线的性质与判定
教学目标:
1、 能够对角平分线的性质定理及逆定理进行严密的证明。
2、 能够灵活运用两个定理进行相关问题的计算或者证明。
教学重点:定理的证明及应用。
教学难点:定理的证明。
教学过程: 一.复习引入:
在第二章,我们利用角的轴对称性质,通过实验的方法,探索出了角平分线的性质。
你还记得角平分线的性质吗?你能用推理的方法证明它们的真实性吗? 角平分线的性质:___________________________________________________ 角平分线的性质的逆命题是: 二、新课学习: 知识点一、证明:角平分线上的点到这个角的两边的距离相等. 已知:OE 是∠AOB 的平分线,F 是OE 上一点,若CF ⊥OA 于点C ,DF ⊥OB 于点D 求证:CF =DF. 证明: 应用格式: 例 1.已知:如图,点B 、C 在∠A 的两边上,且AB=AC ,P 为∠A 内一点,PB=PC , PE ⊥AB ,PF ⊥AC ,垂足分别是E 、F 。
求证:PE=PF
知识点二、证明:到线段两个端点距离相等的点在这条线段的垂直平分线上。
已知:如图5,点P 在∠AOB 的内部,且PC ⊥OA 于C ,PD ⊥OB 于D ,PC =PD 求证:点P 在∠AOB 的平分线上. 证明:
应用格式: 例2. 已知: PA 、PC 分别是△ABC 外角∠MAC 和∠NCA 平分线,它们交于P ,PD ⊥BM 于D ,PF ⊥BN 于F ,求证:BP 为∠MBN 的平分线。
知识点三. 关于三角形三条角平分线交点的定理:
三角形三条角平分线相交于一点,并且这一点到三边的距离相等. 已知:如图6,AP 、BQ 、CR 分别是△ABC 的内角∠BAC 、∠ABC 、∠ACB 的平分线 求证:① AP 、BQ 、CR 相交于一点I ;② 若ID 、IE 、IF 分别垂直于BC 、CA 、AB 于点D 、E 、F ,则DI =EI =FI. 证明:
三、课堂总结:总结本节课的收获 四.课堂检测 1、有一点P 到三角形三条边的距离相等,则点P 一定是 的交点 2.如图2,在△ABD 中,AD=4,AB=3,AC 平分∠BAD ,则= 图4D
O B F E F
D I
P R
Q
A
3.如图3,在△ABC中,∠C=,AD平分∠BAC,DE⊥AB于E,则下列结论:①AD
平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB 。
其中正确的有
4.如图4,AD∥BC,∠D=,AP平分∠DAB,PB平分∠ABC,点P恰好在CD上,则PD与PC的大小关系是PD PC
5、如图所示,在△ABC中,∠BAC=90°,AD⊥BC于D,BE平分∠ABC交AD于E,F
在BC上,并且BF=AB,则下列四个结论:①EF∥AC,②∠EFB=∠BAD,③AE=EF,
④△ABE≌△FBE,其中正确的结论有
5题图 6题图 7题图
6、如图所示,在中,∠C=90°, AC=4㎝,AB=7㎝,AD平分∠BAC交BC
于D,DE⊥AB于E,则EB的长是
7、随着人们生活水平的不断提高,汽车逐步进入到千家万户,小红的爸爸想在本镇
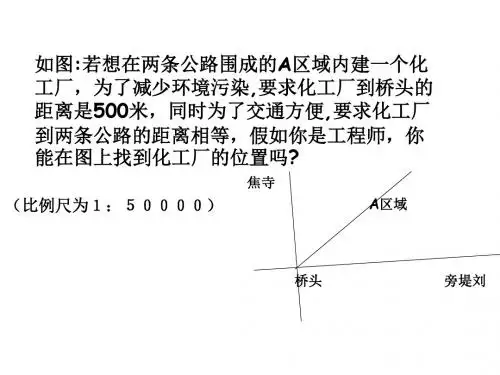
的三条相互交叉的公路(如图所示),建一个加油站,要求它到三条公路的距离相等,这样可供选择的地址有()处。
A、1 B、2 C、3 D、4 8、已知:如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.
求证:(1)∠PAB=∠PBA (2)OP垂直平分AB (3)OA=OB
五.课下作业:
A.作业精,80-81页中,5-8题,13-16题
B.1.如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,
PS⊥AC,垂足分别是R、S.若AQ=PQ,PR=PS,下列结论:
①AS=AR;②PQ∥AR;③△BRP≌△CSP.其中正确的是( ).
(A)①③ (B)②③ (C)①② (D)①②③
2.如图,△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,垂
足分别是E、F,则下列四个结论中:①AD上任意一点到B、C
的距离相等;②AD任意一点到AB、AC的距离相等;③AD⊥BC
且BD=CD;④∠BDE=∠CDF.其中正确的是( ).
(A)②④ (B) ②④ (C)②③④ (D)①②③④
3.已知:如图,∠C=900,AC=BC,AD是∠BAC的角平分线.求证:AC+CD=AB.
4、如图13,△ABC中,P、Q分别是BC、AC上的点,PR⊥AB于R,
PS⊥AC于S,若AQ=PQ,RP=PS。
则PQ与AB是否平行?请说
明理由.
5、已知:如图,在四边形ABCD中,对角线BD平分∠ABC,且∠BAD与∠BCD互补
求证:AD=CD.。