8第八章重组讲义体的筛选

山东理工大学教案第次课教学课型：理论课□ 实验课□ 习题课□实践课□ 技能课□ 其它□主要教学内容（注明：* 重点 # 难点 ）：第八章 立体化学§8-1 手性和对映体*§8-2 旋光性和比旋光度*§8-2 含一个手性碳原子的化合物的对映异构*§8-4 构性表示法确定和标记*§8-5 含多个手法碳原子化合物的立体异构#§8-6 外消旋体的拆分(自学)§8-7 手性合成§8-8 环状化合物的立体异构教学目的要求：1．掌握偏振光、旋光性、比旋光度。

2．掌握手性、对映性、非对映性，内消旋体、外消旋体和不对称性等概念。

3．掌握fischer投影的规则和使用，以及fischer投影式和Newman式，楔形式的转换。

4．掌握含有一个和二个手性碳原子的手性分子的R/S标记法。

5．理解对称元素和对称操作，识别指定结构的对称元素。

6．理解对映异构体理化性质差异及外消旋体的化学拆分原理。

7．了解构型的D、L标记法及手性在自然界的意义。

8．了解手性合成、环状化合物的立体异构。

9．能运用立体化学知识解释烯烃亲电加成反应历程。

教学方法和教学手段：本课程以课堂讲授为主，结合必要的课堂讨论。

教学手段以板书和多媒体相结合。

讨论、思考题、作业：教材：1、①③⑤⑦；3；6、①②；9。

思考：7参考资料：1．邢其毅等，《基础有机化学》.高等教育出版社，19932．胡宏纹主编《有机化学》高等教育出版社19903．王积涛等《有机化学》 南开大学出版社 19934（美）莫里森、博伊德编《有机化学》（第二版），复旦大学化学系有机化学教研室译，科学出版社，1993年。

第八章立体化学对映异构现象的发现早在十九世纪就发现许多天然的有机化合物如樟脑、酒石酸等晶体有旋光性，而且即使溶解成溶液仍具有旋光性，这说明它们的旋光性不仅与晶体有关，而且与分子结构有关。

1848年巴斯德（L.Pasteur）在研究酒石酸钠铵的晶体时发现，没有旋光性的酒石酸钠铵在一定条件下结晶时可生成外形不同的两种晶体，它们之间的关系相当于右手和左手的关系，外形相似，但不能互相重叠。

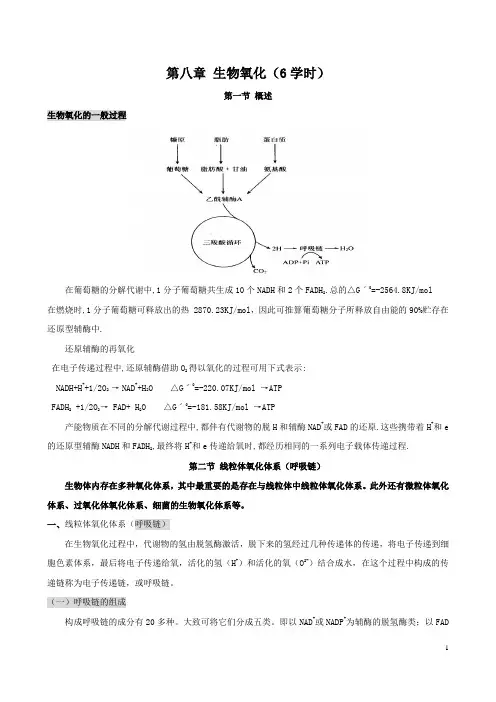
第八章生物氧化（6学时）第一节概述生物氧化的一般过程在葡萄糖的分解代谢中,1分子葡萄糖共生成10个NADH和2个FADH2.总的△Gˊ0=-2564.8KJ/mol在燃烧时,1分子葡萄糖可释放出的热 2870.23KJ/mol，因此可推算葡萄糖分子所释放自由能的90%贮存在还原型辅酶中.还原辅酶的再氧化在电子传递过程中,还原辅酶借助O2得以氧化的过程可用下式表示:NADH+H++1/2O2 →NAD++H2O △Gˊ0=-220.07KJ/mol →ATPFADH2 +1/2O2→ FAD+ H2O △Gˊ0=-181.58KJ/mol →ATP产能物质在不同的分解代谢过程中,都伴有代谢物的脱H和辅酶NAD+或FAD的还原.这些携带着H+和e 的还原型辅酶NADH和FADH2,最终将H+和e传递给氧时,都经历相同的一系列电子载体传递过程.第二节线粒体氧化体系（呼吸链）生物体内存在多种氧化体系，其中最重要的是存在与线粒体中线粒体氧化体系。

此外还有微粒体氧化体系、过氧化体氧化体系、细菌的生物氧化体系等。

一、线粒体氧化体系（呼吸链）在生物氧化过程中，代谢物的氢由脱氢酶激活，脱下来的氢经过几种传递体的传递，将电子传递到细胞色素体系，最后将电子传递给氧，活化的氢（H+）和活化的氧（O2-）结合成水，在这个过程中构成的传递链称为电子传递链，或呼吸链。

（一）呼吸链的组成构成呼吸链的成分有20多种。

大致可将它们分成五类。

即以NAD+或NADP+为辅酶的脱氢酶类；以FAD或FMN为辅基的黄素蛋白酶类；铁硫蛋白类；泛醌和细胞色素类。

依具体功能又可分为递氢体和递电子体。

1．递氢体在呼吸链中即可接受氢又可把所接受的氢传递给另一种物质的成分叫递氢体，包括：（1）NAD+NAD+是不需氧脱氢酶的辅酶。

它们分别可与不同的酶蛋白组成多种功能各异的不需氧脱氢酶。

辅酶分子能可逆地加氢和脱氢。

NAD++2H++2e-→NADH+H+（2）FAD和FMNFAD和FMN是黄素蛋白（又称黄素酶）类的辅基。

正保远程教育旗下品牌网站美国纽交所上市公司(NYSE:DL)中华会计网校会计人的网上家园注册会计师考试辅导《税法》第八章讲义2应税收二、确定增值额的扣除项目（一）对于新建房地产转让，可扣除：1.取得土地使用权所支付的金额，包括：（1）纳税人为取得土地使用权所支付的地价款；（2）纳税人在取得土地使用权时按国家统一规定缴纳的有关费用。

2.房地产开发成本：是指纳税人房地产开发项目实际发生的成本，包括6项：（1）土地征用及拆迁补偿费（2）前期工程费（3）建筑安装工程费（4）基础设施费（5）公共配套设施费（6）开发间接费用等地价款、开发成本，一般情况下，按实际发生额扣除。

另外，要注意和应税收入进行配比，地价款配比时，根据“总支出×开发的项目占用土地面积的比例×出售的部分所占建筑面积的比例”计算扣除项目。

【例题·综合题】（2011年节选）府城房地产开发公司为内资企业，公司于2008年1月～2011年2月开发“东丽家园”住宅项目，发生相关业务如下：（1）2008年1月通过竞拍获得一宗国有土地使用权，合同记载总价款17000万元，并规定2008年3月1日动工开发。

由于公司资金短缺，于2009年5月才开始动工。

因超过期限1年未进行开发建设，被政府相关部门按照规定征收土地受让总价款20%的土地闲置费。

（2）支付拆迁补偿费、前期工程费、基础设施费、公共配套设施费和间接开发费用合计2450万元。

（3）2010年4月开始销售，可售总面积为45000m2，截止2010年8月底销售面积为40500 m2，取得收入40500万元；尚余4500m2房屋未销售。

要求：（1）在计算土地增值税和企业所得税时，对缴纳的土地闲置费是否可以扣除？（2）计算2010年9月进行土增值税清算时可扣除的土地成本金额。

（3）计算2010年9月进行土增值税清算时可扣除的开发成本金额。

[答疑编号3941080104]『正确答案』（1）房地产开发企业逾期开发缴纳的土地闲置费在土地增值税税前不得扣除，但在企业所得税税前可以扣除。

二元一次方程组讲义题型一：二元一次方程（组）的概念①二元一次方程： 含有两个未知数，并且含有未知数项的次数都是1的方程。

注意：满足的四个条件：1、都是整式方程；2、只含有两个未知数；3、未知数的项最高次数都是一次；4、含有未知数的项的系数不为0.②二元一次方程组：含有两个未知数的两个一次方程所组成的一组方程叫二元一次方程组。

注意：1）满足的三个条件：1、每个方程都是一次方程；2、方程组具有两个未知数；3、每个方程均为整式方程。

2）方程组的各个方程中，相同字母必须代表同一数量，否则不能将两个方程合在一起，组成方程组。

①二元一次方程：例1、下列方程①x x 263=+，②3=xy ，③42=-x y ，④y y x 2410=-，⑤21=+y x ，⑥532=+xy x ，⑦03=+-z y x ，⑧1332=+y x 中，二元一次方程有 个。

例2、方程14-=-x y ax 是二元一次方程，则a 的取值范围为 .例3、已知方程()132-=++m y m mx 是关于y x ,的二元一次方程，则m 的取值范围是 . 例4.若关于x ，y 的方程021=+-+n m y x是二元一次方程，则n m +的和为 . 例5、若1342=+--b a y x 是关于x ，y 的二元一次方程，其中3≤+b a ，则=-b a ．②二元一次方程组：例1、下列方程组中，二元一次方程组的个数是 .（1）⎪⎩⎪⎨⎧=+=+21122y x y x ；（2）⎪⎩⎪⎨⎧=-=+211y x y x ；（3）⎪⎩⎪⎨⎧=-=211y x xy ；（4）⎩⎨⎧==+01x y x ；（5）⎪⎪⎩⎪⎪⎨⎧=+=+2111y x y x ；（6）⎩⎨⎧=+=+212z y y x ； （7）⎪⎩⎪⎨⎧=+=+9114yx y x ；（8）⎩⎨⎧=-=-1y x xy y x .；（9）()⎪⎩⎪⎨⎧-=-=+-2312y y x x y x 例5、若方程组()⎩⎨⎧=-=+-+-43332b a y x xy c x 是关于y x ,的二元一次方程组，则代数式c b a ++的值是 ． 题型二：二元一次方程（组）的解的概念①二元一次方程:注意：1)二元一次方程的每一个解，都是一对数值，而不是一个数值；2）二元一次方程的解使方程左右两边相等；3）一般情况下，一个二元一次方程有无数多组解，但并不是说任意一对数值都是它的解，当对解有限制条件时，二元一次方程的解的个数为有限个。

第八章 平面向量一、基础知识定义1 既有大小又有方向的量，称为向量。

画图时用有向线段来表示，线段的长度表示向量的模。

向量的符号用两个大写字母上面加箭头，或一个小写字母上面加箭头表示。

书中用黑体表示向量，如a. |a|表示向量的模，模为零的向量称为零向量，规定零向量的方向是任意的。

零向量和零不同，模为1的向量称为单位向量。

定义2 方向相同或相反的向量称为平行向量（或共线向量），规定零向量与任意一个非零向量平行和结合律。

定理1 向量的运算，加法满足平行四边形法规，减法满足三角形法则。

加法和减法都满足交换律和结合律。

定理2 非零向量a, b 共线的充要条件是存在实数0，使得a= f≠λ.b λ定理3 平面向量的基本定理，若平面内的向量a, b 不共线，则对同一平面内任意向是c ，存在唯一一对实数x, y ，使得c=xa+yb ，其中a, b 称为一组基底。

定义3 向量的坐标，在直角坐标系中，取与x 轴，y 轴方向相同的两个单位向量i, j 作为基底，任取一个向量c ，由定理3可知存在唯一一组实数x, y ，使得c=xi+yi ，则（x, y ）叫做c 坐标。

定义4 向量的数量积，若非零向量a, b 的夹角为，则a, b 的数量积记作a ·b=|a|·|b|cos θθ=|a|·|b|cos<a, b>，也称内积，其中|b|cos 叫做b 在a 上的投影（注：投影可能为负值）。

θ定理4 平面向量的坐标运算：若a=(x 1, y 1), b=(x 2, y 2)， 1．a+b=(x 1+x 2, y 1+y 2), a-b=(x 1-x 2, y 1-y 2)， 2．λa=(λx 1, λy 1), a ·(b+c)=a ·b+a ·c ，3．a ·b=x 1x 2+y 1y 2, cos(a, b)=(a, b 0),222221212121yx y x y y x x +⋅++≠4. a//b x 1y 2=x 2y 1, a b x1x2+y 1y 2=0.⇔⊥⇔定义5 若点P 是直线P 1P 2上异于p 1，p 2的一点，则存在唯一实数λ，使，λ叫P 分21PP P P λ=21P P 所成的比，若O 为平面内任意一点，则。

第八章二元一次方程 二元一次方程组（1）1、 如果2/讪讥3严曲心10是一个二元一次方程，那么数d ・Z? = _______2、 己知x,y,z 满足方程组£一¥ + ：° 求x:y:z 的值是 _________ 。

3、 已知方程12（兀+1）=7©・1）,写出用Y 表示的x 的式子的 ___4 .方程x=3y=9的解是 ________ ・ 5.己知方程组却"不解方程组则x =, y =I3x = 2 y = 156 若(2x — 3y + 5尸 + |x + y — 2| =()则 x= __ Y= ____x+红97.己知二元一•次方程组＜ 4的解为x=a y 二b 则| a-b |的值二 _________-x + y = 17〔5二.解答题8.解下列二元一次方程组:x + y = 7 3(x + y)_7y = 79. 若(3x-y+l)2与|2x+3y —25|互为相反数,求(x-y)2的值.10. 已知a 、b 满足『d + 3b = 3a + 2b = ii •甲、乙两任同求方程，竜i”的整数解，甲正确的求出一个解为和n ,乙把：唸診一看成ax-by = l,求得另一个解为\X = l，试求出a, b 的值. y = 212. 根据下列语句，分别设适当的未知数，列出二元一次方程或方程组（不解答） （1）小明、小芳两人的年龄之和为27岁，且小明比小芳大1岁；(1)1213的值.（2）现有而额为100元和20元的人民币共40张，共计2000元;13•养猴场里的饲养员提了一筐桃来喂喉，如果他给每个猴子14个桃，还剩48个；如果每个猴子18个桃，就还差64个，请问：这个猴场养了多少只猴?饲养员提了多少个桃？4x_2・15•如图5所示，在课间活动屮，小英、小丽和小敏在操场上画出A 、〃两个区域，一起玩投沙包游戏.沙包落在A 区域所得分值与落在〃区域所得分值不同.当毎人各投沙包四次时，其落点和四次总分如图所示.请求出 小敏的四次总分.14•让我们來规定一种运算:=ad 一 be o 例如:3=2x5-3x4 = 10-12 = -2 5x 2再如：1 4按照这种运算的规定解题: 若X 、 y 同时满足x(-6)(-)9=13,3 (一 y)4=4, x 的值。

1.两条异面直线所成角的求法设a,b分别是两异面直线l1,l2的方向向量，则l1与l2所成的角θa与b的夹角β范围（0，错误!][0，π]求法cos θ＝错误!cos β＝错误!2。

直线与平面所成角的求法设直线l的方向向量为a，平面α的法向量为n，直线l与平面α所成的角为θ，a与n的夹角为β，则sin θ＝｜cos β|＝错误!.3.求二面角的大小（1）如图①，AB，CD分别是二面角α－l－β的两个面内与棱l垂直的直线，则二面角的大小θ＝〈错误!，错误!〉.（2）如图②③，n1，n2分别是二面角α－l－β的两个半平面α,β的法向量，则二面角的大小θ满足｜cos θ｜＝|cos<n1，n2〉|，二面角的平面角大小是向量n1与n2的夹角(或其补角)。

【知识拓展】利用空间向量求距离（供选用）(1）两点间的距离设点A(x1，y1，z1),点B（x2，y2，z2）,则AB＝｜错误!｜＝错误!。

(2）点到平面的距离如图所示，已知AB为平面α的一条斜线段，n为平面α的法向量，则B到平面α的距离为|错误!|＝错误!.【思考辨析】判断下列结论是否正确(请在括号中打“√”或“×”)(1）两直线的方向向量所成的角就是两条直线所成的角.(×)（2)直线的方向向量和平面的法向量所成的角就是直线与平面所成的角。

（×)（3)两个平面的法向量所成的角是这两个平面所成的角。

(×)(4)两异面直线夹角的范围是(0,错误!］，直线与平面所成角的范围是［0,错误!］，二面角的范围是［0，π］.(√)（5）直线l的方向向量与平面α的法向量夹角为120°,则l和α所成角为30°.(√)（6）若二面角α－a－β的两个半平面α，β的法向量n1，n2所成角为θ,则二面角α－a－β的大小是π－θ。

（×)1.（2016·南通模拟)已知两平面的法向量分别为m＝（0，1,0)，n＝(0,1,1），则两平面所成的二面角为________.答案45°或135°解析cos<m，n>＝错误!＝错误!＝错误!，即〈m，n>＝45°.∴两平面所成的二面角为45°或180°－45°＝135°。

第八章运动与力知识点1：阻力对物体运动得影响实验器材：小车、斜面、长木板、毛巾、棉布实验设计：（1）改变平面摩擦力得措施：改变平面得粗糙程度。

（2）保证小车到平面时速度相同得措施：让小车从斜面得同一位置由静止开始滑下。

实验结论：平面越光滑，小车运动得距离越远，也就就是说小车受到得阻力越小，速度减小得越慢。

实验结论得推理：如果物体表面绝对光滑，物体受到得阻力为零，速度不会减慢，物体将以不变得速度永远运动下去。

知识点2：牛顿第一定律牛顿第一定律：任何物体在不受任何外力得作用下，总保持匀速直线运动状态或静止状态。

理解要点：（1）牛顿第一定律就是分析事实，由概括、推理得出得，不能通过实验直接验证。

（2）物体得运动不需要力来维持，物体本身就有保持运动状态不变得特性，即力不就是维持物体运动得原因。

（3）力不就是使物体运动得原因，而就是使物体运动状态发生改变得原因。

知识点3：惯性定义：一切物体都有保持原来运动状态不变得性质，这种性质叫做惯性。

惯性得大小：只与物体得质量大小有关，与物体得运动速度大小无关。

理解要点：（1）一切物体（固、液、气）在任何时候都有惯性，静止得物体也有惯性。

（2）惯性就是一种性质，不就是力。

惯性就是物体本身得一种属性，与物体就是否运动、就是否受力、运动速度大小无关。

（3）惯性有利也有弊。

知识点4：平衡力与二力平衡1、平衡状态：（1）运动状态包括：运动速度得大小与运动方向。

（2）静止状态与匀速直线运动状态都属于平衡状态，匀速圆周运动不属于平衡状态。

2、平衡力：（1）物体受到两个或几个力得作用，处于静止或匀速直线运动状态，那么这两个力或几个力就互为平衡力。

（2）二力平衡：物体只受到两个力得作用而处于平衡状态，这就就是所谓得二力平衡。

（3）二力平衡得条件：作用在同一物体上；大小相等；方向相反；在同一直线上。

（同物、等大、反向、同线）（4）二力平衡得应用：平衡得两个力，知道其中一个力得大小与方向，就可以求出另一个力得大小与方向。