清华大学讲义-摄象机模型和外极线几何

学位论文独创性声明本论文是我个人在导师指导下进行的研究工作及取得的研究成果。

论文中除了特别加以标注和致谢的地方外，不包含其他人或其它机构已经发表或撰写过的研究成果。

其他同志对本研究的启发和所做的贡献均已在论文中作了明确的声明并表示了谢意。

作者签名：日期：学位论文使用授权声明本人完全了解南京财经大学有关保留、使用学位论文的规定，即：学校有权保留送交论文的复印件，允许论文被查阅和借阅；学校可以公布论文的全部或部分内容，可以采用影印、缩印或其它复制手段保存论文。

保密的论文在解密后遵守此规定。

作者签名：导师签名：日期：第一章绪论1.1国内外研究方法和现状在计算机视觉领域中，摄像机标定技术是从二维图像中获取三维空间信息的重要且必要的步骤，因此该技术被广泛用于摄影测量、三维重建、导航系统以及视觉监控等一些科研和工程中。

就摄像机标定分类而言，其主要可分为三类: 传统标定[1-4]、主动视觉标定[5-11]和自标定[12-21]。

但此三种标定方法都存在某些方面的优缺点，其具体分析如下：1.1.1传统标定方法1．最优化算法标定方法最优化算法标定方法的优点是，在确定摄像机内参和外参的过程中，可以假设复杂摄像机模型，其中成像的过程亦可假设其复杂性。

但前面起初阶段的假设复杂性却给后面的求解过程带来的不便，归纳如下:1)：优化算法程序运行时间可能较长与一般线性的求解方法相比，无法实时得到精确的标定结果，而在一定情况下不能较快的得到准确的结果，则此算法就无实用性可言；2)：求解摄像机内参和外参最终结果一定程度上取决于所给参数的初值，如所给参数和理想求解值相差较大，则优化算法也较难标定出准确的摄像机参数。

在传统的摄影测量学方法中构造摄像机成像模型如文献[10]的算法。

此方法在进行摄像机标定和三维重建时精度较高，但计算过程复杂且计算量较大。

其中直接线性变换方法(DLT)也属最优化算法标定方法。

如Abdal-Aziz和Karara[11]，提出DLT摄像机定标的方法，此方法中几何关系的线性模型的建立于图像和环境物体之间的关系，但整个求解过程都是在没有考虑到摄像机非线性畸变的情况下，确定方程的线性解和线性模型参数的估计。

1. ys2002090701.htm 1.1 函数与基本不等式函数关系，定义域与值域，反函数与复合函数四类初等性质（广义奇偶性）1.2 极限定义与性质序列与函数极限定义与等价描述极限性质：唯一性，有界性，保号性及推论，比较性质1.3 三个极限存在准则1.4 两个标准极限1.5 无穷小量比阶等价无穷小量，同阶无穷小量与高阶无穷小量。

1.6 极限相关知识点导数概念，变限积分，级数，微分方程，广义积分等。

1.7 连续函数基本概念，定义，连续性与极限的关系，连续性等价描述，连续性的判别闭区间上连续函数的性质，零点定理，最大最小值定理。

2. ys2002090702.htm 1.1 函数与基本不等式函数关系，定义域与值域，反函数与复合函数四类初等性质（广义奇偶性）1.2 极限定义与性质序列与函数极限定义与等价描述极限性质：唯一性，有界性，保号性及推论，比较性质1.3 三个极限存在准则1.4 两个标准极限1.5 无穷小量比阶等价无穷小量，同阶无穷小量与高阶无穷小量。

1.6 极限相关知识点导数概念，变限积分，级数，微分方程，广义积分等。

1.7 连续函数基本概念，定义，连续性与极限的关系，连续性等价描述，连续性的判别闭区间上连续函数的性质，零点定理，最大最小值定理。

3. ys2002090703.htm例15. 设与在有定义，在有间断点，在上连续，且，则（A）在上必有间断点;（B）在上必有间断点;（C）在上必有间断点;（D）在上必有间断点.例16.设，且至少存在一点，使，证明在上有正的最大值。

例17.设，，，证明（1）存在；（2）收敛。

例18.若，则（A）且；（B）且；（C）且；（D）且；例19.若存在, 则 B(A) 。

(B) 之去心邻域, 使当时, 。

(C) 之邻域, 使当时, 。

(D) 。

例20.设定义在, 且都在处连续,若, 则 D(A) 且,(B) 且(C) 且,(D) 且例21.设当是比高阶的无穷小量, 则 A(A) , (B)(C) , (D)4. ys2002090704.htm例15. 设与在有定义，在有间断点，在上连续，且，则（A）在上必有间断点;（B）在上必有间断点;（C）在上必有间断点;（D）在上必有间断点.例16.设，且至少存在一点，使，证明在上有正的最大值。

热态锻件结构光三维测量技术赵　毅　王明辉　马品奎　宋家旺吉林大学,长春,130025摘要:介绍了结合计算机视觉、结构光光栅投影、移相测量原理的热态锻件结构光三维测量技术,该测量技术采用数字滤色技术解决热态工件本身发光干扰的难点,实现热态工件的三维非接触测量。

实验设备可以一次测量1000mm ×800mm 左右的面积,测量时间仅5s ,测量点距1mm 左右,并可以达到0125mm 的精度,这不仅能在车间就近对工件进行高温测量,而且为在线测量的研究提供了技术基础。

关键词:结构光;三维测量;塑性成形;热态工件中图分类号:TG 3 文章编号:1004—132X(2006)S2—0125—04S tr uct ured Light 3D Measurement T echnology of H ot ForgingZhao Y i W ang Minghui Ma Pi nkui Song JiawangJili n Universit y ,Changchun ,130025A bstract :The three dimensional measurement of hot forging part is significant for decreasing met al al 2lowance ,ensuring forging quality and researchi ng t he rule of forging.A new 3D measuri ng met hod usi ng computer vision ,st ructured light ,f ringe projection ,phase shifting and digit al optical filter technology i s pro 2posed for non -contact measurement of hot forging part s.The experimental i nstallation can scan a area of 1000mm ×800mm in a si ngle view ,t he measurement process takes only 5seconds ,and t he accuracy is wit hin 0125mm.K ey w ords :struct ured light ;3D measurement ;plastic forming;hot part收稿日期6—8—8基金项目中国博士后科学基金资助项目(53)0　引言为了有效控制热锻压过程的质量,需对热态锻件进行现场测量。

基础矩阵及其求法同一三维场景在两个不同视点处得到的两幅二维图像之间的几何关系——极几何以及极几何的代数表示——基础矩阵。

两幅图像可以是由两个摄像机在不同位置同时采集的，也可以是同一摄像机顺序采集的，例如摄像机相对场景移动。

对于这两种情况，几何上认为是相等的。

一般地，同一世界坐标系下的同一物体的图像间存在一种几何上的对极约束关系。

在立体视觉中，可以利用图像点的匹配来恢复这种几何关系，反过来，也可以利用这种几何关系来约束匹配，使得对应点的搜索范围由二维平面降低到对应一维极线，使得匹配的鲁棒性、精度都得到很大提高。

对极几何关系在数学上可以用基础矩阵F 来表示，因此，对极几何问题就转化为对基础矩阵F 的估计问题。

精确地计算F 对于标定、寻找精确匹配和三维重建都有重要意义。

2.1 基础矩阵假设在一个立体视觉系统中，有两个摄像机，如图2.1所示，设C和C’分别为两个摄像机的光心，两个摄像机获得的图像分别为I和I’，M为三维空间中任意一点，m和m’是点M 在两个图像上的像点（投影点），称m和m’为一对对应点。

连接光心C和C’的直线称为基线。

空间点M和两个光心C和C’共面，设它们所在的平面为π，该面称为极平面。

极平面与图像平面的交线l和l’称为极线。

因为m（m’）也同时在平面π和像平面I（I’）上。

从这里可以看出，寻找m（m’）的对应点m（m’）时，不必在I（I’）整幅图像中寻找，只需在m（m’）在I（I’）的极线上寻找即可。

这就提供了一个重要的极线约束，将对应点的搜索空间从二维降到了一维。

当三维空间点M移动时，产生的对所有极线都穿过极点e(e’)，极点是极线与图像平面的交点。

图2.1两幅图像间的对极几何2.1.1 参考坐标系为了描述基础矩阵，首先需要定义四个参考坐标系：图像坐标系、成像平面坐标系、摄像机坐标系和世界坐标系。

摄像机采集的数字图像在计算机内可以存储为数组，数组中的每一个元素（称为像素，pixel）的值即是图像点的亮度。

1 精密仪器与机械学系 精密仪器系2013-5-291精密仪器与机械学系 精密仪器系2013-5-292精密仪器与机械学系 精密仪器系一、晶体的双折射现象晶体对两个相互垂直 振动矢量的光n不同 而产生两束折射光 寻常 (o) 光和非寻常(e)光 o 光——遵守折射定律， 在入射面内 e 光——不遵守折射定律， 一般不在入射面内2013-5-29（以单轴晶体为例）方解石（单轴晶体） 天然结构为平行六面体3精密仪器与机械学系 精密仪器系o光和e光与晶体不可分 折射定律的含义:sin i1 v1 = n21 = • 角关系 sin i2 v2• • 入射光线/折射光线与法线共面 界面两侧频率相同2013-5-294精密仪器与机械学系 精密仪器系二、晶体特性1、光轴 双折射晶体中的一个特殊方向， 光束沿这个方向传播时不发生双折射 光轴方向上， o 光和 e 光都遵守折射定律 且：no=ne ， o 、e光 k 相同，v 相同 光轴是一个方向2013-5-29 5精密仪器与机械学系 精密仪器系 2、主截面： 光轴和晶体表面法线确定的平面 当光线在主截面内入射（不与光轴重合）时 o光和e光都在主截面内，但no≠ne光线在一般情况下入射晶体， o光和e光不同面2013-5-29 6精密仪器与机械学系 精密仪器系 3、主平面：光线和光轴组成的面 o 光：振动方向垂直于 o 光主平面 e 光：振动方向在 e 光主平面内 入射光在主截面内时， o光、e光主平面 均为主截面实际使用中， 取入射面与主截面重合2013-5-29 7精密仪器与机械学系 精密仪器系 4、晶体的各向异性 vo>ve，为正晶体；o光 e光 光轴 o光vo<ve，为负晶体e光正：no<ne，e光波面（椭球）在o光波（球）面内 负：no>ne，e光波面（椭球）在o光波（球）面外2013-5-29 8精密仪器与机械学系 精密仪器系 5、晶体的介电张量ur u r 各向同性媒质中， ε 是常数，D // E各向异性媒质中，不同方向光波电矢量的 ε 值不同， 为一个二阶张量，称介电张量ur u r D =εE⎡Dx ⎤ ⎡ε xx ε xy ε xz ⎤ ⎡Ex ⎤ ⎢D ⎥ = ⎢ε ε ε ⎥ ⎢E ⎥ [ε ] = ⎡εij ⎤， ⎢ y ⎥ ⎢ yx yy yz ⎥ ⎢ y ⎥ ⎣ ⎦ ⎢ Dz ⎥ ⎢ε zx ε zy ε zz ⎥ ⎢ Ez ⎥ ⎣ ⎦ ⎣ ⎦⎣ ⎦ur u r D 随 E 而异2013-5-29 9精密仪器与机械学系 精密仪器系 在晶体中可找到x，y，z三个互相垂直的方向 （晶体的主轴方向），建立（主轴）坐标系， 使 ⎡εij ⎤为一对称张量： ⎣ ⎦⎧ Dx = ε x Ex ur ⎪ 主轴坐标系中， D 表示为 ⎨Dy = ε y Ey ⎪D = ε E ⎩ z z z2013-5-29 10⎡ε x 0 0 ⎤ ⎡εij ⎤ = ⎢ 0 ε y 0 ⎥ ⎣ ⎦ ⎢ ⎥ ⎢ 0 0 εz ⎥ ⎣ ⎦主介电常数(ε x , ε y , ε z )结论1：在各向异性晶体中，由于，仅当沿着三主轴之一方向时，光学各向同性晶体单轴晶体双轴晶体//D Eu r u r E u r //D u r Eu rx y z εεε≠≠x y zεεε==x y zεεε=≠x y zεεε≠≠1、法线速度/光线速度晶体中一单色平面波麦克斯韦方程＋晶体中物质方程传播特点B E D t D H j B t∂∇×=−∇⋅=∂∂∇×=+∇⋅=∂u r u r ur uruu r r u r 000exp[()]exp[()]exp[()]E E i t k r H H i t k r D D i t k r ωωω⎧=−−⋅⎪⎪=−−⋅⎨⎪=−−⋅⎪⎩r r r r r r r r r r rr D E B Hεµ==u r u r u r u u r 代入麦氏方程和物质方程：三、单色平面波在晶体中的传播彼此垂直成一右手螺旋系得：,0,0k E H k H D H k E k D D k H k H ωµω⎫×=⎪⎧×=−⊥⎪⎪⇒⎬⎨⋅=⊥⎪⎪⎩⎪⋅=⎭r u r uu rr uu r ur uu r r u r r ur r uu r r r uu r ,,D H k ur uu r r波印廷矢量S E H=×v v v9成一右手螺旋系，故在同一垂直于的平面内。

附录B 摄象机模型和外极线几何B.1 摄象机模型B.1.1 针孔模型和透视投影 B.1.2 摄象机外参数B.1.3 摄象机内参数和归一化摄象机 B.1.4 透视矩阵的一般形式 B.2 透视投影的各种线性近似B.2.1 正投影（orthographic projection ） B.2.2 弱透视（weak perspective ）B.2.3 平行透视（paraperspective projection ） B.2.4 仿射摄象机B.3 透视投影下的外极线几何 B.3.1 外极线几何中的概念B.3.2 归一化坐标系中的外极线方程 B.3.3 像素坐标系中的外极线方程 B.3.4 投影矩阵下的外极线方程 B.3.5 基础矩阵和外极几何变换B.1 摄象机模型在大部分应用环境中可以用理想的针孔模型来近似实际摄象机。

针孔模型的几何关系就是透视投影。

下面我们先介绍透视投影的几何关系。

B.1.1 针孔模型和透视投影针孔摄象机的模型在第五章中已有介绍。

在那里我们使用了矢量代数的表示方法，下面我们用坐标变换的方法来推导之。

我们定义的第一个坐标系是摄象机坐标系。

该坐标系的原点在焦心C ，X 、Y 、Z 轴由A 、H ’和V ’决定，其中A 为光轴方向，H ’和V ’是正交的方向，三者组成右手直角坐标系。

三维点在该坐标系中的坐标M c 记为(X c ,Y c ,Z c )T 。

为表示透视模型我们还需要在图象平面中建立图象坐标系。

这是一个二维坐标系，其原点位于光轴和图象平面的交点c （称为主点，principal point ），两坐标轴与H ’和V ’平行且反向。

在该坐标系中像点m 的坐标表示为(u,v)T 。

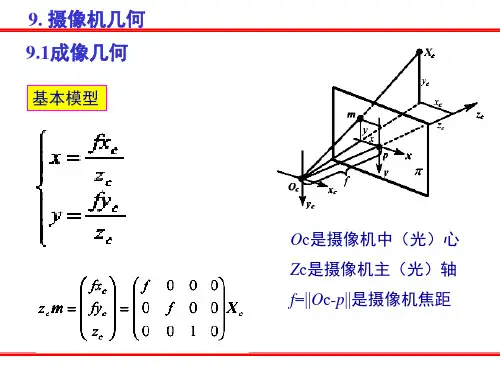
在定义了这两个坐标系后，投影模型可表示为cccZ f Y v X u == (B.1)其中f 为焦心到图象平面的距离，即焦距。

摄象机坐标系和图象坐标系如图B.1所示。

图B.1 针孔模型，其中过焦心C 和图象平面平行的平面称为焦平面在实际应用中物体离焦心的距离一般都远大于焦距。

摄像机标定方法综述摘要：首先根据不同的分类方法对对摄像机标定方法进行分类，并对传统摄像机标定方法、摄像机自标定方法等各种方法进行了优缺点对比，最后就如何提高摄像机标定精度提出几种可行性方法。

关键字：摄像机标定，传统标定法，自标定法，主动视觉引言计算机视觉的研究目标是使计算机能通过二维图像认知三维环境，并从中获取需要的信息用于重建和识别物体。

摄像机便是3D 空间和2D 图像之间的一种映射，其中两空间之间的相互关系是由摄像机的几何模型决定的，即通常所称的摄像机参数，是表征摄像机映射的具体性质的矩阵。

求解这些参数的过程被称为摄像机标定[1]。

近20 多年，摄像机标定已成为计算机视觉领域的研究热点之一，目前已广泛应用于三维测量、三维物体重建、机器导航、视觉监控、物体识别、工业检测、生物医学等诸多领域。

从定义上看，摄像机标定实质上是确定摄像机内外参数的一个过程，其中内部参数的标定是指确定摄像机固有的、与位置参数无关的内部几何与光学参数，包括图像中心坐标、焦距、比例因子和镜头畸变等；而外部参数的标定是指确定摄像机坐标系相对于某一世界坐标系的三维位置和方向关系，可用3 ×3 的旋转矩阵R 和一个平移向量t 来表示。

摄像机标定起源于早前摄影测量中的镜头校正，对镜头校正的研究在十九世纪就已出现，二战后镜头校正成为研究的热点问题，一是因为二战中使用大量飞机，在作战考察中要进行大量的地图测绘和航空摄影，二是为满足三维测量需要立体测绘仪器开始出现，为了保证测量结果的精度足够高，就必须首先对校正相机镜头。

在这期间，一些镜头像差的表达式陆续提出并被普遍认同和采用，建立起了较多的镜头像差模型，D.C.Brown等对此作出了较大贡献，包括推导了近焦距情况下给定位置处径向畸变的表达式及证明了近焦距情况下测得镜头两个位置处的径向畸变情况就可求得任意位置的径向畸变等[2]。

这些径向与切向像差表达式正是后来各种摄像机标定非线性模型的基础。