艺术生高考数学知识点.ppt
- 格式:pdf
- 大小:3.35 MB
- 文档页数:25
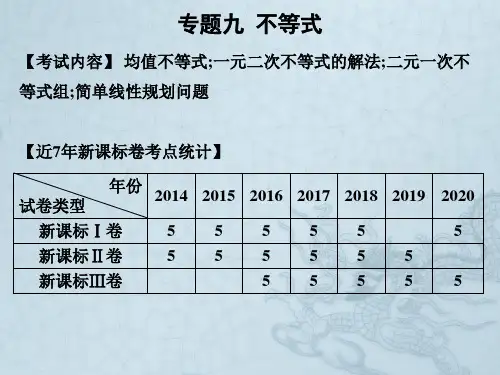


函数的概念与解析式、函数的运算值域、定义域、值域与对应关系统称为函数的三要素.【例1】如下图(1)(2)(3)(4)四个图象各表示两个变量,x y 的对应关系,其中表示y 是x 的函数关系的有 .【例2】下列对应关系是集合P 上的函数是有 .(1)*,P Z Q N ==,对应关系:f “对集合P 中的元素取绝对值与集合Q 中的元素相对应”; (2){1,1,2,2},{1,4}P Q =--=,对应关系::f x →2,,y x x P y Q =∈∈;(3){P =三角形},{|0}Q x x =>,对应关系:f “对P 中三角形求面积与集合Q 中元素对应.”【例3】下列四组函数中,表示为同一函数的是( ) A .2(),()f x x g x x ==B .x x f -=2)(与2)(-=x x gC .21(),()11x f x g x x x -==+- D.2()11,()1f x x x g x x =+⋅-=-【例4】某物体一天中的温度是时间t 的函数:T (t )=t 3-3t +60,时间单位是小时,温度单位为℃,t =0表示12:00,其后t 的取值为正,则上午8时的温度为()A .8℃B .112℃C .58℃D .18℃(4).(3).(2).(1).【巩固训练】1.函数()y f x =的图象与直线1x =的公共点数目是( )A .1B .0C .0或1D .1或22.如图所示,能表示“y 是x 的函数”的是 .3.下列式子能确定y 是x 的函数有 ( )①222=+y x ②111=-+-y x ③x x y -+-=12A .0个B .1个C .2个D .3个4.已知函数()12-=x x f ,则()=-1f函数的表示方法解析法:就是用数学表达式表示两个变量之间的对应关系,这个数学表达式就叫做函数的解析式,简称为解析式.如2260,2,,(0)s t s rl y ax b y ax bx c a π===+=++≠等,都是用解析式法表示的函数关系.【例5】若一个长方体的高为80cm ,长比宽多10cm ,则这个长方体的体积y (3cm )与长方体的宽x (cm )之间的表达式是________________.图象法:就是用图像表示两个变量之间的对应关系. 把一个函数的自变量x 与对应的因变量y 的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做该函数①s OA .s t Os t OstOB .C .D .的图象.这种表示函数关系的方法叫做图象法.【例6】一列货运火车从某站出发,匀加速行驶一段时间后开始匀速行驶,过了一段时间,火车到达下一站停下,装完货以后,火车又匀加速行驶,一段时间后再次匀速行驶,下列图象可以近似地刻画出火车在这段时间内的速度变化情况的是( )列表法:就是列出表格来表示两个变量之间的对应关系.这种表示方法不需要计算就可以直接看出自变量的值所对应的函数值,所以常常用于实际生产与生活中,如银行的利率表,列车的时刻表等.缺点是只能列出部分对应值,难以反映函数的全貌.【巩固训练】1.汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程s 看作时间t 的函数,其图像可能是( )2.矩形球台ABCD 中,4AB dm =,183BC dm =,小球P 以每秒2dm 的速度由A 射出与AB 成θ角前进,碰到BC 上的E 点后又折回与BC 成θ角前进,到达D 后,沿DA 回到A ,设小球P 从A 射出经x 秒后,ABP ∆的面积为2ydm ,求x y 、的关系式.3.某商店经营一种品牌的彩电,每台售价2880元,成本价为销售价的75%.为了扩大经验,拟定出新售价,使商品按新售价的八折优惠销售时,仍能获利,则每台彩电获利y 元与新售价x 元之间的函数解析式为 .O 时间速度O时间速度O时间速度速度函数解析式的求法【例7】设2211(),f x x x x+=+,求()f x 的解析式.【例8】设23)1(2+-=+x x x f ,求)(x f 的解析式【例9】已知()f x 是一次函数,且满足3(1)2(1)217f x f x x +--=+,求()f x 的解析式【例10】已知12()3f x f x x ⎛⎫+= ⎪⎝⎭,求)(x f 的解析式.【例11】用长为l 的铁丝弯成下部为矩形,上部为半圆形的框架.若矩形底边长为x 2,求此框架围成的面积y 与x 的函数解析式,并指出函数的定义域.【巩固训练】1、已知一次函数()f x 满足(())41f f x x =-,求()f x .2.已知21lg f x x ⎛⎫+= ⎪⎝⎭,求)(x f 的解析式.3.已知)(x f 是一个实系数的一次函数,且[]{}78)(+=x x f f f ,求)(x f 的解析式.4.若)(x f 满足x x x f x f -=--2)()(2,则)(x f 的解析式是 .5.在质量分数为%a 的盐水x 克水中加入质量分数为%b 的盐水y 克,变成质量分数为%c 的盐水,则y 关于x 的函数解析式为 .函数的运算函数的和:设函数,,则称为函数与的和;其中。
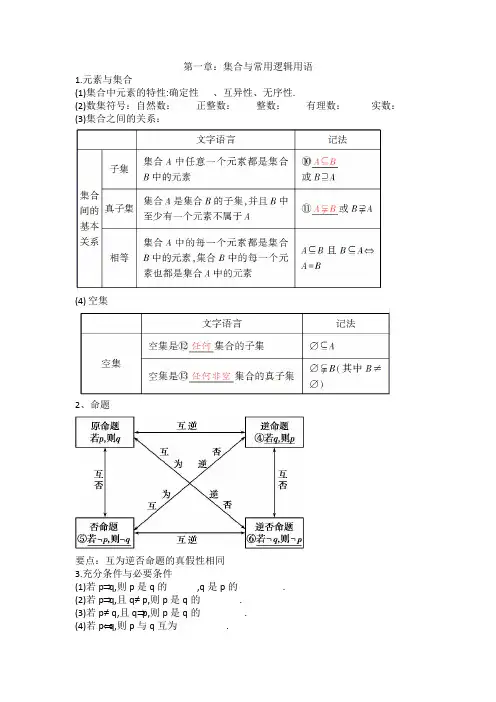
第一章:集合与常用逻辑用语
1.元素与集合
(1)集合中元素的特性:确定性、互异性、无序性.
(2)数集符号:自然数:正整数:整数:有理数:实数:
(3)集合之间的关系:
(4)空集
2、命题
要点:互为逆否命题的真假性相同
3.充分条件与必要条件
(1)若p⇒q,则p是q的,q是p的.
(2)若p⇒q,且q≠ p,则p是q的 .
(3)若p≠ q,且q⇒p,则p是q的 .
(4)若p⇔q,则p与q互为 .
(5)若p≠ q,且q≠ p,则p是q的 .
4、逻辑连接词:
5、含有量词的命题
第二章:函数
2、函数的单调性
3、函数的奇偶性
4、幂函数
5、二次函数
6、指数运算与指数函数
7、对数运算与对数函数
第三章:三角函数、解三角形
解三角形:
正弦定理:=A
a
sin
余弦定理:=2
a 面积公式:==
C ab S sin 2
1
第四章:数列
1、等差数列:
d n a a n )1(1-+=
d n n na a a n S n n 2
)
1(2)(11-+=+=
5371a a a a +=+
2、等比数列
11-=n n q a a
⎪⎩⎪
⎨⎧=≠--=1,1,1)
1(11q na q q q a S n n
5371a a a a ⋅=⋅
第五章:立体几何
2、体积与表面积。
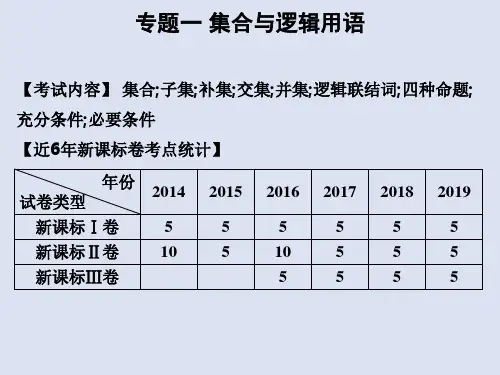

一、集合与简易逻辑:一、理解集合中的有关概念(1)集合中元素的特征:确定性,互异性,无序性 。
(2)集合与元素的关系用符号⊆∈, 表示。
(3)常用数集的符号表示:自然数集 N ;正整数集 N * 、 N + ;整数集 Z ;有理数集 Q 、实数集 R 。
(4)集合的表示法:列举法,描述法,符号法(数轴法,韦恩图法)注意:区分集合中元素的形式:如:}12|{2++==x x y x A ;}12|{2++==x x y y B ;}12|),{(2++==x x y y x C }12|{2++==x x x x D ;},,12|),{(2Z y Z x x x y y x E ∈∈++==;}12|)',{(2++==x x y y x F ;},12|{2xyz x x y z G =++==(5)空集是指不含任何元素的集合。
(}0{、φ和}{φ的区别;0与三者间的关系)空集是任何集合的子集,是任何非空集合的真子集。
注意:条件为B A ⊆,在讨论的时候不要遗忘了φ=A 的情况。
如:}012|{2=--=x ax x A ,如果φ=+R A ,求a 的取值。
二、集合间的关系及其运算(1)符号“∉∈,”是表示元素与集合之间关系的,立体几何中的体现 点与直线(面)的关系 ;符号“⊄⊂,”是表示集合与集合之间关系的,立体几何中的体现 面与直线(面)的关系 。
(2)A ⋂B={ x| x ∈A 且x ∈B} A ⋃B={ x| x ∈A 或x ∈B};C I A={ x| x ∈ I 且x ∉A} (3)对于任意集合B A ,,则:①A B B A =;A B B A =;B A B A ⊆; ②=A B A A ⊆B ;=A B A B ⊆A ;⇔=U B A C U A ⋃B=;⇔=φB A C U A ⋂B=U ;③=B C A C U U )(B A C U ⋃; B C A C U U ⋃)(B A C U =;(4)①若n 为偶数,则=n 2K,(k Z ∈);若n 为奇数,则=n 2k+1, (k Z ∈);②若n 被3除余0,则=n 3k, (k Z ∈);若n 被3除余1,则=n 3k+1(kZ ∈);若n 被3除余2,则=n 3k+2(k Z ∈);三、集合中元素的个数的计算:(1)若集合A 中有n 个元素,则集合A 的所有不同的子集个数为2n ,所有真子集的个数是2n -1,所有非空真子集的个数是2n -2。


2015 艺考生高考数学总复习讲义第一章、集合基本运算一、基础知识:1. 元素与集合的关系:用或表示;2. 集合中元素具有确定性、无序性、互异性•3. 集合的分类:①按元素个数分:有限集,无限集;②按元素特征分;数集,点集。
如数集{y|y=x2}, 表示非负实数集,点集{( x,y)| y=x2}表示开口向上,以y轴为对称轴的抛物线;4. 集合的表示法:①列举法:用来表示有限集或具有显着规律的无限集,如M={0,1, 2, 3,-};②描述法:一般格式: x A p(x),如:{x|x-3>2},{(x,y)|y=x2+1},…;描述法表示集合应注意集合的代表元素,如{(x,y)|y= x 2+3x+2}与{y|y= x2+3x+2}是不同的两个集合③字母表示法:常用数集的符号:自然数集N;正整数集N*或N ;整数集Z;有理数集Q实数集R;5 •集合与集合的关系:用,,二表示;A是B的子集记为A B;A是B的真子集记为A B。
常用结论:①任何一个集合是它本身的子集,记为 A A;②空集是任何集合的子集,记为 A ;空集是任何非空集合的真子集;③如果A B,同时B A,那么A = B ;如果A B,B C,那么A C .④ n个元素的子集有2n个;n个元素的真子集有2n—1个;n个元素的非空真子集有2n—2个.6. 交集A n B={x|x€ A 且x € B};并集A U B={x|x € A,或x € B};补集CA= {x| x € U,且x A},集合U表示全集.7. 集合运算中常用结论:注:本章节五个定义1. 子集定义:一般地,对于两个集合A与B,如果集合A中的任何一个元素都是集合B 的元素,我们就说集合 A 包含于集合B,或集合B 包含集合A ,记作A B (或 B A ),即若任意x A,有x B,则A B (或A B )。
这时我们也说集合A 是集合 B 的子集(subset )。

第1讲 集合【基础知识】一、集合有关概念1、集合中元素的特性:1.确定性; 2.互异性; 3.无序性2、常用数集及其记法:自然数集 ;正整数集 ;整数集 ;有理数集 、实数集 。
二、集合间的基本关系1.子集:A B ⊆.任何一个集合是它本身的子集。
A A2.集合相等: A =B3.真子集:如果AB ,且A B 那就说集合A 是集合B 的真子集,记作A ⊂B (或B ⊃A )4. 空集:不含任何元素的集合叫做空集,记为Φ规定: 空集是任何集合的子集, 空集是任何非空集合的真子集。
三、集合的运算1.交集的定义:}|{B x A x x B A ∈∈=,且I . 2、并集的定义:A ∪B ={x |x ∈A ,或x ∈B }. 3、补集: },|{A x S x x A C S ∉∈=且性质:⇔=A B A I ;⇔=A B A Y ; 四、集合中元素的个数的计算:若集合A 中有n 个元素,则集合A 的所有子集个数为______,所有真子集的个数是______,所有非空真子集的个数是 。
【基础训练】1、(2013·四川高考文科)设集合{1,2,3}A =,集合{2,2}B =-,则A B =I ( )A .∅B .{2}C .{2,2}-D .{2,1,2,3}-2、(2010·福建高考文科)若集合{}13A x x =≤≤,{}2B x x =>,则A B ⋂等于 ( ) (A ){}23x x <≤ (B ){}1x x ≥ (C ){}23x x ≤< (D ){}2x x >3、(2011·全国)已知集合{}{}0,1,2,3,4,1,3,5,,M N P M N ===I 则P 的子集共有( )(A )2个 (B )4个 (C )6个 (D )8个4、(2010·湖南高考文科)已知集合A ={1,2,3},B ={2,m ,4},A ∩B ={2,3},则m = . 【典例分析】1、(2010·北京高考文科)集合2{03},{9}P x Z x M x Z x =∈≤<=∈≤,则P M I = ( )(A ) {1,2} (B ) {0,1,2} (C ){1,2,3} (D ){0,1,2,3}2、(2010·安徽高考文科)若A ={}|10x x +>,B ={}|30x x -<,则A B I =( )(A )(-1,+∞) (B )(-∞,3) (C )(-1,3) (D )(1,3)3. (2013·北京高考文科)已知集合A ={-1,0,1},B ={x |-1≤x <1},则A ∩B = ( )A .{0}B .{-1,0}C .{0,1}D .{-1,0,1}4、(2011·广东)已知集合A =}1,,|),{22=+y x y x y x 且为实数(,B =},,|),{(1=+y x y x y x 且为实数,则A ⋂B 的元素个数为( )(A )4 (B )3 (C )2 (D )1【典型例题讲练】例1 设集合11,,,2442k k M x x k Z N x x k Z ⎧⎫⎧⎫==+∈==+∈⎨⎬⎨⎬⎩⎭⎩⎭,则_______M N练习: 设集合11,,,3663kk P x x k Z Q x x k Z ⎧⎫⎧⎫==+∈==+∈⎨⎬⎨⎬⎩⎭⎩⎭,则______P Q例2已知集合{}2210,,A x ax x x R a =++=∈为实数。

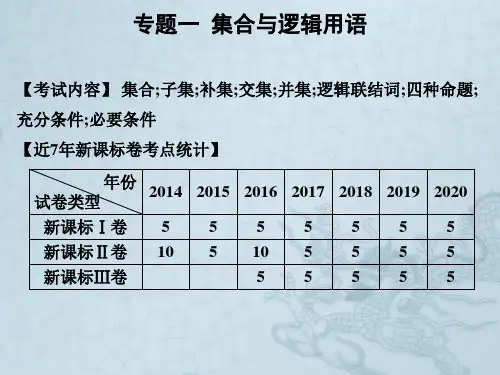
考点四十四 抛物线知识梳理1.抛物线的概念把平面内与一个定点F 和一条定直线l (l 不过F )的距离相等的点的集合叫作抛物线.这个定点F 叫作抛物线的焦点,这条定直线l 叫作抛物线的准线. 用集合语言描述:P ={M ||MF |d=1},即P ={M ||MF |=d }.注意:抛物线的定义中不可忽视“定点不在定直线上”这一条件,当定点在定直线上时,动点的轨迹是过定点且与定直线垂直的直线. 2.抛物线的标准方程与几何性质标准 方程y 2=2px (p >0)y 2=-2px (p >0)x 2=2py (p >0)x 2=-2py (p >0)p 的几何意义:焦点F 到准线l 的距离图形顶点 O (0,0)对称轴 y =0x =0焦点 F ⎝⎛⎭⎫p 2,0F ⎝⎛⎭⎫-p2,0 F ⎝⎛⎭⎫0,p 2 F ⎝⎛⎭⎫0,-p2 离心率 e =1准线方程 x =-p 2x =p 2 y =-p2y =p 2 焦半径 |PF |=p2+x 0|PF |=p2-x 0|PF |=p2+y 0|PF |=p2-y 0开口方向向右向左向上向下3.(1)y 1y 2=-p 2,x 1x 2=p 24. (2)|AB |=x 1+x 2+p =2psin 2θ(θ为AB 的倾斜角).(3) S △AOB =p 22sin θ(4)1|AF |+1|BF |为定值2p. (5)以AB 为直径的圆与准线相切,以AF 或BF 为直径的圆与y 轴相切.(6)当AB 与抛物线的对称轴垂直时,称线段AB 为抛物线的通径,它是焦点弦中最短者,长度等于2p .典例剖析题型一 抛物线的定义及其应用例1 若抛物线y =4x 2上的一点M 到焦点的距离为1,则点M 的纵坐标是__________. 答案1516解析 M 到准线的距离等于M 到焦点的距离,又准线方程为y =-116,设M (x ,y ),则y +116=1,∴y =1516.变式训练 已知抛物线C :y 2=8x 的焦点为F ,准线为l ,P 是l 上一点,Q 是直线PF 与C 的一个交点,若FP →=4FQ →,则|QF |=__________. 答案 3解析 ∵FP →=4FQ →,∴|FP →|=4|FQ →|,∴|PQ ||PF |=34.如图,过Q 作QQ ′⊥l ,垂足为Q ′,设l 与x 轴的交点为A ,则|AF |=4, ∴|PQ ||PF |=|QQ ′||AF |=34, ∴|QQ ′|=3,根据抛物线定义可知|QF |=|QQ ′|=3解题要点 利用抛物线的定义解决此类问题,应灵活地运用抛物线上的点到焦点的距离与到准线距离的等价转化.“看到准线想到焦点,看到焦点想到准线”,这是解决抛物线焦点弦有关问题的有效途径.题型二 抛物线的标准方程求解例2 已知抛物线C :y 2=2px (p >0)过点A (1,-2).求抛物线C 的方程,并求其准线方程; 解析 将(1,-2)代入y 2=2px ,得(-2)2=2p ×1,所以p =2. 故所求的抛物线C 的方程为y 2=4x ,其准线方程为x =-1.变式训练 已知抛物线C 与双曲线x 2-y 2=1有相同的焦点,且顶点在原点,则抛物线C 的方程是__________. 答案 y 2=±42x解析 因为双曲线的焦点为(-2,0),(2,0).设抛物线方程为y 2=±2px (p >0),则p 2=2,所以p =22,所以抛物线方程为y 2=±42x .解题要点 求抛物线的标准方程的方法:①求抛物线的标准方程常用待定系数法,因为未知数只有p ,所以只需一个条件确定p 值即可.②因为抛物线方程有四种标准形式,因此求抛物线方程时,需先定位,再定量. 题型三 抛物线的几何性质例3 如图,过抛物线y 2=2px (p >0)的焦点F 的直线l 依次交抛物线及其准线于点A 、B 、C ,若|BC |=2|BF |,且|AF |=3,则抛物线的方程是________.答案 y 2=3x解析 分别过点A 、B 作准线的垂线AE 、BD ,分别交准线于点E 、D ,则|BF |=|BD |,∵|BC |=2|BF |,∴|BC |=2|BD |,∴∠BCD =30°,又∵|AE |=|AF |=3, ∴|AC |=6,即点F 是AC 的中点,根据题意得p =32,∴抛物线的方程是y 2=3x .变式训练 已知抛物线C :y 2=8x 的焦点为F ,准线为l ,P 是l 上一点,Q 是直线PF 与C 的一个交点,若FP →=4FQ →,则|QF |等于__________. 答案 3解析 ∵FP →=4FQ →,∴|FP →|=4|FQ →|,∴|PQ ||PF |=34.如图,过Q 作QQ ′⊥l ,垂足为Q ′,设l 与x 轴的交点为A ,则|AF |=4,∴|PQ ||PF |=|QQ ′||AF |=34,∴|QQ ′|=3,根据抛物线定义可知|QQ ′|=|QF |=3. 解题要点 应用抛物线性质的技巧:1.利用抛物线方程确定及应用其焦点、准线等性质时,关键是将抛物线方程化成标准方程.2.要结合图形分析,灵活运用平面几何的性质以图助解.3.借助抛物线的定义,在点到焦点间距离和点到准线间距离之间相互转化.当堂练习1.(2015陕西文)已知抛物线y 2=2px (p >0)的准线经过点(-1,1),则该抛物线焦点坐标为__________. 答案 (1,0)解析 由于抛物线y 2=2px (p >0)的准线方程为x =-p 2,由题意得-p2=-1,p =2,焦点坐标为()1,0.2.O 为坐标原点,F 为抛物线C :y 2=42x 的焦点,P 为C 上一点,若|PF |=42,则△POF 的面积为__________. 答案 2 3解析 利用|PF |=x P +2=42,可得x P =32, ∴y P =±2 6.∴S △POF =12|OF |·|y P |=2 3.3. (2014年辽宁卷)已知点A (-2,3)在抛物线C :y 2=2px 的准线上,记C 的焦点为F ,则直线AF 的斜率为__________. 答案 -34解析 ∵点A (-2,3)在y 2=2px 的准线上,∴-p2=-2,∴p =4,∴y 2=2px 的焦点为F (2,0),∴k AF =3-0-2-2=-34.4.(2014·安徽)抛物线y =14x 2的准线方程是__________.答案 y =-1解析 ∵y =14x 2,∴x 2=4y .∴准线方程为y =-1.5.已知A (2,0),抛物线C :x 2=4y 的焦点为F ,射线F A 与抛物线C 相交于点M ,与其准线相交于点N ,则|FM |∶|MN |=________. 答案 1∶ 5解析 MF 的方程为x 2+y =1即x +2y -2=0,MF 的倾斜角为α,则tan α=-12,由抛物线的定义可知|MF |=|MQ |;∴|MF ||MN |=|MQ ||MN |=sin α=55=15. 课后作业一、 填空题1.过点P (-2,3)的抛物线的标准方程是__________. 答案 y 2=-92x 或x 2=43y解析 设抛物线的标准方程为y 2=kx 或x 2=my ,代入点P (-2,3),解得k =-92,m =43,∴y 2=-92x 或x 2=43y .2.抛物线y =4x 2的焦点到准线的距离是__________. 答案 18解析 由x 2=14y ,知p =18,所以焦点到准线的距离为p =18.3.设抛物线的顶点在原点,准线方程为x =-2,则抛物线的方程是__________. 答案 y 2=8x解析 由抛物线的准线方程为x =-2,得焦点F (2,0),∴p2=2,∴p =4,故抛物线的标准方程为y 2=8x .4.在y =2x 2上有一点P ,它到A (1,3)的距离与它到焦点的距离之和最小,则点P 的坐标是__________. 答案 (1,2)解析 如图所示,直线l 为抛物线y =2x 2的准线,F 为其焦点,PN ⊥l ,AN 1⊥l ,由抛物线的定义知,|PF |=|PN |,∴|AP |+|PF |=|AP |+|PN |≥|AN 1|,当且仅当A 、P 、N 三点共线时取等号. ∴P 点的横坐标与A 点的横坐标相同即为1.5.若抛物线y 2=2px 上一点P (2,y 0)到其准线的距离为4,则抛物线的标准方程为__________. 答案 y 2=8x解析 由题意,得2-⎝⎛⎭⎫-p2=4,p =4,所以抛物线的方程为y 2=8x . 6.点M (5,3)到抛物线y =ax 2的准线的距离为6,那么抛物线的方程是__________. 答案 y =112x 2或y =-136x 2解析 将y =ax 2化为x 2=1a y ,当a >0时,准线y =-14a ,由已知得3+14a =6,∴1a =12,∴a =112.当a <0时,准线y =-14a ,由已知得|3+14a |=6, ∴a =-136或a =112(舍).∴抛物线方程为y =x 212或y =-136x 2.7.抛物线y =-2x 2的焦点坐标为__________. 答案 (0,-18)解析 y =-2x 2化为标准方程为x 2=-12y ,其焦点坐标是(0,-18).8.抛物线y 2=4x的焦点到双曲线x 2-y 23=1的渐近线的距离是__________. 答案32 解析 抛物线y 2=4x 的焦点坐标为(1,0),双曲线的渐近线方程为±3x -y =0,则所求距离为d =32. 9.过抛物线y 2=4x 的焦点F 的直线交y 轴于点A ,抛物线上有一点B 满足OB OA AF =+ (O 为坐标原点),则△BOF 的面积是__________. 答案 1解析 由题可知F (1,0),可设过焦点F 的直线方程为y =k (x -1)(可知k 存在),则A (0,-k ),∴B (1,-k ),由点B 在抛物线上,得k 2=4,k =±2,即B (1,±2), S △BOF =12·|OF |·|y B |=12×1×2=1.10.若抛物线y 2=2x 上一点M 到坐标原点O 的距离为3,则点M 到抛物线焦点的距离为________. 答案 32解析 设M (x ,y ),则由⎩⎪⎨⎪⎧y 2=2x ,x 2+y 2=3,得x 2+2x -3=0.解得x =1或x =-3(舍).所以点M 到抛物线焦点的距离d =1--12=32.11.已知抛物线y 2=2px (p >0),过其焦点且斜率为1的直线交抛物线于A 、B 两点,若线段AB 的中点的纵坐标为2,则该抛物线的准线方程为________. 答案 x =-1解析 直线方程为y =x -p 2,由⎩⎪⎨⎪⎧y =x -p 2,y 2=2px ,得y 2-2py -p 2=0.设A 和B 的纵坐标分别为y 1和y 2,由韦达定理知y 1+y 2=2p ,又线段AB 的中点的纵坐标为2,所以p =2.于是抛物线的准线方程为x =-1. 二、解答题12.已知抛物线C :y 2=2px (p >0)的焦点为F ,直线y =4与y 轴的交点为P ,与C 的交点为Q ,且|QF |=54|PQ |.求C 的方程;解析 设Q (x 0,4),代入y 2=2px 得x 0=8p .所以|PQ |=8p ,|QF |=p 2+x 0=p 2+8p .由题设得p 2+8p =54×8p,解得p =-2(舍去)或p =2.所以C 的方程为y 2=4x .13.若抛物线y 2=4x 上一点P 到其焦点F 的距离为3,延长PF 交抛物线于Q ,若O 为坐标原点,求△OPQ 面积S △OPQ .解析 如图所示,由题意知,抛物线的焦点F 的坐标为(1,0),又|PF |=3,由抛物线定义知:点P 到准线x =-1的距离为3,∴点P 的横坐标为2. 将x =2代入y 2=4x 得y 2=8,由图知点P 的纵坐标y =22, ∴P (2,22),∴直线PF 的方程为y =22(x -1).联立直线与抛物线的方程⎩⎨⎧y =22(x -1),y 2=4x ,解之得⎩⎪⎨⎪⎧x =12,y =-2或⎩⎨⎧x =2,y =2 2.由图知Q ⎝⎛⎭⎫12,-2,∴S △OPQ =12|OF |·|y P -y Q |=12×1×|22+2|=322.。