工程力学第3章习题解答教学教材

工程力学教程第4版第3章思考题答案_副本问题1问题描述：请说明受力分析方法的基本原理，并说明在实际工程中使用受力分析的步骤。

答案：受力分析是工程力学中常用的一种方法，用于分析物体所受的力和力的作用方向，以及这些力对物体的影响。

受力分析的基本原理是根据牛顿第二定律，即物体所受的合力等于物体的质量乘以加速度，通过受力分析可以求解物体在受力作用下的运动情况。

在实际工程中，使用受力分析的步骤如下：1.确定受力的作用方向和大小。

根据问题描述和已知条件，确定受力的作用方向和大小。

可使用向量图形表示受力的方向和大小。

2.绘制受力图。

根据受力的作用方向和大小，在纸上绘制受力图。

受力图可以使用箭头表示力的方向和长度表示力的大小。

3.分解力和合力。

根据受力图，可以将受力分解为多个力的合力。

将合力分解为多个力可以使计算更加简单，并且可以更好地理解力的作用。

4.应用牛顿第二定律求解受力的影响。

根据受力的作用方向和大小，使用牛顿第二定律求解受力的影响。

根据物体的质量和加速度，可以计算物体所受的合力。

使用受力分析可以解决物体的运动问题。

5.检查和验证结果。

在完成受力分析后，应对所得结果进行检查和验证。

可以使用其他方法验证受力分析的结果。

通过以上步骤，可以应用受力分析方法解决实际工程中的问题，该方法可以用于求解任何物体的运动情况。

问题2问题描述：请说明轴力和切力的概念，并分别给出它们的计算公式。

答案：轴力和切力是力学中的两个重要概念，用于描述杆件或梁的受力情况。

轴力是指垂直于横截面的力，也可以理解为沿着杆件轴线的力。

轴力的计算公式为：N = A·σ其中，N表示轴力，A表示横截面积，σ表示单位面积上的轴向应力。

切力是指垂直于杆件轴线的力，作用在杆件截面上的力。

切力的计算公式为：Q = A·τ其中，Q表示切力，A表示横截面积，τ表示单位面积上的切应力。

轴力和切力是杆件或梁内力的两个分量，通过计算轴力和切力可以确定杆件或梁在受力状态下的内力分布情况。

方向 作用点
cos( FR, i
)
Fix FR
cos( FR,
j)
Fiy FR
作用于简化中心上
主矩
MO MO (Fi )
F R
(
F x
)2
(
F y
)2
cos(F
, i
)
F x
R
FR
cos(F , R
j) (Fix Fiy Fiy Fix ) (3 2)
Fy 0 FAy P F cos 60 0
解得 FAy 300kN
MA 0
MA M F1l F cos 60 l F sin 60 3l 0
解得 MA 1188kN m
例3-2 已知: F=20kN, q=10kN/m,M 20kNm, L=1m; 求: A,B处的约束力. 解: 取CD梁,画受力图.
节点法与截面法
1、节点法 2、截面法
例3-1 已知：P 100kN, M 20kN m,
q 20kN m, l 1m; F 400kN,
求： 固定端A处约束力。 解：取T型刚架，画受力图。
其中
1
F1
F x
q 3l 30kN 2
0 FAx F1
F
sin 600
0
解得 FAx 316.4kN
解得 F1 10kN (压)
Fix 0 F2 F1 cos 300 0
解得 F2 8.66kN(拉)
取节点C,画受力图.
Fix 0 F4 cos 300 F1' cos 300 0
解得 F4 10kN (压)
Fiy 0 F3 F1' F4 sin 300 0
解得 F3 10kN(拉)

6
力偶的等效条件
作用于刚体上的两个力偶等效的条件是力偶矩矢相等， 即两个力偶矩矢相等的力偶等效。
力偶的性质
性质一 力偶不能与一个力等效,也不能与一个力平衡。 性质二 力偶可在其作用面或平行平面内任意移动,而 不改变力偶对刚体的作用效应。
性质三 只要力偶矩矢的大小与方向不变,即使改变力 与力偶臂的大小，均不改变力偶对刚体的作用效应。
工程力学（静力学与材料力学）
4
§2 力偶矩矢与力偶的性质
力偶
力偶-等值、反向、作用线平行的力F与F’组成的力系, 并用（F,F’）表示。
力偶作用面-两力作用线所在平面
力偶臂-两力作用线间垂直距离d
力偶系-作用于刚体上的一组力偶
平面力偶系-各力偶作用面的方位 相同的力偶系
空间力偶系-各力偶作用面的方位
工程力学（静力学与材料力学）
7
§3 力偶系的合成与平衡条件
力偶系的合成
刚体上两个力偶,力偶矩矢 M1与M2，转换至A与B点,得
M1rF1 M2 rF2
F F1F2 形成M
M rF r(F1F2) rF1rF2
M M1M2 MR
n
MR Mi
i1
空间力偶系可合成为一合力偶，其力偶矩矢等于
系内各分力偶矩矢的矢量和 。
MO (F )Fd
MO (F ) 2ABO
平面力对点之矩是代数量，使刚体绕矩心沿逆时针
方向转动者为正，反之为负。
工程力学（静力学与材料力学）
2
力对点之矩矢
空间力系各力，使刚体绕同一点转动的转轴方位不 同, 力对点之矩应该用矢量表示，即力对点之矩矢。
MO (F ) r F
r-A点对于O点的矢径 rF Frsin Fd

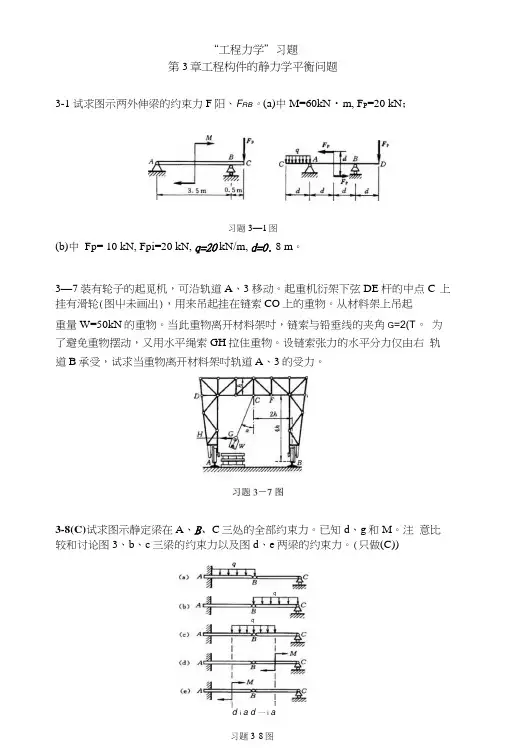
“工程力学”习题第3章工程构件的静力学平衡问题3-1试求图示两外伸梁的约束力F阳、F RB。

(a)中M=60kN・m, F P=20 kN；习题3—1图(b)中Fp= 10 kN, Fpi=20 kN, q=20 kN/m, d=0. 8 m。

3—7装有轮子的起觅机，可沿轨道A、3移动。

起重机衍架下弦DE杆的中点C 上挂有滑轮(图屮未画出)，用来吊起挂在链索CO上的重物。

从材料架上吊起重量W=50kN的重物。

当此重物离开材料架吋，链索与铅垂线的夹角G=2(T。

为了避免重物摆动，又用水平绳索GH拉住重物。

设链索张力的水平分力仅由右轨道B承受，试求当重物离开材料架吋轨道A、3的受力。

3-8(C)试求图示静定梁在A、B、C三处的全部约束力。

已知d、g和M。

注意比较和讨论图3、b、c三梁的约束力以及图d、e两梁的约束力。

(只做(C))qq| Id i a d一i a习题3-8图3-11飞机起落架由弹簧液压杆4D和油缸D以及连杆OB和CB组成，0、A、B、C处均为較链。

假设：飞机起飞或降落时以匀速沿着跑道运动。

轮子所支承的载荷为24 k乂试求A处销钉所受的力。

习题3-11图3-13图示为汽车台秤简图，BCF为整体台面，杠杆AB可绕轴0转动，B、C、D三处均为較链，杆DC处于水平位置。

假设法码和汽车的重量分别为皿和临。

试求平衡时M和M之间的关系。

习题3—13图3-14体重为W的体操运动员在吊环上做十字支撑。

图屮d为两肩关节间的距离。

皿为两臂总重量。

已知/、0、d、阳和假设手臂为均质杆，试求肩关节受力.习题3-14图3-16尖劈起重装置如图所示。

尖劈A的顶角为物块B上受力F Q的作用。

尖劈A与物块B之间的静摩擦因数为/s （有滚珠处摩擦力忽略不计）。

如不计尖劈A和物块B的重量，试求保持平衡时，施加在尖劈A上的力Fp的范围。

习题3-16图3-17砖夹的宽度为250 mm,杆件AGB和GCED在G点较接。

已知：砖的重量为W；提砖的合力为F P,作用在砖夹的对称中心线上；尺寸如图所示；砖夹与砖之间的静摩擦因数；s = 0. 5。

工程力学
Engineering Mechanics
中南大学土木建筑学院力学系
Department of Mechanics of School of Civil Engineering and Architecture of Central South University
第三章 力偶系 §3-1 力对点之矩矢
力偶臂d 力偶臂 1=200mm， ，
，力偶臂d ， F2 = F2' = 120N，力偶臂 2=300mm ， F3 = F3' = 80 N，
M 1 = 100 × 0.2 = 20
N.m N.m
M 2 = 120 × 0.3 = 36
M 3 = 80 × 0.18 = 14.4 N.m
M Rx M Ry = ∑ M y = M 1 = 20 N.m
二、力对轴之矩的 解析表达式
M x ( F ) = M x ( Fy ) + M x ( Fz ) = -zFy + yFz M y ( F ) = M y ( Fz ) + M y ( Fx ) = -xFz + zFx M z ( F ) = M z ( Fx ) + M z ( Fy ) = -yFx + xFy
M R = M1 + M 2 + ⋅ ⋅ ⋅ + M n = ∑ M
M R = M1 + M 2 + ⋅ ⋅ ⋅ + M n = ∑ M
合力偶矩矢的大小 M R = ( ∑ M x ) 2 + ( ∑ M y )2 + ( ∑ M z )2 合力偶矩矢的方向
R
∑M cos( M ，i ) =
cos( M R，j ) = MR

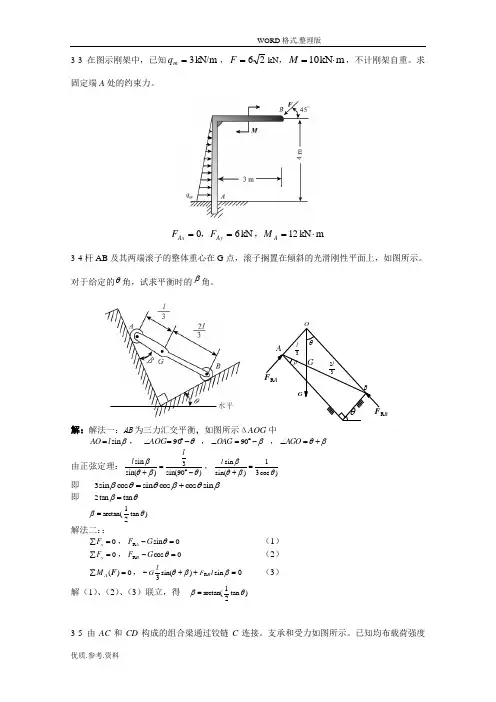
3-3在图示刚架中，已知kN/m 3=m q ，26=F kN ，m kN 10⋅=M ，不计刚架自重。

求固定端A 处的约束力。

m kN 12kN 60⋅===A Ay Ax M F F ，，3-4杆AB 及其两端滚子的整体重心在G 点，滚子搁置在倾斜的光滑刚性平面上，如图所示。

对于给定的θ角，试求平衡时的β角。

B解：解法一：AB 为三力汇交平衡，如图所示ΔAOG 中 βs i n l AO =， θ-︒=∠90AOG ，β-︒=∠90OAG ，βθ+=∠AGO由正弦定理：)90sin(3)sin(sin θβθβ-︒=+ll ，)cos 31)sin(sin θβθβ=+l 即 βθβθθβs i n c o s c o s s i n c o s s i n 3+=即 θβt a n t a n 2=)t a n21a r c t a n (θβ= 解法二：：0=∑x F ，0sin R =-θG F A （1） 0=∑y F ，0cos R =-θG F B（2） 0)(=∑F A M ，0sin )sin(3R =++-ββθl F l G B（3）解（1）、（2）、（3）联立，得 )t a n21a r c t a n (θβ=3-5 由AC 和CD 构成的组合梁通过铰链C 连接。

支承和受力如图所示。

已知均布载荷强度kN/m 10=q ，力偶矩m kN 40⋅=M ，不计梁重。

kN 15kN 5kN 40kN 15===-=D C B A F F F F ；；；解：取CD 段为研究对象，受力如图所示。

0)(=∑F CM，024=--q M F D ；kN 15=D F取图整体为研究对象，受力如图所示。

0)(=∑F AM ，01682=--+q M F F D B；kN 40=B F0=∑yF ，04=+-+D BAyF q F F ；kN 15-=Ay F0=∑x F ，0=AxF3-6如图所示，组合梁由AC 和DC 两段铰接构成，起重机放在梁上。

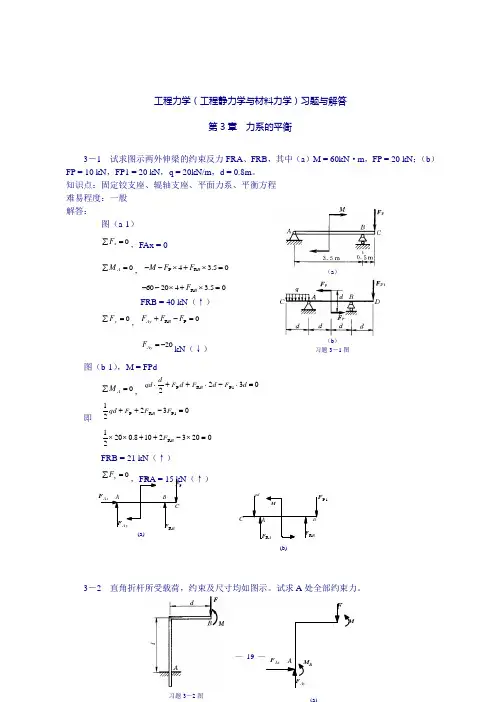
工程力学（工程静力学与材料力学）习题与解答第3章 力系的平衡3－1 试求图示两外伸梁的约束反力FRA 、FRB ，其中（a ）M = 60kN ·m ，FP = 20 kN ；（b ）FP = 10 kN ，FP1 = 20 kN ，q = 20kN/m ，d = 0.8m 。

知识点：固定铰支座、辊轴支座、平面力系、平衡方程 难易程度：一般 解答：图（a-1） 0=∑x F ，FAx = 00=∑A M ，05.34R P =⨯+⨯--B F F M 05.342060R =⨯+⨯--B F FRB = 40 kN （↑）=∑y F ，0P R =-+F F F B Ay20-=Ay F kN （↓）图（b-1），M = FPd 0=∑A M ，03221P R P =⋅-⋅++⋅d F d F d F dqd B即 032211P R P =-++F F F qd B 02032108.02021R =⨯-++⨯⨯B FFRB = 21 kN （↑）=∑y F ，FRA = 15 kN （↑）3－2 直角折杆所受载荷，约束及尺寸均如图示。

试求A 处全部约束力。

A MB Ay F B R F CAx F PF(a) M A B B R F A R F P 1F C qdBD(b)（a ）（b ） 习题3－1图FMB习题3－3图sF W A F ABF BF AN F(a)知识点：固定端约束、平面力系、平衡方程 难易程度：一般 解答： 图（a ）： 0=∑x F ，0=Ax F=∑y F ，=Ay F （↑）0=∑A M ，0=-+Fd M M AM Fd M A -=3－3 图示拖车重W = 20kN ，汽车对它的牵引力FS = 10 kN 。

试求拖车匀速直线行驶时，车轮A 、B 对地面的正压力。

知识点：固定端约束、平面力系、平衡方程 难易程度：一般解答： 图（a ）：0)(=∑F A M 08.214.1NB S =⨯+⨯-⨯-F F W6.13NB =F kN=∑y F ，4.6NA =F kN3－4 图示起重机ABC 具有铅垂转动轴AB ，起重机重W = 3.5kN ，重心在D 。

第三章 平衡方程的应用习题解析3—1静定多跨梁的荷载及尺寸如图3－1所示，长度单位为m ，求支座反力和中间铰处的压力。

图3－1 题3—1图解：a)按照约束的性质画静定多跨梁BC 段受力图（见图3-2），对于BC 梁由平衡条件得到如下方程：图3－2062021660cos ,0)(201=⨯⨯-⨯=∑=NC ni i B F F M ，kN 120=NC F060sin ,001=-=∑=NC Bx ni ix F F F ， kN 9.10360sin 0==NC Bx F F060cos kN 620,001=+⨯-=∑=NC By ni iy F F F ， kN F By 60=故支座反力C 反力kN 120=NC F ，方向垂直与支撑面；中间铰处B 的压力kN 9.103=Bx F 、kN 60=By F 。

如果同学有兴趣，可以进一步计算固定端A 约束反力，按照约束的性质画AB 段受力图（见图3-3），由作用反作用定律得'Bx F Bx F =kN 9.103=、'By F By F =kN 60=。

对于BC 梁由平衡条件得到如下方程：图3-3'1,0Bx Ax ni ix F F F ==∑=kN 9.103=01=∑=ni iy F ， 'By Ay F F =kN 60=0340,0)('1=⨯-⋅-=∑=By A ni i A F m kN M F M ，A M m kN ⋅=220b) 按照约束的性质画静定多跨梁ABC 段、CD 段受力图（见图3-4），对于BC 梁由平衡条件得到如下方程：图3－40m kN 22.521m kN 54,0)(21=⋅⨯⨯-⋅-⨯=∑=ND ni i C F F M ， m kN 5.2⋅=ND F0,01==∑=Cx ni ix F F0kN 25.2,01=+⨯-=∑=ND Cy ni iy F F F ， kN 5.2=Cy F由作用反作用定律得'Cx F Cx F ==0、'Cy F Cy F =kN 5.2=。

《工程力学》第三章精选习题及解答提示3—1 图示空间三力5001=F N ，10002=F N ，7003=F N ，求此三力在x ，y ，z 轴上的投影；并写出三力矢量表达式。

【解】（1）求三力在x ，y ，z 轴上的投影。

力1F的投影： ⎪⎪⎪⎩⎪⎪⎪⎨⎧=⨯=+⨯==⨯=+⨯-=N 224515002110N 447525002122211112211F F y xoz F F F F z y x 轴垂直）坐标面内，与位于—（———＝－－ 力2F 的投影（采用二次投影法）：⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=⨯=++⨯=-=⨯-=+⨯+++⨯-=⨯=+⨯+++⨯-=N 26714110003211N 802143100032132132N 53514210003223213222222222222222222222222F F F F F F z y x ＝－－ 力3F 的投影（3F 位于xoy 坐标面内，与x 轴平行同向）：⎪⎩⎪⎨⎧====00N 7003333z y x F F F F（2）写出三力的矢量表达式： k i k F j F i F F z y x ⋅+⋅-=⋅+⋅+⋅=2244471111 k j i k F j F i F F z y x ⋅+⋅-⋅-=⋅+⋅+⋅=2678025352222 i k F j F i F F z y x ⋅=⋅+⋅+⋅=7003333 3—2 半径为r 的斜齿轮，其上作用有力F ，如图所示。

已知角α和角β，求力F 沿坐标轴的投影及力F 对y 轴之矩。

【解】（1）求力在坐标轴的投影。

根据图中所示的力F 的位置关系，可知本题宜采用二次投影法：⎪⎩⎪⎨⎧⋅-=⋅⋅-=⋅⋅=αβαβαsin cos cos sin cos F F F F F F z y x（2）求力F 对y 轴之矩： 由图可知，力F 可分解为三个分力，分别是：轴向力a F ；径向力r F ；圆周力t F ，即： t r a F F F F ++=由合力矩定理得：βαβαsin cos sin cos 00)()()()(⋅⋅⋅=⋅⋅⋅++=++=r F r F F m F m F m F m t y r y a y y 3—3 铅垂力500=F N ，作用于曲柄上，如图所示，求该力对于各坐标轴之矩。

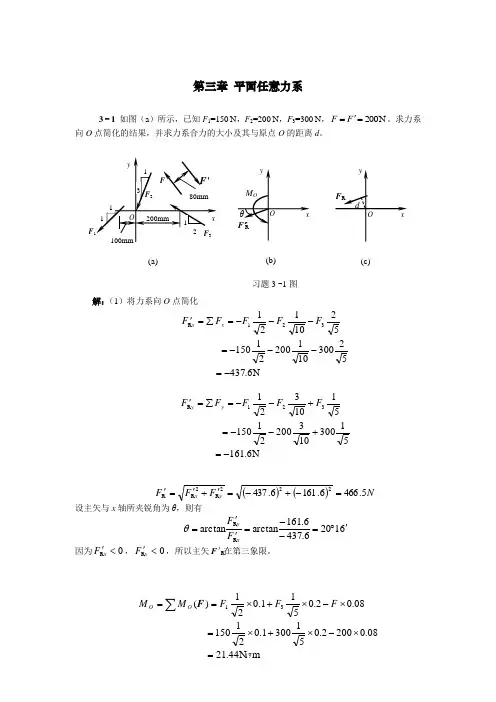
第三章 平面任意力系3-1 如图（a ）所示，已知F 1=150N ，F 2=200N ，F 3=300N ，N 200='=F F 。

求力系向O 点简化的结果，并求力系合力的大小及其与原点O 的距离d 。

解：（1）将力系向O 点简化N6.43752300101200211505210121321R-=---=---=∑='F F F F F x xN6.16151300103200211505110321321R-=+--=+--=∑='F F F F F y y()()N F F F y x 5.4666.1616.437222R 2R R=-+-='+'='设主矢与x 轴所夹锐角为θ，则有61206.4376.161arctanarctanRR '︒=--=''=x y F F θ因为0R <'x F ，0R <'y F ，所以主矢F ＇R在第三象限。

08.02002.0513001.02115008.02.0511.021)(31⨯-⨯+⨯=⨯-⨯+⨯==∑F F F M M O O F(a)(b) (c)将力系向O 点简化的结果如图（b ）。

(2)因为主矢和主矩都不为零，所以此力系可以简化为一个合力如图（c ），合力的大小mm 96.4504596.05.46644.21N 5.466RR R ====='=m F M d F F o3-2重力坝的横截面形状如图（a ）所示。

为了计算的方便，取坝的长度（垂直于图面）l =1m 。

已知混凝土的密度为2.4×103 kg/m 3，水的密度为1×103 kg/m 3，试求坝体的重力W 1，W 2和水压力P 的合力F R ，并计算F R 的作用线与x 轴交点的坐标x 。

解：（1）求坝体的重力W 1，W 2和水压力P 的大小kNN dy y dy y q P mN y dyy dy y q 5.9922105.9922245108.9)45(108.9)()45(108.9)45(8.91011)(3234534533=⨯=⨯⨯=⋅-⨯=⋅=-⨯=-⨯⨯⨯⨯⨯=⎰⎰（2）将坝体的重力W 1，W 2和水压力P 向O 点简化，则kN 5.9922R==∑='P F F x xkN 3057621168940821R-=--=--=∑='W W F F y y()kN 7.32145305765.9922222R 2R R=-+='+'='y x F F FkN N W kN N W 2116810211688.9104.2136)545(2194081094088.9104.218)545(332331=⨯=⨯⨯⨯⨯⨯+==⨯=⨯⨯⨯⨯⨯+=(a) (b) (c)设主矢与x 轴所夹锐角为θ，则有︒=-=''= 02.725.992230576arctanarctanRR x y F F θ因为0R >'x F ，0R <'y F ，所以主矢F ＇R在第四象限，如图（b ）。

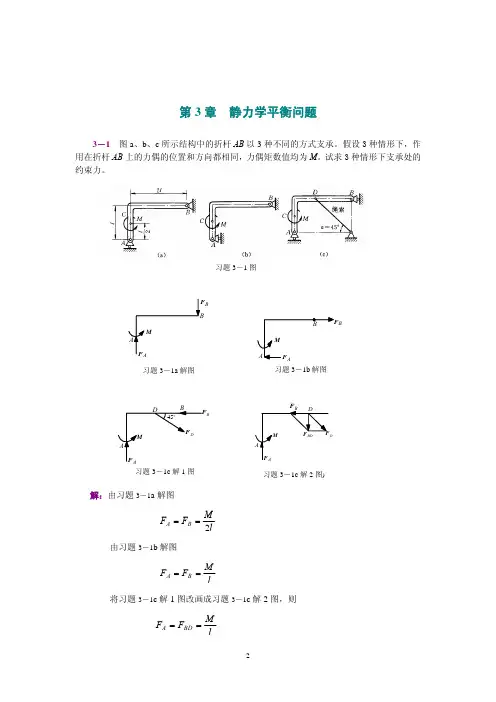
第3章 静力学平衡问题3－1 图a 、b 、c 所示结构中的折杆AB 以3种不同的方式支承。

假设3种情形下，作用在折杆AB 上的力偶的位置和方向都相同，力偶矩数值均为M 。

试求3种情形下支承处的约束力。

解：由习题3－1a 解图lM F F B A 2== 由习题3－1b 解图lM F F B A == 将习题3－1c 解1图改画成习题3－1c 解2图，则lM F F BD A ==习题3－1c 解2图)B习题3－1c 解1图B习题3－1b 解图习题3－1图B习题3－1a 解图'B A习题3－2解2图∴ l M F F BD B ==， lMF F BD D 22==3－2 图示的结构中，各构件的自重都略去不计。

在构件AB 上作用一力偶，其力偶矩数值M ＝800 N·m 。

试求支承A 和C 处的约束力。

解：BC 为二力构件，其受力图如习题3－2解1图所示。

考虑AB 平衡，由习题3－2解图，A 、B 二处的形成力偶与外加力偶平衡。

800269.4N 1.81.2A B M F F BD ′====3－3 图示的提升机构中，物体放在小台车C 上，小台车上装有A 、B 轮，可沿垂导轨ED 上下运动。

已知物体重2 kN 。

试求导轨对A 、B 轮的约束力。

解： W = 2kN ，T = W ΣF x = 0， F A = F BΣM i = 0， 0800300=×−×A F W ，kN 75.083==W FA ，FB = 0.75 kN ，方向如图示。

习题3－2图习题3－3图BF C习题3－2解1图 A F BF习题3－3解图MA习题3－4解1图3－4 结构的受力和尺寸如图所示，求：结构中杆1、2、3杆所受的力。

解：1、2、3杆均为为二力杆 由习题3－4解1图ΣM i = 0，03=−⋅M d F ,dMF =3, F = F 3（压） 由习题3－4解2图ΣF x = 0，F 2 = 0, ΣF y = 0，dMF F ==1（拉）3－5 为了测定飞机螺旋桨所受的空气阻力偶，可将飞机水平放置，其一轮搁置在地秤上。

第三章平面一般力系答案一、填空(将正确的答案填写在横线上)1、作用在物体上的各力的作用线都在同一平面内 ,并呈任意分布的力系,称为平面一般力系。

2、平面一般力系的两个基本问题是平面力系的简化 ,其平面条件的的应用。

3、力的平移定理表明,若将作用在物体某点的力平移到物体上的另一点,而不改变原力对物体的作用效果,则必须附加一力偶,其力偶距等于原来的力对新作用点的距。

4、平面一般力系向已知中心点简化后得到一力和一力偶距。

5平面一般力系的平衡条件为;各力在任意两个相互垂直的坐标轴上的分量的代数和均为零力系中所有的力对平面内任意点的力距的代数和也等零。

6.平面一般力系平衡方程中,两个投影式ΣFix=0 和ΣFiy=0 保证物体不发生移动 ;一个力矩式ΣMo(Fi)=0 保证物体不发生转动。

三个独立的方程,可以求解三个未知量。

7.平面一般力系平衡问题的求解中,固定铰链的约束反力可以分解为相互垂直的两个分力固定端约束反力可以简化为相互垂直的两个分力和一个附加力偶矩。

8.平衡方程ΣMA(Fi)=0、ΣMB(Fi)=0、ΣFiX=0适用于平面一般力系,使其用限制条件为AB连线与X轴不垂直。

9.平衡方程ΣMA(Fi)=0、ΣMB(Fi)=0、ΣMc(Fi)=0的使用限制条约为ABC不在同一直线上。

10.若力系中的各力作用现在同一平面内且相互平行,称为平面平行力系。

它是平面一般力系的特殊情况。

11.平面平行力系有两个独立方程,可以解出两个未知量。

12.平面平行力系的基本平衡方程是：ΣFi X=0，ΣM O(Fi)=0二、判断题（正确的打“√”，错误的打“×”）1.作用于物体上的力,其作用线可在物体上任意平行移动,其作用效果不变。

(×)2.平面一般力系的平衡方程可用于求解各种平面力系的平衡问题。

(√)3.若用平衡方程解出未知力为负值,则表明：(1)该力的真实方向与受力图上假设的方向相反。

(√)(2)该力在坐标轴上的投影一定为负值。

第3章 力系的平衡（一）（平面汇交力系的平衡）3-1 各种支架如题3-1图（a ）、（b ）、（c ）和（d ）所示，由杆AB 与AC 组成，A 、B 与C 均为铰链，在销钉A 上悬挂重量为W 的重物。

试求图示4种情况下，杆AB 与AC 所受的力。

题3-1解：情况如题3-1图（a ）所示，取铰A 为研究对象，作受力图如题3-1图（a1）所示.由平衡方程 0X=∑，cos 600AB AC S S -+=0Y=∑，sin 600A C S W --=得 1.155sin 30A C WS W==(压力)cos 60 1.155cos 600.577AB AC S S W W===（拉力）情况（b ）如题3-1图（b ）所示，取铰A 为研究对象，作受力图如题3-1图（b 1）所示.由平衡方程 0X =∑，cos 700AC AB S S -=0Y=∑，sin 700AB S W -=得 1.064sin 30A B WS W==(拉力)cos 70 1.064cos 700.364AC AB S S W W===（压力）情况（c ）如题3-1图（c ）所示，取铰A 为研究对象，作受力图如题3-1图（c 1）所示.由平衡方程 0X=∑，cos 300AC S W -=0Y=∑，sin 300AB S W -=得 cos 300.866AC S W W == (拉力)sin 300.5AB S W W==（压力）情况（d ）如题3-1图（d ）所示，取铰A 为研究对象，作受力图如题3-1图（d 1）所示.由平衡方程 0X =∑，sin 30sin 300AC AB S S -+=0Y=∑，cos 30cos 300AC AB S S W +-=得 0.5772cos 30A C AB W S S W===(拉力)3-2 题3-2图（a ）所示的电动机重5W kN =，放在水平梁AC 的中间，A 和B 为固定铰链，C 为中间铰链。

ln
=
l n
3－11 厂房构架为三铰拱架，由两片拱架在 C 处铰接而成。桥式吊车沿着垂直于纸面
方向的轨道行驶，吊车梁的重量 W1＝20 kN，其重心在梁的中点。梁上的小车和起吊重物的
重量 W2＝60 kN。两个拱架的重量均为 W3＝60 kN，二者的重心分别在 D、E 二点，正好与
吊车梁的轨道在同一铅垂线上。风的合力为 10 kN，方向水平。试求：当小车位于离左边轨
ΣFy = 0， FAy = FB′y = qd （↑）； （c） 题解：
图（c1）：
ΣFx = 0， FBx = 0
ΣMB
=
0，
−
qd
⋅
d 2
+ FRC
⋅ 2d
= 0 ， FRC
=
qd 4
（↑）
ΣFy = 0， FBy + FRC − qd = 0 ，
FBy
=
3 4
qd
（↑）
图（c2）：
ΣFx = 0，FAx = 0
ΣFy
=
0，
FAy
=
qd
+
FB′y
=
7 4
qd
（↑）
ΣMA
=
0， M A
−
FB′y
⋅ 2d
− qd
⋅
3d 2
=0
（d） 题解：
∴ MA = 3qd 2（逆时针）；
图（d1）：
ΣMB
=
0， FRC
=
M 2d
（↑）
ΣFy
=
0，
FBy
=
M 2d
（↓）
8
(c)
A
q
B

题3-2图试绘下列各轴的扭矩图，并求出 。

已知ma=2o oN ・ m,mb=4OoN.m,mc=6ooN,m.<10<b)弟二早习题3-1试求图视各轴在指定横截面17、2・2和3・3上的扭矩，并在各截面上表示出钮 矩的方向。

3・2试绘岀下列各轴的钮矩图，并求c=©==®zz ©=3m 2m3znm4 税(a)3-4 一传动轴如图所示，已知 ma=i3oN..cm, mb=3OoN.cm , mc=iooN.cm,md=7oN.cm;^$段轴的直径分别为：Dab=5cm, Dbc=7・5cm, Dcd=5cm （1）画出扭矩图；<2）求1-4、2-2、3-3截面的最大切应力。

3・5图示的空心圆轴，外径D=8cm,内径d二6・巧5,承受扭矩m=ioooN.m・（1）求弘、％（2）绘出横截而上的切应力分布图；（3）求单位长度扭转角，已知G=8ooooMpa・3-6已知变截而钢轴上的外力偶矩^^SooN.m, =i2ooN.m,试求最大切应力和最大相对扭矩。

已知G=8o*l沪Pa.题3-6图3-7 一钢轴的转矩n=24o/min.传递功率丹=44」kN.m.已知L可=4ol\4pa,2」」3,G=8o*l，MPa,试按强度和刚度条件计算轴的直径解：轴的直径由强度条件确泄，3-8图示实心轴通过牙嵌离合器把功率传给空心轴。

传递的功率=7-5kw,轴的转速n=ioor/min,试选择实心轴直径和空心轴外径叫2。

己知％/空2 =0.5，[rlL J=4oMpa・3-9图示AB轴的转速 n=i2or/min,AK B 轮上输入功率丹=4okw,此功率的一半通过锥齿轮传给垂直轴V,另一半功率由水平轴H传走。

已知锥齿轮的节圆直径 a=6oomm：各轴宜径为^=ioomm, ^2=8omm, ^3=6omm, t^=2oMPa.试对各轴进行强度校核。

3-1。

船用推进器的轴，一段是实心的，直径为28omm,列一段是空心的，其内径为外径的一半。

sin ( ) 3 cos )
即 3 sin cos sin cos cos sin
习题 3－4 图
即 2 tan tan
1
O
2
注：在学完本书第 3 章后，可用下法求解： Fx 0 ， FRAG sin 0
Fy 0 ， FRBG cos 0
M A (F ) 0
，G
l s3in(
)
FRB
l
解：（a），CD 为二力杆； 图（c）— 力偶系
ΣMi = 0
FRA FRC M 2 M
2
d
d
2
习题 3－11 图
— 11 —
（b）AB 为二力杆
图（d）：ΣMi = 0， FRC FD M ，
d
FRA FD M d
FD
D
A
45
D BM
M
FRA
FRC
C
FRC
FRA
A
FD' B
D
(d)
(e)
(c)
F
q
5 (6 2l) 340l 0
3
l = 1m 即 lmax = 1m
C 6 l (a)
D FR D
l
3－18 木支架结构的尺寸如图所示，各杆在 A、D、E、
F 处均以螺栓连接，C、D 处用铰链与地面连接，在水平杆 AB
的 B 端挂一重物，其重 W = 5kN。若不计各杆的重，试求 C、
G、A、E 各点的约束力。
3－10 试求图示结构中杆 1、2、3 所受的力。 解：杆 3 为二力杆 图（a）：
ΣMi = 0
F3 dM 0 M
F3 d
F = F3 （压） 图（b）：

水平尾翼的约束。
车刀
利用平面任意力系的简化讨论固定端约束（以雨搭为例）：
Fi
A
雨搭
雨搭
简化为一个平面任意力系
MA
A
FA
雨搭
FAy
MA
A
FAx
雨搭
向A处简化，简化结果是 一个主矢加一个主矩
主矢方向待定，用两正交分 量表示
例1：已知F1=150N，F2=200N，F3=300N，F=F ́=200N。求此力 系向原点O简化的结果，并求力系的合力。
2
M=0
FR′≠0
3
M=0
合力
合力
合力作用线通过简化中心
合力作用线距离简化中心距离
4
M≠0
d M O / FR
第三种和第四种结果属于同一种情形。是简化中心选择的不同 引起的。
四、合力矩定理
可以证明，M O ( FR ) M O ( Fi )
i 1
n
由于简化中心可任取，因此上式有普遍意义，可描述为：平 面任意力系的合力对作用面内任一点之矩等于力系中各分力 对于同一点之矩的代数和。
4、在列平衡方程时，最好将力矩方程的矩心取为两个未知力的 交点，而对投影方程的投影轴的选取，应尽可能使其与某些未知 力垂直，为什么？ 答：避免解联立方程，使方程尽量简单。
5、在等腰直角三角形上的A、B、C三点分别作用三个力，各力 的大小和方向如图所示。问该力系是否平衡？为什么？
问题引入：平面任意力系研究物体或物系在受到相关力系作用
下的平衡问题。
吊车：工程中吊车的
起重载荷如何进行计
算？
破碎机：鄂式破碎机是矿山机械中常见的机械设备，颚板作用 给矿石的作用力应如何进行计算？