基于origin7.5的单峰、多峰拟合与面积计算

关于origin计算面积的详解
（一）一般步骤计算曲线与坐标轴间的面积
利用Analysis → mathematics →integrate 命令进行操作：
Input：输入计算区域；
Row：也可以手动选择计算区间；
Area type: 进行积分的方式；
Plot integrated curve：是否画出积分曲线；Result log output：结果是否显示；
例. 计算下图中在区间[10,40]中，曲线与x轴形成的面积。

Analysis → mathematics →integrate，选择行 From 10 To 40 ，点击ok，生成计算结果。

（二）峰面积的计算（曲线和基线形成的面积）例求下图中的各峰面积。

解法1 可以采用多峰积分的方法
Analysis →Spectroscopy →Integrate Multiple Peaks
就会出现以下对话框，峰数选择3，就会出现3个黄色区域，baseline选择connect line，鼠标选中其中的黄色框就可以得到该区域中峰面积。

解法 2 可以采用基线和峰分析向导计算（Baseline and Peaks）
Analysis → Spectroscopy →Baseline and Peaks，出现以下对话框
点击next，进入下一步
峰数选择3，会出现3个黄色框分别包含3个峰（注. 黄色框是可以移动和缩放的，作用是改变选择的区间），接下来的步骤都是点击
next，最后点击finish，完成。

积分结果会在工作表中显示。

如下。

Origin教程｜如何利⽤origin进⾏数据曲线分峰拟合和峰⾯积积分2020-02-06之前，我们分享了Origin教程|如何改变散点图形状、颜⾊、⼤⼩Origin教程|如何快速让数据曲线纵向均匀分布Origin教程|如何给柱状图上加正态分布曲线Origin教程|如何更改Lable和设置⾮均匀坐标Origin教程|如何在origin中拉平曲线基线（XRD、FT-IR、RAMAN等）今天，我们分享Origin教程|如何利⽤origin进⾏数据曲线分峰拟合和峰⾯积积分⾮原创下⾯开始以之前⼀个拉曼数据为例，得到了测试数据，但需要知道两个峰强度⽐值，⽽通过查阅强度⽐值对应则是分峰后对应峰⾯积⽐值，因此在这做个流程教学。

⾸先，这是测试得到的数据这是通过基线矫正得到的曲线过程可参考：Origin教程|如何在origin中拉平曲线基线（XRD、FT-IR、RAMAN等）下⾯开始曲线分峰拟合第⼆步：选中peaks and baseline、multiple peak fit、open dialog 第⼀步第⼀步：选中曲线第⼆步第三步：选中函数Guassian，点击OK第四步：点击明显的峰顶，按enter确认峰位和峰顶第四步第五步第五步：有⼏个明显的峰，结合参考⽂献进⾏拟合（这⼉应该是有两个峰，第⼆个峰位同样的操作）第六步：点击fit进⾏分峰拟合第六步第七步：双击曲线，将曲线的粗度设置为3，使得拟合结果更加明显第七步第⼋步：拟合相关的数据和参数返回可以查看第⼋步下⾯进⾏峰⾯积积分第⼀步：选择需要⾯积积分的峰，单击拟合线，等两秒，再单击⼀次，如下显⽰⽅为选中该峰第⼀步第⼆步：依次点击mathmatics、integrate、open dailog 第⼆步第三步第三步：打开后参数不⽤更改，直接ok第四步：打开原始⽂件旁边的积分表格，可直接读取积分⾯积值（下⾯的37122.145为上图绿第四步⾊峰的⾯积积分，其他的峰也是同样的操作）最后，经过验证，横坐标和纵坐标的设置值不影响积分⾯积，但是为保证准确、有对⽐性，同⼀组数据的应该有同样的横坐标区间，这个很重要。

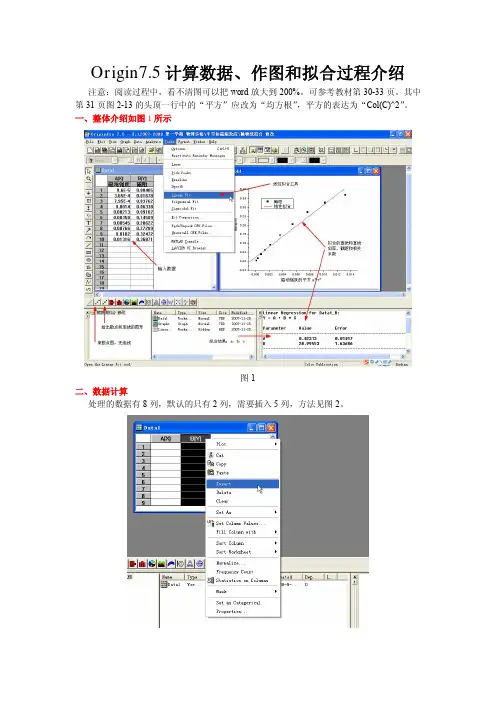
Origin7.5计算数据、作图和拟合过程介绍注意：阅读过程中，看不清图可以把word放大到200%。

可参考教材第30-33页。

其中第31页图2-13的头顶一行中的“平方”应改为“均方根”，平方的表达为“Col(C)^2”。

一、整体介绍如图1所示图1二、数据计算处理的数据有8列，默认的只有2列，需要插入5列，方法见图2。

图2得到8列表格后（见图3），双击“A(X)”后弹出菜单，在左下的“Column label”输入标签文字，方便知道该列数据代表什么物理量，如励磁电流（Im/mA）。

还可以对8列表格的名称按A、B、C、D顺序重新排列，方法见图3的“Column Name”，得到图4的效果。

排序的过程中，若要将“D”列改为“B”列，但是已经存在“B”列了，你可以先将“B”列改为“M”列，然后在修改，其他情况也类似。

图3图4是输入数据后的图，列的名称重新进行了排列。

图4三、计算数据要计算的数据有电阻R，磁感应强度B的平方（并用单位T来表示），以及磁阻MR。

1、在C列上右键，选择“Set Column V alues…”，见图5。

弹出图6的对话框。

将B列的磁场用单位T表示，因此公式为：Col(B)/1000。

图5图62、同样的方法计算F列的电阻R，公式为：Col(D)/Col(E)。

3、计算B2的数据公式为：Col(C)^2，单位用T表示；4、计算MR的公式为：(Col(F)-316.12648)/316.12648，316.12648即为R（0）的电阻值【请注意，Im=0时的电阻为R（0）】，计算结果见图7。

图7中第一MR数据应该为0，但是软件中存在保留位长度不一样，导致不为0，为10-9的一个很小值，手动改为0即可。

图7四、计算机作图作图必须有X轴和Y轴数据，X轴为磁场，Y轴为磁阻。

因此将B（Y）改为B（X），G（Y）改为G（X）。

修改的方法如图3一样，结果见图8。

而且X轴数据列必须在作图的Y轴数据列的前面。

origin计算峰面积
计算峰面积是统计学中重要的一种研究方法，它可以帮助我们快速准确地测量特定数据在某个峰值处的规模。

Origin软件是一款专业的数据处理软件，可以快速、高效地计算峰面积。

本文旨在介绍如何使用Origin来计算数据中峰值处的面积。

首先，用Origin打开所要处理的数据文件。

然后双击打开的文件，会显示一个新的窗口，窗口左侧会有一个边栏，标题为“graph”，在边栏中点击图形工具框，可以看到图表拖拽单元格中的“数据面积”命令，点击放大镜图标以缩放图表。

可以根据图表来决定何时要使用数据面积命令。

一旦确定要计算面积的数据段，就可以在图表拖拽单元中点击“数据面积”命令，会弹出一个窗口，显示数据面积的参数设置。

在右侧的面积范围栏中，可以选择计算数据在哪个峰值处的面积。

同时，可以根据需要设置面积的宽度（不包括峰值点），以及是否将必要的边界点排除在外。

最后点击确定，Origin就会计算出峰值处的面积。

在计算完成后，右下角会显示结果，可以点击结果查看详细信息。

总而言之，使用Origin软件计算峰面积非常容易，只要熟悉参数设置内容，并且搞清楚从数据中选出哪个峰值，就可以准确计算出峰值处的面积。

因此Origin软件是科学家、工程师和统计学家等团体的理想选择，在处理数据面积方面可以节省大量宝贵的时间。

- 1 -。

Origin软件中多峰拟合在化学化工领域的应用摘要：Origin是一款国际通用的具有超强功能的数据分析处理和科学绘图软件,特别适合于绘制一些数据繁多计算复杂的图形。

本文主要介绍了Origin多峰拟合在以化学化工实验数据为基础的数据处理中的具体应用。

体现出Origin强大的图形绘制与数据分析能力。

关键词：Origin软件；多峰拟合1．概述Origin是美国Origin Lab公司(其前身为Microcal公司)开发的图形可视化和数据分析处理软件，该软件主要体现二大功能——数据分析和图形绘制。

Origin的数据分析主要包括数理统计、信号处理、图像处理、峰值分析和曲线拟合等各种完善的数学分析功能。

准备好数据后，进行数据分析时，只需选择所要分析的数据，然后再选择相应的菜单命令即可。

Origin的图形绘制则是基于模板，Origin本身提供了几十种二维和三维绘图模板，而且允许用户自己定制模板。

绘图时，只要选择所需要的模板就行。

用户可以自定义数学函数、图形样式和绘图模板，可以和各种数据库软件、办公软件、图像处理软件等方便的连接。

在化学化工领域的实验数据处理中，经常需要根据两个量的一批测量值来找出这两个量之间所满足的一个关系。

在大多数实验中，两相关变量间的关系满足线性或非线性函数关系。

但是，有些实验数据不能简单地用线性或非线性函数关系来拟合或描述，例如，实验曲线出现多峰情况时。

在这种情形下，采集或确定必要的实验参数和数据往往是很烦琐的事情。

此时可以借助于准确性较高及操作简便的Origin软件的多峰实验曲线数据采集和数据处理的方法。

2．Origin软件中多峰拟合的应用Origin软件中的多峰拟合是采用Guassian或lorentzian峰函数对数据进行拟合。

用户在对话框中确定峰的数量，在图形中的峰中心处双击进行峰的拟合，完成拟合后会自动生成拟合数据报告。

2.1.多峰拟合用于烷基葡萄糖苷临界胶束浓度测量张建华[1]等将高斯多峰拟合用于烷基葡萄糖苷临界胶束浓度测量。

origin多峰拟合峰面积
拟合多峰谱需要使用一个适当的数学模型来描述峰形的特征，并使用数据拟合算法来确定每个峰的面积。

一种常用的数学模型是高斯函数，可以用来描述峰形的对称性和曲率。

高斯函数的数学表达式为:
f(x) = a * exp(-((x-b)/c)^2)
其中a是峰的幅度（或者峰面积），b是峰的位置（即峰的中心点），c是高斯函数的宽度（标准差）。

对于多峰拟合，可以将多个高斯函数线性叠加，形成一个完整的拟合函数。

拟合参数可以通过最小二乘法或其他数值优化方法来确定。

一种常用的拟合算法是非线性最小二乘拟合算法，例如Levenberg-Marquardt算法。

该算法通过迭代优化拟合函数的参数，使得拟合函数与实际数据之间的残差最小。

拟合峰面积可以通过积分拟合函数来计算，即对拟合函数在峰的范围内进行积分。

积分可以使用数值积分方法或解析积分方法来计算。

需要注意的是，在进行拟合之前，需要对数据进行预处理，例如去除背景噪音、调整峰的初始位置等。

总结起来，拟合多峰谱的峰面积需要以下步骤:
1. 选择适当的数学模型来描述峰形特征，例如高斯函数。

2. 使用拟合算法，例如Levenberg-Marquardt算法，来优化拟合函数的参数。

3. 对拟合函数进行积分，计算每个峰的面积。

值得一提的是，拟合多峰谱可能存在一些挑战，例如峰之间的重叠、峰形的非对称性、峰的数量不确定等。

在实际应用中，可能需要根据具体情况选择不同的数学模型和拟合算法，并进行参数调整和模型评估来达到较好的拟合效果。

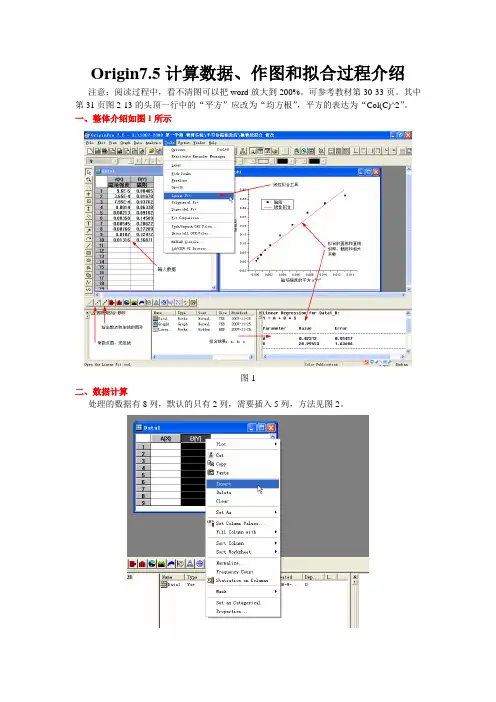
Origin7.5计算数据、作图和拟合过程介绍注意：阅读过程中，看不清图可以把word放大到200%。

可参考教材第30-33页。

其中第31页图2-13的头顶一行中的“平方”应改为“均方根”，平方的表达为“Col(C)^2”。

一、整体介绍如图1所示图1二、数据计算处理的数据有8列，默认的只有2列，需要插入5列，方法见图2。

图2得到8列表格后（见图3），双击“A(X)”后弹出菜单，在左下的“Column label”输入标签文字，方便知道该列数据代表什么物理量，如励磁电流（Im/mA）。

还可以对8列表格的名称按A、B、C、D顺序重新排列，方法见图3的“Column Name”，得到图4的效果。

排序的过程中，若要将“D”列改为“B”列，但是已经存在“B”列了，你可以先将“B”列改为“M”列，然后在修改，其他情况也类似。

图3图4是输入数据后的图，列的名称重新进行了排列。

图4三、计算数据要计算的数据有电阻R，磁感应强度B的平方（并用单位T来表示），以及磁阻MR。

1、在C列上右键，选择“Set Column Values…”，见图5。

弹出图6的对话框。

将B列的磁场用单位T表示，因此公式为：Col(B)/1000。

图5图62、同样的方法计算F列的电阻R，公式为：Col(D)/Col(E)。

3、计算B2的数据公式为：Col(C)^2，单位用T表示；4、计算MR的公式为：(Col(F)-316.12648)/316.12648，316.12648即为R（0）的电阻值【请注意，Im=0时的电阻为R（0）】，计算结果见图7。

图7中第一MR数据应该为0，但是软件中存在保留位长度不一样，导致不为0，为10-9的一个很小值，手动改为0即可。

图7四、计算机作图作图必须有X轴和Y轴数据，X轴为磁场，Y轴为磁阻。

因此将B（Y）改为B（X），G（Y）改为G（X）。

修改的方法如图3一样，结果见图8。

而且X轴数据列必须在作图的Y轴数据列的前面。

origin多峰拟合峰面积拟合峰面积是一项重要的测量分析任务，常用于确定化学分析中存在的多个峰的面积。

对于复杂的数据分析，原始多峰拟合方法被广泛使用，以准确计算每个峰的面积。

Origin软件提供了一个强大的工具来执行多峰拟合峰面积的计算，本文将介绍如何使用Origin软件来进行多峰拟合峰面积的计算。

首先，打开Origin软件并导入需要分析的数据文件。

在Origin的工具栏上选择“文件”>“导入”>“ASCII”，然后选择数据文件并导入到工作空间中。

在数据导入后，可以在Origin的工具栏上选择“分析”>“拟合”>“拟合函数”。

在拟合函数对话框中，选择合适的函数形式来拟合多峰数据。

对于多峰拟合，可以选择高斯分布函数或Lorentzian分布函数。

在此示例中，我们选择高斯分布函数。

在函数对话框中，可以设置每个峰的初值参数，并选择所需的约束条件。

初值参数是对函数拟合过程中所需的起始估计值的设置。

约束条件可用于限制拟合过程中某些参数的取值范围。

完成函数设置后，单击“确定”按钮开始拟合过程。

Origin将自动计算每个峰的面积，并生成拟合曲线。

在拟合完成后，可以通过单击“查看报告”按钮来查看拟合结果。

报告将显示每个峰的面积、拟合曲线和拟合误差等相关信息。

除了基本的多峰拟合峰面积计算，Origin还提供了其他有用的功能来进一步分析数据。

例如，可以使用Origin的积分功能来计算指定峰的积分值，从而得到特定峰的绝对面积。

此外，Origin还提供了数据可视化功能，可以通过绘制峰面积图形来直观地比较不同峰的相对面积大小。

可以选择不同的拟合参数，例如高斯峰的标准方差、Lorentzian峰的半高全宽等，来观察峰面积图形的变化。

综上所述，Origin多峰拟合峰面积是一种强大的分析工具，可用于准确计算化学分析中存在的多个峰的面积。

使用Origin软件，用户可以进行多峰拟合，并根据拟合结果进行进一步的数据分析和可视化展示。

origin 对数坐标分峰拟合在数据分析的过程中，经常会遇到对数坐标下数据进行拟合的情况。

而当数据中存在多个峰值时，我们需要进行分峰拟合，以准确地描述每个峰的特征。

本文将介绍一种常用的方法——origin对数坐标分峰拟合方法，帮助读者更好地理解和应用该方法。

首先，我们先简要介绍一下对数坐标。

对数坐标是以对数作为坐标轴单位的坐标系，它可以有效地展示数据在不同量级下的变化情况，尤其适用于展示极大或极小的数据。

在对数坐标下，数据的大小由其对应的指数值表示，而非传统线性坐标系下的实际数值。

因此，在进行数据拟合时，我们需要特别注意坐标系的选择和相关的数据变化。

那么，对数坐标分峰拟合的方法是如何实现的呢？我们可以使用Origin软件中的分峰拟合工具来完成这一任务。

首先，我们需要将数据导入到Origin软件中，并切换到对数坐标模式。

接下来，选择分峰拟合工具，并按照下面的步骤进行操作：1. 首先，选择适当的拟合函数。

根据数据的特点和需求，选择合适的函数来拟合数据。

常见的拟合函数包括高斯函数、洛伦兹函数等。

根据数据的分布情况，选择具有合适峰形的函数进行拟合。

2. 其次，设置拟合区域。

在分峰拟合中，我们通常关注特定的峰值，而对于其他部分的数据不感兴趣。

因此，我们需要设置拟合区域，将拟合的范围限定在我们关注的峰附近。

3. 然后，进行初始化参数设置。

根据我们对数据的初步了解，我们可以根据经验设定一些初始参数，以帮助拟合算法更好地收敛。

这包括峰的位置、宽度和幅度等参数。

4. 接下来，进行拟合计算。

在设置好参数后，我们可以开始进行拟合计算。

Origin软件会自动应用拟合算法，并给出拟合曲线和相关参数的结果。

5. 最后，进行结果分析和评估。

通过对拟合结果的分析和评估，我们可以判断拟合的质量和适用性。

特别是在分析多峰数据时，我们需要对每个峰的拟合结果进行评估，并进行比较和进一步的分析。

通过以上步骤，我们可以完成对数坐标下的分峰拟合。