spss聚类分析结果解释

•通过比较，可知离差平方和法（Ward’s method）分类 结果较好，将28各样本分为三类： 1.第一类包含6个元素：2、15、10、11、6、7 2.第二类包含10个元素：8、17、28、12、13、18、14、 20、21、22 3.第三类包含9个元素：3、16、23、24、4、27、5、25、 26 另有三个元素1、9、19为孤立点。 •从分类结果可以看出：1、9、19表示北京、上海、广 东三地农民属高消费生活水平；天津等第一类的农民生 活水平较高；安徽等第二类的农民生活水平为中等；陕 西等地的农民生活水平较低。
作用：变换后的数据均值为0，极差为1，且|xij*|<1， 消去了量纲的影响；在以后的分析计算中可以减 少误差的产生。
d) Maximum magnitude of 1
xij max x 1 i n ij * xij x ij 1 min x ij 1 i n 若 max xij 0 i 1, 2, , n j 1, 2, , m 若 max xij 0
以下我们结合实际例子分步进行讨论。
例、下表给出了1982年全国28个省、市、自治区农民家 庭收支情况，有六个指标，是利用调查资料进行聚类分 析，为经济发展决策提供依据。 （详见文件1982―农民生活消费聚类.sav‖） 1. 数据预处理（标准化） 1) 为什么要做数据变换 →指标变量的量纲不同或数量级相差很大，为了使这 些数据能放到一起加以比较，常需做变换。
1) 系统聚类法的产生 系统聚类法的聚类原则决定于样品间的距离（或相 似系数）及类间距离的定义，类间距离的不同定义就 产生了不同的系统聚类分析方法。 2) SPSS中如何选择系统聚类法 从Cluster Method框中 点击向下箭头，将出 现如左可选项，从中 选一即可。

算法步骤：初始 化聚类中心、分 配数据点到最近 的聚类中心、重 新计算聚类中心、 迭代直到聚类中 心不再变化
适用场景：探索 性数据分析、市 场细分、异常值 检测等
注意事项：选择 合适的聚类数目、 处理空值和异常 值、考虑数据的 尺度问题
定义：根据数据点间的距离或相似性，将数据点分为多个类别的过程 常用方法：层次聚类、K-均值聚类、DBSCAN聚类等 适用场景：适用于探索性数据分析，发现数据中的模式和结构 注意事项：选择合适的距离度量方法、确定合适的类别数目等
常见的聚类分析方法包括层次聚类、Kmeans聚类、DBSCAN聚类等。
聚类分析基于数据的相似性或距离度量， 将相似的数据点归为一类，使得同一类 中的数据点尽可能相似，不同类之间的 数据点尽可能不同。
聚类分析广泛应用于数据挖掘、市场细分、 模式识别等领域。
K-means聚类：将数据划分为K个簇，使得每个数据点到所在簇中心的距离之和最小
聚类结果的可视化：通过图表展示聚类结果 聚类质量的评估：使用适当的指标评估聚类效果的好坏 聚类结果的解释：根据实际需求和背景知识，对聚类结果进行合理的解释和解读 聚类结果的应用：探讨聚类结果在各个领域的应用场景和价值
SPSS聚类分析常 用方法
定义：将数据集 划分为K个聚类， 使得每个数据点 属于最近的聚类 中心
聚类结果展示：通过图表或表格展示聚类结果，包括各类别的样本数和占比
聚类质量评估：采用适当的指标评估聚类效果，如轮廓系数、Davies-Bouldin指数等
聚类结果解读：根据业务背景和数据特征，解释各类别的含义和特征 聚类结果应用：说明聚类分析在具体场景中的应用，如市场细分、客户分类等
SPSS聚类分析注 意事项
确定聚类变量：选 择与聚类目标相关 的变量，确保变量 间无高度相关性。

SPSS聚类分析实例讲解SPSS是一款功能强大的统计分析软件，可用于数据清洗、描述统计分析、假设检验和聚类分析等。

聚类分析是一种无监督学习方法，其目标是按照数据的相似性度量，将样本数据划分为多个不同的群组。

下面将以一个实例来讲解如何使用SPSS进行聚类分析。

实例描述：假设有一个超市的销售数据，包含了不同商品的销售额、销售量和利润等信息。

我们希望将商品进行聚类分析，找出相似销售特征的商品群组。

步骤一：数据准备首先，将销售数据保存为一个.SP文件，然后打开SPSS软件。

在主界面上选择“文件”-“打开”-“数据库”-“从SPSS文件”，打开数据文件。

步骤二：变量选择在数据文件中，选择出要进行聚类分析的变量。

在“数据视图”中，选择那些代表销售特征的变量，例如“销售额”、“销售量”和“利润”。

在变量列上按住“Ctrl”键，同时点击这些变量名，选中它们。

步骤三：聚类分析点击菜单上的“数据”-“服务”-“聚类分析”进行聚类分析操作。

会弹出“聚类分析”对话框。

在对话框中，将选中的变量移到右侧的“变量”框中，并选择“K均值聚类”作为聚类方法。

K值是指要分成的群组数量，可以根据实际情况设定。

这里假设将商品分成3个群组，因此设置为3步骤四：聚类结果解读点击“确定”按钮，SPSS将自动进行聚类分析。

完成后，SPSS会在数据文件中生成一个新的变量，用于表示每个样本所属的群组。

在下方的“结果视图”中，可以看到聚类结果的统计数据、聚类中心和变量间的距离。

此外，在“分类变量资料”中，还可以看到每个样本所属的群组编号。

步骤五：聚类结果可视化为了更好地理解聚类结果，可以进行可视化展示。

点击菜单上的“图形”-“散点图”，在对话框中依次选择所属群组变量和销售额、销售量这两个变量。

点击“确定”按钮，即可生成散点图。

散点图可以清楚地显示出不同群组之间的差异和相似性。

根据散点图，可以对聚类结果进行解读。

例如，如果不同群组之间的点比较分散，则说明聚类效果较差；而如果不同群组之间的点比较集中，则说明聚类效果较好。

SPSS聚类分析：K均值聚类分析⼀、概念：（-分类-K均值聚类）1、此过程使⽤可以处理⼤量个案的算法，根据选定的特征尝试对相对均⼀的个案组进⾏标识。

不过，该算法要求您指定聚类的个数。

如果知道，您可以指定初始聚类中⼼。

您可以选择对个案分类的两种⽅法之⼀，要么迭代地更新聚类中⼼，要么只进⾏分类。

可以保存聚类成员、距离信息和最终聚类中⼼。

还可以选择指定⼀个变量，使⽤该变量的值来标记个案输出。

您还可以请求分析⽅差F统计量。

⼆、聚类中⼼（分析-分类-K均值聚类）为获得最佳有效性，可取⼀个个案样本并选择迭代和分类⽅法确定聚类中⼼。

选择最终聚类中⼼另存为。

然后恢复整个数据⽂件并选择仅分类作为⽅法，并选择读取初始聚类中⼼来源以使⽤该样本估计的中⼼对整个⽂件分类。

您可以写⼊和读取⽂件或数据集。

可以在同⼀会话中继续使⽤数据集，但不会将其另存为⽂件，除⾮在会话结束之前明确将其保存为⽂件。

数据集名称必须符合变量命名规则。

三、迭代（分析-分类-K均值聚类-迭代）注意：只有在您从“K均值聚类分析”对话框中选择了迭代和分类⽅法的情况下，这些选项才可⽤。

◎最⼤迭代次数。

限制K均值算法中的迭代次数。

即使尚未满⾜收敛准则，达到迭代次数之后迭代也会停⽌。

此数字必须在1到999之间。

◎收敛性标准。

确定迭代何时停⽌。

它表⽰初始聚类中⼼之间的最⼩距离的⽐例，因此必须⼤于0且⼩于等于1。

例如，如果准则等于0.02，则当完整的迭代⽆法将任何聚类中⼼移动任意初始聚类中⼼之间最⼩距离的2%时，迭代停⽌。

◎使⽤运⾏均值。

允许您请求在分配了每个个案之后更新聚类中⼼。

如果不选择此选项，则会在分配了所有个案之后计算新的聚类中⼼。

四、保存（分析-分类-K均值聚类-保存）1、聚类成员。

创建指⽰每个个案最终聚类成员的新变量。

新变量的值范围是从1到聚类数。

2、与聚类中⼼的距离。

创建指⽰每个个案与其分类中⼼之间的欧式距离的新变量。

五、选项：（分析-分类-K均值聚类-选项）统计量。

1.1 系统聚类本次实验的系统聚类都是凝聚系统聚类，为了控制变量，都采用平方Euclidean距离。

1.1.1 最短距离聚类法最短距离法聚类步骤如下：1.规定样本间的距离，计算样本两两之间的距离，得到对称矩阵。

开始每个样品自成一类。

2.选择对称矩阵中的最小非零元素。

将两个样品之间最小距离记为D1，将这两个样品归并成为一类，记为G1。

3.计算G1与其他样品距离。

重复以上过程直到所有样品合并为一类。

我们在SPSS中实现最短距离分析非常简单。

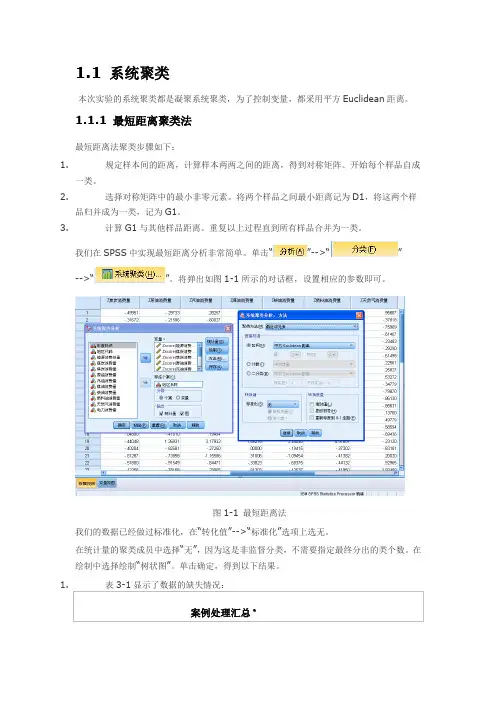
单击“”-->“”-->“”。

将弹出如图1-1所示的对话框，设置相应的参数即可。

图1-1 最短距离法我们的数据已经做过标准化，在“转化值”-->“标准化”选项上选无。

在统计量的聚类成员中选择“无”，因为这是非监督分类，不需要指定最终分出的类个数。

在绘制中选择绘制“树状图”。

单击确定，得到以下结果。

聚类表阶群集组合系数首次出现阶群集下一阶群集1 群集 2 群集 1 群集 21 21 28 .211 0 0 102 12 24 .465 0 0 63 2 27 .491 0 0 54 13 20 .585 0 0 95 2 14 .645 3 0 66 2 12 .678 5 2 77 2 7 .702 6 0 88 2 25 .773 7 0 99 2 13 .916 8 4 1110 21 29 1.085 1 0 1211 2 18 1.106 9 0 12表1-2 聚类过程我们可以通过更加形象直观的树状图来观察整个聚类过程和聚类效果。

如图1-2所示，最短距离法组内距离小，但组间距离也较小。

分类特征不够明显，无法凸显各个省份的能源消耗的特点。

但是我们可以看到广东省能源消耗组成和其他省份特别不同，在其他方法中也显现出来。

12 2 21 1.115 11 10 13 13 2 17 1.360 12 0 14 14 2 26 1.564 13 0 15 15 2 22 1.627 14 0 16 16 2 5 1.649 15 0 17 17 2 8 1.877 16 0 18 18 2 16 3.027 17 0 19 19 2 30 3.543 18 0 20 20 2 11 4.930 19 0 21 21 2 4 5.024 20 0 22 22 2 10 6.445 21 0 24 23 1 9 8.262 0 0 26 24 2 15 10.093 22 0 25 25 2 23 10.096 24 0 26 26 1 2 10.189 23 25 27 27 1 6 11.387 26 0 28 28 1 3 13.153 27 0 29 2911932.36728图1-2 最短距离法聚类图1.1.2 组间联接聚类组间联接聚类法定义为两类之间的平均平方距离，即。

标签: SPSS, 系统聚类, K-mean聚类, Ward法, 最短距离法聚类分析是将物理或者抽象对象的集合分成相似的对象类的过程。

本次实验我将对同一批数据做两种不同的类型的聚类；它们分别是系统聚类和K-mean聚类。

其中系统聚类的聚类方法也采用3种不同方法，来考察对比它们之间的优劣。

由于没有样本数据，因此不能根据其数据做判别分析?。

评价标准主要是观察各聚类方法的所得到的类组间距离和组内聚类的大小。

分析数据依然采用线性回归所使用的标准化?后的能源消费数据。

1.1 系统聚类本次实验的系统聚类都是凝聚系统聚类，为了控制变量，都采用平方Euclidean距离。

1.1.1 最短距离聚类法最短距离法聚类步骤如下：1.规定样本间的距离，计算样本两两之间的距离，得到对称矩阵。

开始每个样品自成一类。

2.选择对称矩阵中的最小非零元素。

将两个样品之间最小距离记为D1，将这两个样品归并成为一类，记为G1。

3.计算G1与其他样品距离。

重复以上过程直到所有样品合并为一类。

我们在SPSS中实现最短距离分析非常简单。

单击“”-->“”-->“”。

将弹出如图1-1所示的对话框，设置相应的参数即可。

图1-1 最短距离法我们的数据已经做过标准化，在“转化值”-->“标准化”选项上选无。

在统计量的聚类成员中选择“无”，因为这是非监督分类，不需要指定最终分出的类个数。

在绘制中选择绘制“树状图”。

单击确定，得到以下结果。

1.表3-1显示了数据的缺失情况：耗的特点。

但是我们可以看到广东省能源消耗组成和其他省份特别不同，在其他方法中也显现出来。

图1-2 最短距离法聚类图1.1.2 组间联接聚类组间联接聚类法定义为两类之间的平均平方距离，即。

类C K 和C L 合并为下一步的C M 则C M 与C J 距离的递推公式为：。

我们依然贴出组间联接法的聚类表和树状图。

1. 聚类表如表1-3所示，相关解释类似于表1-1所述。

表1-2 组间联接聚类法2. 树状图如图1-3所示，可以看到聚类的组间距离较大，组内距离较小。

二、聚类统计量
首先定义一些分类统计指标 —— 刻画样或指标之 间的相似程度（这些统计指标称为聚类统计量） 在市场研究中，样品 —— 用作分类的事物 指标 —— 用来作为分类依据的变量。 （如：年龄、收入、销售量） （一）相似系数（夹角余弦） 一般式：假定每个样品包含有P项指标，若有几个样品 的调查数据
3、步骤：1）首先给出度量“相似”或“关系密切”的 统计指标
指标：（1）统计指标是相似系数。 根据相似性归为一类，否则为另一类。 （2）统计指标是样品（空间的点）之间的距离 将距离近的点归成一类，否则为另一类。 （3）相关系数
（4）关联系数 2）形成一个由小到大的分析系统。
3）把整个分类系统画成一张分类图
CLUSTER过程 开始每个观测值自成一类，然后求两两之间的距离， 将距离最近的两个观测值合成一类。这个过程一直 进行下去，每次减少一类，直到合成一类为止。 聚类方法有11种，可根据问题的性质选用，它们的 区别在于怎样计算两类之间的距离。
METHOD=指定方法
AVERAGE（平均法）、CENTROID（重心法）、 COMPLETE（最大距离法）、DENSITY（密度 法）、MEDIAM（中位数法）等
1
按就近原则将每个观测量选入一个类中，然后计算各个类的中 心位置，即均值，作为新的聚心。 3、使用计算出来的新聚心重新进行分类，分类完毕后继续计 算各类的中心位置，作为新的聚心，如此反复操作，直到两次 迭代计算的聚心之间距离的最大改变量小于初始聚类心间最小 距离的倍数时，或者到达迭代次数的上限时，停止迭代。
观测量概述表
聚类步骤，与图结合看！
4、5
聚类方法有系统聚类和逐步聚类，输入数据集可以是普 通数据集、相关矩阵（CORR过程产生）或协方差矩阵 （FACTOR等过程产生）。SAS提供的聚类过程有：

IBM SPSS Modeler 实验一、聚类分析在数据挖掘中，聚类分析关注的内容是一些相似的对象按照不同种类的度量构造成的群体。

聚类分析的目标就是在相似的基础上对数据进行分类。

IBM SPSS Modeler提供了多种聚类分析模型，其中主要包括两种聚类分析，K-Mean 聚类分析和Kohonen聚类分析，下面对各种聚类分析实验步骤进行详解。

1、K-Means聚类分析实验首先进行K-Means聚类实验。

（1）启动SPSS Modeler 14.2。

选择“开始”→“程序”→“IBM SPSS Modeler 14.2”→“IBM SPSS Modeler 14.2”，即可启动SPSS Modeler程序，如图1所示。

图1 启动SPSS Modeler程序（2）打开数据文件。

首先选择窗口底部节点选项板中的“源”选项卡，再点击“可变文件”节点，单击工作区的合适位置，即可将“可变文件”的源添加到流中，如图2所示。

右键单击工作区的“可变文件”，选择“编辑”，打开如图3的编辑窗口，其中有许多选项可供选择，此处均选择默认设定。

点击“文件”右侧的“”按钮，弹出文件选择对话框，选择安装路径下“Demos”文件夹中的“DRUG1n”文件，点击“打开”，如图4所示。

单击“应用”，并点击“确定”按钮关闭编辑窗口。

图2 工作区中的“可变文件”节点图3 “可变文件”节点编辑窗口图4 文件选择对话框图5 工作区中的“表”节点（3）借助“表（Table）”节点查看数据。

选中工作区的“DRUG1n”节点，并双击“输出”选项卡中的“表”节点，则“表”节点出现在工作区中，如图5所示。

运行“表”节点（Ctrl+E或者右键运行），可以看到图6中有关病人用药的数据记录。

该数据包含7个字段（序列、年龄(Age)、性别(Sex)、血压(BP)、胆固醇含量(Cholesterol)、钠含量(Na)、钾含量(K)、药类含量(Drug)），共200条信息记录。

使用SPSS软件进行因子分析和聚类分析的方法因子分析和聚类分析是一种常用的数据分析方法，可以用于数据降维和分组。

SPSS是一款常用的统计软件，提供了丰富的分析工具和函数，可以方便地进行因子分析和聚类分析。

一、因子分析：因子分析是一种多变量分析方法，可以将一组相关的变量转化为少数几个互相独立的综合变量，称为因子。

因子分析可以用于降低数据的维度，提取主要的因素，并分析因素之间的关系。

以下是使用SPSS软件进行因子分析的步骤：1.打开SPSS软件，并导入要进行因子分析的数据集。

2.菜单栏选择“分析”-“降维”-“因子”。

3.在弹出的因子分析对话框中，选择要进行因子分析的变量，将其添加到“因子”框中。

4.在“提取”选项中，选择提取的因子个数。

可以根据实际需求和经验进行选择。

5. 在“旋转”选项中，选择旋转方法。

常用的旋转方法有方差最大旋转（Varimax），斜交旋转（Oblique）等。

6.点击“确定”按钮，进行因子分析。

7.SPSS会生成因子载荷矩阵、解释方差表、因子得分等结果。

可以根据因子载荷矩阵和解释方差表来解释因子的含义和解释度。

8.根据具体需求和分析目的，可以进行因子得分的计算和因子分组的分析。

二、聚类分析：聚类分析是一种无监督学习方法，可以将一组样本数据自动分成若干互不相交的群组，称为簇。

聚类分析可以用于数据的分组和群体特征的分析。

以下是使用SPSS软件进行聚类分析的步骤：1.打开SPSS软件，并导入要进行聚类分析的数据集。

2.菜单栏选择“分析”-“分类”-“聚类”。

3.在弹出的聚类分析对话框中，选择要进行聚类分析的变量，将其添加到“变量”框中。

可以选择多个变量进行分析。

4.在“距离”选项中，选择计算样本间距离的方法。

常用的方法有欧几里得距离、曼哈顿距离等。

5. 在“聚类方法”选项中，选择聚类算法的方法。

常用的方法有层次聚类（Hierarchical Clustering）、K均值聚类（K-means）等。

25
软件操作
Scores为计算因子的方法
Save as variables：将因子得分保存在 SPSS变量中，method表示计算因子得分的 方法，Regression—回归法 Display factor score coefficient matix： 输出因子得分系数矩阵
采用聚类方法：系统聚类 K均值聚类
3
系统聚类

参与系统聚类的变量选到Variables(s)中 字符型变量作为标记变量选到Lable Cases by中 Cluster中确定聚类类型，是Q型聚类还是R型聚类

Agglomeration schedule：输出聚类过程表 Proximity matrix：输出个体之间的距离矩阵 Cluster Membership 中 None 表示不输出样本 所属类，Single solution表示当分成n类时各样 本所属类，Range of solutions表示当分成m-n 4 类时各样本属性所属类
基本思想：根据所研究的样本或变量在观测数据上表现的不 同亲疏程度，采用不同的聚类方法将亲疏程度较大的样本/ 变量聚合为一类，把另外一些亲疏程度较大的样本/变量聚 合为一类，直到把所有的样本/变量都聚合完毕，形成一个 由小到大的分类系统 。
聚类方法不同： 聚类对象不同时的聚类类型： 亲疏程度的判定 hierarchical cluster），聚类过程是按 系统聚类：又称为层次聚类（ 样本之间的聚类：即Q型聚类分析，常用距离来测度样本之间的亲疏程 照一定层次进行的； 距离：将每一个样本看作p维空间的一个点，并用某种度量测量点与点 度； 之间的距离，距离较近的归为一类，距离较远的点应属于不同的类； 均值聚类（ K-means Cluster ）； K 变量之间的聚类：即 R型聚类分析，常用相似系数来测度变量之间的亲 相似系数：性质越接近的变量或样本，它们的相似系数越接近于1或一l， 疏程度； 而彼此无关的变量或样本它们的相似系数则越接近于0，相似的为一类，不 相似的为不同类；

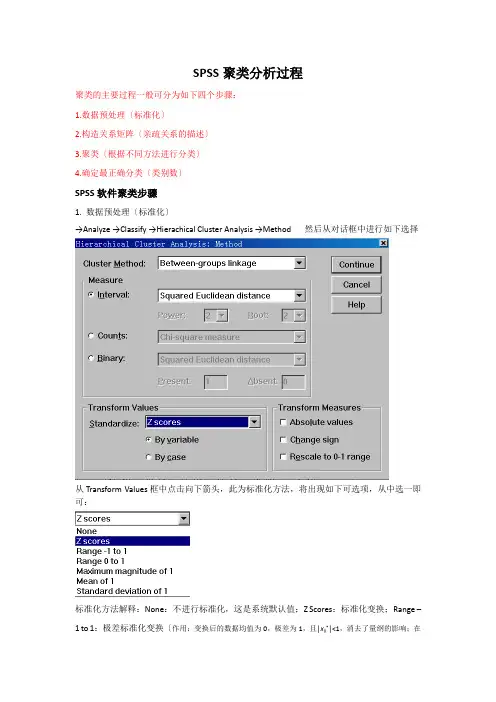
SPSS聚类分析过程聚类的主要过程一般可分为如下四个步骤：1.数据预处理〔标准化〕2.构造关系矩阵〔亲疏关系的描述〕3.聚类〔根据不同方法进行分类〕4.确定最正确分类〔类别数〕SPSS软件聚类步骤1. 数据预处理〔标准化〕→Analyze →Classify →Hierachical Cluster Analysis →Method 然后从对话框中进行如下选择从Transform Values框中点击向下箭头，此为标准化方法，将出现如下可选项，从中选一即可：标准化方法解释：None：不进行标准化，这是系统默认值；Z Scores：标准化变换；Range –1 to 1：极差标准化变换〔作用：变换后的数据均值为0，极差为1，且|x ij*|<1，消去了量纲的影响；在以后的分析计算中可以减少误差的产生。

〕；Range 0 to 1〔极差正规化变换/ 规格化变换〕；2. 构造关系矩阵在SPSS中如何选择测度〔相似性统计量〕:→Analyze →Classify →Hierachical Cluster Analysis →Method 然后从对话框中进行如下选择常用测度〔选项说明〕：Euclidean distance：欧氏距离〔二阶Minkowski距离〕，用途：聚类分析中用得最广泛的距离；Squared Eucidean distance：平方欧氏距离；Cosine：夹角余弦(相似性测度；Pearson correlation：皮尔逊相关系数；3. 选择聚类方法SPSS中如何选择系统聚类法常用系统聚类方法a〕Between-groups linkage 组间平均距离连接法方法简述：合并两类的结果使所有的两两项对之间的平均距离最小。

〔项对的两成员分属不同类〕特点：非最大距离，也非最小距离b〕Within-groups linkage 组内平均连接法方法简述：两类合并为一类后，合并后的类中所有项之间的平均距离最小C〕Nearest neighbor 最近邻法〔最短距离法〕方法简述：用两类之间最远点的距离代表两类之间的距离，也称之为完全连接法d〕Furthest neighbor 最远邻法〔最长距离法〕方法简述：用两类之间最远点的距离代表两类之间的距离，也称之为完全连接法e〕Centroid clustering 重心聚类法方法简述：两类间的距离定义为两类重心之间的距离，对样品分类而言，每一类中心就是属于该类样品的均值特点：该距离随聚类地进行不断缩小。

1. 不同性别学生注册微博时间的比较由表1所示，对不同性别学生注册微博的时间进行比较，男生和女生之间存在统计学差异（P＜0.05）。

男生注册时间不到一个月、1-3个月、3-6个月的例数分别为39、49、67，构成比分别为16.12%、20.25%、27.69%，女生注册时间不到一个月、1-3个月、3-6个月的例数分别为21、49、69，构成比分别为8.11%、18.92%、26.64%，在上述注册微博时间的男生构成比大于女生。

男生注册时间6-12个月、一年以上的例数分别为50、37，构成比分别为20.66%、15.29%，女生注册时间6-12个月、一年以上的例数分别为75、45，构成比分别为28.96%、17.37%，在上述注册微博时间的女生的构成比则大于男生。

表1 不同性别学生注册微博时间的比较不到一个月1-3个月3-6个月6-12个月一年以上合计性别例数构成比例数构成比例数构成比例数构成比例数构成比例数构成比合计60 11.98 98 19.56 136 27.15 125 24.95 82 16.37 242 100.00 男生39 16.12 49 20.25 67 27.69 50 20.66 37 15.29 259 100.00 女生21 8.11 49 18.92 69 26.64 75 28.96 45 17.37 501*100.00 χ210.7859P 0.0291*：排除缺失值后的有效样本量为5012. 不同性别学生平均每天使用微博时间的比较由表2可知，对不同性别学生平均每天使用微博的时间进行比较，男生和女生之间不存在统计学差异（P＞0.05）。

平均每天使用微博时间为10-30分钟的学生最多，有186人，占37.13%，其次为10分钟以内，有162人（32.34%），再次为30-60分钟，为106人（21.16%），平均每天使用微博1-2小时和2小时以上的学生较少，分别有33人（6.59%）和14人（2.79%）。

聚类分析spss
SPSS聚类分析是对数据集进行分类和分析的一种统计过程。

通过SPSS聚类分析，可以将数据集中的观察值划分为较小的簇，并了解每一簇的特点。

SPSS聚类分析的过程主要包括以下几步：
1）定义分类变量：首先，需要确定用于分类的变量类型，例如类别变量，数值变量，以及其他变量。

2）定义聚类目标：根据所选变量的类型，分析者可以自由定义聚类的方法和指标，例如聚类的数量，聚类的最大和最小大小，以及聚类的距离度量标准。

3）数据分析：使用SPSS中提供的聚类算法，根据定义的聚类目标，对数据集进行聚类分析，并计算出聚类的相关结果。

4）结果汇总：聚类分析完成后，SPSS会生成一系列统计图，可以比较不同聚类的结果，以及每组聚类中不同变量的取值情况。

5）结果应用：最后，分析者就可以根据聚类的结果，对数据集进行更有效的分析和解释，从而为业务决策提供合理的依据。

SPSS19.0实战之聚类分析这篇文章与上一篇的回归分析是一次实习作业整理出来的。

所以参考文献一并放在该文最后。

CNBlOG网页排版太困难了，又不喜欢live writer……聚类分析是将物理或者抽象对象的集合分成相似的对象类的过程。

本次实验我将对同一批数据做两种不同的类型的聚类；它们分别是系统聚类和K-mean聚类。

其中系统聚类的聚类方法也采用3种不同方法，来考察对比它们之间的优劣。

由于没有样本数据，因此不能根据其数据做判别分析。

评价标准主要是观察各聚类方法的所得到的类组间距离和组内聚类的大小。

分析数据依然采用线性回归所使用的标准化后的能源消费数据。

1.1 系统聚类本次实验的系统聚类都是凝聚系统聚类，为了控制变量，都采用平方Euclidean距离。

1.1.1 最短距离聚类法最短距离法聚类步骤如下：1.规定样本间的距离，计算样本两两之间的距离，得到对称矩阵。

开始每个样品自成一类。

2.选择对称矩阵中的最小非零元素。

将两个样品之间最小距离记为D1，将这两个样品归并成为一类，记为G1。

3.计算G1与其他样品距离。

重复以上过程直到所有样品合并为一类。

我们在SPSS中实现最短距离分析非常简单。

单击“”-->“”-->“”。

将弹出如图1-1所示的对话框，设置相应的参数即可。

图1-1 最短距离法我们的数据已经做过标准化，在“转化值”-->“标准化”选项上选无。

在统计量的聚类成员中选择“无”，因为这是非监督分类，不需要指定最终分出的类个数。

在绘制中选择绘制“树状图”。

单击确定，得到以下结果。

1.表表1-1 数据汇总我们的数据经过预处理，所以缺失值个数为0.2. 由于相关矩阵过于庞大，无法在文档中贴出，得到的是一个非相似矩阵。

表1-2是样品聚类过程。

样品21和28在第一步合并为一类，它们之间的非相关系数最小，为0.211。

在下一次合并是第十步。

在第五步的时候，样品2、27、14组成一类，出现群集，样品个数为3。

第十讲聚类分析SPSS操作聚类分析是一种数据挖掘的方法，用于将样本数据按照相似性进行分组。

SPSS是一款功能强大的数据分析软件，提供了丰富的聚类分析功能，下面将介绍如何使用SPSS进行聚类分析。

首先，打开SPSS软件，并导入要进行聚类分析的数据文件。

可以通过点击“文件”菜单中的“打开”选项，选择相应的数据文件进行导入，或者直接将数据拖拽到SPSS软件界面上。

导入数据之后，在SPSS软件的数据视图中，可以查看数据的各个变量和观察值（样本）。

接下来，点击“分析”菜单中的“分类”选项，然后选择“聚类”。

在聚类分析对话框中，首先需要选择要进行聚类分析的变量。

可以将所有要分析的变量移动到“变量”列表中，或者点击“添加全部”按钮，将所有变量添加到“变量”列表中。

在聚类分析对话框中，还有一些其他的配置选项，如“距离测度”、“规范化方法”、“分散度”等，可以根据实际需求进行设置。

其中，距离测度指的是计算样本间相似性的方法，常用的有欧几里得距离、曼哈顿距离等；规范化方法用于对变量进行标准化；分散度用于定义聚类的紧密度。

配置好相关选项之后，可以点击“聚类”按钮开始进行聚类分析。

SPSS会根据所选的变量和配置选项，对样本进行聚类，并在输出视图中呈现聚类结果。

聚类分析的输出结果包括聚类分布表、聚类变量表、聚类映射表等。

聚类分布表显示了每个聚类中的样本数量；聚类变量表显示了每个聚类中各个变量的均值；聚类映射表显示了每个观察值所属的聚类。

分析完毕后，可以根据聚类的结果对样本进行分类。

可以基于聚类分布表和聚类映射表，将样本分为不同的类别，并对每个类别进行描述和解释。

此外，可以对每个类别的特点进行进一步的分析，比如对不同类别的平均值进行比较，以了解不同类别之间的差异。

聚类分析还可以进行一些其他的操作，比如对聚类结果进行可视化展示。

可以使用SPSS的图形功能，绘制散点图或热力图，将样本点按照聚类分组进行呈现，以便更直观地了解聚类结果。

聚类分析为了研究全国各地的城镇家庭收支的分布规律，共抽取28个省、市、自治区的农民生活消费支出的6个有关指标的数据资料。

用表中的数据做谱系聚类，画出谱系图，确定消费支出类型。

地区食品支出住房支出衣着支出其他支出北京190 43 60 49天津135 36 44 36河北95 22 22 22山西104 25 9 18内蒙128 27 12 23辽宁145 32 27 39吉林159 33 11 25黑龙江116 29 13 21上海221 38 115 50江苏144 29 42 27浙江169 32 47 34安徽153 23 23 18福建144 21 19 21江西140 21 19 15山东115 30 33 33河南101 23 20 20湖北140 28 18 20湖南164 24 22 18广东182 20 42 36江西139 18 13 20四川137 20 17 16贵州121 21 14 12云南124 19 14 15陕西106 20 10 18甘肃95 16 6 12青海107 16 5 8宁夏113 24 9 22新疆123 38 4 17【结果与分析】一、欧氏距离平方、组间平均距离连接法Case Processing Summary(a)CasesValid Missing Total N Percent N Percent N Percent28 100.0 0 .0 28 100.0a Average Linkage (Between Groups)上表表示进行聚类分析的有效样品是28个，无缺失值。

Agglomeration ScheduleStageCluster CombinedCoefficientsStage Cluster FirstAppearsNext Stage Cluster 1 Cluster 2 Cluster 1 Cluster 21 14 21 15.000 0 0 62 22 23 22.000 0 0 123 4 24 30.000 0 0 104 3 16 45.000 0 0 155 8 27 51.000 0 0 106 14 20 55.500 1 0 87 13 17 67.000 0 0 88 13 14 82.167 7 6 169 12 18 123.000 0 0 1410 4 8 141.000 3 5 1511 25 26 161.000 0 0 1812 5 22 179.000 0 2 1613 2 10 215.000 0 0 1914 7 12 302.500 0 9 2215 3 4 310.750 4 10 1816 5 13 333.600 12 8 2017 11 19 342.000 0 0 2318 3 25 386.000 15 11 2519 2 6 396.500 13 0 2120 5 28 617.250 16 0 2221 2 15 833.667 19 0 2422 5 7 915.222 20 14 2423 1 11 1021.000 0 17 2624 2 5 1225.875 21 22 2525 2 3 1757.844 24 18 2626 1 2 5112.264 23 25 2727 1 9 18396.630 26 0 0上表表示聚类过程，从中可知，聚类共进行27步；第一步首先合并距离最近的14号和21号样品，形成类G1；因为next stage=6，所以在第6步G1和20号进行复聚类，因此，在Stage Cluster First Appears里列的Cluster 1=1，Cluster 2=0；第二步，合并22号和23号样品，形成类G2；因为next stage=12，所以在第12步，G2和第5号样品进行复聚类，且Cluster 1=0，Cluster 2=2；第一次出现类类的合并在第8步，Cluster 1=7，Cluster 2=6，表示第7步和第6步合并形成的类在第8步合并；其余的类似，不再详细叙述。