材料力学课件_平面图形的几何性质.
- 格式:ppt
- 大小:579.00 KB
- 文档页数:13
![材料力学(理工科课件)附录A_平面图形的几何性质()[25P][9.63MB]](https://uimg.taocdn.com/d59f3f242af90242a895e59e.webp)

第五章平面图形的几何性质同济大学航空航天与力学学院顾志荣材料力学的研究对象为杆件,杆件的横截面是具有一定几何形状的平面图形。
杆件的承载能力与其横截面图形的一些几何特性有密切的关系。
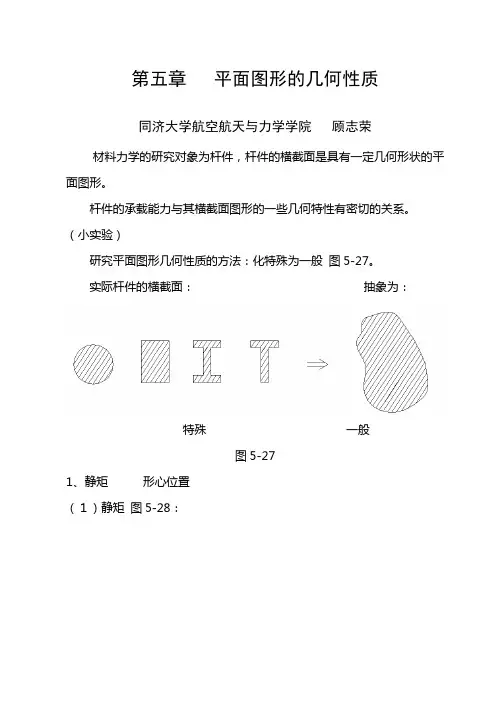
(小实验)研究平面图形几何性质的方法:化特殊为一般图5-27。
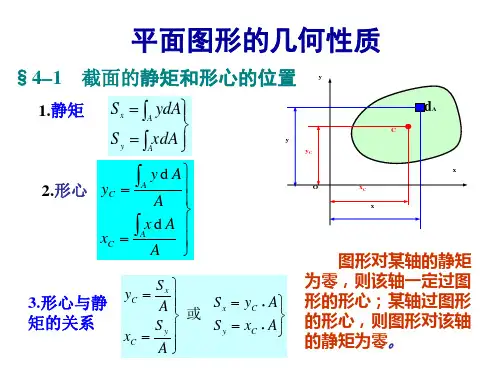
实际杆件的横截面:抽象为:特殊一般图5-271、静矩形心位置(1)静矩图5-28:图5-28微面积dA 与Z 轴、Y 轴间距离的乘积ydA,zdA 分别称为微面积dA 对Z 轴、Y 轴的静矩。
整个截面对Z 轴、Y 轴的静矩可用下式来定义:(若把A 看作力)定义:截面A 对Z 轴:⎪⎭⎪⎬⎫==⎰⎰Ay A ZSZdA S ydA (4-1) 截面A 对Y 轴:计算:①对(4-1)式直接积分:②若已知截面的形心位置C ,则y Z S S ,可以写成:⎭⎬⎫==c Z c Y AY S AZ S (4-2)(2)形心的位置:⎪⎪⎭⎪⎪⎬⎫==A S Z A S Y y C Z C (4-3)性质:①截面对某一轴的静矩等于零,则该轴必通过形心。
②截面对通过形心的轴的静矩恒等于零,即: ;0=ZC S 0=YC S决定因素:静矩与截面尺寸、形状、轴的位置有关。
数值范围:可以为正、或负、或等于零。
单位:333,,m cm mm (3)组合截面的静矩:⎪⎪⎭⎪⎪⎬⎫==∑∑==n i i i y n i i i Z A S Y A z S 11(4-4) 即组合截面的整个图形对于某一轴的静矩,等于各组部分对于同一轴静矩代数和。
(4)组合截面的形心位置:⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎬⎫====∑∑∑∑====n i i ni i i y ni i ni i i z A Z A AS A Y A AS c c z y 1111(4-5) 例题5-7 求图5-29所示截面图形的形心。
图5-29解:把T 形看成为由矩形Ⅰ和Ⅱ组成 ∵y 轴是对称轴 ∴形心必在y 轴上① 求?'=Z S216002080mm A I =⨯= A Ⅱ=2240020120mm =⨯ mm y c 10=I (到Z ′轴) y c Ⅱ=60+20=80mm则:3120800802400101600'mm Y A ni ii z s =⨯+⨯==∑=②求c y=?c y=As z =∑∑==ni ini i i A Y A 11=201202080208000⨯+⨯=52mm 2、惯性矩(形心主惯性矩) 惯性半径 极惯性矩图5-30定义:(1)惯性矩⎪⎭⎪⎬⎫==⎰⎰A yA Z dA Z I dA y I 22(4-6) 定义为截面对z 轴,y 轴的惯性矩。