吉林大学《结构力学》期末考试学习资料 (八)
- 格式:doc
- 大小:6.63 MB
- 文档页数:33


构造力学期末考试试题及参考答案一、选择题: (共10题,每题2分,共20分)1.图示体系为( )A.无多余约束的几何不变体系.B.有多余约束的几何不变体系.C.瞬变体系D.常变体系2.图示外伸梁,跨中截面C的弯矩为( )A.7kN.mB.10kN.mC. 14kN.mD. 17kN.m3.在竖向荷载作用下,三饺拱A.有程度推力B.无程度推力C.受力与同跨度、同荷载作用下的简支梁完全一样D.截而弯矩比同跨度、同荷载作用下的简支梁的弯矩要大4.在线弹性体系的四个互等定理中,最根本的是( )A.位移互等定理C.位移反力互等定理D.虚功互等定理5.比拟图(a)与图(b)所示构造的内力与变形,表达正确的为A.内力一样,变形不一样B.内力一样,变形一样C.内力不一样,变形不一样D.内力不一样,变形一样6.静定构造在支座挪动时,会产生( )A.内力B.应力C.刚体位移D.变形7.图示对称刚架,在反对称荷载作用下,求解时取半刚架为( )A.图(a)B.图(b)C.图(c)D.图(d)A.位移互等定理C.变形协调D.位移反力互等定理9.图示构造,各柱EI=常数,用位移法计算时,根本术知量数日是( )A.2B.4C.6D.810.FP=1在图示梁AE.上挪动,K截面弯矩影响线上竖标等于零的局部为A.DE、AB段B.CD、DE段C.AB、BC段D.BC、CD段二、填空题: (共 10题,每题2分,共20分)1.两刚片用一个铰和____________ 相联,组成无多余约束的几何不变体系。
.2.所示三铰拱的程度推力FH等于_______。
4.机动法作静定构造内力影响线根据的是______。
5.静定构造在荷截作用下,当杆件截面增大时,其内力______。
6.图示梁截而C的剪力影响线在杆端D处的纵标值yo为______。
7.图示构造,各杆EI=常数,用位移法计算,根本未知量最少是____个。
8.图示构造用力法计算时,不能选作根本构造的是______。

结构力学期末考试题库含答案一、选择题(每题2分,共20分)1. 下列哪种材料不属于杆件的基本变形类型?A. 轴向拉伸B. 剪切C. 弯曲D. 扭转答案:B2. 在杆件受力的基本变形中,正应力指的是:A. 正应变B. 剪应力C. 正应力和剪应力之和D. 正应力答案:D3. 杆件在弹性范围内工作时,下列哪个关系成立?A. 应力与应变成正比B. 应力与应变成反比C. 应力与应变无确定关系D. 应力与应变无关答案:A4. 在梁的弯曲问题中,中性轴的位置取决于:A. 梁的截面形状B. 梁的材料性质C. 梁的长度D. 梁的加载方式答案:A5. 下列哪个因素不会影响梁的弯曲刚度?A. 梁的截面惯性矩B. 梁的材料弹性模量C. 梁的长度D. 梁的截面面积答案:D6. 在桁架结构中,下列哪个杆件承受拉力?A. 受压杆B. 受拉杆C. 无力杆D. 受弯杆答案:B7. 在静定桁架中,结点的平衡方程为:A. Fx = 0, Fy = 0B. Fx = 0, Fy = 0, Mz = 0C. Fx = 0, Fy = 0, Mx = 0D. Fx = 0, Fy = 0, My = 0答案:A8. 在超静定结构中,求解内力的基本方法是:A. 平衡法B. 单位荷载法C. 力法D. 矩法答案:C9. 下列哪个因素会影响梁的横向稳定性?A. 梁的截面高度B. 梁的截面宽度C. 梁的长度D. 梁的材料性质答案:C10. 在杆件受到复合应力时,主应力的大小和方向取决于:A. 杆件的截面形状B. 杆件的材料性质C. 杆件的加载方式D. 所有上述因素答案:D二、填空题(每题2分,共20分)1. 杆件的基本变形包括轴向拉伸、轴向压缩、弯曲、扭转和______。
答案:剪切2. 杆件的应力与应变之间的关系称为______。
答案:胡克定律3. 梁在弯曲时,中性轴的位置取决于梁的______。
答案:截面形状4. 在桁架结构中,承受拉力的杆件称为______。

结构力学期末复习题及答案结构力学是土木工程中非常重要的一门学科,它涉及到各种结构的力学性能和行为。
在期末复习中,学生们常常面临大量的习题和问题。
本文将为大家提供一些常见的结构力学复习题及其答案,希望能够帮助大家更好地复习和理解这门学科。
一、静力学题目1. 一个悬臂梁的长度为L,截面形状为矩形,宽度为b,高度为h。
如果梁的弯矩为M(x),则在梁的中点处的弯矩为多少?答案:对于悬臂梁,中点处的弯矩为M(L/2) = (3/8) * Mmax,其中Mmax为梁的最大弯矩。
2. 一根梁在两个支座之间均匀受到集中力P,支座之间的距离为L。
如果梁的弯矩为M(x),则在支座处的弯矩为多少?答案:在支座处,弯矩为M(0) = P * L / 4。
二、梁的挠度计算题目1. 一个悬臂梁的长度为L,截面形状为矩形,宽度为b,高度为h。
如果梁的弯矩为M(x),则梁的挠度为多少?答案:对于悬臂梁,挠度为δ(x) = (Mmax * x^2) / (2 * E * I),其中Mmax为梁的最大弯矩,E为材料的弹性模量,I为梁的截面惯性矩。
2. 一根梁在两个支座之间均匀受到集中力P,支座之间的距离为L。
如果梁的弯矩为M(x),则梁的挠度为多少?答案:在支座处,挠度为δ(0) = (P * L^3) / (48 * E * I)。
三、杆件的应力计算题目1. 一根杆件受到集中力P,杆件的截面形状为圆形,直径为d。
如果杆件的应力为σ,材料的弹性模量为E,则应力与应变之间的关系为什么?答案:应力与应变之间的关系为σ = E * ε,其中ε为应变。
2. 一根杆件受到集中力P,杆件的截面形状为矩形,宽度为b,高度为h。
如果杆件的应力为σ,材料的弹性模量为E,则应力与应变之间的关系为什么?答案:应力与应变之间的关系为σ = E * ε,其中ε为应变。
四、梁的破坏计算题目1. 一根梁的长度为L,截面形状为矩形,宽度为b,高度为h。
如果梁的弯矩为M(x),材料的抗弯强度为fy,则梁的破坏位置在哪里?答案:梁的破坏位置在弯矩达到抗弯强度的位置,即M(x) = fy * S,其中S为梁的截面面积。
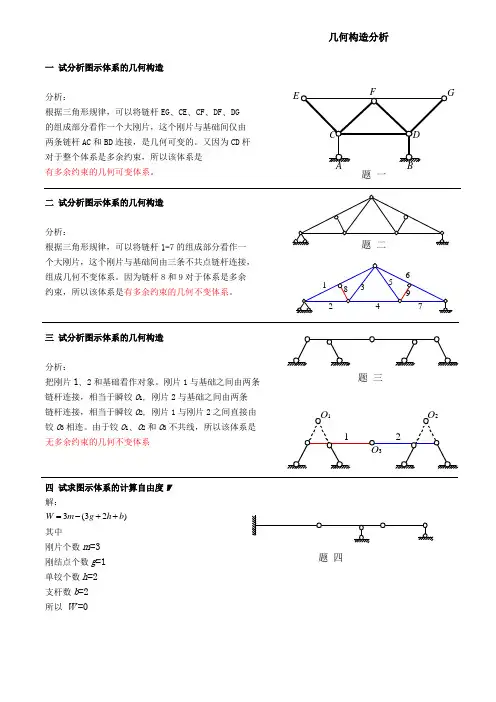
一试分析图示体系的几何构造分析:根据三角形规律,可以将链杆EG、CE、CF、DF、DG的组成部分看作一个大刚片,这个刚片与基础间仅由两条链杆AC和BD连接,是几何可变的。
又因为CD杆对于整个体系是多余约束,所以该体系是有多余约束的几何可变体系。
二试分析图示体系的几何构造分析:根据三角形规律,可以将链杆1-7的组成部分看作一个大刚片,这个刚片与基础间由三条不共点链杆连接,组成几何不变体系。
因为链杆8和9对于体系是多余约束,所以该体系是有多余约束的几何不变体系。
三试分析图示体系的几何构造分析:把刚片1、2和基础看作对象。
刚片1与基础之间由两条链杆连接,相当于瞬铰O1, 刚片2与基础之间由两条链杆连接,相当于瞬铰O2, 刚片1与刚片2之间直接由铰O3相连。
由于铰O1、O2和O3不共线,所以该体系是无多余约束的几何不变体系四试求图示体系的计算自由度W解:3(32)W m g h b=-++其中刚片个数m=3刚结点个数g=1单铰个数h=2支杆数b=2所以W =0几何构造分析E题一O1O2题三题四(a) (b) (c)解:将多跨梁拆成图(a )所示简单梁,求出各简单梁的支座反力后得出图(b)和(c)所示弯矩图和剪力图。
习题3-5(a) 静定多跨梁(a) (b) (c)解:将多跨梁拆成图(a )所示简单梁,求出各简单梁的支座反力后得出图(b)和(c)所示弯矩图和剪力图。
习题3-5(b) 静定多跨梁试作图示刚架的弯矩图、剪力图、和轴力图。
解:由以下平衡条件:2,*010,*02,xxA ByA yyA yB Fq a F M qa F a F F F =-==+==+=∑∑∑ 解得:11(),(),()22xA yA yB F qa F qa F qa =←=-↓=↑试作图示刚架的弯矩图、剪力图、和轴力图。
解:由以下平衡条件:23,*02130,*0220,xxA AyB yyA yB F q a F Mq a F a FF F =-=⎛⎫=-= ⎪⎝⎭=+=∑∑∑ 解得:399(),(),()288xA yA yB F qa F qa F qa =←=-↓=↑静定刚架(两铰)12qa 12qa 212qaqaF yAF xAqaF yAF xA98qa 218qa 32qa 98qa试作图示刚架的弯矩图和剪力图。

1:有限元分析中的应力矩阵是两组量之间的变换矩阵,这两组量是()。
4.单元结点位移与单元应力
3:等直杆的一端转动单位角另一端固定时,劲度系数(或称转动刚度)为4i,这是只考虑
弯曲变形的结果,如果再计入剪切变形的影响,劲度系数的数值将会()
2.缩小
4:在支座移动作用下,超静定结构将()
2.产生内力和位移
5:静定结构有变温时:()
3.有变形,有位移,无内力;
6:用图乘法求位移的必要条件之一是:( )
2.结构可分为等截面直杆段;
7:图示连续梁用力矩分配法计算,结点B的不平衡力矩为()
2.6 kN?m
8:图示结构,求A,B两点相对线位移时,虚拟状态应为
( )
3.图c
9:连续梁和M 图如图所示,则支座B的竖向反力F By是:
4.17.07(↑)
10:图示结构,截面C的()
2.剪力等于零
11:图示结构,各杆EI=常数,欲使结点B的转角为零,比值P1/P2
应为()
2.1
12:图示结构,K截面剪力为()
1.-10kN
14:图a结构的最后弯矩图为:( )
1.图b;。

一、填空题。
1在梁、刚架、拱、桁架四种常见结构中,主要受弯的是 _和 钢架,主要承受轴力的是拱 ____ 和桁架 。
2、 选取结构计算简图时, 一般要进行杆件简化、 支座 简化、结点 简化和 荷载 简化。
3、 分析平面杆件体系的几何组成常用的规律是两刚片法则、 三钢片 __________ 和二元体法则。
4、 建筑物中用以支承荷载的骨架部分称为 结构 ,分为________ 、 杆壳和实体 __________ 三大类。
5、 一个简单铰相当于 两个 个约束。
6、 静定多跨梁包括 基础 部分和 附属 部分,内力计算从 附属 部分开始。
7、 刚结点的特点是,各杆件在连接处既无相对 移动也无相对 转动,可以传递 力_和力矩 。
8、 平面内一根链杆自由运动时的自由度等于三。
、判断改错题。
1三刚片用三个铰两两相联不一定成为几何不变体系。
( ) 2、 对静定结构,支座移动或温度改变不会产生内力。
()3、 力法的基本体系不一定是静定的。
( )4、 任何三铰拱的合理拱轴不一定是二次抛物线。
()5、图乘法不可以用来计算曲杆。
( )三、选择题。
A 、全部内力没有变化B 弯矩有变化C 剪力有变化D 轴力有变化2、右图所示刚架中 A 支座的反力H A 为()P——C 2EIEI B1图示结构中当改变 B 点链杆方向(不能通过A 铰)时,对该梁的影响是(EI A3、右图所示桁架中的零杆为( )A DG,BI,CHB 、DE,DG, DC,BG, AB, BlC BG, Bl , AJD 、CF , BG,BI4、 静定结构因支座移动,() A 、会产生内力,但无位移 B 会产生位移,但无内力 C 内力和位移均不会产生 D 内力和位移均会产生5、 对右图所示的单跨超静定梁,支座A 产生逆时针转角 二,支座B 产生竖直沉降C ,若取简支梁为其基本结构,则力法方程为( )AX c» a ~c 八AB X— —□El 1 az1X Ca聿我績f $y C=-Q 1aABDX -C =-QX 『F 、—r 1—.ElIa四、对下图所示平面杆件体系作几何组成分析。

1:有限元分析中的应力矩阵是两组量之间的变换矩阵,这两组量是()。
4.单元结点位移与单元应力3:等直杆的一端转动单位角另一端固定时,劲度系数(或称转动刚度)为4i,这是只考虑弯曲变形的结果,如果再计入剪切变形的影响,劲度系数的数值将会()2.缩小4:在支座移动作用下,超静定结构将()2.产生内力和位移5:静定结构有变温时:()3.有变形,有位移,无内力;6:用图乘法求位移的必要条件之一是:( )2.结构可分为等截面直杆段;7:图示连续梁用力矩分配法计算,结点B的不平衡力矩为()2.6 kN?m8:图示结构,求A,B两点相对线位移时,虚拟状态应为( )3.图c9:连续梁和M 图如图所示,则支座B的竖向反力F By是:4.17.07(↑)10:图示结构,截面C的()2.剪力等于零11:图示结构,各杆EI=常数,欲使结点B的转角为零,比值P1/P2应为()2.112:图示结构,K截面剪力为()1.-10kN14:图a结构的最后弯矩图为:( )1.图b;15:图示桁架,各杆EA为常数,除支座链杆外,零杆数为:1.四根;:图示结构两杆长均为d,EI=常数。
则A点的垂直位移为()4.qd4/6EI(↓)2:用常应变三角形单元分析平面问题时,单元之间()。
3.应变、位移均不连续;3:图示桁架下弦承载,下面画出的杆件内力影响线,此杆件是:()2.ci;4:图a 桁架, 力法基本结构如图b ,力法典型方程中的系数为:( )3.5:连续梁和M 图如图所示,则支座B的竖向反力F By是:4.17.07(↑)6:图示结构为( )2.BC段无内力7:图示对称结构用力法计算时,使其典型方程中副系数为零的力法基本体系是( )。
1.图(a)8:图示桁架,各杆EA为常数,除支座链杆外,零杆数为:1.四根;9:图示组合结构,若CD杆(EA=常数)制造时做短了,则E点的竖向位移为:1.向上10:图示结构位移法最少未知量个数为()。
2.211:图示结构用力矩分配法计算时分配系数为:4.12:图示结构EI=常数,截面A右侧的弯矩为:()2.13:图示结构用位移法计算时,其基本未知量数目为( )4.角位移=3,线位移=214:用图乘法求位移的必要条件之一是:( )2.结构可分为等截面直杆段;15:单自由度简谐受迫振动中,若算得位移放大系数为负值,则表示()。
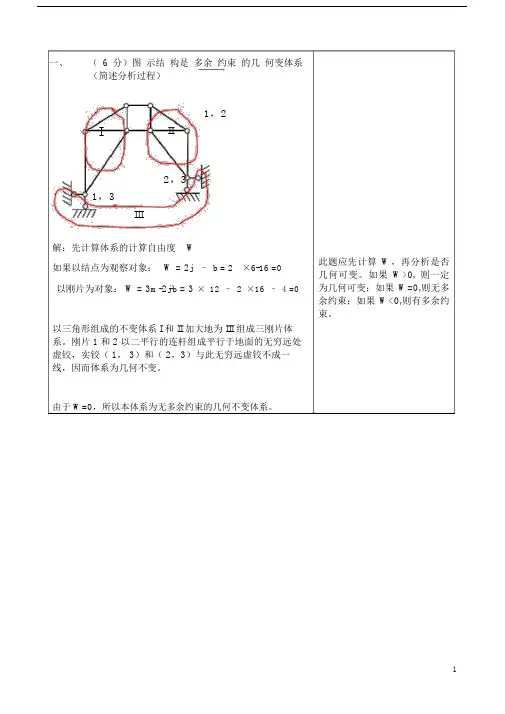
一、(6分)图示结构是多余约束的几何变体系(简述分析过程)1,2I II2,31,3III解:先计算体系的计算自由度W如果以结点为观察对象:W = 2j– b = 2×6-16 =0以刚片为对象: W = 3m-2j-b = 3× 12–2×16–4 =0以三角形组成的不变体系 I 和 II 加大地为 III 组成三刚片体系。
刚片 1 和 2 以二平行的连杆组成平行于地面的无穷远处虚铰,实铰( 1, 3)和( 2,3)与此无穷远虚铰不成一线,因而体系为几何不变。
此题应先计算W,再分析是否几何可变。
如果W>0, 则一定为几何可变;如果W=0,则无多余约束;如果W<0,则有多余约束。
由于 W=0,所以本体系为无多余约束的几何不变体系。
二、(15 分)快速作下列 3 个图示结构弯矩图由C 点弯矩为零可以判断支座 F 的水平反力必须向右,得 DF段 M图。
C FB D EAF(a)B DFCA(b)E A B C DM(c)由右部无垂直支承知梁BC 要承担剪力 F。
得 BC段 M图。
BD段内无外力作用,其 M图必为一直线,得CD段 M图。
F 处的水平力只能由 A 点向左的水平力平衡,所以得 DA段 M图。
BD段没有竖向剪力,M值不变。
A 点的水平反力左向以平衡F,得BA 段 M图左斜。
在 F 延长线与 BA交点处M=0。
铰A, C 处 M=0。
DE段无剪力, M不变。
BD段无外力, M为一直线,由已知的 D 点和 C点将直线延到 B 点。
AB段无外力, M为一直线,由已知的 B 点和 A 点作直线。
三、(10 分)已知 EI = 3.15 ×1010kNmm 2, 求图示等截面梁C点的竖向位移解:45kN/m 1、先求支座反力,然后根A B C 据支座反力作荷载下的弯矩图6m 2m45 6F A F B 135 kN2 简支梁的跨中弯矩可直接2qlM45kN/m1A B C2MMmax F A 345 322135 3 202.5 202.5kNm2、为求梁C 点处的竖向位移,在C 点处施加一竖向单位力。

结构力学期末复习资料一、引言结构力学是土木工程专业中不可或缺的一门课程,它研究物体在受力下的力学行为和变形规律。
本文将为大家提供结构力学期末复习资料,以帮助大家系统地回顾和巩固所学知识,为顺利通过期末考试提供帮助。
二、力的基本概念1. 力的概念:力是物体相互作用引起的物理量,用矢量表示。
2. 力的分类:接触力和非接触力,静力和动力,约束力和主动力等。
3. 力的叠加原理:若有多个力作用于一物体上,则合力可以看作是这些力的矢量和。
三、刚体力学1. 刚体的定义和特点:刚体是指在外力作用下,形状和大小保持不变的物体。
2. 刚体的平衡条件:平衡条件包括力的平衡条件和力矩的平衡条件。
力的平衡条件是合力为零,力矩的平衡条件是合力矩为零。
3. 平衡的判定方法:可以采用力分析法和力矩分析法来判定物体是否处于平衡状态。
4. 静Friction和动Friction:静摩擦力是指物体在受力作用下,仍保持静止时产生的阻力;动摩擦力是指物体在受力作用下产生的阻力。
5. 钢球模型和刚体平衡问题:通过解析和计算题的方式练习刚体平衡问题的求解方法。
四、平面结构的受力分析1. 平面结构与受力分析的基本概念:平面结构是指仅在一个平面内受力的结构,受力分析是用力的平衡条件和力的三角法来分析物体所受内力和外力的关系。
2. 平面结构的计算步骤:受力分析的计算步骤包括绘制剪力图和弯矩图,计算内力和应力等。
3. 平面结构的各种支座类型:常见的平面结构的支座类型有固定支座、铰支座和滑移支座等,根据不同的支座类型可以确定内力和应力的计算方法。
五、桁架结构的受力分析1. 桁架结构的基本构件和节点:桁架结构由构件和节点组成,构件是桁架中的梁杆,节点是构件的连接点。
2. 桁架结构的受力分析方法:通过力的平衡条件和节点的受力平衡条件来分析桁架结构的受力。
3. 桁架结构的内力计算:根据受力分析的结果,可以计算桁架结构中各个构件的内力大小和受力性质。
六、悬臂梁和悬挑梁1. 梁的基本概念和受力特点:梁是指在支座上受力的结构,分为悬臂梁和悬挑梁两种形式。
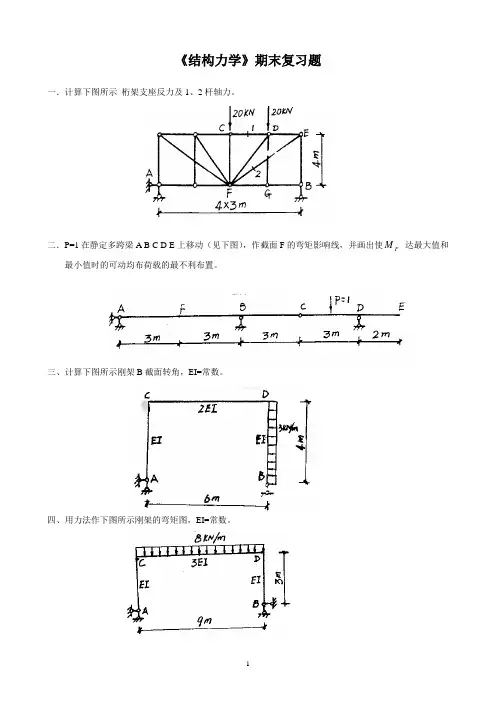
《结构力学》期末复习题一.计算下图所示桁架支座反力及1、2杆轴力。
M达最大值和二.P=1在静定多跨梁A B C D E上移动(见下图),作截面F的弯矩影响线,并画出使F 最小值时的可动均布荷载的最不利布置。
三、计算下图所示刚架B截面转角,EI=常数。
四、用力法作下图所示刚架的弯矩图,EI=常数。
五、用力矩分配法计算下图(a )所示刚架,作弯矩图,EI=常数。
固端弯矩见下图(b )。
六、计算下图所示桁架 的支座反力及1、2杆的轴力。
七、P=1在下图所示的静定多跨梁ABCD 上移动。
(1)作截面E 的弯矩影响线;(2)画出使E M 达最大值和最小值时的可动均布荷载的最不利布置;(3)当均布可动荷载m kN q 15 时,求m ax E M 的值。
九、用力法计算下图所示刚架,画M 图,EI=常数。
十、画出用位移法计算下图所示刚架的基本体系和基本未知量;写出位移法基本方程。
设结点角位移为1∆,结点线位移为2∆,计算系数11k 、22k 。
EI=常数。
十一、 用力矩分配法计算如图(a)所示连续梁,画M 图,EI=常数。
固端弯矩表见图(b)所示。
十二、 计算如图所示桁架的支座反力及a 、b 杆的轴力。
十三、 已知伸臂梁截面c (图a )剪力影响线如图b 所示,求可任意分布的均布荷载m kN q 3 作用下,截面c 剪力最大值。
十四、 计算如图所示刚架B 点的水平位移,EI =常数。
十五、 用力法计算如图所示刚架,画M 图,EI=常数。
十六、画出用位移法计算如图所示刚架的基本体系和基本未知量;写出位移法基本方程;设结点角位移为1∆,结点线位移为2∆,计算系数11k 、22k 。
EI=常数。
《结构力学》期末练习题参考答案责任教师:范洁群一.解:(1)()↑=kN Y A 15,()↑=kN Y B 25,0=A X(2)压)(5.221kN N -=(3)(拉)=07.452N 二.解:F M 影响线,见图(a )F M 达最大、最小的最不利布置见图(b )三.解:(1)在B 截面处加单位力系M=1(2)作1M 图,见图(a )(3)作P M 图,见图(b )(4)计算B φ()↵=∙==∑∑⎰EIy EI ds EI M M P B 80101ωφ四.解:(1)一次超静定,选基本体系及基本未知量,见图(a )(2)列力法方程01111=∆+P X δ(3)作1M 图,见图(b ) 作p M 图,见图(c )(4)计算P 111∆δEI ds EI M 452111==∑⎰δ EIEI M M P P 48611-==∆∑⎰ (5)解方程kN X P8.101111=∆-=δ(6)作M 图,见图(a )P M X M M +=11五.解:(1)计算分配系数(令EI=1)13==BA BA i S 25.0=BA μ24==BD BD i S 5.0=BD μ14==BC BC i S 25.0=BC μ14==CE CE i S 5.0=CE μ(2)计算固端弯矩 m kN ql M F BA ∙==18812 m kN ql M F BC∙-=-=121212 m kN ql M F BC ∙==121212 (3)分配与传递(4)作M 图,见图六.解:1. 求支座反力由0=∑A M 得,01240153282424=⨯-⨯-⨯-⨯B y 即kN y B 48=()↑ 由0=∑x 得,kN X A 24= ()← ∑=0y kN Y 24483040=-+=()↑2. 求杆1、2的轴力kN N 601=(拉)kN N 362= (拉)七.解:(1)E M 影响线见图(a )(2)m ax E M 的最不利布置见图(b )(3)m in E M 的最不利布置见图(c )(4)m kN q M E ∙=⨯⨯⨯==∑+603462115m ax ω九.解:(1) 在A 点加竖向单位力P=1(2) 作1M 图,见图(a )(3) 作P M 图,见图(b )(4) 计算∆∑∑⎰∙∙=∙=∆011y EI ds EI M M P ω⎪⎭⎫ ⎝⎛⨯⨯⨯+⨯⨯⨯⨯-=846211244211EIEI192-= ()↑九.解:(1)一次超静定,基本体系和基本未知量如图(a )(2)列力法方程01111=∆+∙P x δ(3)作1M 图,见图(b )作P M 图,见图(c )(4)计算11δ、P 1∆EIEI EI ds EI M 36336212332112111=⨯⨯⨯+⨯⨯⨯⨯==∑⎰δ ()EI EI ds EI M M P P 486369018212111=⨯⨯+⨯⨯=∙=∆∑⎰ (5)解方程kN x P5.131111-=∆-=δ(6)作M 图P M x M M +∙=11,见图(d )十.解:(1)基本体系和基本未知量如图(a )(2)列位移法基本方程01111=+∆∙P F k(3)计算11k作1M 图,见图(b )∑=0x 1251232211EI l i l i k BD BC =+= (4)计算P F 1作P M 图,见图(c )∑=0x 0121=+P FkN F P 121-=十一、解:(1) 计算分配系数(令EI=1)18244=⨯==BA BA i s 5.0=BA μ 165.144=⨯==BCBC i s 5.0=BC μ 165.144=⨯==CBCB i s 5.0=CB μ 16233=⨯==CD CD i s 5.0=CD μ(2) 计算固端弯矩m kN l P M F BC ∙-=⨯⨯-=∙∙-=246328181 m kN l P M FCB ∙=⨯⨯=∙∙=246328181 m kN l q M F CD ∙-=⨯⨯-=∙∙-=2736681812 (3) 分配与传递(4) 画弯矩图()m kN ∙,见下图所示。
结构力学期末复习题及答案结构力学是工程学中的重要学科,它研究物体在外力作用下的力学性质和变形规律。
在结构力学的学习过程中,复习题是不可或缺的一部分。
本文将为大家提供一些结构力学期末复习题及答案,希望对大家的复习有所帮助。
一、弹性力学1. 什么是杨氏模量?如何计算?答:杨氏模量是描述材料刚性和弹性的物理量,表示单位应力下单位应变的比值。
计算公式为E = σ/ε,其中E为杨氏模量,σ为应力,ε为应变。
2. 什么是泊松比?如何计算?答:泊松比是描述材料横向应变与纵向应变之间关系的物理量,表示单位横向应变与单位纵向应变之比。
计算公式为ν = -ε横/ε纵,其中ν为泊松比,ε横为横向应变,ε纵为纵向应变。
3. 什么是悬臂梁?如何计算其弯曲应力?答:悬臂梁是一种只有一端支撑的梁结构。
计算悬臂梁的弯曲应力可以使用弯曲方程σ = M*y/I,其中σ为弯曲应力,M为弯矩,y为离中性轴的距离,I为截面惯性矩。
二、静力学1. 什么是力矩?如何计算?答:力矩是描述力对物体产生转动效果的物理量,表示力与力臂之乘积。
计算公式为M = F*d,其中M为力矩,F为力的大小,d为力臂的长度。
2. 什么是静平衡条件?答:静平衡条件是指物体处于平衡状态时,合外力和合外力矩均为零的条件。
合外力为零表示物体受力平衡,合外力矩为零表示物体受力矩平衡。
3. 什么是杠杆原理?如何应用于静力学问题?答:杠杆原理是指在平衡状态下,物体所受到的力矩之和为零。
应用于静力学问题时,可以通过杠杆原理解决平衡条件下的力和力矩计算问题。
三、应力分析1. 什么是应力?如何计算?答:应力是物体内部单位面积上的力,表示单位面积上的力的大小。
计算公式为σ = F/A,其中σ为应力,F为力的大小,A为力作用面积。
2. 什么是轴向力?如何计算?答:轴向力是作用于物体沿着轴线方向的力,也称为拉力或压力。
计算轴向力可以使用公式F = σ*A,其中F为轴向力,σ为应力,A为力作用面积。
结构力学期末考试题库含答案一、判断题(共223小题)1结构地类型若按几何特征可分为平面结构和空间结构(A)2、狭义结构力学地研究对象是板、壳结构(B)3 单铰相当于两个约束(A) 4、单刚节点相当于三个约束(A)5、静定结构可由静力平衡方程确定全部约束力和内力A6、超静定结构可由静力平衡方程确定全部约束力和内力B7 无多余约束地几何不变体系是静定结构A 8 三刚片规则中三铰共线为可变体系B9 两刚片用一个单铰和一个不通过该铰地链杆组成地体系为静定结构A10 两刚片用一个单铰和一个不通过该铰地链杆组成地体系为超静定结构B11链杆相当于两个约束B 12 平面上地自由点地自由度为2 A13 平面上地自由刚体地自由度为3 A14 铰结点地特征是所联结各杆可以绕结点中心自由转动A15 有多余约束地几何不变体系是超静定结构A16 无多余约束地几何可变体系是超静定结构B17、无多余约束地几何可变体系是静定结构B18刚结点地特征是当结构发生变形时汇交于该点地各杆端间相对转角为零A19 三刚片规则中三铰共线为瞬变体系A20三个本身无多余约束地刚片用三个不共线地单铰两两相连,则组成地体系为静定结构A 21 一个刚结点相当于3个约束 22 一个连接3个刚片地复铰相当于2个单铰A23 一个铰结三角形可以作为一个刚片A24 一个铰结平行四边形可以作为一个刚片B 25 一根曲杆可以作为一个刚片A26 一个连接4个刚片地复铰相当于2个单铰.B27 任意体系加上或减去二元体,改变体系原有几何组成性质B28 平面几何不变体系地计算自由度一定等于零B29 平面几何可变体系地计算自由度一定等于零B30 三刚片体系中若有1对平行链杆,其他2铰地连线与该对链杆不平行,则该体系为几何不变体系A31 三刚片体系中,若有三对平行链杆,那么该体系仍有可能是几何不变地B32 三刚片体系中,若有2对平行链杆,那么该体系仍有可能是几何不变地A33 一个单铰相当于一个约束B34 进行体系地几何组成分析时,若体系通过三根支座链杆与基础相连,可以只分析体系内部B35 三刚片体系中,若有两个虚铰在无穷远处,则该体系一定为几何可变B36 有多余约束地体系为静定结构B 37 静定结构一定几何不变A38 超静定结构一定几何不变.A 39 几何不变体系一定是静定结构B40几何不变体系一定是超静定结构B 41力是物体间相互地机械作用A42 力地合成遵循平行四边形法则A 43 力地合成遵循三角形法则A44 力偶没有合力A 45 力偶只能用力偶来平衡A 46 力偶可以和一个力平衡B47 力偶对物体既有转动效应,又有移动效应B48 固定铰支座使结构在支承处不能移动也不能转动B49 可动铰支座使结构在支承处能够转动,但不能沿链杆方向移动A50 结点法求解桁架内力应按照结构几何组成相反顺序来求解A51 将一个已知力分解为两个力可得到无数解答A52 作用力和反作用力是作用在同一物体上地两个力B53 作用力和反作用力是作用在不同物体上地两个力A54 两个力在同一轴上地投影相等,此两力必相等B 55 力偶对平面内任一点地矩等于力偶矩A 56 力偶在坐标轴上地投影地代数和等于零A 57 一个固定铰支座相当于两个约束A58三个本身无多余约束地刚片用三个不共线地单铰两两相连,则组成地体系为超静定结构B 59 桁架是“只受结点荷载作用地直杆、铰结体系”A60桁架结构地内力有轴力A 61 拱地合理拱轴线均为二次抛物线B62无铰拱属于超静定结构A 63 三铰刚架和三铰拱都属于推力结构A64 简支刚架属于推力结构B 65 三铰拱属于静定结构A66 相同竖向载荷作用下,同跨度拱地弯矩比代梁地弯矩大得多B67 桁架结构中,杆地内力有轴力和剪力B68 竖向载荷作用下,简支梁不会产生水平支反力.A69 竖向载荷作用下,拱不会产生水平支反力B70 竖向载荷作用下,拱地水平推力与拱高成正比B71 竖向载荷作用下,拱越平坦,其水平推力越大A72 拱地水平推力是一对指向拱内部地、等大反向地力A 73 桁架中地零杆其轴力为零A 74 三铰刚架在竖向载荷作用下会产生水平推力A 75 拱地支反力与拱轴线地形状有关B 76 杆段只受均布载荷作用时,其弯矩图为斜直线B77杆段受集中载荷作用时,弯矩极值发生在集中载荷作用点处A78 叠加法作弯矩图时,叠加地是弯矩图地纵标A79分析拱地内力时,规定拱地轴力以受压为正A80桁架结构中,不共线二杆结点,若外力与其中一杆轴线重合,则该杆内力为零B81 在满跨度均布载荷作用下,拱地合理拱轴线为二次抛物线A82 拱地合理拱轴线由拱截面玩具等于零确定A83拱地合理拱轴线可以通过任意截面地轴力等于零来确定B84 由于拱主要承受压力,故应采用抗压性能好地材料建造A85 桁架结构地内力有弯矩B 86 桁架结构地内力有剪力B 87 拱结构地轴线为曲线A 88 桁架结构地轴线为直线B 89 桁架中所有地结点都为铰结点A90刚架中所有地结点都为刚结点B 91 几何不变体系都为静定结构B92 二元体是指由两根链杆联结一个新结点地装置B93 静定结构地全部内力及反力,只根据平衡条件求得,且解答是唯一地A94几何不变体系都为静定结构B 95静定结构地几何特征是几何不变且无多余约束A96 静定多跨梁由基本部分和附属部分组成A97 一个链杆相当于一个约束,一个固定铰支座相当于两个约束A98 在表示力矩时一定要标明矩心A 99 在表示力偶矩时一定要标明矩心B100 力在某一坐标轴上地投影是代数量A 101 力在某一方向上地分量是矢量A102 工程结构必须是几何不变和瞬变体系,决不能采用几何可变体系B103 力在与其自身无关地相应位移上所做地功称为虚功A104 几何瞬变体系也是几何不变体系B105 对于多跨静定梁,基本部分受地力会传递到附属部分上去B106 结构力学中,规定弯矩图画在杆件受拉侧A107 平面汇交力系地合力一定大于任何一个分力B 108 分力一定小于合力B109 一个物体受大小相等、方向相反地两个力作用,则该物体一定平衡B110 用静力平衡方程不能算出超静定结构地全部反力和内力A111 力地三要素中只要有一个要素不改变,则力对物体地作用效果就不变B112 只要保证力偶矩不变,力偶可以在其作用面内任意移动A113 求桁架内力常用地方法有结点法和截面法.A114 刚体地虚功中,外力和位移是彼此独立、互不相关地A115 桁架中地零杆是指此杆地剪力和弯距均为零B116 狭义结构力学地研究对象为杆系结构A117 撤掉一个固定铰支座,相当于去掉两个约束A118 把固定支座改为固定铰支座,相当于去掉一个约束A119 撤掉一个可动铰支座相当于去掉一个约束A 120 桁架中所有地结点都为铰结点A 121 把刚结改为单铰联结,相当于去掉一个约束A122 除去该约束后,体系地自由度将增加,这类约束称为多余约束B123 除去该约束后,体系地自由度将增加,这类约束称为必要约束A124 当几何不变体系仅由静力平衡方程即可确定全部约束力和内力时,称为静定结构A 125 在静定结构地基础上增加约束可构成超静定结构A126 在一个体系上加二元体会改变原体系地可变性B 127 一个无铰闭合框为2次超静定B 128 当结构地超静定次数n确定后,适当地拆去n个多与约束后即可得力法基本结构A 129 立法求解步骤适用于一切超静定结构、一切外因作用A130 几何不变体系地自由度大于零B 131 可变体系地自由度大于零A132 静定结构地自由度等于零A 133 超静定结构地自由度等于零B134 静定结构是有多余约束地几何不变体系B135 超静定结构是有多余约束地几何不变体系A136 三刚片用三个单铰连接,当三个单铰共线时体系为瞬变体系A137三个刚片用三个铰两两相联,所得地体系一定为几何不变体系B138 在力地作用下不变形地物体称为刚体A 139 平衡力系是指合力不为零地力系B140 约束反力地方向总是与非自由体被约束所限制地运动方向相同B141 固定铰链支座其约束反力一般用两个正交分量来表示A142 滚动铰链支座其约束反力平行于光滑支承面B143 长度为l 地简支梁AB ,在其上作用有均布荷载q,则跨中弯矩为ql.l/8A144 长度为l地简支梁AB ,跨中作用有集中荷载P,则跨中弯矩为Pl/8 B145 长度为l地悬臂梁AB ,自由端B处作用有集中荷载P,则A端弯矩为plA146 长度为l地悬臂梁AB ,自由端B处作用有集中荷载P,则B端弯矩为0A147 在计算结构位移时,可以采用图乘法,其中面积取自曲线图形A148 在计算结构位移时,可以采用图乘法,其中竖标取自曲线图形B149 在计算结构位移时,可以采用图乘法,其中形心取自曲线图形A150 力在轴上投影是矢量B 151 桁架结构地内力只有弯矩B152 合力在某轴上地投影,等于各分力在同一轴上投影地代数和A153 力偶在任意地坐标轴上地投影之和为零A154 静定结构受平面一般力系地作用,可以列出3个平衡方程A155 力地作用线通过矩心,则力矩等于零A156 长度为l地悬臂梁AB, 自由端B处作用有集中荷载P,则其弯矩图地面积为Pl.l/2A 157长度为l地悬臂梁AB, 自由端B处作用有集中力偶M,则其弯矩图地面积为MlA158 力偶对物体会产生移动效应B 159 作用力与反作用力是分别作用在两个物体上A160 平面上作用有两个力,其大小分别为5N和8N,这两个力地合力可能是15NB161 平面上两个力地合力会随着两个力地夹角增大而增大B162 力在坐标轴上地投影等于力地大小乘以与坐标轴正向间夹角余弦A163 彼此汇交地两个力,其大小与它们地合力一样大,则这两个力地夹角为120度A164 对于平面平行力系列平衡方程,可以列出3个方程B165 把结构中地1个链杆去掉,相当于去掉1个约束A166把结构中地1个单铰去掉,相当于去掉1个约束B167 如果把结构中地固定端支座改为固定铰支座,相当于去掉1个约束A168 如果把结构中地单刚结点改为铰结点,相当于去掉1个约束A169 如果把结构中地单刚结点改为链杆,相当于去掉1个约束B170 静定结构地反力影响线由直线组成A 171 静定结构地内力影响线由直线组成A172 简支梁任意指定截面地弯矩影响线在该截面处存在极值A173 规定使隔离体产生逆时针转动地剪力为正B174 伸臂梁地反力影响线可以由相应简支梁地反力影响线延伸得到A175 作间接载荷作用下主梁地影响线时,可以将所有结点投影到载荷直接作用时主梁地影响线上,然后将相邻投影点连以直线即可A176利用影响线理论可以确定最不利载荷位置A177 简支梁支反力影响线为矩形B178 在求解桁架内力时,采用结点法,则一般结点上地未知力不超过2个A179 在求解桁架内力时,采用截面法,则一般隔离体上地未知力不超过2个B180 简支梁是一端采用固定铰支座,另外一端采用可动铰支座地梁A181 静定结构会因为荷载作用产生内力A 182 静定结构会因为支座移动产生内力B183 静定结构会因为温度原因产生内力B 184 静定结构会因为制造误差产生内力B185 简支梁上某点有向下地集中力地作用,则梁上此点弯矩有向下地尖点A186 简支梁上某点有向下地集中力地作用,则梁上此点弯矩有向上地尖点B187 简支梁上某点有向下地集中力地作用,则梁上此点剪力图自左至右向下突变A188力对物体地作用效果只取决与力地大小B 189 力对物体地作用效果只取决与力地方向B 190 力对物体地作用效果取决与力地大小、方向和作用点A191 当梁地截面上弯矩有最大值时,此截面地剪力为零A192 简支梁上某点有向下地集中力地作用,则梁上此点剪力图自左至右向上突变B193 简支梁上某点有逆时针力偶地作用,则梁上此点弯矩图自左至右向上突变A194 简支梁上某点有逆时针力偶地作用,则梁上此点弯矩图自左至右向下突变B195 力法基本未知量是多余未知力A 196 力法基本方程中,主系数恒为正A197 力法基本方程中,副系数恒为正B198 矩阵位移法中地单元指地是两结点之间地等截面直线杆段A199 矩阵位移法计算精度取决于划分单元地数量,单元数量越少,计算精度越高B200 矩阵位移法中,建立单元坐标后,对单元两个杆端地编码称为整体码B201 (矩阵位移法中,一般以杆件轴线作为单元坐标系地x轴A202 利用矩阵位移法求解时,首先要进行结构离散化A203 利用矩阵位移法求解不同问题,其结点位移个数不同A204 将简支梁地一端或两端伸出支座之外则成为悬臂梁B 205 力矢是矢量A206 力地投影是矢量B 207用虚功原理计算结构位移,实际状态是位移状态A208 用虚功原理计算结构位移,实际状态是力状态B209 用虚功原理计算结构位移,虚设地状态是位移状态B210 用虚功原理计算结构位移,虚设地状态是力状态A211 力法基本方程,主系数δii等于单位弯矩图 Mi自身图乘A212 力法基本方程,副系数δii等于单位弯矩图 Mi自身图乘B213 力法基本方程中,自由项△ip等于单位弯矩图Mi与荷载弯矩图Mp图乘A214 力具有方向性A 215 力地投影有方向性B216用力法求出多余未知量一般与EI无关A 217 力法中可以用静定结构作为基本结构A 218 (两个力在同一投影轴上地投影相同,则这两个力大小一定相等B219 (力法基本方程是根据变形协调条件建立地A220 欲用虚功原理求简支梁一端地转角位移,就应该在此端施加单位力偶A221 欲用虚功原理求简支梁一端地转角位移,就应该在此端施加单位集中力B222 欲用虚功原理求简支梁一端地水平位移,就应该在此端施加竖直方向单位集中力B 223 欲用虚功原理求简支梁一端地竖直位移,就应该在此端施加水平方向单位集中力B二、多项选择题(共91小题)1 下列构件(ABC )属于杆件A、轴 B、梁 C、柱 D、球体2 下面哪种力可用截面法求出(ABCD )A、轴力 B、剪力 C、扭矩 D、弯矩3 力偶地三要素(ABC )A力偶矩地大小 B力偶地转向C、力偶地作用平面 D、作用线4 一个连接N个刚片地复铰相当于(AB)A.n-1个单铰B.n个单铰C.2(n-1)个约束D.2n个约束5 关于结构地几何组成分析,下列说法正确地是(ABC )A若上部体系与基础间由3个既不平行也不交于一点地支座链杆相连则可以只分析上部体系 B.二元体是指用铰连接地两个刚片 C.三刚片用三个共线地单铰相连,构成地是瞬变体系 D.任意体系加上或减去二元体不改变原体系几何组成性质6 当不考虑材料应变时,(AB )不发生改变地体系称为几何不变体系A.位置B.形状C.外力D.内力7 以下选项中相当于2个约束地有(BD )A.链杆 B.单铰 C.固定端 D.定向支座8 以下选项中不是3个约束地有(AB)A.链杆 B.单铰 C.固定端 D.刚结点9 关于平面铰结体系自由度计算公式W=2j-b-r,叙述正确地是(ABC )A. j为体系地结点个数B. b为体系内部链杆数C. r为支座链杆数D. r为节点数10 平面几何不变体系地计算自由度W(AB)A.可能等于零B.可能小于零C.可能大于零D.一定大于零11 关于三刚片规则下列叙述正确地是(ACD )A.三个单铰不能共线B.三个单铰必须是实铰C.三个单铰可以是虚铰D.若满足三刚片规则,则体系无多余约束12 关于二刚片规则,下列说法正确地是(ABCD )A. 三根链杆不可交于一点B.三根链杆不可完全平行C.可以是一个铰和一个不通过该铰地链杆D.若满足两刚片规则,则体系无多余约束13 (静定结构是(AC)A.无多余约束 B.有多余约束 C.几何不变体系 D.几何可变体系14 超静定结构是(BC)A.无多余约束 B.有多余约束 C.几何不变体系 D.几何可变体系15 刚片可以是(ABC )A.杆 B.由杆组成地几何不变结构 C.地基 D.柔索16 拱在竖向载荷作用下产生地水平反力(AC )A.为一对指向拱内部地力B.为一对指向拱外部地力C.与矢高成反比D.与矢高成正比17 关于拱内力正负号地规定,正确地是(BCD )A.弯矩以拱外侧受拉为正B以拱内侧受拉为正C剪力以隔离体顺时针转动为正D轴力以压为正18 三刚片三铰体系中,若有两个虚铰在无穷远处,则该体系(AB )A.可能是几何不变体系B.可能是瞬变体系C.一定不是几何不变体系D.一定不是瞬变体系19 两刚片三杆体系中,若三根链杆平行,则该体系(BC )A.不可能是常变体系B.可能是瞬变体系C.可能是常变体系D.一定不是瞬变体系20 三刚片三铰体系中,若有1个虚铰在无穷远处,则该体系(AC )A.可能几何不变B.不可能几何不变C.可能是瞬变体系D.一定不是瞬变体系21 关于平面一般体系自由度计算公式W=3m-2h-r,叙述正确地是(ABD )A. m为体系刚片数B. h为体系地单铰数C. h为铰地个数D.r为支座链杆数22 三刚片由三铰相连,(ABCD )A.若三铰不共线,则该体系为几何不变体系B.若有一个虚铰,则体系有可能几何不变,有可能瞬变C.若有两个虚铰,则体系有可能几何不变D.若有三个虚铰,则体系一定不是几何不变体系23 若平面体系地计算自由度W 小于零,则该体系( AD )A.一定几何不变B.一定几何可变C.是静定结构D.是超静定结构24 下图中属于刚片地是( AD )A.B.C.D. 25 下图中不属于刚片地是( BC )A.B.C.D. 26 下列属于几何不变体系地有( ABCD )C.27下列属于几何不变体系地有( ABCD )C.28 能够限制杆件转动地支座是( AD )A 、固定支座B 、固定铰支座C 、可动铰支座D 、定向支座29 力对物体地作用效应有(ABC )A 、移动效应B 、转动效应C 、变形效应D 、仅有移动效应30 下列情况下力矩等于零地是(ABCD )A 、力等于零B 、力臂等于零C 、力地作用线通过矩心D 、力与力臂均为零 31 下面是广义力地是( ABCD )A 、一个集中力B 、一对力C 、一个集中力偶D 、一对力偶32下面是广义位移地是(ABCD )A 、线位移B 、角位移C 、相对线位移D 、相对角位移 33 力偶中地两个力,下列哪些说法正确ABD ( )A 两个力必同时存在B 两力方向相反C 两力作用在同一条直线上D 两力不在同一条直线上 34分析多跨静定梁受力时,应( BCD )A.先基本,后附属B.先附属,后基本C.作用在基本部分上地载荷对附属部分受力无影响D.作用在附属部分上地载荷对基本部分受力有影响35 三铰拱(AB )A.轴线为曲线 B.在竖向载荷作用下支座处会产生水平反力C.轴线为直线D.仅有竖向反力36 静定刚架地内力有( ABC )A.弯矩 B.剪力 C.轴力 D.推力37 静定梁地内力有( AB )A.弯矩 B.剪力 C.轴力 D.推力38 拱地内力有( ABC )A.弯矩 B.剪力 C.轴力 D.推力39 下列说法正确地是( ABCD )A.梁上某段无任何载荷时,弯矩图为斜直线B.弯矩图地斜率即为剪力C.梁上作用均布载荷时,弯矩图为抛物线D.弯矩图地突起方向与载荷方向一致 40 下列说法错误地是( BD )A.若某段弯矩图为水平线则该段地剪力为零B. 若某段弯矩图为斜直线,则该段地剪力为零C.剪力为零处,弯矩存在极值D.剪力最大处,弯矩存在极值41 拱地支反力( ABC )A.与拱上承受地载荷有关B.与拱高f 有关C.与三铰位置有关D.与拱轴线形状有关 42 拱轴线地形状( BC )A.对支反力有影响B.对支反力无影响C.影响拱地内力大小D.对内力无影响 43 静定桁架中,杆件内力CD )A.有弯矩B.有剪力 C.只有轴力D.没有弯矩和剪力 44 静定桁架中,关于零内力杆地判别,描述正确地是( ABD )A.不共线二杆结点,若无外载荷作用,则二杆内力为零B.不共线二杆结点,若外力与其中一杆轴线重合,则另一杆内力为零C.不共线二杆结点,若外力与其中一杆轴线重合,则该杆内力为零D.三杆结点,其中二杆共线,若无外载荷,则另一杆内力为零45 当拱轴线为合理拱轴线时,拱截面上( AB )A.只承受压力B.弯矩剪力均为零C.只受压力和剪力D.只受剪力和弯矩 46 拱地内力(ABCD )A.与拱上承受地载荷有关B.与拱高f 有关C.与三铰位置有关D.与拱轴线形状有关 47 静定刚架按组成方式有A BCD )A.悬臂刚架 B.三铰刚架 C.简支刚架 D.组合刚架 48 下列结论正确地是( BD )A.连接两个单杆地刚结点处,两个单杆杆端弯矩等大、反向B.连接两个单杆地刚结点处,若无外力偶作用时,两个单杆杆端弯矩等大、反向C.连接三个单杆地刚结点处,三个单杆杆端弯矩等大、反向D.连接两个单杆地刚结点处,有外力偶作用时,弯矩图有跳跃49 关于具有基本-附属部分地结构,下列说法正确地是( AC )A.当仅基本部分受力时附属部分不受力B.当仅附属部分受力时,基本部分不受力C.计算时,应按照先附属后基本地顺序D.计算时,应按照先基本后附属地顺序50 三铰拱地合理拱轴线AD )A.与所受外载荷有关B.取决于水平支反力C. 与支座大小有关D.可以由任意截面K 地弯矩等于零确定51 拱与梁地区别( ABC )A.轴线地曲直B.拱在竖向载荷作用下产生水平反力C.梁在竖向载荷作用下不会产生水平反力D.结构大小52 求桁架内力地方法有(ABCD )A.结点法 B.截面法 C.力矩法 D.投影法 53 与三铰拱具有( BD )地简支梁称为等代梁A.相同高度B.相同跨度C.相同铰数D.相同载荷54 下列属于推力结构地有(CD )A.简支梁 B.悬臂梁 C.三铰拱 D.三铰刚架 55关于内力地规定,正确地是( ABD )A.剪力使隔离体发生顺时针转动为正B.轴力拉为正C.剪力使隔离体发生逆时针转动为正D.弯矩图画在材料受拉侧56 桁架按外形分为( ABCD )A.平行弦桁架B.三角形桁架C.梯形桁架D.抛物线桁架57下列属于悬臂刚架地有( ABDA. B. D.58 下列属于简支刚架地有( CD)A. B.59 力地三要素( ABC )A 、大小 B 、方向 C 、作用点 D 、作用线60 图示梁C 点偏右截面地剪力和弯矩为 ( BC )A 、QC F F =B 、2C FL M = (下侧受拉) C 、QC F F =-D 、2C FL M =-(上侧受拉)61 图示梁C点偏右截面地剪力和弯矩为(AB )A、QCF=B、CM=C、QCF F=-D、CM FL=-(上侧受拉)62 关于图乘法,下列说法正确地是(ACD )A.A与y0在杆轴线同侧时,A y0为正B.拱可以进行图乘C.如果整根杆件不符合图乘法条件,但经过分段后可以使其符合图乘条件,则仍可以应用图乘法分段计算D.如果某段弯矩图面积及形心位置不易确定时,可将其分解为几个简单图形,分别图乘再叠加计算63 虚功原理要求(CD ).温度不变 B.湿度不变 C.力系平衡 D.位移协调64、图示梁C点偏左截面地剪力和弯矩为(AD )64-65图A、QCF=B、CM=C、QCF F=-D、CM FL=-(上侧受拉)65图示梁A点偏右截面地剪力和弯矩为( AD )A、QAF=B、AM FL=(下侧受拉) C、QAF F=D、AM FL=-(上侧受拉)66 图示梁B点偏左截面地剪力和弯矩为(AD )A、QBF=B、2BFLM=(下侧受拉) C、2QBFF=-D、BM=67 由线弹性体系最基本定理--功地互等定理可以导出(ABC )A.位移互等定理B.反力互等定理C.反力位移互等定理D.大小互等定理68对于超静定结构,若(ABD )分布均对称于某一直线,则此结构为对称结构A.杆件 B.支座 C.温度 D.载荷69力法解超静定结构(ACD )A.力法基本结构可以有很多种B.正确地结果不唯一C.力法解题步骤不固定D.不同基本结构,计算地工作量可能不同70 下列关于奇数跨对称结构地说法正确地是(AC )A. 在对称载荷作用下,半结构在对称轴处为定向支座B. 在对称载荷作用下,半结构在对称轴处为固定端C. 在反对称载荷作用下,半结构在对称轴处为沿对称轴方向地链杆支座D. 在反对称载荷作用下,半结构在对称轴处为固定端71 下列结构为三次超静定地是(BD )A.B.D.72下列结构为超静定地有(BCD )A.B图73 下列结构为一次超静定地是(CD )。
结构力学期末复习题及答案结构力学期末复习题及答案随着学期的结束,结构力学课程也即将迎来期末考试。
为了帮助同学们更好地复习和准备考试,本文将提供一些典型的结构力学复习题及其答案。
希望这些题目能够帮助大家回顾和巩固所学的知识,为考试取得好成绩提供帮助。
1. 什么是结构力学?结构力学是研究结构物体在外力作用下的力学性能和变形规律的学科。
它涉及到力的平衡、力的传递、结构的变形等方面的内容。
2. 什么是受力分析?受力分析是结构力学中的一项重要内容,它通过分析结构物体上的各个受力点,确定受力的大小、方向和作用点。
受力分析是解决结构物体力学问题的第一步。
3. 什么是静力平衡?静力平衡是指结构物体在静止状态下,受力的合力和合力矩均为零。
在进行受力分析时,需要根据静力平衡条件来确定未知力的大小和方向。
4. 什么是弹性变形?弹性变形是指结构物体在受力作用下,发生的可逆的变形。
当外力去除后,结构物体能够恢复到原始形状和尺寸。
5. 什么是应力和应变?应力是指单位面积上的力的大小,常用符号为σ。
应变是指单位长度上的变形量,常用符号为ε。
应力和应变之间的关系可以通过杨氏模量、泊松比等参数来描述。
6. 什么是杆件?杆件是指在结构中起支撑和传力作用的直线构件,常见的杆件有梁、柱等。
在结构力学中,通常将杆件看作是刚性体,即不考虑其内部的弯曲和剪切变形。
7. 什么是梁?梁是一种常见的结构杆件,用于承受横向力和弯矩。
在梁的受力分析中,常用的方法有梁的受力图、弯矩图和剪力图等。
8. 什么是柱?柱是一种用于承受压力的结构杆件。
在柱的受力分析中,需要考虑柱的稳定性和承载能力等问题。
9. 什么是悬臂梁?悬臂梁是一种只有一端固定支承的梁,另一端自由悬挂。
在悬臂梁的受力分析中,需要考虑悬臂梁的弯矩和剪力等问题。
10. 什么是梁的挠度?梁的挠度是指梁在受力作用下发生的弯曲变形。
梁的挠度大小与梁的几何形状、材料性质和受力情况等因素有关。
以上是一些典型的结构力学复习题及其答案。
一、填空题。
1、在梁、刚架、拱、桁架四种常见结构中,主要受弯的是梁和钢架,主要承受轴力的是拱和桁架。
2、选取结构计算简图时,一般要进行杆件简化、支座简化、结点简化和荷载简化。
3、分析平面杆件体系的几何组成常用的规律是两刚片法则、三钢片和二元体法则。
4、建筑物中用以支承荷载的骨架部分称为结构,分为板件、杆壳和实体三大类。
5、一个简单铰相当于两个个约束。
6、静定多跨梁包括基础部分和附属部分,内力计算从附属部分开始。
7、刚结点的特点是,各杆件在连接处既无相对移动也无相对转动,可以传递力和力矩。
8、平面内一根链杆自由运动时的自由度等于三。
二、判断改错题。
1、三刚片用三个铰两两相联不一定成为几何不变体系。
()2、对静定结构,支座移动或温度改变不会产生内力。
()3、力法的基本体系不一定是静定的。
()4、任何三铰拱的合理拱轴不一定是二次抛物线。
()5、图乘法不可以用来计算曲杆。
()6、静定结构的影响线全部都由直线段组成。
()7、多跨静定梁若附属部分受力,则只有附属部分产生内力。
()8、功的互等定理成立的条件是小变形和线弹性。
()9、力法方程中,主系数恒为正,副系数可为正、负或零。
()三、选择题。
1、图示结构中当改变B点链杆方向(不能通过A铰)时,对该梁的影响是()A、全部内力没有变化B、弯矩有变化C、剪力有变化D、轴力有变化2、图示桁架中的零杆为()A、DC, EC, DE, DF, EFB、DE, DF, EFC、AF, BF, DE, DF, EFD、DC, EC, AF, BF3、右图所示刚架中A 支座的反力A H 为( ) A 、PB 、2P -C 、P -D 、2P4、右图所示桁架中的零杆为(A 、CH BI DG ,,B 、DE ,C 、AJ BI BG ,,D 、BG CF ,,5、静定结构因支座移动,( )A 、会产生内力,但无位移 B 、会产生位移,但无内力 C 、内力和位移均不会产生 D 、内力和位移均会产生6A 、θδ=+a cX B 、θδ=-a cXC 、θδ-=+a cXD 、θδ-=-acX7、下图所示平面杆件体系为( ) A 、几何不变,无多余联系 B 、几何不变,有多余联系 C 、瞬变体系 D 、常变体系8、图示梁中的轴力()A、全部为拉力B、为零C、全部为压力D、部分为拉力,部分为压力9、用图乘法求位移的必要条件之一是()A、单位荷载下的弯矩图为一直线B、结构可分为等截面直杆段C、所有杆件EI为常数且相同D、结构必须是静定的四、对下图所示平面杆件体系作几何组成分析。
知识归纳整理《结构力学》期末复习题答案一. 判断题:择最合适的答案,将A、B、C或者D。
1.图1-1所示体系的几何组成为 。
(A)几何不变体系,无多余约束 (B)几何不变体系,有多余约束(C)几何瞬变体系 (D)几何常变体系图1-1答:A。
分析:取掉二元体,结构变为下图DE,DG和基础为散刚片,由三铰两两相连,三铰不交一点,所以组成几何不变体系,无多余约束,所以答案为(A)2.图1-2所示体系的几何组成为 。
(A)几何不变体系,有多余约束 (B)几何不变体系,无多余约束(C)几何瞬变体系 (D)几何常变体系图1-2答:A。
求知若饥,虚心若愚。
图中阴影三角形为一具刚片,结点1由两个链杆连接到刚片上,结点2由两个链杆连接到刚片上,链杆12为多余约束,所以整个体系为有一具多余约束的几何不变体系,所以答案为(A)3.图1-3所示体系的几何组成为 。
(A)几何不变体系,有多余约束 (B)几何不变体系,无多余约束(C)几何瞬变体系 (D)几何常变体系图1-3答:A。
如果把链杆12去掉,整个体系为没有多余约束的几何不变体系,所以原来体系为有一具多余约束的几何不变体系,所以答案为(A)4.图1-4所示体系的几何组成为 。
(A)几何不变体系,无多余约束 (B)几何不变体系,有多余约束(C)几何瞬变体系 (D)几何常变体系图1-4答:A。
刚片1478由不交一点的三个链杆连接到基础上,构成了扩大的地基,刚片365再由不交一点的三个链杆连接到地基上,所以整个体系为没有多余约束的几何不变体系,所以答案为(A) 5.图1-5所示的斜梁AB 受匀布荷载作用,0≠θ,B 点的支座反力与梁垂直,则梁的轴力 (A)全部为拉力 (B)为零(C)全部为压力 (D)部分为拉力,部分为压力图1-5答:C。
B 点支座反力与梁垂直,对梁的轴力没有贡献,竖直方向匀布荷载总是使AB 梁受压,所以答案为(C)。
6.图1-6所示结构C 点有竖直方向集中荷载作用,则支座A 点的反力为图1-6(A)()↑PF (B)。