样本量估计

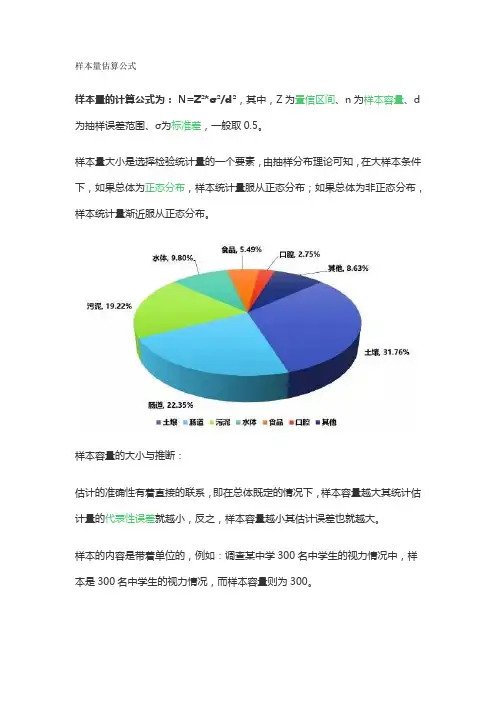
样本量估算公式
样本量的计算公式为： N=Z²*σ²/d²，其中，Z为置信区间、n为样本容量、d 为抽样误差范围、σ为标准差，一般取0.5。

样本量大小是选择检验统计量的一个要素，由抽样分布理论可知，在大样本条件下，如果总体为正态分布，样本统计量服从正态分布；如果总体为非正态分布，样本统计量渐近服从正态分布。

样本容量的大小与推断：
估计的准确性有着直接的联系，即在总体既定的情况下，样本容量越大其统计估计量的代表性误差就越小，反之，样本容量越小其估计误差也就越大。

样本的内容是带着单位的，例如：调查某中学300名中学生的视力情况中，样本是300名中学生的视力情况，而样本容量则为300。

样本容量的大小涉及到调研中所要包括的单元数，样本容量是对于研究的总体而言的，是在抽样调查中总体的一些抽样，比如：中国人的身高值为一个总体，随机取一百个人的身高，这一百个人的身高数据就是总体的一个样本，某一个样本中的个体的数量就是样本容量。

临床医学研究对象样本量的估计临床医学研究对象样本量的估计宁夏医学杂志副主编蒋兴国临床医学研究没有绝对的样本量标准，不同的研究⽅法、研究⽬的，研究要求和研究资料决定了样本量。

⼀般⽽⾔，样本越⼩，结果的估计越精确。

但样本过⼤或过⼩均可影响研究的可⾏性。

因此，科学地确定样本量可增加研究的可靠性，得到可信的研究结果。

1.估计样本量的决定因素[1]1.1 资料性质计量资料如果设计均衡,误差控制得好,样本可以⼩于30例; 计数资料即使误差控制严格,设计均衡, 样本需要⼤⼀些,需要30-100例。

1.2 研究事件的发⽣率研究事件预期结局出现的结局（疾病或死亡），疾病发⽣率越⾼，所需的样本量越⼩，反之就要越⼤。

1.3 研究因素的有效率有效率越⾼，即实验组和对照组⽐较数值差异越⼤，样本量就可以越⼩，⼩样本就可以达到统计学的显著性，反之就要越⼤。

1.4 显著性⽔平即假设检验第⼀类（α）错误出现的概率。

为假阳性错误出现的概率。

α越⼩，所需的样本量越⼤，反之就要越⼩。

α⽔平由研究者具情决定，通常α取0.05或0.01。

1.5 检验效能检验效能⼜称把握度，为1－β，即假设检验第⼆类错误出现的概率，为假阴性错误出现的概率。

即在特定的α⽔准下，若总体参数之间确实存在着差别，此时该次实验能发现此差别的概率。

检验效能即避免假阴性的能⼒，β越⼩，检验效能越⾼，所需的样本量越⼤，反之就要越⼩。

β⽔平由研究者具情决定，通常取β为0.2，0.1或0.05。

即1－β=0.8，0.1或0.95，也就是说把握度为80%，90%或95%。

1.6 容许的误差（δ）如果调查均数时，则先确定样本的均数( )和总体均数(m)之间最⼤的误差为多少。

容许误差越⼩，需要样本量越⼤。

⼀般取总体均数（1－α）可信限的⼀半。

1.7 总体标准差(s)⼀般因未知⽽⽤样本标准差s代替。

1.8 双侧检验与单侧检验采⽤统计学检验时,当研究结果⾼于和低于效应指标的界限均有意义时,应该选择双侧检验,所需样本量就⼤; 当研究结果仅⾼于或低于效应指标的界限有意义时,应该选择单侧检验,所需样本量就⼩。

临床试验样本量的估算介绍临床试验样本量的估算是一个关键性的步骤，它决定了试验结果的可靠性和统计学上的显著性。

样本量的估算需要考虑多个因素，如预期效应大小、研究设计、统计分析方法以及可接受的错误率等。

本文将详细介绍临床试验样本量估算的基本原理和常用方法。

一、样本量估算的目的和原则样本量估算的主要目的是确保试验具有足够的统计功效，能够检测到预期效应的存在或差异的显著性。

同时，也需要避免过大的样本量，以减少资源的浪费和人体试验的风险。

样本量估算的原则如下：1.统计功效要求：根据研究者的预期效应大小，确定试验能够达到的最小统计功效要求。

通常，我们希望试验能够有80%的功效检测到预期效应。

2.显著性水平：选择统计学上的显著性水平，通常为α=0.053.效应大小的估计：根据已有的文献或专家经验，估计预期效应的大小。

4.变异性的估计：估计所研究的指标的标准差或方差。

5.实用性考虑：考虑到资源和时间的限制，选择可实现的最小样本量。

二、常用的样本量估算方法1.基于效应大小的样本量估算方法这种方法根据研究者希望检测到的最小效应大小来估算样本量。

常用的方法有两组均数差异的估算、比例差异的估算以及相关系数的估算。

对于两组均数差异的估算，可使用t检验或方差分析来进行样本量估算。

对于比例差异的估算，可使用Z检验来进行样本量估算。

对于相关系数的估算，可使用相关系数检验来进行样本量估算。

2.基于统计功效的样本量估算方法这种方法以试验的统计功效为基础，确定对于预期效应的检测，需要多大样本量。

常用的方法有功效检验和样本量递推法。

对于功效检验法，可以通过计算给定样本量下的样本估计效应大小，并判断是否满足统计功效要求。

对于样本量递推法，可以根据初步样本量估计和实际效应大小来修正样本量，直到满足统计功效要求。

3.基于生存分析的样本量估算方法这种方法适用于生存分析或生存率的研究。

常用的方法有Kaplan-Meier方法和Cox比例风险模型。

估算样本量的常用方法
估算样本量的常用方法有两种，一种是基于效应大小的计算，另一种是基于统计学功效的计算。

基于效应大小的计算方法是通过先估计所要研究的效应大小，然后推算出需要多少样本才能检测到这个效应，从而确定样本量。

这种方法需要具备一定的先验知识和经验，如果效应大小预估不准，样本量就容易偏小或偏大，影响研究结果的可靠性。

基于统计学功效的计算方法是以研究假设检验的显著性水平和统计功效为依据，通过设定显著性水平和功效，计算出所需的最小样本量。

这种方法更加客观和准确，但需要将显著性水平和统计功效设定得合理才能得到严密的结果。

综合考虑研究对象的特点、研究目的和先前的研究结果，结合合理的方法，才能确定适当的样本量，以确保研究的科学性和可靠性。

样本量估计界值
样本量估计界值是在进行研究或实验设计时的重要考量之一。

它用于确定所需的样本数量，以便能够在统计学上得出有意义的结论。

样本量的大小直接影响结果的可靠性和推广性。

因此，合理地确定样本量界值对于研究的可信度和可行性非常重要。

在确定样本量界值时，需要考虑多个因素。

首先是研究的目的和研究问题的复杂程度。

如果研究问题较为简单，那么所需的样本量可能较小；而如果研究问题涉及多个变量或复杂的关系，那么所需的样本量可能较大。

其次是所用的统计检验方法和效应大小。

不同的统计检验方法对样本量的要求不同，而效应大小则影响着所需的样本量大小。

如果效应较大，那么所需的样本量可能较小；而如果效应较小，那么所需的样本量可能较大。

还需要考虑研究的时间和资源限制。

样本量的增加会带来额外的时间和成本开销，因此需要在合理的范围内确定样本量界值。

同时，还需要考虑样本的代表性和可行性。

样本的代表性是指样本能否真实地反映出总体的特征；而样本的可行性是指样本是否能够被有效地收集和分析。

确定样本量界值是进行研究或实验设计时的重要考虑因素。

合理地确定样本量界值可以提高研究结果的可靠性和推广性，从而为决策提供有意义的依据。

因此，在进行研究或实验设计时，应该根据研究问题的复杂程度、所用的统计检验方法和效应大小、时间和资源
限制以及样本的代表性和可行性等因素来确定合适的样本量界值。

多个样本均数的样本量估算方法多个样本均数的样本量估算方法1. 引言在统计学中，样本量的估算是进行实证研究时的重要步骤之一。

当我们想要对一个或多个总体参数进行推断时，需要选择合适的样本量以获得可靠的结果。

而在研究中涉及到多个样本均数时，如何估算合适的样本量就成为一个关键问题。

本文将介绍多个样本均数的样本量估算方法。

2. 多个样本均数的样本量估算方法在实际的研究中，我们往往需要比较多个群体或处理之间的均值差异。

我们可能要比较两种不同的治疗方法在患者中的疗效，或者比较不同城市的空气质量指标。

为了估算到合适的样本量，我们需要考虑以下几个因素：2.1 效应大小效应大小是指不同群体或处理之间的均值差异。

一般来说，效应大小越大，样本量就越小，因为较大的效应大小意味着我们可以更容易地发现差异。

相反，如果效应大小较小，样本量需要增加以增加统计显著性的能力。

2.2 显著性水平显著性水平是我们对于差异是否真实存在的信心水平。

通常我们选择的显著性水平为0.05或0.01。

选择较小的显著性水平会导致需要更大的样本量，因为我们要求更高的置信度来支持我们的结论。

2.3 统计功效统计功效是指检验能够检测到差异的能力。

通常我们选择的统计功效为0.8或0.9，即80%或90%的概率能够检测到真实存在的差异。

较高的统计功效要求较大的样本量。

2.4 方差方差是影响样本量估算的一个重要因素。

方差反映了数据的离散程度，较大的方差意味着样本量需要增大。

如果预先没有方差的估计，通常可以进行一个小规模的前期研究来估计方差。

根据上述因素，我们可以使用统计学中的样本量估算方法来计算合适的样本量。

以下是一种常用的多个样本均数的样本量估算方法：3. 样本量估算方法示例假设我们想要比较A、B、C三种不同的染料对纺织品色牢度的影响，我们希望能够发现三种染料之间的均值差异。

我们已经知道了染料A的均值为μ1，标准差为σ1；染料B的均值为μ2，标准差为σ2；染料C的均值为μ3，标准差为σ3。

最低样本量的估算公式
在进行样本量估算时，通常会考虑诸多因素，如总体方差、显著性水平、置信度等。

然而，在某些情况下，我们需要尽可能地减少数据采集的成本和时间，因此需要寻找最低样本量的估算公式。

最低样本量的估算公式基于以下假设：
1. 样本来自于一个正态分布的总体；
2. 总体方差未知，但样本方差可用作总体方差的估计量；
3. 期望误差为给定值（通常为总体均值的一定比例）。

根据这些假设，我们可以得到最低样本量的估算公式：
n = (Zα/2 ×σ/ε)
其中，n为最低样本量；Zα/2为给定显著性水平下的标准正态分布的分位数；σ为样本方差的平方根，作为总体方差的估计量；ε为期望误差，即总体均值的一定比例。

需要注意的是，这个公式只适用于正态分布的总体，如果样本来自于一个非正态分布的总体，或者总体方差已知，那么需要使用其他的样本量估算方法。

此外，最低样本量的估算公式只是一个估计值，实际采样时可能需要根据具体情况进行调整。

- 1 -。

如何估算样本量？统计学是一门研究如何从样本数据中推断总体数据的学科。

在进行统计研究时，我们需要考虑到样本大小的问题，即需要多少个观测值才能得到可靠的结论。

本文将介绍如何估算样本量的方法。

一、确定研究目的首先，我们需要明确研究目的，即想要回答什么问题。

例如，我们想要研究某种药物对于某种疾病的治疗效果，那么我们需要确定研究的主要目的是什么，例如想要证明这种药物的疗效是否显著。

二、确定显著性水平和功效接下来，我们需要确定显著性水平和功效。

显著性水平是指我们所允许的犯错率，通常取0.05或0.01。

功效是指我们希望检验的假设能够被发现的概率，通常取0.8或0.9。

三、确定总体方差和效应量然后，我们需要确定总体方差和效应量。

总体方差是指总体数据的变异程度，通常需要通过历史数据或者专家意见来估计。

效应量是指我们所关心的变量之间的差异大小，例如在药物治疗和安慰剂治疗之间的差异。

四、使用样本量估算公式进行计算最后，我们可以使用样本量估算公式进行计算。

样本量估算公式是根据显著性水平、功效、总体方差和效应量等因素推导出来的。

其中，最常用的样本量估算公式是针对两个样本均值比较的t检验，公式如下：n = [(Zα/2 + Zβ) * σ / δ]^2其中，n表示样本量，Zα/2表示显著性水平对应的Z值，Zβ表示功效对应的Z值，σ表示总体方差，δ表示效应量。

举例说明假设我们想要研究某种药物对于某种疾病的治疗效果，我们希望证明这种药物的疗效显著，显著性水平为0.05，功效为0.8。

我们需要估算样本量，以保证研究结果的可靠性。

根据历史数据和专家意见，我们估计总体方差为10，效应量为2。

根据Z表格可知，当显著性水平为0.05时，Zα/2为1.96；当功效为0.8时，Zβ为0.84。

带入样本量估算公式可得：n = [(1.96 + 0.84) * 10 / 2]^2 = 62.74因此，我们需要至少收集63个样本才能保证研究结果的可靠性。