第二章导数与微分

1、极限的实质是：动而不达导数的实质是：一个有规律商的极限。

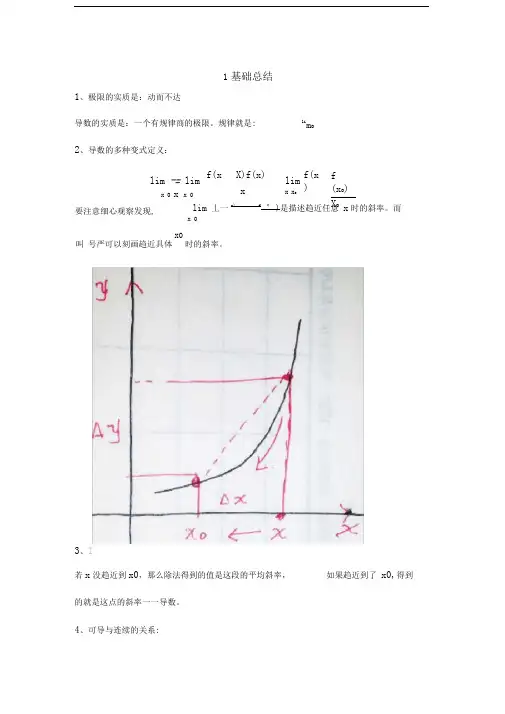
规律就是:2、导数的多种变式定义：lim 丄一x)f°)是描述趋近任意 x 时的斜率。

而x 03、I若x 没趋近到x0，那么除法得到的值是这段的平均斜率， 如果趋近到了 x0,得到的就是这点的斜率一一导数。

4、可导与连续的关系:1基础总结lim -= limx 0 x x 0 f(x X)f(x)xlim x x o f(x )f (x o )X o叫 号严可以刻画趋近具体x0时的斜率。

lim o要注意细心观察发现,导数的实质是定义在某点的左右极限。

既然定义在了某点上，该点自然存在，而 且还得等于左右极限。

因此，可导一定是连续的。

反之，如果连续，不一定可导。

不多说。

同理，如果不连续，肯定某点要么无定义，要么定义点跳跃跑了，肯定 极限有可能存在，但是导数绝不会存在。

同理要注意左右导数的问题。

如果存在左或者右导数，那么在左侧该点一定是存 在的。

如：f(x) x,x 0这个函数，在0点就不存在左导数，只存在右导数。

为什么嫩？看定义:万不要以为导数是一种简单的极限，极限是可以在某点无定义的，而导数却是该 点必须存在! 由此引发了一些容易误判的血案: 例如:A 旦主^謎IC m F 左电鼓 pg 总生戟乞f ( x) f (x)-中的f(x))至u 底是神马。

比如求上图limf(x x) f(x)x 0xlimf(X X)f(0)。

x 0定义里面需要用到f(0)啊！因此，千中 iimf (x)论) x 1x x 0,这个f(x0)千万要等于2/3，而不是1 ！定义解决时候一定要注意问。

X X o由此也可以知道，f (x)2x 3, x 1这个函数是不存在导数的，也不存在左导数,3只存在右导数。

5、反函数的导数与原函数的关系:注意，求反函数时候不要换元。

因为换了元虽然对自身来讲函数形式不变, 与原函数融合运算时候就算是换了一个不是自己反函数的一个函数进行运算 果显然是错误的。

大一上学期《高等数学》知识整理-第二章导数与微分第二章导数与微分1.导数的定义。

对于一个在x0的某个邻域内有定义的函数，当自变量x在x0处取得增量Δx时，相应地函数y取得增量Δy=f(x0+Δx)-f(x0)，如果当Δx→x0时Δy/Δx的极限存在，则称函数y=f(x)在x0点可导，并称这个极限为函数y=f(x)在x0处的导数。

通俗地讲，就是描述某个函数在某点增长或下降的瞬时速度，这个“速度”的单位为y每x，即每变化一个单位的x，y变化多少。

与物理学中定义米/秒是一个性质的。

把函数f(x)的导数看做是关于x的函数，即得到函数f(x)的导函数f'(x)，简称导数。

（以上的“x0”中的“0”都是x 的下标，下同。

）导数也可以用微分的形式记作dy/dx，这个后面会提及。

2.在导数的定义中，如果Δx从左边趋向x0或从右边趋向x0，那么对应的导数被称为左导数和右导数。

只有f(x)在x0处的左导数和右导数相等，才能称f(x)在x0处可导。

举个例子，绝对值函数y=|x|，其在x=0处的左导数是-1（即x每增大1，y减小1），右导数是1，两者不相等，所以该函数在x=0处不可导。

如图所示。

绝对值函数y=|x|的导数是符号函数y=sgn(x)，但是不包含x=0（单独的符号函数y=sgn(x)，当x=0时，y=0）。

3.用定义法可以求初等函数的导数，本质上就是求极限。

比如说求y=x²在x=a处的导数，即就是求Δx→0时((a+Δx)²-a²)/Δx的极限。

求得结果为2a了解即可，还不如求导公式来得快。

下图为求该极限的过程，也就是用定义求y=x²的导数的过程。

4.函数的可导性与连续性的关系。

我们有定理：如果函数y=f(x)在点x0处可导，则f(x)在x0处必连续。

但反过来就不一定了。

归纳为一句话：连续不一定可导，可导一定连续。

y=|x|就是一个例子。

该函数在定义域内处处连续但是在x=0时不可导（因为左右极限不一样）。

第二章 导数与微分数学中研究导数、微分及其应用的部分称为微分学，研究不定积分、定积分及其应用的部分称为积分学. 微分学与积分学统称为微积分学. 微积分学是高等数学最基本、最重要的组成部分，是现代数学许多分支的基础，是人类认识客观世界、探索宇宙奥秘乃至人类自身的典型数学模型之一. . 本章及下一章将介绍一元函数微分学及其应用的内容.第一节 导数概念下列三类问题导致了微分学的产生： (1) 求变速运动的瞬时速度；(2) 求曲线上一点处的切线；(3) 求最大值和最小值.这三类实际问题的现实原型在数学上都可归结为函数相对于自变量变化而变化的快慢程度，即所谓函数的变化率问题. 牛顿从第一个问题出发，莱布尼茨从第二个问题出发，分别给出了导数的概念. 内容要点： 1 导数的定义 2左右导数3导数的几何意义 4函数的可导性与连续性的关系一、引例1、直线运动速度设描述质点运动位置的函数为()s f t =，匀速时：tsv 时间路程=， 平均速度：tsv ∆∆=，因平均速度≠瞬时速度，则0t 到t 的平均速度为00()()f t f t v t t -=-，而0t 时刻的瞬时速度为000()()lim t t f t f t v t t →-=-2、切线问题（曲线在一点处切线的斜率）当点N 沿曲线C 趋于点M 时，若割线MN 绕点M 旋转而趋于极限位置MT ，直线MT 就称为曲线C 在点M 处的切线因0000()()tan y y f x f x yx x x x xφ--∆===--∆ [切线应为割线的极限]当N 沿曲线M C →时，0x x →，故0000()() lim lim x x x f x f x yk x x x ∆→→-∆==∆- 即为割线斜率的极限，即切线斜率。

瞬时速度000()()limt t f t f t v t t →-=-切线斜率000()()limx x f x f x k x x →-=-两个问题的共性:所求量为函数增量与自变量增量之比的极限 .二、导数的定义： 1、函数在一点处的导数设函数()y f x =在点0x 的某个邻域内有定义，当自变量x 在0x 处取得增量x ∆（点0x x +∆仍在该邻域内）时，相应的函数y 取得增量00()()y f x x f x ∆=+∆-；如果y ∆与x ∆之比当0x ∆→时极限存在，则称函数()y f x =在点0x 处可导，并称此极限为函数()y f x =在点0x 处的导数，记为：00000()()limlim x x x x f x x f x y y x x =∆→∆→+∆-∆'==∆∆或0()f x '，x x dy dx=或()x x df x dx =即：已知()f x ，构造yx∆∆，求此增量比的极限，若极限存在，则可导，不存在就不可导（此时切线必垂直于x 轴）。

第二章导数与微分一、教学目的1.理解导数和微分的概念、导数的几何意义，函数的可导性与连续性之间的的关系.2.掌握导数、微分计算的各种方法，会求简单函数的高阶导数的计算. 二、教学重点1.导数的概念及几何意义.2.导数计算的各种方法 三、教学难点复合函数和隐函数的导数 四、课时安排 约16学时2.1 导数的概念◆2.1.1引例◆2.1.2导数的定义 ◆2.1.3求导数举例◆2.1.4 导数与左右导数的关系 ◆2.1.5导数的几何意义◆2.1.6函数的可导性与连续性的关系 ◆2.1.7内容小结2.1.1引例1．瞬时速度设一质点在坐标轴上作非匀速运动, 时刻t 质点的坐标为s , s 是t 的函数: s =f (t ), 求动点在时刻t 0的速度. 考虑到 0000()()s s f t f t v t t t t --==--, 这个比值可认为是动点在时间间隔t -t 0内的平均速度. 如果时间间隔选得越短, 这个比值和动点在时刻t 0的速度越接近.令t -t 0→0, 取比值0)()(t t t f t f --的极限, 如果这个极限存在, 设为v , 即0)()(limt t t f t f v t t --=→我们把这个极限值v 称为动点在时刻t 0的瞬时速度. 2． 产品总成本的变化率设某产品的总成本C 是产量q 的函数，即C ＝f （q ）.当产量0q 变为0q q +∆时，总成本相应的改变量为 00()()C f q q f q ∆=+∆-而产量由0q 变为0q q +∆时，总成本的平均变化率为00()()f q q f q C q q+∆-∆=∆∆ 当0q ∆→时，如果极限000()()limq f q q f q C q q∆→+∆-∆=∆∆存在，称此极限为产量为0q 的总成本的变化率，又称边际成本.2.1.2导数的定义定义2.1.1 设函数y =f (x )在点x 0的某个邻域内有定义, 当自变量x 在x 0处取得增量∆x 时, 相应地函数y 取得增量∆y =f (x 0+∆x )-f (x 0); 如果∆y 与∆x 之比当∆x →0时的极限存在, 则称函数y =f (x )在点x 0处可导, 并称这个极限为函数y =f (x )在点x 0处的导数, 记为)(0x f ',即 xx f x x f x yx f x x ∆-∆+=∆∆='→∆→∆)()(limlim)(00000, 也可记为0|x x y =', 0 x x dx dy =或0)(x x dx x df =. 导数的定义式也可取不同的形式, 常见的有 h x f h x f x f h )()(lim)(0000-+='→, 或 000)()(l i m )(0x x x f x f x f x x --='→. .如果极限xx f x x f x ∆-∆+→∆)()(lim000不存在, 就说函数y =f (x )在点x 0处不可导.如果函数y =f (x )在开区间I 内的每点处都可导, 就称函数f (x )在开区间I 内可导.定义2.1.2如果对任一x ∈I ,函数 f (x )都对应着的一个确定的导数值. 这样就构成了一个新的函数, 这个函数叫做原来函数y =f (x )的导函数, 记作 y ',)(x f ',dx dy , 或dxx df )(. f '(x 0)与f '(x )之间的关系:函数f (x )在点x 0处的导数f '(x )就是导函数f '(x )在点x =x 0处的函数值, 即 0)()(0x x x f x f ='='.导函数f '(x )简称导数, 而f '(x 0)是f (x )在x 0处的导数或导数f '(x )在x 0处的值.2.1.3求导数举例例1．求函数f (x )=C （C 为常数）的导数. 解: hx f h x f x f h )()(lim)(0-+='→0lim 0=-=→h C C h . 即 (C ) '=0.例2. 求xx f 1)(=的导数.解:h x h x h x f h x f x f h h 11lim )()(lim )(00-+=-+='→→2001)(1lim )(lim x x h x x h x h h h h -=+-=+-=→→. 例3. 求x x f =)(的导数.解: hx h x h x f h x f x f h h -+=-+='→→00l i m )()(l i m )(xx h x x h x h h h h 211lim )(lim00=++=++=→→. 例4．求函数f (x )=x n (n 为正整数)在x =a 处的导数. 解: f '(a )a x a f x f ax --=→)()(lima x a x n n a x --=→lim ax →=lim (x n -1+ax n -2+ ⋅ ⋅ ⋅ +a n -1)=na n -1. 把以上结果中的a 换成x 得 f '(x )=nx n -1,即 (x n )'=nx n -1.一般地, 有(x μ)'=μx μ-1 , 其中μ为常数. 例5．求函数f (x )=sin x 的导数. 解: f '(x )hx f h x f h )()(lim-+=→h x h x h sin )sin(lim 0-+=→ 2sin )2cos(21lim 0hh x h h +⋅=→x h hhx h cos 22sin )2cos(lim 0=⋅+=→.即 (sin x )'=cos x .用类似的方法, 可求得 (cos x )'=-sin x . 例6．求函数f (x )= a x (a >0, a ≠1) 的导数. 解: f '(x )hx f h x f h )()(lim-+=→h a a x h x h -=+→0lim h a a h h x 1lim 0-=→t a h =-1令)1(log lim 0t t a a t x +→a a ea x a xln log 1==. 即 '()ln x xa a a =特别地有 (e x )=e x .例7．求函数f (x )=log a x (a >0, a ≠1) 的导数. 解: hx h x h x f h x f x f a ah h log )(log lim )()(lim)(00-+=-+='→→ h xa h a h a h xh x x h h x x x h x h )1(log lim 1)1(log lim 1)(log 1lim 000+=+=+=→→→ax e x a ln 1log 1==. 即 ax x a ln 1)(log =' . :特殊地 xx 1)(l n='. 2.1.4 导数与左右导数的关系:定义2.1.3如果极限hx f h x f h )()(lim 000-+-→存在, 则称此极限值为函数在x 0的左导数.即 f (x )在0x 的左导数:hx f h x f x f h )()(lim )(0000-+='-→-;如果极限hx f h x f h )()(lim 000-++→存在, 则称此极限值为函数在x 0的右导数.即f (x )在0x 的右导数:hx f h x f x f h )()(lim )(0000-+='+→+.定理2.1 函数f (x )在点x 0处可导的充分必要条件是左导数左导数f '-(x 0) 和右导数f '+(x 0)都存在且相等.即: A x f =')(0⇔A x f x f ='='+-)()(00. 如果函数f (x )在开区间(a , b )内可导, 且右导数f '+(a ) 和左导数f '-(b )都存在, 就说f (x )有闭区间[a , b ]上可导.例8．求函数f (x )=|x |在x =0处的导数.解: 1||lim )0()0(lim )0(00-==-+='--→→-h h h f h f f h h , 1||lim )0()0(lim )0(00==-+='++→→+h h hf h f f h h , 因为f '-(0)≠ f '+(0), 所以函数f (x )=|x |在x =0处不可导.2.1.5导数的几何意义函数y =f (x )在点x 0处的导数f '(x 0)在几何上表示曲线y =f (x )在点M (x 0, f (x 0))处的切线的斜率, 即 f '(x 0)=tan α , 其中α是切线的倾角.如果y =f (x )在点x 0处的导数为无穷大, 这时曲线y =f (x )的割线以垂直于x 轴的直线x =x 0为极限位置, 即曲线y =f (x )在点M (x 0, f (x 0))处具有垂直于x 轴的切线x =x 0.由直线的点斜式方程, 可知曲线y =f (x )在点M (x 0, y 0)处的切线方程为 y -y 0=f '(x 0)(x -x 0).过切点M (x 0, y 0)且与切线垂直的直线叫做曲线y =f (x )在点M 处的法线.如果 f '(x 0)≠0, 法线的斜率为)(10x f '-, 从而法线方程为 )()(1000x x x f y y -'-=-.例9. 求等边双曲线x y 1=在点)2 ,21(处的切线的斜率, 并写出在该点处的切线方程和法线方程.解: 21x y -=', 所求切线及法线的斜率分别为4)1(2121-=-==x x k , 41112=-=k k .所求切线方程为)21(42--=-x y , 即4x +y -4=0.所求法线方程为)1(12-=-x y , 即2x -8y +15=0.例10. 求曲线x x y =的通过点(0, -4)的切线方程.解 设切点的横坐标为x 0, 则切线的斜率为 0212302323)()(0x x x x f x x =='='=. 于是所求切线的方程可设为)(230000x x x x x y -=-.根据题意, 点(0, -4)在切线上, 因此 )0(2340000x x x x -=--,解方程得x 0=4.于是所求切线的方程为 )4(42344-=-x y , 即3x -y -4=0.2.1.6函数的可导性与连续性的关系如果函数y =f (x )在点x 处可导, 则函数在该点必连续.另一方面, 一个函数在某点连续却不一定在该点处可导.例11． 函数3)(x x f =在区间(-∞, +∞)内连续, 但在点x =0处不可导. 这是因为函数在点x =0处导数为无穷大h f h f h )0()0(lim-+→+∞=-=→hh h 0lim 30. 2.1.7内容小结1.引例2.导数的定义3.求导数举例4.导数与左右导数的关系5.导数的几何意义6.函数的可导性与连续性的关系2.2 函数的求导法则◆2.2.1函数的和、差、积、商的求导法则 ◆2.2.2反函数的求导法则 ◆2.2.3复合函数的求导法则 ◆2.2.4求导法则与导数公式 ◆2.2.5 隐函数的导数 ◆2.2.6 对数求导法◆2.2.7参数方程所确定的函数的导数 ◆2.2.8内容小结2.2.1函数的和、差、积、商的求导法则定理2.2 如果函数u =u (x )及v =v (x )在点x 可导, 则它们的和、差、积、商(分母不为零)都在点x 具可导, 并且[u (x ) ±v (x )]'=u '(x ) ±v '(x ) ;[u (x )⋅v (x )]'=u '(x )v (x )+u (x )v '(x );)()()()()()()(2x v x v x u x v x u x v x u '-'='⎥⎦⎤⎢⎣⎡.定理2.2中的函数的和、差、积的求导法则可推广到有限多个可导函数的情形. 在函数的积的求导法则中, 如果v =C (C 为常数), 则有 (Cu )'=Cu '. 例1．y =2x 3-5x 2+3x -7, 求y '解: y '=(2x 3-5x 2+3x -7)'= (2x 3)'-(5x 2)'+(3x )'-(7)'= 2 (x 3)'- 5( x 2)'+ 3( x )' =2⋅3x 2-5⋅2x +3=6x 2-10x +3.例2. 2 sin cos 4)(3π-+=x x x f , 求f '(x )及)2 (πf '.解: x x x x x f sin 43)2 (sin )cos 4()()(23-='-'+'='π,443)2 (2-='ππf .例3．y =e x (sin x +cos x ), 求y '.解: y '=(e x )'(sin x +cos x )+ e x (sin x +cos x )' = e x (sin x +cos x )+ e x (cos x -sin x ) =2e x cos x . 例4．y =tan x , 求y '.解:xx x x x x x x y 2cos )(cos sin cos )(sin )cos sin ()(tan '-'='='='x xx x x 22222sec cos 1cos sin cos ==+=.即 (tan x )'=sec 2x .例5．y =sec x , 求y '.解: x x x x x y 2cos )(cos 1cos )1()cos 1()(sec '⋅-'='='='x x2cos sin ==sec x tan x . 即 (sec x )'=sec x tan x .类似的,可求得余切函数及余割函数的导数公式: (cot x )'=-csc 2x ,(csc x )'=-csc x cot x .2.2.2反函数的求导法则定理2.3如果函数x =f (y )在某区间I y 内单调、可导且f '(y )≠0, 那么它的反函数y =f -1(x )在对应区间I x ={x |x =f (y ), y ∈I y }内也可导, 并且)(1])([1y f x f '='-. 或dydx dx dy 1=.即反函数的导数等于直接函数导数的倒数.例6．设x =sin y , ]2 ,2 [ππ-∈y 为直接函数, 则y =arcsin x 是它的反函数. 函数x =sin y 在开区间)2 ,2 (ππ-内单调、可导, 且 (sin y )'=cos y >0.因此, 由反函数的求导法则, 在对应区间I x =(-1, 1)内有 2211sin 11cos 1)(sin 1)(arcsin x y y y x -=-=='='. 即(a r c s i nx '=类似地有: 211)(arccos x x --='.例7．设x =tan y , )2 ,2 (ππ-∈y 为直接函数, 则y =arctan x 是它的反函数. 函数x =tan y在区间)2 ,2 (ππ-内单调、可导, 且 (tan y )'=sec 2 y ≠0.因此, 由反函数的求导法则, 在对应区间I x =(-∞, +∞)内有 22211t a n 11s e c 1)(t a n 1)(a r c t a n xy y y x +=+=='='. 类似地有: 211)cot arc (xx +-='.例8.设x =a y (a >0, a ≠1)为直接函数, 则y =log a x 是它的反函数. 函数x =a y 在区间I y =(-∞, +∞)内单调、可导, 且 (a y )'=a y ln a ≠0.因此, 由反函数的求导法则, 在对应区间I x =(0, +∞)内有 ax a a a x y y a ln 1ln 1)(1)(log =='='. 2.2.3复合函数的求导法则定理2.4如果u =g (x )在点x 可导, 函数y =f (u )在点u =g (x )可导, 则复合函数y =f [g (x )]在点x 可导, 且其导数为 )()(x g u f dx dy '⋅'=或dx du du dydx dy ⋅=. 例9. 3x e y =, 求dxdy . 解： 函数3x e y =可看作是由y =e u , u =x 3复合而成的, 因此32233x u e x x e dxdu du dy dx dy =⋅=⋅=. 例10. 212sinx x y +=, 求dx dy .解： 函数212sinx x y +=是由y =sin u , 212x x u +=复合而成的, 因此2222222212cos )1()1(2)1()2()1(2cos x x x x x x x u dx du du dy dx dy +⋅+-=+-+⋅=⋅=. 对复合函数的导数比较熟练后, 就不必再写出中间变量,而直接写出结果.例11．lnsin x , 求dxdy . 解:)(sin sin 1)sin (ln '⋅='=x xx dx dy x x x cot cos sin 1=⋅=. 例12．3221x y -=, 求dxdy . 解:)21()21(31])21[(2322312'-⋅-='-=-x x x dx dy 322)21(34x x --=. 复合函数的求导法则可以推广到多个中间变量的情形. 例如, 设y =f (u ), u =ϕ(v ), v =ψ(x ),则dxdv dv du du dy dx du du dy dx dy ⋅⋅=⋅=. 例13．y =lncos(e x ), 求dxdy . 解:])[cos()cos(1])cos([ln '⋅='=x x x e e e dx dy)tan()()]sin([)cos(1x x x x x e e e e e -='⋅-⋅=.例14．xe y 1sin =, 求dxdy . 解: )1(1cos )1(sin )(1sin 1sin 1sin '⋅⋅='⋅='=x x e x e e dx dy x x x x e x x 1cos 11sin 2⋅⋅-=. 例15.设x >0, 证明幂函数的导数公式(x μ)'=μ x μ-1.解： 因为x μ=(e ln x )μ=e μ ln x , 所以(x μ)'=(e μ ln x )'= e μ ln x ⋅(μ ln x )'= e μ ln x ⋅μ x -1=μ x μ-1.2.2.4求导法则与导数公式 1．基本初等函数的导数:(1) (C )'=0, (2) (x μ)'=μ x μ-1, (3) (sin x )'=cos x , (4) (cos x )'=-sin x , (5) (tan x )'=sec 2x , (6) (cot x )'=-csc 2x , (7) (sec x )'=sec x ⋅tan x , (8) (csc x )'=-csc x ⋅cot x , (9) (a x )'=a x ln a , (10) (e x )'=e x ,(11) a x x a ln 1)(log =',(12) xx 1)(ln =',(13) 211)(arcsin x x -=', . (14) 211)(arccos x x --=' (15) 211)(arctan x x +=',(16) 211)cot arc (xx +-='.2．函数的和、差、积、商的求导法则 设u =u (x ), v =v (x )都可导, 则(1)(u ±v )'=u '±v ', (2)(C u )'=C u ', (3)(u v )'=u '⋅v +u ⋅v ',(4)2)(v v u v u v u '-'='.3．反函数的求导法则设x =f (y )在区间I y 内单调、可导且f '(y )≠0, 则它的反函数y =f -1(x )在I x =f (I y )内也可导, 并且)(1])([1y f x f ='-. 或dydx dx dy 1=.4．复合函数的求导法则设y =f (x ), 而u =g (x )且f (u )及g (x )都可导, 则复合函数y =f [g (x )]的导数为dxdudu dy dx dy ⋅=或y '(x )=f '(u )⋅g '(x ). 例16. y =sin nx ⋅sin n x (n 为常数), 求y '. 解: y '=(sin nx )' sin n x + sin nx ⋅ (sin n x )'= n cos nx ⋅sin n x +sin nx ⋅ n ⋅ sin n -1 x ⋅(sin x )'= n cos nx ⋅sin n x +n sin n -1 x ⋅ cos x =n sin n -1 x ⋅ sin(n +1)x .2.2.5 隐函数的导数定义2.2.1形如y =f (x )的函数称为显函数. 例如y =sin x , y =ln x +e x 是显函数的例子. 定义2.2.2 由方程F (x , y )=0所确定的函数称为隐函数. 例17求由方程e y +xy -e =0 所确定的隐函数y 的导数. 解: 把方程两边的每一项对x 求导数得 (e y )'+(xy )'-(e )'=(0)', 即 e y ⋅ y '+y +xy '=0, 从而 y ex yy +-='(x +e y ≠0). 在上式两边对x 求导过程中，在遇到含有y 项时，应视y 是x 的函数，利用复合函数的求导法则.例18求由方程y 5+2y -x -3x 7=0 所确定的隐函数y =f (x )在x =0处的导数y '|x =0. 解: 把方程两边分别对x 求导数得5y ⋅y '+2y '-1-21x 6=0,由此得 2521146++='y x y .因为当x =0时, 从原方程得y =0, 所以 21|25211|0460=++='==x x y x y . 例19 求椭圆122=+y x 在)323 ,2(处的切线方程.解: 把椭圆方程的两边分别对x 求导, 得0928='⋅+y y x . 将x =2, 323=y , 代入上式得 03141='⋅+y ,于是 k =y '|x =243-=. 所求的切线方程为)2(43323--=-x y , 即03843=-+y x .2.2.6 对数求导法:这种方法是先在y =f (x )的两边取对数, 然后再求出y 的导数. 设y =f (x ), 两边取对数, 得 ln y = ln f (x ),两边对x 求导, 得 ])([ln 1'='x f y y,y '= f (x )⋅[ln f (x )]'.对数求导法适用于求幂指函数y =[u (x )]v (x )的导数及多因子之积和商的导数. 例20求y =x sin x (x >0)的导数.解法一: 两边取对数, 得 ln y =sin x ⋅ ln x ,上式两边对x 求导, 得 x x x x y y 1sin ln cos 1⋅+⋅=',于是 )1sin ln (cos x x x x y y ⋅+⋅=')sin ln (cos sin xx x x x x +⋅=.解法二: 这种幂指函数的导数也可按下面的方法求:y =x sin x =e sin x ·ln x, )sin ln (cos )ln (sin sin ln sin x x x x x x x e y x x x +⋅='⋅='⋅.例21求函数)4)(3()2)(1(----=x x x x y 的导数.解: 先在两边取对数(假定x >4), 得ln y 21=[ln(x -1)+ln(x -2)-ln(x -3)-ln(x -4)],上式两边对x 求导, 得 )41312111(211-----+-='x x x x y y ,于是 )41312111(2-----+-='x x x x yy .当x <1时, )4)(3()2)(1(x x x x y ----=; 当2<x <3时, )4)(3()2)(1(x x x x y ----=; 用同样方法可得与上面相同的结果.注: 严格来说, 本题应分x >4, x <1, 2<x <3三种情况讨论, 但结果都是一样的.2.2.7参数方程所确定的函数的导数定理2.5 设x =ϕ(t )具有单调连续反函数t =ϕ-1(x ), 且此反函数能与函数y =ψ(t )构成复合函数y =ψ[ϕ-1(x ) ], 若x =ϕ(t )和y =ψ(t )都可导, 则 )()(1t t dtdx dt dy dx dt dt dy dx dy ϕψ''=⋅=⋅=, 即 )()(t t dx dy ϕψ''=或dt dx dt dydx dy =. 例1 设⎩⎨⎧+=-=)1ln(arctan 2t y tt x ，求1=t dx dy . 解：t t t t dt dx dt dydx dy 21111222=+-+== ∴21==t dx dy 例2求椭圆⎩⎨⎧==t b y t a x sin cos 在相应于4 π=t 点处的切线方程. 解:t ab t a t b t a t b dx dy cot sin cos )cos ()sin (-=-='=. 所求切线的斜率为ab dx dyt -==4π. 切点的坐标为224 cos 0a a x ==π, 224sin 0b b y ==π. 切线方程为)22(22a x a b b y --=-, 即 bx +ay 2-ab =0.2.2.8内容小结1.函数的和、差、积、商的求导法则2.反函数的求导法则3.复合函数的求导法则4.求导法则与导数公式5.隐函数的导数6.对数求导法7.参数方程所确定的函数的导数2.3 高阶导数◆2.3.1 高阶导数◆2.3.2 内容小结定义2.3.1如果函数y =f (x )的导数y '=f '(x )仍然是x 的函数. 则称y '=f '(x )的导数叫做函数y =f (x )的二阶导数, 记作 y ''、f ''(x )或22dx y d , 即 y ''=(y ')', f ''(x )=[f '(x )]' , )(22dxdy dx d dx y d =. 相应地, 把y =f (x )的导数f '(x )叫做函数y =f (x )的一阶导数.类似地, 二阶导数的导数, 叫做三阶导数, 三阶导数的导数叫做四阶导数, ⋅ ⋅ ⋅, 一般地, (n -1)阶导数的导数叫做n 阶导数, 分别记作y ''', y (4), ⋅ ⋅ ⋅ , y (n ) 或33dx y d , 44dx y d , ⋅ ⋅ ⋅ , nn dx y d . 函数f (x )具有n 阶导数, 也称函数f (x )为 n 阶可导. 如果函数f (x )在点x 处具有n 阶导数, 那么函数f (x )在点x 的某一邻域内一定具有所有低于n 阶的导数. 二阶及二阶以上的导数统称高阶导数.例1．y =ax +b , 求y ''.解: y '=a , y ''=0.例2．s =sin ω t , 求s ''.解: s '=ω cos ω t , s ''= cos ω t -ω 2sin ω t .例3．验证: 函数22x x y -=是方程y 3y ''+1=0的解.证明: 因为22212222x x x x x x y --=--=', 22222222)1(2x x x x xx x x y -------='')2()2()1(22222x x x x x x x ----+-=32321)2(1yx x -=--=, 所以y 3y ''+1=0.例4．求函数y =e x 的n 阶导数.解：y '=e x , y ''=e x , y '''=e x , y ( 4)=e x ,一般地, 可得 y ( n )=e x , 即 (e x )(n )=e x .例5．求正弦函数与余弦函数的n 阶导数.解: y =sin x ,)2s i n (c o s π+=='x x y , )22s i n ()2 2 s i n ()2 c o s (ππππ⋅+=++=+=''x x x y , )23s i n ()2 2 2s i n ()2 2c o s (ππππ⋅+=+⋅+=⋅+='''x x x y , )24sin()2 3cos()4(ππ⋅+=⋅+=x x y , 一般地, 我们有)2sin()(π⋅+=n x y n , 即)2 sin()(sin )(π⋅+=n x x n .同理, 可得 )2c o s ()(c o s )(π⋅+=n x x n .例6．求幂函数y =x μ (μ是任意常数)的n 阶导数公式.解: y '=μx μ-1,y ''=μ(μ-1)x μ-2,y '''=μ(μ-1)(μ-2)x μ-3,y ( 4)=μ(μ-1)(μ-2)(μ-3)x μ-4,依次类推, 可得y (n )=μ(μ-1)(μ-2) ⋅ ⋅ ⋅ (μ-n +1)x μ-n ,即 (x μ )(n ) =μ(μ-1)(μ-2) ⋅ ⋅ ⋅ (μ-n +1)x μ-n .当μ=n 时, 得到(x n )(n ) = μ(μ-1)(μ-2) ⋅ ⋅ ⋅ 3 ⋅ 2 ⋅ 1=n ! .而 (x n )( n +1)=0 .2.3.2 内容小结高阶导数2.4 函数的微分◆2.4.1微分的定义◆2.4.2微分的几何意义◆2.4.3基本初等函数的微分公式与微分运算法则◆2.4.4微分在近似计算中的应用◆2.4.5内容小结2.4.1微分的定义定义2.4.1 设函数y =f (x )在某区间内有定义, x 0及x 0+∆x 在这区间内, 如果函数的增量 ∆y =f (x 0+∆x )-f (x 0)可表示为∆y =A ∆x +o (∆x ), 其中A 是不依赖于∆x 的常数, 那么称函数y =f (x )在点x 0是可微, 而A ∆x 叫做函数y =f (x )在点x 0相应于自变量增量∆x 的微分, 记作 dy , 即 dy =A ∆x .定理2.6 （函数可微的条件）: 函数f (x )在点x 0可微的充分必要条件是函数f (x )在点x 0可导, 且当函数f (x )在点x 0可微时, 其微分一定是dy =f '(x 0)∆x . .函数y =f (x )在任意点x 的微分, 称为函数的微分, 记作dy 或 d f (x ), 即dy =f '(x )∆x ,例1 求函数y =x 2在x =1和x =3处的微分.解 函数y =x 2在x =1处的微分为 1=x dy =(x 2)'|x =1∆x =2∆x ;函数y =x 2在x =3处的微分为 3=x dy =(x 2)'|x =3∆x =6∆x .例2．求函数 y =x 3当x =2, ∆x =0. 02时的微分.解: 先求函数在任意点x 的微分 dy =(x 3)'∆x =3x 2∆x .再求函数当x =2, ∆x =0. 02时的微分dy |x =2, ∆x =0.02 =3x 2| x =2, ∆x =0.02 =3⨯22⨯0.02=0.24.自变量的微分:因为当y =x 时, dy =dx =(x )'∆x =∆x , 所以通常把自变量x 的增量∆x 称为自变量的微分, 记作dx , 即dx =∆x . 于是函数y =f (x )的微分又可记作dy =f '(x )dx . 从而有 )(x f dxdy '=. 亦即, 函数的微分dy 与自变量的微分dx 之商等于该函数的导数. 因此, 导数也叫做“微商”. 2.4.2微分的几何意义当∆y 是曲线y =f (x )上的点的纵坐标的增量时, dy 就是曲线的切线上点纵坐标的相应增量. 当|∆x |很小时, |∆y -dy |比|∆x |小得多. 因此在点M 的邻近, 我们可以用切线段来近似代替曲线段.2.4.3基本初等函数的微分公式与微分运算法则1. 基本初等函数的微分公式导数公式: 微分公式:(x μ)'=μ x μ-1 d (x μ)=μ x μ-1d x(sin x )'=cos x d (sin x )=cos x d x(cos x )'=-sin x d (cos x )=-sin x d x(tan x )'=sec 2 x d (tan x )=sec 2x d x(cot x )'=-csc 2x d (cot x )=-csc 2x d x(sec x )'=sec x tan x d (sec x )=sec x tan x d x(csc x )'=-csc x cot x d (csc x )=-csc x cot x d x(a x )'=a x ln a d (a x )=a x ln a d x(e x )=e x d (e x )=e x d xax x a ln 1)(log =' dx a x x d a ln 1)(log = x x 1)(ln =' dx xx d 1)(ln = 211)(arcsin x x -=' dx x x d 211)(arcsin -= 211)(arccos x x --=' dx x x d 211)(arccos --=211)(arctan xx +=' dx x x d 211)(arctan += 211)cot arc (xx +-=' dx x x d 211)cot arc (+-= 2. 函数和、差、积、商的微分法则求导法则: 微分法则:(u ±v )'=u '± v ' d (u ±v )=du ±dv(Cu )'=Cu ' d (Cu )=Cdu(u ⋅v )'= u 'v +uv ' d (u ⋅v )=vdu +udv)0()(2≠'-'='v v v u v u v u )0()(2≠-=v dx v udv vdu v u d 乘积的微分法则证明:根据函数微分的表达式, 有d (uv )=(uv )'dx .再根据乘积的求导法则, 有(uv )'=u 'v +uv '.于是 d (uv )=(u 'v +uv ')dx =u 'vdx +uv 'dx .由于u 'dx =du , v 'dx =dv , 所以d (uv )=vdu +udv .3. 复合函数的微分法则设y =f (u )及u =ϕ(x )都可导, 则复合函数y =f [ϕ(x )]的微分为dy =y 'x dx =f '(u )ϕ'(x )dx .于由ϕ'(x )dx =du , 所以, 复合函数y =f [ϕ(x )]的微分公式也可以写成dy =f '(u )du 或 dy =y 'u du .由上式可见, 无论u 是自变量还是中间变量函数的微分形式dy =f '(u )du 保持不变. 这一性质称为微分形式不变性.例3．y =sin(2x +1), 求dy .解: 把2x +1看成中间变量u , 则dy =d (sin u )=cos udu =cos(2x +1)d (2x +1)=cos(2x +1)⋅2dx =2cos(2x +1)dx .运算熟练后，在求复合函数的导数时, 可以不写出中间变量.例4.)1ln(2x e y +=, 求dy .解: )1(11)1ln(222x x x e d e e d dy ++=+= xdx e x d e x x x x 21)(122222⋅⋅=⋅=dx e xe x x 2212+=. 例5．y =e 1-3x cos x , 求dy .解: 应用积的微分法则, 得dy =d (e 1-3x cos x )=cos xd (e 1-3x )+e 1-3x d (cos x )=(cos x )e 1-3x (-3dx )+e 1-3x (-sin xdx )=-e 1-3x (3cos x +sin x )dx .例6．在括号中填入适当的函数, 使等式成立.(1) d ( )=xdx ;(2) d ( )=cos ω t dt .解: (1)因为d (x 2)=2xdx , 所以)21()(2122x d x d xdx ==, 即xdx x d =)21(2. 一般地, 有xdx C x d =+)21(2(C 为任意常数). (2)因为d (sin ω t )=ω cos ω tdt , 所以 ) sin 1() (sin 1 cos t d t d tdt ωωωωω==. 所以 tdt C t d cos ) sin 1(ωωω=+(C 为任意常数). 2.4.4微分在近似计算中的应用如果函数y =f (x )在点x 0处的导数f '(x )≠0, 且|∆x |很小时, 我们有∆y ≈dy =f '(x 0)∆x ,∆y =f (x 0+∆x )-f (x 0)≈dy =f '(x 0)∆x ,f (x 0+∆x )≈f (x 0)+f '(x 0)∆x .若令x =x 0+∆x , 即∆x =x -x 0, 那么又有 f (x )≈ f (x 0)+f '(x 0)(x -x 0).特别当x 0=0时, 有 f (x )≈ f (0)+f '(0)x .这些都是近似计算公式.例7．有一批半径为1cm 的球, 为了提高球面的光洁度, 要镀上一层铜, 厚度定为0. 01cm . 估计一了每只球需用铜多少g (铜的密度是8. 9g/cm 3)?解: 已知球体体积为334R V π=, R 0=1cm , ∆R =0. 01cm . 镀层的体积为∆V =V (R 0+∆R )-V (R 0)≈V '(R 0)∆R =4πR 02∆R =4⨯3. 14⨯12 ⨯0. 01=0. 13(cm 3). 于是镀每只球需用的铜约为 0. 13 ⨯8. 9 =1. 16(g ).例8．利用微分计算sin 30︒30'的近似值.解: 已知30︒30'3606 ππ+=, 6 0π=x , 360π=∆x . sin 30︒30'=sin(x 0+∆x )≈sin x 0+∆x cos x 03606 cos 6 sin πππ⋅+= 5076.03602321=⋅+=π. 即 sin 30︒30'≈0. 5076.常用的近似公式（假定|x |是较小的数值）: (1)x nx n 111+≈+; (2)sin x ≈x ( x 用弧度作单位来表达);(3)tan x ≈x ( x 用弧度作单位来表达);(4)e x ≈1+x ;(5)ln(1+x )≈x .例9．计算05.1的近似值.解: 已知 x nx n 111+≈+, 故025.105.021105.0105.1=⨯+≈+=. 直接开方的结果是02470.105.1=.2.4.5内容小结1.微分的定义2.微分的几何意义3.基本初等函数的微分公式与微分运算法则4.微分在近似计算中的应用。