物理必修一板块模型

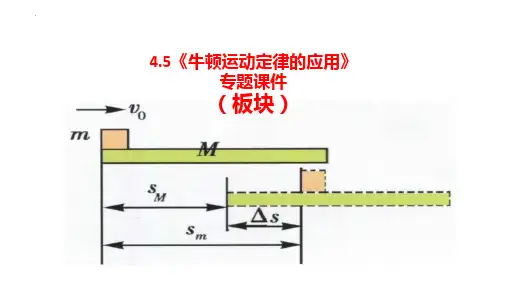
拓展课传送带模型和板块模型（答案在最后）目标要求1.会对传送带上的物体进行受力分析，掌握传送带模型的一般分析方法．2．能正确解答传送带上的物体的运动问题．3．建立板块模型的分析方法．4．能运用牛顿运动定律处理板块问题．拓展1传送带模型【归纳】1．基本类型传送带运输是利用货物和传送带之间的摩擦力将货物运送到其他地方去，有水平传送带和倾斜传送带两种基本模型．2．分析流程3．注意问题求解的关键在于根据物体和传送带之间的相对运动情况，确定摩擦力的大小和方向．当物体的速度与传送带的速度相同时，物体所受的摩擦力有可能发生突变．【典例】例 1 传送带是现代生产、生活中广泛应用的运送货物的运输工具，其大量应用于工厂、车站、机场、地铁站等．如图，地铁一号线的某地铁站内有一条水平匀速运行的行李运输传送带，假设传送带匀速运动的速度大小为v，且传送带足够长．某乘客将一个质量为m的行李箱轻轻地放在传送带一端，行李箱与传送带间的动摩擦因数为μ.当行李箱的速度与传送带的速度刚好相等时，地铁站突然停电，假设传送带在制动力的作用下立即停止运动，求行李箱在传送带上运动的总时间．例 2 某飞机场利用如图所示的传送带将地面上的货物运送到飞机上，传送带与地面的夹角θ＝37°，传送带两端A、B之间的长度L＝11 m，传送带以v＝2 m/s的恒定速度向上运动．在传送带底端A轻轻放上一质量m＝2 kg的货物，货物与传送带间的动摩擦因数μ＝0.8.，sin 37°＝0.6，cos 37°＝0.8)求货物从A端运送到B端所需的时间．(取g＝10ms2例 3 如图所示，传送带与水平地面间的倾角为θ＝37°，从A端到B端长度为s＝16 m，传送带在电机带动下始终以v＝10 m/s的速度逆时针运动，在传送带上A端由静止释放一个质量为m＝0.5 kg的可视为质点的小物体，它与传送带之间的动摩擦因数为μ＝0.5，假设最大静摩擦力与滑动摩擦力大小相同，g取10m，sin 37°＝0.6，求：小物体从A到B所用的s2时间．总结提升倾斜传送带向下传送物体，当物体加速运动与传送带速度相等时：(1)若μ≥tan θ，物体随传送带一起匀速运动；(2)若μ<tan θ，物体不能与传送带保持相对静止，物体将以较小的加速度a＝g sin θ－μg cos θ继续做加速运动．拓展2板块模型【归纳】滑块—木板类(简称板块模型)问题涉及两个或多个物体，并且物体间存在相对滑动，属于多物体多过程问题，知识综合性较强，对能力要求较高．1．解题方法技巧(1)分析题中滑块、木板的受力情况．(2)画好运动草图，找出位移、速度、时间等物理量间的关系．(3)知道每一过程的末速度是下一过程的初速度．(4)两者发生相对滑动的条件：①摩擦力表现为滑动摩擦力；②二者加速度不相等．2．常见的两种位移关系(1)滑块从木板的一端运动到另一端的过程中，若滑块和木板向同一方向运动，则滑块的位移和木板的位移之差等于木板的长度．(2)若滑块和木板向相反方向运动，则滑块的位移和木板的位移之和等于木板的长度．3．注意摩擦力的突变当滑块与木板速度相同时，二者之间的摩擦力通常会发生突变，由滑动摩擦力变为静摩擦力或者消失，或者摩擦力方向发生变化，速度相同是摩擦力突变的一个临界条件．【典例】例 4 长为1.0 m的长木板B静止放在水平冰面上，小物块A以某一初速度从长木板B 的左端冲上长木板B，直到A、B的速度达到相同，大小为v′＝0.4 m/s.再经过t0＝0.4 s的时间A、B一起在水平冰面上滑行了一段距离后停在冰面上．若小物块A可视为质点，它与长木板B的质量相同，A、B间的动摩擦因数μ1＝0.25.(g取10 m/s2)求：(1)长木板与冰面间的动摩擦因数；(2)小物块相对长木板滑行的距离．教你解决问题读题提取信息→ 画运动示意图例5 如图，一平板车以某一速度v0＝5 m/s匀速行驶，某时刻一货箱(可视为质点)无初m，货箱放入车上的同时，平板车开速度地放置于平板车上，货箱离车后端的距离为l＝316始刹车，刹车过程可视为做加速度a＝3 m/s2的匀减速直线运动．已知货箱与平板车之间的.求：摩擦因数为μ＝0.2，g＝10ms2(1)货箱放上平板车时加速度的大小和方向；(2)货箱做匀加速直线运动，平板车做匀减速直线运动，求出速度相等时两者的位移，判断货箱是否从车后端掉下来．例 6 (多选)如图所示，一质量为M的长木板静置于光滑水平面上，其上放置质量为m 的小滑块．木板受到水平拉力F作用时，用传感器测出长木板的加速度a与水平拉力F的关系如图所示，重力加速度g＝10 m/s2，下列说法正确的是()A．小滑块的质量m＝2 kgB．小滑块与长木板之间的动摩擦因数为0.2C．当水平拉力F增大时，小滑块的加速度一定增大D．当水平拉力F＝7 N时，长木板的加速度大小为3 m/s2拓展课八传送带模型和板块模型拓展1[例1] 解析：行李箱所受的合外力等于滑动摩擦力，根据牛顿第二定律有μmg ＝ma ，解得a ＝μg .经过一段时间t 1，行李箱和传送带刚好速度相等，则t 1＝vμg ；停电后，行李箱的加速度大小也是μg ，则减速时间t 2＝v μg，故行李箱在传送带上运动的总时间为t ＝t 1＋t 2＝2vμg.答案：2vμg[例2] 解析：货物放在传送带上，开始相对传送带向下运动，故所受滑动摩擦力的方向沿传送带向上．货物由静止开始做初速度为0的匀加速直线运动．以货物为研究对象，由牛顿第二定律得μmg cos 37°－mg sin 37°＝ma解得a ＝0.4 m/s 2货物匀加速直线运动的时间t 1＝va ＝5 s货物匀加速直线运动的位移x 1＝12at 12＝5 m<L ＝11 m经计算μmg cos 37°>mg sin 37°故此后货物随传送带一起向上做匀速运动，运动的位移x 2＝L －x 1＝6 m 匀速运动的时间t 2＝x2v ＝3 s货物从A 到B 所需的时间t ＝t 1＋t 2＝8 s. 答案：8 s[例3] 解析：开始时，物体相对传送带沿斜面向上滑，所以摩擦力的方向沿斜面向下，由牛顿第二定律，有a 1＝mg sin 37°+μmg cos 37°m ＝10 m/s 2当物体与传送带共速时，物体的位移x 1＝v 2−02a 1＝5 m ，经历的时间t 1＝va 1＝1 s则此时距离B 端的距离x 2＝s －x 1＝11 m又因为mg sin 37°>μmg cos 37°则物体与传送带不能保持相对静止，此后物体的加速度 a 2＝mg sin 37°−μmg cos 37°m＝2 m/s 2根据位移与时间关系有x 2＝vt 2+12at 22代入数据解得t 2＝1 s总耗时为t ＝t 1＋t 2＝2 s ，故物体从A 端运动到B 端需要的时间为2 s. 答案：2 s 拓展2[例4] 解析：(1)设长木板与冰面间的动摩擦因数为μ2，A 、B 一起运动时，根据牛顿第二定律有：2μ2mg ＝2ma又知v ′＝at 0 解得μ2＝0.1.(2)共速前，对A 有：加速度大小a 1＝μ1g ＝2.5 m/s 2 对B 有：μ1mg －μ2×2mg ＝ma 2， 加速度大小a 2＝0.5 m/s 2则知相对运动的时间t ＝v ′a 2＝0.8 s小物块A 的初速度v 0＝v ′＋a 1t ＝2.4 m/s 则相对位移Δx ＝v 0t －12a 1t 2－12a 2t 2代入数据解得：Δx ＝0.96 m. 答案：(1)0.1 (2)0.96 m[例5] 解析：(1)货箱：μmg ＝ma 1，得a 1＝2.0 m/s 2，方向向前． (2)假设货箱能与平板车达到共速，则箱：v ＝a 1t ，车：v ＝v 0－a 2t ，得：t ＝1.0 s ， 箱：s 1＝0+v 2t ＝1 m ，对平板车：s 2＝v 0t －12a 2t 2＝5×1－12×3×1 m ＝3.5 m.此时，货箱相对车向后移动了Δx ＝s 2－s 1＝2.5 m<316 m ，故货箱不会掉下．答案：(1)2 m/s 2，向前 (2)不会 [例6] 解析：由图乙可得，当拉力等于6 N 时，小滑块和长木板刚好要发生相对滑动，以M 、m 为整体，根据牛顿第二定律可得F ＝(M ＋m )a以m 为对象，根据牛顿第二定律可得μmg ＝ma 其中F ＝6 N ，a ＝2 m/s 2联立解得m ＋M ＝3 kg ，μ＝0.2当拉力大于6 N 时，长木板的加速度为a ＝F−μmg M＝F M −μmg M可知a ­F 图像的斜率为k ＝1M ＝2−06−4kg －1＝1 kg －1联立解得M ＝1 kg ，m ＝2 kg ，故A 、B 正确；当水平拉力大于6 N 时，长木板与小滑块已经发生相对滑动，此后F 增大，小滑块的加速度也不再增大，而是保持不变，故C 错误；当水平拉力F ＝7 N 时，长木板的加速度大小为a ＝F−μmg M＝7−0.2×2×101m/s 2＝3 m/s 2，故D 正确；故选ABD.答案：ABD。

物理——板块模型几个要点板块模型几个结论，以下图为例1.有拉力作用的块我们定义为主动块，没有拉力的定义为被动块2.被动块加速度、速度不会大于主动快3.被动块能不能动，取决于AB间摩擦力与B与地面间摩擦力大小。

f ab不大于f地，则无论拉力F多大，B板都不会运动，反之，B板对地运动。

4.若板能相对地面滑动，一定是B板与地面先分开然后才是AB板分开。

5.分开临界条件：整体加速度等于B板最大加速度6.分开瞬间，AB板速度相同，AB间摩擦力为滑动摩擦力，加速度相同，都等于B板的最大加速度。

例1.如图所示，AB两物块的质量分别为2m和m，静止叠放在水平地面上，A、B间的动摩擦因数为μ，B与地面间的动摩擦因数为0.5μ，最大静摩擦力等于滑动摩擦力，重力加速度为g，现对A 施加一水平拉力F，则（）A. 当F<2μmg时，A、B相对地面静止B. 当F=2.5μmg时，A的加速度为0.4μgC. 当F>3μmg时，A相对B滑动D. 无论F为何值，B的加速度不会超过0.5μg例2.如图所示，在光滑平面上有一静止小车，小车上静止地放置着一小物块，物块和小车间的动摩擦因数为μ=0.3，用水平恒力F拉动小车，下列关于物块的加速度a1和小车的加速度a2.当水平恒力F取不同值时，a1与a2的值可能为（当地重力加速度g取10m/s2）（）A. a1=2m/s2，a2=3m/s2B. a1=3m/s2，a2=2m/s2C. a1=5m/s2，a2=3m/s2D. a1=3m/s2，a2=5m/s2解析：被动块m有最大加速度=μg=3m/s2，排除C，在整体加速度不大于3之前，板块不滑动，A 错，被动块加速度不大于主动块，B错，故选D。

变式训练1.如图所示，质量为M的木板A静止在水平地面上，在木板A的左端放置一个质量为m的铁块B，铁块与木板间的动摩擦因数μ1，木板与地面之间的动摩擦因数为μ2，现给铁块施加一由零开始逐渐变大的水平作用力F，下列判断正确的是（ ）A．若μ1＞μ2，则一定是木板A先相对地发生滑动，然后B.相对A发生滑动 B．若μ1mg＞μ2Mg，则一定是木板A先相对地发生滑动，然后B相对A发生滑动C．若铁块B先相对A发生滑动，则当A、B刚发生相对滑动时，F的大小为μ1mgD．若木板A先相对地发生滑动，则当A、B刚发生相对滑动时，F的大小为（ μ 1 m g − μ 2 M g ）（ M + m ）/M变式训练2.如图，一个质量m=1kg的长木板置于光滑水平地面上，木板上放有质量分别为mA=1g和mB=2kg的A、B两物块，A，B两物块与木板之间的动摩擦因数都为μ=0.2，若现用水平恒力F作用在A物块上，重力加速度g取10m/s2）滑动摩擦力等于最大静摩擦力．则下列说法正确的是（ ）A．当F=2N时，A物块和木板开始相对滑动B．当F=1N，则A、B两物块都相对木板静止不动C．若F=4N，则B物块所受摩擦力大小为 4/3N D．若F=6N，则B物块的加速度大小为 2/3m/s2。

板块模型模型分析1、相互作用：滑块和滑板之间靠摩擦力连接,其中静摩擦力是可以变化的;2、相对运动：两物体具有相同的速度和加速度时相对静止;3、通常所说物体运动的位移、速度、加速度都是对地而言的;在相对运动的过程中相互作用的物体之间位移、速度、加速度、时间一定存在关联;它就是我们解决力和运动突破口;4、求时间通常会用到牛顿第二定律加运动学公式或动量定理;5、求位移通常会用到牛顿第二定律加运动学公式或动能定理,应用动能定理时研究对象为单个物体或可以看成单个物体的整体;另外求相对位移时,通常会用到系统能量守恒定律;例题例1：如图所示,物体A、B的质量分别为2kg和1kg,A置于光滑的水平地面上,B 叠加在A上;A、B间的动摩擦因数为,水平向右的拉力F作用在B上,A、B一起相对静止开始做匀加速运动;加速度为s2g =10m/s2求：1力F的大小;2A受到的摩擦力大小和方向;3A、B之间的最大静摩擦力A能获得的最大加速度4要想A、B一起加速相对静止,力F应满足什么条件5要想A、B分离,力F应满足什么条件例2：质量为2kg的长木板B在光滑的水平地面上以4m/s的速度向右运动,将一可视为质点的物体A轻放在B的右端,若A与B之间的动摩擦因数为,A的质量为m=1kg,求g=10 m/s2:1此后A、B分别做什么运动；2分别求出A、B的加速度；3若木板B足够长,A、B的共速后的速度和时间；4当木板B为多长时,A恰好没从B上滑下思考1：质量为2kg的长木板B在光滑的水平地面上以4m/s的速度向右运动,将一可视为质点的物体A轻放在B的右端,若A与B之间的动摩擦因数为,A的质量为m=1kg,求g=10 m/s2:1若B长度为,经过多少时间A从B上滑下；2 A滑离B时,A、B的速度分别为多大A、B的位移分别为多大练习：如图所示,质量M=4kg的木板长L=,静止在光滑的水平地面上,其水平面右端静置一个质量m=1kg的小滑块可视为质点,小滑块与板间的动摩擦因数μ=g取10m/s2,今用水平力F=28N向右拉木板,小滑块将与长木板发生相对滑动;求：1小滑块与长木板发生相对滑动时,它们的加速度各为多少2经过多长时间小滑块从长木板上掉下3小滑块从长木板上掉下时,小滑块和长木板的位移各为多少。

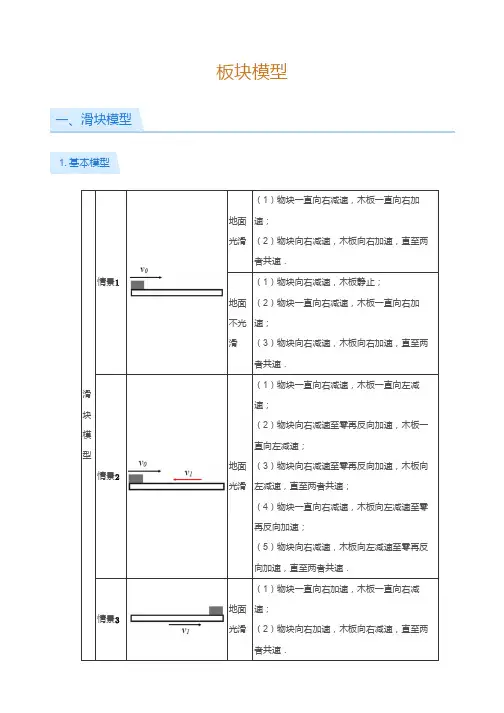
板块模型滑块模型情景地面光滑（1）物块一直向右减速，木板一直向右加速；（2）物块向右减速，木板向右加速，直至两者共速．地面不光滑（1）物块向右减速，木板静止；（2）物块一直向右减速，木板一直向右加速；（3）物块向右减速，木板向右加速，直至两者共速．情景地面光滑（1）物块一直向右减速，木板一直向左减速；（2）物块向右减速至零再反向加速，木板一直向左减速；（3）物块向右减速至零再反向加速，木板向左减速，直至两者共速；（4）物块一直向右减速，木板向左减速至零再反向加速；（5）物块向右减速，木板向左减速至零再反向加速，直至两者共速．情景地面光滑（1）物块一直向右加速，木板一直向右减速；（2）物块向右加速，木板向右减速，直至两者共速．一、滑块模型1.基本模型【注意】位移关系：滑块由木板一端运动到另一端的过程中，滑块和木板同向运动时，位移之差（板长）；滑块和木板反向运动时，位移之和．1如图所示，质量为的小物块以水平速度滑上原来静止在光滑水平面上质量为的小车上，物块与小车间的动摩擦因数为，小车足够长．求：（1）从小物块滑上小车到相对小车静止所经历的时间．（2）小物块相对小车静止时的速度．（3）求从小物块滑上小车直到静止这个过程中小物块在小车表面上相对运动的距离．2如图所示，一个质量为的平板车放在光滑水平面上，在其右端放一个质量为的小木块，，、间动摩擦因数为，现给和以大小相等、方向相反的初速度，使开始向左运动，开始向右运动，最后不会滑离，求：（1）、最后的速度大小和方向．从地面上看，小木块向左运动到离出发点最远的距离．（2）3长为的长木板静止放在水平冰面上，小物块以某一初速度从木板的左端滑上长木板，直到、的速度达到相同，此时、的速度为，然后、又一起在水平冰面上滑行了后停下．若小物块可视为质点，它与长木板的质量相同，、间的动摩擦因数．求：（取）（1）木板与冰面的动摩擦因数．（2）小物块相对于长木板滑行的距离．（3）为了保证小物块不从木板的右端滑落，小物块滑上长木板的初速度应为多大．A.B.C.D.如图所示，一足够长的木板静止在光滑水平面上，一物块静止在木板上，木板和物块间有摩擦．现用水平力向右拉木板，当物块相对木板滑动了一段距离但仍有相对运动时，撤掉拉力，此后木板和物块相对于水平面的运动情况为（ ）物块先向左运动，再向右运动物块向右运动，速度逐渐增大，直到做匀速运动木板向右运动，速度逐渐变小，直到做匀速运动木板和物块的速度都逐渐变小，直到为零4如图所示，质量的小车放在光滑的水平面上，在小车左端加一水平推力，当小车向右运动的速度达到时，在小车前端轻轻地放上一个大小不计，质量为的小物块，小物块与小车间的动摩擦因数，当二者达到相同速度时，物块恰好滑到小车的最左端．取．5小物块放上后，小物块及小车的加速度各为多大．（1）小车的长度是多少．（2）6物体的质量，静止在光滑水平面上的木板的质量为、长，某时刻以的初速度滑上木板的上表面，在滑上的同时，给施加一个水平向右的拉力，若与之间的动摩擦因数，（忽略物体的大小，重力加速度）．试求：滑块加速度大小和方向．（1）（2）为使不从板右侧滑落，拉力应满足的条件．为使不从板左侧滑落，拉力应满足的条件．（3）7如图所示，质量的长木板放在光滑水平面上，质量的小物块（可视为质点）位于木板的左端，木板和物块间的动摩擦因数．现突然给木板一向左的初速度，同时对小物块施加一水平向右的恒定拉力，经过一段时间后，物块与木板相对静止，取，求：物块停在木板上的位置距木板左端多远．运动状态板块速度不相等板块速度相等瞬间板块共速运动处理方法隔离法假设法整体法具体步骤对滑块和木板进行隔离分析，弄清楚每个物体的受力情况与运动过程．假设两物体间无相对滑动，先用整体法算出一起运动的加速度，再用隔离法算出其中一个物体“所需要”的摩擦力；比较与最大静摩擦力的关系，若，则发生相对滑动．将滑块和木板看成一个整体，对整体进行受力分析和运动过程分析．临界条件两者速度达到相等的瞬间，摩擦力可能发生突变；当木板的长度一定时，滑块可能从木板滑下，恰好滑到木板的边缘，二者共速是滑块滑离木板的临界条件．相关知识时间及位移关系式、运动学公式、牛顿运动定律、动能定理、功能关系等．如图所示，质量为的长木板放在水平地面上，在木板的最右端放一质量也为的物块．木板与地面间的动摩擦因数，物块与木板间的动摩擦因数．现用一水平力作用在木板上，使木板由静止开始匀加速运动，经过，撤去拉力．设物块与木板间的最大静摩擦力等于滑动摩擦力．（取）请求解：8拉力撤去时，木板的速度大小．（1）要使物块不从木板上掉下，木板的长度至少多大．（2）在满足（2）的条件下，物块最终将停在距板右端多远处．（3）2.小结3.课有余时9如图所示，质量为的长木板静止在光滑水平面上，现有一质量的小滑块（可视为质点）以的初速度从左端沿木板上表面冲上木板，带动木板一起向前滑动．已知滑块与木板间的动摩擦因数，重力加速度取．求：（1）滑块在木板上滑动过程中，长木板受到的摩擦力大小和方向．（2）滑块在木板上滑动过程中，滑块相对于地面的加速度大小．（3）滑块与木板达到的共同速度．10一长木板在水平地面上运动，从木板经过点时开始计时，在时将一相对于地面静止的小物块轻放到木板上，此后木板运动的图线如图所示．己知木板质量为物块质量的倍，物块与木板间及木板与地面间均有摩擦，物块与木板间的最大静摩擦力等于滑动摩擦力，且物块始终在木板上，取重力加速度的大小，求：（1）物块与木板间的动摩擦因数及木板与地面间的动摩擦因数．（2）木板离点的最终距离．（3）木板的最小长度．11如图所示，物块与木板质量相等，物块与木板间及木板与地面间均有摩擦．起初长木板在水平地面上运动，在时刻将一相对地面静止的物块轻放到木板上，以后木板运动的速度一时间图象如图所示．已知物块始终在木板上，且物体间的最大静摩擦力等于滑动摩擦力．取重力加速度大小．求：（1）根据图象求这段时间内物块和木板的加速度大小和分别是多少．画出这段时间内物块和木板在水平方向受力的示意图，并求物块与木板间、木板（2）与地面间的动摩擦因数和．（3）从时刻到物块与木板均停止运动时，物块相对于木板的位移的大小．12如图所示，物体放在足够长的木板上，木板静止于水平面．已知的质量和的质量均为，、之间的动摩擦因数，与水平面之间的动摩擦因数，最大静摩擦力与滑动摩擦力大小视为相等，重力加速度取．若开始，木板受的水平恒力作用，时改为，方向不变，时撤去．（1）木板受的水平恒力作用时，、的加速度、各为多少．（2）从开始，到、都静止，在上相对滑行的时间为多少．（3）请以纵坐标表示受到的摩擦力，横坐标表示运动时间（从开始，到、都静止），取运动方向为正方向，在图中画出的关系图线（以图线评分，不必写出分析和计算过程）．课堂总结（1）画出物体与板速度方向相反时，物体刚好从板一端移动到另一端的相对位移；（2）假设地面粗糙，物体与木板之间也有摩擦，怎么确定当两者共速以后，接下来两者各自是以不同的加速度运动还是作为一个整体运动？。

专题提升九传送带模型和板块模型[学习目标要求] 1.知道常见传送带模型的特点及分析方法。

2.知道板块模型问题的特点及基本思路方法。

3.注意抓住“三个基本关系”，利用相对运动的思维分析问题。

提升1传送带模型1.传送带的基本模型传送带运输是利用货物和传送带之间的摩擦力将货物运送到其他地方，有水平传送带和倾斜传送带两种基本模型。

2.模型运动情况分析类型图示物体运动情况水平传送带(1)可能一直加速；(2)可能先加速后匀速(1)v0＜v时，可能一直加速，也可能先加速后匀速；(2)v0＞v时，可能一直减速，也可能先减速后匀速(1)传送带较短时，物体一直减速到达左端；(2)传送带较长时，物体先向左运动，减速到零后再向右运动回到右端倾斜传送带(1)可能一直加速；(2)可能先加速后匀速(1)可能一直加速；(2)可能先加速后匀速；(3)可能先以a1加速后以a2加速3.分析思路水平传送带【例1】如图所示，水平传送带两端相距x＝8 m，工件与传送带间的动摩擦因数μ＝0.6，工件滑上A端时速度v A＝10 m/s，设工件到达B端时的速度为v B。

(取g＝10 m/s2)(1)若传送带静止不动，求v B；(2)若传送带顺时针转动，工件还能到达B端吗？若不能，说明理由；若能，求到达B点的速度v B；(3)若传送带以v＝13 m/s逆时针匀速转动，求工件在传送带上划痕的长度。

答案(1)2 m/s(2)能，2 m/s(3)0.75 m解析 (1)根据牛顿第二定律可得 μmg ＝ma 则a ＝μg ＝6 m/s 2工件减速到速度为零时运动的位移x ＝v 2A 2a ＝253 m>8 m ，即工件可运动到B 端 由v 2A －v 2B ＝2ax代入数据得v B ＝2 m/s 。

(2)能，当传送带顺时针转动时，工件受力不变，其加速度不发生变化，仍然始终减速，故工件到达B 端的速度v B ＝2 m/s 。

(3)工件速度达到13 m/s 时所用时间为 t 1＝v －v Aa ＝0.5 s运动的位移为x 1＝v A t 1＋12at 21＝5.75 m<x 传送带的位移x 2＝v t 1＝6.5 m 此后工件与传送带相对静止所以划痕的长度Δx ＝x 2－x 1＝0.75 m 。

专题进阶课八板块模型核心归纳1.模型概述:叠放在一起的滑块—木板之间存在摩擦力,在其他外力作用下它们或者以相同的加速度运动,或者以不同加速度运动,有的题目也可能没有外加的拉力或推力,但板块有初速度。

无论是哪种情况,受力分析和运动过程分析都是解题的关键。

2.一个转折和两个关联:3.三个基本关系:加速度关系如果滑块与木板之间没有发生相对运动,可以用“整体法”求出它们一起运动的加速度;如果滑块与木板之间发生相对运动,应采用“隔离法”分别求出滑块与木板运动的加速度。

应注意找出滑块与木板是否发生相对运动等隐含条件速度关系滑块与木板之间发生相对运动时,明确滑块与木板的速度关系,从而确定滑块与木板受到的摩擦力。

应注意当滑块与木板的速度相同时,摩擦力会发生突变的情况,速度是联系两个运动过程的纽带,上一个过程的末速度是下一个过程的初速度位移关系滑块与木板叠放在一起运动时,应仔细分析滑块与木板的运动过程,明确滑块与木板对地的位移和滑块与木板之间的相对位移之间的关系提醒:运动学公式中的位移都是对地位移。

典题例析角度1有初速度模型【典例1】(2024·深圳高一检测)质量为m 的木板放在水平面上,一质量为2m 的物块以水平速度v 0从木板左端滑上木板,物块与木板之间的动摩擦因数为μ1,木板与地面之间的动摩擦因数为μ2,已知μ1=2μ2,设最大静摩擦力等于滑动摩擦力。

下列说法正确的是()A.若物块不能从木板上滑下,仅增大物块的质量,木板的加速度减小B.若物块不能从木板上滑下,仅增大物块的质量,物块的加速度增大C.若物块能从木板上滑下,仅增大木板的质量,物块在木板上的运动时间更长D.若物块能从木板上滑下,仅增大木板的质量,木板相对于地面运动的总位移将减小【解析】选D 。

由题意,设物块的质量为m 1,木板的质量为m 2,当物块冲上木板时,物块将做减速运动,对物块根据牛顿第二定律有μ1m 1g =m 1a 1,可得a 1=μ1g ;对木板有μ1m 1g -μ2(m 1+m 2)g =m 2a 2,μ1=2μ2,可得a 2=(1-2)2μ2g ,木板将向前做匀加速直线运动,当物块与木板速度相等时,二者将一起减速直至停止。

高中物理板块模型知识点总结一、板块模型的基本概念。

1. 板块模型组成。

- 板块模型通常由一个或多个滑块（可视为质点）和木板组成。

滑块和木板之间存在着摩擦力等相互作用，并且它们在一个平面上运动，这个平面可能是光滑的，也可能存在摩擦力。

2. 研究对象的选取。

- 在板块模型中，我们既可以单独选取滑块或木板作为研究对象，也可以将滑块和木板整体作为研究对象。

当研究它们之间的相对运动时，往往需要分别分析滑块和木板的受力情况；当整体的外力情况比较明确，且不涉及它们之间的内部摩擦力做功等问题时，可以采用整体法。

二、受力分析。

1. 滑块的受力。

- 滑块受到重力G = mg（其中m为滑块质量，g为重力加速度）。

- 如果滑块在木板上滑动，它受到木板对它的摩擦力。

当滑块相对木板滑动时，摩擦力为滑动摩擦力f=μ N，其中μ为动摩擦因数，N为滑块与木板间的正压力（在水平面上N = mg）。

如果滑块有相对木板运动的趋势但未滑动，则受到静摩擦力，静摩擦力的大小根据牛顿第二定律结合物体的运动状态求解，其方向与相对运动趋势方向相反。

2. 木板的受力。

- 木板同样受到重力G'=M g（M为木板质量）。

- 它受到滑块对它的摩擦力，大小与滑块受到的摩擦力相等，方向相反（根据牛顿第三定律）。

如果木板放在水平面上，还受到水平面的支持力F_N=(m + M)g（整体法分析时），若水平面不光滑，木板还受到水平面的摩擦力。

三、运动分析。

1. 加速度的计算。

- 根据牛顿第二定律F = ma计算滑块和木板的加速度。

- 对于滑块，例如受到水平拉力F和摩擦力f时，其加速度a_1=(F - f)/(m)（假设拉力方向与摩擦力方向相反）。

- 对于木板，若受到滑块的摩擦力f和其他外力F'（如水平面的摩擦力等），其加速度a_2=(f+F')/(M)。

2. 相对运动情况。

- 当滑块和木板的加速度不同时，它们之间就会产生相对运动。

判断相对运动的方向可以通过比较它们加速度的大小和方向。

高一物理板块模型专题
高一物理板块的模型专题涉及了许多重要的物理模型，这些模
型有助于我们理解和解释自然界中发生的现象。

在高一物理课程中，模型专题可能包括以下几个方面：
1. 运动学模型，在物理学中，运动学是研究物体运动的学科。

这涉及到描述物体位置、速度、加速度等随时间变化的规律。

在高
一物理板块的模型专题中，学生可能会学习一维运动和二维运动的
模型，包括匀速直线运动、变速直线运动、抛体运动等。

这些模型
有助于学生理解物体在空间中的运动规律。

2. 动力学模型，动力学研究物体的运动是如何受力影响的。

在
高一物理板块的模型专题中，学生可能会学习牛顿运动定律，并应
用这些定律来解决与力、加速度和质量相关的问题。

这些模型有助
于学生理解物体受力情况下的运动规律。

3. 能量模型，能量是物理学中一个重要的概念，它描述了物体
的改变和转化。

在高一物理板块的模型专题中，学生可能会学习动能、势能、机械能守恒定律等能量相关的模型。

这些模型有助于学
生理解能量在物体运动和相互作用中的作用。

4. 波动模型，波动是物理学中另一个重要的研究对象，它涉及到声波、光波等各种波的传播和特性。

在高一物理板块的模型专题中，学生可能会学习波的传播、波的干涉、波的衍射等波动模型。

这些模型有助于学生理解波动现象及其在自然界中的应用。

总的来说，高一物理板块的模型专题涵盖了运动学、动力学、能量和波动等多个方面，通过学习这些模型，学生可以更好地理解物理学中的基本原理和规律，为将来深入学习物理学打下坚实的基础。