光学基础知识：STF原理

光折射偶极光折射光的折射是指光线从一种介质中进入另一种介质时，由于介质密度不同，导致光线传播方向发生改变的现象。

在光学中，折射是一个重要的现象，它在很多领域都有应用，比如眼镜、显微镜、望远镜等。

折射定律当一束光线从一种介质进入另一种介质时，它会发生折射。

根据实验结果和理论分析，我们可以得到一个基本定律——斯涅尔定律（Snell's law），也称为折射定律。

该定律描述了入射角和折射角之间的关系：n1sinθ1 = n2sinθ2其中n1和n2分别是两个介质的折射率，θ1是入射角，θ2是折射角。

这个公式告诉我们，在两个介质之间传播的光线会被弯曲，并且弯曲程度取决于两个介质的特性。

全反射当一束光线从高密度介质（如水）进入低密度介质（如空气）时，如果入射角大于一个特定值（称为临界角），则光线将被完全反射回去，这种现象称为全反射。

在这种情况下，折射角为90度，而入射角等于临界角。

偶极偶极是一个物理概念，用于描述一个系统在外电场作用下的响应。

偶极可以是电偶极或磁偶极，它们分别与电场和磁场有关。

在光学中，我们通常关注的是电偶极。

电偶极电偶极是由两个等量但相反方向的电荷组成的系统。

当该系统处于外电场中时，两个电荷会受到不同大小的力，并产生一个向外指向正电荷的矢量。

这个矢量称为偶极矩（p），它与外电场强度（E）之间有如下关系：p = αE其中α是介质的极化率。

这意味着，在一个给定的外电场中，介质中存在越多的偶极，则其总体响应越强。

光学应用在光学中，我们经常使用折射率和极化率来描述介质对光线的响应。

通过了解这些概念以及它们之间的关系，我们可以更好地理解光的行为，并设计出更有效的光学器件。

例如，在光纤通信中，光信号需要通过长距离的光纤传输。

由于光线在介质之间传播时会发生折射，因此需要使用具有高折射率的材料制成的光纤。

另外，为了保持信号强度，需要在光纤中注入适当的电流以使其极化。

总结在本文中，我们介绍了两个重要的物理概念：光折射和偶极。

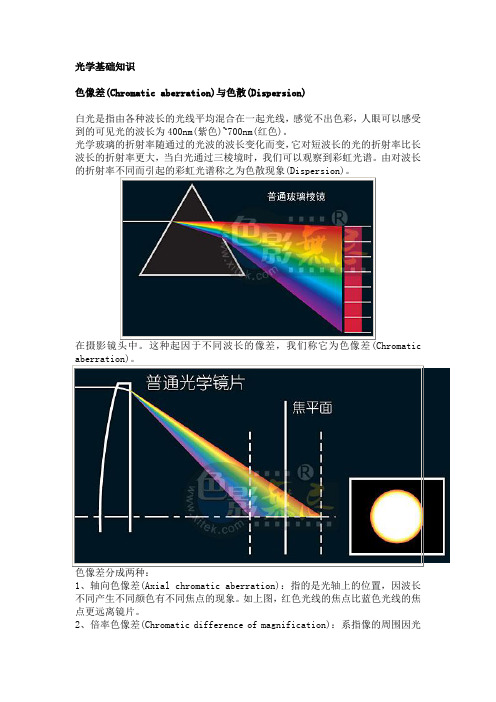
光学基础知识色像差(Chromatic aberration)与色散(Dispersion)白光是指由各种波长的光线平均混合在一起光线，感觉不出色彩，人眼可以感受到的可见光的波长为400nm(紫色)~700nm(红色)。

光学玻璃的折射率随通过的光波的波长变化而变，它对短波长的光的折射率比长波长的折射率更大，当白光通过三棱境时，我们可以观察到彩虹光谱。

由对波长1、轴向色像差(Axial chromatic aberration)：指的是光轴上的位置，因波长不同产生不同颜色有不同焦点的现象。

如上图，红色光线的焦点比蓝色光线的焦点更远离镜片。

2、倍率色像差(Chromatic difference of magnification)：系指像的周围因光线波长的差异，所引起的映像倍率之改变。

这是一种轴外像差，随视场角的增大而增大。

轴向色像差涉及到成像的焦点距离，引起色彩产生松散或光斑(flare)；而倍率色像差别则涉及到成像的大小，在画面周围引起色彩错开，形成扩散的彩色条纹，如镶边(fringing)现象。

色像差不仅影响彩色胶片上成像的色彩再现，也会减低黑白胶片上成像的解像力。

轴向色像差的矫正，一般是采用不同折射率/色散率的镜片来进行组合，使它们的色像差相互抵消。

典型的视采用一个正的冕牌透镜与一个负的火石透镜组合。

会聚的冕牌透镜具有低折射率和小的色散，而发散的火石透镜具有高折射率和更大的色散。

倍率色像差的矫正比较困难，它对像质的劣化作用随焦距增大而加剧，并且不会随光圈缩小而减少。

倍率色像差的有效矫正办法是采用异常/超低色散的光学玻璃。

得鲜锐画质的最重要关键所在。

仅仅仰赖光学玻璃的组合，依然有它的极限，异常/超低色散，才能具有明显的改善。

光的反射、折射、衍射光的传播可以归结为三个实验定律：直线传播定律、反射定律和折射定律。

【光的直线传播定律】：光在均匀介质中沿直线传播。

在非均匀介质种光线将因折射而弯曲，这种现象经常发生在大气中，比如海市蜃楼现象，就是由于光线在密度不均匀的大气中折射而引起的。

为什么光会发生折射光是一种电磁波，在传播过程中常常会发生折射现象。

折射是光线从一种介质传播到另一种介质时改变传播方向的现象。

为了理解为什么光会发生折射，我们需要深入探讨折射的原理和相关概念。

一、光的传播速度差异光在不同介质中的传播速度是不同的，当光从一种介质传播到另一种介质时，介质的光速度差异导致了折射现象的发生。

光速度的差异来自于介质的光密度和折射率的差异。

光密度越高，折射率越大，光速度越小；光密度越低，折射率越小，光速度越大。

当光线从一种介质传播到另一种介质时，介质的光密度和折射率的变化会导致光线传播速度的改变，从而引起光线的折射。

二、斯涅尔定律斯涅尔定律是描述光的折射现象的基本规律，它也被称为折射定律。

斯涅尔定律表明：光线在两种介质之间传播时，入射角与折射角之间的正弦比等于两种介质的折射率之比，即sinθ₁/sinθ₂=n₂/n₁。

其中θ₁为入射角，θ₂为折射角，n₁为第一种介质的折射率，n₂为第二种介质的折射率。

斯涅尔定律说明了光的折射过程中入射角和折射角的关系，以及光在不同介质中传播时的折射率变化。

三、波长与折射光波在折射过程中的波长也会发生变化。

根据斯涅尔定律，光线在不同介质中传播时，由于光速度的改变，波长也会发生变化。

当光从介质A折射到介质B时，如果介质B的光速度比介质A快，那么波长会缩短；如果介质B的光速度比介质A慢，那么波长会延长。

这种波长的变化也是光折射现象的重要表征之一。

四、光的能量传递光的能量在折射过程中也会发生改变。

当光线从一种介质折射到另一种介质时，光的能量会部分传递给新介质。

这是因为光在介质中的传播受到了阻碍或散射，导致部分能量被吸收或转化为其他形式。

因此，在光的折射过程中，光的能量会发生减弱或改变，这也是折射现象的一种重要表现。

总结起来，光发生折射的原因与光速度的差异、折射率的变化、波长的变化以及能量传递等因素密切相关。

通过斯涅尔定律的描述，我们可以了解入射角、折射角和折射率之间的关系，并进一步理解光的折射现象。

§1 几何光学的基本定律1.1 几何光学三定律折射定律的斯涅耳（W. Snell，1621）公式1.2 全反射1.3 棱镜与色散1.4 光的可逆性原理定义：撇开光的波动本性，仅以光的直线传播、反射折射定律为基础，研究光在透明介质中的传播问题。

适用范围：尺度远大于波长，是应用光学的基础特点：原理简单、计算复杂，计算软件（追迹）的发展替代了复杂的计算§1 几何光学的基本定律光线(ray of light)：用一条表示光传播方向的几何线来代表光，称这条几何线为光线1.1 几何光学三定律1. 直线传播定律：在均匀介质中光沿直线传播2. 独立传播定律：不同方向的光线相交，不影响每一光线的传播3. 反射(reflection)、折射(refraction)定律：在两种媒质的界面发生反射、折射例：机场跑道能看多远？夏日机场跑道上方温度梯度较大，导致空气折射率发生变化：()β≈1.5⨯10-6/mn y()=n01+βy人站在跑道的一端，最远能看多远？m n n n n θθθθsin ...sin sin sin 221100====θ光线方程：n 0=1⎧⎪入射光反射光通过内壁上的多次全内反射,从纤维的一端传向另一端。

损耗极低！光纤灯，内窥镜，光纤传感器，……光纤发展历史✧~1840，D Colladon 和J Babinet提出可以依靠光折射现象来引导光线的传播。

✧1854，J Tyndall在英国皇家学会的一次演讲中用实验证实：光线能够沿盛水的弯曲管道传输。

✧1927，JL Baird利用光纤阵列传输图像。

(step index fiber,✧1957，Hirschowitz在美国胃镜学会上展示了研制的光导纤维内窥镜。

✧1961，E Snitzer完成了单模光纤的理论工作。

✧1963，西泽润一提出了使用光纤进行通信的概念。

✧1964，西泽润一发明了渐变折射率光学纤维(gradedindex fiber,GIF)。

简述丝光原理
丝光原理是指在衍射现象中，光通过狭缝或其他有限孔径时，会产生一系列亮暗条纹，这些条纹的间距与孔径大小有关，形成的图案与孔径形状有关。

这种现象在物理学、光学和电子学中都有广泛的应用。

丝光原理最早是由法国科学家菲涅耳在19世纪初发现的。

当光通过一个细小的狭缝射入时，光波在受到阻碍时会发生衍射，产生一系列亮暗相间的条纹，这就是丝光现象。

这些条纹的间距与狭缝的大小有关，当狭缝越小，则条纹越密集，间距越窄。

丝光原理在光学中有着广泛的应用。

例如在显微镜中，光通过物镜的孔径时，会产生丝光现象，这种现象可以帮助我们观察细小的结构，提高显微镜的分辨率。

在照相机中，光通过镜头的孔径时，也会产生丝光现象，这种现象可以用来制造艺术效果，例如夜景拍摄中的星轨效果。

在光栅中，丝光现象可以用来测量光的波长和频率，进而研究物质的性质。

除了光学，丝光原理在电子学中也有着重要的应用。

例如在电子显微镜中，电子通过样品的孔径时，也会产生丝光现象，这种现象可以用于观察材料的微观结构。

在微电子制造中，丝光原理可以用来制造微小的电子元器件，例如芯片上的微处理器和存储器。

丝光原理是一种重要的物理现象，它在各个领域都有着广泛的应用。

理解丝光原理可以帮助我们更好地理解光与物质的相互作用，从而推动科学技术的发展。

偏振分束棱镜原理
偏振分束棱镜是一种光学器件，用于将一个入射光束分成两个偏振光束。

它是由一个三角形棱镜和一个偏振器组成的。

当入射光束通过偏振分束棱镜时，它被分成两个偏振光束，一个是p偏振光束，一个是s偏振光束。

其中，p偏振光束沿着棱镜表面的平面偏振，s偏振光束则垂直于棱镜表面的平面偏振。

偏振分束棱镜的原理是利用棱镜的折射和反射作用，将入射光束沿着不同方向分离出来。

当入射光束通过棱镜时，由于不同偏振方向的光线在棱镜内的折射率不同，因此被分成两个沿不同方向传播的偏振光束。

其中，p偏振光束的折射率比s偏振光束的折射率大，因此p偏振光束向棱镜内弯曲，s偏振光束则向棱镜外弯曲。

偏振分束棱镜广泛应用于光学测量、通信、激光技术等领域。

它可以将入射光束分成两个偏振光束，方便进行各种光学实验和研究。

- 1 -。

光学入门光的折射与全反射光学入门：光的折射与全反射光学是研究光的传播和相互作用的科学领域，其中涉及光的折射与全反射是光学中最基本的知识之一。

本文将介绍光的折射和全反射现象，并探讨其相关的原理和应用。

1. 折射现象当光从一种介质进入另一种介质时，由于介质的密度不同，光的传播速度也会发生改变。

这种由一种介质传到另一种介质时光线改变传播方向的现象称为光的折射。

光的折射现象可以通过斯涅尔定律来描述：入射角与折射角之间的正弦比等于两个介质的折射率之比。

即：$$\frac{{\sin \theta_1}}{{\sin \theta_2}}=\frac{{n_2}}{{n_1}}$$，其中，$\theta_1$为入射角，$\theta_2$为折射角，$n_1$、$n_2$ 分别为两种介质的折射率。

折射现象广泛应用于光学透镜、眼镜、光纤通信等领域。

利用折射现象可以实现焦点的调节、聚光和像的形成等功能。

2. 全反射现象光在从一种介质进入另一种折射率较小的介质时，当入射角超过一定的临界角时，光不再折射出去，而是完全被反射回原来的介质中。

这种现象称为全反射。

全反射现象的产生是由于光从密度较大的介质射入密度较小的介质时，由于折射率的差异，入射角大于临界角时，根据斯涅尔定律，无折射角存在，光线全部反射回原介质中。

全反射在光纤通信中起到重要作用。

当光从光纤中的芯部出射时，由于芯部周围包覆着折射率较小的包层，光线遇到包层与芯部的界面时，当入射角大于临界角时就会发生全反射，光信号得以在光纤中传输。

这种全反射现象实现了光纤通信的快速、高效和长距离传输。

3. 折射与光速光的传播速度在不同介质中是有差异的，当光从一种介质传播到另一种介质时，光速也会发生改变。

根据折射率的定义：光在真空中的速度与光在该介质中的速度之比，即$n=\frac{{c}}{{v}}$，其中，$n$为折射率，$c$为真空中光速，$v$为介质中光速。

根据这个定义，可以推导出斯涅尔定律的等效表达式：$\frac{{\sin \theta_1}}{{\sin \theta_2}} = \frac{{v_1}}{{v_2}} = \frac{{c}}{{cn_2}} = \frac{{1}}{{n_1}}$，其中，$n_1$为入射介质的折射率，$n_2$为出射介质的折射率。