2016年秋北师大版七年级数学上名校课堂练习2.6.2有理数加减混合运算中的简便计算.doc

合用优选文件资料分享七年级数学上册 2.6 有理数的加减混淆运算测试（新北师大版有答案）2.6 有理数的加减混淆运算 1.设 a 是最小的自然数， b 是最大的负整数， c 是绝对值最小的数，则a－b＋c 的值为 ()A．－1B．0 C．1 D．2 2．－6 的相反数与比 5 的相反数小 1 的数的和为 () A．1 B ．0 C．2 D ．11 3 ．若四个有理数之和的 14 是 3，其中三个数是－ 10，＋ 8，－ 6，则第四个数是 () A．＋8 B．－8 C．＋20 D．＋ 11 4 ．某运动员在东西走向的公路上练习跑步，跑步情况记录以下 ( 向东为正，单位：米 ) ：1 000，－1200，1 100，－800,1400，该运动员跑的行程共为 ()A．1500米 B．5 500米 C．4500米 D．3 700 米 5 ．若 a＋b＋c＝0，则以下结论正确的选项是 () A．a ＝b＝c＝0 B．a，b，c 中最罕有两个是负数 C．a，b，c 中能够没有负数 D．a，b，c 中最罕有两个是正数 6 ．把以下各式写成省略括号的和的形式： (1)( ＋7) －( ＋8) ＋( －1) －( －5) ＋( ＋3) ＝____；(2)9 ＋( ＋5) ＋( －6) －( －7) ＝________；(3) －( ＋3) ＋( －4) －( －19) －( ＋11) ＝________； (4) －0.21 ＋( －5.34) －( ＋0.15) －( －1015) ＝________. 7 ．运用互换律和结合律计算：(1)3 －10＋7＝3________7______10＝________； (2) －6＋12－3－5＝______6______3______5______12＝______. 8．有理数 a，b，c 在数轴上的对应点以以下列图，计算a－b＋c________0(填“＞”“＜”或“＝” ) ． 9 ．在以下括号内填上适合的数：(________) －( ＋12)＝－ 13； (________) －( －0.05) ＝10. 10．计算以下各题：(1)(－9) －( －7) ＋( －6) －( ＋4) －( －5) ； (2)(＋4.3)－(－4)＋(－2.3)－(＋4)．11．甲、乙两队拔河，标志物向甲队搬动 0.5 m，又向乙队搬动 0.8 m，对持后又向乙队搬动 0.4 m ，随后向甲队搬动 1.5 m ，接着再向甲队搬动 1.2 m ，按规定标志物向某队搬动 2 m 即获胜，现在甲队获胜了吗？(201 5?河南 ) 计算： 434 －( ＋3.85) －( －314) ＋( －3.15) ．课后作业 1 ．C a＝0，b＝－ 1，c＝0，则 a－b＋c＝1. 2．B－(－6)＋( －5－1) ＝0. 3 ．C 四个有理数之和为 12，所以第四个数是＋20. 4 ．B |1000| ＋| －1200| ＋|1100| ＋| －800| ＋|1400| ＝5500合用优选文件资料分享米． 5 ．C若a＝b＝c＝0时，则三个数中能够没有负数． 6 ．(1)7－8－1＋5＋3 (2)9 ＋5－6＋7 (3) －3－4＋19－11 (4) －0.21 －5.34 －0.15 ＋1015 7．(1) ＋－0 (2) －－－＋－2 8．＞9.16 9.95 10．(1) －7原式＝－9＋7－6－4＋5＝(－9－6－4)＋7＋5＝－ 19＋12＝－ 7； (2)2 原式＝ 4.3 ＋4－2.3 －4＝2. 11 ．解：标志物向甲队搬动的距离为 0.5 －0.8 －0.4 ＋ 1.5 ＋1.2 ＝2(m) ，所以甲队获胜了．中考链接原式＝4.75－3.85＋3.25－3.15＝1.。

有理数的加减混合运算测试题时间：60分钟总分： 100一、选择题（本大题共10小题，共30.0分）1.计算的结果是A. 2B.C. 4D.2.下列说法中，正确的个数有一定是负数；一定是正数；倒数等它本身的数是；绝对值等于它本身的数是1；两个有理数的和一定大于其中每一个加数；如果两个数的和为零，那么这两个数一定是一正一负．A. 1个B. 2个C. 3个D. 4个3.如果两个有理数的积小于零，和大于零，那么这两个有理数A. 符号相反B. 符号相反且绝对值相等C. 符号相反且负数的绝对值大D. 符号相反且正数的绝对值大4.下列各计算题中，结果是零的是A. B. C. D.5.给出20个数：89，91，94，88，93，91，89，87，92，86，90，92，88，90，91，86，89，92，95，则它们的和是A. 1789B. 1799C. 1879D. 18016.两个正数与一个负数相加，和为A. 正数B. 负数C. 零D. 以上都有可能7.已知12与a的积为，则a比4小A. 1B. 2C. 4D. 88.两个数的差是负数，则这两个数一定是A. 被减数是正数，减数是负数B. 被减数是负数，减数是正数C. 被减数是负数，减数也是负数D. 被减数比减数小9.下列式子成立的是A. B. C. D.10.一天，昆明的最高气温为，最低气温为，那么这天的最高气温比最低气温高A. B. C. D.二、填空题（本大题共10小题，共30.0分）11.已知，，，则ab______ 0， ______ 填“、或”12.若a，b，c均为有理数，满足，其中，，请你写出一个满足条件的算式______．13.比3大的数是______．14.计算的结果是______ ．15.若，，则，则的值为______ ．16.纽约与北京的时差是小时，如果现在是北京时间9月11日15时，那么现在的纽约时间是______ ．17.计算的结果是______．2 218.______ ． 19. A ，B ，C 三地的海拔高度分别是米，米，20米，则最高点比最低点高______米20. 在图中，对任意相邻的上下或左右两格中的数字同时加1或减2，这算作一次操作，经过若干次操作后，图能变为图，则图中A 格内的数是______三、计算题（本大题共4小题，共24.0分） 21. 计算．22. 计算：．23. 计算：．24. 计算：四、解答题（本大题共2小题，共16.0分）25.某检修小组乘一辆汽车沿东西向公路检修线路，约定向东为正，某天从A地出发到收工时，行走记录为长度单位：千米：每小题10分，共30分，，，，，，，，，，，，，收工时，检修小组在A地的哪一边？距A地多远？26.已知，，且，求的值．34 4 答案和解析【答案】1. D2. A3. D4. A5. D6. D7. D8. D9. A10. A11. ；12. 答案不唯一13.14. 415.16. 9月11日2时17. 218.19. 9020. 421. 解：原式；原式．22. 解：原式．23. 解：原式．24. 解：25. 解：由题意得：向东路程记为“”，向西路程记为“”，则检修小组离A点的距离为：千米答：小花猫最后在出发点的东边；离开出发点A相距36千米．26. 解：由，得，因为，所以所以．【解析】1. 解：，故选：D．根据同号两数相加的法则进行计算即可．本题主要考查了有理数的加法法则，解决本题的关键是熟记同号两数相加，取相同的符号，并把绝对值相加．2. 解：如果为负数时，则为正数，一定是负数是错的．当时，，一定是正数是错的．倒数等于它本身的数只有，对．绝对值都等于它本身的数是非负数，不只是1，绝对值等于它本身的数是1的说法是错误的．两个负有理数的和小于其中每一个加数，错误．如果两个数的和为零，那么这两个数可能为0，错误．所以正确的说法共有1个．故选A．本题须根据负数、正数、倒数、绝对值、相反数的有关定义以及表示方法逐个分析每个说法，得出正确的个数．本题考查了负数、正数、倒数、绝对值、相反数的有关定义以及表示方法，难度一般．3. 解：两个有理数的积小于零，和大于零，那么这两个有理数符号相反且正数的绝对值大．故选D．根据积小于0，可得两有理数异号，根据和大于零，可得正数的绝对值大，结合选项可得出答案．本题考查了有理数的乘法及有理数的加法法则，属于基础题，掌握各部分的运算法则是关键．4. 解：因为，故选项A的结果是零；因为，故选项B的结果不是零；因为，故选项C的结果不是零；因为，故选项D的结果不是零．故选A．根据四个选项，可以分别计算出它们的结果，进行观察，即可解答本题．本题考查有理数的加法、有理数的减法、去绝对值，解题的关键是正确的运用加法和减法法则进行计算．5. 解：每个数都减去90得，，1，4，，3，1，，，2，，0，2，，0，1，，，2，5，，求和得1，则它们的和为，，故选D．观察这组数的特点，这些数在90上下波动，要这些数都减去90，得出一组新数，把这组新数相加，再加上，即得结果，这样算简便．本题考查了有理数的加法法则，还考查了有理数加法的简便运算．6. 解：，和为正数；，和为0；，和为负数．故选：D．根据有理数的加法，举出例子即可求解．此题考查了有理数加法，在进行有理数加法运算时，首先判断两个加数的符号：是同号还是异号，是否有从而确定用那一条法则在应用过程中，要牢记“先符号，后绝对值”．7. 解：由题意，得，解得，，故选：D．根据有理数的乘法，有理数的减法，可得答案．本题考查了有理数的乘法，利用有理数的乘法、有理数的减法是解题关键8. 解：如果两个数的差是负数，则这两个数一定是被减数比减数小．故选D．56 6两个数的差是负数，说明是较小的数减较大的数的结果，应该是被减数比减数小． 考查有理数的运算方法有理数减法法则：减去一个数等于加上这个数的相反数． 9. 解：A 、原式，正确； B 、原式，错误； C 、原式，错误； D 、原式，错误， 故选A原式各项计算得到结果，即可作出判断．此题考查了有理数的加减混合运算，熟练掌握运算法则是解本题的关键． 10. 解：， 故选：A ．利用最高气温减去最低气温即可．此题主要考查了有理数的减法，关键是掌握减去一个数，等于加上这个数的相反数． 11. 解：，，；，，，．故答案为，． 由，，根据有理数乘法法则得出；由，，，根据有理数加法法则得出．本题考查了有理数的加法与乘法法则用到的知识点：绝对值不相等的异号加减，取绝对值较大的加数符号；两数相乘，异号得负． 12. 解：，，、b 均为负数． 令，则．．故答案为：答案不唯一． 由，可知a 、b 均为负数，然后任意给出符合条件的a 、b 在进行计算即可． 本题主要考查的是有理数的加法法则的应用，根据题意判断出a 、b 均为负数是解题的关键．13. 解：根据题意得：． 故答案为：．根据题意列出算式，利用加法法则计算即可得到结果．此题考查了有理数的加法，熟练掌握加法法则是解本题的关键． 14. 解： 故答案为：4． 先求与2的和，再计算和的绝对值．本题考查了有理数的加法和绝对值的意义理清运算顺序是解决本题的关键． 15. 解：，，且，，；，，则． 故答案为：．根据题意，利用绝对值的代数意义求出x 与y 的值，即可求出的值．此题考查了有理数的乘法，绝对值，以及有理数的加法，熟练掌握运算法则是解本题的关键．16. 解：由题意，得，现在的纽约时间是9月11日2时，故答案为：9月11日2时．根据有理数的减法，可得答案．本题考查了有理数的减法，利用有理数的减法是解题关键．17. 解：．故答案为：2．依据有理数的减法法则进行计算即可本题主要考查的是有理数的减法，熟练掌握有理数的减法法则是解题的关键．18. 解：，，．故答案为：．根据绝对值的性质和有理数的减法运算法则进行计算即可得解．本题考查了有理数的减法运算法则和绝对值的性质，是基础题，熟记运算法则是解题的关键．19. 解：根据题意得：，则最高点比最低点高90米，故答案为：90根据题意列出算式，计算即可求出值．此题考查了有理数的减法，熟练掌握运算法则是解本题的关键．20. 解：如图，将相邻两格用阴影区分出来．由于每次变换都是一个阴影格和相邻的无阴影格中的数据同时加1或减2，所以变换过程中，所有阴影格中的数字之和与所有无阴影格中的数字之和的差不变．图中对应的阴影格的数字之和为：，图中对应的无阴影格的数字之和为：，图中对应的阴影格的数字之和为：，图中对应的无阴影格的数字之和为：，由上述分析可知：，则可得．故答案为：4．每次变换都是在相邻的两格，则将相邻的两格区分出来，如解答中图的有阴影和无阴影由题可知，每次变换都是阴影格中的一个数据和无阴影格中的一个数据同时加1或减2，所以无论变换多少次，所有阴影格中的数字之和与所有无阴影格中的数字之和的差不变．解答此题的关键是将相邻两格区分出来，然后根据两部分之和的差求解．21. 原式结合后，相加即可得到结果；原式结合后，相加即可得到结果．此题考查了有理数的加法，熟练掌握运算法则是解本题的关键．22. 原式结合后，利用加法法则计算即可得到结果．此题考查了有理数的加法，熟练掌握加法法则是解本题的关键．23. 本题主要考查有理数的加减混合运算掌握法则是解题的关键先把减法转化为加法，然后再根据有理数加法的法则计算即可．24. 根据有理数的减法的运算方法，应用加法交换律和加法结合律，求出算式的值是多少即可．此题主要考查了有理数的减法，要熟练掌握，注意加法交换律和加法结合律的应用．25. 首先审清题意，明确“正”和“负”所表示的意义；再根据题意作答．解题关键是理解“正”和“负”的相对性，明确什么是一对具有相反意义的量在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．726. 先由、、确定a 的值，再计算的值．本题考查了有理数的乘法、绝对值及有理数的减法，根据，确定a的值，是解决本题的关键．88。

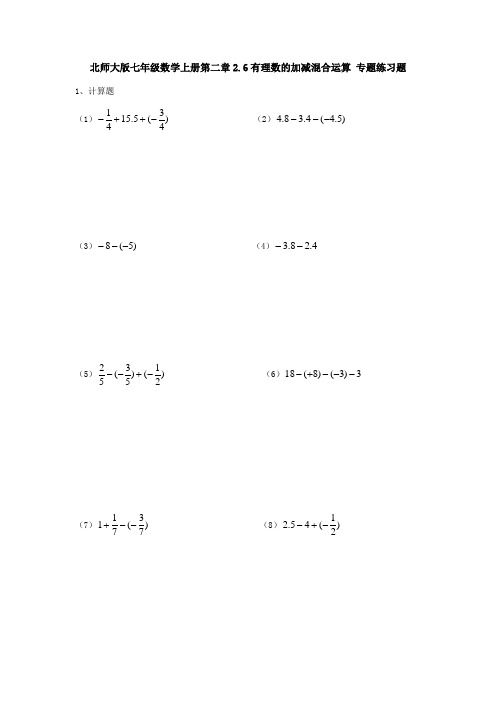
北师大版七年级数学上册第二章2.6有理数的加减混合运算 专题练习题1、计算题 （1）1315.5()44-++- （2）4.8 3.4( 4.5)---（3）)5(8--- （4）4.28.3-- （5）)21()53(52-+-- （6）3)3()8(18---+- （7）131()77+-- （8）12.54()2-+-（9）111324-++ （10）1241()()()2352+---+- （11）2113()()3838---+- (12)23－17－(－7)+(－16)(13)+(－)－1+ (14)(－26.54)+(－6.4)－18.54+6.4(15)(－4)－(－5)+(－4)－3(16)0+1－［(－1)－(－)－(+5)－(－)］+｜－4｜3251318721418173742、已知：a=－2,b=20,c=－3,且a－(－b)+c－d=10,求d的值.3、有十箱梨，每箱质量如下：（单位：千克）51，53，46，49，52，45，47，50，53，48你能较快算出它们的总质量吗？列式计算.4、一条河流在枯水期时，桥面距离年平均水位12.5米，设年平均水位为0米，现在水位为3米，则现在桥面距水面的高度为多少米？（你有几种算法，并作对比）5、一架飞机作特技表演，起飞后的高度变化如如下表：（你有几种算法，并作对比）6、某汽车厂计划半年内每月生产汽车20辆，由于另有任务，每月上班人数不一定相等，实际每月生产量与计划量相比情况如下表（增加为正，减少为负）.1.生产量最多的一天比生产量最少的一天多生产多少辆？2.半年内总生产量是多少？比计划多了还是少了，增或减多少？7、有一架直升飞机从海拔1000米的高原上起飞，第一次上升了1500米，第二次上升上－1200米，第三次上升了1100米，第四次上升了－1700米，求此时这架飞机离海平面多少米？8、10名学生体检测体重，以50千克为基准，超过的数记为正，不足的数记为负，称得结果如下(单位：千克)：2,3,－7.5,－3,5,－8,3.5,4.5,8,－1.5这10名学生的总体重为多少？10名学生的平均体重为多少？。

2.6 有理数的加减混合运算专题一 有理数加减混合运算及实际应用1．把（+7）﹣（﹣10）+（﹣5）﹣（+2）写成省略加号的和的形式为（ ） A ．7+10﹣5+2 B ．7﹣10﹣5﹣2 C ．7+10﹣5﹣2 D ．7+10+5﹣22．用式子表示“引入相反数后，加减混合运算可以统一为加法运算”，下列正确的是（ ） A ．a+b ﹣c=a+b+c B ．a ﹣b+c=a+b ﹣c C ．a+b ﹣c=a+（﹣b ）+（﹣c ） D ．a+b ﹣c=a+b+（﹣c ） 3．下列算式的和为4的是（ ）A ．（﹣2）+（﹣1）B ．（﹣）﹣（﹣）+2C ．0．125+（﹣）﹣（﹣4）D ．4．有人用600元买了一匹马，又以700元的价钱卖了出去，然后，他再用800元把它买回来，最后以900元的价钱卖出．在这桩马的交易中，他（ ） A ．收支平衡 B ．赚了100元 C ．赚了300元 D ．赚了200元5．一个病人每天下午要测量一次血压，下表是该病人星期一至星期六血压变化情况（”+“表示比前一天升的部分；”﹣“表示比前一天降的部分）．该病人上个星期日的血压为160单位，则该病人星期五的血压是（ ）星期一 二三 四 五六血压变化 +30 ﹣20 +17 +18 ﹣20 ﹣5A ．25单位B ．135单位C ．185单位D ．190单位 6．计算：= ．7．一天早晨的气温是﹣5℃，中午上升了10℃，半夜又下降了8℃，则半夜的气温是 ℃． 8．当a= 时，|a+2|﹣2008的最小值为 ． 9．计算：（1）3125.4413151521+-+---；（2）)4.2()7.2()6.1()7.2()5.2(++----+--．10．列式并计算：与的和的绝对值的相反数与的和．11．某汽车厂计划半年内每月生产汽车20辆，由于另有任务，每月上班人数不一定相等，实际每月生产量与计划量相比情况如下表（增加为正，减少为负）：月份一二三四五六增减（辆）+3 ﹣2 ﹣1 +4 +2 ﹣5（1）求实际生产量最多的一个月比生产量最少的一个月多生产了多少辆？（2）半年内总生产量是多少？比计划多了还是少了？增或减多少？12．（1）计算：（+3）+（﹣）+（﹣2）﹣（﹣）；（2）观察下面一列数，探求其规律：﹣1，，﹣，，﹣，，…①写出这列数的第7个数和第8个数；②第2013个数是什么数？如果这一列数无限排列下去，与哪个数越来越近？状元笔记：【知识要点】1．掌握有理数加减混合运算的法则，并能熟练地进行有理数加、减混合运算．2．能根据具体问题，适当使用运算律简化运算．【温馨提示】将加减统一成加法并写成省略加号和括号的“代数和”的形式，带有减法的式子直接进行交换、结合，并不表示减法有结合律、交换律，而是我们利用加法运算律，只是把带有加法的部分省略而已．【方法技巧】直接运用交换律时，需注意将这个数及数前面的符号一起移动．参考答案：1．C 2．D3．C 解析：A ．原式=﹣3≠4，故本选项错误； B ．原式=2≠4，故本选项错误； C ．原式=+4﹣=4，故本选项正确； D ．原式=7+3﹣5=5≠4，故本选项错误． 4．D 解析：设买马的钱为“﹣”，卖马的钱为“+”，则根据题意可得﹣600+700﹣800+900=200（元）．∴在这桩马的交易中，他赚了200元．5．C 解析：根据题意得160+30﹣20+17+18﹣20=185（单位）． 6．﹣7．﹣3 解析：根据题意列式为﹣5+10﹣8=﹣13+10=﹣3（℃）． 8．﹣2 ﹣2008 9．解 ：（1）3125.4413151521+-+---=)312413()5.4151521(++---- =1267556+-=60337-． （2）)4.2()7.2()6.1()7.2()5.2(++----+-- =4.27.26.17.25.2+++-- =4.26.17.27.25.2+++-- =1．5．10．解：由题意得﹣|4+（﹣）|+=﹣|4|+=﹣4+=﹣4．11．解：（1）生产量最多的一个月是四月，生产量最少的一个月是六月，依题意有+4﹣（﹣5）=9（辆）．所以实际生产量最多的一个月比生产量最少的一个月多生产了9辆． （2）半年内计划生产量20×6=120（辆），实际总生产量为20×6+（+3﹣2﹣1+4+2﹣5）=121（辆），所以实际生产量比计划数量多，多了1辆． 12．解：（1）（+3）+（﹣）+（﹣2）﹣（﹣）=3﹣﹣2+=（）﹣（﹣）=（）﹣（）==．（2）①第7个数分母为7，第8个数分母为8，因为7是奇数，所以其分数为负数；因为8是偶数，所以其分数为正数．即第7个数和第8个数分别是．②第2013个数分母为2013，因为2013是奇数，所以其分数为负数，即第2013个数为20131-；随着分母的增大，其分数与0会越来越接近．课时教案课时教案课时教案课题 2.6.3水位的变化教学目标知识与技能：1、能综合运用有理数及其加、减法的有关知识灵活地解决简单的实际问题。

2.6有理数的加减混合运算题型一：将加减混合运算写成省略括号的和的形式【例题1】（2020·江苏苏州市·七年级期末）将-3-（+6）-（-5）+（-2）写成省略括号的和的形式是（）A ．-3+6-5-2B ．-3-6+5-2C ．-3-6-5-2D ．-3-6+5+2【答案】B【分析】原式利用减法法则变形即可得到结果．【详解】解：-3-（+6）-（-5）+（-2）=-3-6+5-2．故选B ．【点睛】此题考查了有理数的加减混合运算，熟练掌握运算法则是解本题的关键．变式训练【变式1-1】（2020·石家庄市·期中）把写成省略括号的和的形式是( ) ．A．B．C．D．【答案】B【分析】先把加减法统一成加法，再省略括号和加号．【详解】解：原式=（+5）+（-3）+（+1）+（-5）=5-3+1-5．故选B．【点睛】本题考查有理数的加减混合运算，将算式写成省略括号的形式必须统一成加法后，才能省略括号和加号．【变式1-2】（2020·河北张家口市·七年级期中）把写成去掉括号的形式，正确的是（）A．B．C．D．【答案】A【分析】先把加减法统一成加法，再省略括号和加号即可．【详解】解：-1-（-2）+（-3）=-1+2-3．故选：A．【点睛】此题考查了有理数的加减混合运算，解题时必须统一成加法后，才能省略括号和加号这是解题的关键．【变式1-3】（2020·成都市三原外国语学校七年级月考）把写成省略括号的和的形式应为（）A．B．C．D．【答案】B【分析】根据有理数的加减法法则及去括号直接进行求解．【详解】解：根据去括号法则，把写成省略括号的和的形式为．故选B．【点睛】本题主要考查有理数的加减法，熟练掌握有理数的加减法是解题的关键．题型二：有理数加减混合运算【例题2】（2018·西藏日喀则市·七年级期中）（－20）＋（＋3）－（－5）－（＋7）；【答案】−19【分析】先化简，再计算加减法即可求解．【详解】(−20)+(+3)−(−5)−(+7)=−20+3+5−7=−27+8=−19，【点睛】此题考查有理数的加减混合运算，解题关键在于掌握运算法则.变式训练【变式2-1】（2019·湖北宜昌市·中考模拟）【答案】－16【分析】根据有理数的加减法法则及绝对值的定义运算即可.【详解】原式=6+6+(－22) -6=12+（－22）-6 =－16【点睛】本题考查有理数的加减混合运算，掌握有理数的加减法法则是关键.【变式2-2】2019·广西河池市·七年级期中）计算：（1）（2）【答案】（1）-2；（2）-10【分析】（1）根据有理数的加、减法法则计算即可；（2）根据有理数的加、减法法则计算即可．【详解】解：（1）==（2）【点睛】此题考查的是有理数的加减法混合运算，掌握有理数的加、减法法则是解决此题的关键．【变式2-3】（2020·辽宁锦州市·太和区第二初中）计算题（1）43 +（-77）+27 +（-43）（2）（-3）+40 +（-32）+（-8）（3）（-72）-（-37）-（-22）-17（4）23- (-76) - 36 - (-105)【答案】(1)-50； (2)-3； (3)-30； (4)168；【分析】(1)根据有理数的加法运算法则，加上一个负数等于减去它的相反数，按式子给出的数字运算即可得到答案；(2)根据有理数的加法运算法则，按式子给出的数字运算即可得到答案；(3)根据有理数的减法运算法则，减去一个非零的数等于加上它的相反数，按式子给出的数字运算即可得到答案；(4)根据有理数的减法运算法则，按式子给出的数字运算即可得到答案；【详解】解：（1）43 +（-77）+27 +（-43）=43-77+27-43=-7-43-50；（2）（-3）+40 +（-32）+（-8）=-3+40-32-8=5-8=-3；（3）（-72）-（-37）-（-22）-17=-72+37+22-17=-13-17=-30；（4）23- (-76) - 36 - (-105)=23+76-36+105=63+105=168；【点睛】本题主要考查有理数的混合运算，有理数的加减法法则：减去一个非零的数等于加上它的相反数，加上一个负数等于减去这个数的相反数，熟练掌握有理数的运算法则是解题的关键；题型三：利用加法运律简化有理数加减混合运算【例题3】（2019·石家庄市第二十八中学七年级月考）计算：（1）；（2）【答案】（1）0；（2）-24【分析】（1）小数化成分数，按照有理数的加减运算法则计算即可；（2）根据绝对值的定义去掉绝对值符号，再按照有理数的加减运算法则计算即可．【详解】（1）；（2）．【点睛】本题考查了有理数的加减混合运算，解题的关键是掌握有理数的混合运算顺序和运算法则．变式训练【变式3-1】计算：【答案】2【分析】（利用加法交换律和结合律可得原式，即可求解．【详解】解：原式．【点睛】本题考查有理数加减的简便运算，根据题目特点灵活应用运算律是解题的关键．【变式3-2】（2019·全国七年级课时练习）计算：(1) ；(2) .【答案】(1) -10，(2) -1，(3) 0.9，(4)【解析】【分析】根据有理数的加减运算法则即可进行求解.【详解】(1)= == =-1(2)==7-5=【点睛】此题主要考查有理数的加减，解题的关键是熟知有理数加减的运算法则.【变式3-3】（1）（2）（3）（4）（5）（6）（7）（8）【答案】（1）-28；（2）0；（3）-25.5；（4）；（5）；（6）；（7）；（8）【分析】各式先化简符号，再利用加法结合律和交换律简化计算即可．【详解】解：（1）==-28；（2）==0；（3）===-25.5；（4）==；（5）===；（6）====；（7）====；（8）=====【点睛】本题主要考查有理数的加减运算，解题的关键是掌握有理数的加法的结合律与交换律．题型四：分组组合法、拆项法、裂项相消法等特殊简便运算【例题4】（2019·云南红河哈尼族彝族自治州·弥勒市一中）计算－1＋2－3＋4－5＋6－…－97＋98－99＋100的结果为( )A．－50B．－49C．49D．50【答案】D【分析】原式结合后，相加即可得到结果．【详解】原式=（-1+2）+（-3+4）+…+（-97+98）+（-99+100）=1+1+…+1=50．故选D．【点睛】此题考查了有理数的加减混合运算，熟练掌握运算法则是解本题的关键．变式训练【变式4-1】（2021·河北张家口市·七年级期末）计算值为（）A．0B．﹣1C．2020D．-2020【答案】D【分析】根据加法的结合律四个四个一组结合起来，每一组的和都等于-4,共505组,计算即可．【详解】解：1+2-3-4+5+6-7-8+9+10-11-12+……+2017+2018-2019-2020=（1+2-3-4）+（5+6-7-8）+（9+10-11-12）+……+（2017+2018-2019-2020）=（-4）+（-4）+（-4）+（-4）+……+（-4）=（-4）×505＝-2020．故选D.【点睛】本题考查了有理数的加减混合运算，观察出规律是解题的关键．【变式4-2】（2020·衡阳市田家炳实验中学七年级期中）阅读下面的计算方法：计算：解：原式====2上面的解法叫拆项法．请你运用这种方法计算：．【答案】-2600【分析】根据题意阅读材料中的拆项法及有理数的运算法则即可求解．【详解】解：（﹣2010）﹣2013+400+1023=﹣2010﹣﹣2013﹣+400++1023+=（﹣2010﹣2013+400+1023）+（﹣﹣++）=﹣2600．【点睛】此题主要考查有理数的运算，解题的关键是根据题意的方法进行求解．【变式4-3】（2020·济南市七贤中学七年级月考）观察下列各式：（1）写出第4个等式：．（2）请你用含n的等式表示第n个等式：．（3）试运用你发现的规律计算：．【答案】（1）（2）（3）【分析】（1）根据已知的等式即可写出；（2）根据已知的等式即可写出第n个等式；（3）根据运算规律即可化简求解．【详解】（1）依题意可得第4个等式为：故答案为：；（2）用含n的等式表示第n个等式：故答案为：；（3）===-1+=．【点睛】此题主要考查有理数的运算，解题的关键是根据题意找到规律进行求解．【变式4-4】（2021·武冈市第二中学九年级开学考试）计算的值为____________．【答案】【分析】根据题目式子的特点，将式子变形，然后裂项作差即可求得所求式子的值．【详解】解：＝+…+＝1﹣+…+＝1﹣＝，故答案为：．【点睛】本题考查了有理数的加减法的简便运算，解答本题的关键是发现题目中式子的特点，裂项作差解答．题型五：有理数加减法与有理数相关概念综合【例题5】（2020·衡阳市田家炳实验中学七年级期中）已知|a|=3，|b|=2，|c|=1，且a＜b＜c，求a+b+c的值．【答案】-6或-4【分析】先根据绝对值和a＜b＜c然后求得a、b、c的值，然后代入求解即可．【详解】解：∵|a|=3、|b|=2、|c|=1，∴a=±3，b=±2，c=±1．∵a＜b＜c，∴a=﹣3，b=﹣2，c=﹣1或1，∴a+b+c=﹣3+（﹣2）+（﹣1）=﹣6或a+b+c=﹣3+（﹣2）+1=﹣4．【点睛】本题主要考查了绝对值的应用和有理数加减运算，运用绝对值和已知条件确定变式训练【变式5-1】（2020·兴化市板桥初级中学七年级月考）若是最大的负整数分别求出的值；求的值．【答案】（1）的值分别为：、、；（2）0或.【分析】（1）由可知，再根据可知，最后根据最大的负整数为从而得出的值即可；（2）将（1）中得出的各数的值代入计算即可.【详解】（1）∵，∴，∵，∴，∵最大的负整数为，∴，∴的值分别为：、、；（2）由（1）可得：的值分别为：、、，∴当，，时，，当，，时，.【点睛】本题主要考查了有理数的加减混合运算，熟练掌握相关概念是解题关键.【变式5-2】（2019·南京市宁海中学七年级月考）若a、b互为相反数，c、d互为倒数，m的绝对值是2，则a+b+m2﹣cd的值为_____．【答案】3【分析】由a、b互为相反数，c、d互为倒数，m的绝对值是2得出a+b＝0、cd＝1，m2＝4，代入计算即可．【详解】∵a、b互为相反数，c、d互为倒数，m的绝对值是2，∴a+b＝0、cd＝1，m2＝4，∴原式＝0+4﹣1＝3，故答案为：3．【点睛】本题综合考查了相反数，倒数和绝对值的相关知识. 在解决该问题时，不应考虑如何求解所有字母的取值，应该利用整体的思想并结合条件将需要求值的式子分解为几个可以求值的部分从而解决问题．【变式5-3】（2020·辉县市文昌中学七年级期中）若互为相反数，互为倒数，数轴上表示数的点到的距离是3，则的值为_______．【答案】或．【分析】利用相反数以及互为倒数、绝对值的性质分别化简得出答案．【详解】解：∵，互为相反数，，互为倒数，数轴上表示数的点到的距离是3，∴，，或，则当时，；当时，；故的值为或．故答案为：或．【点睛】本题主要考查了有理数的混合运算，正确分类讨论是解题关键．题型六：有理数加减法的实际简单应用【例题6】（2020·包头市第六中学七年级期中）一天早晨的气温是﹣5℃，中午又上升了8℃，半夜又下降了10℃，则这天半夜的气温是_____．【答案】-7℃【分析】由题意根据有理数的加减混合运算列式进行运算即可求解．【详解】解：﹣5+8﹣10＝﹣7故答案为：﹣7°C．【点睛】本题考查有理数的加减混合运算，解决本题的关键是根据题意列出算式．变式训练【变式6-1】（2019·郑州市·河南省实验中学七年级月考）小明的爸爸买了一种股票，每股9元，下表记录了在一周内该股票的涨跌情况：星期一二三四五股票涨跌/元0.250.3-0.5-0.350.5（注：用正数记股票价格比前一日上升数，用负数记股票价格比前一日下降数）该股票这星期中每股最低是__________元．【答案】8.7【分析】根据表格中的数据可以求得本周内最低价每股的价格．【详解】解：本周内最低价是周四，每股价格是（元），故答案为：8.7．【点睛】本题考查正数和负数，解答本题的关键是明确正数和负数在题目中表示的实际意义．【变式6-2】（2017·烟台南山东海外国语学校）某公交车上原有乘客16人，经过3个站点时上下车情况如下（上车为正，下车为负）：（+3，-5），（-2，+6），（-4，+7），则现车上有______人【答案】21【解析】16+3－5－2+6－4+7=21.故答案为21.【变式6-3】（2021·山东淄博市·九年级一模）某超市出售的三种品牌月饼袋上分别标有质量为(500±5)g，(500±10)g，(500±20)g的字样，从中任意拿出两袋，它们的质量最多相差( )A．10 g B．20 g C．30 g D．40 g【答案】D【详解】由题意知：任意拿出两袋，最重的是520g，最轻的是480g，所以质量相差520−480=40(g).故选D.题型七：有理数加减法的实际综合运用【例题7】（2020·全国七年级课时练习）小红某星期微信收发红包记录如下：收到22.9元，发出9.9元，收到8.8元，发出35.5元，收到3.7元，发出6.6元，收到4.8元，这时她的微信钱包里的数量是增加了还是减少了？增加或减少了多少钱？【答案】钱包里的钱减少了，减少11.8元.【分析】收到为正，发出为负，然后列式进行有理数的加减混合运算，求出即可．【详解】.钱包里的钱减少了，减少11.8元.【点睛】此题主要考查正负数在实际生活中的意义，学生在学这一部分时一定要联系实际，不能死学．变式训练【变式7-1】某仓库原有某种货物库存200千克，现规定运入为正，运出为负；一天中七次出入如下（单位：千克）第一次第二次第三次第四次第五次第六次第七次（1）在第________次纪录时库存最多．（2）求最终这一天库存增加或减少了多少？（3）若货物装卸费用为每千克0.3元，问这一天需装卸费用多少元？【答案】（1）四；（2）增加了55千克；（3）109.5元【分析】（1）分别算出每一次出入后的库存量，再比较即可；（2）根据表格数据相加计算即可求解；（3）根据总价=单价×数量计算即可求解．【详解】解：（1）第一次库存为：200-30=170千克，第二次库存为：170+80=250千克，第三次库存为：250-10=240千克，第四次库存为：240+100=340千克，第五次库存为：340-90=250千克，第六次库存为：250+30=280千克，第七次库存为：280-25=255千克，∴在第四次纪录时库存最多；（2）-30+80-10+100-90+30-25=55千克，∴最终这一天库存增加了55千克；（3）（30+80+10+100+90+30+25）×0.3=109.5元，∴这一天需装卸费用109.5元．【点睛】此题考查了正数和负数，有理数的混合运算的应用，弄清题意是解本题的关键．【变式7-2】2019年国庆各地风景区游人如织．黄山景区在9月30日的游客人数为0.9万人，接下来的七天中，每天的游客人数变化如下表（正数表示比前一天多的人数，负数表示比前一天少的人数）．日期10月1日10月2日10月3日10月4日10月5日10月6日10月7日人数变化（万人）（1）10月3日的人数为_________万人．（2）八天假期里，游客人数最多是10月________日，达到_______万人．游客人数最少的是10月_______日，达到________万人．（3）请问黄山风景区在这八天内一共接待了多少游客？（结果精确到万位）【答案】（1）5.2；（2）2；5.78；7；0.65；（3）26万【分析】（1）将0.9 加上10月1，2，3的变化量可求解；（2）分别计算每天的游客数量即可求解；（3）将每天的游客数与0.9相加可求解总游客数．【详解】解：（1）0.9+3.1+1.78-0.58=5.2（万人），故10月3日的人数为5.2万人；故答案为5.2；（2）10月1日游客人数为：0.9+3.1=4（万人）；10月2日游客人数为：4+1.78=5.78（万人）；10月3日游客人数为：5.78-0.58=5.2（万人）；10月4日游客人数为：5.2-0.8=4.4（万人）；10月5日游客人数为：4.4-1=3.4（万人）；10月6日游客人数为：3.4-1.6=1.8（万人）；10月7日游客人数为：1.8-1.15=0.65（万人）；故七天假期里，游客人数最多的是10月2日，达到5.78万人．游客人数最少的是10月7日，达到0.65万人．故答案为2；5.78；7；0.65；（3）0.9+4+5.78+5.2+4.4+3.4+1.8+0.65=26.13≈26（万人），答：该风景区在这八天内一共接待了26万游客．【点睛】本题主要考查有理数的加减法混合运算，读懂题意是解题的关键．题型八：有理数加减法的创新应用【例题8】（2019·全国）已知a为有理数，定义运算符号▽：当a＞-2时，▽a=-a；当a＜-2时，▽a=a；当a=-2时，▽a=0．根据这种运算，计算▽［4+▽（2-5）］的值为（ ）A．-7B．7C．-1D．1【答案】C【分析】定义运算符号▽当a>-2时, ▽a=-a;当时a<-2, ▽a=a;当a=-2时, ▽a=0,先判断a的大小,然后按照题中的运算法则求解即可.【详解】且当时, ▽a=a,▽(-3)=-3.4+▽（2-5）=4-3=1>-2,当a>-2时, ▽a=-a,▽［4+▽（2-5）］=▽1=-1.【点睛】本题考查了学生读题做题的能力.关键是理解“▽”这种运算符号的含义,以便从已知条件里找寻规律.变式训练【变式8-1】（2021·河南商丘市·七年级期末）如图，乐乐将﹣3，﹣2，﹣1，0，1，2，3，4，5分别填入九个空格内，使每行、每列、每条对角线上的三个数之和相等，现在a、b、c分别标上其中的一个数，则－2（3a－2b－c）的值为（ ）A．－12B．12C．4D．20【答案】B【分析】根据三个数的和为5+1+(−3)=3,5+1+−3=3，再依次列式计算即可求解．【详解】解：∵5+1+(−3)=3，而每行、每列、每条对角线上的三个数之和相等，∴a+5+0=3， 3+1+b=3，c+(−3)+4=3∴a=−2，b=−1，c=2∴－2（3a－2b－c）==12故选：B．【点睛】本题考查了有理数的混合运算，解题的关键是根据表格，先求出三个数的和，再求出a、b、c的值．【变式8-2】（2020·武汉市第二十一（警予）中学七年级月考）设表示不超过a 的最大整数，例如：，，．（1）求的值；（2）令，求【答案】（1）5；（2）【分析】（1）根据新定义公式和有理数的加减法法则计算即可；（2）根据新定义公式和有理数的加减法法则计算即可．【详解】解：（1），，，；（2），，，，，．【点睛】此题考查的是定义新运算和有理数的加减法混合运算，掌握定义新运算公式和有理数的加减法法则是解决此题的关键．【8-3】（2021·北京房山区·七年级期末）将个互不相同的整数置于一排，构成一个数组．在这个数字前任意添加“+”或“-”号，可以得到一个算式．若运算结果可以为0，我们就将这个数组称为“运算平衡”数组．（1）数组1，2，3，4是否是“运算平衡”数组？若是，请在以下数组中填上相应的符号，并完成运算；1 2 3 4 =（2）若数组1，4，6，是“运算平衡”数组，则的值可以是多少？（3）若某“运算平衡”数组中共含有个整数，则这个整数需要具备什么样的规律？【答案】（1）是，+1-2-3+4=0；（2）m=±1，±3，±9，±11；（3）这n 个整数互不相同，在这个数字前任意添加“+”或“-”号后运算结果为0．【分析】（1）根据“运算平衡”数组的定义即可求解；（2）根据“运算平衡”数组的定义得到关于m的方程，解方程即可；（3）根据“运算平衡”数组的定义可以得到n个数的规律．【详解】解：（1）数组1，2，3，4是“运算平衡”数组，+1-2-3+4=0；（2）要使数组1，4，6，是“运算平衡”数组，有以下情况：1+4+6+m=0；-1+4+6+m=0；1-4+6+m=0；1+4-6+m=0；1+4+6-m=0；-1-4+6+m=0；-1+4-6+m=0；-1+4+6-m=0；1-4-6+m=0；1-4+6-m=0；1+4-6-m=0；-1-4-6+m=0；-1-4+6-m=0，-1+4-6-m=0，1-4-6-m=0；-1-4-6-m=0；共16中情况，经计算得m=±1，±3，±9，±11；（3）这n个整数互不相同，在这个数字前任意添加“+”或“-”号后运算结果为0．【点睛】本题考查了新定义问题，理解“运算平衡”数组的定义是解题关键．。

2.6、有理数的加减混合运算一、课前导学：甲、乙两队进行拔河比赛，甲方在右，乙方在左，平衡位置记为0，如果甲方向右拉1厘米，记作+1 cm,那么乙方向左拉1厘米记作－1 cm.下表记录了双方较量的过程，请你计算一下，并回答：1.平衡位置偏左还是偏右？2.以此可以判断哪方赢了？甲方乙方+10－8+8－6列式计算：平衡位置偏（）（填“左”或“右”）cm,( )方赢.还可以将所列式子写成省略括号的和的形式.思考：有理数加减混合运算适合加法的交换律和结合律吗？二、基础训练：一、计算题1.+3－(－7)=_______.2.(－32)－(+19)=_______.3.－7－(－21)=_______.4.(－38)－(－24)－(+65)=_______.二、填空题1、－4－_______=23.2、36℃比24℃高_______℃，19℃比－5℃高_______℃.3、A、B、C三点相对于海平面分别是－13米、－7米、－20米，那么最高的地方比最低的地方高_______米.4、冬季的某一天，甲地最低温度是－15℃,乙地最低温度是15℃，甲地比乙地低_______℃.三、已知：a=－2,b=20,c=－3,且a－(－b)+c－d=10,求d的值.四、有十箱梨，每箱质量如下：（单位：千克）51，53，46，49，52，45，47，50，53，48你能较快算出它们的总质量吗？列式计算.五、某汽车厂计划半年内每月生产汽车20辆，由于另有任务，每月上班人数不一定相等，实际每月生产量与计划量相比情况如下表（增加为正，减少为负）.月份一二三四五六增减（辆）+3 －2 －1 +4 +2 －51.生产量最多的一天比生产量最少的一天多生产多少辆？2.半年内总生产量是多少？比计划多了还是少了，增或减多少？三、能力提升：1.计算：(1)23－17－(－7)+(－16)(2)32+(－51)－1+31(3)(－26.54)+(－6.4)－18.54+6.4(4)(－487)－(－521)+(－441)－381(5)0+1－［(－1)－(－73)－(+5)－(－74)］+｜－4｜2.有一架直升飞机从海拔1000米的高原上起飞，第一次上升了1500米，第二次上升上－1200米，第三次上升了1100米，第四次上升了－1700米，求此时这架飞机离海平面多少米？3.10名学生体检测体重，以50千克为基准，超过的数记为正，不足的数记为负，称得结果如下(单位：千克)：2,3,－7.5,－3,5,－8,3.5,4.5,8,－1.5这10名学生的总体重为多少？10名学生的平均体重为多少？。

北师大版数学七年级上册2.6 ?有理数的加减混淆运算?课 时作业1. 设 a 是最小的自然数， b 是最大的负整数， c 是绝对值最小的数，那么 a － b ＋c 的值为()A ．－ 1B ． 0C ． 1D ． 22．－ 6 的相反数与比5 的相反数小 1 的数的和为 ()A ． 1B ． 0． 2． 11CD3．假定四个有理数之和的1 10，＋ 8，－ 6，那么第四个数是 ()是 3，此中三个数是－4A ．＋ 8B ．－ 8．＋ 20．＋ 11CD4．某运发动在东西走向的公路上练习跑步，跑步状况记录以下( 向东为正，单位：米 ) ：1000 ，－1200 ，1100 ，－ 800,1 400，该运发动跑的行程共为 ()A ． 1 500 米B ． 5 500 米C ． 4 500 米D ． 3 700 米5．假定 a ＋ b ＋ c ＝ 0，那么以下结论正确的选项是 ()A ． a ＝b ＝ c ＝ 0B ． a ，b ， c 中起码有两个是负数C ． a ，b ， c 中能够没有负数D ． a ，b ， c 中起码有两个是正数6．把以下各式写成省略括号的和的形式：(1)( ＋7) －( ＋8)＋( －1)－( －5) ＋( ＋3) ＝____；(2)9 ＋( ＋ 5) ＋ ( － 6) － ( － 7) ＝ ________；(3) － ( ＋ 3) ＋ ( － 4) － ( －19) － ( ＋11) ＝ ________；1(4) － 0.21 ＋ ( －5.34) － ( ＋ 0.15) － ( － 105) ＝ ________. 7．运用互换律和联合律计算：(1)3 －10＋ 7＝ 3________7______10＝ ________；(2) － 6＋ 12－ 3－ 5＝1 / 4______6______3______5______12 ＝ ______.8．有理数 a，b，c 在数轴上的对应点以下列图，计算a－b＋c________0(填“＞〞“＜〞或“＝〞 ) ．9．在以下括号内填上适合的数：11(________) － ( ＋2) ＝－3；(________) － ( － 0.05) ＝ 10.10．计算以下各题：(1)( －9) －( －7)＋( －6)－( ＋4) －( －5) ；(2)( ＋ 4.3) －( － 4) ＋( － 2.3) －( ＋ 4) ．11．甲、乙两队拔河，标记物向甲队挪动0.5 m，又向乙队挪动0.8 m，对持后又向乙队挪动，随后向甲队挪动，接着再向甲队挪动 1.2 ，按规定标记物向某队挪动2 m m mm即获胜，此刻甲队获胜了吗？2 / 4(2021 ·河南 ) 计算：3144－ ( ＋ 3.85)－ ( －34) ＋ ( －3.15) ．3 / 4课后作业1．C a＝ 0， b＝－ 1， c＝0，那么 a－b＋ c＝ 1.2．B－(－6)＋(－5－1)＝0.3．C四个有理数之和为12，因此第四个数是＋20.4．B |1000|＋ | －1200| ＋ |1100| ＋ | － 800| ＋|1400|＝5500米．5．C 假定 a＝ b＝ c＝ 0 时，那么三个数中能够没有负数．6．(1)7 － 8－1＋ 5＋ 3(2)9 ＋5－ 6＋ 7(3) － 3－4＋ 19－ 11(4) －0.21 － 5.34 －1＋ 1057．(1) ＋－0(2)－－－＋－ 218．＞9. 6 10． (1) － 7原式＝－ 9＋ 7－ 6－4＋ 5＝ ( － 9－ 6－ 4) ＋ 7＋ 5＝－ 19＋ 12＝－ 7；(2)2原式＝ 4.3 ＋ 4－ 2.3 － 4＝ 2.11．解：标记物向甲队挪动的距离为0.5 － 0.8 － 0.4 ＋ 1.5 ＋ 1.2 ＝ 2( ) ，因此甲队获胜m了．中考链接原式＝ 4.75 － 3.85 ＋ 3.25 － 3.15 ＝ 1.4 / 4。

初中数学试卷灿若寒星整理制作2.6.有理数的加减混合运算一、选择题1．在1.17－32－23中把省略的“＋”号填上应得到（）A．1.17＋32＋23 B．－1.17＋（－32）＋（－23）C．1.17＋（－32）＋（－23） D．1.17－（＋32）－（＋23）2．下面说法中正确的是（）A．－2－1－3可以说是－2，－1，－3的和B．－2－1－3可以说是2，－1，－3的和C．－2－1－3是连减运算不能说成和D．－2－1－3＝－2＋3－13．下面说法中错误的是（）A．有理数的加减混合运算都可以写成有理数的加法运算B．－5－（－6）－7不能应用加法的结合律和交换律C．如果和都是的相反数，则D．有理数的加减混合运算都可以写成有理数的减法运算二、填空题1．把下列式子变成只含有加法运算的式子．（1）－9－（－2）＋（－3）－4＝___________；（2）．2．把下列各式写成省略加号的形式．（1）－7－（－15）＋（－3）－（－4）＝____________；（2）3．计算：（1）－5＋7－15－4＋2＝_______________；（2）－0.5＋4.3－9.6－1.8＝_____________；（3）三、解答题1．计算（1）；（2）；（3）；（4）2．计算（1）；（2）；（3）；（4）3．计算（1）；（2）－1999＋2000－2001＋2002－2003．4．存折中有2676元，取出1082元，又存入600元，在不考虑利息的情况下，你能算出存折中还有多少元钱吗？参考答案：一、1． C 2． A 3．B二、1．（1）－9＋2＋（－3）＋（－4），（2）；2．（1）－7＋15－3＋4，（2）；3．（1）－15，（2）－7.6，（3）．三、1．（1）（2）（3）－17 （4）2．（1）（2）（3）（4）3．（1）－15.2 （2）－20014．2194元。

七年级上册第二章第六节有理数的加减混合运算课时练习一、选择题（共10题）1．下列关于有理数的加法说法错误的是（）A.同号两数相加，取相同的符号，并把绝对值相加B.异号两数相加，绝对值相等时和为0C.互为相反数的两数相加得0D.绝对值不等时，取绝对值较小的数的符号作为和的符号答案：D解析：解答：D选项应该是有理数相加时，如果绝对值不等时，取绝对值较小的数的符号作为和的符号分析：考查有理数的的加法法则2．计算—3+2—1=（）A.0B.1C.—2D.3答案：C解析：解答：根据有理数的加减法则可知：—3+2—1=—1—1=—2分析：考查有理数的加减混合运算3．—2—（—3）+（—7）=（）A.5B.3C.2D.—6答案：D解析：解答：—2—（—3）+（—7）=1+（—7）=—6分析：考查有理数的加减混合运算4. —5+（—2）—（—7）=（）A.0B.3C.1D.2答案：A解析：解答：根据有理数的加减混合运算法则可以得到：—5+（—2）—（—7）=—7+7=0 分析：考查有理数的加减混合运算5.—5+2—（—20）=（）A.3B.—3C.17D.2答案：C解析：解答：—5+2—（—20）=—3+20=17分析：考查有理数的加减混合运算6.—12—2+（—6）=（）A.4B.8C.—20D.不能确定答案：C解析：解答：—12—2+（—6）=—14+（—6）=—20分析：注意运算顺序7.—6+0—（—10）=（）A.0B.4C.—6D.6或0答案：B解析：解答：—6+0—（—10）=—6+10=4分析：注意一个数和0相加，还得这个数8.—278—3+（—6）+278=（）A.0B.6C.3D.—9答案：D解析：解答：—278—3+（—6）+278=—278+278+（—3）+（—6）=0+（—9）=—9 分析：注意互为相反数的两个数相加之和等于0.9.如果a＝—14，b＝－2, c＝－234，那么︱a︱+︱b︱－︱c︱等于（）A.－12B.112C.12D.112-答案：A解析：解答：︱a︱+︱b︱－︱c︱=131 22442 +-=-分析：注意先算出绝对值10.a—b =a+（）A.—bB.bC.aD.—a答案：A解析：解答：有理数的减法法则：减去一个数等于加上这个数的相反数分析：考查有理数的加法法则二、填空题（共10题）11. 有理数的加减混合运算一般遵循________运算顺序答案：从左向右解析：解答：加减运算是同级运算，一般遵循从左向右的顺序运算分析：考查运算顺序，有简单方法的用简单方法12.在有理数的减法中，减去一个数等于加上这个数的__________答案：相反数解析：解答：有理数的减法法则：减去一个数等于加上这个数的相反数分析：考查有理数的减法法则13.数轴上与原点之间的距离小于5的所有整数的相加之和是_______答案：0解析：解答：在数轴上与原点距离小于5的所有整数是—4、—3、—2、—1、0、1、2、3、4；根据有理数的加法法则，这几个数相加之和等于0分析：考查数轴和有理数的加法法则.M ，N=3，那么M—N =______14.若10答案：7或—13解析：解答：因为M为+10或是—10，所以M—N =10—3=7或是—10—3=—13分析：考查绝对值和有理数的减法问题15.—5+（—9）—15=____答案：—29解析：解答：原式=—14+（—15）=—29分析：考查有理数的加减计算16.15+（—20）—3=___________答案：—8解析：解答：原式=—5+（—3）=—8分析：考查有理数的加减混合运算17.21+2—（—23）= _________答案：46解析：解答：原式=23+23=46分析：注意运算顺序，从左向右18.数轴上A点表示原点左边距离原点3个单位长度、B点在原点右边距离原点2个单位长度，那么两点所表示的有理数的和与10的差是________答案：—11解析：解答：可以从数轴上得到A表示—3，B点表示2，根据有理数的加法法则可以得到两数之和是—1，那么—1—10=—11；故答案是—11分析：考查数轴上点的计算问题19.15+（—22）—____=12答案：—19解析：解答：根据题意可知15+（—22）—12=—7+（—12）=—19分析：考查有理数的加减混合运算20. —6+0—10=____答案：—16解析：解答：原式=—6+（—10）=—16分析：考查有理数的加减混合运算三、解答题（共5题）21. 已知230a b ++-=,则a +b 等于？答案：根据绝对值的非负性可以得到a +2=0、b —3=0，可以得到a =—2、b =3，所以a +b =—2+3=1解析：注意绝对值的非负性是解决问题的关键22.答案：原式解析： 考查有理数的加法23. 答案：原式 解析：解答：有理数的加法，注意运用好加法法则 24.计算133244⎛⎫⎛⎫-+- ⎪ ⎪⎝⎭⎝⎭+10—1.5 答案：6)432413()432()413(-=+-=-+-+10—1.5=2.5 解析：考查有理数的加减混合运算25.()()()8 1.20.6 2.4-+---+-答案：原式=—9.2+0.6+（—2.4）=—8.6+（—2.4）=—11解析：考查有理数的加减混合运算)2()6()8()20()15(++-+++-++)6()20()2()8()15(-+-++++++=1)26()25(-=-++=)819()125.0()5.2()712()25()72(-+-+++-+-++)819()81()5.2()25()712()72(-+-+++-+-++=)25(0)710(-++-=1455)1435()1420(-=-+-=。