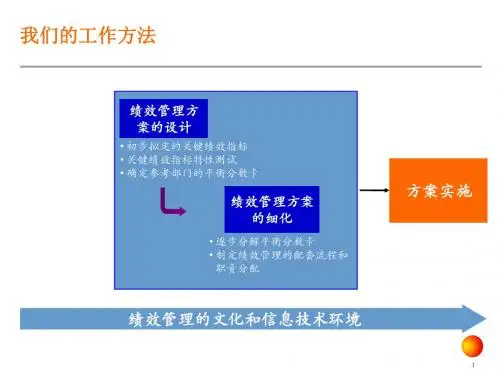
n j i 1
1
2
, xn , 并
记 x x ,求最小的 m ,使得
i 1 i
n
x
i 1
miLeabharlann x a (a为小于 1 的常数,称为重要性
常数) , x ,x ,
1 2
, xn , 对应的指标 I1 , I 2 ,
, I n 即为重要性指标。
2019
-
9
的选取并无定量规定,应视实际情况而定,一般取 a 0.7 。经 验表明,取 a 0.7 是合适的,能较好地满足下面两个要求: (1) 所选的指标是重要的 (2) 重要的指标已被选上。 下面举例说明重要性指标筛选的过程。 在高新企业管理中,评价职工绩效考核的因素很多,现拟订 32 项指标,请 43 位专家给每项指标打分。通过 Delphi 法,得到 32 项指标的最后得分及重要性排序(5 分赋值) ,列于下表 Word 表格 1
从表中可以看出: 若取 a 0.9, 则得m 28, 若取 a 0.8, 则得m 24, 若取 a 0.7, 则得m 21, 即所选的指标至少是 21 项,而 21 32 0.7 ,显然,这样并没有将 指标之和的得分拉开。事实上, 32 项指标中,最高分与最低分之比为
211
2019
83
2.5 ,指标的重要性分辨率不强。 -
11
现在我们对专家的最初打分进行改进,尝试以 等比数列代替 5 分制等差数列。规定最低分为 1 ,最高分为 50,由 c4 50 得等比系数 c 2.65 。 分别以 1,3,7,18,50 代替 1,2,3,4,5 重新对指标赋植,统计指标得分并作重要性排 序,得到下列结果 Word 表格 2
M
Q