(完整版)角的和差倍分专项训练题2

成功是必须的:两角和与差及其二倍角公式知识点及典例知识要点： 1、 两角和与差的正弦、余弦、正切公式 C( a — 3 ): cos( a — 3 )= S( a + 3 ): sin( a + 3 )=T( a + 3 ): tan( a + 3 )=2、 二倍角的正弦、余弦、正切公式 S 2 : sin2 a = C( a + 3 ): cos( a + 3 )= S( a — 3 ): T( a — 3 )： 2h例 2 设 cos a —21 9’T 2 : tan2 . asin 2 — 23,其中n 2,n0, 2，求 cos( a+ 3).sin( a — 3 )= tan( a — 3 )= C 2 : cos2 a =— — ,3、 在准确熟练地记住公式的基础上 ，要灵活运用公式解决问题：如公式的正用、逆用和变形用等。

如T( a± 3可变形为：tan a± tan 3= 考点自测： 1、已知tan A 、7 11 B、 tan 3 = 3, 7 11 变式2:已知03.ncos(— 4 435，sin( 4)—,求 sin( a + 3 )的值. 13则 tan( a C 、？ 13 tan a an 3= 3)=( 13 题型3给值求角已知三角函数值求角，一般可分以下三个步骤：(1)确定角所在的范围;值(要求该三角函数应在角的范围内严格单调 )；(3)求出角。

1 1例 3 已知 a, 3^ (0, n,且 tan (a — 3 ="2, tan 3=— 7 求 2 a — 3 的值.(2)求角的某一个三角函数n a — 6 +A —症A . 5 2、已知cos 3、在厶ABC 中，若 sin a= 43」 B辺B.5 4 q 5cosA = 5，cosB = 13, B 56 B.65sin 7 n a+舀的值是( C . — 4 5 则cosC 的值是( c 丄或56 C.65或65 4、若 cos2 9+ cos 0= 0,贝U sin2 0+ sin B 的值等于( )C . 0 或 3 4D ・516 65 0或土 3A . 0B . ± 3 一.卜 2cos55 — j‘3sin55、二角式 A 辽 2 题型训练 题型1给角求值 一般所给出的角都是非特殊角，利用角的关系(与特殊角的联系)化为特殊角 cos5B.o■值为( 例 1 求[2si n50 sin 10 (1 3tan10)]? 2sin 280 的值• 11变式3:已知tan a =, tan 3 =-，并且a , 3均为锐角，求a +23的值.7 3题型4辅助角公式的应用J 22asinx bcosx a b sin x (其中 角所在的象限由 a, b 的符号确定，角的值由btan —确定)在求最值、化简时起着重要作用。

精心整理和差倍练习题21、果篮里共有苹果和梨共21个,如果把3个苹果换成3个梨,苹果还是比梨多1个.问:苹果原来有多少个?2、动物园里共有老虎、狮子和猎豹共有100只,其中老虎比狮子多3只,狮子比猎豹多2只,那么动物里有老虎多少只?3、学校举办跳绳比赛,第一名跳的个数是第二名的2倍,第二名跳的个数又是第三名的3倍,前三名一共跳了1000个,那么第一名跳了多少个?4、三个火枪手共有子弹64发,小个火枪手的子弹数目比中个火枪手的2倍多4颗,中个火枪手的子5、200元的话,6、,问每桶7等,8、6厘米.910111222枚.13,结果长14920克.1516件的317,只有25厘米.它们吃面条的速度相同,过了一段时间后,长面条的长度是短面条的2倍.那么此时短面条还剩多少厘米?18、一满瓶水可以装7杯水,如果从中倒出5杯水,剩下的水和瓶子共重520克；如果倒出3杯水,那么剩下的水和瓶子共重880克.请问：空瓶重多少克?19、卡莉娅和萱萱都在织围巾,现在两人已经织好的围巾长度相同,但萱萱织得比较快.在接下来的两个月里,萱萱可以织120厘米,而卡莉娅只能织45厘米,因此两个月后,萱萱围巾的长度将会是卡莉娅的2倍.那么现在卡莉娅的围巾有多长?20、墨莫想买一台电脑,有高端和低端两种选择,高端电脑的价格比低端的2倍少1300元,低端电脑的价格则要比高端电脑的2倍少7300元.请问：低端电脑的价格是多少?21、有甲、乙两个仓库,原来甲仓库存有65吨货物,乙仓库存有25吨货物.请问：从甲仓库调运多少精心整理吨货物到乙仓库,才能使得乙仓库的库存量变为甲仓库的2倍?22、有两支粗细、材料都相同的蜡烛,长的能烧100分钟,短的能烧70分钟.同时点燃这两支蜡烛,过多少时间后,长蜡烛长度是短蜡烛的3倍?23、在饭盒里装鸡蛋,如果放入3个鸡蛋,那么连盒共重250克；如果放入7个鸡蛋,则连盒共重470克.请问：一个鸡蛋有多重?(假设每个鸡蛋重量相同)24、萱萱送给小山羊和卡莉娅两人一样多的饼干.小山羊比较贪吃,过了几天,小山羊已经吃了39块饼干,而卡莉娅只吃了17块.此时卡莉娅剩下的饼干数量是小山羊的3倍,请问：卡莉娅原来有多少饼干?25、一次考试,墨莫的得分比卡莉娅的2倍少30分,而卡莉娅的得分比墨莫的2倍少120分,那么卡莉娅考了多少分?1,。

， ：两角和与差及其二倍角公式知识点及典例2，22 2 2知识要点：1、两角和与差的正弦、余弦、正切公式 C(α － β )： cos(α － β )＝ ； C(α ＋ β )： cos(α ＋ β )＝ ； S(α ＋ β)： sin(α ＋β )＝ ； S(α － β )： sin(α － β )＝；T( α＋ β )： tan( α ＋ β )＝ ； T( α－ β )： tan( α － β )＝；例 2 设 cos α－ β＝－ 1 2 9 α 2－ β＝ 2 ，其中 α∈ 3 π 2，π， β∈ 0 π，求 cos(α＋β)． 2 2、二倍角的正弦、余弦、正切公式 变式 2： 已知 0π 3 ππ,cos( )3,sin( 3 π5), 求 sin( α+β ) 的值. S 2 ：sin2α ＝ ； T 2 ：tan2α ＝ ； 4 4 45 413C 2 ：cos2α＝ ＝＝；3、在准确熟练地记住公式的基础上 ,要灵活运用公式解决问题 :如公式的正用、逆用和变形用等。

如 T( α± β)可变形为 : tan α± tan β= ； tan αtan β==.考点自测：题型 3 给值求角已知三角函数值求角，一般可分以下三个步骤：(1) 确定角所在的范围； (2) 求角的某一个三角函数值( 要求该三角函数应在角的范围内严格单调 ) ；（ 3） 求出角。

1、已知 tan α ＝ 4，tan β＝ 3，则 tan( α ＋ β) ＝ ()例 3 已知 α， β∈(0， π)，且 tan(α－ β)＝ 1 ， tan β＝－ 1，求 2α－β的值． 7 7C 7 72 7A 、B 、-1111、 D 、-13132、已知 cos α－π＋ sin α＝ 43，则 sin α＋7π的值是 ( ) 6 A ．－ 2 3 5 B.2 3 6 C ．－ 4D.4变式 3： 已知 tan α = 1， tan β = 1，并且 α , β 均为锐角 , 求 α +2β 的值 .5 5 55 733、在△ ABC 中，若 cosA ＝ 4， cosB ＝ 5，则 cosC 的值是 ( ) 5 16 56 A. B. 13 C.16或5616D ．－65 65 65 65 65 题型 4 辅助角公式的应用4、若 cos2θ＋ cos θ＝ 0，则 sin2θ＋ sin θ的值等于 ( )A ． 0B ． ± 3C ． 0 或 3D ． 0 或± 3asin x bcosxa2b 2sin x(其中 角所在的象限由 a, b 的符号确定， 角的值由2cos55 －° 3sin5 °b 5、三角式 3 cos5 °值为 ( )tan确定 ) 在求最值、化简时起着重要作用。

板块一、差倍问题【例1】李爷爷家养的鸭比鹅多18只，鸭的只数是鹅的3倍，你知道李爷爷家养的鸭和鹅各有多少只吗？【巩固】两个书架，甲书架存书相当于乙书架存书量的5倍，甲书架比乙书架存书多120本，则乙书架存书多少本？【巩固】某小学原来参加室外活动的人数比参加室内活动的人数多480人，现在把室内活动的50人改为室外活动，这样室外活动的人数正好是室内人数的5倍，则参加室内、室外活动的共有多少人?【例2】有两根铁丝，第一根长18米，第二根长10米，两根铁丝用去同样长的一段后，第一根剩下的长度是第二根剩下长度的3倍，两根铁丝各剩下多少米？【巩固】有两条纸带，一条长21厘米，一条长13厘米，两条纸带都剪下同样的一段后，长纸带剩下的长度是短纸带剩下的3倍，问剪下的一段有多长？【巩固】二⑴班的图书角里有故事书和连环画共47本，如果故事书拿走7本后，故事书的本数就是连环画的4倍.原有连环画和故事书各有多少本？【例3】有两根同样长的绳子，第一根截去12米，第二根接上14米，这时第二根长度是第一根长的3【巩固】有甲、乙两艘货船，甲船所载货物是乙船的3倍．若甲船增加货物1200吨，乙船增加货物900吨，则甲船所载货物是乙船的2倍．甲船原载货物多少吨?【例4】某迎春茶话会上，买来苹果4箱，已知每箱苹果取出24千克后，剩余的各箱苹果总和等于原来一箱苹果的重量，问原来一箱苹果多重？【巩固】菜站运来的白菜是萝卜的3倍，卖出白菜1800千克，萝卜300千克，剩下的两种蔬菜的重量相等，菜站运来的白菜和萝卜各是多少千克？【例5】有大小两个桶原来水一样多，如果从小桶倒8千克水到大桶，则大桶中水是小桶的3倍，求原来大桶有水多少千克？【巩固】某校五年级比六年级人数少154人，若六年级学生再转来46人，则六年级学生是五年级学生的3倍，问五、六年级各有多少人？【巩固】小云比小雨少20本书，后来小云丢了5本书，小雨新买了11本书，这时小雨的书比小云的书多2倍.问：原来两人各有多少本书？【例6】甲、乙俩人存款若干元，甲存款是乙存款的3倍．如果甲取出80元，乙存入20元，甲、乙的存款正好相等．问甲、乙俩人原来各存款多少元？【巩固】甲、乙各有若干本书,若甲给乙45本,则二人的书相等,若乙给甲45本则甲的本数是乙的4倍,甲、乙各有书多少本？【例7】(2008年第八届“春蕾杯”小学数学邀请赛初赛)兄妹俩人去买文具，哥哥带的钱是妹妹的两倍，哥哥用去180元，妹妹用去30元，这时兄妹俩人剩下的钱正好相等，哥哥带了________元钱，妹妹带了________元钱．【巩固】食堂里有94千克面粉，138千克大米，每天用掉面粉和大米各9千克，几天后剩下的大米是面粉的3倍？【例8】幼儿园大班每人发17张画片，小班每人发13张画片，小班人数是大班人数的2倍，小班比大班多发126张画片，那么小班有多少人？【巩固】实验小学一校区人数比实验小学二校区人数少540人，因为第三校区建成，从两个校区各调走200人，这时实验小学二校区人数恰好是实验小学一校区人数的4倍，那么实验小学一校区和实验小学二校区原来各有多少人？【例9】有两盘苹果，如果从第一盘中拿2个放到第二个盘里，那么两盘的苹果数相同；如果从第二个盘中拿2个放到第一盘里，那么第一盘的苹果数是第二盘的2倍．第一盘有苹果多少个?【巩固】小青和小红每人都有一些水彩笔，如果小青给小红1支，两人就一样多，如果小红给小青1支，小青的水彩笔就是小红的2倍，那么小青和小红各有多少支水彩笔？【巩固】小明和小刚各有玻璃弹球若干个.小明对小刚说：“我若给你两个，我们的玻璃弹球一样多.”小刚说：“我若给你两个，你的弹球数量将是我的3倍.”小明和小刚共有玻璃弹球多少个？【例10】小新家有大小两个书架，大书架上的书的本数是小书架的3倍，如果从大书架上取走150本放到小书架上，那么两个书架上的书一样多，大小书架上原来各有多少本书?【巩固】甲、乙两桶油重量相等，甲桶取走16千克油，乙桶加入14千克油后，乙桶油的重量是甲桶油的重量的4倍．甲桶原来有油多少千克？【巩固】两根绳，第一根长64米，第二根长52米，剪去同样长后，第一根是第二根的3倍，求每根绳减去几米？【巩固】两个筐中各有苹果若干千克，第一个筐中的苹果是第二筐中的苹果的4倍，如果从第一个筐中取出26千克苹果，从第二个筐中取出2千克苹果，则两筐苹果的重量相等．你知道这两个筐中原来各有苹果多少千克吗?【巩固】两块同样长的花布，第一块卖出31米，第二块卖出19米后，第二块是第一块的4倍，求每块花布原有多少米？【例11】学而思学校买来白粉笔比彩色粉笔多15箱，白粉笔的箱数比彩色笔的4倍还多3箱，学而思学校买来白粉笔和彩色粉笔各多少箱？【巩固】学而思学校买来白粉笔比彩色粉笔多15箱，白粉笔的箱数比彩色笔的4倍少3箱，学而思学校买来白粉笔和彩色粉笔各多少箱？【例12】甲、乙、丙三所小学学生人数的总和为1999，已知甲校学生人数的2倍，乙校学生人数减3，丙校学生人数加4都是相等的，问：甲、乙、丙各校的人数是多少？【巩固】红旗小学三年级有甲、乙、丙三个班，一共有学生162人．如果从甲班转出2个人到乙班，则甲、乙两班人数相同．如果这时再从丙班转出3个人到乙班，则乙、丙两班人数相同．请问：甲班原来有多少人？【例13】小明、小红、小玲共有73块糖．如果小玲吃掉3块，那么小红与小玲的糖就一样多；如果小红给小明2块糖，那么小明的糖就是小红的糖的2倍．问小红有多少块糖？【巩固】甲、乙、丙三数的和是78，甲比乙的2倍多4，乙比丙的3倍少2．求这三个数．【例14】小丸子家养了一些鸡，黄鸡比黑鸡多13只，比白鸡少18只，白鸡的只数是黄鸡2倍，白鸡、黄鸡、黑鸡一共多少只？【例15】某养殖厂养鸡、鸭、鹅共1462只，鸡的只数比鸭的4倍多132只，鹅的只数比鸭的2倍少70只．这个养殖厂养的鸡、鸭、鹅各有多少只？【例16】甲、乙两个小朋友各有一袋糖，每袋糖不到20粒．如果甲给乙一定数量的糖后，甲的糖就是乙的糖粒数的2倍；如果乙给甲同样数量的糖后，甲的糖就是乙的糖粒数的3倍．那么甲、乙两个小朋友共有多少粒糖？【巩固】在一次考试中，甲、乙两人考试结果如下：甲答错了全部试题的13，乙答错了7道题，甲、乙都答错的题目占全部试题的15，则甲、乙两人都答对的题目最少多少道？【例17】在期末考试中，哥哥的数学成绩比语文高7分，弟弟的数学成绩是语文的67．又知道弟弟的数学成绩比哥哥的数学成绩的56高4分，总成绩比哥哥低3分，那么弟弟的语文成绩是多少分？【例18】一小、二小两校春游的人数都是10的整数倍，出行时两校人员不合乘一辆车，且每辆车尽量坐满．现在知道，若两校都租用14座的旅游车，则两校共需租用这种车72辆；若两校都租用19座的旅游车，则二小要比一小多租用这种车7辆．问两校参加这次春游的人数各是多少？板块二、年龄问题的和差与差倍【例19】爸爸妈妈现在的年龄和是72岁；五年后，爸爸比妈妈大6岁．今年爸爸妈妈二人各多少岁？【例20】爸爸妈妈现在的年龄和是72岁；六年后，爸爸比妈妈大4岁.今年爸爸妈妈二人各多少岁？【巩固】爸爸今年38岁，佳佳今年2岁，问：几年后，父亲的年龄是佳佳的5倍？【例21】姐姐今年13岁，弟弟今年9岁，几年后姐弟俩岁数和是40岁？姐姐到时多少岁了？【例22】新老运动员把话谈，手拉手儿笑微微.老将说：“我比你大10岁.”新手说：“上次你比我大一倍.”运动会四年开一次，两人年龄各几岁？【例23】兄弟俩今年的年龄和是30岁，当哥哥像弟弟现在这样大时，弟弟的年龄恰好是哥哥年龄的一半．问：哥哥今年几岁？【巩固】哥哥现在的年龄是弟弟当年年龄的3倍，哥哥当年的年龄与弟弟现在的年龄相同，哥哥与弟弟现在的年龄和为30岁．问：哥哥现在多少岁？【巩固】妈妈的年龄是小红的5倍，奶奶的年龄比小红大9倍，已知奶奶比妈妈大35岁，求三人年龄各多少岁？。

：两角和与差及其二倍角公式知识点及典例知识要点：1、两角和与差的正弦、余弦、正切公式C(α－β)：cos(α－β)＝ ； C(α＋β)：cos(α＋β)＝ ； S(α＋β)：sin(α＋β)＝ ； S(α－β)：sin(α－β)＝ ； T(α＋β)：tan(α＋β)＝ ； T(α－β)：tan(α－β)＝ ； 2、二倍角的正弦、余弦、正切公式2S α：sin2α＝ ； 2T α：tan2α＝ ；2C α：cos2α＝ ＝ ＝ ；3、在准确熟练地记住公式的基础上,要灵活运用公式解决问题:如公式的正用、逆用和变形用等。

如T(α±β)可变形为:tan α±tan β=___________________； tan αtan β= = . 考点自测：1、已知tan α＝4，tan β＝3，则tan(α＋β)＝( )711A 、 711B 、- 713C 、 713D 、-2、已知cos ⎝⎛⎭⎫α－π6＋ sin α＝453，则 sin ⎝⎛⎭⎫α＋7π6的值是( ) A ．－235 B.235 C ．－45 D.453、在△ABC 中，若cos A ＝45，cos B ＝513，则cos C 的值是( )A.1665B.5665C.1665或5665 D ．－1665 4、若cos2θ＋cos θ＝0，则sin2θ＋sin θ的值等于( )A ．0B ．±3C ．0或 3D ．0或±35、三角式2cos55°－3sin5°cos5°值为( )A.32B.3 C ．2 D ．1 题型训练题型1 给角求值一般所给出的角都是非特殊角，利用角的关系（与特殊角的联系）化为特殊角例1求[2sin50sin10(1)]︒︒︒+.变式1：化简求值：2cos10sin 20.cos 20︒︒︒- 题型2给值求值三角函数的给值求值问题解决的关键在于把“所求角”用“已知角”表示．如()()ααββαββ=+-=-+，2()()ααβαβ=++-，2()()αβαβα=+--，22αβαβ++=⋅，()()222αββααβ+=---例2 设cos ⎝⎛⎭⎫α－β2＝－19，sin ⎝⎛⎭⎫α2－β＝23，其中α∈⎝⎛⎭⎫π2，π，β∈⎝⎛⎭⎫0，π2，求cos(α＋β)．变式2：π3π33π50π,cos(),sin(),4445413βααβ<<<<-=+=已知求sin(α+β)的值.题型3给值求角已知三角函数值求角，一般可分以下三个步骤：(1)确定角所在的范围；(2)求角的某一个三角函数值(要求该三角函数应在角的范围内严格单调)；（3）求出角。

差倍问题已知两个数的差与它们的倍数关系，求两个数各是多少，这一类题称为“差倍问题”。

解答方法是：两个数的差÷倍数的差=1倍数，然后根据差或倍求另一个数。

例1.小明到市场去买水果，他买的苹果个数是梨的3倍，苹果比梨多18个。

小明买苹果和梨各多少个？例2.两个书架所存书的本数相等，如果从第一个书架里取出200本书，而第二个书架再放入40本书，那么第二个书架的本数是第一个书架的3倍。

问两个书架原来各存书多少本？例3.甲乙两人分别带了150元和70元去买东西，两人买了同样的东西之后，剩下的钱甲是乙的5倍。

甲乙两人各剩下多少钱？每人花了多少钱？例4.小明的爸爸办了一个养鸡场，今年比去年多养了4000只小鸡，且今年的小鸡数比去年的3倍少2000只。

今年、去年各养了多少只？例5.被除数比除数大252，商是7，被除数、除数各是多少？例6.有甲、乙两桶色拉油，如果向甲桶中倒入8千克，则两桶色拉油就一样重；如果向乙桶中倒入12千克，乙桶的色拉油就是甲桶的5倍。

甲、乙两桶原来各有色拉油多少千克？例7.两个数相除，商是4，被除数、除数、商的和是124。

被除数和除数各是多少？例8.育红小学买了一些足球、排球和篮球，已知足球比排球多7只，排球比篮球多11只，足球的只数是篮球的3倍。

足球、排球和篮球各买了多少只？姓名得分1.学校合唱组，女同学人数是男同学的4倍，女同学比男同学多42人。

合唱组有男、女同学各多少人？2.一件皮衣价钱是一件羽绒服价钱的5倍，又已知一件皮衣比一件羽绒服贵960元。

皮衣与羽绒服各多少元？3.哥哥种的树是弟弟的3倍，哥哥比弟弟多种了26棵树。

兄弟两人各种了多少棵树？4.两个仓库所存粮食重量相等，如果从第一个仓库里取出200千克，而第二个仓库再存入40千克，那么第二个仓库的粮食重量就是第一个仓库的7倍。

两个仓库原来各存粮食多少千克？5.小红和小明的铅笔枝数相等，如果奶奶再给小红16枝铅笔，给小明2枝铅笔，那么小红的铅笔枝数就是小明的3倍。

7.5画角的和、差、倍（分层练习）【夯实基础】一、填空题1．（2020春·六年级校考单元测试）已知∠AOB ＝78°，射线OE 是∠AOB 的平分线，∠AOE ＝_____．2．（2021春·上海浦东新·七年级上海民办建平远翔学校校考期末）如图，射线OA 与射线OB 的夹角为40°，将射线OC 绕点O 顺时针旋转一周，若射线OA 、OB 、OC 中恰有一条射线平分另两条射线的夹角时，则∠AOC 的度数为______．3．（2022秋·上海奉贤·七年级统考期中）如图，点O 与量角器中心重合，OA 与零刻度线叠合，OB 与量角器刻度线叠合，OD 是BOC Ð的角平分线，那么BOD Ð=______．4．（2021春·上海浦东新·六年级校考期末）如图，OB 为∠AOD 的角平分线，:2:3BOC COD ÐÐ=，∠BOC ＝20°，则∠AOB ＝______．5．（2021春·上海长宁·六年级上海市延安初级中学校考期末）如图，O 为直线DA 上一点，120AOB Ð=°，OE 为AOB Ð的平分线，90COB Ð=°，则EOC Ð的度数是_______．6．（2021春·上海浦东新·六年级上海市进才中学北校校考期末）如图，已知AOB Ð是直角，60BOC Ð=°，OE 平分AOC Ð，OF 平分BOC Ð，那么EOF Ð=______°．7．（2022春·上海·六年级校考期末）如图，∠AOB ＝84°，∠BOC ＝44°．OD 平分∠AOC ，则∠COD ＝_____．8．（2021春·上海金山·六年级校考期末）如图，将一张长方形纸按照如图所示的方法对折，两条虚线为折痕，这两条折痕构成的角的度数是__________．9．（2020春·六年级校考单元测试）如图：根据图形填空∠BOC ＝∠AOD －_____－_____＝_____－∠AOB ＝_____－∠DOC ；∠BOD ＝∠AOD －_____＝∠DOC ＋_____．10．（2021春·上海浦东新·六年级校联考期末）∠AOB ＝60°，OC 平分∠AOB ，以OC 为一边作∠COP ＝15°，则∠BOP 的度数为__________．11．（2021春·上海普陀·六年级期末）如图，OP 、OQ 分别是∠AOB 、∠BOC 的平分线，如果∠POQ ＝28°，那么∠AOC ＝____°．12．（2021·上海·六年级期末）如图，85AOB Ð=°，45BOC Ð=°．OD 平分AOC Ð，则AOD Ð=_______．13．（2021春·上海闵行·六年级统考期末）如图，∠AOB ＝62°，OC 平分∠AOB ，∠COD ＝90°，则∠AOD ＝_____度．14．（2021春·上海静安·六年级上海市民办扬波中学校考期末）如图，OP 、OQ 分别是AOB Ð，BOC Ð的平分线，如果5226POQ ¢Ð=°，那么AOC Ð=______．（结果用度、分、秒表示）15．（2021春·上海长宁·六年级华东政法大学附属中学校考期末）如图所示，已知OB 是AOC Ð的角平分线90BOD Ð=°，120AOC Ð=°，那么COD Ð=______．16．（2022春·七年级单元测试）如图，直线,AB CD 相交于O ，OE 平分,Ð^AOC OF OE ，若46BOD Ð=°，则DOF ∠的度数为______°．17．（2021春·上海浦东新·六年级上海市浦东模范中学东校校考期末）已知140AOB Ð=°，OC 是AOB Ð的角平分线，射线OD 在AOB Ð的内部，50AOD Ð=°，那么DOC Ð=______．二、解答题18．（2022春·上海·七年级专题练习）如图，直线AB 、CD 相交于点O ，OE 平分∠AOB ，OB 平分∠DOF ，若∠DOE ＝50°，求∠DOF 的度数．19．（2022春·上海·七年级期末）（1）已知：如图1，P 是直角三角板ABC 斜边AB 上的一个动点，CD 、CE分别是∠ACP和∠BCP的平分线，试探究：当点P在斜边AB上移动时，∠DCE的大小是否会发生变化，请说明你的理由．（2）把直角三角板的直角顶点C放在直尺的一边MN上，点A和点B在直线MN的上方（如图2），此时∠ACM与∠BCN的数量关系是∠ACM+∠BCN＝；当把这把直角三角板绕顶点C旋转到点A在直线MN的下方，点B仍然在直线MN的上方时（如图3），∠ACM与∠BCN的数量关系是；当把这把直角三角板绕顶点C旋转到点A和点B都在直线MN的下方时（如图4），∠ACM与∠BCN的数量关系是．20．（2020春·六年级校考单元测试）如图已知点O为直线AC上一点，OE平分∠AOB，∠DOB：∠DOC＝1：3，∠EOD＝65°，求∠DOC的度数？21．（2020春·六年级校考单元测试）已知∠α、∠β，用量角器画出∠AOB=∠α+∠β．（不写作法，标明字母）22．（2020春·六年级校考单元测试）已知∠α、∠β，用尺规画出∠AOB=∠α+2∠β．（不写作法，标明字母）【能力提升】一、填空题1．（2022春·上海闵行·六年级校考期末）如图，OP 、OQ 分别是AOB Ð、BOC Ð的平分线，如果5226POQ Ð=°¢，那么AOC Ð=______．2．（2021春·上海松江·六年级统考期末）已知：如图，OC 和OD 为∠AOB 内的射线，OE 平分∠AOC ，OF 平分∠DOB ，若∠EOF ＝60°，∠COD ＝20°，则∠AOB 的度数为 _______．3．（2021春·上海·六年级上海同济大学附属存志学校校考期末）如图，OM 平分AOB Ð，2MON BON Ð=Ð，AON Ð与BON Ð的差为80°，则AOB Ð=__________．4．（2021春·上海·六年级上海市西南模范中学校考期末）已知80AOB Ð=°，30AOC Ð=°，OD 平分BOC Ð，则BOD Ð的大小为___________．二、解答题5．（2021春·上海松江·六年级校考期末）如图，点A 、O 、C 在一直线上，AOB Ð比BOC Ð大20°，OE 是BOC Ð的平分线，90EOF Ð=°．(1)求BOC Ð的度数．(2)求DOF ∠的度数．6．（2020春·六年级校考单元测试）如图，作∠A 、∠B 的平分线，并作出它们的交点O ，再连接OC ，用量角器度量比较∠ACO 、∠BCO 的大小．（不写作法，保留作图痕迹）7．（2022春·上海·七年级专题练习）如图，直线AB，CD相交于点O，OE⊥AB，OF⊥CD．(1)若OC恰好是∠AOE的平分线，则OA是∠COF的平分线吗？请说明理由；(2)若∠EOF＝5∠BOD，求∠COE的度数．8．（2022春·上海·七年级专题练习）（1）已知：如图1，P是直角三角板ABC斜边AB上的一个动点，CD、CE分别是∠ACP和∠BCP的平分线．当点P在斜边AB上移动时，∠DCE＝ °；（2）把直角三角板的直角顶点C放在直尺的一边MN上：①点A和点B在直线MN的上方（如图2），此时∠ACM与∠BCN的数量关系是∠ACM+∠BCN＝ ；②当把这把直角三角板绕顶点C旋转到点A在直线MN的下方、点B仍然在直线MN的上方时（如图3），∠ACM与∠BCN的数量关系是 ；③当把这把直角三角板绕顶点C旋转到点A和点B都在直线MN的下方时（如图4），∠ACM与∠BCN的数量关系是 ．。

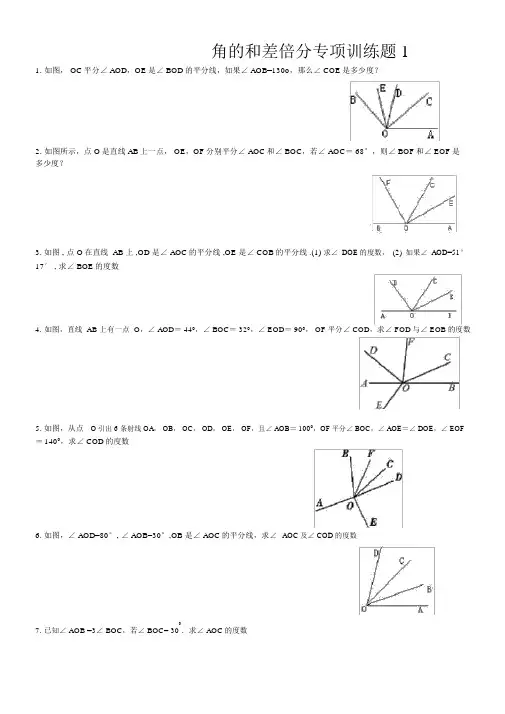
角的和差倍分专项训练题11.如图， OC平分∠ AOD，OE是∠ BOD的平分线，如果∠ AOB=130o，那么∠ COE是多少度？2.如图所示，点 O是直线 AB上一点， OE，OF分别平分∠ AOC和∠ BOC，若∠ AOC＝ 68°，则∠ BOF和∠ EOF是多少度？3. 如图 , 点 O在直线 AB 上 ,OD 是∠ AOC的平分线 ,OE 是∠ COB的平分线 .(1)求∠ DOE的度数，(2)如果∠ AOD=51°17′ , 求∠ BOE的度数4.如图，直线 AB 上有一点 O，∠ AOD＝ 440，∠ BOC＝ 320，∠ EOD＝ 900， OF平分∠ COD，求∠ FOD与∠ EOB的度数5. 如图，从点O引出 6 条射线 OA， OB， OC， OD， OE， OF，且∠ AOB＝ 1000，OF平分∠ BOC，∠ AOE＝∠ DOE，∠ EOF ＝1400，求∠ COD的度数6. 如图，∠ AOD=80°, ∠ AOB=30°,OB 是∠ AOC的平分线，求∠AOC及∠ COD的度数7. 已知∠ AOB =3∠ BOC，若∠ BOC= 30 ．求∠ AOC的度数8. 如图，∠ BAE =750，∠ DAE= 150， AC 是∠ BAD 的平分线，求∠ CAD 的度数9. 如图， BD 平分∠ ABC ， BE 分∠ ABC 为 2： 5 两部分，∠ DBE=24，求∠ ABE 的度数0 0 10. 如图，∠ AOC+∠ AOB=180，OM 、 ON 分别是∠ BOC 、∠ AOB 的平分线，∠MON=60，求∠ AOC 和∠ AOB 的度数11. 已知∠ AOB ，过 O 点作射线 0OC ，若∠ AOC=0.5∠AOB ，且∠ AOC=22，求∠ BOC 的度数 12. 0 0 DOE 的度数已知∠ AOB=60，∠ BOC=120， OD 平分∠ AOB ， OE 是∠ BOC 的一条三等分线，求∠13. 如图，已知∠ 0 0AOC=90，∠ DOC 比∠ DOA 大 28 ， OB 是∠ AOC 的平分线，求∠ BOD 的度数0 14. 如图，已知∠ AOC=150， OB 是∠ AOC 的平分线， OE ， OF 分别是∠ AOB ，∠ BOC 的平分线 , 求∠ EOF 的度数15. 直线 AB 、 CD 相交于点 0 0 与∠ 3 的度数 O ， OE 平分∠ AOD ，∠ FOC=90，∠ 1=40 ，求∠ 2。

两角和与差的三角函数及倍角公式练习及答案一、选择题： 1、若)tan(,21tan ),2(53sin βαβπαπα-=<<=则的值是A ．2B ．－2C ．211D ．-2112、如果sin cos ,sin cos x x x x =3那么·的值是A ．16B ．15C ．29D ．3103、如果的值是那么)4tan(,41)4tan(,52)tan(παπββα+=-=+A ．1318B ．322C ．1322D ．-13184、若f x x f (sin )cos ,=⎛⎝⎫⎭⎪232则等于A ．-12B ．-32C ．12D ．325、在∆ABC A B A B 中，··sin sin cos cos ,<则这个三角形的形状是 A ．锐角三角形 B ．钝角三角形C ．直角三角形D ．等腰三角形二、填空题：6、角αβαβ终边过点，角终边过点，则(,)(,)sin()4371--+=；8、已知=+-=⎪⎭⎫⎝⎛+θθθθθπsin 2cos cos sin 234cot ，则 ；12、的值。

，求已知)tan 1)(tan 1(43βαπβα--=+ 两角和与差练习题一、选择题：2．已知)2,0(πα∈,sin(6πα+)=53,则cos α的值为( )A ．－10334+ B ．10343- C ．10334- D ．10334+7．已知cos(α－π6)＋sin α＝453，则sin(α＋7π6)的值是 ( )A ．－235 B.235 C ．－45 D.458.f(x)＝sinx cosx1＋sinx ＋cosx 的值域为( )A ．(―3―1,―1) ∪(―1, 3―1)B ．[－2－12,―1] ∪(―1, 2－12)C ．(－3－12,3－12)D ．[－2－12,2－12]解析：令t ＝sin x ＋cos x ＝2sin(x ＋π4)∈[―2,―1]∪(―1, 2)． 则f(x)＝t 2－121＋t ＝t －12∈[－2－12,―1]∪(―1, 2－12)．B9 .sin()cos()cos()θθθ+︒++︒-+︒7545315的值等于（ ） A. ±1B. 1C. -1D. 010．等式sin α＋3cos α＝4m －64－m有意义，则m 的取值范围是( ) A ．(－1,73)B ．[－1,73]C ．[－1,73]D ．[―73,―1]11、已知αβγ，，均为锐角，且1tan 2α=，1tan 5β=，1tan 8γ=，则αβγ++的值（ ） Ａ．π6Ｂ．π4Ｃ．π3Ｄ．5π412．已知α,β是锐角，sin α=x,cos β=y,cos(α+β)=－53，则y 与x 的函数关系式为（ ） A ．y=－5321x -+54x (53<x<1) B ．y=－5321x -+54x (0<x<1)C ．y=－5321x -－54x (0<x<53)D ．y=－5321x -－54x (0<x<1)13、若函数()(1)cos f x x x =+，02x π≤<，则()f x 的最大值为（ ）A ．1B ．2 C1 D2 15. 设0)4tan(tan 2=++-q px x 是方程和θπθ的两个根，则p 、q 之间的关系是（ ）A ．p+q+1=0B ．p －q+1=0C ．p+q －1=0D ．p －q －1=016.若()1cos 3A B -=, 则()()22cos cos sin sin B A B A +++的值是（ ）A. 83-B . 83 C. 73D. 5317. 若()()17tan 411tan 4=-+βα,则()βα-tan 的值为（ ） A. 14 B. 12C . 4 D. 1218. 已知)tan(),sin(4sin ,cos βαβααβ++==则a 的值是 （ ）A ．412--a aB ．－412--a aC ．214a a --±D ．412--±a a19．已知)cos(,32tan tan ,7)tan(βαβαβα-=⋅=+则的值 （ ）A ．21B ．22C ．22-D ．22±21．已知tan α,tan β是方程x 2+4=0的两根,且2π-<α<2π,2π-<β<2π,则α+β等于 （ ）A ．23π- B ．3π C ．3π或23π- D ．－3π或23π22．如果sin()sin()m n αβαβ+=-，那么tan tan βα等于（ ）Ａ．m n m n -+ Ｂ．m nm n+- Ｃ．n mn m-+ Ｄ．n mn m+-23．在△ABC 中，已知2sinAcosB ＝sinC ，则△ABC 一定是( )A ．直角三角形B ．等腰三角形C ．等腰直角三角形D ．正三角形24．在ABC ∆中,若3tan =C , 且()B B B A sin 120cos cos sin 0-=,则ABC ∆的形状是（ ）A. 等腰三角形B.等腰但非直角三角形C. 等腰直角三角形 D . 等边三角形25．若A B ，为锐角三角形的两个锐角，则tan tan A B 的值（ ） Ａ．不大于1 Ｂ．小于1 Ｃ．等于1 Ｄ．大于126．在ABC △中，90C >，sin E C =，sin sin F A B =+，cos cos G A B =+，则E F G ，，之间的大小关系为（ ） Ａ．G F E >> Ｂ．E F G >>Ｃ．F E G >> Ｄ．F G E >>27.ABC ∆中，若135cos ,53in ==B A s ，则C cos 的值是（ ） Ａ。

两角和差练习题一、选择题1. 已知角A = 30°，角B = 45°，则角A + 角B 的度数是：A. 50°B. 75°C. 60°D. 75°2. 已知角X = 110°，角Y = 40°，则角X - 角Y 的度数是：A. 70°B. 80°C. 50°D. 90°3. 若角M + 角N = 135°，角M - 角N = 45°，则角M 和角N 的度数分别是：A. 40°和55°B. 80°和55°C. 90°和45°D. 90°和80°4. 将角P用两个锐角表示，则这两个锐角的大小分别是：A. 45°和90°B. 60°和90°C. 60°和80°D. 45°和80°二、填空题1. 已知角A = 80°，角B = 120°，则角A + 角B 的度数是__________。

2. 已知角X = 90°，角Y = 30°，则角X - 角Y 的度数是__________。

3. 若角M + 角N = 180°，角M - 角N = 60°，则角M 和角N 的度数分别是__________。

4. 将角P用两个锐角表示，这两个锐角的大小分别是__________。

三、解答题1. 推导过程: 已知角D = 70°，角E = 45°，求角D + 角E 的度数。

解：根据角度和差公式：角D + 角E = 70° + 45° = 115°。

2. 推导过程: 已知角F = 140°，角G = 30°，求角F - 角G 的度数。

和差、和倍、差倍专项训练题姓名：一、和差问题练习1、张先生投资股票，2006 年和2007 年一共盈利40 万元，其中2006 年比2007 年少盈利14 万元．张先生2007年盈利多少万元？（★）2、甲、乙两位火炬手负责把火炬从A 地传递到B 地．先由甲从A 地出发，并在途中将火炬传递给乙；乙接过火炬后继续慢跑前往B 地．已知A ，B 两地相距2400 米，并且甲比乙多跑了600 米．请问：甲跑了多少米？（★）3、两筐水果共重150 千克，第一筐比第二筐多8 千克，两筐水果各多少千克？（☆）4、果园里有桃树和梨树共150 棵，桃树比梨树多20 棵，两种果树各有多少棵？（☆）5、用锡和铝制成500 千克的合金，铝的重量比锡多100 千克，锡和铝各是多少千克？（☆）6、甲、乙两个学校共有学生1245 人，如果从甲校调20 人去乙校后，甲校比乙校还多5 人，两校原有学生各多少人？（☆☆）7、甲、乙两个工程队共有1980 人，甲队为了支援乙队，抽出285 人加入乙队，这时乙队人数还比甲队少24人，求甲、乙两队原有工人多少人？（☆☆）8、甲乙两校共有学生864 人，为了照顾学生就近入学，从甲校调入乙校32 名同学，这样甲校学生还比乙校多48 人，问甲、乙两校原来各有学生多少人？（☆☆）9、某工厂去年与今年的平均产值为96 万元，今年比去年多10 万元，今年与去年的产值各是多少万元？（☆☆）二、和差倍综合练习1、费叔叔买来三箱水果，总重100 千克．其中前两箱重量相差11 千克，且前两箱的总重量是第三箱的3倍．请问：这三箱水果中最重的那箱重多少千克？（★★）2、甲、乙、丙三个物体的总重量是93 千克，甲物体比乙、丙两个物体的重量之和轻1 千克，乙物体比丙物体重量的2 倍还重2 千克，那么甲、乙、丙各重多少千克？（★★★）3、四年级有3 个班，如果把甲班的1 名学生调整到乙班，两班人数相等；如果把乙班1 名学生调到丙班，丙班比乙班多2 人，问甲班和丙班哪班人数多？多几人？（☆☆☆）4、育才小学三年级有3 个班，一共有学生126 人．如果一班比二班多4 人，二班比三班多4 人，那么这三个班分别有多少人？（★★）5、三国时期，魏国、蜀国、吴国三国交战．已知吴国军队比蜀国军队多20 万人；魏国军队人数是吴国的 2 倍，又是蜀国的3 倍．魏国军队有多少人？（★★★）6、甲、乙两个人一起去商店买东西，两人一共带了80 元钱．甲用自己带的钱的一半买了一本漫画书，乙花10 元钱买了一盘磁带．这时甲的钱恰好是乙的3 倍．开始时乙带了多少元钱？（★★★）7、姐妹俩一起做数学、语文两科作业．姐姐花在数学作业上的时间比妹妹多10 分钟；而妹妹花在语文作业上的时间比姐姐多4 分钟．已知姐姐一共花了88 分钟做完作业，妹妹做数学作业的时间比语文作业少12 分钟．请问：妹妹做语文作业花了多少分钟？（★★★）8、游泳池里男生的人数比女生的6 倍少11 人，比女生的4 倍多13 人，那么男生有多少人？（★★★）9、红旗小学三年级有甲、乙、丙三个班，一共有学生162 人．如果从甲班转出2 个人到乙班，则甲、乙两班人数相同．如果这时再从丙班转出3 个人到乙班，则乙、丙两班人数相同．请问：甲班原来有多少人？（★★★）三、和倍练习题1、甲班和乙班共有图书160本。

和差倍问题专项测习题集团标准化办公室：[VV986T-J682P28-JP266L8-68PNN]和差倍练习题21、果篮里共有苹果和梨共21个,如果把3个苹果换成3个梨,苹果还是比梨多1个.问:苹果原来有多少个2、动物园里共有老虎、狮子和猎豹共有100只,其中老虎比狮子多3只,狮子比猎豹多2只,那么动物里有老虎多少只3、学校举办跳绳比赛,第一名跳的个数是第二名的2倍,第二名跳的个数又是第三名的3倍,前三名一共跳了1000个,那么第一名跳了多少个4、三个火枪手共有子弹64发,小个火枪手的子弹数目比中个火枪手的2倍多4颗,中个火枪手的子弹是大个火枪手的3倍,那么小个火枪手有多少发子弹5、商场里大电视机和小电视机的售价之和为3000元,而如果大电视机降价400元,小电视机提价200元的话,两种电视机的售价就相同了,那么小电视机的售价是多少元6、两个桶里共盛水30斤,如果把第一桶里的水倒6斤到第二个桶里,两个桶里的水就一样多,问每桶各有多少斤水？7、甲仓所存面粉是乙仓的3倍,如从甲仓运出850公斤,从乙仓运出50公斤,则两仓所在了的面粉相等,两仓原有面粉多少公斤？8、卡莉娅、萱萱和墨莫的身高之和恰好是400厘米,卡莉娅比墨莫矮5厘米,而萱萱比墨莫高6厘米.请问：萱萱身高多少厘米9、小高、墨莫和卡莉娅帮老师搬书,一共搬了352本,小高搬的书比墨莫的2倍多2本,而墨莫搬的书是卡莉娅的2倍,那么卡莉娅搬了几本书10、纺织厂有职工480人，其中女职工人数是男职工人数的3倍.请问：男、女职工各有几人？11、12、学校合唱团成员中，女生人数是男生的3倍，而且女生比男生多80人.合唱团里男生和女生各有多少人？13、14、小悦和冬冬玩游戏,每玩一局,输的就要给赢的1枚棋子.一开始小悦有18枚棋子,冬冬则有22枚.玩了若干局之后,小悦反而比冬冬多了10枚棋子.请问：此时小悦有多少枚棋子15、16、阿奇家有两根绳子,长的那根有163米,短的只有97米,他把两根绳子剪去同样长的一段,结果长绳所剩长度比短绳所剩长度的7倍还多6米.那么两根绳子都剪去了多少米17、18、用杯子往一个空瓶里倒水,如果倒进6杯水,连瓶共重680克,如果倒进9杯水,连瓶共重920克.求空瓶的重量.19、有两根粗细不同但长度相同的蜡烛,把它们同时点燃,1小时后细蜡烛缩短了15厘米,而粗蜡烛只缩短了3厘米,此时粗蜡烛长度正是细蜡烛的3倍.请问：粗蜡烛还能烧多久20、21、拍卖行卖出了两件艺术品,第一件的拍卖价格比第二件的3倍多3万元,而第二件的价钱比第一件的3倍少73万元.请问：这两件艺术品一共卖了多少万元22、23、两只老鼠“叽叽”和“喳喳”在吃面条,“叽叽”吃的面条比较长,有40厘米；“喳喳”吃的比较短,只有25厘米.它们吃面条的速度相同,过了一段时间后,长面条的长度是短面条的2倍.那么此时短面条还剩多少厘米24、25、一满瓶水可以装7杯水,如果从中倒出5杯水,剩下的水和瓶子共重520克；如果倒出3杯水,那么剩下的水和瓶子共重880克.请问：空瓶重多少克26、27、卡莉娅和萱萱都在织围巾,现在两人已经织好的围巾长度相同,但萱萱织得比较快.在接下来的两个月里,萱萱可以织120厘米,而卡莉娅只能织45厘米,因此两个月后,萱萱围巾的长度将会是卡莉娅的2倍.那么现在卡莉娅的围巾有多长28、29、墨莫想买一台电脑,有高端和低端两种选择,高端电脑的价格比低端的2倍少1300元,低端电脑的价格则要比高端电脑的2倍少7300元.请问：低端电脑的价格是多少30、31、有甲、乙两个仓库,原来甲仓库存有65吨货物,乙仓库存有25吨货物.请问：从甲仓库调运多少吨货物到乙仓库,才能使得乙仓库的库存量变为甲仓库的2倍32、33、有两支粗细、材料都相同的蜡烛,长的能烧100分钟,短的能烧70分钟.同时点燃这两支蜡烛,过多少时间后,长蜡烛长度是短蜡烛的3倍34、35、在饭盒里装鸡蛋,如果放入3个鸡蛋,那么连盒共重250克；如果放入7个鸡蛋,则连盒共重470克.请问：一个鸡蛋有多重(假设每个鸡蛋重量相同)36、萱萱送给小山羊和卡莉娅两人一样多的饼干.小山羊比较贪吃,过了几天,小山羊已经吃了39块饼干,而卡莉娅只吃了17块.此时卡莉娅剩下的饼干数量是小山羊的3倍,请问：卡莉娅原来有多少饼干37、38、一次考试,墨莫的得分比卡莉娅的2倍少30分,而卡莉娅的得分比墨莫的2倍少120分,那么卡莉娅考了多少分39、思考题：1、一条鱼分为鱼头、鱼身、鱼尾三段.如果鱼尾重4千克,鱼头重量等于鱼身的一半加上鱼尾的重量,鱼身重量等于鱼头加鱼尾的重量.请问:这条鱼有多重。

练习15 两角和与差的三角函数与二倍角公式1.sin 22cos82cos22sin82︒︒︒︒-的值是（ ）A.12B.12-C.2D.2答案：D【详解】由题意，()()sin 22cos82cos 22sin82sin 2282sin 60︒︒-︒︒=︒-︒=-︒=2. 已知tan 3β=，()tan 5αβ-=，则tan α的值为（ ）A.47-B.47 C .18 D.18- 答案：A【详解】()()()tan tan 534tan tan 1tan tan 1537αββααββαββ-++=-+===-⎡⎤⎣⎦---⨯.3. 在ABC △中，34cos ,cos 55A B ==，则()cos A B -=（ ）A.725-B.0C.925D.2425答案：D【详解】在ABC 中， ()0A B π∈、，.因为34cos ,cos 45A B ==，所以4sin 5A ===，3sin 5===B ，所以()344324cos cos cos sin sin 555525A B A B A B -=+=⨯+⨯=. 4. 函数cos22sin y x x =+的值域为（ ）A.[]1,3B.[]3,1-C.31,2⎡⎤⎢⎥⎣⎦D.33,2⎡⎤-⎢⎥⎣⎦答案：D【详解】2cos22sin 12sin 2sin y x x x x =+=-+，令sin [1,1]t x =∈-，则22132212()22y t t t =-++=--+，有12t =时，max 32y =，1t =-时，min 3y =-，函数cos22sin y x x =+的值域为33,2⎡⎤-⎢⎥⎣⎦.5. 已知等腰三角形顶角的余弦值等于45，则这个三角形底角的正弦值为（ ）A. 10B.C. 10D.－10答案：C【详解】底角为锐角，()4cos 205πθ-=>，即24cos 212sin ,sin 5θθθ=-=-=6． 已知α，β均为锐角，且sin α=cos β=，则αβ-的值为（ ）A ．π4B ．π4- C ．3π4D ．3π4-【答案】B【详解】∵α，β均为锐角，且sin α，cos β=∴cos α==，sin β==∴()sin sin cos cos sin αβαβαβ-=-==. 又∵α，β均为锐角 ∴ππ22αβ-<-<. ∴π4αβ-=-.故选：B.7. 已知ππ,,tan 242αα⎡⎤∈=⎢⎥⎣⎦，则22πsin 2cos 14αα⎛⎫--+ ⎪⎝⎭的值为___________. 答案：710【详解】因为ππ,42α⎡⎤∈⎢⎥⎣⎦，所以π2,π2α⎡⎤∈⎢⎥⎣⎦，因为tan 2α=，所以2222sin cos 2tan 4sin 22sin cos sin cos 1tan 5ααααααααα====++ 22222222cos sin 1tan 143cos 2cos sin cos sin 1tan 145ααααααααα---=-====-+++，22π1cos 2π2sin 2cos 1cos 242αααα⎛⎫-- ⎪⎛⎫⎝⎭--+=- ⎪⎝⎭411sin 2375cos 222510αα--⎛⎫=-=--= ⎪⎝⎭ 8. 函数()cos2cos sin 2sin f x x x x x =-的最小正周期为________. 答案：23π【详解】()()cos 2cos sin 2sin cos 2cos3f x x x x x x x x =⋅-⋅=+=，所以最小正周期为23π 9. 已知353sin(),cos()41345αβππ+=-=，且3044αβπ<<<<π，则()sin αβ+的值是________.答案：5665【详解】因35sin()413πα+=，即5sin[()]2413ππα++=，则5cos()413πα+=又04πα<<，即442πππα<+<，则12sin()413πα+==， 而3cos()45πβ-=，344πβπ<<，即042ππβ<-<，4sin()45πβ-=，则有s i n ()s i n [()(44444πππππαβαβαβ+=++-=+-123545613513565=⋅+⋅=. 10. 已知3sin 45x π⎛⎫-= ⎪⎝⎭，则sin 2x =__________.答案：725【详解】因为3sin 45x π⎛⎫-= ⎪⎝⎭，所以sin 2cos 2cos 224x x x ππ⎛⎫⎛⎫⎛⎫=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭223712sin 124525x π⎛⎫⎛⎫=--=-⨯=⎪ ⎪⎝⎭⎝⎭. 11. 设当x θ=时，函数()sin 2cos f x x x =-取得最大值，则cos θ=_________. 答案：【详解】f (x )＝sin x －2cos xx x ⎫⎪⎪⎝⎭x －φ)，其中sin φcos φ＝x －φ＝2kπ＋2π (k ∈Z)时，函数f (x )取得最大值，即θ＝2kπ＋2π＋φ时，函数f (x )取到最大值，所以cos θ＝－sin φ12．函数()2sin()sin()44f x x x ππ=+-的图象的对称轴方程为_________________．【答案】π,2k x k =∈Z 【详解】因为ππsin()cos 44x x ⎛⎫+=- ⎪⎝⎭所以πππππ2sin sin =2sin cos sin 22cos 244444x x x x x x ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+⋅---=-⨯=- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭，故()f x 对称轴为π2π=2k x k x k =⇒∈Z ，.故答案为:,2k x k π=∈Z。

和差倍角1．在△ABC 中，已知2sinAcosB ＝sinC ，则△ABC 一定是 ( ) A ．直角三角形 B ．等腰三角形 C ．等腰直角三角形 D ．正三角形2．2cos10°－sin20°sin70°的值是( ) A ．12B ．32C ． 3D ． 23．f(x)＝sinx cosx1＋sinx ＋cosx 的值域为( )A ．(―3―1,―1) ∪(―1, 3―1)B ．[－2－12,―1] ∪(―1, 2－12)C ．(－3－12,3－12)D ．[－2－12,2－12]4．已知x ∈(－π2,0)，cosx ＝45，则tan2x 等于( ) A ．724B ．－724C ．247D ．－2475．已知sin(θ＋π)＜0，cos(θ－π)＞0，则下列不等关系中必定成立的是( )A ．tan θ2＜cot θ2，B ．tan θ2＞cot θ2，C ．sin θ2＜cos θ2，D ．sin θ2＞cos θ2．6．已知0＜α＜π2，tan α2＋cot α2＝52，则sin(α－π3)的值为( )A ．4＋3310B ．4－3310C ．33－410D ．－4＋33107．等式sin α＋3cos α＝4m －64－m 有意义，则m 的取值范围是( )A ．(－1,73)B ．[－1,73]C ．[－1,73]D ．[―73,―1]8．在△ABC 中，tanA tanB ＞1是△ABC 为锐角三角形的 ( ) A ．充要条件B ．仅充分条件 C ．仅必要条件D ．非充分非必要条件 9．已知α.β是锐角，sin α＝x ，cos β＝y ，cos(α＋β)＝－35，则y 与x 的函数关系式为( )A ．y ＝―351―x 2＋45x (35＜x ＜1) B ．y ＝―351―x 2＋45x (0＜x ＜1) C ．y ＝―351―x 2―45x (0＜x ＜35＝ D ．y ＝―351―x 2―45x (0＜x ＜1＝10．已知α∈(0,π)，且sin α＋cos α＝15，则tan α的值为( )A ．－43B ．－43 或－34C ．－34D ．43 或－3411．在△ABC 中，已知tan A ＋B2＝sinC ，则以下四个命题中正确的是( )(1)tanA ·cotB ＝1．(2)1＜sinA ＋sinB ≤2．(3)sin 2A ＋cos 2B ＝1．(4)cos 2A ＋cos 2B ＝sin 2C ． A ．①③ B ．②④ C ．①④ D ．②③二、填空题：13．若x ＝π3是方程2cos(x ＋α)＝1的解，α∈(0,2π)，则α＝___________14．已知cos θ＋cos 2θ＝1，则sin 2θ＋sin 6θ＋sin 8θ＝___________ 15．函数y ＝5sin(x ＋20°)－5sin(x ＋80°)的最大值是___________16．若圆内接四边形的四个顶点A 、B 、C 、D 把圆周分成AB ︵∶BC ︵∶CD ︵∶DA ︵＝4∶3∶8∶5，则四边形四个内角A 、B 、C 、D 的弧度数为___________三、解答题17．设cos(α－β2)＝－19，sin(α2－β)＝23，且π2＜α＜π，0＜β＜π2，求cos （α＋β）．18．已知f(x)＝2asin 2x －22asinx ＋a ＋b 的定义域是[0, π2]，值域是[－5,1]，求a 、b 的值．19．已知6sin 2α＋sin αcos α－2cos 2α＝0，α∈[π2,π]，求sin(2α＋π3)的值．20．在△ABC 中，sinA ＋cosA ＝22，AC ＝2，AB ＝3，求tanA 的值和△ABC 的面积．21．在矩形ABCD 中，AB ＝a ，BC ＝2a ，在BC 上取一点P ，使得AB ＋BP ＝PD ，求tan ∠APD 的值．22．是否存在锐角α和β，使α＋2β＝2π3①，且tan α2tan β＝2－3②，同时成立？若存在，求出α和β的值；若不存在，请说明理由．参考答案：1．B 由2sinAcosB ＝sin(A ＋B)⇒sin(B －A)＝0⇒B ＝A ．2．C 原式＝2cos(30°―20°)―sin20°cos20°＝3cos20°cos20°＝3．3．B 令t ＝sin x ＋cos x ＝2sin(x ＋π4)∈[―2,―1]∪(―1, 2)．则f(x)＝t 2－121＋t＝t －12∈[－2－12,―1]∪(―1, 2－12)．4．D ．5．B ∵sin θ＞0，cos θ＜0，tan θ2－cot θ2＝sinθ2cos θ2－cos θ2sinθ2＝－2cos θsin θ＞0．∴tanθ2＞cot θ2．6．B tanα2＋cot α2＝2sin α＝52．∴sin α＝45．cos α＝35． sin(α－π3)＝12sin α－32cos α＝4－3310． 7．C 8．A9．A y ＝cos β＝cos[(α＋β)－α]＝cos(α＋β)cos α＋sin(α＋β)sin α ＝―351―x 2＋45x ＞0⇒4x ＞31―x 2⇒35＜x ＜1．10．A 解：当α∈(0,π2)时，sin α＋cos α＝2sin(α＋π4)＞1．故α∈(π2,π)． ∴sin α＞0,cos α＜0．且|sin α|＞|cos α|∴|tan α|＞1． 由(sin α＋cos α)2＝125⇒sin2α＝－2425⇒2tan α1＋tan 2α＝－2425⇒tan α＝－43或tan α＝－34(舍)． 11．B 解：由tan A ＋B 2＝1－cos(A ＋B)sin(A ＋B)＝1＋cosC sinC ＝sinC 。

角的和差倍分专项训练题21.如图，已知OB是∠AOC的平分线，OD是∠COE的平分线，如果∠AOE=140°，∠BOC比∠COD的2倍还多10°，那么∠AOB是多少度？2.如图，OB是∠AOC的平分线，OD是∠COE的平分线．（1）如果∠AOB=50°，∠DOE=30°，那么∠BOD是多少度？（2）如果∠AOE=160°，∠COD=30°，那么∠AOB是多少度？3.如图，OB是∠AOC的角平分线，OD是∠COE的角平分线．∠DOE= －（1）∠AOC= ＋；∠BOD= ＋；∠DOE= －；∠AOB= －；（2）如果∠AOB=400，∠DOE=300，那么∠BOD是多少度？（3）如果∠AOE=1400，∠COD=300，那么∠AOB是多少度？4.如图，已知∠AOC：∠BOC=1：3，∠AOD：∠BOD=5：7，若∠COD=150，求∠AOB的度数5.将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起.（1）如果∠DCE=36°，则∠ACB的度数为；（2）写出图中相等的角．如果∠DCE≠36°，它们还会相等吗？（3）若∠DCE变小，∠ACB如何变化？（4）在下图中利用能够画直角的工具再画一个与∠DCB相等的角6.如图，将两块直角三角尺的直角顶点O叠放在一起．（1）若∠BOC=400，试求∠AOD的度数．（2）若∠AOD=1350，试求∠BOC的度数．（3）若∠BOC=α，∠AOD=β，请写出α与β的大小关系式，并说明理由7.如图，将一副三角尺的两个直角顶点O重合在一起，在同一平面内旋转其中一个三角尺．（1）如图1，若∠BOC=700，则∠AOD= ；（2）如图2，若∠BOC=500，则∠AOD= ；（3）如图1，请猜想∠BOC与∠AOD 的关系，并写出理由8.如图所示，将两块三角尺的直角顶点重合，（1）写出以C为顶点的相等的角；（2）若∠A=1500，求∠DCE的度数；（3）写出∠ACB与∠DCE之间所具有的数量关系；（4）当三角尺ACD不动，将三角尺ECB的EC边与AC边重合，然后绕点C按顺时针或逆时针方向任意转动一个角度，当∠ACE（00＜∠ACE ＜900）等于多少度时，这两块三角尺各有一条边互相垂直，直接写出∠ACE角度的所有可能值，不用说明理由。

六年级角的和差练习题一、填空题1. 一个角的补角是120°，这个角的度数是______°。

2. 两个角的和是180°，其中一个角是30°，另一个角是______°。

3. 若一个角是100°，则它的余角是______°。

4. 两个锐角的和是______°。

5. 一个直角和一个钝角的和是______°。

二、选择题1. 下列哪个角的补角是它本身？A. 45°B. 90°C. 180°D. 0°2. 两个角的和是360°，那么这两个角可能是：A. 两个锐角B. 一个锐角和一个直角C. 一个锐角和一个钝角D. 两个钝角3. 一个角的补角比它的余角大______°。

A. 45°B. 90°C. 135°D. 180°4. 下列哪个角的和是一个直角？A. 30°和60°B. 45°和45°C. 60°和60°D. 70°和20°三、判断题1. 两个角的和是180°，则这两个角互为补角。

（）2. 一个角的补角比它的余角大90°。

（）3. 两个锐角的和一定小于180°。

（）4. 一个钝角和一个锐角的和一定大于180°。

（）四、计算题1. 已知一个角的补角是130°，求这个角的度数。

2. 两个角的和是255°，其中一个角是125°，求另一个角的度数。

3. 一个角的补角比它的余角大75°，求这个角的度数。

4. 已知三个角的和是360°，其中第一个角是90°，第二个角是120°，求第三个角的度数。

5. 一个角的补角和它的余角的和是180°，求这个角的度数。

两角和与差、二倍角的三角函数公式课时作业1.若tan α＝3，tan β＝3，则tan(α－β)等于( )A ．－3B ．－13 C ．32．求值：⎝ ⎛⎭⎪⎫cos π12－sin π12⎝ ⎛⎭⎪⎫cos π12＋sin π12＝( )A ．－32 B ．－123．已知α∈⎝ ⎛⎭⎪⎫π2，π，sin α＝35，则tan ⎝ ⎛⎭⎪⎫α＋π4等于( )B ．7C ．－17D ．－74．已知sin(α－β)cos α－cos(α－β)sin α＝35，那么cos 2β的值为( )C ．－725D ．－18255．已知0<α<π，sin α＋cos α＝12，则cos 2α的值为( )B ．－74C ．±74 D ．－346．已知α，β为锐角且cos α＝110，cos β＝15，则α＋β的值等于________．7已知α，β∈⎝ ⎛⎭⎪⎫3π4，π，sin(α＋β)＝－35， sin ⎝ ⎛⎭⎪⎫β－π4＝1213，则cos ⎝ ⎛⎭⎪⎫α＋π4＝________.8已知α，β均为锐角，且sin α－sin β＝－12，cos α－cos β＝13，则cos(α－β)＝________.年在北京召开的国际数学家大会，会标是我国以古代数学家赵爽的弦图为基础设计的．弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如右图)．如果小正方形的面积为1，大正方形的面积为25，直角三角形中较小的锐角为θ，那么cos 2θ的值等于________．10已知cos ()α＋β＝45，cos ()α－β＝－45，且32π<α＋β<2π， π2<α－β<π，分别求cos 2α和cos 2β的值．11已知函数f (x )＝sin x ＋sin(x ＋π2)，x ∈R .(1)求f (x )的最小正周期；(2)求f (x )的最大值和最小值，并求出取得最值时的x 的值； (3)若f (α)＝34，求sin 2α的值．12设f (x )＝6cos 2x －3sin 2x . (1)求f (x )的最大值及最小正周期；(2)若锐角α满足f (α)＝3－23，求tan 45α的值．参考答案1．D 7，－5665,8..59729．解析：图中小正方形的面积为1，大正方形的面积为25，∴ 每一个直角三角形的面积是6，设直角三角形的两条直角边长分别为a ，b ，则⎩⎪⎨⎪⎧a 2＋b 2＝2512ab ＝6 ，∴ 两条直角边的长分别为3,4，直角三角形中较小的锐角为θ，cos θ＝45，cos 2θ＝2cos 2θ－1＝725. 答案：72510．cos 2α＝－725，cos 2β＝－111．(1)2π (2)当x ＝π4＋2k π，k ∈Z 时，f (x )max ＝2当x ＝－3π4＋2k π，k ∈Z 时，f (x )min ＝－2(3)－71612．(1)f (x )的最大值为23＋3；最小正周期为T ＝π. (2)3。