第十一页,共46页。
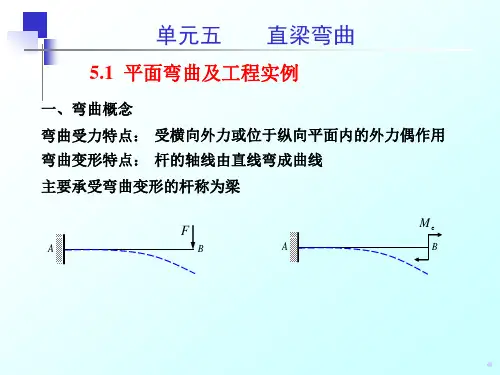
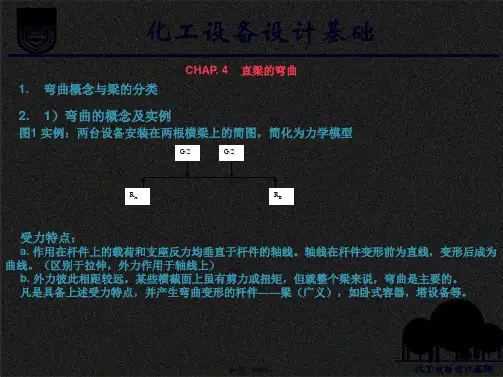
CHAP. 4 直梁的弯曲
l
l
a. 纵向纤维由直变弯。o1o2以上部分,m1m2缩短,o1o2以下部分,m1m2伸长,而o1o2不变。 这说明梁的上半部分受到纵向压缩,梁的下半部分受到纵向拉伸,而且离开o1o2线越远的纵向 线,它们被拉长或缩短的数量越大。
b. 各条横向线a1b1,c1d1,a2b2仍为直线。由此假设,梁的横截面的变形后仍是一 个平面,且仍与已经成为弧线的m1m2,n1n2相重合。并且仍垂直于变形后梁的轴线。 (平面假设)->试验理论得到证明。
剪力、弯矩均有二种D 方向,须规定其“正负”:由于Q,M均是内力,其正负要 根据变形而定。
第十五页,共46页。
CHAP. 4 直梁的弯曲
1)剪力正负的规定 根据剪切变形的方向,规定剪力Q的正负。通常规定:如果产生图(a)所示的变形, (此变形是使截面左边的梁发生相对截面右侧梁的向上滑动)那么伴随这种变形产生的
x2
D
lx
la
)
2
q (x 2
l )2 2
ql (l 4a) 8
x
l 2
,
M
极值=
ql 8
(l
4a)
BD段
MA
M
qa 2
q2(l
,MB
x)2
qa 2 2
2
第二十二页,共46页。
目的―分析找出梁内
的大小及其横截面所在位置(危险截面),从而进行梁
的强度计算。
Qmax , Mmax
D
下面分别讨论集中力、集中力偶、均布载荷作用下的Q、M图。
第十八页,共46页。
CHAP. 4 直梁的弯曲 例1:集中力作用 AC=a=0.25m,BE=b=0.2m,AB=l=1m,P1=500N,P2=1000N,P3=300N