11-3 波的能量要点
- 格式:ppt
- 大小:295.00 KB
- 文档页数:8


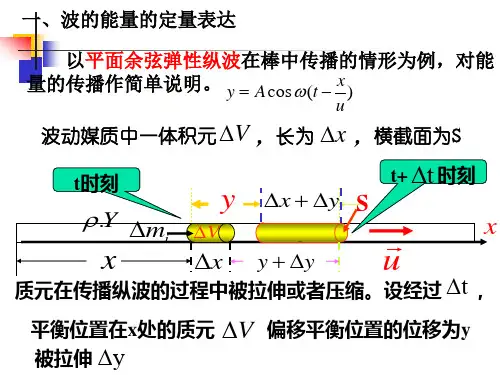
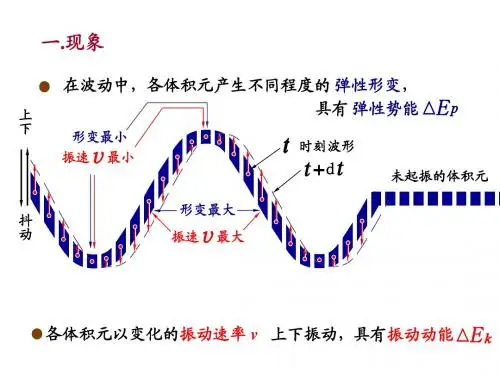
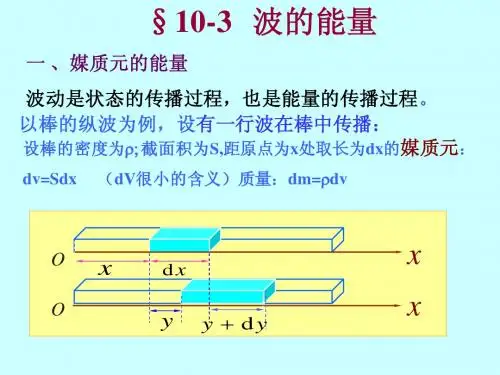
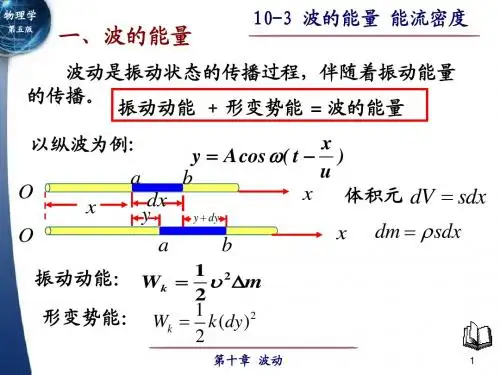
第4节 波的能量一、 波的能量密度 绳上横波 质量线密度μ )(cos[),(ω-=cx t A t x y x m ∆=∆μ, ])(sin[ϕωω+--=∂∂=cx t A t y V ])([sin 21212222ϕωω+-∆=∆=cx t A m mV E k 伸长量x l ∆-∆=]1)(1[)()(222-∂∂+∆=∆-∆+∆xy x x y x 小振幅条件下,xy ∂∂(波形曲线切线斜率)及其平方很小 +∂∂+=∂∂+22/12)(211])(1[xy x y x l ∆-∆≈21()02y x x∂∆≈∂,则 T T T =≈21 ≈∆-∆=T x l E P )(xT xy ∆∂∂2)(21 ])(sin[ϕωω+-=∂∂cx t A c x y ,2c T μ= ])([sin 2122222ϕωωμ+-∆=c x t A cx c E P =])([sin 21222ϕωω+-∆cx t A m =E k E +P E =])([sin 222ϕωω+-∆cx t A m 结论:(1)k E 、P E 都是时间的周期函数,且k E =P E(2)E 是时间的周期函数平衡位置→最大位移处,能量↓最大位移处→平衡位置,能量↑(3)能量的传播速度也是c无限大各向同性均匀媒质也成立V m ∆=∆ρ ∆ =E k E +P E =])([sin 222ϕωωρ+-∆cx t A V 能量密度:V E w ∆==])([sin 222ϕωρω+-cx t A平均能量密度220211A wdt T w T ρω==⎰ 二、 能流密度(波的强度):单位时间内通过与波的传播方向c相垂直的单位面积的平均能量c A c w I 2221ρω==c A c wI 2221ρω==,2A I ∝ 三、 平面和球面谐波的振幅1、 平面谐波 S I S I 21=cS A cS A 2222122121ρωρω= 21A A = ])(c o s [),(ϕω+-=cx t A t x y , 2、 球面谐波2211S I S I =2222221212421421r c A r c A πρωπρω=2211r A r A =,2112r r A A =,r A 1∝,I ∝])(cos[)(),(ϕωξ+-=cr t r A t r m r 10=,0A ,r r A r A )(00=,rA r A 0)(= ])(cos[),(0ϕωξ+-=cr t r A t r第5节 惠更斯原理一、 惠更斯原理(1690年)“媒质中波动传到的各点都可以看作发射子波的波源,在其后任意时刻这些子波的包络面(公切面)就是新的波阵面”例t 1r t t ∆+ t c ∆t c r r ∆+=12二、 波的绕射(衍射)当波在传播过程中遇到障碍物时,其传播方向会发生变化,并且能够绕过障碍物的边缘继续向前传播:波的绕射波的传播方向第6节 波的干涉一、 波的独立传播原理和迭加原理当几列波在媒质中相遇时,每一列波的振幅、频率、波长、 振动方向及传播方向不因其它波的存在而受影响,或者说 每一列波都保持其独立的传播特性——波的独立传播原理 当几列波在媒质中相遇时,媒质质点的振动位移等于每列波 单独引起位移的矢量和——波的迭加原理二、 波的干涉1、 波的干涉现象,p146如果两列波在相遇区域迭加的结果使得某些点上振动始终加强 某些点上振动始终减弱,形成稳定的干涉花样:波的干涉现象2、 相干条件同振向、同频率、位相差恒定——相干条件相干波,相干波源3、 定量分析)c o s (11010ϕω+=t A y )c o s (22020ϕω+=t A y 1S])(c o s[1111ϕω+-=cr t A y ])(c o s [2222ϕω+-=cr t A y 2S 21y y y +==])(cos[111ϕω+-c r t A +])(cos[222ϕω+-c r t A ϕ∆++=c o s 2212221A A A A Aϕ∆++=c o s 22121I I I I I ,(2A I ∝) -+-=∆])([22ϕωϕc r t ])([11ϕω+-cr t =)(1212r r c ---ωϕϕ=)(21212r r ---λπϕϕ =∆ϕ)(21212r r ---λπϕϕ:两列波在P 点的相位差 δ=-12r r :波程差=∆ϕπk 2±, 2,1,0=k ,21A A A +=最大,21212I I I I I ++=,干涉加强=∆ϕπ)12(+±k , 2,1,0=k ,21A A A -=最小,21212I I I I I -+=,干涉相消如果21ϕϕ=,=∆ϕ)(212r r --λπ 干涉加强条件=∆ϕπλπk r r 2)(212±=-- λδk r r ±=-=12, 2,1,0=k干涉相消条件=∆ϕπλπ)12()(212+±=--k r r λλδ)21(2)12(12+±=+±=-=k k r r , 2,1,0=k 4、 (1)干涉加强或相消是指合振幅或波的强度最大或最小 而不是合位移最大或最小(2)位相差恒定要求两个波源在观察时间内持续振动(3)ϕ∆由两部分组成(4)干涉后,波的能量重新分布例:A ,B 两个相干波源,等振幅 x P 20-x同频率=ν100Hz ,初相差π相距20m,波速s m c /200= A 20m B 求:A ,B 连线上因干涉而静止的点解:=∆ϕ)(21212r r ---λπϕϕ =2(20)()x x c πνπλν---=)220(x --ππ=π)12(+k k x +=10 , 10,2,1,0±±±= k20,,1,0 =x m例:声波干涉仪 EC 每移动8cm ,声音减弱一次 x 求:声波的频率(空气中声速s m c /340=)解:21ϕϕ=λλ)21(2)12(12+=+=-k k r r (1) λ)211(212++=-+k r x r (2) νλc x ==2,Hz x c 212508.023402=⨯==ν。