亥姆霍兹线圈磁场实验

（B1 B2 ) x 曲线与上述叠加曲 线，以及这两条曲线的叠加的曲线，再做
线进行比较，验证磁场叠加原理。 6. 切断仪器电源，整理实验台。
实验数据处理：
表一 亥姆霍兹线圈磁感应强度表
x(cm)
-7.00 -6.00 -5.00 -4.00 -3.00 -2.00 -1.00 0.00 1.00 2.00 3.00 4.00 5.00 6.00 7.00
亥姆霍兹线圈的磁场测量 实验目的： 测量亥姆霍兹线圈中 O1 线圈的磁感应强度沿轴线的分布 ； 测量 O2 线 （B1 x）
圈磁感应 强度沿 轴线的 分布 ；测量亥 姆霍兹 线圈的 磁感应 强度沿 轴线的 分 布 （B2 x）
（B1 B2 ) x ;验证磁场叠加原理。
实验原理：
亥姆霍兹线圈是用以产生均匀弱磁场的一种组合线圈，它由一对半径为 R，匝数为 N， 相互平行，同轴放置的圆形线圈同相串联组成。并且，这对线圈的距离 O1O2 R 。 当两线圈分别同以电流 I 时，产生的磁感应强度分别是：
百分比 （%） 0.53 1.50 0 0.68 0.45 0 0.44 0.22 0.44 0.22 0.67 0.46 0.94 0.49 0.53
B
8 0 NI 2 5 3 R
，N=500，I=100mA=0.1A , R=10cm
0 4 10 7 H m
由此可求得 B=1.7190mH
B1 (mT )
-0.295 -0.309 -0.312 -0.308 -0.294 -0.278 -0.255 -0.228 -0.195 -0.174 -0.149 -0.126 -0.109 -0.095 -0.082
B2 (mT )

亥姆霍兹线圈的磁场实验报告实验目的：观察亥姆霍兹线圈中的磁场分布情况。

实验原理：亥姆霍兹线圈是由两个平行的同轴圆形线圈组成，两个线圈中电流方向相同。

通过改变电流大小和方向，可以控制磁场的强度和方向。

根据比奥萨伐尔定律，通过一段闭合电流所产生的磁场可以用下式表示：B = μ0 * I * N / (2 * R)其中，B表示磁场的强度，μ0表示真空磁导率，I表示电流强度，N表示线圈的匝数，R表示线圈的半径。

实验器材：1. 亥姆霍兹线圈2. 电源3. 电流表4. 磁场传感器5. 连接线实验步骤：1. 将亥姆霍兹线圈的两个线圈放置在水平的平面上，并调整它们的距离，使得两个线圈之间的距离与半径相等。

2. 将磁场传感器放置在线圈中央的位置，并使其与线圈轴线垂直。

3. 连接线圈和电流表，并接通电源。

4. 通过调节电流表上的电流大小和方向，改变电流强度。

5. 使用磁场传感器测量不同位置处的磁场强度，并记录数据。

6. 重复步骤4和5，改变电流强度和方向，记录更多的数据。

实验结果：根据实验数据，绘制电流强度与磁场强度的关系曲线图。

实验讨论：1. 分析实验数据，观察磁场强度与电流强度的关系。

根据比奥萨伐尔定律的公式，验证实验结果是否与理论值吻合。

2. 讨论磁场强度随距离的变化趋势，检验亥姆霍兹线圈中磁场分布的均匀性。

3. 探讨如何通过改变电流强度和方向来控制磁场的强度和方向。

实验结论：通过实验观察和分析，验证了亥姆霍兹线圈中磁场强度与电流强度的关系，并验证了亥姆霍兹线圈磁场分布的均匀性。

同时，通过改变电流强度和方向，可以控制磁场的强度和方向。

亥姆霍兹线圈磁场实验报告一、实验目的本实验旨在通过亥姆霍兹线圈的磁场实验，探究磁场的基本性质，了解磁场的产生和作用规律，以及掌握测量磁场强度的方法。

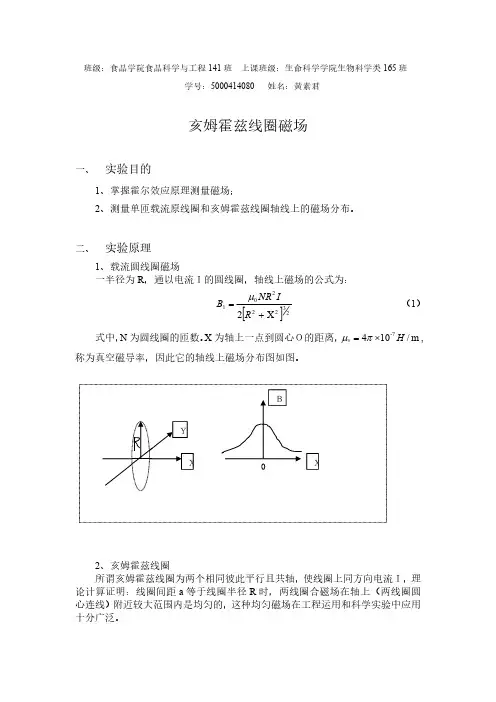
二、实验原理亥姆霍兹线圈是由两个相同的圆形线圈组成的，它们的轴线重合，且两个线圈的半径相等。

当两个线圈通以相同方向的电流时，它们产生的磁场在轴线上方的区域内是均匀的。

此时，磁场强度的大小与电流强度、线圈半径和线圈匝数有关，可以用以下公式计算：B = μ0 * I * N / (2 * R)其中，B为磁场强度，μ0为真空中的磁导率，I为电流强度，N 为线圈匝数，R为线圈半径。

三、实验器材1. 亥姆霍兹线圈2. 直流电源3. 万用表4. 磁场探测器四、实验步骤1. 将亥姆霍兹线圈放置在水平面上，调整两个线圈的距离和电流强度，使得磁场在轴线上方的区域内是均匀的。

2. 将直流电源接入亥姆霍兹线圈，调节电流强度，使得磁场强度在合适的范围内。

3. 使用万用表测量电流强度，并记录下来。

4. 使用磁场探测器测量磁场强度，并记录下来。

5. 重复以上步骤，改变电流强度和线圈半径，测量不同条件下的磁场强度。

五、实验结果在本次实验中，我们测量了不同条件下的磁场强度，结果如下表所示：| 电流强度（A） | 线圈半径（m） | 磁场强度（T） || -------------- | -------------- | -------------- || 0.5 | 0.1 | 0.0000314 || 0.5 | 0.2 | 0.0000785 || 0.5 | 0.3 | 0.000141 || 1 | 0.1 | 0.0000628 || 1 | 0.2 | 0.000157 || 1 | 0.3 | 0.000282 || 1.5 | 0.1 | 0.0000942 || 1.5 | 0.2 | 0.000235 || 1.5 | 0.3 | 0.000423 |从上表可以看出，磁场强度与电流强度、线圈半径和线圈匝数有关。

亥姆霍兹线圈磁场测定-实验报告实验目的：1. 掌握亥姆霍兹线圈原理及其构造；2. 熟悉磁场测定的基本方法；3. 使用亥姆霍兹线圈测定磁场的强度，了解其精度；4. 熟悉使用万用表和数字万用表进行电量测量。

实验原理：亥姆霍兹线圈是一种特殊的线圈结构，由两个同轴的环形线圈组成，两个线圈的半径相等，通电方向相反，电流强度相等，在同一轴向上构成匀强磁场。

如果通过两线圈流同向电流，其磁场强度将会倍增。

由于外界物体的磁场强度对线圈的磁场有一定的影响，因此在实验过程中，需要先测定环境中的磁场强度，再将线圈放置于恒定的磁场中，通过测量线圈中的磁场强度差，求得外磁场的强度。

实验器材：亥姆霍兹线圈、数字万用表、长板子、短板子、直流电源等。

实验步骤：1. 将亥姆霍兹线圈放置于平稳的桌面上，用数字万用表测定环境中的磁场强度，记录下读数。

2. 在同一位置，保持线圈不动，通过调节直流电源输出电压，使亥姆霍兹线圈中的磁场强度降低至为0。

记录下此时的电压值，并将其记作$U_0$。

5. 测量亥姆霍兹线圈本身的参数：使用数字万用表测量亥姆霍兹线圈中圈数，环半径等参数。

6. 计算环境中的磁场强度B0：根据数字万用表测量得到的环境磁场强度读数，使用其对应的磁场表值作为环境磁场强度B0。

7. 计算磁场强度B：由均匀磁场的定义，设线圈中磁场$B_1$和$B_2$分别为直流电源输出电压为$U_1$和$U_2$时线圈中磁场的强度，则有$B=\frac{1}{2}(B_1+B_2)$。

8. 计算外界磁场的强度B': 由于亥姆霍兹线圈内自带磁场，需要在计算磁场强度B 时，减去线圈的自感磁场强度$B_{self}$。

因此，有$B'=B-B_{self}$。

9. 计算磁场强度的不确定度：需考虑设备测量误差和环境影响因素的影响，根据不确定度的综合误差计算公式$U=\sqrt {\sum_{i=1}^n u_i}$，其中n为误差项的数目，$u_i$为每一误差项的保守评估。

【注意事项】
1. 霍尔传感器探头必需沿着线圈中心轴线移动。 2.每测量一个数据前，需对微特斯拉计调零，方 可记录数据。 3. 实验中，测试架位置保持不动，实验仪相互间 保持一定距离。 4. 不要拔白色芯线（专用连接线）。
【数据记录与处理】
1. 数据记录表格(注d=R=10cm,N=500匝， I=100mA)
3. 调整传感器位置，使其在两线圈的轴线上。
二、载流圆线圈轴线上各点磁感应强度的测量
1. 单线圈a轴线上各点的磁感应强度Ba
只给固定线圈a通电，旋转电流调节旋纽， 令电流I为100mA。取标尺零点为坐标原点O，通 过O的横刻线为OX轴。把传感器探头从一侧沿OX 轴移动,每移动1.00cm测一磁感应强度Ba，测出一 系列与坐标x对应的磁感应强度Ba .测量区域为6cm—+19cm。
注意事项：每测量一个数据后，先将电流调节旋 钮调零，再移动线圈到下一位置，然后将微特斯 拉计调零，最后才将电流调回100mA，微特斯拉 计示值稳定后，方可记录数据。
二、载流圆线圈轴线上各点磁感应强度的测量
2. 单线圈b轴线上各点的磁感应强度Bb 只给单线圈b通电，旋转电流调节旋纽，令电流I
为100mA。以上述同样的测量方法，测出一系列X— Bb数据。测量区域为-6cm—+19cm。
RH称为霍尔系数
2. 霍尔传感器
UH
RH
IB d
KH IB
并且传感器的工作电流已设定为标准工作电流 （定值）。即KHI＝K（常数）
UH＝KB 所以由UH值可得出B的示值。
【实验仪器】
一、FB511型霍尔法亥姆霍兹线圈磁场测试架 二、 FB511型霍尔法亥姆霍兹线圈磁场测试仪
【实验仪器】

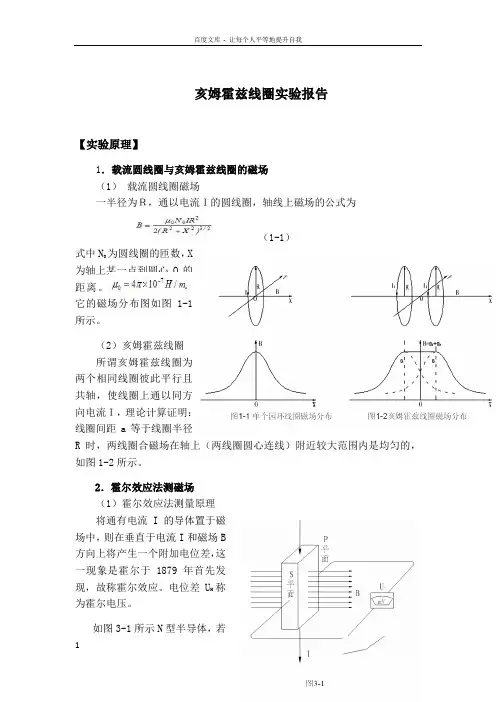
亥姆霍兹线圈实验报告【实验原理】1．载流圆线圈与亥姆霍兹线圈的磁场（1）载流圆线圈磁场一半径为Ｒ，通以电流Ｉ的圆线圈，轴线上磁场的公式为（1-1）式中N0为圆线圈的匝数，X为轴上某一点到圆心O的距离。

它的磁场分布图如图1-1所示。

（2）亥姆霍兹线圈所谓亥姆霍兹线圈为两个相同线圈彼此平行且共轴，使线圈上通以同方向电流Ｉ，理论计算证明：线圈间距a等于线圈半径R时，两线圈合磁场在轴上（两线圈圆心连线）附近较大范围内是均匀的，如图1-2所示。

2．霍尔效应法测磁场（1）霍尔效应法测量原理将通有电流I的导体置于磁场中，则在垂直于电流I和磁场B方向上将产生一个附加电位差，这一现象是霍尔于1879年首先发现，故称霍尔效应。

电位差U H称为霍尔电压。

如图3-1所示N型半导体，若在MN两端加上电压U，则有电流I沿X轴方向流动（有速度为V运动的电子），此时在Z轴方向加以强度为B的磁场后，运动着的电子受洛伦兹力F B的作用而偏移、聚集在S平面；同时随着电子的向S平面（下平面）偏移和聚集，在P平面（上平面）出现等量的正电荷，结果在上下平面之间形成一个电场E H（此电场称之为霍尔电场）。

这个电场反过来阻止电子继续向下偏移。

当电子受到的洛伦兹力和霍尔电场的反作用力这二种达到平衡时，就不能向下偏移。

此时在上下平面（S、P平面）间形成一个稳定的电压U H（霍尔电压）。

（2）霍尔系数、霍尔灵敏度、霍尔电压设材料的长度为l，宽为b，厚为d，载流子浓度为n，载流子速度v，则与通过材料的电流I有如下关系：I=nevbd霍尔电压 U H=IB/ned=R H IB/d=K H IB式中霍尔系数R H=1/ne，单位为m3/c；霍尔灵敏度K H=R H/d，单位为mV/mA由此可见，使I为常数时，有U H= K H IB =k0B，通过测量霍尔电压U H，就可计算出未知磁场强度B。

本实验使用的仪器用集成霍尔元件，已经与显示模块联调，直接显示磁场强度。

三、 实验仪器
4501A 型亥姆霍兹线圈磁场实验仪
四、
实验步骤
1、测量载流圆线圈轴线上磁场的分布 （1）仪器使用前，请先开机预热 10min 接好电路，调零。 （2）调节磁场实验仪的输出功率，使励磁电流有效值为 I=200mA，以圆电
流线圈中心为坐标原点，每隔 10.00mm 测一个 Bmax 值，测量过程中注意保持励 磁电流值不变，记录数据并作出磁场分布曲线图。 2、测量亥姆霍兹线圈轴上磁场分布 （1）关掉电源，把磁场实验仪的两组线圈串联起来（注意极性不要接反）， 接到磁场测试仪的输出端钮，调零。 （2）调节磁场实验仪的输出功率，使励磁电流有效值为 I=200A，以圆电流 线圈中心为坐标原点，每隔 10.00mm 测一个 Bmax 值，测量过程中注意保持励磁 电流值不变，记录数据并作出磁场分布曲线图。
实验数据及处理1圆电流线圈轴线上磁场分布的测量数据记录注意坐标原点设在圆心处要求列表记录表格中包括测点位置并在表格中表示出各测点位置对应的理论值在坐标纸上画出实验曲线
班级：食品学院食品科学与工程 141 班
上课班级：生命科学学院生物科学类 165 班 姓名：黄素君
学号：5000414080
亥姆霍兹线圈磁场
一、
实验目的
1、掌握霍尔效应原理测量磁场； 2、测量单匝载流原线圈和亥姆霍兹线圈轴线上的磁场分布。
二、
实验原理
1、载流圆线圈磁场 一半径为 R，通以电流Ｉ的圆线圈，轴线上磁场的公式为：
B1 2 R2 X2

0 NR 2 I

3
2
（1）
式中， N 为圆线圈的匝数。 X 为轴上一点到圆心Ｏ的距离， 0 4 10 -7 H / m , 称为真空磁导率，因此它的轴线上磁场分布图如图。

O1与O2在轴上一点合成磁感应强 度为
B B 1 2 3 3 2 R 2 2 2 R 2 2 2 [ R ( x )] 2 [ R ( x )] 2 2
NR I 0
2
NR I 0
2
D=R
D=2R
D=R/2
两线圈电流反向
二 实验原理
3.霍尔传感器测量磁场的原理
平衡时
UH=KI0B
x
fm=fe
三 仪器介绍
四 实验任务
X(cm) B1(mT) -7.00 … 0.00 … 7.00
B2(mT)
B1 +B2(mT)
B(1+2)(mT)
四 实验任务
分别测量亥姆霍兹线圈中O1和O2线
圈的磁感应强度沿轴线的分布曲线 （B1~χ）, （B2~χ）,(B1+B2~x). 测量亥姆霍兹线圈的磁感应强度沿 轴线的分布B( 1+2)~χ. 验证磁场迭加原理。 计算线圈O1在圆心位置B的理论值, 并与测量值比较,计算. B理 B测 100% B理
BA
0 NR I
2
I
2( R x )
2 2
3 2
o
x
在线圈的中心O点，x=0, 磁感应强度 为
BA0
0 NI
2R
返回
2载流亥姆霍兹线圈的磁场
亥姆霍兹线圈是由一对半径为R， 匝数 分别为N，相互平行，同轴放 置的圆形线圈同向串联组成。并且 这对线圈的距离O1O2= R 。
图1 亥姆霍兹线圈
实验四十三 亥姆霍兹线圈的磁场 测量
戚非
一.实验目的
测量载流亥姆霍兹线圈
的磁感应强度沿其轴线 的分布。 验证磁场叠加原理

与理论曲线。
表1
轴向距离 X（mm） -120.0 -110.0 -100.0
┅┅ 100.0
110.0
120.0
B(mT)
（2）将亥姆霍兹线圈轴线上的磁场分布的测量数据记录于表 2(注意坐标原点设在两个
线圈圆心连线的中点 O 处)，在方格坐标纸上画出实验曲线。
带电粒子(电子或空穴)被约束在固体材料中，这种偏转就导致左垂直电流和磁场的方向上产 生正负电荷在不同侧的聚积，从而形成附加的横向电场。如图 6 所示，磁场 B 位于 Z 的正向， 与之垂直的半导体薄片上沿 X 正向通以电流 Is(称为工作电流)，假设载流子为电子(N 型半导 体材料)，它沿着与电流 Is 相反的 X 负向运动。
（2）亥姆霍兹线圈
亥姆霍兹线圈是一对彼此平行且连通的共轴圆形线圈，。两线圈内的电流方向一致，大小 相同。线圈之间距离 d 正好等于圆形线圈的半径 R。这种线圈的特点是能在其公共轴线中点 附近产生较广的均匀磁场区，故在生产和科研中有较大的实用价值，也常用于弱磁场的计量 标准。
设 z 为亥姆霍兹线圈中轴线上某点离中心点 O 处的距离，则亥姆霍兹线圈轴线上任一点 的磁感应强度为
图 3 亥姆霍兹线圈磁场测试架
图 4 型亥姆霍兹线圈磁场测试架面板 2.主要技术性能 （1）环境适应性：工作温度 5～35℃；相对湿度 25~85％。
图 5 亥姆霍兹线圈磁场测量仪面板 （2）亥姆霍兹线圈架
二个励磁线圈：线圈有效半径 1lOmm 单个线圈匝数 500 匝 二线圈中心间距 llOmm 温升不大于 IO0C 时的最大负荷电流不小于 O.5A 测量磁场传感器：SS495A 型霍尔元件 移动装置：轴向可移动距离 230mm，径向可移动距离 75mm，距离分辨率 lmm （3）亥姆霍兹磁场实验仪 亥姆霍兹磁场实验仪由可调恒流源和测量磁场的高斯计二部分组成。内置恒流源部分： 输出电流：O～0.5A，最大电压 24V；3 位半数显表，最小分辨率 lmA。内置磁场测量部分(高 斯计)：当与亥姆霍兹线圈架内的霍尔传感器相配套工作时，测量磁场范围 O～2.200mT，最 小 分 辨 力 0.001mT 。 电 源 ： 220V ± 10 ％ ， 功 耗 ： 50VA 外 形 尺 寸 ： 亥 姆 霍 兹 线 圈 架 340×270×250mm。磁场测试仪 320×300×120mm。 （四）使用方法 1.准备工作：仪器使用前，先开机预热 10 分钟。这段时间内，请使用者熟悉亥姆霍兹线 圈测试架和磁场测量仪的构成，各个接线端子的正确连线方法，以及仪器的正确操作方法。 2.亥姆霍兹线圈架与磁场测量仪之间的连线 用随机带来的两头都是同轴插头的连接线将测量仪的偏置电压端与测试架的偏置电压端 相连．将测量仪的霍尔电压端与测试架的霍尔电压端相连。

亥姆霍兹线圈磁场实验报告1. 背景亥姆霍兹线圈是一种用于产生均匀磁场的装置，由两个相同半径和间距的同轴圆线圈组成。

在实验中，我们将使用亥姆霍兹线圈来测量其产生的磁场强度与电流的关系，并验证其是否为均匀磁场。

2. 实验目的1.理解亥姆霍兹线圈的结构和原理；2.掌握使用亥姆霍兹线圈测量磁场强度的方法；3.验证亥姆霍兹线圈产生的磁场是否为均匀磁场；4.分析实验结果，得出结论并提出建议。

3. 实验装置和方法3.1 实验装置•亥姆霍兹线圈（包括两个同轴圆线圈、电源和电流控制器）•磁场计•电流表•直流电源•连接线3.2 实验方法1.将亥姆霍兹线圈放置在水平桌面上，调整线圈间距与半径，使其符合实验要求。

2.将直流电源和电流控制器连接到亥姆霍兹线圈上，将电流表连接到电流控制器上，确保电路连接正确。

3.打开直流电源，调节电流控制器使得电流稳定在设定值，记录电流强度。

4.将磁场计垂直放置于亥姆霍兹线圈的中心位置，记录磁场强度值。

5.调节直流电源的电流值，重复步骤3和4，记录一系列不同电流强度下的磁场强度值。

4. 分析与结果4.1 实验数据我们采集了一系列不同电流强度下的磁场强度值，并绘制了磁场强度与电流强度的关系图：电流强度（A）磁场强度（T）0.1 0.0250.2 0.0500.3 0.0750.4 0.1000.5 0.1254.2 数据处理根据测得的磁场强度值和电流强度值，我们可以绘制磁场强度与电流强度的关系图。

在这个图中，我们可以观察到一个线性关系，并计算出磁场强度与电流强度之间的比例系数。

根据电流对磁场产生的影响可以得到以下关系式：B=μ0⋅I⋅N 2⋅R其中，B为磁场强度，μ0为真空介质中磁导率，I为电流强度，N为线圈匝数，R为线圈半径。

通过线性拟合，我们可以得到磁场强度与电流强度之间的比例系数k。

4.3 结果分析通过拟合得到的结果，我们得到了磁场强度与电流强度之间的线性关系，证明亥姆霍兹线圈可以产生均匀的磁场。

实验十一 亥姆霍兹线圈磁场测定一、概述亥姆霍兹线圈磁场测定仪是综合性大学和工科院校物理实验教学大纲重要实验之一。

该实验可以学习和掌握弱磁场测量方法，证明磁场迭加原理，根据教学要求描绘磁场分布等。

传统的亥姆霍兹线圈磁场测量实验，一般用探测线圈配以指针交流电压表测量磁感应强度。

由于线圈体积大，指针式交流电压表等级低等原因，测量的误差较大。

近年来，在科研和工业中，集成霍耳传感器由于体积小，测量准确度高，易于移动和定位，所以被广泛应用于磁场测量。

例如：A SS 95型集成霍耳传感器就是一种高灵敏度的优质磁场传感器，它的体积小（面积mm mm 34⨯，厚mm 2），其内部具有放大器和剩余电压补偿电路，采用此集成霍耳传感器（配直流数字电压表）制成的高灵敏度毫特计，可以准确测量mT 000.20～的磁感应强度，其分辨率可达T 6101-⨯。

因此，用它探测载流线圈及亥姆霍兹线圈的磁场，准确度比用探测线圈高得多。

用高灵敏度集成霍耳传感器测量T T 35102101--⨯⨯～弱交、直流磁场的方法已在科研与工业中广泛应用。

本仪器采用先进的95A 型集成霍耳传感器作探测器,用直流电压表测量传感器输出电压,探测亥姆霍兹线圈产生的磁场,测量准确度比探测线圈优越得多,仪器装臵固定件牢靠，实验内容丰富。

本仪器经复旦大学物理实验教学中心使用,取得良好的教学效果。

二、原理(1)根据毕奥—萨伐尔定律，载流线圈在轴线（通过圆心并与线圈平面垂直的直线）上某点的磁感应强度为：I N x R R B ⋅+⋅=2/32220)(2μ （1）式中0μ为真空磁导率，R 为线圈的平均半径，x 为圆心到该点的距离，N 为线圈匝数，I 为通过线圈的电流强度。

因此，圆心处的磁感应强度0B 为：I N RB ⋅=200μ （2）轴线外的磁场分布计算公式较为复杂，这里简略。

(2)亥姆霍兹线圈是一对彼此平行且连通的共轴圆形线圈，两线圈内的电流方向一致，大小相同,线圈之间的距离d 正好等于圆形线圈的半径R 。

用亥姆霍兹线圈测磁场所谓亥姆霍兹线圈为两个相同线圈彼此平行且共轴，使线圈上通以同方向电流Ｉ，理论计算证明：线圈间距a 等于线圈半径R 时，两线圈合磁场在轴上（两线圈圆心连线）附近较大范围内是均匀的，如图5所示。

这种均匀磁场在工程运用和科学实验中应用十分广泛。

【实验目的】1、了解亥姆霍兹线圈的结构和工作原理；2、掌握载流圆线圈轴线上磁场的测量方法；3、掌握和亥姆霍兹线圈轴线上磁场的测量方法。

【实验仪器】亥姆霍兹线圈磁场实验仪。

实验仪由二部分组成，它们分别为励磁线圈架和磁场测量仪（见图 3，上部为励磁线圈架，下部为磁场测量仪），亥姆霍兹线圈架部分有一传感器盒，盒中装有用于测量磁场的感应线圈。

仪器参数：二个励磁线圈有效半径为105mm ，单个线圈匝数400匝，二线圈中心间距为105mm ；传感器盒横向移动范围250mm ，纵向移动范围70mm ，距离分辨率1mm ；传感器盒中探测线圈匝数为1000匝，旋转角度360o ； 【实验原理】一、载流圆线圈与亥姆霍兹线圈的磁场 1、 单个载流圆线圈磁场一半径为Ｒ，通以电流Ｉ的圆线圈，轴线上磁感应强度的计算公式为2/322200)(2X R IRN B +=μ （1）式中0N 为圆线圈的匝数，X 为轴上某一点到圆心O 的距离。

m H /10470-⨯=πμ。

轴线上磁场的分布如图2所示。

本实验取Ｎ０＝400匝，Ｒ＝105mm 。

当f=120Hz ，Ｉ＝60m Ａ（有效值）时，在圆心O 处x ＝0，可算得单个线圈的磁感应强度为：B=0.144mT 2、亥姆霍兹线圈设X 为亥姆霍兹线圈中轴线上某点离中心点O 处的距离，则亥姆霍兹线圈轴线上该点的磁感应强度为：}])2([])2({[212/3222/322200'---++++=X RR X R R IR N B μ （2） 而在亥姆霍兹线圈轴线上中心O 处，X =0，磁感应强度为：RIN RIN B O 002/300'7155.058μμ=⨯=（3）图1亥姆霍兹线圈磁场实验仪及接线方法架圈线仪量测图 2 单个圆环线圈磁场分布 图 3亥姆霍兹线圈磁场分布当实验取Ｎ０＝400匝，Ｒ＝105mm 。

亥姆霍兹线圈磁场实验——【ANSYS精】亥姆霍兹线圈是一种非常常见的磁场实验装置，其主要用于产生均匀的磁场。

本文将使用ANSYS软件进行亥姆霍兹线圈磁场实验的模拟，并进行结果分析。

1. 实验原理亥姆霍兹线圈是一种由两个同轴平行圆形线圈组成的装置，两个线圈的电流方向相反。

亥姆霍兹线圈的磁场是由两个线圈的磁场叠加而成的。

当两个线圈间的距离等于线圈半径的一半时，线圈中心的磁场是均匀的。

2. 实验建模2.1 建立几何模型首先，在ANSYS中建立一个几何模型。

我们可以通过几何建模工具创建一个直径为10cm的圆线圈。

然后，将该圆线圈复制一份，并旋转180度，使其与原始线圈同轴平行放置，且两个线圈电流方向相反。

最后，将两个线圈的距离设置为线圈半径的一半，即5cm。

2.2 设置材料属性在ANSYS中，我们需要为线圈设置合适的材料属性。

在本实验中，我们假设线圈是由纯铜制成的，因此在材料库中选择铜作为材料属性。

2.3 设置边界条件在实际的实验中，亥姆霍兹线圈是通过电源进行驱动的。

然而，在模拟实验中，我们需要为线圈设置边界条件，以模拟电源的驱动。

在本实验中，我们为线圈设置电流密度的边界条件，将其设置为2A/mm²。

同时，我们需要将线圈上表面设置为绝缘条件，以避免电流从线圈中逸出。

3. 实验分析在设置好几何模型、材料属性和边界条件之后，我们需要运行模拟并分析实验结果。

3.1 计算磁场强度在ANSYS中，我们可以使用磁场分析工具计算亥姆霍兹线圈中心的磁场强度。

在本实验中，我们假设线圈中的电流为2A，计算线圈中心的磁场强度分布。

根据分析结果，当线圈电流为2A时，亥姆霍兹线圈中心的磁场强度约为3.14mT。

这表明实验结果符合预期，即亥姆霍兹线圈能够产生一个均匀的磁场。

3.2 分析磁场分布我们也可以使用磁场分析工具来分析亥姆霍兹线圈中磁场的分布情况。

通过分析磁场分布，我们可以确定实验中可接受的偏差范围。

根据磁场分布分析结果，亥姆霍兹线圈中心附近的磁场强度分布非常均匀。

（5）
式中： EH 为霍尔电场强度，VH 为霍尔电势， l 为霍尔元件宽度。
当达到动态平衡时：
f L = − f E ， VB = VH / l
(6)
设霍尔元件宽度为 l ，厚度为 d，载流子浓度为 n，则霍尔元件的工作电流为
I S = neVld
(7)
由(6)、(7)两式可得：
VH
=
EH l
=
1 ne
图 6 DH4501A 型亥姆霍兹线圈磁场实验仪接线示意图 如果只是用二个线圈中的某一个产生磁场时，可选择左边或者右边的线圈，从测量仪的 励磁电流两端用两头都是插片的连接线接至测试架的励磁线圈两端．红接线柱与红接线柱相 连，黑接线柱与黑接线柱相连．用亥姆霍兹线圈(双个线圈)产生磁场时，将励磁线圈(左)的 黑色端子与励磁线圈(右)的红色端子用短接片短接。 亥姆霍兹线圈的中心设有二维移动装置，其中长的一个移动装置用于测量轴向的磁场分 布：短的一个移动装置用于测量径向磁场分布，如图 3 所示。慢慢转动手轮，移动装置上的 霍尔磁传感器盒随之移动，通过转动二个移动架的手轮，可将霍尔磁传感器移动到需要的位 置上。磁传感器的位置，也就是磁场的位置由相应的指示标尺确定。 3.高斯计的使用方法 仪器内置的磁场测量部分(高斯计)，它的测量范围为 O～2.200mT，采用 4 位数码管显示。 由于有地磁场和大楼建筑等的影响，当亥姆霍兹线圈没有电流流过时，显示值也不为零。 因此在进行亥姆霍兹线圈磁场测量实验时，需要对这个固定偏差值进行修正，即在数据处理 中扣除这个初始偏差值，否则的话，测量出的值是在线圈产生的磁场上面叠加上了一个偏差 值，会引起较大的测量误差。为此测量仪内，设计有一个零位偏差值白动修正电路，能将这 个偏差值记忆在仪器中，自动补偿地磁场引起的固定偏差值。具体使用方法如下： 将测量仪与测试架连线如图 6 所示连好。打开电源，将测量仪的励磁电流电位器逆时针 旋到底，电流表显示为零，线圈没有产生磁场。但这时由于存在地磁场，以及内部电路的失 调电压，毫特计的显示往往不为 O。预热 10～20 分钟后，按下测量仪面板上的“零位凋节” 按钮，直到数码管上的显示从 llll 变到 3333 再放开按钮。这个过程大约需要 2 秒。此时毫 特表头应显示 0，如果没有到零，请重复上述过程。 调零完毕后，即可进入正常亥姆霍兹线圈磁场测量过程。 （五）实验内容及数据处理 1.实验内容 （1）测量圆电流线圈轴线上磁场的分布

开放性实验实验报告——亥姆霍兹线圈磁场测定姓名学号班级亥姆霍兹线圈是一对相同的、共轴的、彼此平行的各有N匝的圆环电流。

当它们的间距正好等于其圆环半径R时，称这对圆线圈为亥姆霍兹线圈。

在亥姆霍兹线圈的两个圆电流之间的磁场比较均匀。

在生产和科研中经常要把样品放在均匀磁场中作测试，利用亥姆霍兹线圈是获得一种均匀磁场的比较方便的方法。

一、实验目的1. 熟悉霍尔效应法测量磁场的原理。

2. 学会亥姆霍兹磁场实验仪的使用方法。

3. 测量圆线圈和亥姆霍兹线圈上的磁场分布，并验证磁场的叠加原理二、实验原理同学们注意，根据自己的理解，适当增减，不要太多，有了重点就可以了。

1．霍尔器件测量磁场的原理图3—8—1 霍尔效应原理如图3—8—1所示，有－N型半导体材料制成的霍尔传感器，长为L，宽为b，厚为d，其四个侧面各焊有一个电极1、2、3、4。

将其放在如图所示的垂直磁场中，沿3、4两个侧面通以电流I，电流密度为J，则电子将沿负J方向以速度运动，此电子将受到垂直方向磁场B的洛仑兹力作用，造成电子在半导体薄片的1测积累过量的负电荷，2侧积累过量的正电荷。

因此在薄片中产生了由2侧指向1侧的电场，该电场对电子的作用力，与反向，当两种力相平衡时，便出现稳定状态，1、2两侧面将建立起稳定的电压，此种效应为霍尔效应，由此而产生的电压叫霍尔电压，1、2端输出的霍尔电压可由数显电压表测量并显示出来。

如果半导体中电流I是稳定而均匀的，则电流密度J的大小为（3—8—1）式中b为矩形导体的宽，d为其厚度，则bd为半导体垂直于电流方向的截面积。

如果半导体所在范围内，磁场B也是均匀的，则霍耳电场也是均匀的，大小为（3—8—2）霍耳电场使电子受到一与洛仑兹力F m相反的电场力F e，将阻止电子继续迁移，随着电荷积累的增加，霍耳电场的电场力也增大，当达到一定程度时，F m与F e大小相等，电荷积累达到动态平衡，形成稳定的霍耳电压，这时根据F m=F e有（3—8—3）将（3—8—2）式代入（3—8—3）式得（3—8—4）式中、容易测量，但电子速度难测，为此将变成与I有关的参数。

亥姆霍兹线圈磁场测定实验一、实验目的：1. 掌握霍尔效应原理测量磁场；2. 测量单个载流圆线圈和亥姆霍兹线圈轴线上的磁场分布；3. 验证磁场叠加原理。

二、实验仪器与器件亥姆霍兹线圈磁场测定仪一套，导线若干，霍尔元件传感器。

三、实验原理：根据毕奥—萨伐尔定律，单个载流线圈在轴线（通过圆心并与线圈平面垂直的直线）上某点的磁感应强度为：20223/22()R B N I R x μ⋅=⋅+式中0μ为真空磁导率，R 为线圈的平均半径，x 为轴线上圆心到该点的距离，N 为线圈匝数，I 为通过线圈的电流强度。

因此，圆心处的磁感应强度0B 为：亥姆霍兹线圈因德国物理学者赫尔曼·冯·亥姆霍兹而命名，是一对彼此平行且连通的共轴圆形线圈，两线圈内的电流方向一致，大小相同，线圈之间的距离d 正好等于圆形线圈的半径R 。

这种线圈的特点是能在 附近产生小范围区域均匀磁场，由于亥姆霍兹线圈具有开敞性质，很容易地可以将其它仪器置入或移出，也可以直接做视觉观察，所以，是物理实验常使用的器件。

设z 为亥姆霍兹线圈中轴线上某点离中心点O （如图1）处的距离，则亥姆霍兹线圈轴线上任意一点的磁感应强度为：⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-++⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛++⋅⋅⋅='--2/3222/322202221z R R z R R R I N B μ图1 亥姆霍兹线圈示意图由上式可知，在亥姆霍兹线圈上中心O 处（0z =）的磁感应强度'0B 为：R I N B ⋅⋅='02/3058μ四、实验内容：1. 测量单个载流圆线圈轴线上各点磁感应强度（实验装置如图2）：图2 实验装置如图2，选定其中一个线圈为载流线圈a ，测其轴线上不同位置磁感应强度B (a )的测量结果填写至表1，并与相应的理论值作比较。

要求电流I =100mA ，已知线圈平均半径10.00R cm =，线圈匝数N =500，真空磁导率70410/T m A μπ-=⨯⋅。

实验四十三亥姆霍兹线圈的磁场测量资料讲解
本实验旨在通过测量亥姆霍兹线圈的磁场，研究亥姆霍兹线圈的工作原理和磁场分布
规律。

亥姆霍兹线圈由两个相等的同向螺线管组成，它们刚好射线方向的中心轴上，并能
通过电源供电。

当两个螺线管通以相等的电流时，它们合成的磁场沿轴心方向，大小均匀，且磁感应强度与轴心距的平方成正比。

实验采用的仪器设备有亥姆霍兹线圈、直流电源、数字万用表、磁场探头等。

在进行
实验前，首先需要将亥姆霍兹线圈的内外半径、匝数等参数测量并记录好；同时将磁场探
头垂直于轴心放置，并用数字万用表检查并记录好其灵敏度。

实验步骤如下：
1.按照实验要求，调节电源电压和电流并用数字万用表确认电流大小。

2.将磁场探头沿轴心线移动测量磁感应强度，每次移动固定距离并记录数据。

3.移动磁场探头到亥姆霍兹线圈轴心上方一定距离处，测量此处的磁感应强度。

4.分别测量单个螺线管通电时的磁感应强度，并与两个螺线管通电时的磁感应强度进
行比较。

在进行实验测量时，需要注意以下几点：
1.在每组测量数据前，需要将电源电压和电流调至零并等待一段时间，确保仪器处于
稳态。

2.在移动磁场探头时，应该保持探头位置和朝向的一致性，并确保探头的垂直方向与
轴心平行。

3.每组数据的测量应该重复多次，并求取平均值以提高测量精度。

本实验测量到的结果可为今后深入研究电磁现象和应用提供基础数据和理论依据，对
于提高学生的实验能力和科学素养也具有一定的指导意义。