运筹学图与网络
- 格式:doc
- 大小:1.46 MB
- 文档页数:10









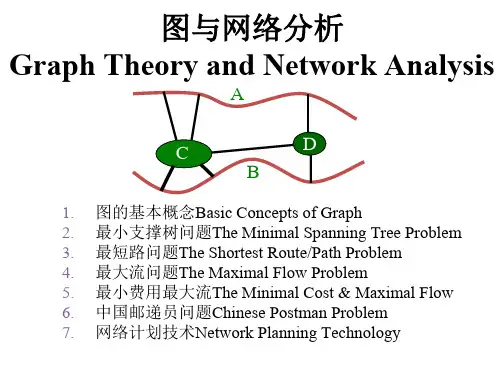
第二节 最大流和最小割一、割若S 为V 的一个子集,S y S V S S x ∈-=∈,,,记),(S S K =为起点在S 中,终点在S 中的全体有向边的集合,即{}S v S u v u K ∈∈=,),( (11-4)我们称边集),(S S K =为网络G 的一个割,称∑∈Ke e C )(为K 的容量,记为Cap K 。
例5 给运输网络如图11-8所示,试求与给定的j S (j =1,2,3)相对应的Cap j K 。
解取{}11,v x S =,{}),(),,(),,(221311v x v v v v K =,Cap 1K =10+6+9=25。
图11-8 取 {}4212,,,v v v x S =,{}),(),,(),,(5254312v v v v v v K =, Cap 2K =10+6+13=29。
取 {}54213,,,,v v v v x S =, {}),(),,(5313y v v v K =, Cap 3K =10+10=20。
可见,若把割K 的边全从G 中移去,G -K 不一定分离成两部份(如例5中,3K G -仍为一个连通图),但是它一定把G 的全部自源x 到汇y 的路断开,也就是说此时流不能在G 上发生。
故从直观上不难理解,G 的任一流f 的流值Val f 不能超过任一割的容量。
二、最大流与最小割 若∙f 为满足下列条件的流:Val ∙f ={}的一个流为G f Valf max , (11-5)则称∙f 为G 的最大流。
若∙K 为满足下列条件的割。
Cap ∙K ={}的一个割为G K K Cap min , (11-6) 则称∙K 为G 的最小割。
例1 这个运输问题,就是一个在图11-6中求x 至y 的最大流问题。
对此,我们不难建立线性规划模型来求出最优解。
但由于网络模型结构的特殊性,我们可以建立有效的求最大流的算法,且求出的最优解是一个整数解。
定理1 对于G 中任一流f 和任一割),(S S K =,有Val )()(s f S f f -+-=其中,∑∈+=),()()(S S e e f S f ,∑∈-=),()()(S S e e f S f例如,在图11-7中,取{}11,,v x x S =,则{}),(),,(),,(),,(),,(),(221412121x x x x v v v v v x S S = {}),(),(12v x S S =4815510315)(=++++=+S f8)(=-S f可见,Val )()(40S f S f f -+-==定理1说明,通过G 的任一横截面的净流值都为Val f ,亦即Val f 为任一横截面的输出量与输入量的代数和。
若f 为G 上一个流,对任E e ∈,若)()(e C e f =,称边e 为f 饱和边;若)(e f <)(e C ,称边e 为f 不饱和边;若)(e f >0,称边e 为f 正边;若)(e f =0,称e 为f 零边。
定理2 对于G 上任一流f 和任一割),(S S K =,有 1.Val f ≤Cap K ;2.Val f =Cap K 的充要条件为:任),(S S e ∈,边e 为f 饱和边;任),(S S e ∈,边e 为f 零边。
证 1.∑∈+=),()()(S S e e f S f ≤∑∈=Ke CapK e C )(又 )(S f -≥0,故 Val )()(S f S f f -+-=≤)(S f +≤Cap K2.Val ∑∑∈∈-+-=-=),(),()()()()(S S e S S e e f e f S f S f f ≤Cap K =∑∈),()(S S e e C注意到)(e f ≤)(e C ,故要使Val =f Cap K ,当且仅当任),(S S e ∈,有)()(e C e f =,任),(S S e ∈,有)(e f =0。
本定理说明,若f 为G 的一个最大流,K 为G 的最小割,则必有Val f ≤Cap K 。
定理3 设f 为G 的一个流,而K 是一个割,且Val f = Cap K ,则f 为G 的最大流,而K 是一个最小割。
证 设∙f 是G 的最大流,∙K 是G 的最小割,则Val f ≤Val ∙f ,Cap ∙K ≤Cap K 。
而由定理2知:Val ∙f ≤Cap ∙K 。
现在Val f = Cap K ,故有Val f =Val ∙f =Cap ∙K =Cap K 。
即得f 为最大流,K 为最小割。
三、增流链设t uv x Q =为G 的一条初等链,若G 中有u 到v 的有向边),(v u ,称边),(v u 为Q 的前向边;若G 中有v 到u 的有向边),(u v ,称边),(u v 为Q 的后向边。
例如图11-8中,取312v v xv Q =,则边),(),,(312v v v x 为Q 的前向边,边),(21v v 为Q 的后向边。
若f 为G 上的流,对)(Q E e ∈,令:⎩⎨⎧-=,Q e e f ,Q e e f e C e l 的一条后向边是当的一条前向边是当)()()()( (11-7))(min )(e l Q l Qe ∈= (11-8)当0)(=Q l ,称Q 为f 饱和链;当)(Q l >0,称Q 为f 不饱和链。
例6 对图11-8给一个流f 如图11-9图11-9取43121v v v xv Q =,边),(2v x ,),(31v v 和),(43v v 为1Q 的前向边,2),(2=v x l ,0),(31=v v l ,2),(43=v v l ;边),(21v v 为1Q 的后向边,0),(21=v v l ,故0)(1=Q l ,1Q 为f 饱和链。
取y v v v xv Q 34522=,边),(2v x ,),(52v v 和),(3y v 为2Q 的前向边,2),(2=v x l ,6),(52=v v l ,),(3y v l =6;边),(54v v 和),(43v v 为2Q 的后向边,若Q 为f 不饱和链,则Q 的前向边都为f 不饱和边,后向边全为f 正边。
一条从源x 至汇y 的f 不饱和链,称为f 增流链。
例如图11-9中,就是一条f 增流链。
若网络G 中存在一条f 增流链,我们可得G 上一个新流f ˆ:⎪⎩⎪⎨⎧-+=其它的后向边是当的前向边是当)()()()()()(ˆe f Q e Q l e f Q e Q l e f e f (11-9)此时Val f ˆ=Val f +)(Q l 。
我们称f ˆ为f 基于Q 的修改流。
对于f ˆ而言,Q 中至少有一条前向边为f ˆ饱和边,或至少有一条后向边是f ˆ零边,即Q 是f ˆ饱和链。
如图11-9,可得f 基于y v v v xv Q 3452=的修改流f ˆ如图11-10。
图11-10四、最大流最小割定理定理4 流f 为G 的最大流的充要条件为G 中不存在f 增流链。
证 必要性:反之,若G 中存在f 增流链Q ,)(Q l >0,则可得f 基于Q 的修改流f ˆ,Val f ˆ=Val f +)(Q l >Val f 。
矛盾,故G 中不存在f 增流链。
充分性:令{G v S =中存在一条f 不饱和链}v x Q =,且定义S x ∈。
由设知,S y ∈,故),(S S K =为G 的一个割,它具有如下特点:若边K u u e ∈=),(21,则e 为一条f 饱和边;若),(),(12S S u u e ∈=,则e 为一条f 零边。
反之,若K u u e ∈=),(21,而e 为一条f 不饱和边,因S u ∈1,故存在一条f 不饱和链1u x Q =,则21u u x 也为f 不饱和链,从而S u ∈2,但S u ∈2,矛盾。
若),(),(12S S u u e ∈=,e 为一条f 正边,因S u ∈1,故存在一条f 不饱和链1u x ,则21u u x 也为f 不饱和链,边),(12u u 为其后向边,故S u ∈2,但S u ∈2,矛盾。
由定理2知,Val f =Cap K ;由定理3知,f 为G 的最大流(同时,K 为最小割)。
由定理4的充分性证明,我们可得最大流最小割定理: 定理5 在运输网络中,最大流的流值等于最小割的容量。
第三节 最大流算法一、算法思想定理4为我们提供了寻求运输网络中最大流的一个方法。
若给网络G 上一个初始流f (例如平凡流),我们判别一下G 中有无f 增流链,若无f 增流链,则f 即为最大流;若有f 增流链Q ,可得f 基于Q 的修改流f ˆ,Val f ˆ=Val f +)(Q l ,再将f ˆ视为f ,继续迭代。
但是,到此时算法还不能说已经建立成功了,因为如何寻求f 的增流链这个问题还没有解决,故下面我们先讨论寻求f 增流链的方法,然后建立求最大流的算法。
我们采用标号的方法来寻找x 至y 的增流链。
若f 为网络G 的一个流,G 中满足下列条件的树T 称为以x 为根的f 不饱和树(边是带有方向的)。
1.)(T V x ∈;2.任)(T V v ∈,x v ≠。
T 内有唯一的一条初等链v x Q v =为f 不饱和链)(v Q l >0。
每个点)(T V v ∈,都按下述方法给以标记: 若T 中x 至v 的初等链uv x Q v =:(1)如果边),(v u 为G 中的边,则给v 以标号))(,,(v l u +,其中第一个标号u 表明在v Q 中v 的前驱点为u ,第二个标号表明),(v u 在v Q 中为前向边,第三个标号)()(v Q l v l =()(v Q l 由式(11-8)给出)。
显然{}),(),(),(m in )(v u f v u C u l v l -= (11-10)(2)如果),(u v 为G 中的边,则给v 以标号))(,,(v l g u ,其中第一个标号u 表明在v Q 中v 的前驱点为u ,第二个标号表明),(u v 在v Q 中为后向边,第三个标号)()(v Q l v l =。
显然,此时{}),(),(m in )(u v f u l v l = (11-11)例如,图11-11为图11-9的一棵f 不饱和树。
我们通过以x 为根的f 不饱和树T 的不断“生长”以及“标记法”来探寻G 中f 增流链。
初始时,先给x 以标号),,0(∞+。
图11-11一般地,若已得x 为根的f 不饱和树T (如图11-11),T 中每个点都有标号,而)(T V y ∈,可将)(T V S =中点分成两部份:一部份点已查视过,即已生长了枝的点(例如图11-11中的点x ,2v 和5v ),或判定不能生长枝的点(如图11-11中的点1v );另一部份点未查视过(如图11-11中的点4v ),我们将T 中全部未查视过的点记为A (A 为有顺序的集合,先标记的点排在前,这是由于本算法的特点为:先标记的点先查视,即先生长枝)。