小方块涂色问题

29涂色问题涂色问题是数学竞赛中较为典型的问题，可以直接用抽屉原则解决涂色问题。

另一方面，也可以将别的有关问题“涂色”，转化为涂色问题，涂色问题本身，有其深刻的数学背景。

有些问题，本来就属于图论的内容。

有些问题的解决，则需要用到数论、组合数学的理论和方法。

这里介绍，只是中学数学竞赛中的有关问题。

1．小方格染色问题最简单的染色问题是从一种民间游戏中发展起来的方格盘上的染色问题.解决这类问题的方法后来又发展成为解决方格盘铺盖问题的重要技巧.2．线段染色和点染色(1)线段染色.较常见的一类染色问题是发样子组合数学中图论知识的所谓“边染色”（或称“线段染色”），主要借助抽屉原则求解.（2）点染色.先看离散的有限个点的情况.例题讲解1．把正方形ABCD的一边AB分成n段，使奇数号的线段长度之和等于偶数号的线段长度之和（如图01—01）。

过各分点作平行于AD的线段，得到n个矩形。

每一个矩形又被对角线BD分成两部分。

将奇数号矩形左部及偶数号矩形的右部涂上同一颜色。

证明：在对角线BD两侧的有同色的部分，其面积和相等。

2．在一张无限方格纸的某些方格上涂上红色，其余方格涂上蓝色，每一个2×3的六方格矩形内恰好2个红方格。

试问：一个9×11的99方格矩形内包含多少个红方格？3．在n×n（n≥2）个方格的正方形表中，有n－1个格子里涂了色，求证：通过交换两行或两列的位置，总可以将所有涂色的方格移到正方形表的左上角顶点到右下角顶点的对角线下方。

4．有n×n（n≥3）个方格表中，先在表中任意选出n－1个方格都涂成黑色，然后将那些凡是至少与两个已涂色的方格相邻的方格也都涂黑色。

求证：不论怎样选择最初的n－1个方格，都不能按这样的法则，将表中的所有方格全涂黑。

5．设ABC为正三角形，E为线段BC，CA，AB上点的集合（包括A，B，C在内）。

将E分成两个子集，求证：总有一个子集中含有一个直角三角形的顶点。

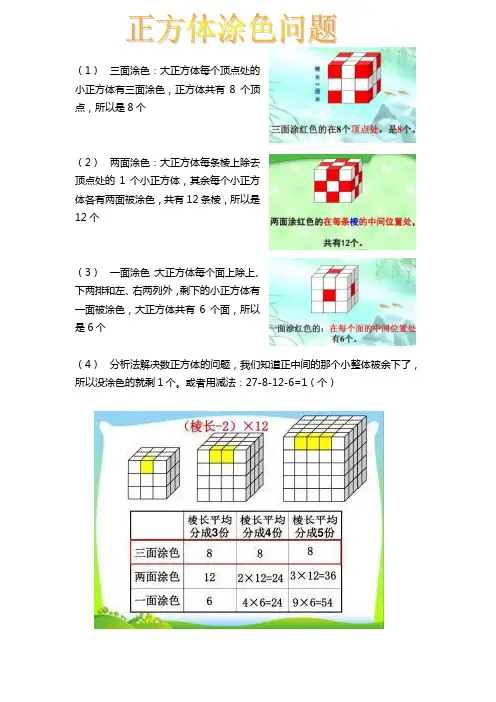
（1）三面涂色：大正方体每个顶点处的
小正方体有三面涂色，正方体共有8个顶
点，所以是8个
（2）两面涂色：大正方体每条棱上除去
顶点处的1个小正方体，其余每个小正方
体各有两面被涂色，共有12条棱，所以是
12个
（3）一面涂色：大正方体每个面上除上、
下两排和左、右两列外，剩下的小正方体有
一面被涂色，大正方体共有6个面，所以
是6个
（4）分析法解决数正方体的问题，我们知道正中间的那个小整体被余下了，所以没涂色的就剩1个。

或者用减法：27-8-12-6=1（个）
正方体涂色专项练习
【练习1】
如图是用27个小正方体拼成的一个大正方体，把它的
表面都涂成红色
请你数一数，算一算：每条棱上3个小正方体，a=3
（1）三面涂成红色的小正方体有（8）块；
（2）两面涂成红色的小正方体有（12）块；
（3）一面涂成红色的小正方体有（6）块；
（4）没有涂成红色的小正方体有（1）块。

【方法总结】
用若干个小正方体拼成一个大正方体，并将拼成的大正方体的表面涂色。

如果大正方体的每条棱上有a个小正方体，则
三面涂色的小正方体在顶点处，共有8 个；
两面涂色的小正方体在棱上，共有[(a-2)×12] 个；
一面涂色的小正方体在面上，共有[(a-2)×(a-2)×6] 个。

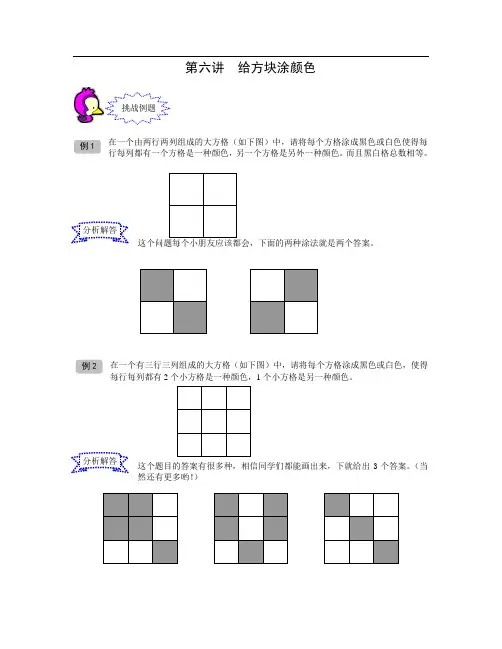
第六讲 给方块涂颜色在一个由两行两列组成的大方格（如下图）中，请将每个方格涂成黑色或白色使得每行每列都有一个方格是一种颜色，另一个方格是另外一种颜色。

而且黑白格总数相等。

在一个有三行三列组成的大方格（如下图）中，请将每个方格涂成黑色或白色，使得每行每列都有2个小方格是一种颜色，1个小方格是另一种颜色。

这个题目的答案有很多种，相信同学们都能画出来，下就给出3个答案。

（当然还有更多哟！）在一个有4行4（1） 每行每列都有2个方格是一种颜色，另2个方格是另一种颜色。

（2） 每行每列都有3个方格是一种颜色，另一个方格是另一种颜色。

对于（1）并不难想出一些符合要求的解答来，例如下面的4个图形就满足要求。

对于（2）最容易想到的是下面的涂法：下面我们采用“调整”的方法，将右下角的一个小黑格与前面3列中的任意一列左右平移对调，就可以得到一种新的满足要求的涂法：类似的小黑格与第2列、第1列左右对调，就得到如下另外两种合乎要求的涂法：若回到（2）的第一个涂法，右下角的小黑格与前3行做上下平移对调，又可得到三种新的涂法。

在4×4的正方形方格纸中，将小方格涂上黑白两种颜色，得到两种不同的染色图。

如果将图上任意一横行或任意一竖行的四格全部改变颜色（黑格变白格，白格变成黑格），我们称之为一个交换。

能否经过若干次变换将A 图变成B 图？A B不能。

在一次变换中是将一横行或一竖行的四格全部改变颜色，所以变换前黑格如果是单数个，变换后黑格仍然是单数个；变换前黑格如果是双数个，变换后黑格仍是双数个。

白格也是如此。

在A 图与B 图的左下角2×2方格中，A 图的黑白格各2个，都是双数，无论经过多少次变换，变换后黑白格的个数仍都是双数，而B 图中黑白格的个数是3白1黑，所以A 图不能通过变换成为B图。

在8×8方格棋盘中，去掉左上角和右上角的小方格，剩下的62个方格能不能用31个1×2的“日”型覆盖？不能。

五年级下《表面涂色的正方体》在五年级的数学学习中，我们会遇到一个有趣且富有挑战性的问题——表面涂色的正方体。

这个问题看似简单，却蕴含着丰富的数学知识和思维方法。

首先，让我们来思考一下什么是表面涂色的正方体。

想象一下，有一个正方体的木块，我们在它的表面涂上颜色。

那么，这个被涂色的正方体就成为了我们研究的对象。

当我们面对一个表面涂色的正方体时，第一个要探究的问题就是：不同位置的小正方体的涂色情况是怎样的？为了更好地理解，我们不妨从最简单的情况开始。

假设这个正方体的棱长为 3。

那么，这个正方体一共由 27 个小正方体组成。

位于正方体顶点处的小正方体，它们是三面涂色的。

因为顶点处的小正方体同时属于三个面，所以有三个面被涂上了颜色。

正方体一共有 8 个顶点，所以就有 8 个三面涂色的小正方体。

接下来，看看正方体棱上的小正方体。

它们是两面涂色的。

每条棱上除去顶点处的两个小正方体，中间部分的小正方体就是两面涂色的。

正方体有 12 条棱，每条棱上有 1 个两面涂色的小正方体，所以一共有12 个两面涂色的小正方体。

再看正方体每个面中间部分的小正方体，它们是一面涂色的。

每个面上除去棱上的小正方体，中间部分的就是一面涂色的。

一个面上有 1 个一面涂色的小正方体，正方体有 6 个面，所以一共有 6 个一面涂色的小正方体。

最后，位于正方体内部的小正方体，它们没有被涂色。

通过对这个棱长为 3 的正方体的分析，我们可以总结出一些规律。

当正方体的棱长为 n 时，三面涂色的小正方体永远有 8 个，因为正方体的顶点数量不变。

两面涂色的小正方体数量为 12×（n 2) 个。

一面涂色的小正方体数量为 6×（n 2)²个。

而没有涂色的小正方体数量则为（n 2)³个。

了解了这些规律，我们就可以解决很多与表面涂色的正方体相关的问题。

比如，有一个棱长为 5 的表面涂色的正方体，问三面、两面、一面涂色以及没有涂色的小正方体各有多少个？根据我们总结的规律，三面涂色的小正方体有 8 个。

方格涂色计数的规则
嘿，朋友！今天咱来说说方格涂色计数这超有趣的事儿呀！
想象一下，你面前有一张大大的方格纸，就像一个充满无限可能的神秘世界。

（这不就像我们的人生嘛，有那么多选择和可能性等待着我们去发掘！）每个方格都等着被你涂上颜色呢！
规则其实很简单啦。

比如说，一个 2x2 的方格，你可以选择用一种颜色涂满它，这很容易理解吧？但如果变成 3x3 的方格呢？（哎呀，这可就有点挑战性了吧！）你就得好好思考下怎么涂啦。

我们假设方格的颜色只有红色和蓝色两种，那这其中的变化可就多了去了！你可以把四个角涂成红色，中间涂蓝色，或者反过来呀。

（这是不是就像我们搭配衣服，不同的组合会有不同的效果呢！）又或者一部分方格涂红色，一部分涂蓝色，排列组合超多的！
再复杂一点，假设是个 4x4 的方格，哇，那简直就是色彩的狂欢节呀！（你能想象那得有多少种涂法吗？）而且，你还可以自己设定规则，比如每行每列不能有相同颜色的方格相邻，那可就更刺激啦！
两个人一起玩就更有意思了。

比如说你和你的小伙伴一起比赛，看谁在规定时间内想出的涂法更多。

（嘿，这时候可就得拼脑子啦！）然后互相展示、交流，说不定还能碰撞出更多新点子呢。

在方格涂色计数里，你可以尽情发挥你的想象力和创造力，没有什么是不可能的！就像我们的生活，充满着惊喜和未知，只要你敢去尝试，就会发现无数的精彩。

所以呀，方格涂色计数绝对是个能让你沉浸其中、乐此不疲的好玩意儿呀！
我的观点就是：方格涂色计数简单又有趣，还能锻炼我们的思维能力，真的非常值得一试哦！。

生活趣味数学题：涂色的正方体一个棱长1分米的正方体木块，表面涂满了红色，把它切成棱长1厘米的小正方体。

在这些小正方体中：（1）三个面涂有红色的有多少个？（2）两个面涂有红色的有多少个？（3）一个面涂有红色的有多少个？（4）六个面都没有涂色的有多少个？下面我们结合图示，分别来看看这几个问题。

（1）三个面都涂有红色的小正方体在大正方体的顶点处，正方体有8个顶点，所以三个面涂有红色的有8个。

（2）两个面都涂有红色的小正方体在大正方体的棱上，每条棱上有8个，正方体有12条棱，所以两个面涂有红色的有8×12=96个。

（3）一个面都涂有红色的小正方体在大正方体的面上，每个面上有8×8=64个，正方体有6个面，所以一个面涂有红色的有8×8×6=3 84个。

(4)六个面都没有涂色的在大正方体的中间，有两种算法：1. 1000－8－96－384=512（个）；2. 8×8×8=512（个）。

注意正方体有8个顶点、12条棱、6个面假设把棱n等分（n≥3），那么:N的三次方个小立方体组成的立方体的表面图涂上颜色, 则未被涂色的小立方体有(n-2)的三次方个.则一面被涂色的小立方体为(n-2)*(n-2)*6两面被涂色的小立方体有(n-2)*12三面被涂色的有8长方体, 有a*b*c个立方体组成的长方体表面涂上颜色.则未被涂色的小立方体有(a-2)*(b-2)*(c-2)个一面被涂色的小立方体有(a-2)* (b-2)*2+(b-2)* (c-2)*2+(c-2)* (a-2)*2两面被涂色的小立方体有(a-2)*4+(b-2)*4+(c-2)*4三面被涂色的有8个选择是难，更何况是心灵选择。

高渐离为了荆轲，他选择了死；马本斋母亲为了革命，她选择了牺牲；祝英台为了真挚爱情，她选择了化蝶。

在这友情、亲情与爱情之间选择，他们是这样做。