第6讲 二次函数几何综合(1)(教师版)
- 格式:pdf
- 大小:8.15 MB
- 文档页数:28

二次函数(h ánsh ù)与几何(j ǐ h é)综合典题题例1.已知抛物线的顶点(d ǐngdi ǎn)坐标为(3,-2),且与轴两交点(ji āodi ǎn)间的距离为4,求其解析(ji ě x ī)式。
例2.已知二次函数)0(2≠++=a c bx ax y 的图像与x 轴交于不同的两点A 、B ,点A 在点B 的左边,与轴交于点C ,若△AOC 与△BOC 的面积之和为6,且这个二次函数的图像的顶点坐标为(2,-a ),求这个二次函数的解析式。
例3.已知二次函数)0(2≠++=a c bx ax y 的图像过点E (2,3),对称轴为x =1,它的图像与x 轴交于两点A 。
(1)求二次函数的解析式;(2)在(1)中抛物线上是否存在点P ,使△POA 的面积等于△EOB 的面积?若存在,求出P 点的坐标;若不存在,说明理由。
例4.如图,抛物线)0(2≠++=a c bx ax y 与x 轴、轴分别相交于A (-1,0)、B (3,0)、C(0,3)三点,其顶点为D 。
(1)求经过A 、B 、C 三点的抛物线的解析式; (2)求四边形ABDC 的面积;(3)试判断△BCD与△COA是否相似?若相似写出证明过程;若不相似请说明理由。
例5:如图,已知抛物线的图像(tú xiànɡ)与X轴交于A、C两点。
l的解析(jiě xī)式;(1)若抛物线与关于(guānyú)x轴对称,求2l上一动(yīdòng)点(B不与A,C重合(chónghé)),以(2)若点B是抛物线1AC为对角线,A,B,C三点为顶点的平行四边形的第四个顶点记为D,求l上;证:点D在2l在x轴上、下两部分的图像上时,平行四边形(3)探索:当点B分别位于1ABCD的面积是否存在最大值或最小值?若存在,判断它们是何种特殊平行四边形并求出它的面积;若不存在,请说明理由。
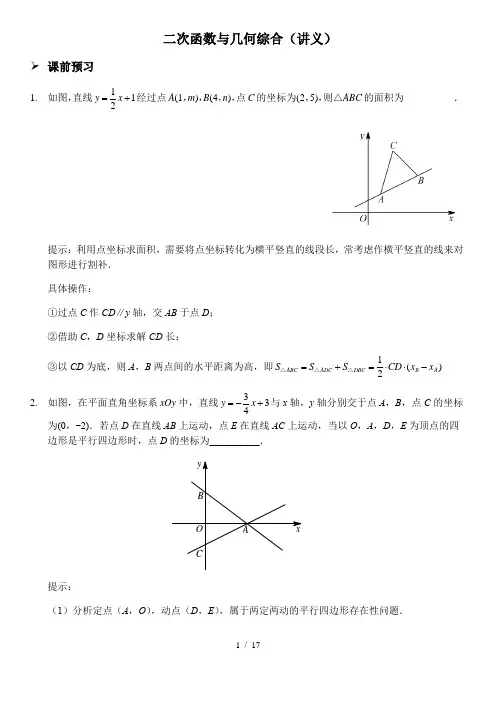
二次函数与几何综合(讲义)➢ 课前预习1. 如图,直线112y x =+经过点A (1,m ),B (4,n ),点C 的坐标为(2,5),则△ABC 的面积为__________.提示:利用点坐标求面积,需要将点坐标转化为横平竖直的线段长,常考虑作横平竖直的线来对图形进行割补. 具体操作:①过点C 作CD ∥y 轴,交AB 于点D ; ②借助C ,D 坐标求解CD 长;③以CD 为底,则A ,B 两点间的水平距离为高,即1()2ABC ADC DBC B A S S S CD x x =+=⋅⋅-△△△2. 如图,在平面直角坐标系xOy 中,直线334y x =-+与x 轴,y 轴分别交于点A ,B ,点C 的坐标为(0,-2).若点D 在直线AB 上运动,点E 在直线AC 上运动,当以O ,A ,D ,E 为顶点的四边形是平行四边形时,点D 的坐标为__________.y xCB AO提示:(1)分析定点(A ,O ),动点(D ,E ),属于两定两动的平行四边形存在性问题.(2)连接两定点得定线段,考虑:①若定线段作为平行四边形的边,则通过平移确定点的坐标;②若定线段作为平行四边形的对角线,则绕定线段中点旋转,利用中点坐标公式确定点的坐标. (3)利用函数特征和几何特征求解后,结合图形进行验证.➢ 知识点睛1. “函数与几何综合”问题的处理原则:_________________,_____________________. 2. 研究背景图形:①研究函数表达式.二次函数关注____________,一次函数关注__________.②___________________________.找特殊图形、特殊位置关系,寻求边长和角度信息. 3. 二次函数之面积问题的常见模型①割补法——铅垂法求面积:1()2APB B A S PM x x =⋅⋅-△ 1()2APB B A S PM x x =⋅⋅-△②转化法——借助平行线转化:若S △ABP =S △ABQ ,若S △ABP =S △ABQ , 当P ,Q 在AB 同侧时, 当P ,Q 在AB 异侧时, PQ ∥AB .AB 平分PQ .➢ 精讲精练1. 如图,抛物线y =-x 2+2x +3经过A ,B ,C 三点.点M 是直线BC 上方抛物线上的点(不与B ,C 重合),过点M 作MN ∥y 轴交线段BC 于点N ,连接MB ,MC .(1)若设点M 的横坐标为m ,四边形OBMC 的面积为S ,则S 与m 的函数关系式为________________.(2)四边形OBMC 的最大面积为________,此时点M 的坐标为____________.2.如图,在平面直角坐标系中,抛物线y=-x2+2x+3经过A,B,C三点,点D的坐标为(0,1),直线AD与抛物线交于另一点E.(1)若M是直线AD上方抛物线上的一个动点,则△AME面积的最大值为__________.=6时,点G的坐标为_______________.(2)在直线AD下方的抛物线上有一动点G,当S△AEG3.如图,已知抛物线y=ax2-2ax-b(a>0)与x轴交于A,B两点,点A在点B的右侧,且点B的坐标为(-1,0),与y轴的负半轴交于点C,顶点为D.连接AC,CD,∠ACD=90°.(1)直接写出抛物线的解析式;(2)若点M在抛物线上,且以点M,A,C以及另一点N为顶点的平行四边形ACNM的面积为12,设M的横坐标为m,求m的值.4.如图,已知二次函数y=x2-3x-4的图象与x轴交于点A,B,且经过点C(2,-6),连接AC,二次函数图象的对称轴记为l.(1)点D(m,n)(-1<m<2)是二次函数图象上一动点,当△ACD关于l的对称点为E,求点E的坐标.(2)在(1)的条件下,能否在二次函数图象和直线l上分别找到点P,Q,使得以点D,E,P,Q为顶点的四边形为平行四边形.若能,求出点P的坐标;若不能,请说明理由.5. 如图,抛物线y =ax 2-5ax+4(a <0)经过△ABC 的三个顶点,已知BC ∥x 轴,点A 在x 轴上,点C 在y 轴上,且AC =BC . (1)求抛物线的解析式;(2)已知点D 在抛物线对称轴上,点E 在抛物线上,且以A ,B ,D ,E 为顶点的四边形是平行四边形,求点E 的坐标;(3)已知点F 是抛物线上的动点,点G 是直线y =-x 上的动点,且以O ,C ,F ,G 为顶点的四边形是平行四边形,求点G 的横坐标.【参考答案】➢课前预习1.9 22.1126 () 55D,,2286 () 55D,➢知识点睛1.利用横平竖直的线段长,函数特征与几何特征互转2.①四点一线;k,b②坐标转线段长➢精讲精练(2)(3,0)或(-2,-5)3.(1)y=x2-2x-3;(2)m=4或m=-1.二次函数与几何综合(习题)➢例题示范例1:如图,抛物线y=ax2+2ax-3a与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,且OA=OC,连接AC.(1)求抛物线的解析式.(2)若点P是直线AC下方抛物线上一动点,求△ACP面积的最大值.(3)若点E在抛物线的对称轴上,抛物线上是否存在点F,使以A,B,E,F为顶点的四边形是平行四边形?若存在,求出所有满足条件的点F的坐标;若不存在,请说明理由.第一问:研究背景图形【思路分析】读题标注,注意到题中给出的表达式中各项系数都只含有字母a,0),对称轴为直线x=-1;结合题中给出的OA=OC,可得C(0,-3)析式.再结合所求线段长来观察几何图形,发现△AOC 【过程示范】解:(1)由y=ax2+2ax-3a=a(x+3)(x-1)可知A(-3,0),B(1,0),∵OA=OC,∴C(0,-3),将C(0,-3)代入y=ax2+2ax-3a,解得,a=1,∴y=x2+2x-3.(2+2x-3第二问:铅垂法求面积 【思路分析】(1)整合信息,分析特征:由所求的目标入手分析,目标为S △ACP 的最大值,分析A ,C 为定点,P 为动点且P 在直线AC 下方的抛物线上运动,即 -3<x P <0; (2)设计方案:注意到三条线段都是斜放置的线段,需要借助横平竖直的线段来表达,所以考虑利用铅垂法来表达S △ACP . 【过程示范】如图,过点P 作PQ ∥y 轴,交AC 于点Q , 易得l AC :y =-x -3设点P 的横坐标为t ,则P (t ,t 2+2t -3), ∵PQ ∥y 轴, ∴Q (t ,-t -3),∴PQ =y Q -y P =-t -3-(t 2+2t -3)=-t 2-3t (-3<t <0), ∴2139()222ACP C A S PQ x x t t =⋅-=--△(-3<t <0) ∵302-<, ∴抛物线开口向下,且对称轴为直线32t =-,∴当32t =-时,S △ACP 最大,为278.第三问:平行四边形的存在性 【思路分析】 分析不变特征:以A ,B ,E ,F 为顶点的四边形中,A ,B 为定点,E ,F 为动点,定点A ,B 连接成为定线段AB .分析形成因素:要使这个四边形为平行四边形.首先考虑AB在平行四边形中的作用,四个顶点用逗号隔开,位置不确定,则AB既可以作边,也可以作对角线.画图求解:先根据平行四边形的判定来确定EF和AB之间应满足的条件,再通过平移和旋转来尝试画图,确定图形后设计方案求解.①AB作为边时,依据平行四边形的判定,需满足EF∥AB且EF=AB,要找EF,可借助平移.点E在对称轴上,沿直线容易平移,故将线段AB拿出来沿对称轴上下方向平移,确保点E在对称轴上,来找抛物线上的点F.注意:在对称轴的左、右两侧分别平移.找出点之后,设出对称轴上E点坐标,利用平行且相等表达抛物线上F点坐标,代入抛物线解析式求解.②AB作为对角线时,依据平行四边形的判定,需满足AB,EF互相平分,先找到定线段AB的中点,在旋转过程中找到EF恰好被AB中点平分的位置,因为E和AB中点都在抛物线对称轴上,说明EF所在直线即为抛物线对称轴,则与抛物线的交点(抛物线顶点)即为F点坐标.结果验证:画图或推理,根据运动范围考虑是否找全各种情形.【过程示范】(3)①当AB为边时,AB∥EF且AB=EF,如图所示,设E点坐标为(-1,m),当四边形是□ABFE时,由A(-3,0),B(1,0)可知,F1(3,m),代入抛物线解析式,可得,m=12,∴F1(3,12);当四边形是□ABEF时,由A(-3,0),B(1,0)可知,F2(-5,m),代入抛物线解析式,可得,m=12,∴F2(-5,12).②当AB为对角线时,AB与EF互相平分,AB的中点D(-1,0),设E(-1,m),则F(-1,-m),代入抛物线解析式,可得,m=4,∴F3(-1,-4).综上:F1(3,12),F2(-5,12),F3(-1,-4).➢巩固练习1.如图,直线12y x=-与抛物线2164y x=-+交于A,B两点,C是抛物线的顶点.(1)在直线AB上方的抛物线上有一动点P,当△ABP的面积最大时,点P的坐标为__________________.(2)若点M在抛物线上,且以点M,A,B以及另一点N为顶点的平行四边形ABNM的面积为240,则M,N两点的坐标为_______________.2.已知抛物线y=-mx2+4x+2m与x轴交于点A(α,0),B(β,0),且112αβ+=-.抛物线的对称轴为直线l,与y轴的交点为点C,顶点为点D,点C关于l的对称点为点E.(1)抛物线的解析式为_________.(2)连接CD,在直线CD下方的抛物线上有一动点G,当S△CDG=3,点G的坐标为______________.(3)若点P在抛物线上,点Q在x轴上,当以点D,E,P,Q为顶点的四边形是平行四边形时,点Q的坐标为_______.3.已知抛物线y=ax2-4ax+b的对称轴为直线x=2,顶点为P,与x轴交于A,B两点,与y轴交于点C,其中A(1,0),连接BC,PB,得到∠PBC=90°.(1)求抛物线的解析式.(2)抛物线上是否存在异于点P的一点Q,使△BCQ与△BCP的面积相等?若存在,求出点Q的坐标;若不存在,请说明理由.(3)若点E是抛物线上一动点,点F是x轴上一动点,是否存在以B,C,E,F为顶点的四边形是平行四边形?若存在,求出点F的坐标;若不存在,请说明理由.4.如图,在平面直角坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2).抛物线y=ax2-ax-b与y轴交于点D,且经过点C,连接AD,可得AB=AD.(1)求抛物线的解析式.(2)平移该抛物线的对称轴所在直线l.当l移动到何处时,恰好将△ABC的面积分为相等的两部分?(3)点P是抛物线上一动点,点Q是抛物线对称轴l上一动点,是否存在点P,使以P,Q,A,B为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,说明理由.【参考答案】1.(1)23 (1)4,;(2)M1(-10,-19),N1(-20,-14);M2(12,-30),N2(2,-25) 2.(1)y=-x2+4x+2;(2)G1(-1,-3),G2(3,5);(3)1(40)Q,2(40)Q,3(0)Q,40)Q3.(1)y=-x2+4x-3;(2)存在,Q1(1,0),237 (22Q --,,337(22Q+-+,;(3)存在,F1(7,0),F2(-1,0).4. (1)211222y x x =--;(2)3x =(3)存在,1313()28P -,,2113()28P --,,3117()28P -,.。

二次函数与几何综合专题--角问题【模型解读】二次函数与角综合问题,常见的主要有三种类型: 1. 特殊角问题:(1) 利用特殊角的三角函数值找到线段之间的数量关系(2) 遇到特殊角可以构造特殊三角形,如遇到45°构造等腰直角三角形,遇到30°、60°构造等边三角形,遇到90°构造直角三角形2.角的数量关系问题(1)等角问题:借助特殊图形的性质、全等和相似的性质来解决;构造圆,利用圆周角的性质来解决 (2)二倍角问题:利用角平分线的性质、等腰三角形的性质、对称、辅助圆等知识来解答 (3)角的和差问题3.角的最值问题:利用辅助圆等知识来解答【引例】如图,在平面直角坐标系xOy 中,抛物线2y x bx c =++与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,3OA OC ==,顶点为D ,对称轴交x 轴于点E . (1)求抛物线的解析式、对称轴及顶点D 的坐标.(2)在抛物线上是否存在点P ,使PAO OCE ∠=∠,若存在,求出点P 的坐标;若不存在,说明理由.(3)该抛物线上是否存在点P,使得PCA CAD∠=∠?若存在,求出所有点P的坐标;若不存在,请说明理由.∠的平分线与y轴的交点M的坐标.(4)直线AC与抛物线的对称轴交于点F,请求出CDF∠=∠,若存在,求出点P的坐标;若不存在,请说明理(5)在抛物线上是否存在点P,使得POC PCO由.(6)过点B 的直线交直线AC 于点M ,当直线AC 与BM 的夹角等于ACB ∠的2倍时,求点M 的坐标.(7)在y 轴上是否存在点N ,使得BCO BNO BAC ∠+∠=∠,若存在,求出点N 的坐标;若不存在,请说明理由.(8)在对称轴左侧的抛物线上有一点M ,在对称轴右侧的抛物线上有一点N ,满足90MDN ∠=︒.求证:MN 恒过定点,并求出定点坐标.【答案】(1)223y x x =+-,对称轴为:直线x =-1,顶点坐标为:D (-1,-4);(2)存在,P 的坐标为(43,139)或(23,119-);(3)存在,点P 的坐标为(-4,5)或(52-,74-);(4)点M 的坐标为(0-3);(5)存在,P 1,-32)或(1-,-32);(6)点M 的坐标为(52-,12-)或(12,72-);(7)在y 轴上存在点N ,点N 的坐标为(0,±2);(8)见解析,(-1,-3).【详解】答案:(1)解:∵3OA OC ==, ∴A (-3,0),C (0,-3),∴()20333b c c ⎧=--+⎪⎨-=⎪⎩,解得:23b c =⎧⎨=-⎩,∴抛物线的解析式为:223y x x =+-,对称轴为:直线x =-1,顶点坐标为:D (-1,-4). (2)解:假设存在,如图,当点P 在x 轴上方时,过点P 作PH ⊥x 轴于点H ,设点P 的坐标为(a ,223a a +-), 则90PHA COE ∠=∠=︒,∵点A (-3,0),点C (0,-3),点E (-1,0),点P (a ,223a a +-), ∴AH =a -(-3)=a +3,PH =223a a +-,OC =3,EO =1,∵PAO OCE ∠=∠,90PHA COE ∠=∠=︒, ∴PHA EOC △∽△, ∴PH AHEO OC=, ∴223313a a a +-+=, 解得:143a =,23a =-(不符合题意,舍去), 此时2164132323939a a +-=+⨯-=, ∴点P 的坐标为(43,139),当点P 在x 轴下方时,如图,过点P '作P F '⊥x 轴于点F ,设点P '的坐标为(b ,223b b +-), 则90P FA COE '∠=∠=︒,∵点A (-3,0),点C (0,-3),点E (-1,0),点P '(b ,223b b +-), ∴AF =b -(-3)=b +3,P F '=223b b --+,OC =3,EO =1, ∵P AO OCE '∠=∠,90P FA COE '∠=∠=︒, ∴P FA EOC '△∽△, ∴P F AFEO OC'=, ∴223313b b b --++=,解得:123b =,23b =-(不符合题意,舍去), 此时242112323939b b +-=+⨯-=-, ∴点P '的坐标为(23,119-), 综上所述,在抛物线上存在点P ,使PAO OCE ∠=∠,此时点P 的坐标为(43,139)或(23,119-).(3)解:假设存在,如图,当点P 在直线AC 的右上方时,设直线AD 为y kx b =+,将A (-3,0),D (-1,-4)代入,得304k b k b -+=⎧⎨-+=-⎩, 解得:26k b =-⎧⎨=-⎩,∴直线AD 为26y x =--, ∵PCA CAD ∠=∠, ∴//PC AD ,∴设直线PC 为12y x b =-+, 将C (0,-3)代入,得13b =-, ∴直线PC 为23y x =--,将23y x =--与223y x x =+-联立方程,得22323x x x +-=--,解得:14x =-,20x =(不符合题意,舍去) 当4x =-时,235y x =--=, ∴点P 的坐标为(-4,5);如图,当点P '在直线AC 的左下方时,延长CP '交x 轴于点G ,延长AD 交y 轴于点H ,∵直线AD 为26y x =--, ∴当x =0时,y =-6, ∴OH =6,∵P CA CAD '∠=∠,45OCA OAC ∠=∠=︒, ∴P CA OCA CAD OAC '∠+∠=∠+∠, 即:P CO OAD '∠=∠, ∴在△GOC 与△HOA 中,OCG OAH OC OA COG AOH ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△GOC ≌△HOA (ASA ), ∴OG =OH =6,∴点G 的坐标为(-6,0), 设直线CG 为22y k x b =+,将G (-6,0),C (0,-3)代入,得603k b b -+=⎧⎨=-⎩,解得:123kb⎧=-⎪⎨⎪=-⎩,∴直线CG为132y x=--,将132y x=--与223y x x=+-联立方程,得21 2332x x x+-=--,解得:15 2x=-,20x=(不符合题意,舍去)当52x=-时,17324y x=--=-,∴点P的坐标为(52-,74-),综上所述,抛物线上存在点P,使得PCA CAD∠=∠,此时点P的坐标为(-4,5)或(52-,74-).(4)解:如图,过点D作DH⊥y轴于点H,∵点D为(-1,-4),点C为(0,-3),∴DE=OH=4,OC=3,DH=1,∴CH=OH-OC=1,∴在Rt△CDH中,CD∵DM平分CDF∠,∴∠CDM=∠FDM,∵DF//y轴,∴∠CMD=∠FDM,∴∠CMD=∠CDM,∴CM=CD∴OM=OC-CM=3又∵点M在y轴的负半轴上,∴点M 的坐标为(03). (5)解:假设存在,∵POC PCO ∠=∠, ∴PC =PO ,∴点P 在OC 的垂直平分线上, ∵O (0,0),C (0,-3),∴OC 的垂直平分线为直线y =-32,将y =-32代入223y x x =+-,得23232x x +-=-,解得:11x ,21x =,∴在抛物线上存在点P ,使得POC PCO ∠=∠,此时点P 1,-32)或(1,-32). (6)解:若点M 在点C 的左上方时,满足2AMB ACB ∠=∠,如图,过点M 作MH ⊥AB 于点H ,过点C 作CG ⊥MH ,交HM 的延长线于点G ,∵2AMB ACB MBC ACB ∠=∠+∠=∠, ∴ACB MBC ∠=∠, ∴MB MC =,设直线AC 为y kx b =+,将A (-3,0),C (0,-3)代入,得303k b b -+=⎧⎨=-⎩, 解得:13k b =-⎧⎨=-⎩,∴直线AC 为3y x =--, ∵点M 在直线AC 上,∴设点M 的坐标为(x ,-x -3), 又∵点B (1,0),点C (0,-3),∴MH =x +3,BH =1-x ,MG =-x -3-(-3)=-x ,CG =-x , ∴在Rt △MHB 中,22222(3)(1)MB MH BH x x =+=++-, 在Rt △MGC 中,222222()()2MC MG CG x x x =+=-+-=, ∵MB MC =, ∴22MB MC =, ∴222(3)(1)2x x x ++-=, 解得:52x =-,将52x =-代入3y x =--,得12y =-,∴此时点M 的坐标为(52-,12-),若点M '在点C 的右下方时,满足2PM B ACB '∠=∠, 如图,过点M '作M N AB '⊥于点N ,∵2PM B ACB '∠=∠,2AMB ACB ∠=∠,∴AMB PMB '∠=∠, ∴MBMB '=, 设点M '的坐标为(m ,-m -3),又∵点B (1,0),点M (52-,12-),∴MH =52-+3=12,BH =1-(52-)=72,M 'N =-m -3,BN =1-m ,∴在Rt △MHB 中,222221725()()222MB MH BH =+=+=, 在Rt M NB '△中,22222(3)(1)M B M N BN m m ''=+=--+-,∵MBMB '=, ∴22M B MB '=, ∴2225(3)(1)2m m --+-=, 解得:112m =,252m =-(不符合题意,舍去), 将12x m ==代入3y x =--,得72y =-,∴此时点M '的坐标为(12,72-),综上所述,当直线AC 与BM 的夹角等于ACB ∠的2倍时,点M 的坐标为(52-,12-)或(12,72-).(7)解:假设在y 轴的正半轴上存在点N ,使得BCO BNO BAC ∠+∠=∠,如图,过点N 作NM ⊥BN ,交CB 的延长线于点M ,过点M 作MH ⊥y 轴于点H , 则∠MHN =∠MNB =∠BON =90°,∵点A (-3,0),点C (0,-3), ∴OA =OC =3, 又∵∠AOC =90°, ∴∠BAC =∠OCA =45°, ∴45BCO BNO BAC ∠+∠=∠=︒, ∴45MBN BCO BNO ∠=∠+∠=︒, ∵∠MNB =90°,∴∠NMB =∠MBN =45°, ∴NB =MN ,∵∠MHN =∠MNB =90°,∴∠HMN +∠HNM =∠ONB +∠HNM =90°, ∴∠HMN =∠ONB , ∴在△HMN 与△ONB 中,MHN NOB HMN ONB MN BN ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△HMN ≌△ONB (AAS ), ∴HM =ON ,HN =OB , ∵点B 坐标为(1,0), ∴HN =OB =1,设HM =ON =a ,则OH =ON +HN =a +1, ∴点M 的坐标为(a ,a +1), 设直线BC 为y kx b =+,将B (1,0),C (0,-3)代入,得3k b b +=⎧⎨=-⎩, 解得:33k b =⎧⎨=-⎩,∴直线BC 为33y x =-, 将点M (a ,a +1)代入得:133a a +=-,解得:2a =,∴点N 的坐标为(0,2),当点N 在y 轴的负半轴时,如图所示,根根轴对称的性质可得此时点N 的坐标为(0,-2), 综上所述,在y 轴上存在点N ,使得BCO BNO BAC ∠+∠=∠,此时点N 的坐标为(0,±2). (8)解:如图,过点D 作直线l ⊥y 轴,过点M 、N 分别作直线l 的垂线,垂足分别为点H 、G ,设点M 的坐标为(m ,223m m +-),点N 的坐标为(n ,223n n +-), ∵顶点D 的坐标为(-1,-4),且M 、N 分别位于点D 的左右两侧, ∴2223(4)21MH m m m m =+---=++,1HD m =--,2223(4)21NG n n n n =+---=++,(1)1DG n n =--=+,根据题意可得90MHD DGN MDN ∠=∠=∠=︒, ∴90MDH HMD MDH GDN ∠+∠=∠+∠=︒, ∴HMD GDN ∠=∠, ∴HMD GDN △∽△, ∴MH HDDG NG=, ∴22211121m m mn n n ++--=+++,即22(1)(1)1(1)m m n n +-+=++, ∴(1)(1)1m n -++=, 整理得:20mn m n +++=, 设直线MN 为y kx b =+,将M (m ,223m m +-),N (n ,223n n +-)代入,得222323km b m m kn b n n ⎧+=+-⎨+=+-⎩, 解得:23k m n b mn =++⎧⎨=--⎩,∴直线MN 为(2)3y m n x mn =++--, ∵20mn m n +++=, ∴2m n mn ++=-,∴直线MN 为3(1)3y mnx mn mn x =---=-+-, ∴当10x +=即=1x -时,=3y -,∴无论m ,n 取何值,直线MN 总会经过定点(-1,-3), ∴直线MN 恒过定点,该定点坐标为(-1,-3).【模型实例】1.如图,在平面直角坐标系xOy 中,抛物线()2y a x h k =-+与x 轴相交于O ,A 两点,顶点P 的坐标为()2,1-.点B 为抛物线上一动点,连接,AP AB ,过点B 的直线与抛物线交于另一点C .(1)求抛物线的函数表达式;(2)若点B 的横坐标与纵坐标相等,ABC OAP ∠=∠,且点C 位于x 轴上方,求点C 的坐标;(3)若点B 的横坐标为t ,90ABC ∠=︒,请用含t 的代数式表示点C 的横坐标,并求出当0t <时,点C 的横坐标的取值范围.【答案】(1)214y x x =-或21(2)14y x =--;(2)点C 的坐标为(6,3)或51,4⎛⎫- ⎪⎝⎭;(3)164t t --+;12C x ≥【分析】(1)设抛物线的解析式为()221y a x =--,把点O (0,0)代入即可求解;(2)求得B (0,0)或B (8,8),分两种情况讨论,①当点B 的坐标为(0,0)时,过点B 作BC ∥AP 交抛物线于点C ,利用待定系数法求得直线BC 的解析式为12y x =,解方程组即可求解;②点B 的坐标为(8,8)时,作出如图的辅助线,利用三角形函数以及轴对称的性质求得M (85,165),同①可求解;(3)作出如图的辅助线,点B 的坐标为(t ,214t t -),得到AH =4t -,BH =214t t -,OH =t =MN ,由AH =4t -,BH =214t t -,OH =t =MN ,△ABH ~△BMN 得到M (0,2144t t -+),求得BC 的解析式为:24144y x t t t =-+-+,解方程组求得点C 的横坐标为164t t--+,即可求解.【详解】(1)∵抛物线的顶点坐标为P (2,-1),∴设抛物线的解析式为()221y a x =--, ∵抛物线经过原点O ,即经过点O (0,0), ∴()20021a =--, 解得:14a =, ∴抛物线的解析式为()22112144y x x x =--=-; (2)在()21214y x =--中,令y x =, 得:()21214x x =--, 解得0x =或8x =, ∴B (0,0)或B (8,8),①当点B 的坐标为(0,0)时,过点B 作BC ∥AP 交抛物线于点C , 此时∠ABC =∠OAP ,如图:在()21214y x =--中,令0y =, 得:()212104x --=, 解得:0x =或4x =, ∴A (4,0),设直线AP 的解析式为1y kx b =+, 将A (4,0),P (2,-1)代入得110412k b k b =+⎧⎨-=+⎩,解得:1122k b ⎧=⎪⎨⎪=-⎩, ∴直线AP 的解析式为122y x =-,∵BC ∥AP ,∴设直线BC 的解析式为212y x b =+, 将B (0,0)代入得20b =, ∴直线BC 的解析式为12y x =, 由()2121214y x y x ⎧=⎪⎪⎨⎪=--⎪⎩,得:00x y =⎧⎨=⎩(此点为点O ,舍去)或63x y =⎧⎨=⎩, ∴点C 的坐标为(6,3);②点B 的坐标为(8,8)时,过点P 作PQ ⊥x 轴于点Q ,过点B 作BH ⊥x 轴于点H ,作H 关于AB 的对称点M ,作直线BM 交抛物线于C ,连接AM ,如图:∵A (4,0),P(2,-1), ∴PQ =1,AQ =2,在Rt △APQ 中,1tan 2PQ OAP AQ ∠==, ∵A (4,0),B (8,8), ∴AH =4,BH =8,在Rt △ABH 中,1tan 2AH ABH BH ∠==, ∴∠OAP =∠ABH ,∵H 关于AB 的对称点为M , ∴∠ABM =∠ABH ,∴∠ABC =∠OAP ,即C 为满足条件的点, 设M (x ,y ),∵H 关于AB 的对称点为M ,∴AM =AH =4,BM =BH =8,∴()()()()222222404888x y x y ⎧-+-=⎪⎨-+-=⎪⎩ 两式相减得:82x y =-,代入即可解得: 80x y =⎧⎨=⎩(此点为点H ,舍去)或85165x y ⎧=⎪⎪⎨⎪=⎪⎩, ∴M (85,165),同理求得BM 的解析式为:324y x =+, 解()23241214y x y x ⎧=+⎪⎪⎨⎪=--⎪⎩得:88x y =⎧⎨=⎩(此点为点B ,舍去)或154x y =-⎧⎪⎨=⎪⎩,∴点C 的坐标为(-1,54); 综上,点C 的坐标为(6,3)或(-1,54); (3)设BC 交y 轴于点M ,过点B 作BH ⊥x 轴于点H ,过点M 作MN ⊥BH 于点N ,如图:∵点B 的横坐标为t ,∴点B 的坐标为(t ,214t t -),又A (4,0),∴AH =4t -,BH =214t t -,OH =t =MN , ∵∠ABC =90°,∴∠MBN =90°-∠ABH =∠BAH , 且∠N =∠AHB =90°, ∴△ABH ~△BMN ,∴AH BH BN MN=,即2144t t t BN t--=, ∴BN =224414t tt t -=-,∴HN =2144t t -+,∴M (0,2144t t -+),同理求得BC 的解析式为:24144y x t t t =-+-+,由22144144y x x y x t t t ⎧=-⎪⎪⎨⎪=-+-+⎪⎩,得22141444x x x t t t -=-+-+,解得x t =(点B 的横坐标),或2416164t t x t t t-+=-=--+,∴点C 的横坐标为164t t --+,当0t <时,164C x t t=--+224=++212=+,=C x 的最小值是12,此时4t =-;∴当0t <时,点C 的横坐标的取值范围是12C x ≥. 【点睛】本题考查二次函数综合知识,涉及解析式、锐角三角函数、对称变换、两条直线平行、两条直线互相垂直、解含参数的方程等,综合性很强,难度较大,解题的关键是熟练掌握、应用各种综合知识,用含字母的式子表示线段长度及函数解析式.2.如图,在平面直角坐标系xOy 中,抛物线E :y =﹣(x ﹣m )2+2m 2(m <0)的顶点P 在抛物线F :y =ax 2上,直线x =t 与抛物线E ,F 分别交于点A ,B . (1)求a 的值;(2)将A ,B 的纵坐标分别记为y A ,y B ,设s =y A ﹣y B ,若s 的最大值为4,则m 的值是多少? (3)Q 是x 轴的正半轴上一点,且PQ 的中点M 恰好在抛物线F 上.试探究:此时无论m 为何负值,在y 轴的负半轴上是否存在定点G ,使∠PQG 总为直角?若存在,请求出点G 的坐标;若不存在,请说明理由.【分析】(1)由抛物线的顶点式可直接得出顶点P的坐标,再代入抛物线F即可得出结论;(2)根据题意可分别表达A,B的纵坐标,再根据二次函数的性质可得出m的值;(3)过点Q作x轴的垂线KN,分别过点P,G作x轴的平行线,与KN分别交于K,N,则△PKQ∽△QNG,设出点M的坐标,可表达点Q和点G的坐标,进而可得出结论.【解答】解:(1)由题意可知,抛物线E:y=﹣(x﹣m)2+2m2(m<0)的顶点P的坐标为(m,2m2),∵点P在抛物线F:y=ax2上,∴am2=2m2,∴a=2.(2)∵直线x=t与抛物线E,F分别交于点A,B,∴y A=﹣(t﹣m)2+2m2=﹣t2+2mt+m2,y B=2t2,∴s=y A﹣y B=﹣t2+2mt+m2﹣2t2=﹣3t2+2mt+m2=﹣3(t﹣m)2+m2,∵﹣3<0,∴当t=m时,s的最大值为m2,∵s的最大值为4,∴m2=4,解得m=±,∵m<0,∴m=﹣.(3)存在,理由如下:设点M的坐标为n,则M(n,2n2),∴Q(2n﹣m,4n2﹣2m2),∵点Q在x轴正半轴上,∴2n﹣m>0且4n2﹣2m2=0,∴n=﹣m,∴M(﹣m,m2),Q(﹣m﹣m,0).如图,过点Q作x轴的垂线KN,分别过点P,G作x轴的平行线,与KN分别交于K,N,∴∠K=∠N=90°,∠QPK+∠PQK=90°,∵∠PQG=90°,∴∠PQK+∠GQN=90°,∴∠QPK=∠GQN,∴△PKQ∽△QNG,∴PK:QN=KQ:GN,即PK•GN=KQ•QN.∵PK=﹣m﹣m﹣m=﹣m﹣2m,KQ=2m2,GN=﹣m﹣m,∴(﹣m﹣2m)(﹣m﹣m)=2m2•QN解得QN=.∴G(0,﹣).3.如图,在平面直角坐标系中,抛物线y=ax2+bx+2经过A(,0),B(3,)两点,与y轴交于点C.(1)求抛物线的解析式;(2)点P在抛物线上,过P作PD⊥x轴,交直线BC于点D,若以P、D、O、C为顶点的四边形是平行四边形,求点P的横坐标;(3)抛物线上是否存在点Q,使∠QCB=45°?若存在,请直接写出点Q的坐标;若不存在,请说明理由.【分析】(1)根据待定系数法,将点A,点B代入抛物线解析式,解关于b,c的二元一次方程组,即可求得抛物线的解析式;(2)设出点P的坐标,确定出PD∥CO,由PD=CO,列出方程求解即可;(3)过点D作DF⊥CP交CP的延长线于点F,过点F作y轴的平行线EF,过点D作DE⊥EF于点E,过点C作CG⊥EF于点G,证明△DEF≌△FGC(AAS),由全等三角形的性质得出DE=FG,EF=CG,求出F点的坐标,由待定系数法求出直线CF的解析式,联立直线CF和抛物线解析式即可得出点P的坐标.【解答】解:(1)将点A(﹣,0),B(3,)代入到y=ax2+bx+2中得:,解得:,∴抛物线的解析式为y=﹣x2+x+2;(2)设点P(m,﹣m2+m+2),∵y=﹣x2+x+2,∴C(0,2),设直线BC的解析式为y=kx+c,∴,解得,∴直线BC的解析式为y=x+2,∴D(m,m+2),∴PD=|﹣m2+m+2﹣m﹣2|=|m2﹣3m|,∵PD⊥x轴,OC⊥x轴,∴PD∥CO,∴当PD=CO时,以P、D、O、C为顶点的四边形是平行四边形,∴|m2﹣3m|=2,解得m=1或2或或,∴点P的横坐标为1或2或或;(3)①当Q在BC下方时,如图,过B作BH⊥CQ于H,过H作MN⊥y轴,交y轴于M,过B作BN⊥MH于N,∴∠BHC=∠CMH=∠HNB=90°,∵∠QCB=45°,∴△BHC是等腰直角三角形,∴CH=HB,∴∠CHM+∠BHN=∠HBN+∠BHN=90°,∴∠CHM=∠HBN,∴△CHM≌△HBN(AAS),∴CM=HN,MH=BN,∵H(m,n),∵C(0,2),B(3,),∴,解得,∴H(,),设直线CH的解析式为y=px+q,∴,解得,∴直线CH的解析式为y=﹣x+2,联立直线CF与抛物线解析式得,解得或,∴Q(,);②当Q在BC上方时,如图,过B作BH⊥CQ于H,过H作MN⊥y轴,交y轴于M,过B作BN⊥MH于N,同理得Q(,).综上,存在,点Q的坐标为(,)或(,).4.如图1,在平面直角坐标系中.抛物线y=ax2+bx+2与x轴交于A(﹣4,0)和B(1,0),与y轴交于点C,连接AC,BC.(1)求该抛物线的解析式;(2)如图2,点M为直线AC上方的抛物线上任意一点,过点M作y轴的平行线,交AC于点N,过点M作x轴的平行线,交直线AC于点Q,求△MNQ周长的最大值;(3)点P为抛物线上的一动点,且∠ACP=45°﹣∠BAC,请直接写出满足条件的点P的坐标.【分析】(1)用待定系数法可得抛物线的解析式为y=﹣x2﹣x+2;(2)设直线AC解析式为y=kx+2,用待定系数法得直线AC解析式为y=x+2,设M(x,﹣x2﹣x+2),则N(x,x+2),即得MN=﹣x2﹣2x,可证△QMN∽△AOC,有==,故MQ=2MN,NQ=MN,可得△MNQ周长MN+MQ+NQ=MN+2MN+MN=﹣(x﹣2)2+6+2,即得当x=2时,△MNQ周长最大值为6+2;(3)在x轴负半轴上取D,使OC=OD,连接CD交抛物线于P,此时∠ACP=45°﹣∠BAC,P是满足条件的点,由C(0,2),D(2,0),得直线CD解析式为y=x+2,即可解得P(﹣5,﹣3),作D关于直线AC的对称点E,连接CE并延长交抛物线于P',由对称性知∠ACP'=∠ACP,P'是满足条件的点,设E (m,n),可得,可解得E(﹣,),从而可得直线CE解析式为:y=x+2,即可解得P'(﹣,).【解答】解:(1)把A(﹣4,0)和B(1,0)代入y=ax2+bx+2得:,解得,∴抛物线的解析式为y=﹣x2﹣x+2;(2)由y=﹣x2﹣x+2可得C(0,2),设直线AC解析式为y=kx+2,把A(﹣4,0)代入得:﹣4k+2=0,解得k=,∴直线AC解析式为y=x+2,设M(x,﹣x2﹣x+2),则N(x,x+2),∴MN=﹣x2﹣x+2﹣(x+2)=﹣x2﹣2x,∵MQ∥x轴,MN∥y轴,∴∠MQN=∠CAO,∠NMQ=∠AOC=90°,∴△QMN∽△AOC,∴==,即==,∴MQ=2MN,NQ=MN,∴△MNQ周长MN+MQ+NQ=MN+2MN+MN=(3+)MN=(3+)×(﹣x2﹣2x)=﹣(x+2)2+6+2,∵﹣<0,∴当x=﹣2时,△MNQ周长最大值为6+2;(3)在x轴负半轴上取D,使OC=OD,连接CD交抛物线于P,如图:∴D(﹣2,0),∠CDO=45°,此时∠ACP=45°﹣∠BAC,P是满足条件的点,∵C(0,2),D(2,0),∴直线CD解析式为y=x+2,由得或,∴P(﹣5,﹣3),作D关于直线AC的对称点E,连接CE并延长交抛物线于P',由对称性知∠ACP'=∠ACP,P'是满足条件的点,设E(m,n),根据AE=AD,CE=CD可得:,解得或,∴E(﹣,),由E(﹣,),C(0,2)可得直线CE解析式为:y=x+2,解得或,∴P'(﹣,),综上所述,P的坐标为(﹣5,﹣3)或(﹣,).5.抛物线y=x2﹣4x+c与直线I:y=kx交于点G(1,m)和点H,﹣1≤m<0,直线x=m﹣1交直线l于点A,交抛物线于点B.(1)求c和k的值(用含m的代数式表示);(2)过点A作x轴的平行线交抛物线于M,N两点(M在N的左侧),交y轴于点C.求的取值范围;(3)在(2)的条件下,过点B作x轴的平行线,与抛物线另一个交点为D,若点E是线段BD的中点,探究∠MEN与∠ABC的数量关系,并说明理由.【分析】(1)把点G(1,m)分别代入y=x2﹣4x+c与y=kx,即可求得答案;(2)由题意可得A(m﹣1,m2﹣m),B(m﹣1,m2﹣5m+8),M(m+1,m2﹣m),求得==﹣2m+4,再根据一次函数的性质即可求得的取值范围;(3)先求出D(﹣m+5,m2﹣5m+8),E(2,m2﹣5m+8),F(2,m2﹣m),利用三角函数定义可得:tan ∠ABC==,tan∠MEF==,tan∠NEF==,得出∠MEF=∠NEF=∠ABC,进而可得∠MEN=2∠ABC.【解答】解:(1)∵抛物线y=x2﹣4x+c与直线I:y=kx交于点G(1,m),∴m=12﹣4×1+c,m=k×1,∴c=m+3,k=m;(2)∵直线x=m﹣1交直线l于点A,∴y=m(m﹣1)=m2﹣m,∴A(m﹣1,m2﹣m),∵直线x=m﹣1交抛物线于点B,∴y=x2﹣4x+m+3=(m﹣1)2﹣4(m﹣1)+m+3=m2﹣5m+8,∴B(m﹣1,m2﹣5m+8),∴AB=﹣4m+8,∵过点A作x轴的平行线交抛物线于M,N两点(M在N的左侧),交y轴于点C,∴C(0,m2﹣m),点M的纵坐标与点A的纵坐标相等,∴m2﹣m=x2﹣4x+m+3,解得:x1=m+1,x2=﹣m+3,∴M(m+1,m2﹣m),N(﹣m+3,m2﹣m),∴AM=m+1﹣(m﹣1)=2,∴==﹣2m+4,∵﹣2<0,且﹣1≤m<0,∴的值随着m的增大而减小,当m=﹣1时,=﹣2×(﹣1)+4=6,当m=0时,=﹣2×0+4=4,∴4≤≤6;(3)∠MEN=2∠ABC.理由如下:∵BD∥x轴,∴点D的纵坐标与点B的纵坐标相等,∴m2﹣5m+8=x2﹣4x+m+3,解得:x1=m﹣1,x2=﹣m+5,∴D(﹣m+5,m2﹣5m+8),∵点E是线段BD的中点,∴E(2,m2﹣5m+8),如图,设直线x=2交直线MN于点F,则F(2,m2﹣m),∴MF=NF=﹣m+1,EF=m2﹣5m+8﹣(m2﹣m)=﹣4m+8,∵AC=0﹣(m﹣1)=﹣m+1,AB=﹣4m+8,∴tan∠ABC==,∵tan∠MEF==,tan∠NEF==,∴∠MEF=∠NEF=∠ABC,∴∠MEN=2∠ABC.6.抛物线y=ax2﹣2ax﹣3a与x轴交于A、B两点(点A在点B的左边),与y轴的正半轴交于C点,△ABC的面积为6.(1)直接写出点A、B的坐标为A(﹣1,0),B(3,0);抛物线的解析式为y=﹣x2+2x+3.(2)如图1,连结AC,若在第一象限抛物线上存在点D,使点D到直线AC的距离为,求点D的坐标;(3)如图2,平行于AC的直线交抛物线于M、N两点,在抛物线上存在点P,当PQ⊥y轴时,PQ恰好平分∠MPN,求P点坐标.【分析】(1)令y=0,可求出x的值,进而可得出A,B的坐标;令x=0,可求出y的值,可得出点C的坐标,得出线段OC的长,利用三角形的面积公式可得出a的值;(2)过点O作OQ⊥AC于点Q,根据三角形面积的等积法可求出OQ的长,进可得出点D的位置,利用全等三角形的性质求出直线QA′的解析式,联立可求出点D的坐标;(3)过点M作ME⊥DE于E,过点N作NF⊥DE于F,根据∠MPE=∠NPE,∠MEP=∠NFP=90°,可得△MPE∽△NPF,设出M、N、P三点的坐标(只设横坐标,纵坐标用横坐标表示),分别用横坐标之差、纵坐标之差表示出两个相似三角形的直角边,列出比例等式;设出MN的解析式,与抛物线方程联立,得出两根之和的关系式,结合前面的比例等式解出P点的横坐标,进而算出纵坐标.【解答】解:(1)令y=0,即ax2﹣2ax﹣3a=0,解得x=﹣1或x=3,∴A(﹣1,0),B(3,0);令x=0,则y=﹣3a,∴C(0,﹣3a),即OC=﹣3a,∴S=×4×(﹣3a)=6,解得a=﹣1,∴函数解析式为:y=﹣x2+2x+3.故答案为:A(﹣1,0),B(3,0);y=﹣x2+2x+3.(2)由(1)知,A(﹣1,0),B(3,0),C(0,3),∴OA=1,OC=3,AB=,过点O作OG⊥AC于点G,∴S△OAC=•OA•OB=•AC•OG∴×1×3=וOG,∴OG=,设点D到直线AC的距离h==2OG,延长GO到点G′,使得OG′=OG,过点G′作AC的平行线与x轴交于点A′,与抛物线在第一象限内交于点D,∴∠GAO=∠G′A′O,∵∠GOA=∠G′OA′,∴△GAO≌△G′A′O(AAS),∴OA=OA′=1,∴A′(1,0),∵A(﹣1,0),C(0,3),∴直线AC的解析式为:y=3x+3,∴直线A′G′的解析式为:y=3x﹣3,令3x﹣3=﹣x2+2x+3,解得x=2或x=﹣3,∵点D在第一象限,∴D(2,3).(3)如图,过点M作ME⊥DE于E,过点N作NF⊥DE于F,设M(x1,﹣x12+2x1+3),N(x2,﹣x22+2x2+3),P(x0,﹣x02+2x0+3),则:ME=﹣x12+2x1+3﹣(﹣x02+2x0+3)=﹣x12+2x1+x02﹣2x0=﹣(x1﹣x0)(x1+x0)+2(x1﹣x0)=(x0+x1﹣2)(x0﹣x1),PE=x0﹣x1,FN=﹣x02+2x0+3﹣(﹣x22+2x2+3)=﹣(x0+x2﹣2)(x0﹣x2),PF=x0﹣x2,∵PQ恰好平分∠MPN,即∠MPE=∠NPE,∠MEP=∠NFP=90°,∴△MPE∽△NPF,∴=,∴=,∴x0=,∵A(﹣1,0),C(0,﹣3),∵MN∥AC,∴设直线MN的解析式为y=3x+b,令3x+b=﹣x2+2x+3,由消去y整理得:x2+x﹣3+b=0,由韦达定理可知:x1+x2=﹣1,∴x=,∴x−2x−3=,∴P(,).7.如图,抛物线y=mx2+3mx﹣2m+1的图象经过点C,交x轴于点A(x1,0),B(x2,0)(点A在点B左侧),且x2﹣x1=5,连接BC,D是AC上方的抛物线一点.(1)求抛物线的解析式;(2)连接BC,CD,S△DCE:S△BCE是否存在最大值?若存在,请求出其最大值及此时点D的坐标;若不存在,请说明理由;(3)第二象限内抛物线上是否存在一点D,DF垂直AC于点F,使得△DCF中有一个锐角等于∠BAC的两倍?若存在,求点D的横坐标,若不存在,请说明理由.【分析】(1)利用抛物线与x轴的交点的横坐标与一元二次方程根的联系,用一元二次方程根与系数的关系定理列出关于m的方程,解方程即可得出结论;(2)过点D作DH⊥x轴于点H,交AC于点M,过点B作BN⊥x轴于点B,交直线AC于点N,利用待定系数法求得直线AC的解析式,设D(a,a+2),则M(a,a+2),求得线段DM,BN的长,利用同高的三角形的面积关系列出S△DCE:S△BCE关于a的等式,利用配方法和二次函数的性质解答即可;(3)利用分类讨论的思想方法分两种情况讨论解答:①当∠DCF=2∠BAC时,②当∠FDC=2∠BAC时:取AB的中点P,连接OP,过点D作DR⊥y轴于点R,延长交AC于点G,利用勾股定理的逆定理判定△ABC为直角三角形,∠ACB=90°,设D(a,a+2),则DR=﹣a,OR=a+2,利用直角三角形的边角关系定理列出关于a的方程,解方程即可得出结论.【解答】解:(1)∵抛物线y=mx2+3mx﹣2m+1的图象交x轴于点A(x1,0),B(x2,0),∴x1,x2是方程mx2+3mx﹣2m+1=0的两根,∴x1+x2=﹣3,x1•x2=.∵x2﹣x1=5,∴=25.即:﹣4x1•x2=25,∴9﹣4×=25.解得:m=﹣.∴抛物线的解析式为y=﹣﹣x+2.(2)S△DCE:S△BCE存在最大值,此时点D的坐标为(﹣2,3),理由:令y=0,则﹣﹣x+2=0,解得:x=﹣4或1,∴A(﹣4,0),B(1,0),令x=0,则y=2,∴C(0,2).设直线AC的解析式为y=kx+b,∴,解得:,∴直线AC的解析式为y=x+2.过点D作DH⊥x轴于点H,交AC于点M,过点B作BN⊥x轴于点B,交直线AC于点N,如图,则DM∥BN,∴△EDM∽△EBN,∴.设D(a,a+2),则M(a,a+2),∴DM=(a+2)﹣(a+2)=﹣﹣2a.当x=1时,y=×1+2=,∴N(1,).∴BN=.∵等高的三角形的面积比等于底的比,∴S△DCE:S△B∁E=.∴S△DCE:S△B∁E==﹣﹣a=﹣(a+2)2+,∵<0,∴当a=﹣2时,S△DCE:S△BCE有最大值为,此时点D(﹣2,3);(3)第二象限内抛物线上存在一点D,DF垂直AC于点F,使得△DCF中有一个锐角等于∠BAC的两倍,点D的横坐标为﹣2或﹣,理由:∵A(﹣4,0),B(1,0),C(0,2),∴OA=4,OB=1,OC=2,∴AC==2,BC==,AB=OA+OB=5.∵AC2+BC2=25=AB2,∴△ABC为直角三角形,∠ACB=90°.取AB的中点P,连接OP,则P(﹣,0),∴OP=.∴P A=PB=PC=,∴∠BAC=∠PCA.∵∠CPB=∠BAC+∠PCA,∴∠CPB=2∠BAC.过点D作DR⊥y轴于点R,延长交AC于点G,如图,①当∠DCF=2∠BAC时,设D(m,m+2),则DR=﹣m,OR=m+2,∴CR=OR﹣OC=m.∵DR⊥y轴,OA⊥y轴,∴DR∥AB,∴∠G=∠BAC.∵∠DCF=∠G+∠CDG,∠DCF=2∠BAC,∴∠CDG=∠G=∠BAC.∵tan∠BAC=,∴tan∠CDR=.∴,∴解得:m=﹣2或0(舍去),∴m=﹣2.∴点D的横坐标为﹣2;②当∠FDC=2∠BAC时,∵∠CPB=2∠BAC,∴∠FDC=∠CPB.∵tan∠CPB=,∴tan∠FDC=,∵tan∠FDC=,∴,设FC=4n,则DF=3n,∴CD==5n.∵tan∠G=tan∠BAC=,∴tan∠G=,∴FG=6n.∴CG=FG﹣FC=2n.∵tan∠G=,∴RC=n,∴DR==n,∴,解得:a=或0(舍去),∴a=﹣,即点D的横坐标为﹣,综上,第二象限内抛物线上存在一点D,DF垂直AC于点F,使得△DCF中有一个锐角等于∠BAC的两倍,点D的横坐标为﹣2或﹣.【课后练习】1.如图1,抛物线y=ax2+bx+3经过A(1,0)、B(3,0)两点,与y轴交于点C,(1)求抛物线的函数解析式;(2)如图2,M是x轴下方的抛物线上一点,连接MO、MB、MC,若△MOC的面积是△MBC面积的3倍,求点M的坐标;(3)如图3,连接AC、BC,在抛物线上是否存在一点N(不与点A重合),使得∠BCN=∠ACB?若存在,求点N的横坐标;若不存在,请说明理由.【分析】(1)由于抛物线y=ax2+bx+3过A(1,0)、B(3,0)两点,那么可以得到方程ax2+bx+3=0的两根为x=1或x=3,然后利用根与系数即可确定a、b的值.(2)利用待定系数法求出直线BC的解析式,设点M(m,m2﹣4m+3),过点M作MN∥y轴,交BC于点N,则N(m,﹣m+3),根据△MOC的面积是△MBC面积的3倍,即可得到点M的坐标;(3)过点B作BE⊥AB交CN与E,证明△ABC≌△EBC(ASA),根据全等三角形的性质得BE=AB=2,求得E的坐标,由点E、C的坐标可得直线CN的解析式,联立y=x2﹣4x+3即可求得N点的坐标.【解答】解:(1)∵抛物线y=ax2+bx+3过A(1,0)、B(3,0)两点,∴方程ax2+bx+3=0的两根为x=1或x=3,∴1+3=﹣,1×3=,∴a=1,b=﹣4,∴二次函数解析式是y=x2﹣4x+3;(2)∵二次函数解析式是y=x2﹣4x+3,∴C(0,3).设直线BC的解析式为y=kx+t(k≠0),则,解得:.∴直线BC的解析式为y=﹣x+3.设点M(m,m2﹣4m+3),过点M作MN∥y轴,交BC于点N,∴N(m,﹣m+3),∴MN=﹣m+3﹣m2+4m﹣3=﹣m2+3m,∵A(1,0)、B(3,0),C(0,3).∴S△MOC=OC•m=m,S△MBC=MN•OB=﹣m2+m,∵△MOC的面积是△MBC面积的3倍,∴m=3(﹣m2+m),∴m=0(舍去)或,∴点M的坐标为(,﹣);(3)抛物线上存在一点N,使得∠BCN=∠ACB.过点B作BE⊥AB交CN与E,∵B(3,0),C(0,3).∴OB=OC=3,∴∠OBC=45°,∴∠OBC=∠EBC=45°,∵BC=BC,∠BCN=∠ACB.∴△ABC≌△EBC(ASA),∴BE=AB=2,∴E(3,2),设直线CN的解析式为y=mx+n,∴,解得,∴直线CN的解析式为y=﹣x+3,联立y=x2﹣4x+3得,或(舍去),∴抛物线上存在一点N,使得∠BCN=∠ACB.点N的横坐标为.2.如图,抛物线与x轴交于点A和点C(﹣1,0),与y轴交于点B(0,3),连接AB,BC,对称轴PD交AB与点E.(1)求抛物线的解析式;(2)如图2,试探究:线段BC上是否存在点M,使∠EMO=∠ABC,若存在,求出点M的坐标;若不存在,请说明理由;(3)如图3,点Q是抛物线的对称轴PD上一点,若以点Q、A、B为顶点的三角形是锐角三角形,请直接写出点Q纵坐标n的取值范围.【分析】(1)用待定系数法即可求解;(2)先求出A(4,0),可得抛物线的对称轴为x==,证明∠ACB=∠ABC,△MCO∽△EBM,可得MC•BM=BE•CO,求出MC,即可求解;(3)当∠BAQ为直角时,求出直线BQ的表达式为y=x+3,得到n=5;当∠BQA为直角时,利用解直角三角形的方法求出n=;当∠BAQ为直角时,同理可得,n=﹣,进而求解.【解答】解:(1)由题意得:,解得,故抛物线的表达式为y=﹣x2+x+3;(2)对于y=﹣x2+x+3,令y=﹣x2+x+3=0,解得x=4或﹣1,故点A的坐标为(4,0),∵点A(4,0),B(0,3),C(﹣1,0),∴抛物线的对称轴为x==,直线AB的表达式为y=﹣x+3,AB==5=AC.∴∠ACB=∠ABC,点E(,),∵∠CME=∠CMO+∠OME=∠ABC+∠MEB,∠ABC=∠OME,∴∠CMO=∠BEM.∴△MCO∽△EBM,∴,∴MC•BM=BE•CO,∵B(0,3),E(,),∴BE==,∴MC•BM=,∵MC+BM=BC==.∴MC=或MC=.∴=或=,如图,过M作MK⊥x轴于K,则MK∥y轴,∴△CMK∽△CBO,∴=或,即=或,∴MK=或,∵B(0,3),C(﹣1,0),∴直线BC的解析式为y=3x+3,∴M的﹣横坐标为﹣或﹣,∴点M的坐标为(﹣,)或(﹣,);(3)设点Q的坐标为(,n),当∠ABQ为直角时,如图,设BQ交x轴于点H,∵∠ABQ=90°,∴∠BAO+∠BHA=90°,∵∠BAO+∠ABO=90°,∴∠ABO=∠BHA,∵tan∠ABO=,∴tan∠BHO=,故设直线BQ的表达式为y=x+t,∵该直线过点B(0,3),∴t=3,∴直线BQ的表达式为y=x+3,当x=时,y=x+3=5,即n=5;②当∠BQA为直角时,过点Q作直线MN交y轴于点N,交过点A与y轴的平行线于点M,∵∠BQN+∠MQA=90°,∠MQA+∠MAQ=90°,∴∠BQN=∠MAQ,∴tan∠BQN=tan∠MAQ,即,则,解得n=;③当∠BAQ为直角时,同理可得,n=﹣;综上,以点Q、A、B为顶点的三角形是锐角三角形,则△ABQ不为直角三角形,故点Q纵坐标n的取值范围为﹣<n<或<n<5.3.如图1,抛物线y=ax2﹣x+c与x轴交于A(﹣2,0)、B(4,0)两点,与y轴交于点C,直线l与抛物线交于A、D两点,其中D点的横坐标为2.(1)求抛物线的解析式以及直线AD的解析式;(2)点P是抛物线上位于直线AD下方的动点,过点P作x轴,y轴的平行线,交AD于点E、F,当PE+PF取最大值时,求点P的坐标;(3)如图2,连接AC,点Q在抛物线上,且满足∠QAB=2∠ACO,求点的坐标.【分析】(1)将A(﹣2,0),B(4,0)代入y=ax2﹣x+c,求出抛物线的解析式,求出D点坐标后,利用待定系数法求直线AD的解析式;(2)由题意可得PF=PE,设P(x,x2﹣x﹣4),F(x,﹣x﹣2),则PF=﹣x2+2,当PF最大时,PF+PE就最大,由此求解即可;(3)在BO上截取ON=OA,连接CN,过点A作AH⊥CN,证明△OCN≌△OCA(SAS),则可推导出∠QAB=∠NCA,再由S△ANC=AN×OC=AH×CN,求出tan∠NCA=,分两种情况讨论:当点Q在AB的下方时,设AQ与y轴交于点I,tan∠NCA=tan∠QAB=,可求点I(0,﹣),求出直线AQ解析式为y=﹣x﹣,联立方程组得:,可求点Q坐标为(,﹣),当点Q在AB的上方时,同理可求直线AQ解析式为:y=x+,联立方程组得:,可求点Q坐标为(,).【解答】解:(1)将A(﹣2,0),B(4,0)代入y=ax2﹣x+c,得,解得,∴抛物线解析式为y=x2﹣x﹣4,当x=2时,y=﹣4,∴D(2,﹣4),设直线AD的解析式为y=kx+b,将A(﹣2,0)D(2,﹣4)代入,得,解得,∴直线AD的解析式为y=﹣x﹣2;(2)根据题意作图,如图1,在y=﹣x﹣2上,当x=0时,y=﹣2,∴AD与y轴的交点M的坐标为(0,﹣2),∴OA=OM,∠AOM=90°,∴∠OAB=45°,∵PE∥x轴,PF∥y轴,∴∠PEF=∠OAB=45°,∠EPF=90°,∴PF=PE,设P(x,x2﹣x﹣4),F(x,﹣x﹣2),∴PF=﹣x2+2,∵P在AD的下方,∴﹣2<x<2,当x=0时,PF有最大值为2,此时PF+PE最大,∴P(0,﹣4);(3)在BO上截取ON=OA,连接CN,过点A作AH⊥CN,如图2,∵点A(﹣2,0),点C(0,﹣4),∴OA=2,OC=4,∴AC=2,∵ON=OA,∠CON=∠COA=90°,OC=OC,∴△OCN≌△OCA(SAS),∴∠ACO=∠NCO,CN=AC=2,∴∠NCA=2∠ACO,∵∠QAB=2∠ACO,∴∠QAB=∠NCA,∵S△ANC=AN×OC=AH×CN,∴AH=,∴CH=,∴tan∠NCA=,如图3,当点Q在AB的下方时,设AQ与y轴交于点I,∵∠QAB=∠NCA,∴tan∠NCA=tan∠QAB=,∴OI=,∴点I(0,﹣),又∵点A(﹣2,0),∴直线AQ解析式为:y=﹣x﹣,联立方程组得:,解得:或(不合题意舍去),∴点Q坐标为(,﹣),当点Q在AB的上方时,同理可求直线AQ解析式为:y=x+,联立方程组得:,解得:(不合题意舍去)或,∴点Q坐标为(,),综上所述:点Q的坐标为(,﹣)或(,).。

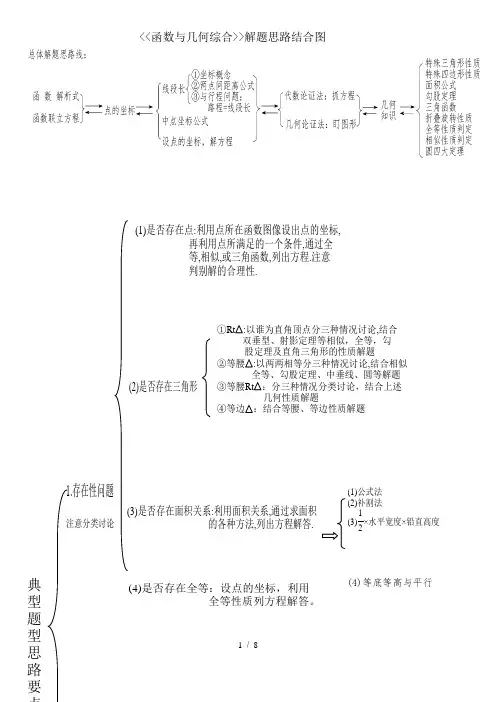
<<函数与几何综合>>解题思路结合图(1)公式法(2)补割法(3)12×水平宽度×铅直高度注意分类讨论1.存在性问题(1)是否存在点:利用点所在函数图像设出点的坐标, 再利用点所满足的一个条件,通过全 等,相似,或三角函数,列出方程.注意 判别解的合理性.典型题型 (2)是否存在三角形①Rt :以谁为直角顶点分三种情况讨论,结合 双垂型、射影定理等相似,全等,勾 股定理及直角三角形的性质解题②等腰:以两两相等分三种情况讨论,结合相似 全等、勾股定理、中垂线、圆等解题③等腰Rt :分三种情况分类讨论,结合上述 几何性质解题④等边:结合等腰、等边性质解题(3)是否存在面积关系:利用面积关系,通过求面积 的各种方法,列出方程解答.(4)是否存在全等:设点的坐标,利用 全等性质列方程解答。
(4)等底等高与平行(5)是否存在相似:一般利用等角分两种情况分类讨论,利用相似性质列方程解答(7)是否存在矩形、菱形、正方形:结合点的坐标, 利用它们的判定或性质及相似等列方程解答。
2.最值问题(1)线段最值①求解析式,利用二次函数配方求最值; ②垂线段最短、两点间线段最短 (转化为同一线段、将军饮马问题)(2)线段和差或周长最值:①解析式求最值;②将军饮马问题(3)面积最值:利用面积三种方法,列解析式求最值3.取值范围问题:①善于抓住图形位置特点,确定最大/小值; ②求解析式解不等式方程.4.线段定值问题:①直接计算;②如果题目没给出定值的,可利用特殊位置、 极端位置先探求出定值,然后加以一般化证明。
(6)是否存在平行四边形①几何论证法:以已知边为长边、短边及对角线去找图②代数论证法:选三点,以两两的连线为对角线,利用中点坐标公式分三种情况讨论计算出第四点坐标③平行四边形顶点的横纵坐标的差相等,利用平移表示 各点坐标,计算上可以简化,用于表示各顶点坐标①点动:依解析式设动点坐标②线动总体思路:圆只是周围是曲线的多边形 全等或相似勾股等照常用①求角或三角函数:直接求或等量替换 圆心或圆周角定理 切线性质,内接四边形对角性质 弦切角性质②求线段:垂径定理 切线性质③辅助线:(1)连半径,构造等腰(2)见弦必做弦心距,构造RT △(3)见切线必连圆心与切点,构造RT △ (4)见直径,构造90°圆周角基本思路:在变化中找到不变的性质③面动:折叠,平移,旋转5.动态问题6.圆典型题型思路要点与行程问题结合的动态问题:先用字母表示出各线段,根据 各线位置,结合相似全等等几 何知识列方程解答题型解读1 二次函数与几何综合题的两种解题方法【分析思路】在二次函数与几何综合的各种题型中,只有一条总体分析思路线:解析式(方程)←→点的坐标←→线段长←→几何问题,但在具体解题分析过程中,求点的坐标或线段长时,思考方向却有两种:可以由左往右思考,即“由解析式或方程求点的坐标,由点的坐标求线段长”,这是“代数论证方法”;也可以由右往左思考,即“由几何问题求线段长,由线段长求点的坐标”,这是“几何论证方法”。

二次函数y=a (x-h)2+k(a ≠0)的图象与性质—知识讲解(提高)【学习目标】1.会用描点法画出二次函数(a 、h 、k 常数,a ≠0)的图象.掌握抛物线与图象之间的关系;2.熟练掌握函数的有关性质,并能用函数的性质解决一些实际问题;3.经历探索的图象及性质的过程,体验与、、之间的转化过程,深刻理解数学建模思想及数形结合的思想方法.【要点梳理】要点一、函数2()(0)y a x h a =-≠与函数2()(0)y a x h k a =-+≠的图象与性质1.函数2()(0)y a x h a =-≠的图象与性质2.函数2()(0)y a x h k a =-+≠的图象与性质要点诠释:二次函数的图象常与直线、三角形、面积问题结合在一起,借助它的图象与性质.运用数形结合、函数、方程思想解决问题.要点二、二次函数的平移 1.平移步骤:2()y a x h k =-+2()y a x h k =-+2y ax =2()y a x h k =-+2()y a x h k =-+2()y a x h k =-+2()y a x h k =-+2y ax =2y ax k =+2()y a x h =-2()+(0y a x h k a =-≠)⑴ 将抛物线解析式转化成顶点式,确定其顶点坐标; ⑵ 保持抛物线的形状不变,将其顶点平移到处,具体平移方法如下:2.平移规律:在原有函数的基础上“值正右移,负左移;值正上移,负下移”.概括成八个字“左加右减,上加下减”. 要点诠释:⑴沿轴平移:向上(下)平移个单位,变成(或)⑵沿x 轴平移:向左(右)平移个单位,变成(或)【典型例题】类型一、二次函数2()(0)y a x h k a =-+≠图象及性质1. 已知是由抛物线向上平移2个单位长度,再向右平移1个单位长度得到的抛物线.(1)求出a 、h 、k 的值;(2)在同一坐标系中,画出与的图象; (3)观察的图象,当x 取何值时,y 随x 的增大而增大;当x 取何值时,y 随x 增大而减小,并求出函数的最值;(4)观察的图象,你能说出对于一切x 的值,函数y 的取值范围吗? 【答案与解析】()2y a x h k =-+()h k ,2y ax =()h k,h k c bx ax y ++=2y m c bx ax y ++=2m c bx ax y +++=2m c bx ax y -++=2c bx ax y ++=2m c bx ax y ++=2c m x b m x a y ++++=)()(2c m x b m x a y +-+-=)()(22()y a x h k =-+212y x =-2()y a x h k =-+212y x =-2()y a x h k =-+2()y a x h k =-+(1)∵ 抛物线向上平移2个单位长度, 再向右平移1个单位长度得到的抛物线是, ∴ ,1h =,. (2)函数与的图象如图所示.(3)观察的图象知,当时,y 随x 的增大而增大; 当时,y 随x 增大而减小,当x =1时,函数y 有最大值是2.(4)由图象知,对于一切x 的值,总有函数值y ≤2. 【总结升华】先根据平移的性质求出抛物线平移后的抛物线的解析式,再对比得到a 、h 、k 的值,然后画出图象,由图象回答问题.举一反三:【变式】把二次函数的图象先向左平移2个单位,再向上平移4个单位,得到二次函数的图象. (1)试确定a 、h 、k 的值;(2)指出二次函数的开口方向,对称轴和顶点坐标,分析函数的增减性. 【答案】(1).(2)开口向下,对称轴x=1, 顶点坐标为(1,-5), 当x ≥1时,y 随x 的增大而减小; 当x <1时,y 随x 的增大而增大.212y x =-21(1)22y x =--+12a =-2k =21(1)22y x =--+212y x =-21(1)22y x =--+1x <1x >212y x =-2()y a x h k =-+2()y a x h k =-+21(1)12y x =-+-2()y a x h k =-+1,1,52a h k =-==-2. 已知函数,则使y=k 成立的x 值恰好有三个,则k 的值为( ) A .0B .1C .2D .3【答案】D ;【解析】函数 的图象如图: ,根据图象知道当y=3时,对应成立的x 恰好有三个,∴k=3. 故选D .【总结升华】此题主要考查了利用二次函数的图象解决交点问题,解题的关键是把解方程的问题转换为根据函数图象找交点的问题.类型二、二次函数2()(0)y a x h k a =-+≠性质的综合应用3.(2019秋•滨海县期末)已知:二次函数y=x 2﹣4x+3. (1)求出该二次函数图象的对称轴和顶点坐标; (2)求出该抛物线与x 轴的交点坐标; (3)当x 取何值时,y <0. 【解析】解:(1)∵y=x 2﹣4x+3,∵y=(x ﹣2)2﹣1, ∵对称轴为:直线x=2, ∵顶点(2,﹣1); (2)令y=0,则,x 2﹣4x+3=0, ∵(x ﹣1)(x ﹣3)=0, ∵x 1=1,x 2=3,∵与x 轴的交点坐标为(1,0),(3,0); (3)当1<x <3时,y <0.【总结升华】本题考查了二次函数的性质,抛物线与x 轴坐标的求解方法,二次函数与不等式,熟记性质并把函数解析式整理成顶点式形式求解更简便. 举一反三:【变式】(2019秋•岑溪市期末)已知抛物线y=2(x ﹣1)2﹣8. (1)直接写出它的顶点坐标: ,对称轴: ;()()()()22113513x x y x x ⎧--⎪=⎨--⎪⎩≤>()()()()22113513x x y x x ⎧--⎪=⎨--⎪⎩≤>(2)x 取何值时,y 随x 增大而增大? 【答案与解析】解:(1)抛物线y=2(x ﹣1)2﹣8的顶点坐标为(1,﹣8),对称轴为直线x=1;故答案为(1,﹣8),直线x=1; (2)当x >1时,y 随x 增大而增大.4. 如图所示,抛物线的顶点为C ,与y 轴交点为A ,过点A 作y 轴的垂线,交抛物线于另一点B .(1)求直线AC 的解析式; (2)求△ABC 的面积;(3)当自变量x 满足什么条件时,有? 【答案与解析】(1)由知抛物线顶点C(-1,0),令x =0,得,∴ .由待定系数法可求出,∴(2)∵ 抛物线的对称轴为x =-1,根据抛物线对称性知.∴ . (3)根据图象知或时,有.【总结升华】 图象都经过A 点和C 点,说明A 点、C 点同时出现在两个图象上,A、C 两点的坐标均满足两个函数的解析式,解答这类题时,要画出函数图象,结合几何图形的性质,运用数形结合的思想和抛物线的对称性,特别要慎重处理平面直角坐标系中的坐标(数)与线段长度(形)之间的关系,不要出现符号上的错误,充分利用函数图象弄清函数值与自变量的关系,利用图象比较函数值的大小,或根据函数值的大小,确定自变量的变化范围.二次函数y=a (x -h)2+k(a ≠0)的图象与性质—巩固练习(提高)【巩固练习】 一、选择题213(1)y x +2y kx b =+12y y >211)y x +y =A b =k =2y 211)y x +(B -122ABC S =⨯=△0x >1x <-12y y >1. 不论m 取任何实数,抛物线y=a(x+m)2+m(a ≠0)的顶点都( )A.在y=x 直线上B.在直线y=-x 上C.在x 轴上D.在y 轴上 2.二次函数的最小值是( ).A .-2B .2C .-lD .13.如图所示,直角坐标系中,两条抛物线有相同的对称轴,下列关系不正确的是( ). A . B . C . D .,0n <第3题 第5题4.(2019•牡丹江)将抛物线y=(x ﹣1)2+3向左平移1个单位,得到的抛物线与y 轴的交点坐标是( ).A .(0,2)B .(0,3)C .(0,4)D .(0,7) 5.如图所示,抛物线的顶点坐标是P(1,3),则函数y 随自变量x 的增大而减小的x 的取值范围是( ). A . B . C . D .6.若二次函数.当≤l 时,随的增大而减小,则的取值范围是( )A .=lB .>lC .≥lD .≤l二、填空题 7.(2019•巴中模拟)抛物线y=x 2+2x+7的开口向 ,对称轴是 ,顶点是 .8.若点A (3,-4)在函数的图象上,则_ _.这个抛物线的对称轴是 ;点A关于抛物线对称轴的对称点是 .9.如果把抛物线向上平移-3个单位,再向右平移3个单位长度后得到抛物线,则求的值为 ;的值为 . 10.请写出一个二次函数,图象顶点为(-1,2),且不论x 取何值,函数值y 恒为正数.则此二次函数为______ __. 11.若二次函数中的x 取值为2≤x ≤5,则该函数的最大值为 ;最小值为 .12.已知抛物线y=x 2+x+b 2经过点,则y 1的值是_____.三、解答题2(1)2y x =-+h m =k n =k n >0k>3x >3x <1x >1x <2()1y x m =--x y x m m m m m 2)(m x y --==m 2)(b x a y +=3)2(212-+=x y a b 23(1)2y x =-+13.抛物线y=3(x-2)2与x轴交于点A,与y轴交于点B,求△AOB的面积和周长.14.(2019秋•湘西州期末)已知二次函数y=﹣x2+2(m﹣1)x+2m﹣m2的图象关于y轴对称,其顶点为A,与x轴两交点为B、C.(1)求B、C两点的坐标.(2)求∵ABC的面积.15.如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A,D不重合).BE•的垂直平分线交AB于M,交DC于N.(1)设AE=x,四边形ADNM的面积为S,写出S关于x的函数关系式;(2)当AE为何值时,四边形ADNM的面积最大?最大值是多少?【答案与解析】 一、选择题 1.【答案】B ;【解析】抛物线y=a(x+m)2+m(a ≠0)的顶点为(-m,m ),所以顶点在直线y=-x 上. 2.【答案】B ;【解析】当时,二次函数有最小值为2. 3.【答案】B ;【解析】由两抛物线对称轴相同可知,且由图象知,,0n <. 4.【答案】B ;【解析】抛物线y=(x ﹣1)2+3的顶点坐标为(1,3),把点(1,3)向左平移1个单位得到点的坐标为(0,3), 所以平移后抛物线解析式为y=x 2+3,所以得到的抛物线与y 轴的交点坐标为(0,3). 故选:B .5.【答案】C ;【解析】由顶点坐标P(1,3)知抛物线的对称轴为直线,因此当时,y 随x 的增大而减小. 6.【答案】C ;【解析】画出草图进行分析得出结论.二、填空题 7.【答案】上,x=﹣1,(﹣1,6). 【解析】∵y=x 2+2x+7,而a=1>0, ∵开口方向向上,∵y=y=x 2+2x+7=(x 2+2x+1)+6=(x+1)2+6, ∵对称轴是x=﹣1,顶点坐标是(﹣1,6).8.【答案】5或1; 直线x=5或直线x=1; 或(-1,-4);【解析】因为点A (3,-4)在函数的图象上,所以把点A (3,-4)代入函数得或;对称轴是直线x=5或直线x=1;点A关于抛物线对称轴的对称点是或(-1,-4).9.【答案】 ,; 【解析】抛物线向上平移-3个单位得到,再向右平移3个单位长度得到,即与相同,故,.1x =2(1)2y x =-+h m =k n >0k >1x =1x >(7,4)-2)(m x y --=2)(m x y --=5m =1m =(7,4)-12a =5b =2)(b x a y +=2()3y a x b =+-2(3)3y a x b =+--2(3)3y a x b =+--3)2(212-+=x y 12a =5b =10.【答案】 等;【解析】答案不唯一,只要抛物线开口向上即可,即,所以或等均可. 11.【答案】50;5.【解析】由于函数的顶点坐标为(1,2),,当时,y 随x 的增大而增大,当x =5时,函数在2≤x ≤5范围内的最大值为50; 当x =2时,函数的最小值为.12.【答案】;【解析】把1(,)4a -代入y=x 2+x+b 2得22104a a b +++=,221()02a b ++=, ,代入即可求得.三、解答题13.【答案与解析】∵ 抛物线y=3(x -2)2与x 轴交于点A ,与y 轴交于点B , ∴ A(2,0),B(0,12),∴ S △AOB =12,△AOB 的周长为14十.14.【答案与解析】解:由二次函数y=﹣x 2+2(m ﹣1)x+2m ﹣m 2的图象关于y 轴对称,得m ﹣1=0. 解得m=1.函数解析式为y=﹣x 2+1, 当y=0时,﹣x 2+1=0. 解得x 1=﹣1,x 2=1, 即B (﹣1,0),C (1,0); (2)当x=0时,y=1,即A (0,1), S △ABC =×2×1=1. 15.【答案与解析】(1)连接ME ,设MN 交BE 交于P , 根据题意得MB=ME ,MN ⊥BE .2(1)2y x =++0a >2(1)2y x =++22(1)2y x =++23(1)2y x =-+30a =>1x >23(21)25y =⨯-+=最小过N 作NF ⊥AB 于F ,在Rt △MBP 和Rt △MNF 中,∠MBP+∠BMN=90°, ∠FNM+∠BMN=90°,∠MBP=∠MNF ,又AB=FN ,Rt △EBA ≌Rt △MNF ,MF=AE=x . 在Rt△AME 中,由勾股定理得 ME 2=AE 2+AM 2,所以MB 2=x 2+AM 2,即(2-AM )2=x 2+AM 2,解得AM=1-x 2. 所以四边形ADNM 的面积S=×2=AM+AM+MF=2AM+AE=2(1-x 2)+x=-x 2+x+2. 即所求关系式为S=-x 2+x+2. (2)S=-x 2+x+2=-(x 2-2x+1)+=-(x-1)2+. 当AE=x=1时,四边形ADNM 的面积S 的值最大,此时最大值是.1422AM DN AM AF AD ++⨯=141212121252125252。

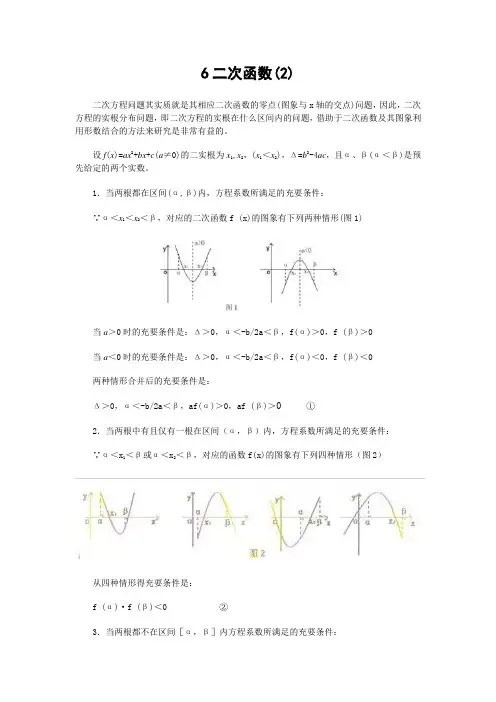
6二次函数(2)二次方程问题其实质就是其相应二次函数的零点(图象与x轴的交点)问题,因此,二次方程的实根分布问题,即二次方程的实根在什么区间内的问题,借助于二次函数及其图象利用形数结合的方法来研究是非常有益的。
设f(x)=ax2+bx+c(a≠0)的二实根为x1,x2,(x1<x2),Δ=b2-4ac,且α、β(α<β)是预先给定的两个实数。
1.当两根都在区间(α,β)内,方程系数所满足的充要条件:∵α<x1<x2<β,对应的二次函数f (x)的图象有下列两种情形(图1)当a>0时的充要条件是:Δ>0,α<-b/2a<β,f(α)>0,f (β)>0当a<0时的充要条件是:Δ>0,α<-b/2a<β,f(α)<0,f (β)<0两种情形合并后的充要条件是:Δ>0,α<-b/2a<β,af(α)>0,af (β)>0 ①2.当两根中有且仅有一根在区间(α,β)内,方程系数所满足的充要条件:∵α<x1<β或α<x2<β,对应的函数f(x)的图象有下列四种情形(图2)从四种情形得充要条件是:f (α)·f (β)<0 ②3.当两根都不在区间[α,β]内方程系数所满足的充要条件:(1)两根分别在区间[α,β]之外的两旁时:∵x1<α<β<x2,对应的函数f(x)的图象有下列两种情形(图3):当a>0时的充要条件是:f (α)<0,f (β)<0当a>0时的充要条件是:f (α)>0,f (β)>0两种情形合并后的充要条件是:af (α)<0,af (β)<0 ③(2)两根分别在区间[α,β]之外的同旁时:∵x1<x2<α<β或α<β<x1<x2,对应函数f(x)的图象有下列四种情形(图4):当x1<x2<α时的充要条件是:Δ>0,-b/2a<α,af (α)>0 ④当β<x1<x2时的充要条件是:Δ>0,-b/2a>β,af (β)>0 ⑤二次函数与二次不等式前面提到,一元二次不等式的解集相应于一元二次函数的正值、负值区间。

二次函数与几何综合(习题)➢例题示范例1:如图,抛物线y=ax2+2ax-3a 与x 轴交于A,B 两点(点A 在点B 的左侧),与y 轴交于点C,且OA=OC,连接AC.(1)求抛物线的解析式.(2)若点P 是直线AC 下方抛物线上一动点,求△ACP 面积的最大值.(3)若点E 在抛物线的对称轴上,抛物线上是否存在点F,使以A,B,E,F 为顶点的四边形是平行四边形?若存在,求出所有满足条件的点F 的坐标;若不存在,请说明理由.yA OB xC第一问:研究背景图形【思路分析】读题标注,注意到题中给出的表达式中各项系数都只含有字母a,可以求解A(-3,0),B(1,0),对称轴为直线x=-1;结合题中给出的OA=OC,可得C(0,-3),代入表达式,即可求得抛物线解析式.再结合所求线段长来观察几何图形,发现△AOC 为等腰直角三角形.【过程示范】解:(1)由y=ax2+2ax-3a=a(x+3)(x-1)可知A(-3,0),B(1,0),∵OA=OC,∴C(0,-3),将C(0,-3)代入y=ax2+2ax-3a,解得,a=1,∴y=x2+2x-3.1第二问:铅垂法求面积【思路分析】(1)整合信息,分析特征:由所求的目标入手分析,目标为S△ACP的最大值,分析A,C 为定点,P 为动点且P 在直线AC 下方的抛物线上运动,即-3<x P<0;(2)设计方案:注意到三条线段都是斜放置的线段,需要借助横平竖直的线段来表达,所以考虑利用铅垂法来表达S△ACP.第三问:平行四边形的存在性【思路分析】分析不变特征:以A,B,E,F 为顶点的四边形中,A,B 为定点,E,F 为动点,定点A,B 连接成为定线段AB.分析形成因素:要使这个四边形为平行四边形.首先考虑AB 在平行四边形中的作用,四个顶点用逗号隔开,位置不确定,则AB 既可以作边,也可以作对角线.画图求解:先根据平行四边形的判定来确定EF 和AB 之间应满足的条yA Q OB xPC23件,再通过平移和旋转来尝试画图,确定图形后设计方案求解.①AB 作为边时,依据平行四边形的判定,需满足 EF ∥AB 且 EF =AB ,要找 EF ,可借助平移.点 E 在对称轴上,沿直线容易平移,故将线段 AB 拿出来沿对称轴上下方向平移,确保点 E 在对称轴上,来找抛物线上的点 F .注意:在对称轴的左、右两侧分别平移.找出点之后,设出对称轴上 E 点坐标,利用平行且相等表达抛物线上 F 点坐标,代入抛物线解析式求解.②AB 作为对角线时,依据平行四边形的判定,需满足 AB , EF 互相平分,先找到定线段 AB 的中点,在旋转过程中找到 EF 恰好被 AB 中点平分的位置,因为 E 和 AB 中点都在抛物线对称轴上,说明 EF 所在直线即为抛物线对称轴,则与抛物线的交点(抛物线顶点)即为 F 点坐标.画图或推理,根据运动范围考虑是否找全各种情形. 【过程示范】(3)①当 AB 为边时,AB ∥EF 且 AB =EF , 如图所示,设 E 点坐标为(-1,m ), 当四边形是□ABFE 时,由 A (-3,0),B (1,0)可知,F 1(3,m ), 代入抛物线解析式,可得,m =12, ∴F 1(3,12);当四边形是□ABEF 时,由 A (-3,0),B (1,0)可知,F 2(-5,m ), 代入抛物线解析式,可得,m =12, ∴F 2(-5,12).②当 AB 为对角线时,AB 与 EF 互相平分, AB 的中点 D (-1,0),设 E (-1,m ),则 F (-1,-m ), 代入抛物线解析式,可得,m =4, ∴F 3(-1,-4).综上:F 1(3,12),F 2(-5,12),F 3(-1,-4).结果验证:➢巩固练习1.如图,直线y =-1x 与抛物线y =-1x2 + 6 交于A,B 两点,2 4C 是抛物线的顶点.(1)在直线AB 上方的抛物线上有一动点P,当△ABP 的面积最大时,点P 的坐标为.(2)若点M 在抛物线上,且以点M,A,B 以及另一点N 为顶点的平行四边形ABNM 的面积为240,则M,N 两点的坐标为.yCBO xAyCBO xA42.已知抛物线y=-mx2+4x+2m 与x 轴交于点A(α,0),B(β,0),且1+1=-2 .抛物线的对称轴为直线l,与y 轴的交点为点αβC,顶点为点D,点C 关于l 的对称点为点E.(1)抛物线的解析式为.(2)连接CD,在直线CD 下方的抛物线上有一动点G,当S△CDG=3,点G 的坐标为.(3)若点P 在抛物线上,点Q 在x 轴上,当以点D,E,P,Q 为顶点的四边形是平行四边形时,点Q 的坐标为.53.已知抛物线y=ax2-4ax+b 的对称轴为直线x=2,顶点为P,与x 轴交于A,B 两点,与y 轴交于点C,其中A(1,0),连接BC,PB,得到∠PBC=90°.(1)求抛物线的解析式.(2)抛物线上是否存在异于点P 的一点Q,使△BCQ 与△BCP 的面积相等?若存在,求出点Q 的坐标;若不存在,请说明理由.(3)若点E 是抛物线上一动点,点F 是x 轴上一动点,是否存在以B,C,E,F 为顶点的四边形是平行四边形?若存在,求出点F 的坐标;若不存在,请说明理由.64.如图,在平面直角坐标系xOy 中,△ABC 是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2).抛物线y=ax2-ax-b 与y 轴交于点D,且经过点C,连接AD,可得AB=AD.(1)求抛物线的解析式.(2)平移该抛物线的对称轴所在直线l.当l 移动到何处时,恰好将△ABC 的面积分为相等的两部分?(3)点P 是抛物线上一动点,点Q 是抛物线对称轴l 上一动点,是否存在点P,使以P,Q,A,B 为顶点的四边形是平行四边形?若存在,求出点P 的坐标;若不存在,说明理由.75.如图,二次函数图象的顶点为坐标系原点O,且经过点A(3,3),一次函数的图象经过点A和点B(6,0).(1)求二次函数与一次函数的解析式;(2)如果一次函数图象与y轴相交于点C,点D在线段AC上,与y轴平行的直线DE与二次函数图象相交于点E,∠CDO=∠OED,求点D的坐标;(3)当点D在直线AC上的一个动点时,以点O、C、D、E为顶点的四边形能成为平行四边形吗?请说明理由.6.已知关于二次函数y=x2﹣(4k+2)x+4k2+3k的图象与x轴有两个交点.(1)求k的取值范围;(2)若二次函数与x轴的两个交点坐标为(a,0),(b,0),并满足(a﹣b)2=2,求k的值,并写出二次函数的表达式;(3)如图所示,由(2)所得的抛物线与一次函数y=﹣3x +的图象相交于点C、点D,求三角形CDP的面积.7.如图1,二次函数y=a(x2﹣x﹣6)(a≠0)的图象过点C(1,﹣),与x轴交于A,B两点(点A在x轴的负半轴上),且A,C两点关于正比例函数y=kx(k≠0)的图8象对称.(1)求二次函数与正比例函数的解析式;(2)如图2,过点B作BD⊥x轴交正比例函数图象于点D,连接AC,交正比例函数的图象于点E,连接AD,CD.如果动点P从点A沿线段AD方向以每秒2个单位的速度向D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个点到达终点时,另一个点随之停止运动,连接PQ,QE,PE,设运动时间为t秒,是否存在某一刻,使PE,QE分别平分∠APQ和∠PQC?若存在,求出t的值;若不存在,请说明理由.8.如图,二次函数图象的顶点为坐标原点O,y轴为对称轴,且经过点A(3,3),一次函数的图象经过点A和点B(6,0).(1)求二次函数与一次函数的解析式;(2)如果一次函数图象与y轴相交于点C,E是抛物线上OA段上一点,过点E作y轴平行的直线DE与直线AC交于点D,∠DOE=∠EDA,求点E的坐标;(3)点M是线段AC延长线上的一个动点,过点M作y轴的平行线交抛物线于F,以点O、C、M、F为顶点的四边形能否为菱形?若能,求出点F的坐标;若不能,请说明理由.9.小明在学习时遇到这样一个问题:如果二次函数y=a1x2+b1x+c1(a1≠0,a1,b1,c1是常数)与y=a2x2+b2x+c2(a2≠0,a2,9b,c2是常数)满足a1+a2=0,b1=b2,c1+c2=0,则称这两个函数互为“旋转函2数”.求y=﹣x2+3x﹣2函数的“旋转函数”.小明是这样思考的:由y=﹣x2+3x﹣2函数可知a1=﹣1,b1=3,c1=﹣2,根据a1+a2=0b1=b2,c1+c2=0,求出a2,b2,c2,就能确定这个函数的“旋转函数”.请参考小明的方法解决下面的问题:(1)写出函数y=﹣x2+3x﹣2的“旋转函数”;(2)若函数y=﹣x2+mx﹣2与y=x2﹣2nx+n互为“旋转函数”,求(m+n)2016的值;(3)已知函数y =﹣(x+1)(x﹣4)的图象与x轴交于A,B两点,与y轴交于点C,点A,B,C关于原点的对称点分别是A,B1,C1,试证明经过点A1,B1,C1的二次函数与函1数y =﹣(x+1)(x﹣4)互为“旋转函数”.10.如图,已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0),C(0,3),与x轴交于另一点B,抛物线的顶点为D.(1)求此二次函数解析式;(2)连接DC、BC、DB,求证:△BCD是直角三角形;(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.11.如图,抛物线y=ax2+bx+c与x轴交与A(1,0),B(4,0)两点,与y轴交于点C (0,4)(1)求抛物线的解析式.(2)点P为抛物线上一动点,满足S△PBC =S△ABC,求P点的坐标.(3)点D为抛物线对称轴上一点,若△BCD是锐角三角形,求点D的纵坐标n的取值范围.1012.如图,已知直线y=x+2交x轴、y轴分别于点A、B,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x =﹣,且抛物线经过A、B两点,交x轴于另一点C.(1)求抛物线的解析式;(2)点M是抛物线x轴上方一点,∠MBA=∠CBO,求点M的坐标;(4)过点A作AB的垂线交y轴于点D,平移直线AD交抛物线于点E、F两点,连结EO、FO.若△EFO为以EF为斜边的直角三角形,求平移后的直线的解析式.13.在平面直角坐标系xOy中,对于图形G,若存在一个正方形γ,这个正方形的某条边与x轴垂直,且图形G上的所有的点都在该正方形的内部或者边上,则称该正方形γ为图形G的一个正覆盖.很显然,如果图形G存在一个正覆盖,则它的正覆益有无数个,我们将图形G的所有正覆盖中边长最小的一个,称为它的紧覆盖,如图所示,图形G为三条线段和一个圆弧组成的封闭图形,图中的三个正方形均为图形G的正覆盖,其中正方形ABCD就是图形G的紧覆盖.(1)对于半径为2的⊙O,它的紧覆盖的边长为.(2)如图1,点P为直线y=﹣2x+3上一动点,若线段OP的紧覆盖的边长为2,求点P的坐标.(3)如图2,直线y=3x+3与x轴,y轴分别交于A,B,11①以O为圆心,r为半径的⊙O与线段AB有公共点,且由⊙O与线段AB组成的图形G的紧覆益的边长小于4,直接写出r的取值范围;②若在抛物线y=ax2+2ax﹣2(a≠0)上存在点C,使得△ABC的紧覆益的边长为3,直接写出a 的取值范围.14.如图1,在平面直角坐标系中,矩形OABC如图所示放置,点A在x轴上,点B的坐标为(n,1)(n>0),将此矩形绕O点逆时针旋转90°得到矩形OA′B′C′,抛物线y=ax2+bx+c(a≠0)经过A、A′、C′三点.(1)求此抛物线的解析式(a、b、c可用含n的式子表示);(2)若抛物线对称轴是x=1的一条直线,直线y=kx+2(k≠0)与抛物线相交于两点D (x1,y1)、E(x2、y2)(x1<x2),当|x1﹣x2|最小时,求抛物线与直线的交点D和E 的坐标;(3)若抛物线对称轴是x=1的一条直线,如图2,点M是抛物线的顶点,点P是y轴上一动点,点Q是坐标平面内一点,四边形APQM是以PM为对角线的平行四边形,点Q′与点Q 关于直线CM对称,连接MQ′、PQ′,当△PMQ′与平行四边形APQM重合部分的面积是平行四边形的面积的时,求平行四边形APQM的面积.1215.如图①,在平面直角坐标系中,抛物线y =x2﹣x﹣2分别与x轴交于A,B两点,与y轴交于C点,直线EF垂直平分线段BC,分别交BC于点E,y轴于点F,交x轴于D.(1)判定△ABC的形状;(2)在线段BC下方的抛物线上有一点P,当△BCP面积最大时,求点P的坐标及△BCP面积的最大值;(3)如图②,过点E作EH⊥x轴于点H,将△EHD绕点E逆时针旋转一个角度α(0°≤α≤90°),∠DEH的两边分别交线段BO,CO于点T,点K,当△KET为等腰三角形时,求此时KT的值.16.如图,在平面直角坐标系中,抛物线y =﹣x2+bx+c与x轴交于点A,B,与y轴交于点C,直线BC的解析式为y=﹣x+6.(1)求抛物线的解析式;(2)点M为线段BC上方抛物线上的任意一点,连接MB,MC,点N为抛物线对称轴上任意一13点,当M到直线BC的距离最大时,求点M的坐标及MN+NB的最小值;(3)在(2)中,点M到直线BC的距离最大时,连接OM交BC于点E,将原抛物线沿射线OM 平移,平移后的抛物线记为y′,当y′经过点M时,它的对称轴与x轴的交点记为H.将△BOE绕点B逆时针旋转60°至△BO1E1,再将△BO1E1沿着直线O1H平移,得到△B 1O2E2,在平面内是否存在点F,使以点C,H,B1,F为顶点的四边形是以B1H为边的菱形.若存在,直接写出点B1的横坐标;若不存在,请说明理由.【参考答案】1415。
二次函数与几何综合专题----面积问题【模型解读】1.比例问题大部分题目的处理方法可以总结为两种:(1)计算;(2)转化. 策略一:运用比例计算类 策略二:转化面积比如图,B 、D 、C 三点共线,考虑△ABD 和△ACD 面积之比.转化为底:共高,面积之比化为底边之比:则.更一般地,对于共边的两三角形△ABD 和△ACD ,连接BC ,与AD 交于点E ,则.策略三:进阶版转化 在有些问题中,高或底边并不容易表示,所以还需在此基础上进一步转化为其他线段比值,比如常见有:“A ”字型线段比、“8”字型线段比. “A ”字型线段比:.DCBA::ABDACDSSBD CD =HABCD :::ABDACDSSBM CN BE CE ==M N EDCBA :::ABDACDSSBD CD BA AM ==“8”字型线段比:.转化为垂线:共底,面积之比化为高之比:.面积能算那就算,算不出来就转换; 底边不行就作高,还有垂线和平行.2.铅垂高求三角形的面积是几何题中常见问题之一,可用的方法也比较多,比如面积公式、割补、等积变形、三角函数甚至海伦公式,本文介绍的方法是在二次函数问题中常用的一种求面积的方法——铅垂法. 【问题描述】在平面直角坐标系中,已知()1,1A 、()7,3B 、()4,7C ,求△ABC 的面积.MDCBA:::ABDACDSSBD CD AB CM ==MDCBA:::ABDACDSSBD CD BM CN ==MNABCD【分析】显然对于这样一个位置的三角形,面积公式并不太好用,割补倒是可以一试,比如这样:构造矩形ADEF ,用矩形面积减去三个三角形面积即可得△ABC 面积. 这是在“补”,同样可以采用“割”:()111222ABCACDBCDSSSCD AE CD BF CD AE BF =+=⋅+⋅=+ 此处AE +AF 即为A 、B 两点之间的水平距离.由题意得:AE +BF =6. 下求CD :根据A 、B 两点坐标求得直线AB 解析式为:1233y x =+由点C 坐标(4,7)可得D 点横坐标为4, 将4代入直线AB 解析式得D 点纵坐标为2, 故D 点坐标为(4,2),CD =5, 165152ABCS=⨯⨯=.【方法总结】 作以下定义:A 、B 两点之间的水平距离称为“水平宽”;过点C 作x 轴的垂线与AB 交点为D ,线段CD 即为AB 边的“铅垂高”.如图可得:=2ABCS⨯水平宽铅垂高【解题步骤】(1)求A 、B 两点水平距离,即水平宽;(2)过点C 作x 轴垂线与AB 交于点D ,可得点D 横坐标同点C ; (3)求直线AB 解析式并代入点D 横坐标,得点D 纵坐标; (4)根据C 、D 坐标求得铅垂高; (5)利用公式求得三角形面积.引例1:如图,在平面直角坐标系xOy 中,抛物线2y x bx c =++与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,3OA OC ==,顶点为D ,对称轴交x 轴于点E . (1)求抛物线的解析式、对称轴及顶点D 的坐标.解:∵3OA OC ==, ∴A (-3,0),C (0,-3),∴()20333b c c ⎧=--+⎪⎨-=⎪⎩,解得:23b c =⎧⎨=-⎩,∴抛物线的解析式为:223y x x =+-,对称轴为:直线x =-1,顶点坐标为:D (-1,-4).(2)求四边形ABCD 的面积.解:由例题可知该二次函数的解析式为223y x x =+-,()()()()3,0,1,0,0,3,1,4A B C D ----, 连接OD ,如图所示,∴DOC △的底为OC ,高为点D 的纵坐标的绝对值, ∵AODDOCBOCABCD S SSS=++四边形,∴1113431139222ABCD S =⨯⨯+⨯⨯+⨯⨯=四边形(3)抛物线上是一点P ,若△PAC 面积为1,求P 点坐标(4)抛物线上是否存在点P ,使得ABP ABC S S =△△,若存在,求出点P 的坐标;若不存在,请说明理由.解:设点()2,23P m m m +-,点()0,3C -,由ABP ABC S S =△△可知:△ABP 与△ABC 同底,为AB ,则有点P 与点C 的纵坐标的绝对值相等, ∴P C y y =,∴2233m m +-=-或3,①当2233m m +-=-时,解得:2m =-或0m =(舍去), 此时点P 的坐标为()2,3--;②当2233m m +-=时,解得:1m ==-,此时点P 的坐标为()1-或()1-,综上所述:当ABP ABC S S =△△时,点P 的坐标为()2,3--或()1-或()1-(5)抛物线上是否存在点P ,使得ACPACDSS=,若存在,求出点P 的坐标;若不存在,请说明理由.解:过点D 作DM ∥y 轴,交AC 于点M ,过点P 作PN ∥y 轴,交AC 延长线于点N ,如图所示:∵()1,4D --,∴点M 的横坐标为-1,代入直线AC 的解析式3y x =--得:=2y -, ∴2DM =,根据铅垂法可知13232ADCACPSS =⨯⨯==,设()2,23P a a a +-,则有(),3N a a --,由铅垂法可把△ACP 的面积看作以AC 为水平宽,PN 为铅垂高,∴222333PN a a a a a =+-++=+,∴213332ACPSa a =⨯⨯+=,即232a a +=,∴当232a a +=时,解得:12a a =,此时点P 的坐标为⎝⎭或⎝⎭; 当232a a +=-时,解得:122,1a a =-=-(不符合题意,舍去), 此时点P 的坐标为()2,3--;综上所述:当ACPACDSS=时,点P 的坐标为()2,3--或⎝⎭或⎝⎭(6)抛物线上是否存在点P ,使得12ACPACD S S =(32ACPACD SS =),若存在,求出点P 的坐标;若不存在,请说明理由.(7)抛物线上是否存在点P ,使得AOPCOPSS=,若存在,求出点P 的坐标;若不存在,请说明理由.解:∵()()3,0,0,3A C --, ∴3OA OC ==,∴AOP 与COP 的底相等, ∴当AOPCOPSS=时,则AOP 与COP 的高也相等,由题意知AOP 的高是点P 的纵坐标的绝对值,而COP 的高是点P 的横坐标的绝对值,设()2,23P a a a +-,∴223a a a =+-,∴当223a a a =+-时,解得:12a a =,此时点P 的坐标为⎝⎭或⎝⎭;当223a a a =--+时,解得:12a a ==此时点P 的坐标为⎝⎭或⎝⎭;综上所述:当AOPCOP SS=时,点点P 的坐标为⎝⎭或⎝⎭或⎝⎭或⎝⎭(8)抛物线上是否存在点P ,使得BP 平分ABC 的面积,若存在,求出点P 的坐标;若不存在,请说明理由.解:设直线BP 与线段AC 交于点H ,如图所示:∵BP 平分ABC 的面积,∴线段BH 是ABC 的中线,即点H 是线段AC 的中点, ∵()()3,0,0,3A C --,∴根据中点坐标公式可得33,22H ⎛⎫-- ⎪⎝⎭,设直线BH 的解析式为y kx b =+,把点()33,,1,022H B ⎛⎫-- ⎪⎝⎭代入得:33220k b k b ⎧-+=-⎪⎨⎪+=⎩,解得:3535k b ⎧=⎪⎪⎨⎪=-⎪⎩, ∴直线BH 的解析式为3355y x =-, 联立抛物线与直线解析式得:2332355x x x +-=-, 解得:1212,15x x =-=(不符合题意,舍去), ∴1251,525⎛⎫-- ⎪⎝⎭(9)抛物线上是否存在点P ,使得BP 把ABC 的面积分为1:2,若存在,求出点P 的坐标;若不存在,请说明理由.(10)直线AC 下方的抛物线上有一动点P ,过点P 作PM x ⊥轴于点M ,使得AC 平分APM △的面积,若存在,求出点P 的坐标;若不存在,请说明理由.解:设直线AC 与线段PM 交于点Q ,如图所示:设()2,23P a a a +-,∵PM x ⊥轴, ∴(),0M a ,∵AC 平分APM △的面积,∴线段AQ 是APM △的中线,即点Q 是PM 的中点,∴根据中点坐标公式可得213,22Q a a a ⎛⎫+- ⎪⎝⎭,∵点Q 在直线AC 上,∴213322a a a +-=--, 解得:121,3a a =-=-(不符合题意,舍去), ∴()1,4P --(11)直线AC 下方的抛物线上有一动点P ,过点P 作PM x ⊥轴于点M ,交直线AC 于点N ,使得:2:1AMNANPSS=,若存在,求出点P 的坐标;若不存在,请说明理由.解:由:2:1AMNANPS S=,可知:2:1MN NP =,∴23MN MP =, 设()2,23P a a a +-,则有223MP a a =--+,∴224233MN a =--+,∴224,233N a a a ⎛⎫+- ⎪⎝⎭,∵点N 在直线AC 上,∴2242333a a a +-=--,化简得22730a a ++=, 解得:121,32a a =-=-(不符合题意,舍去),∴115,24P ⎛⎫-- ⎪⎝⎭(12)过E 点的直线l 将四边形ABCD 的面积分成2:7两部分,求直线l 的解析式.解:由(2)可得9ABCD S =四边形,①当过点E 的直线l 靠近点B 时,交直线BC 于点F ,把四边形ABCD 的面积分成2:7两部分,如图所示:∵点E 在抛物线的对称轴上, ∴BE =2,设点F 的纵坐标为y F , ∴2929EBFS=⨯=,即1222EBFy S F =⨯⨯=, ∴2y F =-,(2不符合题意,舍去),设BC 的解析式为:y kx b =+,则把点()()1,0,0,3B C -代入得:03k b b +=⎧⎨=-⎩,解得:33k b =⎧⎨=-⎩, ∴BC 的解析式为:33y x =-, ∵点F 在直线BC 上, ∴233x -=-,解得:13x =,∴1,23F ⎛⎫- ⎪⎝⎭,设直线l 的解析式为11y k x b =+,把点E 、F 代入得: 11111230k b k b ⎧+=-⎪⎨⎪-+=⎩,解得:113232k b ⎧=-⎪⎪⎨⎪=-⎪⎩, ∴直线l 的解析式为3322y x =--; ②当过点E 的直线l 靠近点A 时,交直线AD 于点G ,把四边形ABCD 的面积分成2:7两部分,如图所示:由①可知2AE =,1222AEGy S G =⨯⨯=, ∴2y G =-,设直线AD 的解析式为:y mx n =+,则把点()()3,0,1,4A D ---代入得:304m n m n -+=⎧⎨-+=-⎩,解得:26m n =-⎧⎨=-⎩, ∴直线AD 的解析式为:26y x =--, ∵点G 在直线AD 上,∴226x -=--,解得:2x =-, ∴()2,2G --,设直线l 的解析式为11y m x n =+,把点E 、G 代入得:1111220m n m n -+=-⎧⎨-+=⎩,解得:1122m n =⎧⎨=⎩, ∴直线l 的解析式为22y x =+;综上所述:当直线l 把四边形ABCD 的面积分成2:7两部分时,则直线l 的解析式为22y x =+或3322y x =--(13)抛物线上有一点P ,其横坐标为t ,抛物线上另有一点Q ,其横坐标为4t +,线段PQ 上有一点M ,作//MN y 轴交抛物线于点N ,求PNQ 面积的最大值.解:由抛物线上有一点P ,其横坐标为t ,抛物线上另有一点Q ,其横坐标为4t +,可知:()()22,23,4,1021P t t t Q t t t +-+++,设直线PQ 的解析式为y kx b =+,把点()()22,23,4,1021P t t t Q t t t +-+++代入得:()222341021tk b t t t k b t t ⎧+=+-⎪⎨++=++⎪⎩,解得:22643k t b t t =+⎧⎨=---⎩, ∴直线PQ 的解析式为()22643y t x t t =+---, 设点()2,23N m m m +-,∵//MN y 轴,∴()()2,2643M m t m t t +---,∴()()2222264323244MN t m t t m m m t m t t =+-----+=-++--,由铅垂法可知,P Q 的水平距离即为水平宽,即为44t t +-=,MN 为铅垂高, ∴()22142442PNQSm t m t t ⎡⎤=⨯⨯-++--⎣⎦ =()2224828m t m t t -++--=()2228m t ---+, ∵-2<0,开口向下,∴当2m t =+时,PNQ 的面积有最大值,最大值为8引例2:如图,已知抛物线过A (4,0)、B (0,4)、C (-2,0)三点,P 是抛物线上一点 (1)求抛物线解析式答案:2142x x -++(2)若P 在直线AB 上方,求四边形PBCA 面积最大值,(3)点D 是点B 关于关于x 轴的对称点,连接CD ,点P 是第一象限上一点,求△PCD 面积最大值△APB 面积为:12PH •△△AO (AO 是PBH ,PAH 两个三角形高之和)设P (m ,-12m ²+m +4),H (m ,-m +4)PH=-12m ²+2m (上面的点减去下面的点)当m =-b2a时,PH 取最大值2△分离出面积为定值的ABCH过动点P作y轴平行线交对边(延长)与点HS △PCD =S △PCH -S △PDH =12PH •CO=PH推导过程如下:以PH为底,设△PHC的高为h1,△PDH的高为h212PH •h1-12PH •h2=12PH •h1-h2()=12PH •CO(4)若P 在直线AB 上方,作PF ⊥AB ,交线段AB 于F,作PE ∥y 轴交AB 于E ,求△PEF 面积的最大值(5)若P 在直线AB 上方,连接OP ,交AB 于D ,求PDOD的最大值(6)若P 在直线AB 上方,连接CP ,交AB 于D ,△PDA 面积为S 1,△CDA 面积为S 2,求21S S 的最小值x第一步:面积比转换为共线的边之比S 2S 1=CD PD第二步:构造,共线的边之比转换成平行边之比CD PD =CG PH =6PH1.将抛物线y=ax2(a≠0)向左平移1个单位,再向上平移4个单位后,得到抛物线H:y=a(x﹣h)2+k.抛物线H与x轴交于点A,B,与y轴交于点C.已知A(﹣3,0),点P是抛物线H上的一个动点.(1)求抛物线H的表达式;(2)如图,点P在线段AC上方的抛物线H上运动(不与A,C重合),过点P作PD⊥AB,垂足为D,PD交AC 于点E.作PF⊥AC,垂足为F,求△PEF的面积的最大值;【解答】解:(1)由题意得抛物线的顶点坐标为(﹣1,4),∴抛物线H:y=a(x+1)2+4,将A(﹣3,0)代入,得:a(﹣3+1)2+4=0,解得:a=﹣1,∴抛物线H的表达式为y=﹣(x+1)2+4;(2)如图,由(1)知:y=﹣x2﹣2x+3,令x=0,得y=3,∴C(0,3),设直线AC的解析式为y=mx+n,∵A(﹣3,0),C(0,3),∴,解得:,∴直线AC的解析式为y=x+3,设P(m,﹣m2﹣2m+3),则E(m,m+3),∴PE=﹣m2﹣2m+3﹣(m+3)=﹣m2﹣3m=﹣(m+)2+,∵﹣1<0,∴当m=﹣时,PE有最大值,∵OA=OC=3,∠AOC=90°,∴△AOC 是等腰直角三角形, ∴∠ACO =45°, ∵PD ⊥AB , ∴∠ADP =90°, ∴∠ADP =∠AOC , ∴PD ∥OC ,∴∠PEF =∠ACO =45°, ∵PF ⊥AC ,∴△PEF 是等腰直角三角形, ∴PF =EF =PE ,∴S △PEF =PF •EF =PE 2,∴当m =﹣时,S △PEF 最大值=×()2=;2.如图,抛物线212y x bx c =++与x 轴交于点()1,0A -和点B ,与y 轴交于点()0,2C -,连接AC ,BC . (1)求抛物线的解析式;(2)点P 在第四象限的抛物线上,设ABC 的面积为1S ,PBC 的面积为2S ,当2S =451S 时,求点P 的坐标3.在平面直角坐标系中,抛物线y =ax 2+bx +c (a ≠0)与x 轴的两个交点分别为A (﹣3,0)、B (1,0),与y 轴交于点D (0,3),过顶点C 作CH ⊥x 轴于点H (1)求抛物线的解析式和顶点C 的坐标;(2)连结AD 、CD ,若点E 为抛物线上一动点(点E 与顶点C 不重合),当△ADE 与△ACD 面积相等时,求点E 的坐标;4.如图1,平面直角坐标系xOy中,抛物线y=ax2+bx+c(a<0)与x轴分别交于点A和点B(1,0),与y轴交于点C,对称轴为直线x=﹣1,且OA=OC,P为抛物线上一动点.(1)直接写出抛物线的解析式;(2)如图2,连接AC,当点P在直线AC上方时,求四边形PABC面积的最大值,并求出此时P点的坐标;5.在平面直角坐标系中,抛物线y=﹣x2+2mx的顶点为A,直线l:y=x﹣1与x轴交于点B.(1)如图,已知点A的坐标为(2,4),抛物线与直线l在第一象限交于点C.①求抛物线的解析式及点C的坐标;②点M为线段BC上不与B,C重合的一动点,过点M作x轴的垂线交x轴于点D,交抛物线于点E,设点M的横坐标t.当EM>BD时,求t的取值范围;(2)过点A作AP⊥l于点P,作AQ∥l交抛物线于点Q,连接PQ,设△APQ的面积为S.直接写出①S关于m的函数关系式;②S的最小值及S取最小值时m的值.6.如图,已知二次函数的图象交x轴于点B(﹣8,0),C(2,0),交y轴点A.(1)求二次函数的表达式;(2)连接AC,AB,若点P在线段BC上运动(不与点B,C重合),过点P作PD∥AC,交AB于点D,试猜想△PAD的面积有最大值还是最小值,并求出此时点P的坐标.7.在平面直角坐标系xOy中,已知抛物线:y=ax2+bx+c交x轴于A(﹣1,0),B(3,0)两点,与y轴交于点C(0,﹣).(1)求抛物线的函数解析式;(2)如图1,点D为第四象限抛物线上一点,连接OD,过点B作BE⊥OD,垂足为E,若BE=2OE,求点D的坐标;(3)如图2,点M为第四象限抛物线上一动点,连接AM,交BC于点N,连接BM,记△BMN的面积为S1,△ABN的面积为S2,求的最大值.8.抛物线y=ax2+c的顶点为C(0,1),与直线y=kx+3(k为常数)相交于A(x1,y1),B(x2,y2)两点.当k=0时,点B的横坐标恰好为2(如图1).(1)求a、c的值;(2)当k=0时,若点P是抛物线上异于A、C的一点,且满足2PC2=AB2+2AP2,试判断△PAC的形状,并说明理由;(3)若直线y=﹣1交y轴于点F,过点A、B分别作该直线的垂线,垂足分别为D、E,连接AF、BF(如图2).设△ADF、△ABF、△BEF的面积分别为S1、S2、S3,是否存在常数t,使S22=t•S1S3?若存在,求出t的值;若不存在,请说明理由.【模型解读】1.如图,抛物线y=ax2+x+c与x轴交于点A,B,与y轴交于点C,已知A,C两点坐标分别是A(1,0),C(0,﹣2),连接AC,BC.(1)求抛物线的表达式和AC所在直线的表达式;(2)将△ABC 沿BC 所在直线折叠,得到△DBC ,点A 的对应点D 是否落在抛物线的对称轴上?若点D 在对称轴上,请求出点D 的坐标;若点D 不在对称轴上,请说明理由;(3)若点P 是抛物线位于第三象限图象上的一动点,连接AP 交BC 于点Q ,连接BP ,△BPQ 的面积记为S 1,△ABQ 的面积记为S 2,求的值最大时点P 的坐标.2.如图,已知抛物线2y x bx c =-与一直线相交于1,023A C -,,两点,与y 轴交于点N .其顶点为D . (1)抛物线及直线AC 的函数关系式;(2)设点()3,M m ,求使MN MD +的值最小时m 的值;(3)若P 是抛物线上位于直线AC 上方的一个动点,求APC △的面积的最大值.3.如图,在平面直角坐标系中,抛物线y=ax2+bx+2与直线y=x﹣2交于点A(m,0)和点B(﹣2,n),与y轴交于点C.(1)求抛物线的解析式及顶点D的坐标;(2)若向下平移抛物线,使顶点D落在x轴上,原来的抛物线上的点P平移后的对应点为P′,若OP′=OP,求点P的坐标;(3)在抛物线上是否存在点Q,使△QAB的面积是△ABC面积的一半?若存在,直接写出点Q的坐标;若不存在,请说明理由.4.点A,B在抛物线y=ax2(a>0)上,AB交y轴于点C.(1)过点C作DC⊥y轴交抛物线于点D,若AB∥OD,AB的解析式为y=x+2,求a的值;(2)过点B作BG⊥x轴交x轴于点G,BG的延长线交AO的延长线于点H,连接AG交y轴于点K,求OK•BH的值;(3)若a=1,将抛物线平移后交x轴于点A(﹣1,0),B(2,0)两点,点P为y轴正半轴上一点,AP,BP交抛物线于点M,N,设△PNA的面积为S1,△PMB的面积为S2,△PBA的面积为S3,若,求点P的坐标.。
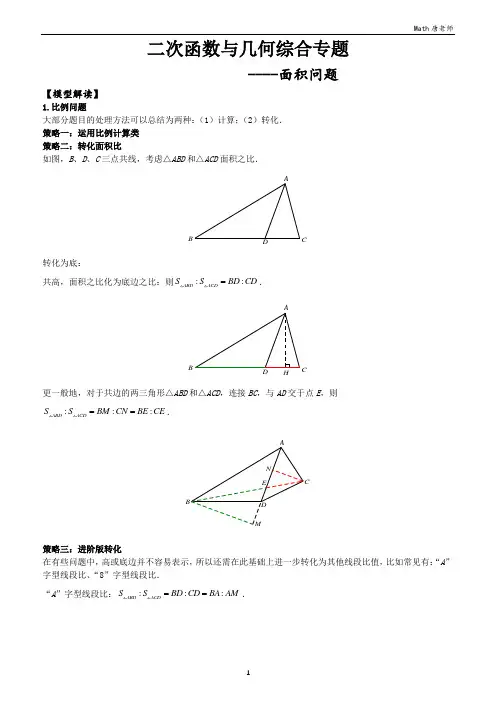
专项11 二次函数与几何综合-面积问题【方法1直接法】一般以坐标轴上线段或以与轴平行的线段为底边【方法2 铅锤法】铅锤高水平宽⨯=21S 【方法3 其他面积方法】如图1,同底等高三角形的面积相等.平行线间的距离处处相等.如图2,同底三角形的面积比等于高的比.如图3,同高三角形的面积比等于底的比.如图1 如图2 如图3【方法4 利用相似性质】利用相似图形,面积比等于相似比的平方。
【方法1 铅锤法求面积】【典例1】(聊城)如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于点A(﹣2,0),点B(4,0),与y轴交于点C(0,8),连接BC.又已知位于y轴右侧且垂直于x轴的动直线l,沿x轴正方向从O运动到B(不含O点和B点),且分别交抛物线、线段BC以及x轴于点P,D,E.(1)求抛物线的表达式;(2)作PF⊥BC,垂足为F,当直线l运动时,求Rt△PFD面积的最大值.【答案】(1)y=﹣x2+2x+8 (2)【解答】解:(1)将点A、B、C的坐标代入二次函数表达式得:,解得:,故抛物线的表达式为:y=﹣x2+2x+8;(2)在Rt△PFD中,∠PFD=∠COB=90°,∵l∥y轴,∴∠PDF=∠OCB,∴Rt△PFD∽Rt△BCO,∴,∴S△PDF=•S△BOC,而S△BOC=OB•OC==16,BC==4,∴S△PDF=•S△BOC=PD2,即当PD取得最大值时,S△PDF最大,将B、C坐标代入一次函数表达式并解得:直线BC的表达式为:y=﹣2x+8,设点P(m,﹣m2+2m+8),则点D(m,﹣2m+8),则PD=﹣m2+2m+8+2m﹣8=﹣(m﹣2)2+4,当m=2时,PD的最大值为4,故当PD=4时,∴S△PDF=PD2=【变式1-1】(娄底)如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),点B(3,0),与y轴交于点C,且过点D(2,﹣3).点P、Q是抛物线y=ax2+bx+c上的动点.(1)求抛物线的解析式;(2)当点P在直线OD下方时,求△POD面积的最大值.【答案】(1):y=x2﹣2x﹣3 (2)①﹣m2+m+3 ②【解答】解:(1)函数的表达式为:y=a(x+1)(x﹣3),将点D坐标代入上式并解得:a=1,故抛物线的表达式为:y=x2﹣2x﹣3…①;(2)设点P(m,m2﹣2m﹣3),①当点P在第三象限时,设直线PD与y轴交于点G,设点P(m,m2﹣2m﹣3),将点P、D的坐标代入一次函数表达式:y=sx+t并解得:直线PD的表达式为:y=mx﹣3﹣2m,则OG=3+2m,S△POD=×OG(x D﹣x P)=(3+2m)(2﹣m)=﹣m2+m+3,②当点P在第四象限时,设PD交y轴于点M,同理可得:S△POD=×OM(x D﹣x P)=﹣m2+m+3,综上,S△POD=﹣m2+m+3,∵﹣1<0,故S△POD有最大值,当m=时,其最大值为;【变式1-2】(2021秋•龙江县校级期末)综合与探究如图,已知抛物线y=ax2+bx+4经过A(﹣1,0),B(4,0)两点,交y轴于点C.(1)求抛物线的解析式,连接BC,并求出直线BC的解析式;(2)请在抛物线的对称轴上找一点P,使AP+PC的值最小,此时点P的坐标是(,);(3)点Q在第一象限的抛物线上,连接CQ,BQ,求出△BCQ面积的最大值.(4)点M为x轴上一动点,在抛物线上是否存在一点N,使得以A、C、M、N四点为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.【解答】解:(1)把A(﹣1,0),B(4,0)代入y=ax2+bx+4,得到,解得,∴y=﹣x2+3x+4;在y=﹣x2+3x+4中,令x=0,则y=4,∴C(0,4),设BC的解析式为y=kx+b,∵B(4,0),C(0,4),∴,∴,∴直线BC的解析式为y=﹣x+4;(2)如图1中,由题意A,B关于抛物线的对称轴直线x=对称,连接BC交直线x=于点P,连接P A,此时P A+PC的值最小,最小值为线段BC的长==4,∵直线BC的解析式为y=﹣x+4,∴x=时,y=﹣+4=,∴此时P(,).故答案为:(,);(3)设Q(m,﹣m2+3m+4)过Q作QD⊥x轴,交BC于点D,则D(m,﹣m+4),∴QD=(﹣m2+3m+4)﹣(﹣m+4)=﹣m2+4m,∵B(4,0),∴OB=4,,当m=2时,S△BCQ取最大值,最大值为8,∴△BCQ面积的最大值为8;【变式1-2】(2022春•南岸区月考)如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x 轴交于A(﹣1,0),B(3,0),交y轴于点C,且OC=3.(1)求该抛物线的解析式;(2)点P为直线BC下方抛物线上的一点,连接AC、BC、CP、BP,求四边形PCAB 的面积的最大值,以及此时点P的坐标;【解答】解:(1)∵OC=3,∴C(0,﹣3),将点A(﹣1,0),B(3,0),C(0,﹣3)代入y=ax2+bx+c,得,解得,∴y=x2﹣2x﹣3;(2)∵S四边形PCAB=S△ABC+S△PBC,∴当S△PBC面积最大时,S四边形PCAB的面积最大,设BC的直线解析式y=kx+b,∴,解得,∴y=x﹣3,过点P作PQ⊥x轴交BC于点Q,设P(t,t2﹣2t﹣3),则Q(t,t﹣3),∴当PQ最大时,S△PBC面积最大,∴PQ=t﹣3﹣t2+2t+3=﹣t2+3t=﹣(t﹣)2+,当t=时,PQ取最大值,∴P(,﹣),∵A(﹣1,0),B(3,0),C(0,3),∴AB=4,∴S四边形PCAB=S△ABC+S△PBC=×4×3+××3=;【方法2 其他方法】【典例2】(深圳)如图抛物线y=ax2+bx+c经过点A(﹣1,0),点C(0,3),且OB =OC.(1)求抛物线的解析式及其对称轴;(2)点P为抛物线上一点,连接CP,直线CP把四边形CBP A的面积分为3:5两部分,求点P的坐标.【答案】(1)y=﹣x2+2x+3 ;x=1(2)P的坐标为(4,﹣5)或(8,﹣45)【解答】解:(1)∵OB=OC,∴点B(3,0),则抛物线的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3)=ax2﹣2ax﹣3a,故﹣3a=3,解得:a=﹣1,故抛物线的表达式为:y=﹣x2+2x+3…①,函数的对称轴为:x=1;(2)如图,设直线CP交x轴于点E,直线CP把四边形CBP A的面积分为3:5两部分,又∵S△PCB:S△PCA=EB×(y C﹣y P):AE×(y C﹣y P)=BE:AE,则BE:AE=3:5或5:3,则AE=或,即:点E的坐标为(,0)或(,0),将点E的坐标代入直线CP的表达式:y=kx+3,解得:k=﹣6或﹣2,故直线CP的表达式为:y=﹣2x+3或y=﹣6x+3…②联立①②并解得:x=4或8(不合题意值已舍去),故点P的坐标为(4,﹣5)或(8,﹣45).【变式2-1】(2021秋•合川区)如图,抛物线y=ax2+bx+6(a≠0)与x轴交于A(﹣1,0),B(6,0),与y轴交于点C,点P为第一象限内抛物线上一动点,过点P作x轴的垂线,交直线BC于点D,交x轴于点E,连接PB.(1)求该抛物线的解析式;(2)当△PBD与△BDE的面积之比为1:2时,求点P的坐标;【答案】(1)y=﹣x2+5x+6 (2)P(,)【解答】解:(1)∵抛物线y=ax2+bx+6(a≠0)与x轴交于A(﹣1,0),B(6,0),∴,∴,∴抛物线的解析式为y=﹣x2+5x+6;(2)∵抛物线y=﹣x2+5x+6过点C,∴C(0,6),设直线BC的解析式为y=kx+n,∴,∴,∴直线BC的解析式为y=﹣x+6,设P(m,﹣m2+5m+6),则D(m,﹣m+6),∴PE=﹣m2+5m+6,DE=﹣m+6,∵△PBD与△BDE的面积之比为1:2,∴PD:DE=1:2,∴PE:DE=3:2,∴3(﹣m+6)=2(﹣m2+5m+6),解得,m2=6(舍去),∴P(,);【典例3】(淮安)如图,已知二次函数的图象与x轴交于A、B两点,D为顶点,其中点B的坐标为(5,0),点D的坐标为(1,3).(1)求该二次函数的表达式;(2)试问在该二次函数图象上是否存在点G,使得△ADG的面积是△BDG的面积的?若存在,求出点G的坐标;若不存在,请说明理由.【答案】(1)y=﹣(x﹣1)2+3(2)G的坐标为(0,)或(﹣15,﹣45).【解答】解:(1)依题意,设二次函数的解析式为y=a(x﹣1)2+3将点B代入得0=a(5﹣1)2+3,得a=﹣∴二次函数的表达式为:y=﹣(x﹣1)2+3(2)存在点G,当点G在x轴的上方时,设直线DG交x轴于P,设P(t,0),作AE⊥DG于E,BF⊥DG于F.由题意:AE:BF=3:5,∵BF∥AE,∴AP:BP=AE:BF=3:5,∴(﹣3﹣t):(5﹣t)=3:5,解得t=﹣15,∴直线DG的解析式为y=x+,由,解得或,∴G(0,).当点G在x轴下方时,如图2所示,∵AO:OB=3:5∴当点G在DO的延长线上时,存在点G使得S△ADG:S△BDG=3:5,此时,DG的直线经过原点,设直线DG的解析式为y=kx,将点D代入得k=3,故y=3x,则有整理得,(x﹣1)(x+15)=0,得x1=1(舍去),x2=﹣15当x=﹣15时,y=﹣45,故点G为(﹣15,﹣45).综上所述,点G的坐标为(0,)或(﹣15,﹣45).【变式3】(2021秋•南阳)如图,对称轴为x=﹣1的抛物线y=ax2+bx+c(a≠0)与x 轴相交于A,B两点,其中点A的坐标为(﹣3,0).(1)求点B的坐标.(2)已知a=1,C为抛物线与y轴的交点.①求抛物线的解析式.②若点P在抛物线上,且S△POC=4S△BOC,求点P的坐标.【答案】(1)点B的坐标为(1,0)(2)①y=x2+2x﹣3②点P的坐标为(4,21)或(﹣4,5)【解答】解:(1)∵对称轴为直线x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,∴A、B两点关于直线x=﹣1对称,∵点A的坐标为(﹣3,0),∴点B的坐标为(1,0);(2)①a=1时,∵抛物线y=x2+bx+c的对称轴为直线x=﹣1,∴=﹣1,解得b=2,将B(1,0)代入y=x2+2x+c,得1+2+c=0,解得c=﹣3,∴抛物线的解析式为y=x2+2x﹣3;②∵抛物线的解析式为y=x2+2x﹣3,∴抛物线与y轴的交点C的坐标为(0,﹣3),OC=3,设P点坐标为(x,x2+2x﹣3),∵S△POC=4S△BOC,∴×OC×|x|=4××OC×OB,即×3×|x|=4××3×1,∴|x|=4,解得x=±4,当x=4时,x2+2x﹣3=16+8﹣3=21,当x=﹣4时,x2+2x﹣3=16﹣8﹣3=5,∴点P的坐标为(4,21)或(﹣4,5);1.(2021秋•日喀则市月考)如图,二次函数y=﹣x2+4x+5的图象与x轴交于A,B两点,与y轴交于点C,M为抛物线的顶点.(1)求M点的坐标;(2)求△MBC的面积;【解答】解:(1)y=﹣x2+4x+5=﹣(x﹣2)2+9,∴M(2,9);(2)令y=0,得﹣x2+4x+5=0,解得x=﹣1或x=5,∴A(﹣1,0),B(5,0),令x=0,得y=﹣x2+4x+5=5,∴C(0,5),过点M作ME⊥y轴于点E,∴S△MBC=S四边形MBOE﹣S△MCE﹣S△BOC==15;2.(2022•东方二模)如图,抛物线y=x2+bx+c经过B(3,0)、C(0,﹣3)两点,与x 轴的另一个交点为A,顶点为D.(1)求该抛物线的解析式;(2)点E为该抛物线上一动点(与点B、C不重合),当点E在直线BC的下方运动时,求△CBE的面积的最大值;【解答】解:(1)将B(3,0),C(0,﹣3)代入y=x2+bx+c得:,解得,∴抛物线的解析式为y=x2﹣2x﹣3;(2)连接CE、BE,经过点E作x轴的垂线FE,交直线BC于点F,设直线BC的解析式为y=kx+m,将B,C两点的坐标代入得:,解得:,∴直线BC的解解析式为y=x﹣3,设点F(x,x﹣3),点E(x,x2﹣2x﹣3),∴EF=(x﹣3﹣x2+2x+3)=﹣x2+3x,∴S△CBE=S△CEF+S△BEF=EF•OB=(﹣x2+3x)=﹣(x﹣)2+,∵a=﹣<0,且0<x<3,∴当x=时,S△CBE有最大值,最大值是,此时E点坐标为(,﹣);3.(2022•广东)如图,抛物线y=x2+bx+c(b,c是常数)的顶点为C,与x轴交于A,B 两点,A(1,0),AB=4,点P为线段AB上的动点,过P作PQ∥BC交AC于点Q.(1)求该抛物线的解析式;(2)求△CPQ面积的最大值,并求此时P点坐标.【解答】(1)∵抛物线y=x2+bx+c(b,c是常数)的顶点为C,与x轴交于A,B两点,A(1,0),AB=4,∴B(﹣3,0),∴,解得,∴抛物线的解析式为y=x2+2x﹣3;(2)过Q作QE⊥x轴于E,过C作CF⊥x轴于F,设P(m,0),则P A=1﹣m,∵y=x2+2x﹣3=(x+1)2﹣4,∴C(﹣1,﹣4),∴CF=4,∵PQ∥BC,∴△PQA∽△BCA,∴,即,∴QE=1﹣m,∴S△CPQ=S△PCA﹣S△PQA=P A•CF﹣P A•QE=(1﹣m)×4﹣(1﹣m)(1﹣m)=﹣(m+1)2+2,∵﹣3≤m≤1,∴当m=﹣1时S△CPQ有最大值2,∴△CPQ面积的最大值为2,此时P点坐标为(﹣1,0).4.(2022春•青秀区校级期末)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c,与y 轴交于点A,与x轴交于点E、B.且点A(0,5),B(5,0),抛物线的对称轴与AB 交于点M.(1)求二次函数的解析式;(2)若点P是直线AB上方抛物线上的一动点,连接PB,PM,求△PMB面积的最大值;【解答】解:(1)∵点A(0,5),B(5,0)在抛物线y=﹣x2+bx+c上,∴,∴,∴二次函数的解析式为y=﹣x2+4x+5;(2)如图,∵A(0,5),B(5,0),∴直线AB的解析式为y=﹣x+5,∵点M是抛物线的对称轴与直线AB的交点,∴M(2,3),由(1)知,二次函数的解析式为y=﹣x2+4x+5,过点P作PH∥y轴交AB于H,设P(m,﹣m2+4m+5)(0<m<5),∴H(m,﹣m+5),∴PH=﹣m2+4m+5﹣(﹣m+5)=﹣m2+5m,∴S△PMB=PH(x B﹣x M)=(﹣m2+5m)(5﹣2)=﹣(x﹣)2+,∴当x=时,S△PMB最大=,即△PMB面积的最大值为;5.(2022春•南岸区月考)如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于A (﹣1,0),B(3,0),交y轴于点C,且OC=3.(1)求该抛物线的解析式;(2)点P为直线BC下方抛物线上的一点,连接AC、BC、CP、BP,求四边形PCAB 的面积的最大值,以及此时点P的坐标;【解答】解:(1)∵OC=3,∴C(0,﹣3),将点A(﹣1,0),B(3,0),C(0,﹣3)代入y=ax2+bx+c,得,解得,∴y=x2﹣2x﹣3;(2)∵S四边形PCAB=S△ABC+S△PBC,∴当S△PBC面积最大时,S四边形PCAB的面积最大,设BC的直线解析式y=kx+b,∴,解得,∴y=x﹣3,过点P作PQ⊥x轴交BC于点Q,设P(t,t2﹣2t﹣3),则Q(t,t﹣3),∴当PQ最大时,S△PBC面积最大,∴PQ=t﹣3﹣t2+2t+3=﹣t2+3t=﹣(t﹣)2+,当t=时,PQ取最大值,∴P(,﹣),∵A(﹣1,0),B(3,0),C(0,3),∴AB=4,∴S四边形PCAB=S△ABC+S△PBC=×4×3+××3=;6.(2022•兴宁区校级模拟)如图,抛物线y=﹣x2+bx+c过点A、B,抛物线的对称轴交x 轴于点D,直线y=﹣x+3与x轴交于点B,与y轴交于点C,且.(1)求抛物线的解析式;(2)点M(t,0)是x轴上的一个动点,点N是抛物线对称轴上的一个动点,当DN=2t,△MNB的面积为时,求出点M与点N的坐标;【解答】解:(1)对于直线y=﹣x+3,令y=0,即﹣x+3=0,解得:x=3,令x=0,得y=3,∴B(3,0),C(0,3),∵A为x轴负半轴上一点,且OA=OB,∴A(﹣1,0).将点A、B的坐标分别代入y=﹣x2+bx+c中,得,解得,∴抛物线的解析式为y=﹣x2+2x+3;(2)由(1)知:A(﹣1,0),B(3,0),D(1,0),∴BM=|3﹣t|,∵S△MNB=BM•DN=,即•|3﹣t|•2t=,当t<3时,•(3﹣t)•2t=,化简得:4t2﹣12t+15=0,∵Δ=(﹣12)2﹣4×4×15=﹣96<0,∴方程无解;当t>3时,•(t﹣3)•2t=,解得t1=,t2=(舍),∴DN=2t=3+2,∴点M的坐标为(,0),点N的坐标为(1,3+2);7.(2022•烟台)如图,已知直线y=x+4与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c经过A,C两点,且与x轴的另一个交点为B,对称轴为直线x=﹣1.(1)求抛物线的表达式;(2)D是第二象限内抛物线上的动点,设点D的横坐标为m,求四边形ABCD面积S 的最大值及此时D点的坐标;【解答】解:(1)当x=0时,y=4,∴C(0,4),当y=0时,x+4=0,∴x=﹣3,∴A(﹣3,0),∵对称轴为直线x=﹣1,∴B(1,0),∴设抛物线的表达式:y=a(x﹣1)•(x+3),∴4=﹣3a,∴a=﹣,∴抛物线的表达式为:y=﹣(x﹣1)•(x+3)=﹣x2﹣x+4;(2)如图1,作DF⊥AB于F,交AC于E,∴D(m,﹣﹣m+4),E(m,m+4),∴DE=﹣﹣m+4﹣(m+4)=﹣m2﹣4m,∴S△ADC=OA=•(﹣m2﹣4m)=﹣2m2﹣6m,∵S△ABC===8,∴S=﹣2m2﹣6m+8=﹣2(m+)2+,∴当m=﹣时,S最大=,当m=﹣时,y=﹣=5,∴D(﹣,5);。
教学过程一、课堂导入1、在平面直角坐标系中,已知点A(4,4)、B(-4,4),试在x轴上找出点P,使△APB为直角三角形,请直接写出所有符合条件的P点的坐标2、在平面直角坐标系中找出所有的点C,使得△ABC是以AB为腰的等腰三角形,且C点的横坐标与纵坐标为自然数.画出C点的位置并写出C点的坐标.问题:这是我们在平面直角坐标系那章学习的内容,如果我们将二次函数容纳其中,在抛物线上求作一点,使得三角形是等腰三角形(等边三角形、直角三角形等)并求出该点坐标时,又该如何解答呢?二、复习预习根据实际问题列二次函数关系式:1、列二次函数解应用题与列整式方程解应用题的思路和方法是一致的,不同的是,学习了二次函数后,表示量与量的关系的代数式是含有两个变量的等式.对于应用题要注意以下步骤:(1)审清题意,弄清题中涉及哪些量,已知量有几个,已知量与变量之间的基本关系是什么,找出等量关系(即函数关系).(2)设出两个变量,注意分清自变量和因变量,同时还要注意所设变量的单位要准确.(3)列函数表达式,抓住题中含有等量关系的语句,将此语句抽象为含变量的等式,这就是二次函数.(4)按题目要求,结合二次函数的性质解答相应的问题。
(5)检验所得解是否符合实际:即是否为所提问题的答案.(6)写出答案.2、常见题目类型(1)几何类(三角形、四边形、圆等)一般问题是求图形的面积,首先可以根据特殊图形的面积公式来求解,这时关键是表示出公式里各个部分的代数式;其次,如果不是特殊的图形,可以通过特殊图形的面积相加减来表示;最后,还可以通过构造特殊图形来进行表示求解;总之,要根据题目给的条件实际运用。
(2)桥梁问题这类题型是出现较多的类型,首先应该建立适当的直角坐标系,将桥梁的拱形转化为二次函数来进行求解,强调的是特殊点的表示与运用。
(3)销售问题这类题型会在考试中频繁出现,解题的方法就是:围绕总利润=(售价-进价)×数量这个公式去进行,难度大一点的就是会涉及提价跟降价两种情况,关键是要根据题意分别表示出降价或者提价后商品的售价、数量(进价一般不变),然后再通过公式将各个部分组合在一起就可以了。
二次函数与几何综合专题----线段最值问题将军饮马:这个将军饮的不是马,是数学!原理:两点间线段最短;点到直线的垂直距离最短;对称(翻折)、平移.策略:对称(翻折)→化同为异、化异为同;化折为直.两村一路(异侧)和最小两村一路(同侧)和最小两路一村和最小两村两路和最小两村一路和最小两村一路(同侧)差最大两村一路(异侧)差最大例:如图,在平面直角坐标系xOy 中,抛物线2y x bx c =++与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,3OA OC ==,顶点为D ,对称轴交x 轴于点E . (1)求抛物线的解析式、对称轴及顶点D 的坐标.PN y轴交AC于N,求线段PN的最大值及此时点P (2)直线AC下方的抛物线上有一动点P,过点P作//的坐标.于H,求线段PH的最大值及此时点P的坐标.(3)直线AC下方的抛物线上有一动点P,过点P作PH AC(4)直线AC 下方的抛物线上有一动点P ,过点P 作//PN y 轴交AC 于N ,过点P 作PH AC 于H ,求PNH △周长的最大值及此时点P 的坐标.(5)在抛物线对称轴上找一点N ,使得BCN △的周长最小,求BCN △周长的最小值及此时点N 的坐标.⊥交AC于点M,求CM的最小值.(6)在线段OA上找一点N,连接NC,作NM NCMN=,求四边形BNMC周长的最小值及(7)在抛物线对称轴上有两动点N、M(点N在点M上方),且1此时M的坐标.(8)在对称轴上找一点N ,使得NA NC -最大,求点N 的坐标.【答案】(1)223y x x =+-,对称轴为:直线x =-1,顶点坐标为:D (-1,-4);(2)PN 的最大值为94,此时P (-32,154-);(3)当PN 最大为94时,PH 92P (-32,154-);(4)当PNH △周9294,此时P (-32,154-);(5)1032N (-1,-2);(6)1262-(7)6105(8)10131,M (713-,-);(9)N 的坐标为:(-1,-6). 【详解】(1)解:∵3OA OC ==, ∴A (-3,0),C (0,-3),∴()20333b c c ⎧=--+⎪⎨-=⎪⎩,解得:23b c =⎧⎨=-⎩,∴抛物线的解析式为:223y x x =+-,对称轴为:直线x =-1,顶点坐标为:D (-1,-4). (2)解:设P (x ,223x x +-),则N (x ,-x -3),∴PN =-x -3-(223x x +-)=23x x --=23924x ⎛⎫-++ ⎪⎝⎭,∴当x =-32时,PN 的最大值为94,此时P (-32,154-).(3)解:过点P 作PN ∥y 轴,交AC 于点N , ∵OA =OC =3, ∴∠ACO =45°, ∵PN ∥y 轴,∴∠PNH =45°,即:PNH 是等腰直角三角形,∴PH 2PN , 设P (x ,223x x +-),则N (x ,-x -3),∴PN =-x -3-(223x x +-)=23x x --=23924x ⎛⎫-++ ⎪⎝⎭,∴当x =-32时,PN 的最大值为94,∴当PN 最大为94时,PH 最大值=94×22=928,此时P (-32,154-).(4)解:∵OA =OC =3, ∴∠ACO =45°, ∵PN ∥y 轴,∴∠PNH =45°,即:PNH 是等腰直角三角形, ∴PH =NH 2, ∴PNH △周长= PH +NH +PN 22PN 22PN + PN =(21)PN , 设P (x ,223x x +-),则N (x ,-x -3),∴PN =-x -3-(223x x +-)=23x x --=23924x ⎛⎫-++ ⎪⎝⎭,∴当x =-32时,PN 的最大值为94,∴当PN 最大为94时,PNH △周长最大值=94×)219294,此时P (-32,154-).(5)解:连接AC 交对称轴于点N ′,∵A、B关于对称轴对称,∴AN′=BN′∴BCN△的周长=BC+CN′+BN′=BC+CN′+AN′=BC+AC,∴此时BCN△的周长最小值=BCN'的周长=BC+AC222213331032++∵直线AC的解析式为:y=-x-3,∴当x=-1时,y=-2,即N(-1,-2).(6)解:由题意得:点N在以CM为直径的圆上,设CM的中点为E,连接EN,则当圆E与x轴相切时,即:EN⊥x轴时,EN最小,此时CM=2EN最小,设M(x,-x-3),则E(622x x--,),∴EN=62x+,CM()222332x x x+--+=∴2×62x +22x 662x =-62x =+, ∴M (662-629), ∴CM ()()2266262931262-+-+-(7)解:过点N 作作NQ ∥MC 交y 轴于点Q ,连接AQ 交DE 于点N ′,连接BN ′,则Q (-2,0),∵NQ ∥MC ,MN ∥CQ , ∴四边形MNQC 是平行四边形, ∴CM =QN ,∴四边形BNMC 的周长=BC +BN +MN +CM =BC +BN +1+QN 101+BN +QN , ∵B 、A 关于DE 对称, ∴AN ′=BN ′,∴四边形BNMC 101+BN ′+QN ′101+AN ′+QN 101+AQ 101+222310131+,∵直线AQ 的解析式为:223y x =--,∴N ′(413-,-),∴此时M (713-,-).(8)解:连接BC ,并延长交ED 于点N ′,连接BN ,∵A 、B 关于DE 对称, ∴AN =BN ,∴NA NC -=NB NC -≤BC =N B N C ''-, ∵B (1,0),C (0,-3), ∴直线BC 的解析式为:33y x =-, 令x =-1代入33y x =-得:y =-6, ∴N ′(-1,-6),∴NA NC -最大时,N 的坐标为:(-1,-6).二次函数与几何综合专题---- 胡不归和阿氏圆问题【胡不归最值问题】 求BC +kAC 的最小值.解决思路:构造射线AD 使得sin ∠DAN=k ,即CHk AC,CH=kAC .将问题转化为求BC+CH 最小值,过B 点作BH ⊥AD 交MN 于点C ,交AD 于H 点,此时BC+CH 取到最小值,即BC+kAC 最小.1.已知抛物线y =ax 2+bx +c 与x 轴交于A (﹣1,0),B (5,0)两点,C 为抛物线的顶点,抛物线的对称轴交x 轴于点D ,连结BC ,且tan ∠CBD =43,如图所示. (1)求抛物线的解析式;(2)设P 是抛物线的对称轴上的一个动点.①过点P 作x 轴的平行线交线段BC 于点E ,过点E 作EF ⊥PE 交抛物线于点F ,连结FB 、FC ,求△BCF 的面积的最大值;②连结PB ,求35PC +PB 的最小值.CH=kACsin α=CH AC=kHDαA BCM MCBAαDH2.在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于点A(﹣3,0)、B(1,0),交y轴于点N,点M 为抛物线的顶点,对称轴与x轴交于点C.(1)求抛物线的解析式;(2)如图1,连接AM,点E是线段AM上方抛物线上一动点,EF⊥AM于点F,过点E作EH⊥x轴于点H,交AM于点D.点P是y轴上一动点,当EF取最大值时:①求PD+PC的最小值;②如图2,Q点为y轴上一动点,请直接写出DQ+14OQ的最小值.3.如图,抛物线y =ax 2﹣2ax +c 的图象经过点C (0,﹣2),顶点D 的坐标为(1,−83),与x 轴交于A 、B 两点.(1)求抛物线的解析式.(2)连接AC ,E 为直线AC 上一点,当△AOC ∽△AEB 时,求点E 的坐标和AE AB的值.(3)在(2)的条件下,点F (0,y )是y 轴上一动点,当y 为何值时,√55FC +BF 的值最小.并求出这个最小值.(4)点C 关于x 轴的对称点为H ,当√55FC +BF 取最小值时,在抛物线的对称轴上是否存在点Q ,使△QHF 是直角三角形?若存在,请求出点Q 的坐标;若不存在,请说明理由.4.如图1,抛物线y=x2+(m﹣2)x﹣2m(m>0)与x轴交于A,B两点(A在B左边),与y轴交于点C.连接AC,BC.且△ABC的面积为8.(1)求m的值;(2)在(1)的条件下,在第一象限内抛物线上有一点T,T的横坐标为t,使∠ATC=60°.求(t﹣1)2的值.(3)如图2,点P为y轴上一个动点,连接AP,求CP+AP的最小值,并求出此时点P的坐标.【阿氏圆最值问题】计算PA k PB +的最小值时,利用两边成比例且夹角相等构造母子型相似三角形问题:在圆上找一点P 使得PA k PB +的值最小,解决步骤具体如下: ①如图,将系数不为1的线段两端点与圆心相连即OP ,OB ②计算出这两条线段的长度比OPk OB= ③在OB 上取一点C ,使得OC k OP =,即构造△POM ∽△BOP ,则PCk PB=,PC k PB = ④则=PA k PB PA PC AC ++≥,当A 、P 、C 三点共线时可得最小值1.如图,抛物线2y ax bx c =++与x 轴交于(3A 0),B 两点(点B 在点A 的左侧),与y 轴交于点C ,且33OB OA OC ==,OAC ∠的平分线AD 交y 轴于点D ,过点A 且垂直于AD 的直线l 交y 轴于点E ,点P 是x 轴下方抛物线上的一个动点,过点P 作PF x ⊥轴,垂足为F ,交直线AD 于点H . (1)求抛物线的解析式;(2)设点P 的横坐标为m ,当FH HP =时,求m 的值; (3)当直线PF 为抛物线的对称轴时,以点H 为圆心,12HC 为半径作H ,点Q 为H 上的一个动点,求14AQ EQ +的最小值.2.如图1,抛物线y=ax2+bx+c与x轴正半轴交于点A,点B(点A在点B的左侧),与y轴交于点C.若线段AB绕点A逆时针旋转120°,点B刚好与点C重合,点B的坐标为(3,0).(1)求抛物线的表达式;(2)抛物线的对称轴上是否存在一点P,使△ACP为直角三角形?若存在,请求出点P的坐标,若不存在,请说明理由;(3)如图2,以点B为圆心,以1为半径画圆,若点Q为⊙B上的一个动点,连接AQ,CQ,求AQ+CQ 的最小值.3.如图,已知抛物线y=﹣x2+2x+3与x轴交于点A,B(点A在点B的右侧),与y轴交于点C.(1)如图①,若点D为抛物线的顶点,以点B为圆心,3为半径作⊙B.点E为⊙B上的动点,连接A,DE,求DE+AE的最小值.(2)如图②,若点H是直线AC与抛物线对称轴的交点,以点H为圆心,1为半径作⊙H,点Q是⊙H 上一动点,连接OQ,AQ,求OQ+AQ的最小值;(3)如图③,点D是抛物线上横坐标为2的点,过点D作DE⊥x轴于点E,点P是以O为圆心,1为半径的⊙O上的动点,连接CD,DP,PE,求PD﹣PE的最大值.4.如图1,抛物线y=ax2+bx﹣4与x轴交于A、B两点,与y轴交于点C,其中点A的坐标为(﹣1,0),抛物线的对称轴是直线x=.(1)求抛物线的解析式;(2)若点P是直线BC下方的抛物线上一个动点,是否存在点P使四边形ABPC的面积为16,若存在,求出点P的坐标若不存在,请说明理由;(3)如图2,过点B作BF⊥BC交抛物线的对称轴于点F,以点C为圆心,2为半径作⊙C,点Q为⊙C 上的一个动点,求BQ+FQ的最小值.【课后训练】1.如图,直线y=x+2与抛物线y=x2﹣2mx+m2+m交于A、B两点(A在B的左侧),与y轴交于点C,抛物线的顶点为D,抛物线的对称轴与直线AB交于点M.(1)当四边形CODM是菱形时,求点D的坐标;(2)若点P为直线OD上一动点,求△APB的面积;′(3)作点B关于直线MD的对称点B',以点M为圆心,MD为半径作⊙M,点Q是⊙M上一动点,求QB'+QB的最小值.2.如图,已知二次函数y=ax2+bx+c的图象经过点C(2,﹣3),且与x轴交于原点及点B(8,0),点A为抛物线的顶点.(1)求二次函数的表达式;(2)在抛物线的对称轴上是否存在点M,使△ABM是等腰三角形?如果存在,请求出点M的坐标.如果不存在,请说明理由;(3)若点P为⊙O上的动点,且⊙O的半径为,求的最小值.3.抛物线y=ax2+bx﹣5的图象与x轴交于A、B两点,与y轴交于点C,其中点A坐标为(﹣1,0),一次函数y=x+k的图象经过点B、C.(1)试求二次函数及一次函数的解析式;(2)如图1,点D(2,0)为x轴上一点,P为抛物线上的动点,过点P、D作直线PD交线段CB于点Q,连接PC、DC,若S△CPD=3S△CQD,求点P的坐标;(3)如图2,点E为抛物线位于直线BC下方图象上的一个动点,过点E作直线EG⊥x轴于点G,交直线BC于点F,当EF+√22CF的值最大时,求点E的坐标.4.如图①,直线y=﹣x﹣3分别与x轴、y轴交于点B,C,抛物线y=ax2+bx+c经过B,C两点,且与x轴的另一交点为A(1,0).(1)求抛物线的函数解析式;(2)如图①,点P在第三象限内的抛物线上.①连接AC,PB,PC,当四边形ABPC的面积最大时,求点P的坐标;②在①的条件下,G为x轴上一点,当PG+√55AG取得最小值时,求点G的坐标;(3)如图②,Q为x轴下方抛物线上任意一点,D是抛物线的对称轴与x轴的交点,直线AQ,BQ分别交抛物线的对称轴于点M,N.问:DM+DN是否为定值?如果是,请求出这个定值;如果不是,请说明理由.21Math唐老师22。
二次函数与几何综合07年课改后,最后一题普遍为抛物线和几何结合(主要是与三角形结合)的代数几何综合题,计算量较大。
几何题可能想很久都不能动笔,而代数题则可以想到哪里写到哪里,这就让很多考生能够拿到一些步骤分。
因此,课改之后,武汉市数学中考最后一题相对来说要比以前简单不少,而这也符合教育部要求给学生减轻负担的主旨,因此也会继续下去。
要做好这最后一题,主要是要在有限的时间里面找到的简便的计算方法。
要做到这一点,一是要加强本身的观察力,二是需要在平时要多积累一些好的算法,并能够熟练运用,最后就是培养计算的耐心,做到计算又快又准。
题目分析及对考生要求(1)第一问通常为求点坐标、解析式:本小问要求学生能够熟练地掌握待定系数法求函数解析式,属于送分题。
(2)第二问为代数几何综合题,题型不固定。
解题偏代数,要求学生能够熟练掌握函数的平移,左加右减,上加下减。
要求学生有较好的计算能力,能够把题目中所给的几何信息进行转化,得到相应的点坐标,再进行相应的代数计算。
(3)第三问为几何代数综合,题型不固定。
解题偏几何,要求学生能够对题目所给条件进行转化,合理设参数,将点坐标转化为相应的线段长,再根据题目条件合理构造相似、全等,或者利用锐角三角函数,将这些线段与题目构建起联系,再进行相应计算求解,此处要求学生能够熟练运用韦达定理,本小问综合性较强。
在我们解题时,往往有一些几何条件,我们直接在坐标系中话不是很好用,这时我们需要对它进行相应的条件转化,变成方便我们使用的条件,以下为两种常见的条件转化思想。
1、遇到面积条件:a.不规则图形先进行分割,变成规则的图形面积;b.在第一步变化后仍不是很好使用时,根据同底等高,或者等底同高的三角形面积相等这一性质,将面积进行转化;c.当面积转化为一边与坐标轴平行时,以这条边为底,根据面积公式转化为线段条件。
2、遇到角度条件:找到所有与这些角相等的角,以这些角为基础构造相似、全等或者利用锐角三角函数,转化为线段条件。