下载文档原格式
土力学与地基基础第五版课后答案一、单向选择题（每题1分，共13分）1.下列哪种地基不属于人工地基（Ａ）。
[第一章]A.第四纪沉积土地基为B.换填碎石土地基C.弱夯粘土地基2.在一般高层建筑中，基础工程造价约占总造价的（Ｂ）。
[第一章]A.5%B.25%C.55%3.下列三种粘土矿物中，（Ａ）含量高的土可塑性最高。
[第二章]A.蒙脱石B.伊利石C.高岭石4.对于级配连续的土，（Ｃ）级配良好。
[第二章]A.Cu<5B.Cu=5C.Cu>55.满足条件（Ｂ）的土为级配良好的土。
[第二章]A.Cu<5，cc>3~6B.Cu>5，Cc=1~3C.Cu<5，cc>2~56.若将地基视为均质的半无限体，土体在自重作用下只能产生（Ａ）。
[第三章]A.横向变形B.侧向位移C.剪切变形7.单向偏心荷载作用在矩形基础上，偏心距e满足条件（Ｃ）时，基底压力呈梯形分布。
（L为矩形基础偏心方向边长）[第三章]A.e>L/6B.e=L/6C.e8.上软下硬双层地基中，土层中的附加应力比起均质土时，存在（Ａ）现象。
[第三章]A.应力集中B.应力扩散C.形变维持不变9.土的压缩之中，下列三个部分中，（Ｃ）所占的压缩量最大。
[第四章]A.液态土颗粒被放大；B.土中水及封闭气体被压缩；C.水和气体从孔隙中被抽走。
10.土的压缩试验中，压缩仪（固结仪）中的土样在压缩过程中（Ｂ）。
[第四章]A.只出现侧向变形B.只发生竖向变形C.同时出现横向变形和侧向变形11.土的压缩系数a1-2位于（Ａ）范围时，土为低压缩性土。
[第四章]A. a1-2<0.1MPa-1B.0.1MPa-1≤a1-2＜0.5 MPa-1C. a1-2≥MPa-112.采用规范法计算地基沉降时，沉降经验系数ψs与（Ｃ）无关。
[第四章]A.基底额外压力值B.沉降计算深度范围内压缩模量的当量值C.基础底面形状13.超固结比（OCR）指的是（Ａ）。
高等教育自学考试土力学及地基基础测试题五一、单项选择题(本大题共24小题，每小题1分，共24分)。
1. 钢筋混凝土预制桩的优点在于（ A ）。
A.桩身质量易于保证B.直径大C.对周围环境影响小D.适用所有土层2. 预制桩的最小间距为（ B ）。
A.2.5dB.3dC.3.5dD.4d3. 在桩身强度达到设计要求的前提下，对于砂土，静载荷试验要求的间歇时间不得少于（ A ）天。
A.7B.15C.25D.284. 用静载试验确定单桩承载力时，如果Q-S曲线呈缓变型，则常取桩顶总沉降量为一定值时所对应的荷载为单桩竖向极限承载力，该沉降量宜取（ B ）。
A.10mmB.40mmC.100mmD.150mm5. 对于打入式预制桩，设置桩之后，宜隔一段时间才开始进行静载试验，如果桩所穿过的土层是一般粘性土，一般间歇时间不少于（ C ）。
A.3dB.7dC.15dD.30d6. 当桩的长径比l／d较小，桩身穿越软弱土层，桩端设置在密实砂层、碎石类土层或微风化岩层中，这类桩宜按（A）。
A.端承桩设计B.摩擦桩设计C.摩擦端承桩设计D.端承摩擦桩设计7. 桩端进入粘性土持力层的深度不宜小于（ C ）。
A.0.5倍桩径B.2倍桩径C.4倍桩径D.5倍桩径8. 以承受竖向荷载为主的桩基础，桩顶嵌入承台的长度不宜小于（ C ）。
A.10mmB.20mmC.50mmD.150mm9. 端承型群桩基础，群桩效应系数η的值为（B）。
A.0.8B.1.0C.1.25D.1.6710. 当桩产生负摩擦阻力时，桩相对于地基土的位移是（ A ）。
A.向上B.向下C.相对不动D.侧向11. 桩侧负摩阻力的产生，将使桩的（ B ）。
A.竖向承载力增加，桩身轴力加大B.竖向承载力减小，桩身轴力加大C.竖向承载力减小，桩身轴力减小D.竖向承载力增加，桩身轴力减小12. 相同条件下的桩基静载荷试验桩数不少于总桩数的（ A ）。
A.1％，且不少于3根B.2％，且不少于3根C.3％，且不少于3根D.5％，且不少于3根13. 其他条件相同时，下列情况中，对应的群桩效应系数最小的是（ B ）。
（第二次作业）2-1 某办公楼工程地质勘察中取原状土做试验，用体积为1003cm 的环刀取样试验，用天平测得环刀加湿土的质量为245.00g ，环刀质量为55.00g ，烘干后土样质量为170.00g ，土粒比重为2.70。
计算此土样的天然密度、干密度、饱和密度、天然含水率、孔隙比、孔隙率以及饱和度，并比较各种密度的大小。
解：已知：V=100 cm 3；M=245-55=190g ；M s =170g ；土粒比重Gs=M s /V s =2.70； M w = M - Ms=186-170=16g ，ρw=1 g/cm 3；所以V w =16cm 3； 土粒比重G s =M s /V s =2.70；所以V s = M s /2.70=62.96cm 3； V=100 cm 3；Vs=62.96cm 3；Vw=16cm 3；所以V v =V-V s =100-62.96=37.04cm 3；V a =V v -V w =37.04-16=21.04 cm 3； 因此：天然密度Vm=ρ=190/100=1.90 g/cm 3； 干密度/ds m Vρ= =170/100=1.70 g/cm 3；饱和密度()/sat s v w m V V ρρ=+=(16+170+21.04×1)/100=2.07 g/cm 3；天然含水率%42.9%10017016%100=⨯=⨯=s w m m w 孔隙比/v s e V V == 37.04/62.96=0.588孔隙率()/100v n V V =⨯%=V v/V=37.04/100=37.04%饱和度()/100rw v S V V =⨯%=16/37.04=43.2%综上所述：ρsat ＞ρ＞ρd2-3某住宅地基土的试验中，已测得土的干密度d ρ=1.643/cm g ，含水率w =21.3﹪，土粒比重S G =2.65。
计算土的e 、n 和r S 。
第1章 作业参考答案P401-5 :含水量44.34%；孔隙比1.20；孔隙度（率）54.54%；饱和密度1.77g/cm 3；浮密度0.77g/cm 3；干密度1.22g/cm 3；饱和重度17.7 kN/cm 3；浮重度7.7kN/cm 3；干重度12.2kN/cm 3 1-8：天然孔隙比e=0.64；相对密实度Dr=0.57，中密。
1-10：夯实地基干重度15.37kN/cm 3，D=0.97>0.95，夯实合格。
1-13：解：基坑体积318003600m h A V =⨯=⋅=土粒质量kg g Vm d s631088.21018001016⨯=⨯⨯=⋅=ρ现有土料质量s s m m ='，则需要现有土料质量为：kg w m m s 660102256.3%)121(1088.2)1(⨯=+⨯⨯=+'=' 现有土料体积3220056.14180016/m V ggVgm m V d d =⨯=⋅=⋅='='='γγγγγρ每立方米土料需要加水kg V w w m m o op sw522200%)12%16(1088.2)(6=-⨯⨯='-'='1-15：131.30 cm 3，粉质黏土，流塑。
第二章 作业补充2-3 通过变水头试验测定某粘土的渗透系数k ，土样横断面面积230cm A =，长度cm L 4=，渗透仪水头管（细玻璃管）断面积21256.0cm a =，水头差从cm h 1301=∆降低到cm h 1102=∆所需时间min 8=t 。
试推导变水头试验法确定渗透系数的计算公式，并计算该粘土在试验温度是的渗透系数k 。
解：变水头试验试验过程中水头差一直在随时间而变化，试验时，测记起始水头差1h ∆，经过时间t 后，再测记终了水头差2h ∆，通过建立瞬时达西定律，即可推出渗透系数k 的表达式。
设试验过程中任意时刻作用于试样两端的水头差为h ∆，经过dt 时段后，水头管中水位下降dh ，则dt 时间内流入试样的水量为adh dq -=1式中，右端的负号表示水量随h ∆的减少而增加。
第一章 土的物理性质及其工程分类P 60[2-2] 解：V=21.7cm 3，m=72.49－32.54＝39.95g ，m S =61.28－32.54＝28.74g ，m W =72.49－61.28=11.21g7.2195.39==V m ρ＝1.84g/ cm 3，74.2821.11==sw m m w ＝39％ 07.1184.1)39.01(174.21)1(=-+⨯⨯=-+=ρωρW S d eP 60[2-3] 解：963.0185.1)34.01(171.21)1(=-+⨯⨯=-+=ρωρWS d e 963.01963.071.21++=++=e e d s sat ρ＝1.87 g/ cm 3，87.0187.1=-=-='W sat ρρρ g/ cm 3g ργ'='＝0.87×10＝8.7 kN/m 3P 60[2-4] 解：已知77.1=ρg/cm 3, w ＝9.8％，s d ＝2.67，461.0min =e ,943.0max =e∴656.0177.1)098.01(167.21)1(=-+⨯⨯=-+=ρωρW S d e ，∈=--=--=6.0461.0943.0656.0943.0min max max e e e e D r （0.33，0.67）∴该砂土处于中密状态。
P 60[2-5] 解：已知s d ＝2.73，w ＝30％，=L w 33％，=P w 17％土样完全饱和→1=r S ，sat ρρ=819.073.23.01=⨯=⇒==e e wd S S r ，819.01819.073.21++=++=e e d s sat ρ＝1.95 g/ cm 3 3.0195.11+=+=w d ρρ＝1.5 g/ cm 3，161733=-=-=P L p w w I 81.0161730=-=-=P P LI w w I 10＜16=p I ≤17→该土为粉质粘土0.75＜81.0=L I ≤1→该土处于软塑状态[附加1-1]证明下列换算公式：（1）w s d e d ρρ+=1；（2）γee S sw r ++=1γγ；（3）n n w S w s r γγ)1(-=（1）证明：设e V V V V V Ve V S V V SV S +=+===⇒=1,1w s s w s s s s d ed V V d V V V m ρρρρ+====1 （2）证明：设e V V V V V Ve V S V V SV S +=+===⇒=1,1V g V V V g m m V mg V G s s w w s w )()(ρργ+=+===ee S V V V S sw r s s w v r ++=+=1γγγγ （3）证明：设n V n V n VVV s v v -==⇒==1,,1∴nn w gV gV w V V w V V m m V m V V S w s v w s s v w s s ss v w s wv w w v w r γγρρρρρρρ)1(-====== [附加1-2]解：V=72cm 3，m=129.5g ，m S =121.5g ，m W =129.5－121.5=8g%6.65.1218===⇒S W m m ω 6.0172/5.129)066.01(17.21)1(=-+⨯⨯=-+=ρωρW S d e %7.296.07.2066.0=⨯==e d S S r ω 0.1872105.129=⨯===V mg V G γkN/m 36.20106.16.07.21=⨯+=++=W S sat e e d γγkN/m 36.10106.20=-=-='W sat γγγkN/m 39.16106.17.21=⨯=+=W S d e d γγkN/m 3∴γγγγ'>>>d sat[附加1-3]解：已知s d ＝2.68，w ＝32％，土样完全饱和→1=r S86.068.232.01=⨯=⇒==e ed S Sr ω02.1986.1)32.01(1068.286.01)1(=+⨯⨯=⇒=-+=γγωγW S d e kN/m 3[附加1-4]解：已知66.1=ρg/cm 3,s d ＝2.69，（1）干砂→w ＝0 ∴62.0166.1)01(169.21)1(=-+⨯⨯=-+=ρρw d e W S（2）置于雨中体积不变→e 不变∴%2.969.262.04.04.0=⨯=⇒==w e wd S S r [附加1-5]解：已知m=180g ，1w ＝18％，2w ＝25％，sss s s w m m m m m m m w -=-==18011＝18％→s m ＝152.54g∴)(12w w m m s w -=∆＝152.54×（0.25－0.18）＝10.68g[附加1-6]实验室内对某土样实测的指标如下表所示，计算表土中空白部分指标。
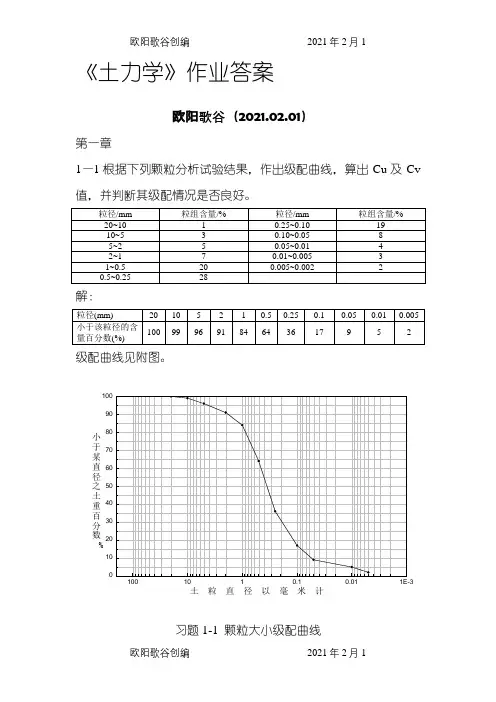
《土力学》作业答案欧阳歌谷（2021.02.01）第一章1—1根据下列颗粒分析试验结果，作出级配曲线，算出Cu及Cv 值，并判断其级配情况是否良好。
解：级配曲线见附图。
小于某直径之土重百分数%土粒直径以毫米计习题1-1 颗粒大小级配曲线由级配曲线查得：d 60=0.45，d 10=0.055，d 30=0.2； C u >5，1<C c <3； 故，为级配良好的土。
1—2有A 、B 、C 三种土，各取500g ，颗粒大小分析结果如表：要求：（1）绘出级配曲线；（2）确定不均匀系数Cu 及曲率系数Cv ，并由Cu 、Cv 判断级配情况。
解：级配曲线见附图。
1001010.10.011E-3102030405060708090100土粒直径以毫米计小于某直径之土重百分数%习题1-2 颗粒大小级配曲线由级配曲线查得d 10、d 30、d 60，并计算C u 、C c ：d 10d 30 d 60 C u C c 级配情况 A 0.0125 0.045 0.12 9.6 1.35 良好 B 0.19 0.41 0.69 3.63 1.28 不良 C0.1350.252.9021.480.16不良1—3某土样孔隙体积等于颗粒体积，求孔隙比e 为若干？ 若Gs=2.66，求d =? 若孔隙为水所充满求其密度和含水量W 。
解：111===s v V V e ； 3/33.1266.2cm g V M s d ===ρ； 3/83.12166.2cm g V M M w s =+=+=ρ；%6.3766.21===s w M M ω。
1—4在某一层土中，用容积为72cm 3的环刀取样，经测定，土样质量129.1g ，烘干后质量121.5g ，土粒比重为2.70，问该土样的含水量、密度、饱和密度、浮密度、干密度各是多少？ 解：3457.25.121cm G M V s s s ===； 3274572cm V V V s V =-=-=；%26.60626.05.1215.1211.129==-==s w M M ω； 3/79.1721.129cm g V M ===ρ； 3/06.2722715.121cm g V V M v w s sat =⨯+=+=ρρ；3/06.1724515.121'cm g V V M s w s =⨯-=-=ρρ；[或3/06.1106.2'cm g w sat =-=-=ρρρ]；3/69.1725.121cm g V M s d ===ρ。
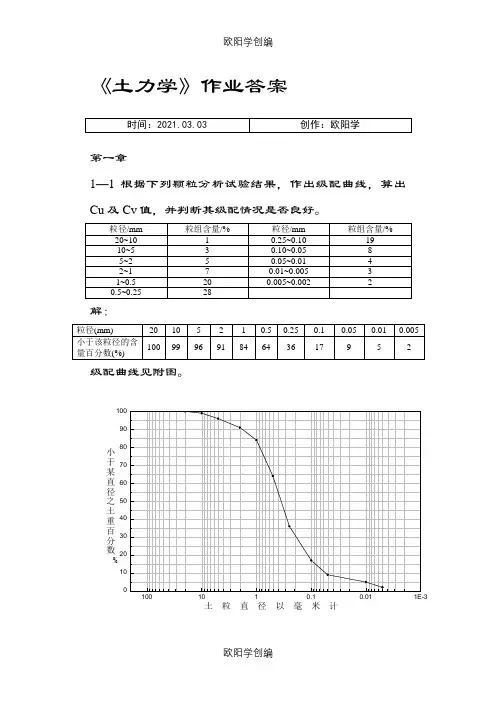
《土力学》作业答案第一章1—1根据下列颗粒分析试验结果，作出级配曲线，算出Cu及Cv值，并判断其级配情况是否良好。
解：级配曲线见附图。
小于某直径之土重百分数%土粒直径以毫米计习题11 颗粒大小级配曲线由级配曲线查得：d60=0.45，d10=0.055，d30=0.2；Cu>5，1<Cc<3；故，为级配良好的土。
1—2有A、B、C三种土，各取500g，颗粒大小分析结果如表：要求：（1）绘出级配曲线；（2）确定不均匀系数Cu及曲率系数Cv，并由Cu、Cv判断级配情况。
解：级配曲线见附图。
102030405060708090100土粒直径以毫米计小于某直径之土重百分数%习题12 颗粒大小级配曲线由级配曲线查得d10、d30、d60，并计算Cu 、Cc ：d10d30 d60 Cu Cc 级配情况 A 0.0125 0.045 0.12 9.6 1.35 良好 B 0.19 0.41 0.69 3.63 1.28 不良 C0.1350.252.9021.480.16不良1—3某土样孔隙体积等于颗粒体积，求孔隙比e 为若干？ 若Gs=2.66，求d=? 若孔隙为水所充满求其密度和含水量W 。
解：111===s v V V e ； 3/33.1266.2cm g V M s d ===ρ； 3/83.12166.2cm g V M M w s =+=+=ρ；%6.3766.21===s w M M ω。
1—4在某一层土中，用容积为72cm3的环刀取样，经测定，土样质量129.1g ，烘干后质量121.5g ，土粒比重为2.70，问该土样的含水量、密度、饱和密度、浮密度、干密度各是多少？ 解：3457.25.121cm G M V s s s ===； 3274572cm V V V s V =-=-=；%26.60626.05.1215.1211.129==-==s w M M ω； 3/79.1721.129cm g V M ===ρ； 3/06.2722715.121cm g V V M v w s sat =⨯+=+=ρρ；3/06.1724515.121'cm g V V M s w s =⨯-=-=ρρ；[或3/06.1106.2'cm g wsat =-=-=ρρρ]；3/69.1725.121cm g V M s d ===ρ。
土力学第五次作业答案-标准化文件发布号：（9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII1.在荷载为100kPa 作用下，非饱和土样孔隙比e=1.0，饱和度为80%，当荷载增加之200kPa 时，饱和度为90%，试问土样的压缩系数a 为多少？并求出土样的压缩模量s E 。
解：由sr G S eω⨯=可知，当w V 、s V 不变（也即wsV V ω=不变时），r S e 为常数。
12280% 1.00.88990%r r S e e S ==⨯= 压缩系数61122110.8891.1110 1.11()200100e e a Pa MPa p p -----===⨯=--压缩模量1111.801.11s e E MPa a ++=== 2.一个饱和土样，含水率为40%，重度18kN/m 3，土粒比重G s 为2.70，在压缩试验中，荷载从0增至150kPa ，土样含水率变为34%，试问土样的压缩量和此时的重度各位多少（ 环刀高度为2cm ）解：加荷前土体的孔隙比330(1)1 2.710/(140%)/18/1 1.10s w G e kN m kN m γωγ+=-=⨯+-=加荷后土体的孔隙比，饱和土中eω为定值。
00/0.34 1.1/0.400.935e e ωω==⨯=压缩量0(1.10.935)20 1.57(1)1 1.1e H H mm mm e ∆-∆==⨯=++33(1)/(1) 2.710/(10.34)/(10.935)18.7/s w G e kN m kN m γγω=++=⨯++=3.从一黏土层中取样做室内压缩试验，试样成果列于表5—9中。
试求：（1）该黏土的压缩系数a 1-2及相应的压缩模量E s,1-2，并评价其压缩性；（2）设黏土层厚度为2m ，平均自重应力σc =50kPa ，试计算在大面积堆载p 0=100kPa 的作用下，黏土层的固结压缩量。
表 黏土层压缩试验资料解：（1）11212120.7100.6500.60.20.1e e a MPa p p ----===--1,1212110.710 2.850.6s e E MPa a --++=== 该土属高压缩性土。
（2）050,100,p kPa p kPa =∆=12210.7100.6500.199lg lg lg 200lg100c e e C p p --===--000lg[()/]/(1)10.265c c s HC p p p e cm =+∆+=4.地面以下4~8m 范围内有一层软粘土，含水率42%ω=，重度317.5/kN m γ=，土粒重度 2.70s G =，压缩系数a=1.35MPa -1，4m 以上为粉质粘土，重度316.25/kN m γ=，地下水位在地表处，若地面作用一无限均布荷载q=100kPa ，求4~8m 深度这层软粘土的最终沉降量？首先思考几个问题：1）沉降是什么力产生的？目前我们认识到的土层中的应力有自重应力和附加应力，那么必须要明确的是产生土层沉降的力为附加应力。
2）作为对1）中的叙述的补充，有些时候对新填土层，会有土层还没有完成自重应力固结的情况，这样，我们才会去考虑自重应力产生的沉降，这是一种特殊情况，这里自然不必考虑。
借此，同学可以考虑0~4m 土层对下卧土层的沉降有没有影响，请说明原因！ 提示：外荷载作用前，地基土已在自重应力作用下完成固结。
解：4~8m 层软粘土303(1)2.7010/(10.42)11 1.1917.5/s w G kN m e kN m γωγ+⨯+=-=-=11.351000.135e a p MPa kPa -∆=•∆=⨯=00.135/(1 1.19)40024.65(1)eS H cm cm e ∆==+⨯=+说明：本题只是要求4~8米软土层的沉降，地面作用的无限均布荷载100kPa 在地基土不同深度产生的应力增量为100kPa ，故不必分层,也可以从另一个角度来说明不必分层计算——分层厚度h<0.4*b,而此处b 为无限长。
因为“外荷载作用前，地基土已在自重应力作用下完成固结”，所以不考虑上部对下部土层的作用力。
5.某墙下单独基础，基底尺寸3.0m*2.0m ，传至地面的荷载为300kN ，基础埋置深度为1.2m ，地下水位在基底以下0.6m ，地基土室内压缩实验成果如表所示，用分层总和法求基础中点的沉降量。
地基剖面描述如下：地面以下2.4m 内为粘土，317.6/kN m γ=，320.0/sat kN m γ=；粘土以下为粉质粘土，318.0/kN m γ=。
粉质粘土318.0/sat kN m γ=解：（1）地基分层考虑地层厚度不超过0.4b=0.8m 以及地下水位，基底以下厚度1.2m 的粘土层分成两层，层厚均为0.6m ，其下粉质黏土层厚度取为0.8m 。
（2）计算自重应力计算分层处的自重应力。
地下水位以下取有效重度进行计算 第2点处的自重应力：1.8*17.6+0.6*（20-10）=37.68kPa计算各个分层上下界面处自重应力的平均值，作为该分层受压前所受侧限竖向应力，各个分层点得自重应力值以及各个分层的平均自重应力值列于表中。
（3）计算竖向附加应力 基底平均附加应力0300 3.0 2.0 1.2201.217.652.93.0 2.0p kPa +⨯⨯⨯=-⨯=⨯利用应力系数a α（见第四章表4-4，查不到的数值可以利用线性插值法）计算各分层点的竖向附加应力，如第1点得附加应力为：a 452.940.23152.948.9kPa kPa α⨯=⨯⨯=计算各个分层上下界面处附加应力的平均值，各分层点附加应力值及各分层的平均附加应力值列于表中。
（4）各个分层自重应力平均值和附加应力平均值之和作为该分层受压后所受总应力。
（5）确定压缩层深度一般按照0.2z sz σσ<来确定压缩层深度，在3.6m 处，就已经有9.67kPa<56.88*0.2=11.38kPa ，故到此为止。
（6）计算各分层的压缩量 利用1211i i ie e s h e ⎛⎫-=⎪+⎝⎭或者相关公式计算各分层沉降量，各分层压缩量列于表中。
7.89 6.3512.68 6.58 3.4736.9737i s s mm mm ==++++=≈∑6.由于建筑物传来的荷载，地基中某一饱和黏土层产生梯形分布的竖向附加应力，该层顶面和底面的附加应力分别为σZ '=240kPa 和σZ ''=160kPa ，顶底面透水，土层平均k=0.2cm/年，e=0.88，a=0.39MPa -1，Es=4.82MPa 。
试求：①该土层的最终沉降量；②当达到最终沉降量之半所需的时间；③当达到120mm 沉降所需的时间；④如果该饱和黏土层下卧不透水层，则达到120mm 沉降所需的时间。
σ’解：①求最终沉降630.39102401601040.166166110.882z a s H m mm e σ-⨯+⎛⎫==⨯⨯== ⎪++⎝⎭②50%tt S U S==（双面排水，分布1型） 查平均固结度与时间因数的关系曲线中曲线得0.2v T =223(1)0.210(10.88)0.964/0.391010v w k e c m a γ--+⨯+===⨯⨯年 由2v v c t T H =，可知2240.220.830.964v v T H t c ⎛⎫⨯ ⎪⎝⎭===年③当120t S mm =时72%tt S U S== 查平均固结度与时间因数的关系曲线中曲线得0.42v T =2240.22 1.740.964v v T H t c ⎛⎫⨯ ⎪⎝⎭===年④当下卧层不透水，120t S mm =时,③比较，相当于由双面排水改为单面排水，即1.744t=年，所以 1.744 6.96t =⨯=年7.设基础置于厚8m 的饱和粘土层上，其下为不透水的坚硬岩层，基底有透水沙层。
已知地基附加应力分布为，基底处p a =140kPa ，岩面处p b =70kPa ，土层的初始孔隙比e 0=0.85，压缩系数a=0.4MPa -1，渗透系数k=0.59*10-7cm/s （即0.018m/年）。
试问： （1） 加荷1年后，基础沉降量是多少？81.9mm （2） 若饱和粘土层（底面）亦有一排透水砂层，则上述两问题有何不同？142mm因为'''z a z b p p p p =>=，基础加荷1年后的沉降量0.45*18281.9t s U s mm mm =•==（本结果比较粗略） 特别提醒：本问不可以直接查表，可以分开计算（矩形均布+三角分布，结果的表达形式=12.1cm*0.4+6.1cm*0.55=81.95mm ），也可以按上述公式计算总的U 。
为“万能公式”，最常用到的还是那个图表。
（2）双面排水，按曲线（1）计算 查图表，U=0.78，沉降量S t =0.78*182mm=142mm注意：当土层上下应力相同时为曲线1的情况，这时当采用双面排水时，也同为曲线1的情况，这时当沉降相同时，时间因数v T 相同，这时才有“双面排水需要的时间是单面排水的1/4”。
而我们这个题，当单面排水时不是曲线1，所有的双面排水都是情况1的情况，所以有些同学直接按（2）的结果1/4倍计算的方法是错误的，当然结果更错误，因为你们第二问的结果本身都是不对的。
8.请解释地震中的液化现象（包含什么是液化，产生的机理）。
答：少粘性土受地震力作用后，使使土体积体积缩小、孔隙压力猛增，从而使有效压力减小，使土迅速减小或完全丧失抗剪强度，使土提如液体一样流动或喷出地面，称为地基液化。
地震液化产生的条件内因：有的说砂土，实践证明叫“少粘性土”更好一些，有的粉土轻壤土也可能液化。
外因：饱和+地震动如果是常年干燥状态，不会液化，如果地震烈度是小于6度，也认为不发生液化。
主要应用有效应力原理解释！。
