工程力学教程篇(第二版)习题第7章答案

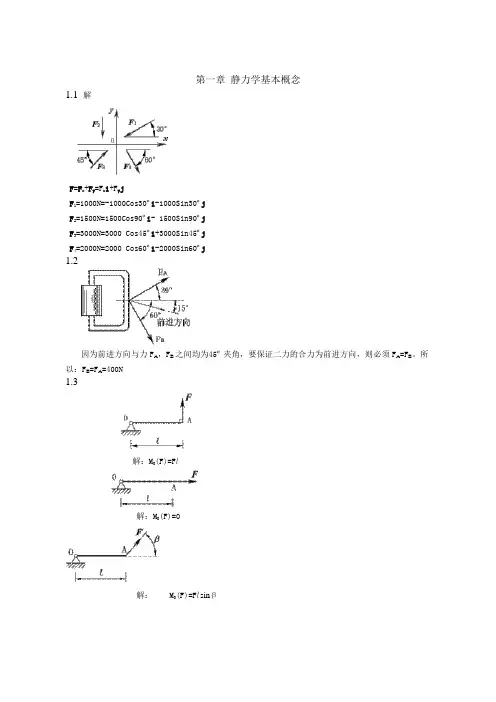
第一章静力学基本概念1.1 解F=F x+F y=F x i+F y jF1=1000N=-1000Cos30ºi-1000Sin30ºjF2=1500N=1500Cos90ºi- 1500Sin90ºjF3=3000N=3000 Cos45ºi+3000Sin45ºjF4=2000N=2000 Cos60ºi-2000Sin60ºj1.2因为前进方向与力F A，F B之间均为45º夹角，要保证二力的合力为前进方向，则必须F A=F B。

所以：F B=F A=400N1.3解：M O(F)=F l解：M O(F)=0解： M O(F)=F l sinβ解： M O(F)=F l sinθ解： M O(F)= -F a解：M O(F)= F(l＋r)解:1.4解:1.5解：1位置：M A(G)=02位置：M A(G)=-G l sinθ3位置：M A(G)=-G l1.6解：M O(F n)=-F n cosθ·D/2=-75.2N·m 1.71.8第二章平面力系2.1 力系简化解：（1）主矢大小与方位：F/R x＝∑F x＝F1cos45º+F3+F4cos60º＝100Ncos45º+200N+250cos60º＝395.7N F/R y＝∑F y＝F1sin45º-F2-F4sin60º＝100Nsin45º-150N-250sin60º＝-295.8N（2）主矩大小和转向：M O＝∑M O(F)＝M O(F1)+M O(F2)+M O(F3)+M O(F4)+m＝0-F2×0.3m+F3×0.2m+F4sin60×0.1m+F×0.1m＝0-150N×0.3m+200N×0.2m+250Nsin60×0.1m+50N×0.1m ＝21.65N·m( )向O点的简化结果如图所示。

工程力学（第2版）第7章 弯 曲题 库： 主观题7-1 长度为250mm ，截面尺寸为0.8mm 25mm h b ⨯=⨯的薄钢板卷尺，由于两端外力偶的作用而弯成中心角为030的圆弧。

已知弹性模量52.110MPa E =⨯。

试求钢尺横截面上的最大正应力。

解：由题知302250mm 360πρ⋅= ，故480mm ρ= 卷尺最外层纤维应变最大，且为4max 0.428.3310480hερ-===⨯ 由拉压胡克定律可知 54max max 2.1108.3310176MPa E σε-==⨯⨯⨯=即钢尺横截面上的最大正应221(0.250.23)760.573kN /m 4q π=-⨯=力为176MPa .知识点：1．梁横截面的应力。

参考页: P145。

学习目标: 2（掌握梁横截面上的应力计算方法，会利用应力计算公式计算正应力） 难度: 1.0提示一：该题考察知识点：1. 梁横截面上的应力计算。

提示二：无 提示三：无 提示四（同题解） 题解：1、利用正应力计算公式计算正应力。

7-2 一外径为250mm ，壁厚为10mm ，长度l=12m 的铸铁水管，两端搁在支座上，管中充满着水，如图所示。

铸铁的容量3176kN /m γ=，水的容重3210kN /m γ=。

试求管内最大拉、压正应力的数值。

解：每米铸铁水管的重量 每米水柱的重量22220.2310.231100.415kN /m 44q y ππ=⨯⨯⨯=⨯⨯⨯=故水管所受均布荷载120.988kN /m q q q =+=在水管中部有弯矩最大值22max 110.9881217.784kN m 88M ql ==⨯⨯=⋅最大弯曲正应力为3max max343217.7841040.7MPa 2300.25[1()]250z M W σπ⨯⨯===⨯⨯-故管内最大拉、压正应力的数值为,max ,max 40.7MPa t c σσ==。

知识点：1．梁横截面的应力。

工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A，构件AB，BC或ABC的受力图，未标重力的物体的重量不计，所有接触处均为光滑接触。

（a）（b）（c）（d）（e）（f）（g）1-2 试画出图示各题中AC杆（带销钉）和BC杆的受力图（a）（b）（c）（a）1-3 画出图中指定物体的受力图。

所有摩擦均不计，各物自重除图中已画出的外均不计。

（a）（b）（c）（d）（e）（f）（g）第二章 平面力系2-1 电动机重P=5000N ，放在水平梁AC 的中央，如图所示。

梁的A 端以铰链固定，另一端以撑杆BC 支持，撑杆与水平梁的夹角为30 0。

如忽略撑杆与梁的重量，求绞支座A 、B 处的约束反力。

题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN，用绳子挂在支架的滑轮B上，绳子的另一端接在绞车D上，如图所示。

转动绞车，物体便能升起。

设滑轮的大小及轴承的摩擦略去不计，杆重不计，A 、B 、C 三处均为铰链连接。

当物体处于平衡状态时，求拉杆AB 和支杆BC 所受的力。

题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示，输电线ACB 架在两电线杆之间，形成一下垂线，下垂距离CD =f =1m ，两电线杆间距离AB =40m 。

电线ACB 段重P=400N ，可近视认为沿AB 直线均匀分布，求电线的中点和两端的拉力。

题2-3图以AC 段电线为研究对象，三力汇交NF N F F F FF F F C A GA yC A x 200020110/1tan sin ,0,cos ,0=======∑∑解得：ααα2-4 图示为一拔桩装置。

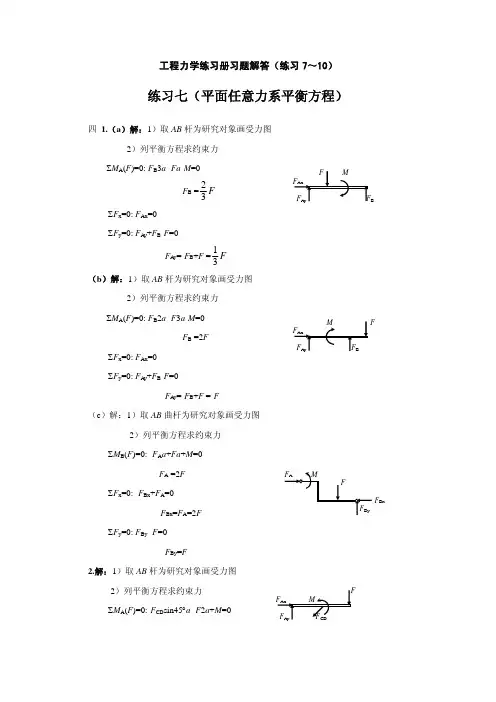
工程力学练习册习题解答（练习7～10）练习七（平面任意力系平衡方程）四 1.（a）解：1）取AB杆为研究对象画受力图2）列平衡方程求约束力∑M A(F)=0:F B3a-Fa-M=0F B=F32∑F x=0:F Ax=0∑F y=0:F A y+F B-F=0F A y=-F B+F=F31（b）解：1）取AB杆为研究对象画受力图2）列平衡方程求约束力∑M A(F)=0:F B2a-F3a-M=0F B=2F∑F x=0:F Ax=0∑F y=0:F A y+F B-F=0F A y=-F B+F=-F（c）解：1）取AB曲杆为研究对象画受力图2）列平衡方程求约束力∑M B(F)=0:-F A a+Fa+M=0F A=2F∑F x=0:-F Bx+F A=0F Bx=F A=2F∑F y=0:F By-F=0F By=F2.解：1）取AB杆为研究对象画受力图2）列平衡方程求约束力∑M A(F)=0:-F CD sin45︒a-F2a+M=0F CD =Fa Fa245sin -=-∑F x =0:F Ax -F CD con45︒=0F Ax =F CD con45︒=-F∑F y =0:F A y -F CD sin45︒-F =0F A y =F CD sin45︒+F =03.解：1）滿载向右倾倒时，F A =0∑M B (F )=0:Q (a +b )-Ge -Fl =0Q =36102505.1500+⨯+⨯=++ba Fl Ge =361.1kN 2）空载向左倾倒时，F B =0∑M A (F )=0:Qa -G (b +e )=0Q =6)5.13(500)(+=+a e b G =375kN 所以，361.1kN ≤Q ≤375kN练习八（固定端约束均布载荷求力矩）二 1.（a ）解：1）取AC 杆为研究对象画受力图2）列平衡方程求约束力∑M A (F )=0:F B 2a +M –q 2a ·a –F 3a =0F B =aqa qa qa 232222-+=2qa ∑F x =0:F Ax =0∑F y =0:F A y +F B -2qa -F =0F A y =-F B +2qa +F =qa（b ）解：1）取AB 杆为研究对象画受力图2）列平衡方程求约束力∑M A (F )=0:F B 3a +M –q 3a ·1.5a –F 2a =0F B =qaa qa qa qa 611325.4222=-+∑F x =0:F Ax =0∑F y =0:F A y +F B -3qa -F =0F A y =-F B +3qa +qa =qa 613（c ）解：1）取AB 杆为研究对象画受力图2）列平衡方程求约束力∑M A (F )=0:M A +M –q 2a ·a –F 2a =0M A =2qa 2+2qa 2–qa 2=3qa 2∑F x =0:F Ax =0∑F y =0:F A y -2qa -F =0F A y =2qa +F =3qa（d ）解：1）取AB 杆为研究对象画受力图2）列平衡方程求约束力∑M B (F )=0:M B +qa ·2.5a +Fa =0M B =–2.5qa 2–qa 2=–227qa ∑F x =0:F Bx =0∑F y =0:F By -qa -F =0F A y =qa +F =2qa2.解：1）取AB 杆为研究对象画受力图2）列平衡方程求约束力∑M A (F )=0:F CD sin45︒a -qa ·1.5a +M =0F CD =qaa qa qa 2245sin 5.122=- ∑F x =0:F Ax +F CD con45︒=0F Ax =-F CD con45︒=qa 21-∑F y =0:F A y +F CD sin45︒-qa =0F A y =-F CD sin45︒+qa =qa 21练习九（物体系统的平衡）四 1.解：1）分别取AB 、BC 杆为研究对象画受力图2）对AB 杆列平衡方程求约束力∑M B (F )=0:–F A ·3+q 2·1=0F A =31152⨯⨯=10kN ∑F x =0:F Bx =0∑F y =0:F By +F A -2q ·1=0F By =-F B +2q ·1=20kN3）对BC 杆列平衡方程求约束力∑M C (F )=0:M C +M +F By ·2=0M C =–M –2F By =–60kN ·m∑F x =0:F Bx -F Cx =0F Cx =F Bx =0∑F y =0:-F By +F Cy =0F Cy =F By =20kN2.解：1）分别取AB 、CD 杆为研究对象画受力图2）对CD 杆列平衡方程求约束力∑M D (F )=0:–F N ·0.4+M =0F N =4.044.0=M =10kN ∑F x =0:-F Dx +F N =0F x =F N =10kN∑F y =0:F Dy =03）对AB 杆列平衡方程求约束力∑M A (F )=0:–F N ·0.4+F ·0.2=0F =2.0104.0⨯=20kN ∑F x =0:F Ax +F -F N =0F Ax =-F +F N =-20+10=-10kN∑F y =0:F A y =03.解：1）分别取BCE 称台、AB 称杆为研究对象画受力图2）对BCE 称台列平衡方程求约束力F By ，∑F y =0:F By -G =0F By =G3）对AB 称杆列平衡方程求Q ,∑M O (F )=0:Q ·l -F By ·a =0Ql =F By a =G aal Q G =练习十（考虑摩擦时构件的平衡）四、1.解：1）分别取A 物块、B 物块为研究对象画受力图2）对A 物块列平衡方程求未知力∑F y =0:F N1-G A =0F N1=G A∑F x =0:F –F fA =0F =F fA补充方程：F fA =F N1·μ=μG A 所以F =μG A3）对B 物块列平衡方程求约束力∑F y =0:F N2-F N1-G B =0F N2=F N1+G B =G A +G B∑F x =0:–F fB +F fA =0F fB =F fA =μG A <μF N2=μ(G A +G B )结果表明，B 与接触面间摩擦力F fB 没有达到最大值。

第七章 杆类构件的应力分析与强度计算习 题7.1 图示阶梯形圆截面杆AC ，承受轴向载荷1200 kNF =与2100 kN F =, AB 段的直径mm 401=d 。

如欲使BC 与AB 段的正应力相同，试求BC 段的直径。

题7.1图解：如图所示：物体仅受轴力的作用，在有两个作用力的情况下经分析受力情况有：AB 段受力：1NAB F F = BC 段受力：12NBC F F F =+AB 段正应力：1221440.04NAB NAB AB AB F F F A d σππ⨯===⨯ BC 段正应力：()12222244NBC NBC BCBC F F F F A d d σππ+⨯===⨯ 而BC 与AB 段的正应力相同 即，BC AB σσ= 解出：249d mm ==7.2 图示轴向受拉等截面杆，横截面面积2500 mm A =，载荷50 kN F =。

试求图示斜截面()o30=α m-m 上的正应力与切应力，以及杆内的最大正应力与最大切应力。

mm题7.2图解：拉杆横截面上的正应力605000010050010N F F Pa MPa A A σ︒-====⨯ 应用斜截面上的正应力和剪应力公式：2300cos σσα︒︒= 030sin 22στα︒︒=有图示斜截面m-m 上的正应力与切应力为：3075MPa σ︒= 3043.3MPa τ︒=当0=α时，正应力达到最大，其值为max 0100MPa σσ︒== 即：拉压杆的最大正应力发生在横截面上，其值为100MPa 。

当45=α时，切应力最大，其值为0max 502MPa στ︒==即拉压杆的最大切应力发生在与杆轴成45的斜截面上，其值为50MPa 。

7.3图示结构中AC 为钢杆，横截面面积21200 mm A =，许用应力[]1160 Mpa σ=;BC 为铜杆，横截面面积22300 mmA =，许用应力[]2100 Mpa σ=。

⼯程⼒学第7章答案第7章简单的弹性静⼒学问题7－1 有⼀横截⾯⾯积为A 的圆截⾯杆件受轴向拉⼒作⽤，若将其改为截⾯积仍为A 的空⼼圆截⾯杆件，其他条件不变，试判断以下结论的正确性：（A ）轴⼒增⼤，正应⼒增⼤，轴向变形增⼤；（B ）轴⼒减⼩，正应⼒减⼩，轴向变形减⼩；（C ）轴⼒增⼤，正应⼒增⼤，轴向变形减⼩；（D ）轴⼒、正应⼒、轴向变形均不发⽣变化。

正确答案是 D 。

7－2 韧性材料应变硬化之后，材料的⼒学性能发⽣下列变化：（A ）屈服应⼒提⾼，弹性模量降低；（B ）屈服应⼒提⾼，韧性降低；（C ）屈服应⼒不变，弹性模量不变；（D ）屈服应⼒不变，韧性不变。

正确答案是 B 。

7－3 关于材料的⼒学⼀般性能，有如下结论，试判断哪⼀个是正确的：（A ）脆性材料的抗拉能⼒低于其抗压能⼒；（B ）脆性材料的抗拉能⼒⾼于其抗压能⼒；（C ）韧性材料的抗拉能⼒⾼于其抗压能⼒；（D ）脆性材料的抗拉能⼒等于其抗压能⼒。

正确答案是 A 。

7－4 低碳钢材料在拉伸实验过程中，不发⽣明显的塑性变形时，承受的最⼤应⼒应当⼩于的数值，有以下四种答案，试判断哪⼀个是正确的：（A ）⽐例极限；（B ）屈服强度；（C ）强度极限；（D ）许⽤应⼒。

正确答案是 B 。

7－5 根据图⽰三种材料拉伸时的应⼒—应变曲线，得出的如下四种结论，试判断哪⼀种是正确的：（A ）强度极限)3()2()1(b b b σσσ>=，弹性模量E(1)>E(2)>E(3)，延伸率δ（1）>δ（2）>δ（3）⽐例极限；（B ）强度极限)2()1()3(b b b σσσ<<，弹性模量E(2)>E(1)>E(3)，延伸率δ（1）>δ（2）>δ（3）⽐例极限；（C ）强度极限)3()1()2(b b b σσσ>>，弹性模量E(3)>E(1)>E(2)，延伸率δ（3）>δ（2）>δ（1）⽐例极限；（D ）强度极限)3()2()1(b b b σσσ>>，弹性模量E(2)>E(1)>E(3)，延伸率δ（2）>δ（1）>δ（3）⽐例极限；正确答案是 B 。

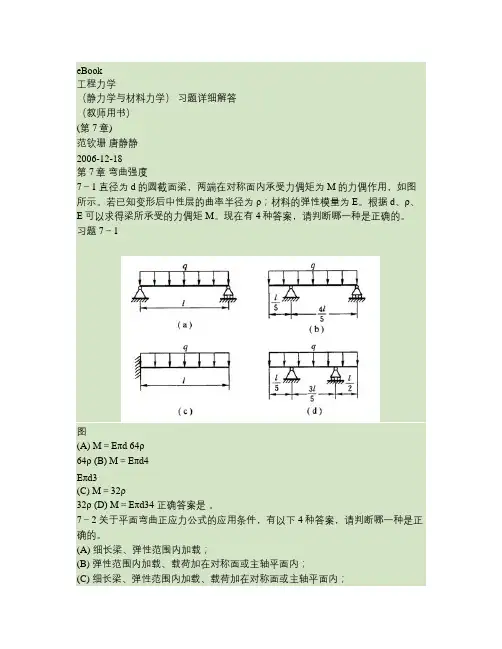
eBook工程力学（静力学与材料力学）习题详细解答（教师用书）(第7章)范钦珊唐静静2006-12-18第7章弯曲强度7－1 直径为d的圆截面梁，两端在对称面内承受力偶矩为M的力偶作用，如图所示。

若已知变形后中性层的曲率半径为ρ；材料的弹性模量为E。

根据d、ρ、E可以求得梁所承受的力偶矩M。

现在有4种答案，请判断哪一种是正确的。

习题7－1图(A) M＝Eπd 64ρ64ρ (B) M＝Eπd4Eπd3(C) M＝32ρ32ρ (D) M＝Eπd34 正确答案是。

7－2 关于平面弯曲正应力公式的应用条件，有以下4种答案，请判断哪一种是正确的。

(A) 细长梁、弹性范围内加载；(B) 弹性范围内加载、载荷加在对称面或主轴平面内；(C) 细长梁、弹性范围内加载、载荷加在对称面或主轴平面内；(D) 细长梁、载荷加在对称面或主轴平面内。

正确答案是 C _。

7－3 长度相同、承受同样的均布载荷q作用的梁，有图中所示的4种支承方式，如果从梁的强度考虑，请判断哪一种支承方式最合理。

l 5习题7－3图正确答案是7－4 悬臂梁受力及截面尺寸如图所示。

图中的尺寸单位为mm。

求：梁的1－1截面上A、 2B两点的正应力。

习题7－4图解：1. 计算梁的1－1截面上的弯矩：M=−⎜1×10N×1m+600N/m×1m×2. 确定梁的1－1截面上A、B两点的正应力：A点：⎛⎝31m⎞=−1300N⋅m 2⎟⎠⎛150×10−3m⎞−20×10−3m⎟1300N⋅m×⎜2My⎝⎠×106Pa=2.54MPa(拉应力)σA=z=3Iz100×10-3m×150×10-3m()12B点：⎛0.150m⎞1300N⋅m×⎜−0.04m⎟My⎝2⎠=1.62×106Pa=1.62MPa(压应力)σB=z=3Iz0.1m×0.15m127－5 简支梁如图所示。

工程力学习题答案第一章 静力学基础知识思考题：1. ×;2. √;3. √;4. √;5. ×;6. ×;7. √;8. √习题一1．根据三力汇交定理，画出下面各图中A 点的约束反力方向。

解：（a ）杆AB 在A 、B 、C 三处受力作用。

由于力和的作用线交于点O 。

如图（a ）所示，根据三力平衡汇交定理， 可以判断支座A 点的约束反力必沿 通过A 、O 两点的连线。

（b ）同上。

由于力和的作用线 交于O 点，根据三力平衡汇交定理， 可判断A 点的约束反力方向如 下图（b ）所示。

2．不计杆重，画出下列各图中AB 杆的受力图。

解：（a ）取杆AB 为研究对象，杆除受力外，在B 处受绳索作用的拉力，在A 和E 两处还受光滑接触面约束。

约束力和的方向分别沿其接触表面的公法线，并指向杆。

其中力与杆垂直，力通过半圆槽的圆心O 。

AB 杆受力图见下图（a ）。

(b)由于不计杆重，曲杆BC 只在两端受铰销B 和C 对它作用的约束力和，故曲杆BC 是二力构件或二力体，此两力的作用线必须通过B 、C 两点的连线，且=。

研究杆AB ，杆在A 、B 两点受到约束反力和，以及力偶m 的作用而平衡。

根据力偶的性质，和必组成一力偶。

(d)由于不计杆重，杆AB 在A 、C 两处受绳索作用的拉力和，在B 点受到支座反力。

和相交于O 点，根据三力平衡汇交定理，可以判断必沿通过pB RpB Rp B T A N E N E N A N B N C N BN CN A N B N A N B N A T C T B N A T C TB NB、O两点的连线。

见图(d).第二章 力系的简化与平衡思考题：1. √;2. ×;3. ×;4. ×;5. √;6. ×;7. ×;8. ×;9. √.1． 平面力系由三个力和两个力偶组成，它们的大小和作用位置如图示，长度单位为cm ，求此力系向O 点简化的结果，并确定其合力位置。

力学（第二版）漆安慎习题解答第七章刚体力学第七章刚体力学一、基本知识小结1•刚体的质心定义：r c = 7 m i r i/ m r c = rdm/ dm求质心方法：对称分析法，分割法，积分法。

2•刚体对轴的转动惯量定义：I 八mm2I = j r2dm平行轴定理I o = I c+md2正交轴定理I z = I x+I y.常见刚体的转动惯量：（略）3•刚体的动量和质心运动定理p = mv c v F = ma c4•刚体对轴的角动量和转动定理L = I 二* I -5.刚体的转动动能和重力势能E k 詔I ' E p = mgy c6•刚体的平面运动=随质心坐标系的平动+绕质心坐标系的转动动力学方程：a F二ma。

a .c=I「c （不必考虑惯性力矩）动能：E k = 2mV c2 i Ij J7•刚体的平衡方程'、■ F = 0,对任意轴x =0二、思考题解答7.1火车在拐弯时所作的运动是不是平动？答：刚体作平动时固联其上的任一一条直线，在各时刻的位置（方位）始终彼此平行。

若将火车的车厢看作一个刚体，当火车作直线运行时，车厢上各部分具有平行运动的轨迹、相同的运动速度和加速度，选取车厢上的任一点都可代替车厢整体的运动，这就是火车的平动。

但当火车拐弯时，车厢上各部分的速度和加速度都不相同，即固联在刚体上任一条直线，在各时刻的位置不能保持彼此平行，所以火车拐弯时的运动不是平动。

7.2对静止的刚体施以外力作用，如果合外力为零，刚体会不会运动？答：对静止的刚体施以外力作用，当合外力为了零，即时，刚体的质心将保持静止，但合外力为零并不表明所有的外力都作用于刚体的同一点。

所以，对某一确定点刚体所受合外力的力矩"八",八* 口Fi不一定为零。

由刚体的转动定律M=J可知，刚体将发生转动。

比如，置于光滑水平面上的匀质杆，对其两端施以大小相同、方向相反，沿水平面且垂直于杆的两个作用力时，杆所受的外力的合力为零，其质心虽然保持静止，但由于所受合外力矩不为零，将作绕质心轴的转动。

七 扭 转某圆轴作用有四个外力偶矩11=m m kN ⋅，6.02=m m kN ⋅，2.043==m m m kN ⋅。

(1) 试作轴扭矩图；(2) 若1m 、2m 位置互换，扭矩图有何变化？解：(2)AC ，主动轮A 传递外扭矩11=m m kN ⋅，从C 分别传递外扭矩为4.02=m m kN ⋅，6.03=m m kN ⋅，已知轴的直径4=d cm ，各轮间距50=l cm ，剪切弹性模量80=G GPa ，试求：(1) 合理布置各轮位置；(2) 求出轮在合理位置时轴的最大剪应力、轮A 与轮C之间的解：1．由扭矩图可以看出：按原先的布置，轴的最大扭矩为m kN 0.1⋅； 当主动轮A位于中间位置时，轴的最大扭矩降低为m kN 6.0⋅，因此，将主动轮A 布置在两从动轮B 和C 中间较为合理。

2．47.7MPa Pa 10416106.0633t max =⨯⨯⨯==-πτW T AC854.0r a d 0149.01043210801050106.084923p==⨯⨯⨯⨯⨯⨯⨯==--πϕGI l T AC AC 或 22tp max d GW lT GI l T d G l AC AC AC ===τϕ一空心圆轴的外径90=D mm ，内径60=d mm ，试计算该轴的t W ；若在横截面面积不变的情况下，改用实心圆轴，试比较两者的抗扭截面模量t W ，计算结果说明了什么？ 解：1．空心圆轴的抗扭截面模量()()()34444444t mm 105.119016609016232⨯=⨯-=-=-=πππDd D D d D W2．实心圆轴的抗扭截面模量 设实心圆轴的直径为d '，由实心圆轴与空心圆轴的横截面面积相等，即()22244d Dd -='ππ，可得mm 1.6760902222=-=-='d D d 故实心圆轴的抗扭截面模量为 343t mm 109.516⨯='='d W π3．比较1和2可知：在横截面相同的情况下，空心圆截面要比实心圆截面的抗扭截面模量大，因而，在扭转变形中，采用空心圆截面要比实心圆截面合理。

第七章基本知识小结⒈刚体的质心定义：∑⎰⎰==dm dm r r mr m r c i i c//求质心方法：对称分析法，分割法，积分法。

⒉刚体对轴的转动惯量定义：∑⎰==dm r I r m Iii 22平行轴定理 I o = I c +md 2 正交轴定理 I z = I x +I y. 常见刚体的转动惯量：（略） ⒊刚体的动量和质心运动定理∑==cca m F v m p⒋刚体对轴的角动量和转动定理∑==βτωI I L⒌刚体的转动动能和重力势能c p k mgy E I E ==221ω⒍刚体的平面运动=随质心坐标系的平动+绕质心坐标系的转动动力学方程：∑∑==cc ccI a m F βτ（不必考虑惯性力矩）动能：221221cc c k I mv E ω+=⒎刚体的平衡方程∑=0F， 对任意轴∑=0τ7.1.2 汽车发动机的转速在12s 内由1200rev/min 增加到3000rev/min.⑴假设转动是匀加速转动，求角加速度。

⑵在此时间内，发动机转了多少转？解：⑴260/2)12003000(/7.15s rad ===-∆πωβ⑵rad 2)60/2)(12003000(1039.26222202⨯===∆--πωωθ对应的转数=42010214.3239.262≈⨯=⨯∆πθ7.1.3 某发动机飞轮在时间间隔t 内的角位移为):,:(43s t rad ct bt at θθ-+=。

求t 时刻的角速度和角加速度。

解：23212643ct bt ct bt a d d -==-+==ωθβω7.1.4 半径为0.1m 的圆盘在铅直平面内转动，在圆盘平面内建立o-xy 坐标系，原点在轴上，x 和y 轴沿水平和铅直向上的方向。

边缘上一点A 当t=0时恰好在x 轴上，该点的角坐标满足θ=1.2t+t 2 (θ:rad,t:s)。

⑴t=0时，⑵自t=0开始转45º时，⑶转过90º时，A 点的速度和加速度在x 和y 轴上的投影。

第7章 刚体的平面运动习题7-1 直杆AB 长为l ，两端分别沿着水平和铅直方向运动，已知点A 的速度A υ为常矢量，试求当 60=θ时，点B 的速度和杆AB 的角速度。

（a ） （b ）解法一（如图a ）1.运动分析：杆AB 作平面运动。

2.速度分析：A B A B v v v +=，作速度矢量合成图 IA AB υυυ360tan == A A BA υυυ260cos /==A BAlAB υυω2==解法二（如图b ）1.运动分析：杆AB 作平面运动。

2.速度分析：杆AB 的速度瞬心是点I 。

ωυ⨯=AP A A All υυω260cos ==A AB ll BP υυωυ3260sin =⨯⨯=⨯=s rad /6=ω，试求图示位置时，滑块B 的速度以及连杆AB 的角速度。

解：1.运动分析：杆AB 均作一般平面运动，滑块作直线运动，杆OA 作定轴转动。

2.速度分析：对杆AB ，s m OA A /12=⨯=ωυA B A B v v v +=或AB B AB A v v ][][=30cos B A υυ=s m B /38=υs m A BA /3430tan =⨯=υυ s rad ABBAAB /2==υω7-3 图示机构，滑块B 以s m /12的速度沿滑道斜向上运动，试求图示瞬时杆OA 与杆AB 的角速度。

解：AB 杆运动的瞬心为I 点。

AB B BP ωυ⨯= s r a d BAB /325.043=⨯=υωs m AP AB A /2.7323.043=⨯⨯=⨯=ωυ 4.0⨯=OA A ωυ s rad OA /184.02.7==ω 或利s /m .B A 2753==υυOA=2m ，，圆轮半径为2m ，s rad /60=ω，试求图示位置时，轮心的速度，圆轮的角速度及连杆AB 的角速度。

解：1.运动分析：圆轮和杆AB 均作一般平面运动。

杆OA 作定轴转动。

力学（第二版）漆安慎习题解答第七章刚体力学第七章 刚体力学 一、基本知识小结⒈刚体的质心定义：∑⎰⎰==dm dm r r mr m r c i i c //ρρρρ求质心方法：对称分析法，分割法，积分法。

⒉刚体对轴的转动惯量定义：∑⎰==dm r I r m I ii 22平行轴定理 I o = I c +md 2 正交轴定理 I z = I x +I y.常见刚体的转动惯量：（略） ⒊刚体的动量和质心运动定理∑==c c a m F v m p ρρρρ ⒋刚体对轴的角动量和转动定理∑==βτωI I L⒌刚体的转动动能和重力势能c p k mgy E I E ==221ω⒍刚体的平面运动=随质心坐标系的平动+绕质心坐标系的转动动力学方程：∑∑==c c c c I a m F βτρρ（不必考虑惯性力矩）动能：221221cc c k I mv E ω+= ⒎刚体的平衡方程 ∑=0F ρ， 对任意轴∑=0τ二、思考题解答7.1 火车在拐弯时所作的运动是不是平动？答：刚体作平动时固联其上的任一一条直线，在各时刻的位置（方位）始终彼此平行。

若将火车的车厢看作一个刚体，当火车作直线运行时，车厢上各部分具有平行运动的轨迹、相同的运动速度和加速度，选取车厢上的任一点都可代替车厢整体的运动，这就是火车的平动。

但当火车拐弯时，车厢上各部分的速度和加速度都不相同，即固联在刚体上任一条直线，在各时刻的位置不能保持彼此平行，所以火车拐弯时的运动不是平动。

7.2 对静止的刚体施以外力作用，如果合外力为零，刚体会不会运动？答：对静止的刚体施以外力作用，当合外力为了零，即0i c F ma ==∑r r 时，刚体的质心将保持静止，但合外力为零并不表明所有的外力都作用于刚体的同一点。

所以，对某一确定点刚体所受合外力的力矩i i iM M r F ==⨯∑∑不一定为零。

由刚体的转动定律M J α=可知，刚体将发生转动。