SPSS分析-T检验

SPSS统计分析教程-独立样本T检验.docSPSS统计分析教程：独立样本T检验一、简介独立样本T检验（Independent Sample T-test）是统计分析中常见的一种方法，主要用于比较两组数据的均值是否存在显著差异。

这种检验的前提假设是，两组数据来自正态分布的独立样本。

独立样本T检验在SPSS中的实现相对简单，下面将详细介绍其操作步骤和解读结果。

二、数据准备在进行独立样本T检验之前，需要准备好数据。

数据通常存储在Excel或SPSS数据文件中。

为了方便起见，我们将使用SPSS数据文件进行说明。

三、操作步骤1.打开SPSS软件，点击“分析”（Analyze）菜单，然后选择“比较均值”（Compare Means）中的“独立样本T检验”（Independent Sample T-test）。

2.在弹出的对话框中，将左侧的“组别”（Grouped By）字段设置为一组变量，如“性别”（Gender），将右侧的“组1”（Group 1）和“组2”（Group 2）字段设置为另一组变量，如“年龄”（Age）。

3.点击“确定”（OK）按钮开始进行独立样本T检验。

四、结果解读1.假设检验（Hypothesis Test）：在结果中，可以看到假设检验的结果。

如果p值小于显著性水平（通常为0.05），则拒绝原假设（即两组数据的均值无显著差异），认为两组数据的均值存在显著差异。

反之，如果p值大于显著性水平，则接受原假设，认为两组数据的均值无显著差异。

2.均值（Mean）：在结果中，可以看到每组数据的均值。

如果两组数据的均值存在显著差异，则可以通过均值的大小来判断哪组数据更好或更优。

3.标准差（Standard Deviation）：在结果中，还可以看到每组数据的标准差。

标准差反映了数据分布的离散程度，标准差越大，说明数据分布越不集中。

4.t统计量（t-statistic）：t统计量是用来衡量两组数据之间差异大小的一个指标。

你的分析结果有T值，有sig值，说明你是在进行平均值的比较。

也就是你在比较两组数据之间的平均值有没有差异。

从具有t值来看，你是在进行T检验。

T检验是平均值的比较方法。

T检验分为三种方法：1. 单一样本t检验（One-sample t test）是用来比较一组数据的平均值和一个数值有无差异。

例如，你选取了5个人，测定了他们的身高，要看这五个人的身高平均值是否高于、低于还是等于1.70m，就需要用这个检验方法。

2. 配对样本t检验（paired-samples t test）是用来看一组样本在处理前后的平均值有无差异。

比如，你选取了5个人，分别在饭前和饭后测量了他们的体重，想检测吃饭对他们的体重有无影响，就需要用这个t检验。

注意，配对样本t检验要求严格配对，也就是说，每一个人的饭前体重和饭后体重构成一对。

3. 独立样本t检验（independent t test）是用来看两组数据的平均值有无差异。

比如，你选取了5男5女，想看男女之间身高有无差异，这样，男的一组，女的一组，这两个组之间的身高平均值的大小比较可用这种方法。

总之，选取哪种t检验方法是由你的数据特点和你的结果要求来决定的。

t检验会计算出一个统计量来，这个统计量就是t值，spss根据这个t值来计算sig值。

因此，你可以认为t值是一个中间过程产生的数据，不必理他，你只需要看sig值就可以了。

sig值是一个最终值，也是t检验的最重要的值。

sig值的意思就是显著性（significance），它的意思是说，平均值是在百分之几的几率上相等的。

一般将这个sig值与0.05相比较，如果它大于0.05，说明平均值在大于5%的几率上是相等的，而在小于95%的几率上不相等。

我们认为平均值相等的几率还是比较大的，说明差异是不显著的，从而认为两组数据之间平均值是相等的。

如果它小于0.05，说明平均值在小于5%的几率上是相等的，而在大于95%的几率上不相等。

我们认为平均值相等的几率还是比较小的，说明差异是显著的，从而认为两组数据之间平均值是不相等的。

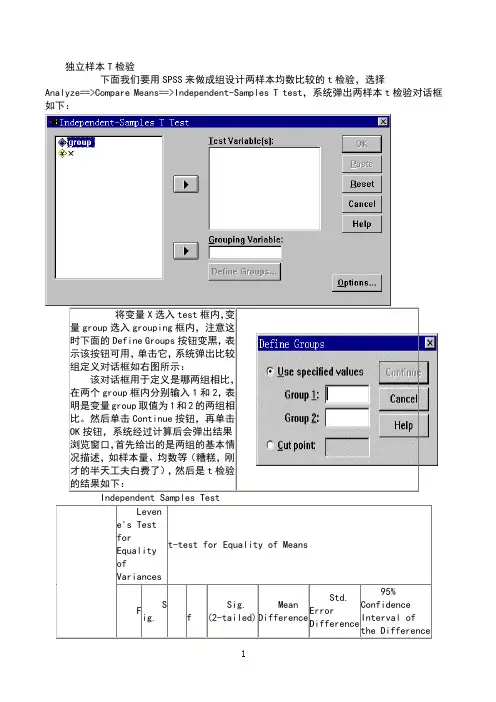
独立样本T检验下面我们要用SPSS来做成组设计两样本均数比较的t检验，选择Analyze==>Compare Means==>Independent-Samples T test，系统弹出两样本t检验对话框如下：将变量X选入test框内，变量group选入grouping框内，注意这时下面的Define Groups按钮变黑，表示该按钮可用，单击它，系统弹出比较组定义对话框如右图所示：该对话框用于定义是哪两组相比，在两个group框内分别输入1和2，表明是变量group取值为1和2的两组相比。

然后单击Continue按钮，再单击OK按钮，系统经过计算后会弹出结果浏览窗口，首先给出的是两组的基本情况描述，如样本量、均数等（糟糕，刚才的半天工夫白费了），然后是t检验的结果如下：Levene's TestforEqualityofVariancest-test for Equality of MeansFSig.tdfSig.(2-tailed)MeanDifferenceStd.ErrorDifference95%ConfidenceInterval ofthe Difference体方差是否齐，这里的戒严结果为F = ，p = ，可见在本例中方差是齐的；第二部分则分别给出两组所在总体方差齐和方差不齐时的t检验结果，由于前面的方差齐性检验结果为方差齐，第二部分就应选用方差齐时的t检验结果，即上面一行列出的t= ，ν=22，p=。

从而最终的统计结论为按α=水准，拒绝H0，认为克山病患者与健康人的血磷值不同，从样本均数来看，可认为克山病患者的血磷值较高。

SPSS对数据进行T检验统计分析下面将做此项目的最后一个环节，即使用SPSS进行统计分析。

先用SPSS来做组设计两样本均数比较的T检验，其步骤如下。

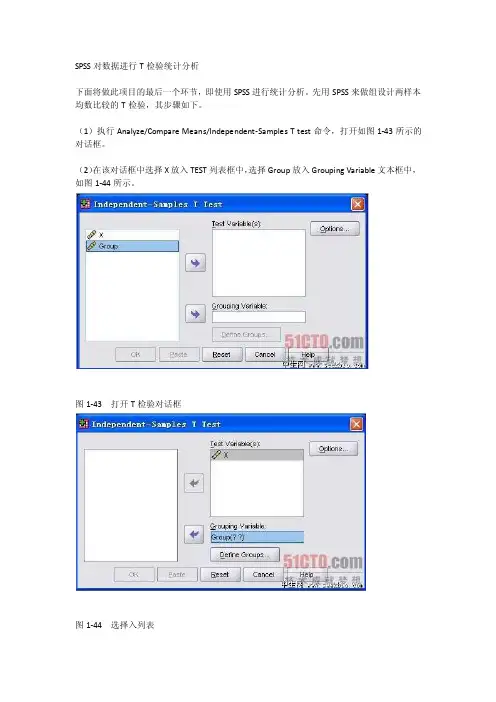
（1）执行Analyze/Compare Means/Independent-Samples T test命令，打开如图1-43所示的对话框。

（2）在该对话框中选择X放入TEST列表框中，选择Group放入Grouping Variable文本框中，如图1-44所示。

图1-43 打开T检验对话框图1-44 选择入列表（3）单击Define Groups按钮，系统弹出比较组定义对话框，如图1-45所示。

（4）在该对话框中的两个值框中分别输入1和2，然后单击Continue按钮，如图1-46所示。

图1-45 比较组定义对话框图1-46 输入值（5）单击T检验对话框中的OK按钮，如图1-47所示。

图1-47 进行T检验（6）系统经过计算后，会弹出结果浏览窗口。

首先给出的是两组的基本情况描述，如样本量、均数等，然后是T检验的结果，如图1-48所示。

图1-48 T检验结果从上图中可见，结果分为两大部分：第一部分为Levene's方差检验，用于判断两体方差是否齐，这里的检验结果为F=0.032，p=0.860，可见在本例中方差齐；第二部分则分别给出两组所在部体方差齐和方差不齐时的T检验结果，即上面一行列出的T=2.542，V=22，p=0.019。

从而最终的统计结论为按=0.05水准，拒绝H0，认为克山病患者与健康人的血磷值是不同的。

从样本均数来看，可以确定克山病患者的血磷值较高。

《证券理论与实务》模块八考试精要（证券市场基础知识）模块八考试精要一、单项选择题1、涉及证券市场的法律、法规第一个层次是指（）。

A、法律B、行政法规C、厂纪厂规D、部门规章2、涉及证券市场的法律、法规第二个层次是指（）。

A、法律B、行政法规C、厂纪厂规D、部门规章3、涉及证券市场的法律、法规第三个层次是指（）。

使用“住房状况调查”数据，对不同性别、户口状况的居民现住面积进行独立样本T检验并解释其结果。

答：对不同性别的居民现住面积进行独立样本T检验：①SPSS操作：第一步：点击“分析”、依次选择“比较平均值”、“独立样本T检验”；第二步：将“现住面积”选入“检验变量”，“性别”选入“分组变量”，在点击“定义组”，在“组1”中键入1，在“组2”中键入2，点击“继续”、“确定”。

②结果输出：③结果解读：先用F检验对不同性别的居民现住面积的方差是否向相等加以验证，然后利用t检验对不同性别的居民现住面积的均值是否存在差异进行检验。

从独立样本检验输出图中可以看到：F统计量为1.598，p值为0.206，在显著性水平0.05下，p值大于0.05，不拒绝原假设，即认为不同性别的居民现住面积的方差相等，没有差别。

由于不同性别的居民现住面积的方差没有差别，t检验将看假定等方差一栏。

t统计量为2.982，p值为0.003，在显著性水平0.05下，p值小于0.05，拒绝原假设，即认为不同性别的居民现住面积的均值有显著性差异。

对不同户口状况的居民现住面积进行独立样本T检验：④SPSS操作：第一步：点击“分析”、依次选择“比较平均值”、“独立样本T检验”；第二步：将“现住面积”选入“检验变量”，“户口状况”选入“分组变量”，在点击“定义组”，在“组1”中键入1，在“组2”中键入2，点击“继续”、“确定”。

⑤结果输出：⑥结果解读：先用F检验对不同户口状况的居民现住面积的方差是否向相等加以验证，然后利用t检验对不同户口状况的居民现住面积的均值是否存在差异进行检验。

从独立样本检验输出图中可以看到：F统计量为5.966，p值为0.015，在显著性水平0.05下，p值小于0.05，拒绝原假设，即认为不同户口状况的居民现住面积的方差存在显著差异。

由于不同户口状况的居民现住面积的方差存在显著差异，t检验将看不假定等方差一栏。

t统计量为3.314，p值为0.001，在显著性水平0.05下，p值小于0.05，拒绝原假设，即认为不同户口状况的居民现住面积的均值有显著性差异。

用SPSS进行T检验什么是T检验？T检验是统计学中的常用方法之一，用于检验两组样本的均值是否有显著差异。

它是通过计算样本的t值来确定两组样本均值差异是否显著。

因此，如果两组样本的t值越大，则它们之间的差异就越明显。

在进行T检验之前，我们首先需要明确两组样本是否满足正态分布的要求。

如果样本呈正态分布，则我们可以使用独立样本T检验或配对样本T检验进行检验。

如果不符合正态分布条件，我们需要使用非参数检验方法，例如Wilcoxon符号秩检验或Mann-Whitney U检验。

如何用SPSS进行T检验？下面我们将演示如何使用SPSS进行独立样本T检验和配对样本T检验。

独立样本T检验独立样本T检验用于检验两个独立样本的均值是否有差异。

例如，我们想知道男性和女性在身高上是否有显著差异，则可以使用独立样本T检验来验证。

我们使用一个示例数据集来展示如何进行独立样本T检验。

该数据集包含两组样本：一组是男子的身高，另一组是女子的身高。

在SPSS中，我们可以按照以下步骤进行独立样本T检验：1.打开SPSS软件并载入数据集。

2.单击菜单栏中的“分析”（Analyze），然后选择“比较均值”（CompareMeans），再选“独立样本T检验”（Independent-Samples T Test）。

3.在“独立样本T检验”对话框中，将男性身高和女性身高变量分别放到“变量1”和“变量2”框中。

4.点击“OK”按钮，SPSS将自动计算并输出T检验的结果和描述性统计数据。

下面是一个示例的SPSS的输出：执行男子控制女子均值174.609 161.164标准差 6.971 6.098标准误差均值 1.760 1.53595% CI（下限）171.023 158.126T 17.915df 38Sig。

（双尾）.000T检验结果显示，在本例中，男性和女性的身高之间存在显著差异。

T值为17.915，df值为38，Sig值小于0.05，表明这两组数据的差异不是由于随机因素导致的，而是由于不同的性别所导致的。

SPSS中t检验全都集中在分析—比较均值菜单中。

关于t检验再简单说一下，我们知道一个统计结果需要表达三部分内容，即集中性、变异性、显著性。

集中性的表现指标是均值变异的的表现指标是方差、标准差或标准误显著性的则是根据统计量判断是否达到显著性水平由于t分布样本均值的抽样分布，那么基于t分布的t检验就是样本均值的检验，是对均值差异的显著性检验。

t检验可以在以下三种分析中使用1.样本均数与总体均数的差异性分析（单样本t检验）2.配对设计样本均数或两非独立两样本均数差异性分析（配对t检验）3.两独立样本均数差异性分析（独立样本t检验）==============================================一、分析—比较均值—单样本T检验单样本T检验用来分析样本均值与总体均值的差异，以此来判断这个样本来自总体的均值是否等于（大于或小于）某个已知总体的均值，适用条件是样本数据分布呈正态分布，小样本情况下需要检验，大样本情况下近似正态，该方法比较稳健，只要不是严重偏态都可以使用。

二、分析—比较均值—配对样本T检验当配对设计的数据为连续变量时，可以使用配对T检验，配对T检验认为如果两种处理实际上没有差异，则每对数据的差值的总体均值应该为0，实际上就是已知均值为0的单样本T检验，因此适用条件也和单样本T检验一样。

三、分析—比较均值—独立样本T检验和配对设计相对应，独立样本t检验是针对成组设计，数据资料被分为两组，也就是两个样本，它们之间是相互独立的，检验的目的是判断这两个样本来自的总体均值是否存在差异。

由于涉及到两个总体，而每个总体的离散程度即方差也不一定相同，因此需要先对两样本的方差齐性做出检验，并且根据结果分为方差相同和方差不同两种算法。

独立样本t检验和配对样本t检验的区别：1.独立样本t检验用于检验两个独立样本是否来自具有相同均值的总体，也就是检验两个正态分布的总体均值是否相等。

配对样本t检验用于检验两个相关样本是否来自具有相同均值的正态总体，也就是检验两相关样本的差值的均值和零均值之间的差异显著性2.独立样本是指不同样本均值的比较，配对样本是相同样本均值的比较，例如同一个体的两次测量，如果分为实验组和对照组，那么就应该是独立样本。

6、输出结构的第二个表格表示的统计分析结果。

时间应激为例，在时间应激上t=2.030,df=95,Sig.=0.045。

在此处Sig就是统计学上的p值，其值小于0.05则差异显著，小于0.01则非常显著，小于0.001则极其显著。

在时间应激上，Sig也就是p值为0.045小于0.05，这就说明男性和女性在时间应激方面存在差异，由上表我们知道，其中男性的平均分为23.87，女性的平均分为21.63，因此男性高于女性，且这个差异具有显著性。

Independent Samples TestLevene's Testfor Equality ofVariances t-test for Equality of MeansF Sig. t dfSig.(2-tailed)MeanDifferenceStd. ErrorDifference95% ConfidenceInterval of theDifferenceLower Upper时间应激Equalvariancesassumed.043 .836 2.030 95 .045 2.23 1.100 .049 4.416 Equalvariancesnotassumed2.021 55.255 .048 2.23 1.105 .018 4.446焦虑Equalvariancesassumed.116 .734 .922 95 .359 .80 .871 -.926 2.533 Equalvariancesnotassumed.932 57.354 .355 .80 .862 -.922 2.529上司支持Equalvariancesassumed.009 .924 -1.020 95 .310 -.58 .567 -1.704 .547Equalvariancesnotassumed-1.004 53.732 .320 -.58 .577 -1.735 .577同事支持Equalvariancesassumed.041 .841 -1.089 95 .279 -.68 .624 -1.920 .559 Equalvariancesnotassumed-1.091 56.066 .280 -.68 .623 -1.929 .569家人朋友Equalvariances.420 .518 -.635 95 .527 -.28 .447 -1.172 .604assumedEqualvariancesnotassumed-.625 53.787 .535 -.28 .455 -1.196 .627内在满意Equalvariancesassumed20.916 .000 -4.278 95 .000 -10.87 2.542 -15.919 -5.827 Equalvariancesnotassumed-3.758 42.490 .001 -10.87 2.893 -16.710 -5.036外在满意Equalvariancesassumed11.579 .001 .046 95 .963 .09 1.889 -3.662 3.836Equalvariancesnotassumed.057 91.141 .955 .09 1.530 -2.951 3.125整体满意Equalvariancesassumed.774 .381 -2.506 95 .014 -10.76 4.292 -19.277 -2.235 Equalvariancesnotassumed-2.518 56.493 .015 -10.76 4.272 -19.312 -2.200内外倾向Equalvariancesassumed.000 .987 -2.064 95 .042 -2.19 1.062 -4.298 -.084 Equalvariancesnotassumed-2.135 60.646 .037 -2.19 1.026 -4.243 -.139F检验F检验主要用来考察三组以上变量间的关系。

SPSS均值检验（均数分析单样本T检验独⽴样本T检验）在统计学中，我们往往从样本的特性推知随机变量总体的特性。

但由于总体中个体之间存在差异，样本的统计量和总体的参数之间往往会有误差。

因此，均值不相等的样本未必来⾃不同分布的总体，⽽均值相等的样本未必来⾃有相同分布的总体。

也就是说，如何从样本均值的差异推知总体的差异，这就是均值⽐较的内容。

SPSS提供了均值⽐较过程，在主菜单栏单击“Analyze”菜单下的“Compare Means”项，该项下有5个过程，如图4-1。

平均数⽐较Means过程⽤于统计分组变量的的基本统计量。

这些基本统计量包括：均值（Mean）、标准差(Standard Deviation)、观察量数⽬(Number of Cases)、⽅差(Variance)。

Means过程还可以列出⽅差表和线性检验结果。

[例⼦]调查了棉铃⾍百株卵量在暴⾬前后的数量变化，统计暴⾬前和暴⾬后的统计量，其数据如下：暴⾬前 110 115 133 133 128 108 110 110 140 104 160 120 120暴⾬后 90 116 101 131 110 88 92 104 126 86 114 88 112该数据保存在“DATA4-1.SAV”⽂件中。

1）准备分析数据在数据编辑窗⼝输⼊分析的数据，如图4-2所⽰。

或者打开需要分析的数据⽂件“DATA4-1.SAV”。

图4-2 数据窗⼝2）启动分析过程在SPSS主菜单中依次选择“Analyze→Compare Means→Means”。

出现对话框如图4-3。

图4-3 Means设置窗⼝3）设置分析变量从左边的变量列表中选中“百株卵量”变量后，点击变量选择右拉按钮，该变量就进⼊到因⼦变量列表“Dependent List:”框⾥，⽤户可以从左边变量列表⾥选择⼀个或多个变量进⾏统计。

从左边的变量列表中选中“调查时候”变量，点击“Independent List”框左边的右拉按钮，该变量就进⼊分组变量“IndependentList”框⾥，⽤户可以从左边变量列表⾥选择⼀个或多个分组变量。

计量资料的统计分析-均数比较两个均数比较的t 检验(t-test / Student’s t-test)就是以t分布为基础的假设检验方法，实际应用时，应弄清各种检验方法的用途、适用条件和注意事项。

SPSS在其分析菜单下的的均值比较中提供的t 检验方法过程有： 单样本t检验配对样本t检验独立样本t检验例3-5 某医生测量了36名从事铅作业男性工人的血红蛋白含量，算得其均数为130.83g/L，标准差为25.74g/L。

问从事铅作业工人的血红蛋白是否不同于正常成年男性平均值140g/L？附：36名从事铅作业男性工人的血红蛋白含量的原始数据112，137， 129，126，88， 90， 105， 178，130， 128，126，103，172，116，125， 90， 96， 62，157，151，135，113，175，129， 165， 171，128， 128，160，110，140，163，100， 129， 116，127。

SPSS软件操作-例3-051） 建立数据文件数据格式：1列36行，1个反应变量，变量名为“hb”。

2）过程操作界面SPSS软件操作-例3-053）结果N均值标准差均值的标准误血红蛋白含量36130.833325.74102 4.29017单个样本统计量单个样本检验检验值=140T df Sig.(双侧)均值差值差分的95%置信区间下限上限血红蛋白含量-2.13735.040-9.16667-17.8762-.4572例3-6 为比较两种方法对乳酸饮料中脂肪含量测定结果是否不同，随机抽取了10份乳酸饮料制品，分别用脂肪酸水解法和哥特里－罗紫法测定其结果如表3-5第(1)~(3)栏。

问两法测定结果是否不同？表3-5 两种方法对乳酸饮料中脂肪含量的测定结果（%）编号（1）哥特里-8罗紫法（29）脂肪酸水解法（3）差值d（4）=（2）-（3）10.8400.5800.260 20.5910.5090.082 30.6740.5000.174 40.6320.3160.316 50.6870.3370.350 60.9780.5170.461 70.7500.4540.291 80.7300.5120.218 9 1.2000.9970.203 100.8700.5060.364合计-- 2.724SPSS软件操作-例3-061） 建立数据文件数据格式：2列10行，2个反应变量，变量名为“x1”和“x2”。