中科院物理所考博试题(固体物理)

第一章 晶体结构和X 射线1、试证体心立方和面心立方各自互为正、倒格子2、如果基矢a,b,c 构成正交关系，证明晶面族（h k l ）的面间距满足：222)()()(1c l b k a hd hkl ++=3、证明以下结构晶面族的面间距：（1） 立方晶系：d hkl =a [h 2+k 2+l 2]-1/2（2） 六角晶系：2/12222])()(34[-+++=c l ahk k h d hkl 4、等体积的硬球堆积成体心立方结构和面心立方结构，试求他们在这两种结构中的致密度分别为0.68和0.74。

5、试证密积六方结构中，c/a=1.633。

6、在立方晶胞中，画出（1 0 1），（0 2 1），（221）和（012）晶面。

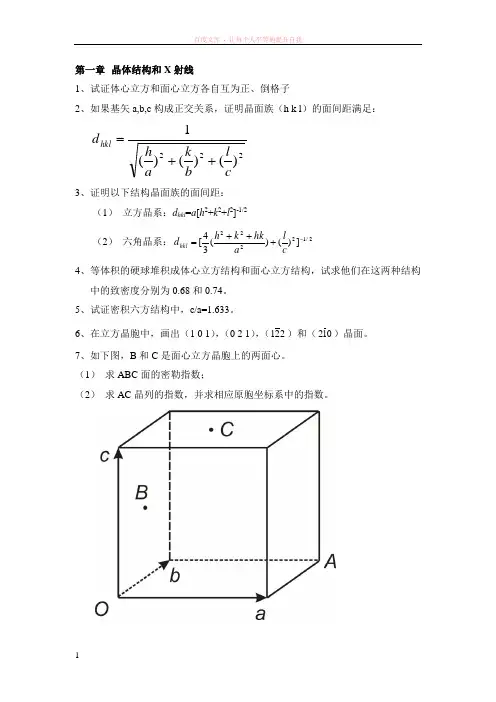
7、如下图，B 和C 是面心立方晶胞上的两面心。

（1） 求ABC 面的密勒指数；（2） 求AC 晶列的指数，并求相应原胞坐标系中的指数。

8、六角晶胞的基矢为.,223,223k c c j a i a b j a i a a =+-=+=求其倒格子基矢。

9、求晶格常数为a 的面心立方和体心立方晶体晶面族（h 1 h 2 h 3）之间的面间距（指导p30,10）。

10、讨论六角密积结构，X 光衍射的消光条件。

11、求出体心立方、面心立方的几何因子和消光条件。

12、原胞和晶胞的区别？13、倒空间的物理意义？14、布拉格衍射方程，原子和几何结构因子在确定晶格结构上分别起何作用？15、什么是布拉格简单格子，什么是复式格子？第二章 自由电子气1、设有一个长度为L 的一维金属线，它有N 个导电电子，若把这些导电电子看成自由电子气，试求：（1） 电子的状态密度（2） 绝对零度下的电子费米能级，以及费米能级随温度的变化关系。

（3） 电子的平均能量。

（4） 电子的比热。

2、二维电子气的能态密度2)( πm E N =，证明费米能 ]1ln[/2-=T mk n B F b eT k E π 3、求出一维金属中自由电子的能态密度、费米能级、电子的平均动能以及一个电子对于比热的贡献。

前 言本资料主要用于中科院的固体物理考研参考。

中科院的很多研究所的硕士入学考试都有固体物理(均为可选)，例如半导体所、高能物理所、物理所、金属所、上海应用物理研究所、上海技术物理研究所和上海硅酸盐研究所等，这表明固体物理这门课程对我们以后在研究生阶段的学习和研究是非常重要的，因此我们在这门课程的复习过程中要认真对待，对教材的相关内容要理解透彻。

本资料不作理论研究用，仅用于考研复习参考资料，主要是参照中科院的新大纲来编写的。

大纲中给出的参考资料有两本，分别为教材一《固体物理基础》(阎守胜编)和教材二《固体物理学》(黄昆编)，另外，根据很多同学的推荐本人再向大家推荐一本教材，就是方俊鑫和陆栋主编的《固体物理学(上册)》，在本资料里把它称为教材三。

这三本教材中最重要的还是教材二，其中主要是前六章，希望大家都能仔细复习。

本资料按照新大纲要求分为七章，每章都分为三部分(除第三章外)：考试指导、基本知识点和试题分析。

考试指导是来自于本人考研复习的经验，纯属个人意见，希望能对大家有帮助。

基本知识点大多都是考试重点，不是重点内容的将会说明。

试题分析是很重要的部分，我们要通过例题来加强对知识的理解和掌握，通过分析解题来进一步抓住考点。

另外，本资料例题均选自于往年考试真题，因为真题最具有参考性，解题过程中最重要的是知识点分析，其答案仅供参考。

由于本人知识有限，本资料在编写过程中定有一些不妥或错误之处，诚恳大家在以后的交流中批评、指正。

中科院研究生院硕士研究生入学考试《固体物理》考试大纲本《固体物理》考试大纲适用于中国科学院凝聚态物理及相关专业的硕士研究生入学考试。

《固体物理》是研究固体的结构、组成粒子的相互作用以及运动规律的学科，是物理研究的一个重要组成部分，是许多学科专业的基础课程，其主要内容包括晶体结构、晶格振动、能带理论和金属电子论等内容。

要求考生深入理解其基本概念，有清楚的物理图象，能够熟练掌握基本的物理方法，并具有综合运用所学知识分析问题和解决问题的能力。

中科院物理所面试推免面试题目不完全整顿
我（第三批）被问到旳题目：
1. 狭义相对论公式，详细怎样推导出来（电磁、电动）
2. 氢原子半径公式及其详细数值（原子物理）
3. 电冰箱旳工作机制，规定说出详细怎么工作旳，氟利昂旳作用等（热学）
4. 怎样在试验室辨别金属，半导体，绝缘体（固体物理）
5. 一台电子显微镜能否辨别一种原子（辨别本领，艾里斑）（光学）
6. 什么算符跟什么算符对易（量子力学）
没学固体物理，就提前告诉老师你没学这本书
英语问题：talk about your college. 没有英语自我简介。

英语比重没有专业问题那么重要。

中国科学院物理所考博固体物理试题5套中国科学院物理研究所固体物理博士入学试题(20XX年）1.填空题①．NaCl 石墨铜钠其中一个的点群与其它不同是②.在低温，金刚石比热与温度的关系是③.高压晶体体积变小，能带宽度会④.石墨中原子之间通过键结合成固体。

2.推导bloch定理；写出理想情况下表面态的波函数的表达式，并说明各项的特点。

3.推导出一维双原子的色散关系。

4.在紧束缚近似条件下，求解周期势场中的波函数和能量本征值。

5.某面心立方晶体，其点阵常数为a①画出晶胞，（１，１，１），（２，２，０），（１，１，３）晶面；②计算三面的面间距；③说明为什么（１，０，０）晶面衍射强度为零。

6.重费米系统、接触电势、安德森转变。

７．为什么金属电子自由程是有限的但又远远大于原子间距？８．硅本征载流子浓度为９．６５×１０９ｃｍ－３，导带有效密度为２．８６×１０１９ｃｍ－３，若掺入每立方厘米１０１６的Ａｓ原子，计算载流子浓度。

９．磁畴１０．原激发１１．对理想金属可以认为其介电常数虚部为零。

请以Ａｌ为例，给出理想金属对的反射率Ｒ随频率的变化（公式、频率值、示意图）１２．分析说明小角晶界的角度和位错的间距的关系，写出表达式。

１３．试通过数据说明，为什么处理硅、锗等半导体的可见光吸收时，采用垂直跃迁的近似是合理的。

１４．试根据超导Ｂ＝０，推导出超导临界温度和外加磁场的定性关系。

１５．论述固体内部的位错类型，并且画出示意图。

20XX年第一部分（共6题，选作4题，每题15分，共计60分；如多做，按前4题计分）1. 从成键的角度阐述Ⅲ-Ⅴ族和Ⅱ-Ⅵ族半导体为什么可以形成同一种结构:闪锌矿结构。

2. 请导出一维双原子链的色散关系，并讨论在长波极限时光学波和声学波的原子振动特点。

3. 从声子的概念出发，推导并解释为什么在一般晶体中的低温晶格热容量和热导率满足T3关系。

4. 设电子在一维弱周期势场V(x)中运动，其中V(x)= V(x+a)，按微扰论求出k=±π/a处的能隙。

中科院考研固体物理试题（1997~2012）一九九七年研究生入学考试固体物理试题一好多元素晶体拥有面心立方构造，试：1绘出其晶胞形状，指出它所拥有的对称元素2说明它的倒易点阵种类及第一布里渊区形状3面心立方的 Cu 单晶（晶格常熟 a=? ）的 x 射线衍射图（x 射线波长λ＝ ? ）中，为何不出现（ 100），（ 422），（511）衍射线？4它们的晶格振动色散曲线有什么特色？二已知原子间互相作用势 U ( r )r n ，此中α，β， m,n 均为 >0 的常数，r mn>m。

试证明此系统能够处于稳固均衡态的条件是三已知由 N 个质量为 m，间距为的同样原子构成的一维单原子链的色散关系为142qasinm21试给出它的格波态密度g，并作图表示2试绘出其色散曲线形状，并说明存在截止频次max 的意义四半导体资料的价带基本上填满了电子（近满带），价带中电子能量表示式34 2E k 1.016 10 k ( J ) ，此中能量零点取在价带顶。

这时若k 1 10 6 cm 处电子被激发到更高的能带（导带）而在该处产生一个空穴，试求此空穴的有效质量，波矢，准动量，共有化运动速度和能量。

（已知 1.054 10 34 J s ，m0 9.1095 1035w s3cm2 ）五金属锂是体心立方晶格，晶格常数为 a 3.5 ?，假定每一个锂原子贡献一个传导电子而构成金属自由电子气，试推导 T 0K 时，金属自由电子气费米能表示式，并计算出金属锂费米能。

（已知 eV1.602 1019J）1六 二维自由电子气的电子能量表达式是2 22k 2E kkx y2m2m当kz方向有磁场入射时， 电子能量本征值将为一系列 Landau 能级。

Landau 能级是高简并度分立能级，试导出其简并度。

一九九八年研究生入学考试固体物理试题一 简要回答以下问题（ 20 分）1试绘图表示 NaCl 晶体的结晶学原胞、布拉菲原胞、基元和固体物理学原胞。

宝鸡文理学院试题课程名称 固体物理 适 用 时 间 2011年1月 试卷类别 A 适用专业、年级、班 2008级物理教育专业一、简答题（每题6分，共6×5=30分)1、试述离子键、共价键、金属键、范德瓦尔斯和氢键的基本特征.2、试述晶态、非晶态、准晶、多晶和单晶的特征性质。

3、什么叫声子？对于一给定的晶体，它是否拥有一定种类和一定数目的声子？4、周期性边界条件的物理含义是什么？引入这个条件后导致什么结果？如果晶体是无限大，q 的取值将会怎样？5、倒格子的实际意义是什么？一种晶体的正格矢和相应的倒格矢是否有一一对应的关系？二、试证明体心立方格子和面心立方格子互为正倒格子。

（20分)三、一维晶格，晶格由两种离子组成,间距为R 0,计算晶格的Madelung 常数α。

（15分）四、用钯靶αK X 射线投射到NaCl 晶体上，测得其一级反射的掠射角为5。

9°，已知NaCl 晶胞中Na ＋与Cl －的距离为2.82×10—10m ，晶体密度为2.16g/cm 3.求:（1）X 射线的波长；（2）阿伏加德罗常数。

(20分）五、写出量子谐振子系统自由能，证明在经典极限，自由能为：（15分） ⎪⎪⎭⎫ ⎝⎛+≈∑KT hw KT U F q q o ln宝鸡文理学院试题参考答案与评分标准课程名称 固体物理 适 用 时 间 2011年1月 试卷类别 A 适用专业、年级、班07物理教育一、简答题(每小题6分，5×6=30分）1、试述离子键、共价键、金属键、范德瓦尔斯和氢键的基本特征。

解：（1）离子键：无方向性，键能相当强;（2）共价键:饱和性和方向性,其键能也非常强；（3）金属键：有一定的方向性和饱和性，其价电子不定域于2个原子实之间，而是在整个晶体中巡游，处于非定域状态,为所有原子所“共有”；（4）范德瓦尔斯键:依靠瞬时偶极距或固有偶极距而形成，其结合力一般与7r 成反比函数关系，该键结合能较弱；（5）氢键：依靠氢原子与2个电负性较大而原子半径较小的原子（如O,F,N 等)相结合形成的。

固体物理题库第⼀章晶体的结构第⼀章晶体的结构⼀、填空体（每空1分）1. 晶体具有的共同性质为长程有序、⾃限性、各向异性。

2. 对于简⽴⽅晶体，如果晶格常数为a，它的最近邻原⼦间距为 a ，次近邻原⼦间，原胞与晶胞的体积⽐1：1 ，配位数为 6 。

3. 对于体⼼⽴⽅晶体，如果晶格常数为a a2，次近邻原⼦间距为 a ，原胞与晶胞的体积⽐1：2 ，配位数为8 。

4. 对于⾯⼼⽴⽅晶体，如果晶格常数为a邻原⼦间距为 a ，原胞与晶胞的体积⽐1：4 ，配位数为12 。

5. ⾯指数(h1h2h3)所标志的晶⾯把原胞基⽮a1,a2,a3分割,其中最靠近原点的平⾯在a1,a2,a3上的截距分别为__1/h1_,_1/h2__,__1/h3_。

6. 根据组成粒⼦在空间排列的有序度和对称性，固体可分为晶体、准晶体和⾮晶体。

7. 根据晶体内晶粒排列的特点，晶体可分为单晶和多晶。

8. 常见的晶体堆积结构有简⽴⽅（结构）、体⼼⽴⽅（结构）、⾯⼼⽴⽅（结构）和六⾓密排（结构）等，例如⾦属钠（Na）是体⼼⽴⽅（结构），铜（Cu）晶体属于⾯⼼⽴⽅结构，镁（Mg）晶体属于六⾓密排结构。

9. 对点阵⽽⾔，考虑其宏观对称性，他们可以分为7个晶系，如果还考虑其平移对称性，则共有14种布喇菲格⼦。

10.晶体结构的宏观对称只可能有下列10种元素：1 ，2 ，3 ，4 ，6 ，i ，m ，3，4，6，其中3和6不是独⽴对称素，由这10种对称素对应的对称操作只能组成32个点群。

11. 晶体按照其基元中原⼦数的多少可分为复式晶格和简单晶格，其中简单晶格基元中有 1 个原⼦。

12. 晶体原胞中含有 1 个格点。

13. 魏格纳-塞茨原胞中含有 1 个格点。

⼆、基本概念1. 原胞原胞：晶格最⼩的周期性单元。

2. 晶胞结晶学中把晶格中能反映晶体对称特征的周期性单元成为晶胞。

3. 散射因⼦原⼦内所有电⼦在某⼀⽅向上引起的散射波的振幅的⼏何和，与某⼀电⼦在该⽅向上引起的散射波的振幅之⽐。

固体物理试题库一. 填空(20分, 每题2分)1.对晶格常数为a 的SC 晶体,与正格矢R =a i +2a j +2a k 正交的倒格子晶面族的面指数为( ), 其面间距为( ).2.典型离子晶体的体积为V , 最近邻两离子的距离为R , 晶体的格波数目为( ), 长光学波的( )波会引起离子晶体宏观上的极化.3. 金刚石晶体的结合类型是典型的( )晶体, 它有( )支格波.4. 当电子遭受到某一晶面族的强烈反射时, 电子平行于晶面族的平均速度( )零, 电子波矢的末端处在( )边界上.5. 两种不同金属接触后, 费米能级高的带( )电. 对导电有贡献的是 ( )的电子.二. (25分)1. 证明立方晶系的晶列[hkl ]与晶面族(hkl )正交.2. 设晶格常数为a , 求立方晶系密勒指数为(hkl )的晶面族的面间距.三. (25分)设质量为m 的同种原子组成的一维双原子分子链, 分子内部的力系数为β1, 分子间相邻原子的力系数为β2, 分子的两原子的间距为d , 晶格常数为a ,1. 列出原子运动方程.2. 求出格波的振动谱ω(q ).四. (30分)对于晶格常数为a 的SC 晶体1. 以紧束缚近似求非简并s 态电子的能带.2. 画出第一布里渊区[110]方向的能带曲线, 求出带宽.3.当电子的波矢k =i +j 时,求导致电子产生布拉格反射的晶面族的面指数.a πa π1.1 在结晶学中, 晶胞是按晶体的什么特性选取的?[解答]在结晶学中, 晶胞选取的原则是既要考虑晶体结构的周期性又要考虑晶体的宏观对称性.1.2六角密积属何种晶系? 一个晶胞包含几个原子?[解答]六角密积属六角晶系, 一个晶胞(平行六面体)包含两个原子.1.3在晶体衍射中，为什么不能用可见光？[解答]晶体中原子间距的数量级为米，要使原子晶格成为光波的衍射光栅，光波的波长应小于米. 但可见光的波长为7.6−4.0米, 是晶体中原子间距的1000倍. 因此, 在晶体衍射中，不能用可见光.2.1共价结合, 两原子电子云交迭产生吸引, 而原子靠近时, 电子云交迭会产生巨大的排斥力, 如何解释?[解答]共价结合, 形成共价键的配对电子, 它们的自旋方向相反, 这两个电子的电子云交迭使得体系的能量降低, 结构稳定. 但当原子靠得很近时, 原子内部满壳层电子的电子云交迭, 量子态相同的电子产生巨大的排斥力, 使得系统的能量急剧增大.2.2为什么许多金属为密积结构?[解答]金属结合中, 受到最小能量原理的约束, 要求原子实与共有电子电子云间的库仑能要尽可能的低(绝对值尽可能的大). 原子实越紧凑, 原子实与共有电子电子云靠得就越紧密, 库仑能就越低. 所以, 许多金属的结构为密积结构.3.1什么叫简正振动模式？简正振动数目、格波数目或格波振动模式数目是否是一回事？[解答]为了使问题既简化又能抓住主要矛盾，在分析讨论晶格振动时，将原子间互作用力的泰勒级数中的非线形项忽略掉的近似称为简谐近似. 在简谐近似下, 由N 个原子构成的晶体的晶格振动, 可等效成3N 个独立的谐振子的振动. 每个谐振子的振动模式称为简正振动模式, 它对应着所有的原子都以该模式的频率做振动, 它是晶格振动模式中最简单最基本的振动方式. 原子的振动, 或者说格波振动通常是这3N 个简正振动模式的线形迭加.简正振动数目、格波数目或格波振动模式数目是一回事, 这个数目等于晶体中所有原子的自由度数之和, 即等于3N .3.2长光学支格波与长声学支格波本质上有何差别?[解答]长光学支格波的特征是每个原胞内的不同原子做相对振动, 振动频率较高, 它包含了晶格振动频率最高的振动模式. 长声学支格波的特征是原胞内的不同原子没有相对位移, 原胞做整体运动, 振动频率较低, 它包含了晶格振动频率最低的振动模式, 波速是一常数. 任何晶体都存在声学支格波, 但简单晶格(非复式格子)晶体不存在光学支格波.3.3温度一定，一个光学波的声子数目多呢, 还是声学波的声子数目多?[解答]频率为的格波的(平均) 声子数为.因为光学波的频率比声学波的频率高, ()大于(), 所以在温度1010-1010-710-⨯ω11)(/-=T k B e n ωω O ωA ω1/-T k B O eω 1/-T k B A e ω一定情况下, 一个光学波的声子数目少于一个声学波的声子数目.3.4长声学格波能否导致离子晶体的宏观极化?[解答]长光学格波所以能导致离子晶体的宏观极化, 其根源是长光学格波使得原胞内不同的原子(正负离子)产生了相对位移. 长声学格波的特点是, 原胞内所有的原子没有相对位移. 因此, 长声学格波不能导致离子晶体的宏观极化.3.5你认为简单晶格存在强烈的红外吸收吗？[解答]实验已经证实, 离子晶体能强烈吸收远红外光波. 这种现象产生的根源是离子晶体中的长光学横波能与远红外电磁场发生强烈耦合. 简单晶格中不存在光学波, 所以简单晶格不会吸收远红外光波.3.6爱因斯坦模型在低温下与实验存在偏差的根源是什么?[解答]按照爱因斯坦温度的定义, 爱因斯坦模型的格波的频率大约为, 属于光学支频率. 但光学格波在低温时对热容的贡献非常小, 低温下对热容贡献大的主要是长声学格波. 也就是说爱因斯坦没考虑声学波对热容的贡献是爱因斯坦模型在低温下与实验存在偏差的根源.3.7在甚低温下, 德拜模型为什么与实验相符?[解答]在甚低温下, 不仅光学波得不到激发, 而且声子能量较大的短声学格波也未被激发, 得到激发的只是声子能量较小的长声学格波. 长声学格波即弹性波. 德拜模型只考虑弹性波对热容的贡献. 因此, 在甚低温下, 德拜模型与事实相符, 自然与实验相符.4.1 波矢空间与倒格空间有何关系? 为什么说波矢空间内的状态点是准连续的?[解答]波矢空间与倒格空间处于统一空间, 倒格空间的基矢分别为, 而波矢空间的基矢分别为, N 1、N 2、N 3分别是沿正格子基矢方向晶体的原胞数目.倒格空间中一个倒格点对应的体积为,波矢空间中一个波矢点对应的体积为,即波矢空间中一个波矢点对应的体积, 是倒格空间中一个倒格点对应的体积的1/N . 由于N 是晶体的原胞数目, 数目巨大, 所以一个波矢点对应的体积与一个倒格点对应的体积相比是极其微小的. 也就是说, 波矢点在倒格空间看是极其稠密的. 因此, 在波矢空间内作求和处理时, 可把波矢空间内的状态点看成是准连续的.4.2在布里渊区边界上电子的能带有何特点?[解答]电子的能带依赖于波矢的方向, 在任一方向上, 在布里渊区边界上, 近自由电子的能带一般会出现禁带. 若电子所处的边界与倒格矢正交, 则禁带的宽度, 是周期势场的付里叶级数的系数.不论何种电子, 在布里渊区边界上, 其等能面在垂直于布里渊区边界的方向上的斜率为零, 即电子的等能面与布里渊区边界正交4.3当电子的波矢落在布里渊区边界上时, 其有效质量何以与真实质量有显著差别?[解答]Hz 1013321 b b b 、、32N N / / /321b b b 、、1N 321 a a a 、、*321) (Ω=⨯⋅b b b N N b N b N b *332211)(Ω=⨯⋅n K )(2n K V E g =)(n K V晶体中的电子除受外场力的作用外, 还和晶格相互作用. 设外场力为F , 晶格对电子的作用力为F l , 电子的加速度为.但F l 的具体形式是难以得知的. 要使上式中不显含F l , 又要保持上式左右恒等, 则只有.显然, 晶格对电子的作用越弱, 有效质量m*与真实质量m 的差别就越小. 相反, 晶格对电子的作用越强, 有效质量m *与真实质量m 的差别就越大. 当电子的波矢落在布里渊区边界上时, 与布里渊区边界平行的晶面族对电子的散射作用最强烈. 在晶面族的反射方向上, 各格点的散射波相位相同, 迭加形成很强的反射波. 正因为在布里渊区边界上的电子与晶格的作用很强, 所以其有效质量与真实质量有显著差别4.4电子的有效质量变为的物理意义是什么?[解答]仍然从能量的角度讨论之. 电子能量的变化 .从上式可以看出，当电子从外场力获得的能量又都输送给了晶格时, 电子的有效质量变为. 此时电子的加速度,即电子的平均速度是一常量. 或者说, 此时外场力与晶格作用力大小相等, 方向相反.4.5紧束缚模型下, 内层电子的能带与外层电子的能带相比较, 哪一个宽? 为什么?[解答]以s 态电子为例. 由图5.9可知, 紧束缚模型电子能带的宽度取决于积分的大小, 而积分的大小又取决于与相邻格点的的交迭程度. 紧束缚模型下, 内层电子的与交叠程度小, 外层电子的与交迭程度大. 因此, 紧束缚模型下, 内层电子的能带与外层电子的能带相比较, 外层电子的能带宽.4.6等能面在布里渊区边界上与界面垂直截交的物理意义是什么？[解答]将电子的波矢k 分成平行于布里渊区边界的分量和垂直于布里渊区边界的分量k ┴. 则由电子的平均速度得到 , .)(1l m F F a +=F a *1m =*m ∞m E m E m E 晶格对电子作的功外场力对电子作的功外场力对电子作的功)d ()(d )(d *+=[]电子对晶格作的功外场力对电子作的功)d ()(d 1E E m -=*m ∞01*==F a m s J rR r R r r r d )()]()([)(*n at s n at N at s s V V J ----=⎰ϕϕΩ)(r ats ϕ)(n at s R r -ϕ)(r at s ϕ)(n at s R r -ϕ)(r at s ϕ)(n at s R r -ϕ//k )(1k E k ∇= ν////1k E ∂∂=ν⊥⊥∂∂=k E1ν等能面在布里渊区边界上与界面垂直截交, 则在布里渊区边界上恒有=0, 即垂直于界面的速度分量为零. 垂直于界面的速度分量为零, 是晶格对电子产生布拉格反射的结果. 在垂直于界面的方向上, 电子的入射分波与晶格的反射分波干涉形成了驻波.5.1一维简单晶格中一个能级包含几个电子?[解答]设晶格是由N 个格点组成, 则一个能带有N 个不同的波矢状态, 能容纳2N 个电子. 由于电子的能带是波矢的偶函数, 所以能级有(N /2)个. 可见一个能级上包含4个电子.5.2本征半导体的能带与绝缘体的能带有何异同?[解答]在低温下, 本征半导体的能带与绝缘体的能带结构相同. 但本征半导体的禁带较窄, 禁带宽度通常在2个电子伏特以下. 由于禁带窄, 本征半导体禁带下满带顶的电子可以借助热激发, 跃迁到禁带上面空带的底部, 使得满带不满, 空带不空, 二者都对导电有贡献.6.1你是如何理解绝对零度时和常温下电子的平均动能十分相近这一点的?[解答]自由电子论只考虑电子的动能. 在绝对零度时, 金属中的自由(价)电子, 分布在费密能级及其以下的能级上, 即分布在一个费密球内. 在常温下, 费密球内部离费密面远的状态全被电子占据, 这些电子从格波获取的能量不足以使其跃迁到费密面附近或以外的空状态上, 能够发生能态跃迁的仅是费密面附近的少数电子, 而绝大多数电子的能态不会改变. 也就是说, 常温下电子的平均动能与绝对零度时的平均动能一定十分相近.6.2为什么温度升高, 费密能反而降低?[解答]当时, 有一半量子态被电子所占据的能级即是费密能级. 温度升高, 费密面附近的电子从格波获取的能量就越大, 跃迁到费密面以外的电子就越多, 原来有一半量子态被电子所占据的能级上的电子就少于一半, 有一半量子态被电子所占据的能级必定降低. 也就是说, 温度升高, 费密能反而降低.6.3为什么价电子的浓度越大, 价电子的平均动能就越大?[解答]由于绝对零度时和常温下电子的平均动能十分相近，我们讨论绝对零度时电子的平均动能与电子浓度的关系.价电子的浓度越大价电子的平均动能就越大, 这是金属中的价电子遵从费密-狄拉克统计分布的必然结果. 在绝对零度时, 电子不可能都处于最低能级上, 而是在费密球中均匀分布. 由(6.4)式可知, 价电子的浓度越大费密球的半径就越大,高能量的电子就越多, 价电子的平均动能就越大. 这一点从(6.5)和(6.3)式看得更清楚. 电子的平均动能正比与费密能, 而费密能又正比与电子浓度: ,.所以价电子的浓度越大, 价电子的平均动能就越大.6.4对比热和电导有贡献的仅是费密面附近的电子, 二者有何本质上的联系?[解答]对比热有贡献的电子是其能态可以变化的电子. 能态能够发生变化的电子仅是费密面附近的电子. 因为, 在常温下, 费密球内部离费密面远的状态全被电子占据, 这些电子从格波获取的能量不足以使其跃迁到费密面附近或以外的空状态上, 能够发生能态跃迁的仅是费密面附近的电子, 这些电子吸收声子后能跃迁到费密面附近或以外的空状态上.⊥∂∂k E /⊥ν0≠T 3/120)3(πn k F =E 0F E 3/2n ()3/22232πn m E F =()3/2220310353πn m E E F ==对电导有贡献的电子, 即是对电流有贡献的电子, 它们是能态能够发生变化的电子. 由(6.79)式可知, 加电场后,电子分布发生了偏移. 正是这偏移部分才对电流和电导有贡献. 这偏移部分是能态发生变化的电子产生的. 而能态能够发生变化的电子仅是费密面附近的电子, 这些电子能从外场中获取能量, 跃迁到费密面附近或以外的空状态上. 而费密球内部离费密面远的状态全被电子占拒, 这些电子从外场中获取的能量不足以使其跃迁到费密面附近或以外的空状态上. 对电流和电导有贡献的电子仅是费密面附近电子的结论从(6.83)式和立方结构金属的电导率看得更清楚. 以上两式的积分仅限于费密面, 说明对电导有贡献的只能是费密面附近的电子.总之, 仅仅是费密面附近的电子对比热和电导有贡献, 二者本质上的联系是: 对比热和电导有贡献的电子是其能态能够发生变化的电子, 只有费密面附近的电子才能从外界获取能量发生能态跃迁.6.5为什么价电子的浓度越高, 电导率越高?[解答]电导是金属通流能力的量度. 通流能力取决于单位时间内通过截面积的电子数(参见思考题18). 但并不是所有价电子对导电都有贡献, 对导电有贡献的是费密面附近的电子. 费密球越大, 对导电有贡献的电子数目就越多. 费密球的大小取决于费密半径.可见电子浓度n 越高, 费密球越大, 对导电有贡献的电子数目就越多, 该金属的电导率就越高.6.6磁场与电场, 哪一种场对电子分布函数的影响大? 为什么?[解答]磁场与电场相比较, 电场对电子分布函数的影响大. 因为磁场对电子的作用是洛伦兹力, 洛伦兹力只改变电子运动方向, 并不对电子做功. 也就是说, 当只有磁场情况下, 非磁性金属中价电子的分布函数不会改变. 但在磁场与电场同时存在的情况下, 由于产生了附加霍耳电场, 磁场对非磁性金属电子的分布函数的影响就显现出来. 但与电场相比, 磁场对电子分布函数的影响要弱得多.)(00ε⋅∂∂+=v τe E f f f )(0ε⋅∂∂v τe E f x k S x x E S v e j F ετπ∇=⎰d 4222ES v e k S x F ∇=⎰d 4222τπσσ3/12)3(πn k F =答案：一. 填空(20分, 每题2分)1.对晶格常数为a 的SC 晶体,与正格矢R =a i +2a j +2a k 正交的倒格子晶面族的面指数为( 122 ), 其面间距为( ).2.典型离子晶体的体积为V , 最近邻两离子的距离为R , 晶体的格波数目为( ), 长光学波的( 纵 )波会引起离子晶体宏观上的极化.3. 金刚石晶体的结合类型是典型的(共价结合)晶体, 它有( 6 )支格波.4. 当电子遭受到某一晶面族的强烈反射时, 电子平行于晶面族的平均速度(不为 )零, 电子波矢的末端处在(布里渊区)边界上.5. 两种不同金属接触后, 费米能级高的带(正)电.对导电有贡献的是 (费米面附近)的电子.二. (25分)1.设为晶面族的面间距为, 为单位法矢量, 根据晶面族的定义,晶面族将分别截为等份， 即(,)==a (,)=,(,)= a (,) =,(,)= a (,) =.于是有=++=(++). (1)其中, 、、分别为平行于三个坐标轴的单位矢量. 而晶列的方向矢量为++=(++).(2)由(1)、（2）两式得=,即与平行. 因此晶列与晶面正交.2. 立方晶系密勒指数为(hkl )的晶面族的面间距a 32π33R Vd ()hkl n ()hkl c b a 、、l k h 、、a =⋅n a cos a n cos a n hd b =⋅n b cos b n cos b n kd c =⋅n c cos c n cos c n ld n a d h i a d k j a d l k a dh i k j l k i j k c b a 、、[]hkl =R ha i ka j la k a h i k j l k n 2a dR n R []hkl ()hkl三. (25分)1.原子运动方程1. 1. 格波的振动谱ω(q )＝四. (30分)1. 紧束缚近似非简并s 态电子的能带2.[110]方向的能带曲线带宽为8J s 。

固体物理试题1答案固体物理试题1——参考答案⼀、填空题（每⼩题2分，共12分）1、体⼼⽴⽅晶格的倒格⼦是⾯⼼⽴⽅点阵，⾯⼼⽴⽅晶格的倒格⼦是体⼼⽴⽅点阵。

2、晶体宏观对称操作的基本元素分别是 1、2、3、4、6、i、m（2）、4等⼋种。

3、N 对钠离⼦与氯离⼦组成的离⼦晶体中，独⽴格波波⽮数为 N ，声学波有 3 ⽀，光学波有 3 ⽀，总模式数为 6N 。

4、晶体的结合类型有⾦属结合、共价结合、离⼦结合、范德⽡⽿斯结合、氢键结合及混合键结合。

5、共价结合的主要特点为⽅向性与饱和性。

6、晶格常数为a的⼀维晶体电⼦势能V(x)的傅⽴叶展开式前⼏项(单位为eV)为:,在近⾃由电⼦近似下, 第⼆个禁带的宽度为 2（eV）。

⼆、单项选择题（每⼩题 2分，共 12 分）1、晶格常数为a的NaCl晶体的原胞体积等于（ D ）.A、B、C、 D、.2、⾦刚⽯晶体的配位数是（ D ）。

A、12B、8C、6D、4.3、⼀个⽴⽅体的点对称操作共有（ C ）。

A、 230个B、320个C、48个D、 32个.4、对于⼀维单原⼦链晶格振动的频带宽度，若最近邻原⼦之间的⼒常数β增⼤为4β，则晶格振动的频带宽度变为原来的（ A ）。

A、 2倍B、4倍C、 16倍D、 1倍.5、晶格振动的能量量⼦称为（ C ）。

A、极化⼦B、激⼦C、声⼦D、光⼦.6、三维⾃由电⼦的能态密度，与能量E的关系是正⽐于（ C ）A 、 12E-B 、0EC 、2/1ED 、E .三、问答题（每⼩题4分，共16分） 1、与晶列垂直的倒格⾯的⾯指数是什么解答正格⼦与倒格⼦互为倒格⼦。

正格⼦晶⾯与倒格⽮垂直,则倒格晶⾯与正格⽮正交。

即晶列与倒格⾯垂直。

2、晶体的结合能、晶体的内能、原⼦间的相互作⽤势能有何区别解答⾃由粒⼦结合成晶体过程中释放出的能量, 或者把晶体拆散成⼀个个⾃由粒⼦所需要的能量, 称为晶体的结合能。

原⼦的动能与原⼦间的相互作⽤势能之和为晶体的内能。

目的:考核基本知识。

1、晶格常数为的体心立方晶格，原胞体积等于 C 。

A. B. C. D.2、面心立方密集的致密度是 B 。

A. 0.76B. 0.74C. 0.68D. 0.623、表征晶格周期性的概念是 A 。

A. 原胞或布拉伐格子B. 原胞或单胞C. 单胞或布拉伐格子D.原胞和基元4、晶格常数为的一维单原子链，倒格子基矢的大小为 D 。

A. B. C. D.5、晶格常数为a的简立方晶格的(010)面间距为 A 。

A. aB. 3aa D. 5a C. 46、晶格振动的能量量子称为 CA. 极化子B. 激子C. 声子D. 光子7、由N个原胞组成的简单晶体，不考虑能带交叠，则每个s能带可容纳的电子数为 C 。

A. N/2B. NC. 2ND. 4N8、二维自由电子的能态密度，与能量的关系是正比于 B 。

A. B. C. D.9、某种晶体的费米能决定于 C 。

A. 晶体的体积B.晶体中的总电子数C.晶体中的电子浓度D. 晶体的形状10、晶体结构的实验研究方法是 A 。

A. X射线衍射B.中子非弹性散射C.回旋共振D.霍耳效应1、波矢空间与倒格空间（或倒易空间）有何关系? 为什么说波矢空间内的状态点是准连续的?波矢空间与倒格空间处于统一空间, 倒格空间的基矢分别为, 而波矢空间的基矢分别为, N1、N2、N3分别是沿正格子基矢方向晶体的原胞数目.倒格空间中一个倒格点对应的体积为,波矢空间中一个波矢点对应的体积为,即波矢空间中一个波矢点对应的体积, 是倒格空间中一个倒格点对应的体积的1/N. 由于N 是晶体的原胞数目，数目巨大，所以一个波矢点对应的体积与一个倒格点对应的体积相比是极其微小的。

也就是说，波矢点在倒格空间看是极其稠密的。

因此, 在波矢空间内作求和处理时，可把波矢空间内的状态点看成是准连续的。

2、在甚低温下, 德拜模型为什么与实验相符?在甚低温下, 不仅光学波得不到激发, 而且声子能量较大的短声学格波也未被激发, 得到激发的只是声子能量较小的长声学格波. 长声学格波即弹性波. 德拜模型只考虑弹性波对热容的贡献. 因此, 在甚低温下, 德拜模型与事实相符, 自然与实验相符.3、解释导带、满带、价带和带隙对于导体：电子的最高填充能带为不满带，称该被部分填充的最高能带为导带，在电场中具有被部分填充的能带结构的晶体具有导电性。

2000年博士入学考试试题 固体物理
1. 正格子和倒格子
2. 已知某晶体中相距为r 的相邻原子的相互作用势能可表示为：
n m r
B r A r U +-=)(，其中A 、B 、m>n 都是>0的常数，求： （1）平衡时两原子间的距离；
（2）平衡时结合能；
晶体平衡时原子之间具有数值相等、方向相反的吸引力和排斥力，写出平衡时原子之间的吸引力的表达式。

3. 试述电介质物理中洛仑兹有效场理论。

理论有何局限性？
4. 结合你的理解对晶体中的两种面缺陷进行描述
（1）堆垛层错
（2）小角度晶界
5. 已知扩散与温度之间的关系式：KT D D ε-⋅=exp 0，其中D0是常数，EA 是激活能；K 为波尔兹曼常数1.38×10-23J/K 。

下面是某元素在某晶体中的扩散实验数据，
T (K) 878 1007 1176 1253 1322
D (m 2/s) 1.6×10-20 4.0×10-19 1.1×10-18 4.0×10-17 1.0×10-16 求D 0和
E A 。

第 1 页 共 1 页 中国科学院固体物理入学试题
1. 晶体有几种关于旋转的点对称操作，晶体学的点群和空间群各有多少个？(10分)
2. 写出七种晶系的名称和结构特征，并说出金刚石属于那一个晶系。

(10分)
3. 晶体中布拉伐格子表示晶体的什么性质？晶体中布拉伐格子有多少种？(5分)
4. 密勒指数（h,k,l ）的物理意义是什么？ (5分)
5. 设晶体中的晶胞参数为a 1,a 2, a 3, 写出倒格子基矢的定义，倒格子所组成的空间和正格子所组成的空间在物理意义上有什么不同？(10分)
6. 说明固体比热的爱因斯坦模型的物理近似，并导出其比热表达式。

（10分）
7. 固体的热膨胀是什么原因引起的，它与简谐振动有什么关系？（10分）
8. 铁电体晶体具有什么物理特征，举出三种典型的铁电体的名称。

（10分）
9. 写出费米统计函数的表达式，解释费米能级的物理意义，说明在金属和半导体中费米能级如何确定。

（15分）
10. 稀土离子Ho 3+是顺磁离子, 其电子组态为f 10, 利用洪德规则求出该离子基态谱项并计算该离子的顺磁磁矩M 。

(15分) （提示：磁矩单位为波尔磁子，朗德因子：(1)(1)(1)12(1)
J J J S S L L g J J +++-+=+
+）。

中科院2005年秋季博士生固体物理及半导体物理入学试题2005年秋季入学博士生固体物理及半导体物理试题一、问答题：（8小题选5题，每题8分，共40分）1. 以GaAs 体材料为例，简述几种常见的散射机制与温度的关系；2. 简单说明pn 结的作用及同质结与异质结的不同之处；3. 分子束外延（MBE ）和金属有机物化学气相淀积（MOCVD ）技术；4. 自发发射和受激发射，实现受激发射的基本条件什么？5. GaAlAs/GaAs 二维电子气（2DEG ）；6. 解释重掺杂半导体使禁带宽度变窄的原因；7. 写出费米分布函数，f （x ），的表达式，讨论不同温度下f （x ）随E -E f 的变化关系，其中E f 是费米能级；8. 以GaAs 和Si 为例，讨论直接禁带半导体与间接禁带半导体之间的区别。

二、具有金刚石结构的硅的晶格常数a 0 = 0.543nm ，试求：(1) 晶体中的原子密度；(2) (100)、(110)和(111)晶面的原子密度和面间距；(3) 说明金刚石结构和闪锌矿结构的解理面。

（15分）三、试证明：电导率为最小值时硅的霍尔系数为 bn b q R i H 411-=，其中p n b μμ/=，μn 、μp 分别是电子和空穴的迁移率，q 为电子电荷，n i 是本征载流子浓度（不考虑载流子的速度统计分布）。

（10分）四、假设半导体导带底附近的电子在z 方向上的运动受到宽度为d 的无限深势阱的限制，而在xy 平面内可以自由运动，(1) 试分析电子本征能量分布的特点；(2) 求出电子的状态密度g(E )，并用图形表示出来；(3) 当电子在x 、y 和z 方向上的运动都受到限制时，它的本征能量和状态密度发生什么改变？（20分）五、试证明在一维晶体中：（15分）（1）电子的本征能量E n (k )是k 的偶函数，即)()(k E k E n n =-；（2）电子的平均速度υn (k )是k 的奇函数，即))(k k n n υυ-=-；（3）在布里渊区的边界，即在a l k π=0 ( ,2,1±±=l )处，0)(0=k n υ。

第一章晶体结构一、填空1、晶面有规则，对称配置的固体，具有长程有序特点的固体称为；在凝结过程中不经过结晶（即有序化）的阶段，原子的排列为长程无序的固体称为。

由晶粒组成的固体，称为。

2、化合物半导体材料GaAs晶体属于闪锌矿类结构，晶格常数为a，其配位数为。

一个惯用元胞（结晶学元胞）内的原子数，其布喇菲格子是。

其初基原胞（固体物理学原胞）包含原子数，体积为。

初基元胞的基矢为，，。

3、半导体材料Si具有金刚石型晶体结构，晶格常数为a，其配位数为。

一个惯用元胞（结晶学元胞）内的原子数。

属于布喇菲格子。

写出其初基元胞（固体物理学元胞）的基矢________，_______，_______。

晶格振动色散关系中支声学波，支光学波，其总的格波数。

4、简立方结构如果晶格常数为a，其倒格子元胞基矢为是_______，______，_________ 。

在倒格子空间中是结构，第一布里渊区的形状为______，体积为______ 。

5、某元素晶体的结构为体心立方布喇菲格子，其格点面密度最大的晶面的密勒指数____ ，并求出该晶面系相邻晶面的面间距________。

（设其晶胞参数为a ）。

6、根据三个基矢的大小和夹角的不同，十四种布喇菲格子可归属于_____ 晶系，其中当 90,=====γβαc b a 时称为 _____类晶系，该晶系的布喇菲格子有 ______ 。

7、NaCl 晶体是由两个 _ 格子沿体对角线滑移1/4长度套构而成；设惯用原胞的体积为a 3，一个惯用元胞内的原子数 ；其配位数为 ，最近邻距离 ；初基原胞体积为 ，第一布里渊区体积为______；晶体中有 支声学波， 支光学波。

8、对晶格常数为a 的SC ，与倒格矢 242K i j k a a aπππ=+- 正交的晶面族的晶面指数为____，其面间距为 __ 。

9、半导体材料Si 具有金刚石型晶体结构，晶格常数为a ，一个惯用元胞内的原子数 ，一个固体物理学原胞内的原子数 ；固体物理学原胞的体积 ，倒格子原胞的体积 __ ，第一布里渊区的体积为 ；晶格振动色散关系中 支声学波，______ 支光学波。

中科院物理所固体物理考博试题2003第一部分（共6题，选作4题，每题15分，共计60分；如多做，按前4题计分）1. 从成键的角度阐述 ?-? 族和 ?-? 族半导体为什么可以形成同一种结构:闪锌矿结构。

2. 请导出一维双原子链的色散关系，并讨论在长波极限时光学波和声学波的原子振动特点。

3. 从声子的概念出发，推导并解释为什么在一般晶体中的低温晶格热容量和热导率满足T3关系。

4. 设电子在一维弱周期势场V(x)中运动，其中V(x)= V(x+a)，按微扰论求出k=?π/a处的能隙。

5. 假设有一个理想的单层石墨片，其晶格振动有两个线性色散声学支和一个平方色散的声学支，分别是ω=c1k，ω=c2k，ω=c3k（其中c1，c2和c3(π/a)是同一量级的量，a是晶格常数）。

1）试从Debye模型出发讨论这种晶体的低温声子比热的温度依赖关系，并作图定性表示其函数行为；2）已知石墨片中的每一个碳原子贡献一个电子，试定性讨论电子在k空间的填充情况及其对低温比热的贡献情况。

6. 画出含有两个化合物并包含共晶反应和包晶反应的二元相图，注明相应的共晶和包晶反应的成分点和温度，写出共晶和包晶反应式。

第二部分（共9题，选做5题，每题8分，总计40分；如多做，按前5题计分）1. 从导电载流子的起源来看，有几种半导体？2. 举出3种元激发，并加以简单说明。

3. 固体中存在哪几种抗磁性？铁磁性和反铁磁性是怎样形成的？铁磁和反铁磁材料在低温和高温下的磁化有什么特点？4. 简述固体光吸收过程的本证吸收、激子吸收及自由载流子吸收的特点，用光吸收的实验如何确定半导体的带隙宽度？5. 利用费米子统计和自由电子气体模型说明低温下的电子比热满足T线性关系。

6. 超导体的正常态和超导态的吉布斯自由能的差为μ0Hc2(T)，这里Hc是超导体的临界磁场，说明在无磁场时的超导相变是二级相变，而有磁场时的相变为一级相变。

7. 什么是霍耳效应？何时会出现量子霍耳效应？8. 假设一体心立方化合物的点阵常数为a，写出前5条衍射线的晶面间距d 值。

中科院物理所面试整理（1）1。

什么是能带？2。

什么是位移电流？是由谁引入的?其物理实质是什么？3. 简述原胞和单胞的区别。

4。

什么是宏观对称素和微观对称素？5. 简述热力学四大定律.6. 晶体可能有的独立的点对称元素有几种？7。

康普顿散射证明了什么？8。

比热反映了什么，它的微观本质是什么？9。

简述量子力学的发展.10. 电子单缝实验及其物理内涵？11。

什么是倒格子?引入倒格子的意义是什么？12。

什么事俄歇电子？是怎么产生的？13。

Maxwell方程组及其各项的物理意义？14. 现在介观物理研究的尺寸范围是多少？15. 分析力学的基本方法？16。

在实验上用什么方法分析晶体的结构？17. 为什么会有半导体,导体,绝缘体?18. 什么是布拉格反射？19。

量子力学中为什么要引入算符？20。

正格子和倒格子之间关系是什么？21。

简述量子力学的基本假设.22. 你认为量子力学的精髓是什么?23。

什么是布里渊区？24。

大致说明一下晶体中电阻率随温度的变化关系。

剩余电阻率都来自哪?25。

什么是得哈斯—范阿尔芬效应?26。

什么是声子？什么是德拜温度？格林－埃森常数代表什么物理意义？27。

Maxwell 方程组的实验基础和假设是什么?28。

矩阵力学最早是由谁引入的？29。

较详细的介绍下你做过的一个近代物理实验？30。

能带论的三个基本假定是什么？简要阐述固体物理中的Born—Oppenheimer 近似。

31。

什么是布洛赫定理？32. 什么是Zeemann效应?介绍下斯特恩－盖拉赫干涉仪?33。

什么是纠缠态？大概介绍下EPR佯谬和薛定谔猫实验。

34。

介绍下你对自旋的认识。

自旋谁发现的，怎样发现的？35。

什么是剩余电阻？36. 介绍下你对狭义相对论的认识。

说说狭义相对论的基本原理。

写出洛伦兹变换的表达式。

37. 什么是霍尔效应?类比电荷霍尔效应,自旋霍尔效应应该怎么定义？38。

什么是Stark效应?39。

什么是超导现象？大概介绍下高温超导。