第四章 多组分系统热力学
- 格式：doc
- 大小：275.01 KB
- 文档页数：16
下载文档原格式
合集下载
第4章 多组分热力学
第四章 多组分系统热力学
前面所讨论的是：单组分单相（两相）系统或多 组分组成恒定的系统。 但常见系统绝大部分是：多组分变组成系统。因 此必须研究处理多组分系统。
多组分系统除了两个变量之外，还需确定各组分 的物质的量才能确定系统的状态。 多组分系统分为：单相、多相
本章主要讨论多组分单相系统。
1
第四章 多组分系统热力学
B
dA SdT pdV BdnB
B
•适用条件 W ' 0 ，单相系统
31
2.多组分单相系统的热力学公式
•广义定义
B
U nB
S ,V ,nC
H nB
S , p,nC
A nB
T ,V ,nC
G nB
T , p,nC
保持特征变量和除B以外其它组分不变，某热力
学函数随其物质的量 nB的变化率称为化学势。
2 偏摩尔量相对于某一组分而言，本身是强度量；
3 偏摩尔量与浓度有关，与系统的总量无关。
4 偏摩尔量 X B ( nX，B )下T ,标p,n必C 须是
。T , p, nC
15
2.偏摩尔量
•偏摩尔量的物理意义
•两种理解 1 在恒温恒压下，于极大量的某恒定组成的系统中加
入1mol组分B时所引起系统广度量X的改变量。
混合物的摩尔体积：
Vm
xB M B /
B
Vm xBVB
B
21
5.吉布斯—杜亥姆方程
X
X
dX
( T
) p,nB
dT
(
p
)T ,nB
dp
B
X BdnB
•恒温恒压多组分系统
dX X BdnB
B
前面所讨论的是：单组分单相（两相）系统或多 组分组成恒定的系统。 但常见系统绝大部分是：多组分变组成系统。因 此必须研究处理多组分系统。
多组分系统除了两个变量之外，还需确定各组分 的物质的量才能确定系统的状态。 多组分系统分为：单相、多相
本章主要讨论多组分单相系统。
1
第四章 多组分系统热力学
B
dA SdT pdV BdnB
B
•适用条件 W ' 0 ，单相系统
31
2.多组分单相系统的热力学公式
•广义定义
B
U nB
S ,V ,nC
H nB
S , p,nC
A nB
T ,V ,nC
G nB
T , p,nC
保持特征变量和除B以外其它组分不变，某热力
学函数随其物质的量 nB的变化率称为化学势。
2 偏摩尔量相对于某一组分而言，本身是强度量；
3 偏摩尔量与浓度有关，与系统的总量无关。
4 偏摩尔量 X B ( nX，B )下T ,标p,n必C 须是
。T , p, nC
15
2.偏摩尔量
•偏摩尔量的物理意义
•两种理解 1 在恒温恒压下，于极大量的某恒定组成的系统中加
入1mol组分B时所引起系统广度量X的改变量。
混合物的摩尔体积：
Vm
xB M B /
B
Vm xBVB
B
21
5.吉布斯—杜亥姆方程
X
X
dX
( T
) p,nB
dT
(
p
)T ,nB
dp
B
X BdnB
•恒温恒压多组分系统
dX X BdnB
B
第四章 多组分系统1
由集合公式：X =
B B B B B
B
（2）
此式与前式相减得：
n dX 0 除以 n= n → x dX 0
等ＴＰ，
B
B
B
B
B
B
B
——吉布斯－杜亥姆方程
B
例：
二组分系统， nAdX A nB dX B ＝０
或
xAdX A xB dX B ＝０
5.偏摩尔量间函数关系
H B = U B p VB
Ｇ＝Ｇ（Ｔ,Ｐ,ｎA,ｎB,……ｎｋ）
G G ) P ,n dT ＋ ( )T , n dP ｄＧ＝ ( T P
＋
B A
k
G ( )T , P,nC dnB nB
G G 组成不变：有 ( ) P,n S， ( )T ,n V T p
dG＝－ＳｄＴ＋ＶｄＰ＋
B
G 定义式：μ Ｂ＝ ( )T , P ,nC nB
X 引起系统容量性质 dX 的改变值 ( )T , p ,nC nB
注意：
1）必须在等 TP 下的偏微商
其它条件下不是偏摩尔量
X XB =( )T , p ,nC nB
GB
X ( )T ,V ,nC ≠ X B nB
G ( )T ,V ,nC nB
=
G ( )T , p ,nC nB
k
Z Z dp dZ= ( ) p ,nA ,nB ,n C nk dT + ( ) p T Z Z )T , p ,nA ,nC nK dnB +( ) p ,nB ,n C nk dnA + ( nB nA Z + ……+ ( )T , p ,nA ,nB , nk 1 dnk nk
B B B B B
B
（2）
此式与前式相减得：
n dX 0 除以 n= n → x dX 0
等ＴＰ，
B
B
B
B
B
B
B
——吉布斯－杜亥姆方程
B
例：
二组分系统， nAdX A nB dX B ＝０
或
xAdX A xB dX B ＝０
5.偏摩尔量间函数关系
H B = U B p VB
Ｇ＝Ｇ（Ｔ,Ｐ,ｎA,ｎB,……ｎｋ）
G G ) P ,n dT ＋ ( )T , n dP ｄＧ＝ ( T P
＋
B A
k
G ( )T , P,nC dnB nB
G G 组成不变：有 ( ) P,n S， ( )T ,n V T p
dG＝－ＳｄＴ＋ＶｄＰ＋
B
G 定义式：μ Ｂ＝ ( )T , P ,nC nB
X 引起系统容量性质 dX 的改变值 ( )T , p ,nC nB
注意：
1）必须在等 TP 下的偏微商
其它条件下不是偏摩尔量
X XB =( )T , p ,nC nB
GB
X ( )T ,V ,nC ≠ X B nB
G ( )T ,V ,nC nB
=
G ( )T , p ,nC nB
k
Z Z dp dZ= ( ) p ,nA ,nB ,n C nk dT + ( ) p T Z Z )T , p ,nA ,nC nK dnB +( ) p ,nB ,n C nk dnA + ( nB nA Z + ……+ ( )T , p ,nA ,nB , nk 1 dnk nk
物理化学：第4章_多组分系统热力学_
Vm*,B Vm*,C Vm*,B xC
真实混合物：实曲线
Vm xBVB xCVC VB (VC VB)xC
当混合物组成改变时，两组 分偏摩尔体积随之改变，且二者 变化相互关联。
组成接近某纯组分，其偏摩 尔体积也接近该纯组分摩尔体积。
5. 吉布斯 − 杜亥姆方程
对广度量 X (T , p, nB, nC , nD ,) 求全微分：
dX
X T
p,nB
dT
X p
T ,nB
dp
B
X nB
dnB T , p,nC
恒温、恒压
另一方面，由加和公式
，恒温恒压下求导：
比较两式，得
或
或
吉布斯-杜亥姆方程－－在一定温度压力下，当混合物
组成变化时，各组分偏摩尔量变化的相互依赖关系。
➢ 系统中各组分的偏摩尔量并非完全独立，而是相 互依存的。
➢ 例：固体溶解、过饱和溶液析出、…
组分B在α、β两相中迁移达平衡的条件：该组分
在两相中的化学势相等。
➢ 物质总是从其化学势高的相向化学势低的相迁移， 直至物质迁移达平衡时为止，此时系统中每个组分在 其所处的相中的化学势相等。
化学势 判据
② 化学平衡
<0：自发不可逆； =0：平衡、可逆
任一化学反应，假定系统已处于相平衡，
任一组分B在每个相中的化学势都相等： Bα B
B
B
整个系统中B组分物质的量的变化量： dnBα dnB
α
BdnB
B
化学平衡时
平衡条件：与化学反应达到平衡的方式无关。
§4.3 气体组分的化学势
1、纯理想气体的化学势 2、理想气体混合物中任一组分的化学势 3、纯真实气体的化学势 4、真实气体混合物中任一组分的化学势
真实混合物：实曲线
Vm xBVB xCVC VB (VC VB)xC
当混合物组成改变时，两组 分偏摩尔体积随之改变，且二者 变化相互关联。
组成接近某纯组分，其偏摩 尔体积也接近该纯组分摩尔体积。
5. 吉布斯 − 杜亥姆方程
对广度量 X (T , p, nB, nC , nD ,) 求全微分：
dX
X T
p,nB
dT
X p
T ,nB
dp
B
X nB
dnB T , p,nC
恒温、恒压
另一方面，由加和公式
，恒温恒压下求导：
比较两式，得
或
或
吉布斯-杜亥姆方程－－在一定温度压力下，当混合物
组成变化时，各组分偏摩尔量变化的相互依赖关系。
➢ 系统中各组分的偏摩尔量并非完全独立，而是相 互依存的。
➢ 例：固体溶解、过饱和溶液析出、…
组分B在α、β两相中迁移达平衡的条件：该组分
在两相中的化学势相等。
➢ 物质总是从其化学势高的相向化学势低的相迁移， 直至物质迁移达平衡时为止，此时系统中每个组分在 其所处的相中的化学势相等。
化学势 判据
② 化学平衡
<0：自发不可逆； =0：平衡、可逆
任一化学反应，假定系统已处于相平衡，
任一组分B在每个相中的化学势都相等： Bα B
B
B
整个系统中B组分物质的量的变化量： dnBα dnB
α
BdnB
B
化学平衡时
平衡条件：与化学反应达到平衡的方式无关。
§4.3 气体组分的化学势
1、纯理想气体的化学势 2、理想气体混合物中任一组分的化学势 3、纯真实气体的化学势 4、真实气体混合物中任一组分的化学势
hx04多组分系统热力学
VB def
V n B T , p,nC(CB)
U B def
U n B T , p,nC(CB)
H B def
H n B T , p,nC(CB)
SB def
S n B T , p,nC(CB)
AB def
A n B T , p,nC(CB)
GB def
G n B T , p,nC(CB)
上一内容 下一内容 回主目录
返回
2024/7/4
4.2.2 偏摩尔量的定义
(4) 偏摩尔量是两个广度性质X、nB之比，因此它是一强度性质，与体积的量无关。
上一内容 下一内容 回主目录
返回
2024/7/4
4.2.3 偏摩尔量的加和公式
已知
k X
dX
B=1
nB
T , p,nC(CB)
dnB
量和除B以外的其他组分不变时，热力学函数对B 物质的量求偏导。
上一内容 下一内容 回主目录
返回
2024/7/4
4.3.2 化学势的定义
把化学势的广义定义代入热力学函数的微分式：
dU TdS pdV BdnB B
dH TdS Vdp BdnB B
dA SdT pdV BdnB B
溶剂，含量少的称为溶质。
上一内容 下一内容 回主目录
返回
2024/7/4
4.1.2 多组分系统的组成表示法
1. B的物质的量浓度
cB def
nB V
溶质 B 的物质的量与溶液体积V 的比
值称为溶质 B 的物质的量浓度，或称为溶
质 B 的浓度.
物质的量浓度的单位 mol ×m-3
或
mol ×dm-3
第四章 多组分系统1
3.物质的量浓度cB（molarity， Substance amount concentration ）
cB
def
nB V
溶质B的物质的量与溶液体积V的比值称为溶质 B的物质的量浓度，或称为溶质B的浓度，单位是 。 mol m3，但常用单位是 mol dm3
4.质量分数wB（mass fraction）
偏摩尔焓
T ,p ,n C
偏摩尔熵
T ,p ,n C
偏摩尔亥姆霍兹函数
T ,p ,n C
偏摩尔吉布斯函数
T ,p ,n C
设X代表多组分系统中任一广度性质 X = f ( T, p, n1, n2,…)
X X X X dX dn1 dn2 dT p dp n n T p,ni T ,ni 1 T , p , n j 1 2 T , p , n j 2
B
另一方面，由于恒温、恒压下 X =
å
B
n BX B ，则
B
dX =
邋n BdX B +
B
X B dn B
因此：在等T，p条件下：
å
n B dX B = 0 或
B
å
x B dX B = 0
B
此即吉布斯 − 杜亥姆方程。该方程指出，系统中各组分的 偏摩尔量并非完全独立，而是相互依存的。 (1) 对二元溶液
G B = H B - T S B = U B - T S B + T S B = A B + pV B
G (抖 B
p ) = VB T
G (抖 B
T )p = - S B
A nB AB
物理化学4 多组分体系热力学 1
几点说明
（1）偏摩尔量只对体系中某组分才具有的，对整体而 言无所谓偏摩尔量的概念； （2）只有体系的广度性质才有偏摩尔量（质量除外） ； （3）偏摩尔量本身是强度性质； （4）注意右下角标的条件； （5）任何偏摩尔量都是T、p、组成的函数； （6）纯物质的偏摩尔量就是摩尔量； （7）偏摩尔量可能是负值。 （8）偏摩尔量是1mol B对整体热力学性质的贡献量， 而不应该理解为它在混合体系中所具有的量。
分类
气态混合物：空气 混合物液态混合物：甲醇 + 乙醇 固态混合物：Cu + Ni 气态溶液：萘溶解于高压CO 2中 非电解质溶液：糖水 − − − 本章 溶液液态溶液 电解质溶液：盐水 - - -电化学 固态溶液：单体溶解于聚合物中 − − − 又称固溶体
§4-2 化学势 化学势μ μB
• 4-2-1 化学势定义 • 4-2-2 平衡判据与平衡条件 • 4-2-3 理想气体的化学势表达式
4-2-1 化学势定义
混合物或溶液中，组分B的偏摩尔吉布斯函数 GB在化学热力学中有特殊的重要性，又把它叫 做化学势，用符号μB表示。
∂G µ B = GB = ∂nB T , p ,nc≠B
dX = ∑ X B dnB
B =1 k
（ 2）
• 可得Gibbs-Duhem方程：
∑ n dX
B B=1
k
B
=0
∑ x dX
B B=1
k
B
=0
Gibbs-Duhem方程的意义： (1) 某一偏摩尔量的变化可从其它偏摩尔量的变 化中求得。 (2) 对一个含有K个组分的均相体系，K个偏摩 尔量Xi中，只有 K－１个是独立的。
如果在溶液中不按比例地添加各组分，则溶液浓 度会发生改变，这时各组分的物质的量和偏摩尔量均 会改变。 根据集合公式
第4章多组分系统热力学分解
第四章 多组分系统热力学
p/Pa
R
p gh
p
p = kx,B xB 服从Henry定律
h
W
pP
稀溶液
纯B
纯溶剂
* A
* pB = pB xB
A
半透膜
A
实际曲线 xA xB
B
基本内容
§ 4.1 § 4.2 § 4.3 § 4.4 § 4.5 § 4.6 § 4.7 § 4.8 § 4.9 偏摩尔量 化学势 气体组分的化学势 逸度及逸度因子 拉乌尔定律和亨利定律 理想液态混合物 理想稀溶液 活度与活度因子 稀溶液的依数性
GB 骣 ¶G 琪 =琪 桫 ¶n B
T ,p ,n C
因此：
T ,n B
禳 骣 镲 ?G 镲 琪 = 睚 琪 ?nB 镲 镲 铪p桫 禳 镲 抖 骣G 镲 琪 = 睚 琪 桫p 抖 n 镲 B 镲 铪 骣 ¶V 琪 =琪 桫 ¶n B
T ,p ,n C T ,n B
T ,n B T ,p ,n C
V nBVm , B nCVm ,C
理想混合溶液
★将0.5摩尔的水与0.5摩尔的乙醇混合，溶液体积：
V≠（0.5×18.09十0.5×58.35）cm3 =38.22cm3 ＝37.2cm3
实际混合溶液 V nBVm n V ,B C m,C
★乙醇与水溶液混合的体积与浓度的关系
多组分系统可以是单相的也可以是多相的。
但对多组分多相系统可以拆解为多个多组分单相系统来研究。
多组分单相系统：是由两种或两种以上物质以分子大小粒
子相互均匀混合成一相的系统。
混合物——系统中的各组分以同等条件予以研究 溶 液——系统中的组分区分为溶剂和溶质予以研究
p/Pa
R
p gh
p
p = kx,B xB 服从Henry定律
h
W
pP
稀溶液
纯B
纯溶剂
* A
* pB = pB xB
A
半透膜
A
实际曲线 xA xB
B
基本内容
§ 4.1 § 4.2 § 4.3 § 4.4 § 4.5 § 4.6 § 4.7 § 4.8 § 4.9 偏摩尔量 化学势 气体组分的化学势 逸度及逸度因子 拉乌尔定律和亨利定律 理想液态混合物 理想稀溶液 活度与活度因子 稀溶液的依数性
GB 骣 ¶G 琪 =琪 桫 ¶n B
T ,p ,n C
因此：
T ,n B
禳 骣 镲 ?G 镲 琪 = 睚 琪 ?nB 镲 镲 铪p桫 禳 镲 抖 骣G 镲 琪 = 睚 琪 桫p 抖 n 镲 B 镲 铪 骣 ¶V 琪 =琪 桫 ¶n B
T ,p ,n C T ,n B
T ,n B T ,p ,n C
V nBVm , B nCVm ,C
理想混合溶液
★将0.5摩尔的水与0.5摩尔的乙醇混合，溶液体积：
V≠（0.5×18.09十0.5×58.35）cm3 =38.22cm3 ＝37.2cm3
实际混合溶液 V nBVm n V ,B C m,C
★乙醇与水溶液混合的体积与浓度的关系
多组分系统可以是单相的也可以是多相的。
但对多组分多相系统可以拆解为多个多组分单相系统来研究。
多组分单相系统：是由两种或两种以上物质以分子大小粒
子相互均匀混合成一相的系统。
混合物——系统中的各组分以同等条件予以研究 溶 液——系统中的组分区分为溶剂和溶质予以研究
物理化学 第四章 多组分系统热力学
Vm
T,p一定
V*m,C VC
V*m,B VB
d c· b·
0 B
a xC
C
图4.1.2 二组分液态混合物的 偏摩尔体积示意图
若B，C形成真实液态混合物： 则混合物体积为由V*m,B至V*m,C的曲线。对于任一 组成a时，两组分的偏摩尔体积可用下法表示： 过组成点a所对应的系统体积点d作Vm-xC曲线的 切线，此切线在左右两纵坐标上的截距即分别 为该组成下两组分的偏摩尔体积VB，VC。
B
系统中各广度量的偏摩尔量： 对于多组分系统中的组分B，有： 偏摩尔体积： VB=(ƽV/ƽnB)T,p,n C 偏摩尔热力学能： UB=(ƽU/ƽnB)T,p,n C 偏摩尔焓： HB=(ƽH/ƽnB)T,p,n C 偏摩尔熵： SB=(ƽS/ƽnB)T,p,n C 偏摩尔亥姆霍兹函数：AB=(ƽA/ƽnB)T,p,n C 偏摩尔吉布斯函数： GB=(ƽG/ƽnB)T,p,n
C
几点说明： (1)偏摩尔量为两个广度性质之比，所以为强度 性质； (2)偏摩尔量的定义中明确是在恒温、恒压及系 统组成不变的条件下，偏导数式的下标为T，p 时才是偏摩尔量； (3)同一物质在相同温度、压力但组成不同的多 组分均相系统中，偏摩尔量不同； (4)若系统为单组分系统，则该组分的偏摩尔量 与该组分的摩尔量相等，即： XB=X*B，m
C
=VB (数学知识：二阶偏导与求导的顺序无关) 得证。
4.2化学势 4.2化学势
1.化学势的定义 混合物(或溶液中)组分B的偏摩尔吉布斯函数GB 定义为B的化学势，用符号μB表示：
μB = GB=(ƽG/ƽnB)T,p,n
def
C
对于纯物质，其化学势等于它的摩尔吉布斯函 数。
04多组分体系热力学
B
B
吉布斯–杜亥姆方程
xBdXB 0
B
二元系统： xAdX A xBdXB 0
Gibbs-Duhem公式可以表明在温度、压力恒定下，混合物的组 成发生变化时，各组分偏摩尔量变化的相互依赖关系。某一偏 摩尔量的变化可从其它偏摩尔量的变化中求得，即一组分的偏 摩尔量增大，另一组分的偏摩尔量就减小，且增大或减小的比 例与混合物中两组分的摩尔分数成反比。
( nB
)T , p,nC (CB)
B
3.偏摩尔量的测定法举例
以二组分体系的偏摩尔体积为例，说明 测定偏摩尔量的方法原理
Vm
V n1 n2
n1V1,m n2V2,m n1 n2
X1V1,m
X V2 2,m
偏摩尔量的实验测定
以偏摩尔体积为例：
T、P一定，向物质的量 为nC的液体C中，不断 加入B形成混合物，以混 合物体积V和B的物质的 量nB作图。图中任一点 作曲线的切线，其斜率
适用于只做体积功时的任何可逆或不可逆过程：包括封闭或开 放的多组分多相系统发生PVT变化、相变化和化学变化过程。
3.化学势判据及应用举例
dG SdT Vdp B ( )dnB ( )
B
适用于恒温恒压
下封闭系统只做
B ( )dnB ( ) 0
B
体积功时相变化 和化学变化的平
衡判据
dAT ,V dGT , p
混合物中对体积的贡献量VB，等于在无限大量该组成的 混合物中加入单位物质的量的B(混合物组成未变)引起系
统体积的增加值，也等于在有限量的该组成的混合物中
加入dnB的B (混合物组成未变)引起系统体积增加量dV折
合成加入单位物质的量的B时的增量，称为物质B的偏摩
物理化学第四版 第四章 多组分系统热力学2014.2
)
p,n
(
B
)
,V
(
G P
)T
,n(
B
)
k
dG SdT VdP BdnB
证毕
B 1
14
又 dA d(G PV ) dG pdV Vdp
将上式dG 代入，整理得：
k
dA sdT PdV BdnB ……..(3) B 1
同理可得出另二个热力学基本方程。
因 A=A(T,V,n1,n2…….nk)
B
B
B
........
n B
相平衡条件
有N 个组分，就有N 个这样的式子
19
例：在、 两相中均含有A和B两种物质，达到相平衡时，下列
各式正确的是（
）。
A、
A
B
B、
B
B
C、
A
B
D、
B
A
例：组分B从相扩散入相中，则以下说法正确的有（ A、总是从浓度低的相扩散入浓度高的相 B、平衡时两相浓度相等 C、总是从化学势高的相移向低化学势低的相
dA
(
A T
)V
,n
(
B
)
dT
( A V
)T ,n(B)
dV
k B 1
(
A n(B)
)T
,V
,n
(
c,c
B)
dnB
将式（4）和式（3）比较
B
A ( nB
)T ,V ,n(c,cB)
同样可得出
B
U ( nB
)S ,V ,n(c,cB)
H ( nB
)S ,P.n(c,cB)
…..(4)
15
例 2： 下列偏导数中那些是偏摩尔量?那些是化学势?
第四章 多组分系统热力学
多组分系统热力学
前两章－单组分均相封闭系统，如：纯物质或某种 理想气体系统。 科学研究及生产实践－多组分系统 纯物质单相封闭系统：确定n（对于单相封闭系统， 此为一定值）、T、p，系统的状态即可确定。此时， 系统的一切性质，不只是强度性质而且全部容量性 质都有了确定值。若以X代表任意一种容量性质， 如V、U、S、G等，对于物质的量固定的纯物质单 相系统，都有： X=f(T,p) 其微小改变量为：
10
XB物理意义为：在恒温、恒压、均相封闭系统中， 只增加任一组分B，同时不引起原来nj改变，且不 发生缔合、沉淀、化学反应时： （1）dnB量B物质的加入，系统容量性质X对nB的变 化率。或在原有nB中加入dnB的B，使X改变了dX的 比值； （2）条件同前，在一个无限大的系统中，加入1 mol 的B物质，引起容量性质X的改变量。 如：向一大缸某白酒中，加入1 mol的水，引起V增 大了17.0 ml (<18.0 ml), 则此时V水=17.0 ml· -1。 mol
X X X dp dX dT d n1 p n T p , ni T , ni 1 T , p , n2 , n3 ,nk
X n 2 X d n2 n T , p , n1 , n3 ,nk k d nk T , p , n1 , n2 ,nk 1
W (乙) 10
W (水) 90
V (乙) 12.67
V (水) 90.36
V 103.30
V (实) 101.84
V 1.19
20 g乙醇+180 g水，其V=2×1.19=2.38 ml
7
描述一多组分均相系统的状态，除指明系统的T和p， 还必须指明系统的组成ni。为此，需要引入偏摩尔 量（XB）来代替单组分系统中的摩尔量（Xm）。 一、偏摩尔量的定义 含有k个组分的均相系统，其任一容量性质X (可为 V, U, H, S, A, G)可写成下列函数式： X=f(T,p,n1,n2,…nk) 2+k个变量 当系统的T、p及各组分的n均发生一微小变化时， 该容量性质X也相应发生微小变化。根据状态函数的 性质，此变化可用全微分表示，即：
前两章－单组分均相封闭系统，如：纯物质或某种 理想气体系统。 科学研究及生产实践－多组分系统 纯物质单相封闭系统：确定n（对于单相封闭系统， 此为一定值）、T、p，系统的状态即可确定。此时， 系统的一切性质，不只是强度性质而且全部容量性 质都有了确定值。若以X代表任意一种容量性质， 如V、U、S、G等，对于物质的量固定的纯物质单 相系统，都有： X=f(T,p) 其微小改变量为：
10
XB物理意义为：在恒温、恒压、均相封闭系统中， 只增加任一组分B，同时不引起原来nj改变，且不 发生缔合、沉淀、化学反应时： （1）dnB量B物质的加入，系统容量性质X对nB的变 化率。或在原有nB中加入dnB的B，使X改变了dX的 比值； （2）条件同前，在一个无限大的系统中，加入1 mol 的B物质，引起容量性质X的改变量。 如：向一大缸某白酒中，加入1 mol的水，引起V增 大了17.0 ml (<18.0 ml), 则此时V水=17.0 ml· -1。 mol
X X X dp dX dT d n1 p n T p , ni T , ni 1 T , p , n2 , n3 ,nk
X n 2 X d n2 n T , p , n1 , n3 ,nk k d nk T , p , n1 , n2 ,nk 1
W (乙) 10
W (水) 90
V (乙) 12.67
V (水) 90.36
V 103.30
V (实) 101.84
V 1.19
20 g乙醇+180 g水，其V=2×1.19=2.38 ml
7
描述一多组分均相系统的状态，除指明系统的T和p， 还必须指明系统的组成ni。为此，需要引入偏摩尔 量（XB）来代替单组分系统中的摩尔量（Xm）。 一、偏摩尔量的定义 含有k个组分的均相系统，其任一容量性质X (可为 V, U, H, S, A, G)可写成下列函数式： X=f(T,p,n1,n2,…nk) 2+k个变量 当系统的T、p及各组分的n均发生一微小变化时， 该容量性质X也相应发生微小变化。根据状态函数的 性质，此变化可用全微分表示，即：
多组分系统热力学
第四章 多组分系统热力学§4.1 偏摩尔量 partial molar quantity 热力学状态函数：U 、H 、S 、A 、G 、 V 广度量X=X （T ，p ，n 1，n 2，…）偏摩尔量：,,,C B B mB T p n X X n ≠⎛⎫∂= ⎪∂⎝⎭1212,12,,,,,1,12,2,,0,01,12,2,.........i i i i i ip n T n T p n T p n m m p n T n dT dp m m B m BBX X X X dX dT dp dn dn T p n n X X dT dp X dn X dn T p X dn X dn X dn ≠≠==⎛⎫⎛⎫⎛⎫∂∂∂∂⎛⎫=++++ ⎪ ⎪ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫∂∂⎛⎫=++++ ⎪ ⎪∂∂⎝⎭⎝⎭=++=∑ 恒温恒压恒组成条件下，X B ，m为定值，积分上式，得11,22,,...m m B B m BX n X n X n X =++=∑此即偏摩尔量的集合公式组成变化时，X B ，m 随之变化，恒温恒压下对集合公式求微分，得,,B B m B m B BBdX n dX X dn =+∑∑比较，可得,0B B mBn dX=∑ 或,0BB m Bx dX =∑此即吉布斯-杜亥姆方程 Gibbs-Duhem ’s equation§4.2 化学势 chemical potential,,,C BB B mB T p n G G n μ≠⎛⎫∂== ⎪∂⎝⎭∵ G=G(T ，p ，n 1，n 2，…)1212,12,,,,,...i i i i p n T n T p n T p n B BBG G G G dG dT dp dn dn T p n n SdT Vdp dn μ≠≠⎛⎫⎛⎫⎛⎫∂∂∂∂⎛⎫=++++ ⎪ ⎪ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭⎝⎭⎝⎭=-++∑∵ U=G －pV ＋TS ，H=G ＋TS ，A=G －pV∴B BBB BBB BBdU TdS pdV dn dH TdS Vdp dn dA SdT pdV dn μμμ=-+=++=--+∑∑∑此即普遍形式的热力学基本方程。
第4章 多组分系统热力学1
§4.2 化学势
1.化学势的定义 混合物（或溶液）中组分B的偏摩尔吉布斯函 数GB 定义为B的化学势，用μB表示。
定义为 G B GB nB T .P.nC
对于纯物质，其化学势就是它的摩尔吉布斯函数。
化学势是最重要的热力学函数，系统中的其它偏摩 尔量均可以通过化学势、它的偏导数或组合表示。
B
得到
dA B ( )dnB ( ) 0
B
自发 平衡
化学势判据
封闭系统恒温恒压，W’=0 ，由dGT,p≤0，
dG SdT Vdp B ( )dnB ( )
B
得到
dG B ( )dnB ( ) 0
B
<自发 =平衡
化学势判据
化学势在多相平衡中的应用
设系统有α和β两相，两相中均不仅一种物 质。在恒温恒压下若α 相中有dnB的 B物质 转移到β相，则 若上述转移是自发进行的，则有
相dnB ( )
相
相转移
dGT . p 0
即
B( ) B( )
dG 0
即
当系统达平衡时
B( ) B( )
μ
B（α ）=μ B（β ）
= …=μ
B（ρ ）
如果有某物质在各相中的化学势不等，则根据 dGT，p<0为自发过程的原理，该物质必然要从化学 势较大的相向化学势较小的相转移。
化学势在化学平衡中的应用
参加反应的物质都有化学势，平衡条件为
dG vi i (产物) vi i (反应物) 0
B
dA SdT pdV B ( ) dnB ( )
物理化学 第四章 多组分系统热力学
AB
( nB
)T , p ,nC
G
GB
( nB
)T , p ,nC
注意：偏摩尔量的下脚标为：T，P，C（C≠ B)
使用偏摩尔量时应注意： 1.偏摩尔量的含义是：在等温、等压、保持B物质 以外的所有组分的物质的量不变的条件下，广度性 质X的随组分B的物质的量的变化率。
2.只有广度性质才有偏摩尔量，而偏摩尔量是强度 性质。
六、偏摩尔量之间的函数关系
对于组分B：VB、UB、HB、SB、AB、GB之间的关系：
HB= UB +PVB ，
AB= UB －ＴSB
GB = HB －ＴSB＝ UB +PVB －ＴSB UB ＝AB+PVB
(
GB P
)T
,nA
VB
(
GB T
)
P,nA
SB
( GB )
[T T
]P,nB
3.纯物质的偏摩尔量就是它的摩尔量。
4.任何偏摩尔量都是T，p和组成的函数。
偏摩尔量的集合公式
设一个均相体系由1、2、 、k个组分组成，则体 系任一广度量Z应是T，p及各组分物质的量的函数，即：
X X (T , p, n1, n2,, nk )
在等温、等压条件下：
X
X
dX
( n1
···········
dG= dG(α) ＋ dG(β) +·········
恒T，p时 dG SdT Vdp
B
dnB
B
同理，有
dU TdS pdV B ( )dnB ( ) B
dH TdS Vdp B ( )dnB ( ) B
第四章 多组分系统热力学
⎛ ∂A ⎞
C
≠ nB
于是化学势就有4个偏微商表达式:
μB = ⎜ ⎜ ∂n ⎟ ⎟ ⎝ B ⎠ S ,V ,n
⎛ ∂U ⎞ ⎛ ∂H =⎜ ⎜ ∂n ⎝ B ⎞ ⎛ ∂A ⎟ ⎜ = ⎟ ⎜ ∂n ⎠ S , p ,nC ≠ nB ⎝ B ⎞ ⎛ ∂G ⎟ ⎜ = ⎟ ⎜ ∂n ⎠ T ,V ,nC ≠ nB ⎝ B ⎞ ⎟ ⎟ ⎠ T , p ,nC ≠ nB
第四章 多组分系统热力学 Thermodynamics of multi-component systems
引
言
实际系统绝大多数为多组分系统或变组成系统, 必 须掌握处理多组分系统的热力学方法. 混合物 气态混合物 理想液态混合物 真实液态混合物 理想稀溶液 真实溶液
多组分均相系统
各 组 分 液态混合物 l1 + l2 + … 等同对待
⎛ ∂X ⎞ ⎛ ∂X ⎞ ⎟ ⎜ ⎟ +⎜ dnB + ⎜ dnC + ⋅ ⋅ ⋅ ⎟ ⎟ ⎜ ⎝ ∂nB ⎠T , p ,nC ,nD ⋅⋅⋅ ⎝ ∂nC ⎠T , p ,nB ,nD ⋅⋅⋅
定义
def ⎛ ∂X ⎞ XB ⎜ ⎜ ∂n ⎟ ⎟ ⎝ B ⎠T , p,nC ≠nB
XB ⎯偏摩尔量
偏摩尔体积 偏摩尔内能 偏摩尔焓
⎛ ∂V VB = ⎜ ⎜ ∂n ⎝ B
UB ⎛ ∂U =⎜ ⎜ ∂n ⎝ B
⎞ ⎟ ⎟ ⎠ T , p ,nC ≠ nB
⎞ ⎟ ⎟ ⎠ T , p ,nC ≠ nB
⎛ ∂H HB = ⎜ ⎜ ∂n ⎝ B ⎛ ∂S SB = ⎜ ⎜ ∂n ⎝ B
⎛ ∂A AB = ⎜ ⎜ ∂n ⎝ B
B
dH = TdS + Vdp + ∑ μBdnB
多组分系统热力学
第四章 多组分系统热力学 主要内容1.混合物和溶液（1）多组分系统的分类含一个以上组分的系统称为多组分系统。
多组分系统可以是均相（单相）的，也可以是非均相（多相）的。
将多组分均相系统区分为混合物和溶液,并以不同的方法加以研究：（Ⅰ）混合物：各组分均选用同样的标准态和方法处理；（Ⅱ）溶液：组分要区分为溶剂及溶质，对溶剂及溶质则选用不同的标准态和方法加以研究。
（2）混合物及溶液的分类混合物有气态混合物液态混合物和固态混合物；溶液亦有气态溶液液态溶液和固态溶液。
按溶液中溶质的导电性能来区分，溶液又分为电解质溶液和非电解质溶液（分子溶液）。
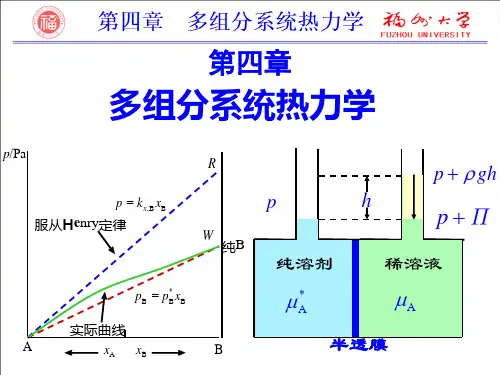
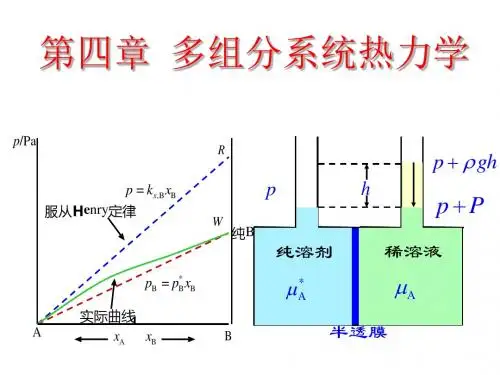
2.拉乌尔定律与亨利定律拉乌尔定律与亨利定律是稀溶液中两个重要的经验规律。
（1）拉乌尔定律平衡时，稀溶液中溶剂A 在气相中的蒸气分压A p 等于纯溶剂在同一温度下的饱和蒸气压与该溶液中溶剂的摩尔分数A x 的乘积。
这就是拉乌尔定律。
用数学式表达拉乌尔定律为 A *A Ax p p = （2）亨利定律一定温度下，微溶气体B 在溶剂A 中的溶解度B x 与该气体在气相中的分压B p 成正比。
也可表述为：一定温度下，稀溶液中挥发性溶质B 在平衡气相中的分压力B p 与该溶质B 在平衡液相中的摩尔分数B x 成正比。
这就是亨利定律。
用数学式表达亨利定律为： B B ,B x k p x =B ,x k 、B ,b k 为以不同组成标度表示的亨利系数，其单位分别为Pa ，Pa·kg·mol -1。
应用亨利定律时，要注意其不同表达式所对应的亨利系数及其单位。
还要注意亨利定律适用于稀溶液中的溶质分子同气相同种分子相平衡，即亨利定律适用于稀溶液中的溶质在液相及气相中具有相同分子形态的场合。
3.偏摩尔量（1）偏摩尔量的定义设X 代表V ,U ,H,S ,A ,G 这些广度性质，则对多组份系统（混合物或溶液）即 X =f (T ,p ,n A ,n B ,…)定义 ()B C C,,,B B def ≠⎪⎪⎭⎫ ⎝⎛∂∂n p T n X X式中，X Ｂ称为广度性质X （X=V ,U ,H ,S ,A ,G 等）的偏摩尔量，它们分别为只有系统的广延量才具有偏摩尔量，偏摩尔量是强度量。
多组分体系热力学.ppt
常用的偏摩尔量：
XB
def
X nB
T , p,nC
U nBUB B
H nB HB B
A nB AB B
S nB SB B
G nBGB B
U
UB
( nB
)T , p,nC (CB )
偏摩尔热力学能
H
HB
( nB
)T ,
p,nC (CB)
A
AB
( nB
)T , p,nC (CB )
dp
B
nB
T , p,nC
dnB
偏摩尔量
X B def
X nB
T , p,nC
X
X
dX
T
p,nB
dT
p
T ,nB
dp
B
X BdnB
2、偏摩尔量的物理含义：
X B def
X nB
T , p,nC
偏摩尔量XB是在恒温、恒压及除组分B以外其余各 组分的物质的量均保持不变的条件下，系统广度量X随 组分B的物质的量的变化率
四、同一组分的各种偏摩尔量之间的关系 对单组分系统有:
H=U＋pV A=U－TS G=H－TS
G S T p
对多组分系统有:
G p
T
V
HB=UB＋pVB AB=UB－TSB GB=HB－TSB
GB T
p
SB
GB p
T
VB
§4.2 化学势
定义：
B
GB
( G nB
)T , p,nC (CB)
3、偏摩尔量的加和公式
X nB X B
B
多组分系统的广度量X为系统各组分的物质的量与其偏摩尔量 XB乘积的加和。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第四章 多组分系统热力学4.1 有溶剂A 与溶质B 形成一定组成的溶液。
此溶液中B 的浓度为c B ，质量摩尔浓度为b B ，此溶液的密度为。
以M A ，M B 分别代表溶剂和溶质的摩尔质量，若溶液的组成用B 的摩尔分数x B 表示时，试导出x B 与c B ，x B 与b B 之间的关系。
解：根据各组成表示的定义()/B BB cBB B BB R RR BA B A Bx n n x c x MV M n x M M M x ρρρ===⎛⎫⎪⎝⎭=+-∑∑∑()()BBB A A B B A B A B x x c x M x M M M M x ρρ==++-⎡⎤⎣⎦()001BB B B cc c A A A AR Rn n x b m x M x M x M →→====-∑∑4.2 D-果糖()6126C H O B 溶于水（A ）中形成的某溶液，质量分数0.095B w =，此溶液在20℃时的密度31.0365/Mg m ρ-=。
求：此溶液中D-果糖的（1）摩尔分数；（2）浓度；（3）质量摩尔浓度。
解：质量分数的定义为()B B B B BB A B A A B B A B B A m nx M x M w m m nx M nx M M x M M ===+++-()()0.09518.0152180.15720.095180.157218.01520.0104B B B B B B A w M x M w M M ⨯==---⨯-=()()331.0365100.010418.01520.0104180.157218.01520.547BB A BA B x c M M M x mol dm ρ-⨯⨯==+⨯-+-⎡⎤⎣⎦=⋅()()10.01040.583110.010418.0152B B B A x b molKg x M -===--⨯4.3 在25℃，1 kg 水（A ）中溶有醋酸（B ），当醋酸的质量摩尔浓度b B 介于10.16mol kg -⋅和12.5mol kg -⋅之间时，溶液的总体(){}(){}2311/1002.93551.832/0.1394/B B V cm b mol kg b mol kg --=+⋅+⋅（1） 把水（A ）和醋酸（B ）的偏摩尔体积分别表示成b B 的函数关系。
（2） 11.5B b mol kg -=⋅时水和醋酸的偏摩尔体积。
解：根据定义,,,,,,A AAB B B B B T P n T P n T P n b V V V n b n ⎛⎫⎛⎫⎛⎫∂∂∂==• ⎪ ⎪⎪∂∂∂⎝⎭⎝⎭⎝⎭1,,1AB B T P n b kg n -⎛⎫∂= ⎪∂⎝⎭()31131/151.8320.2788/D D V cm mol b mol kg cm mol ---⎡⎤=⨯+⋅⎣⎦{}2111000/18.015218.01521002.9350.1394/1000B B B BA AB V n V V kgb V V n b mol kg ---==⎡⎤=-⎢⎥⎣⎦g {}2131A V 18.0681 1.0025/B b mol kg cm mol --⎡⎤=-⋅⋅⎢⎥⎣⎦当11.5B b mol kg -=⋅时[]31351.8320.2788 1.552.25B V cm mol cm -=+⨯⋅=231318.06810.0025 1.518.0625A V cm mol cm -⎡⎤=-⨯⋅=⎣⎦4.4 60℃时甲醇的饱和蒸气压是84.4 kPa ，乙醇的饱和蒸气压是47.0 kPa 。
二者可形成理想液态混合物。
若混合物的组成为二者的质量分数各50 %，求60 °C 时此混合物的平衡蒸气组成，以摩尔分数表示解：质量分数与摩尔分数的关系为()B BB B B B A w M x M w M M =--求得甲醇的摩尔分数为0.546.06880.589832.0420.514.0268B x ⨯==+⨯根据Raoult 定律()()()()()()()()()3333332510.589883.40.589883.410.589847.00.7184x CH OH P CH OH y CH OH x CH OH P CH OH x CH OH P C H OH ***=+-⨯=⨯+-⨯=()2510.71840.2816y C H OH =-=4.5 80 °C 是纯苯的蒸气压为100 kPa ，纯甲苯的蒸气压为38.7 kPa 。
两液体可形成理想液态混合物。
若有苯-甲苯的气-液平衡混合物，80 °C 时气相中苯的摩尔分数()0.300y =苯，求液相的组成。
解：根据Raoult 定律()()()()()()()()1x P y x P x P ***=--苯甲苯苯苯甲苯苯甲苯()()()()()()()()0.30038.71000.30038.71000.142y P x P y P P ****⨯==+⨯-⎡⎤+-⎣⎦=苯甲苯苯苯苯甲苯苯()()10.858x x =-=甲苯苯4.6 在18 °C ，气体压力101.352 kPa 下，1 dm 3的水中能溶解O 2 0.045 g ，能溶解N 2 0.02g 。
现将 1 dm 3被202.65 kPa 空气所饱和了的水溶液加热至沸腾，赶出所溶解的O 2和N 2，并干燥之，求此干燥气体在101.325 kPa ，18 °C 下的体积及其组成。
设空气为理想气体混合物。
其组成体积分数为：()00221O ϕ=，()00279N ϕ=解：显然问题的关键是求出O 2和N 2的Henry 常数。
18 °C ，气体压力101.352 kPa 下，O 2和N 2的质量摩尔浓度分别为()3120.045 1.40610131.9988molb O mol kg kg --==⨯⋅ ()4120.027.13910128.0134molb N mol kg kg --==⨯⋅这里假定了溶有气体的水的密度为11mol dm -⋅（无限稀溶液）。
根据Henry 定律，1 dm 3被202.65 kPa 空气所饱和了的水溶液中O 2和N 2的质量摩尔浓度分别为()()()()2222322121410.21202.651.40610101.3255.905210x b y O P y O P b O b O k P mol kg ---⨯===⨯=⨯⋅，()()()()2222422121310.79202.657.13910101.3251.12810x b y O P y N P b N b N k P mol kg ---⨯===⨯=⨯⋅，()33530.5905 1.128108.314291.15101.3251041.11041.1nRT V P m cm ---+⨯⨯⨯==⨯=⨯=()()()()422322 5.9052100.52361.12310y b O y N b N --⨯===⨯22O()()0.6560.343y N y O ==22，4.7 20 °C 下HCl 溶于苯中达平衡，气相中HCl 的分压为101.325 kPa 时，溶液中HCl 的摩尔分数为0.0425。
已知20 °C 时苯的饱和蒸气压为10.0 kPa ，若20°C 时HCl 和苯蒸气总压为101.325kPa ，求100 g 笨中溶解多少克HCl 。
解：设HCl 在苯中的溶解符合Henry 定律()()()()()()()11101.325100.04250.03831101.325p x P HCl x HCl x HCl P HCl k HCl P HCl -===⨯=，()()()()()()()()1n HCl n benzene x HCl x HCl n HCl n HCl n benzene x HCl =⇒=+-()()()()()()()()1x HCl n benzene M HCl m HCl n HCl M HCl x HCl M benzene ==-()0.0383110036.461.85910.383178.114m HCl g⨯==-4.8 H 2, N 2与100 g 水在40 °C 时处于平衡，平衡总压为105.4 kPa 。
平衡气体经干燥后的组成分数()00240H ϕ=。
假设可以认为溶液的水蒸气压等于纯水的蒸气压，即40 °C 时的7.33kPa 。
已知40 °C 时H 2, N 2在水中的Henry 系数分别为7.61 GPa 及10.5 GPa ，求40 °C 时水中溶解H 2, N 2在的质量。
解：假设（1）H 2, N 2在水中的溶解符合Henry 定律；（2）气相可看作理想气体。
在此假设下()()()()2222x x P H k x H P N k x N ==，()()()()()()()222222223P H H P H P N P P H O P N N ϕϕ==+=-，()()()()22223255P P H O P P H O P N P H --⎡⎤⎡⎤⎣⎦⎣⎦==， ()[]6262105.47.33 5.15481057.6310x H -⨯-==⨯⨯⨯()[]6263105.47.33 5.60410510.510x N -⨯-==⨯⨯⨯()()()()()()()2222222n N n H x N n H n N n H O n H O =≈++()()()222n H x H n H O ≈()()()()222261005.154810 2.015957.6818.015m H x H n H O M H g μ-≈=⨯⨯⨯=()()()()222261005.6041028.013871.418.015m N x N n H O M N g μ-≈=⨯⨯⨯=4.9 试用Gibbbs-Duhem 方程证明在稀溶液中若溶质服从Henry 定律，则溶剂必服从Raoult 定律。
证明：设溶质和溶剂分别用B ，A 表示。
根据Gibbbs-Duhem 方程B B A A x d x d μμ=-（const. T and const. p ）。
溶质B 的化学势表达式为ln lnBB B B B B P RT a RT P μμμ*=+=+B x B B P k x =， ，ln lnx B B B B B B B k x RT a RT P μμμ*=+=+，()B B BRTd dx constT and const P x μ⋅⋅=ln B A B A AA B Ax RT RTd dx dx RT x x x x μ=-==ln A A A RT x μμ=+AA A A A AAP a x P x P P ==⇒=即溶剂A 服从Raoult 定律。