自感和互感

电学电磁感应中的自感与互感比较自感和互感是电学电磁感应领域中重要的概念。

它们在电路设计、电力传输和电器工作中起到了至关重要的作用。

本文将比较自感和互感的定义、特性和应用，并探讨它们在电学电磁感应中的差异。

一、自感的定义和特性自感是指任何一段导体或线圈的电流变化会在自身产生感应电动势。

自感现象是由于电流通过线圈产生的磁场变化而引起的。

自感的大小与线圈的匝数和电流变化速率有关。

自感的单位是亨利（H）。

自感现象具有以下几个特性：1. 自感电动势的方向与电流变化的方向相反。

这意味着当电流增加时，自感电动势的方向是阻碍电流变化的。

2. 自感电动势的大小与电流变化速率成正比。

电流变化越快，自感电动势越大。

3. 自感只与线圈的几何形状和电流有关，与周围的其他线圈或导体无关。

二、互感的定义和特性互感是指两个或多个线圈之间由于磁场的相互作用而产生的感应电动势。

互感现象常见于变压器和电感器等设备中。

互感的大小与线圈匝数、线圈之间的距离以及电流变化速率有关。

互感的单位也是亨利（H）。

互感现象具有以下几个特性：1. 互感电动势的方向可以相互吸引或相互排斥，具体方向取决于线圈之间的位置和电流变化的方向。

2. 互感电动势的大小与电流变化速率和线圈之间的相对位置有关。

线圈之间的距离越近，互感电动势越大。

3. 互感不仅与线圈本身有关，还与周围的其他线圈或导体有关。

三、自感与互感的应用自感和互感在电学电磁感应中具有广泛的应用。

以下是它们在实际应用中的一些例子：1. 自感应用：自感常用于稳定电压和电流的电路中。

通过合理设计线圈的自感，可以实现对电流和电压的平滑控制，减小电路中的涌流和噪声。

2. 互感应用：互感主要应用于变压器、电感器和共振电路中。

变压器利用互感现象实现了电能的高效传输和变压功能。

电感器则利用互感调节电路的工作频率，起到滤波和隔离的作用。

共振电路则利用互感使电路对特定频率的信号产生放大的效果。

综上所述，自感和互感在电学电磁感应中扮演着重要的角色。

电磁场中的自感与互感在电磁学中，电磁场是一种由电荷所产生的力场，具有电场和磁场两个成分。

而自感与互感则是电磁场中非常重要的两个概念。

在本文中，我们将探讨电磁场中的自感与互感的概念、特性以及在实际应用中的重要性。

一、自感（自电感）的概念自感是指导体中流过电流时，由于磁场的存在而产生的感应电动势。

它是由电流与导体自身所形成的磁场相互作用所产生的。

自感的大小与导体的物理属性、电流强度以及线圈的形状和参数等有关。

二、互感的概念互感是指两个或多个导体线圈之间，由于磁场的交变而产生的感应电动势。

互感是指两个或多个线圈之间通过磁场相互耦合所产生的现象。

互感的大小与线圈之间的相对位置、线圈的形状与参数以及磁场的交变频率等因素相关。

三、自感与互感的特性与计算自感与互感有一些共同的特性，例如它们都与电流的变化有关，其大小与时间导数成正比。

自感和互感的计算通常采用数学公式进行，其中自感的计算公式可表示为L=μ0N^2A/l，其中L代表自感，μ0代表真空中的磁导率，N代表线圈中的线圈数，A代表线圈的横截面积，l代表线圈的长度。

而互感则可以通过公式M=k√(L1L2)，其中M代表互感，k代表耦合系数，L1和L2分别代表两个线圈的自感。

四、自感与互感在实际应用中的重要性自感与互感在电磁学中有广泛的应用。

其中，自感的效应在交流电路中非常重要，例如自感线圈可用于电感、变压器等电器元件的制造中。

而互感的效应则广泛应用于变压器、互感器、电感耦合通信等领域，具有非常重要的作用。

同时，自感和互感的研究也对电磁场的理论研究具有深远的意义。

通过对自感与互感的研究，我们可以更好地理解电磁场的产生、传播和作用机制，为电磁学的发展提供理论基础。

结论自感与互感作为电磁场中重要的概念，具有广泛的应用价值。

它们在电磁学的理论研究和实际应用中扮演着重要的角色。

我们需要深入理解自感与互感的概念、特性和计算方法，以更好地应用于电子、通信、电力等领域，并为进一步探索电磁学的奥秘做出贡献。

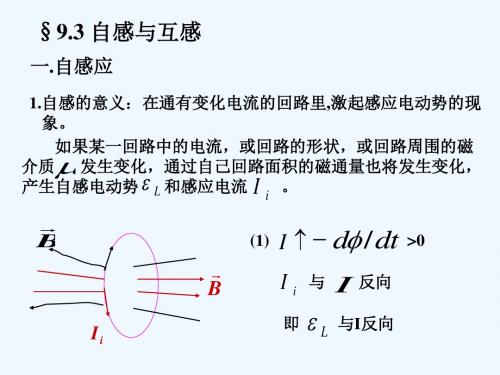
电磁感应中的自感与互感在研究电磁感应现象时，我们经常会涉及到自感与互感的概念。

自感和互感是电磁感应中非常重要的性质，深入理解它们对于我们理解电磁现象的本质和应用于实际情况具有重要意义。

本文将着重探讨电磁感应中的自感与互感。

一、自感自感是指当电流通过一个导线时，所产生的磁场会影响到这个导线本身，从而使导线内部产生感应电动势，这种现象称为自感。

自感可以通过下面这个式子来计算：L = (μ₀N²A)/l其中，L代表自感系数，N代表线圈的匝数，A代表线圈的面积，l代表线圈的长度，μ₀代表真空中的磁导率。

从这个式子可以看出，自感与线圈的匝数、形状以及长度都有关系，匝数越多、面积越大、长度越长，自感就越大。

自感的一个重要性质是，它与电流的变化有关。

当电流发生变化时，自感会阻碍电流的变化，产生一个逆电动势。

这也是为什么在闭合电路中开关突然断开时，会产生火花的原因，因为自感阻碍了电流突然减小的变化。

二、互感互感是指当两个或更多个线圈靠近时，它们之间会相互影响，产生电磁感应。

这种现象称为互感。

互感可以通过下面这个式子来计算：M = k√(L₁L₂)其中，M代表互感系数，L₁和L₂分别代表两个线圈的自感系数，k代表线圈的耦合系数。

从这个式子可以看出，互感与线圈的自感系数和耦合系数都有关系，自感系数越大，互感也就越大。

互感的一个重要应用是变压器。

变压器通过互感的原理，实现了将交流电的电压从一个电路传输到另一个电路。

变压器中的一个线圈称为“初级线圈”，另一个线圈称为“次级线圈”。

当初级线圈中的电流变化时，次级线圈中也会有相应的电压变化。

这样，变压器就实现了电压的升降。

三、自感与互感的关系自感和互感有密切的关系。

实际上，互感本质上就是两个线圈之间的自感。

当两个线圈靠近时，它们的自感相互影响，从而产生互感。

自感和互感的大小不仅取决于线圈的特性，还取决于材料的性质和频率。

自感和互感对于交流电路的特性有很大的影响，我们在设计电路时需要充分考虑它们的影响。

电磁感应中的自感与互感自感（自感应）和互感（互感应）是电磁感应中的两个重要概念。

它们描述了电流变化所产生的磁场对电路中其他线圈或电流的影响。

本文将详细介绍自感和互感的定义、原理及应用。

一、自感（自感应）自感是指电流通过线圈时，在线圈内部产生的磁场引起的感应电动势。

当电流通过一个线圈时，线圈内部的磁场变化，产生感应电动势。

根据法拉第电磁感应定律，感应电动势的大小与电流的变化率成正比。

自感系数L用来描述线圈的自感大小，单位为亨利（H）。

自感现象在电路中具有重要的作用。

首先，自感限制了电流的变化速度。

当电路开关打开或关闭时，线圈内的自感会阻碍电流变化，导致电流的“冲击”效应。

这也是为什么要在开关电路中使用电感等元件的原因之一。

其次，自感也影响电路中的交流信号。

交流信号在线圈中产生交变的磁场，从而引起感应电动势。

自感使得线圈对不同频率的交流信号具有不同的阻抗。

在高频电路中，自感对电路的阻抗有显著影响。

二、互感（互感应）互感是指当两个或更多的线圈靠近时，其中一个线圈中的变化电流在其他线圈中引起感应电动势。

互感现象的存在基于电磁感应定律，即磁场的变化会导致感应电动势的产生。

互感是电磁感应的重要应用之一。

它在变压器中起着关键作用，实现了电压和电流的变换。

变压器由两个或更多线圈组成，当其中一个线圈中的交流电流变化时，产生的磁场被其他线圈感应，从而在这些线圈中引起电压的变化。

此外，互感还广泛应用于电子领域中的滤波器、耦合电容器等元件中。

通过合理设计线圈之间的互感关系，可以实现信号的转换、过滤和传递等功能。

总结：电磁感应中的自感和互感是描述线圈中磁场变化对电路的影响的重要概念。

自感影响电路中电流的变化速度和交流信号的阻抗，而互感实现了电压和电流的转换。

它们在电路设计和电子技术中有着广泛的应用，对于实现各种功能和优化电路性能起着关键作用。

注：本文内容仅供参考，如需详细了解电磁感应中的自感和互感，请参考相关教材或专业资料。

电感的自感与互感现象电感是电路中常见的元件，它具有自感和互感两种重要的物理现象。

本文将详细介绍电感的自感和互感现象。

一、自感现象自感是指电流在电感中产生的磁通量对电流自身的感应作用。

当电流通过一个线圈时，会形成一个磁场，这个磁场会将一部分能量储存起来，形成磁能。

当电流发生变化时，线圈的磁场也随之变化，产生电动势。

这种电动势的方向与电流变化的方向相反，试图阻止电流变化。

这种现象称为自感现象。

自感现象的数学表达式为：ε = -L * dI/dt其中，ε表示自感电动势，L表示电感的自感系数，dI/dt表示电流变化的速率。

根据这个公式，我们可以看出，自感电动势与电流变化的速率呈线性关系。

二、互感现象互感是指两个或者多个线圈之间通过磁场相互感应产生的电动势现象。

当一个线圈中的电流发生变化时，将会生成一个磁场，这个磁场会穿过另一个线圈，从而在另一个线圈中产生电动势。

这种现象称为互感现象。

互感现象的数学表达式为：ε = -M * dI1/dt其中，ε表示互感电动势，M表示互感系数，dI1/dt表示第一个线圈电流的变化速率。

互感系数M与线圈的结构有关，正比于线圈的匝数和相对位置。

互感现象不仅存在于两个线圈之间，还可以存在于一个线圈的不同部分。

当线圈自身的一部分对另一部分产生感应时，也会发生互感现象。

三、电感对电路的影响电感具有阻碍电流变化的特性，这对电路有着重要的影响。

1. 自感对电路的影响：在直流电路中，自感会形成一个扼流圈，阻碍电流的变化。

这可以用来稳定直流电压，避免电流的突变。

在交流电路中，自感会引起电路的阻抗变化。

阻抗由电阻和电感共同决定，而电感对不同频率的电流具有不同的阻抗。

这使得电感在交流电路中可以用作滤波器、隔直流器等。

2. 互感对电路的影响：互感在变压器、电感耦合放大器等电路中起着重要作用。

变压器利用互感现象将电压变换到合适的水平，实现电能传输和变压变流。

电感耦合放大器则通过互感将信号传递到输出电路，增加信号的幅度。

自感与互感的概念及计算自感（Self-inductance）和互感（Mutual inductance）是电磁学中重要的概念，它们描述了电流和磁场之间的相互作用关系。

本文将对自感和互感的概念进行详细解析，并讨论其计算方法。

1. 自感的概念自感是指通过一根导线中的电流激发出的磁场引起的自身感应电动势。

当电流通过导线时，其周围会形成一个磁场，而这个磁场又会影响导线中的电流。

自感的大小取决于导线的几何形状和电流的变化速率。

自感可以用以下公式来表示：L = (μ0 * N^2 * A) / l其中，L代表自感的系数，单位为亨利（H）；μ0是真空中的磁导率，约等于4π×10^(-7) H/m；N表示导线的匝数；A是导线截面积；l是导线的长度。

2. 互感的概念互感是指两根导线之间的电流激发出的磁场引起的互相感应电动势。

当两根导线靠近并且电流变化时，它们之间会产生互感现象。

互感的大小取决于导线之间的几何关系、电流的变化速率以及它们之间的距离。

互感可以用以下公式来表示：M = k * sqrt(L1 * L2)其中，M代表互感的系数，单位为亨利（H）；k是一个比例常数，0 < k ≤ 1，表示两根导线之间的耦合系数；L1和L2分别代表两根导线的自感系数。

3. 计算示例假设有两根平行的长直导线，它们之间的距离为d，导线1的电流为I1，导线2的电流为I2。

现在我们来计算它们之间的互感系数M。

首先，我们需要计算导线1和导线2的自感系数L1和L2：L1 = (μ0 * N1^2 * A1) / l1L2 = (μ0 * N2^2 * A2) / l2其中，N1和N2分别代表两根导线的匝数，A1和A2分别代表导线1和导线2的截面积，l1和l2分别代表导线1和导线2的长度。

然后，根据互感的计算公式：M = k * sqrt(L1 * L2)通过以上计算，我们可以得到两根导线之间的互感系数M。

互感系数的大小反映了导线之间的电磁相互作用的强度。

电磁感应中的自感与互感现象电磁感应是电磁学中的重要概念之一，它描述了磁场和电场之间的相互作用。

在电磁感应中，自感和互感是两个重要的现象。

本文将探讨自感和互感的概念、原理以及其在实际应用中的重要性。

一、自感的概念与原理自感是指电流在变化时所产生的电动势。

当电流通过一个线圈时，线圈本身就会产生一个磁场。

当电流发生变化时，磁场也会发生变化，从而产生一个自感电动势。

自感电动势的大小与电流的变化速率成正比，而与线圈的形状和材料有关。

自感现象可以用法拉第定律来描述，即自感电动势等于自感系数乘以电流的变化率。

自感系数取决于线圈的形状和材料，通常用亨利（H）来表示。

自感系数越大，线圈的自感效应越强。

二、互感的概念与原理互感是指两个或多个线圈之间通过磁场相互作用而产生的电动势。

当一个线圈中的电流变化时，它所产生的磁场会穿过附近的另一个线圈，从而在另一个线圈中产生一个互感电动势。

互感电动势的大小与电流变化率以及线圈之间的耦合系数有关。

互感现象可以用法拉第定律来描述，即互感电动势等于互感系数乘以电流的变化率。

互感系数取决于线圈之间的物理距离、线圈的形状和材料，通常用亨利（H）来表示。

互感系数越大，线圈之间的互感效应越强。

三、自感与互感的应用自感和互感在电磁学中有着广泛的应用。

其中一个重要的应用是变压器。

变压器利用互感现象将交流电能从一个线圈传输到另一个线圈。

当一个线圈中的电流变化时，它所产生的磁场会穿过另一个线圈，从而在另一个线圈中产生一个互感电动势。

通过合理设计线圈的匝数比例，可以实现电压的升降。

另一个重要的应用是感应电动机。

感应电动机利用自感和互感现象将电能转化为机械能。

当电流通过线圈时，线圈本身会产生一个磁场，这个磁场会与定子产生的磁场相互作用，从而产生一个力矩，驱动电动机转动。

此外，自感和互感还应用于电子设备中的滤波器、变频器等电路中。

通过合理设计线圈的参数，可以实现对电流和电压的调节和控制。

总结电磁感应中的自感和互感是两个重要的现象。