大一高等数学定积分定义

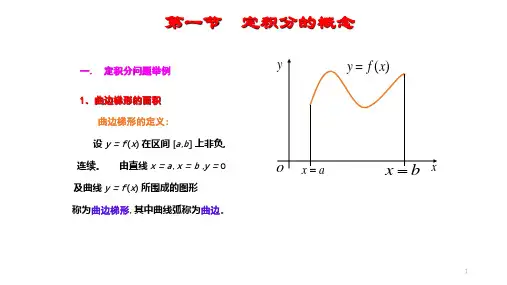
解释定积分的概念
定积分是积分的一种，是函数f(x)在区间[a,b]上积分和的极限。

具体来说，定积分定义如下：设函数f(x) 在区间[a,b]上连续，将区间[a,b]分成n个子
区间[x₀,x₁], (x₁,x₂], (x₂,x₃], …, (xₙ-1,xₙ]，其中x₀=a，xₙ=b。

a叫做积分下限，b叫做积分上限，区间[a, b]叫做积分区间，函数f(x)叫做被积函数，x
叫做积分变量，f(x)dx 叫做被积表达式，∫ 叫做积分号。

同时，应注意定积分与不定积分之间的关系：若定积分存在，则它是一个具体的数值，而不定积分是一个函数表达式，它们仅仅在数学上有一个计算关系（牛顿-莱布尼茨公式）。

一个函数，可以存在不定积分，而不存在定积分；也可以存在定积分，而不存在不定积分。

一个连续函数，一定存在定积分和不定积分；若只有有限个间断点，则定积分存在；若有跳跃间断点，则原函数一定不存在，即不定积分一定不存在。

以上内容仅供参考，如需更多信息，建议查阅相关文献或咨询数学专业人士。

大一数学定积分知识点定积分是微积分学中的一个重要概念，是对某个区间上的函数在该区间上的总体积进行刻画的数学工具。

它有着广泛的应用，在科学、工程等领域都有着重要的地位。

在本文中，我们将介绍大一数学中的定积分的基本概念、性质以及一些常见的计算方法。

一、定积分的概念定积分的概念可以从求和的角度进行理解。

给定一个函数 f(x)在闭区间 [a, b] 上连续，我们将 [a, b] 上的区间等分成 n 个小区间，每个小区间的长度为Δx=(b-a)/n。

选取每个小区间的一个代表点x_i，将函数在这些点上的取值 f(x_i) 求和，然后将这个和乘以Δx，当 n 趋向于无穷大时，这个乘积的极限就是定积分。

定积分通常用符号∫ 表示，表示对函数 f(x) 在区间 [a, b] 上进行积分。

其表示方式为∫[a,b] f(x) dx，其中 f(x) 为被积函数，a 和 b分别为积分下限和上限，dx 表示积分变量。

二、定积分的性质1. 线性性质：对于任意的实数 k，以及在区间 [a, b] 上连续的函数 f(x) 和 g(x)，有∫[a,b] (kf(x)+g(x)) dx = k∫[a,b] f(x) dx + ∫[a,b] g(x) dx。

2. 区间可加性：对于连续函数 f(x)，在区间 [a, b] 上和区间 [b,c] 上进行积分的和等于在整个区间 [a, c] 上进行积分，即∫[a,c] f(x) dx = ∫[a,b] f(x) dx + ∫[b,c] f(x) dx。

3. 切割性质：将一个区间分割成几个小区间，对于每个小区间进行积分的和等于整个区间进行积分，即若 [a, b] 表示为 [a, c] 和[c, b] 的和，那么有∫[a,b] f(x)dx = ∫[a,c] f(x) dx + ∫[c,b] f(x) dx。

三、定积分的计算方法1. 几何意义计算：对于一些简单的图形，我们可以利用几何意义来计算定积分。

高数定积分公式大全在高等数学中，定积分是通过积分来求解某一特定函数的不定积分的一种特殊方法，是计算物理量变化，寻找函数极值点以及在区间内求定积分的有效工具。

定积分的定义如下：如果函数f(x)在给定区间[a,b]上可导，那么定积分的定义为：∫a^bf(x)dx = F(b) - F(a)其中F(x)是f(x)的某个不定积分，解析法求解定积分的步骤为：首先将函数f(x)分解为常数、x、x^2、x^n多项式，其次对于每一项分别求解其不定积分，最后再将每一项求得的不定积分相加，即可得出整体定积分的解析解。

定积分中常见的公式有：一、定积分中的基本公式1. 不定积分的基本公式：∫x^ndx = 1/n+1*x^n+1 + C2. 二次方程不定积分的公式：∫x^2dx = 1/3*x^3 + C3.用的其他不定积分的公式：(1)∫sinx dx = -cosx + C(2)∫cosx dx = sinx + C(3)∫1/(1+x^2)dx = arctanx + C(4)∫lnx dx = xlnx - x + C二、高阶定积分的公式1. 一阶定积分：∫ax+b dx = 1/a*(ax+b) + C2. 二阶定积分：∫ax^2 + bx + c dx = 1/3a*x^3 + 1/2b*x^2 + cx + C3.用的其他高阶定积分的公式：(1)∫sinax dx = -1/a*cosax + C(2)∫e^x dx = e^x + C(3)∫lnax dx = xlnax - x + C三、复合定积分的公式定积分可以复合求解，以求解复合定积分为例，复合定积分公式为：∫a^b f(x)dx =a^x f(x)dx +x^b f(x)dx其中f(x)为一个标量函数，[a,b]为被积函数的定积区间，求解步骤如下：1.根据f(x)的表达式求出该函数的不定积分F1(x)；2.复合定积分拆分成两部分，先求∫a^x f(x)dx，即F1(x)的定积分，再求∫x^b f(x)dx，即F2(x)的定积分；3.后将两部分求得的结果相加，即可得出复合定积分的解析解，解析解为F1(b) - F1(a) + F2(b) - F2(a)。

用定向集概念定义定积分
定积分是一种重要的高等数学概念，早在17世纪被提出来。

它可以用定向集的概念来理解。

当我们将一组定向的集合定义为一个定向集时，它就包含了一个函数的零点及其附近的所有极值点（对应于极大值点和极小值点），这些极点表明该函数在此处达到边界值。

定积分就是从函数的边界值表达式求出的函数在某一区域内的积分，该区域的边界由定向的定向集确定。

从这个意义上说，定积分就是一种数学定义，它表示了一个函数在一个有限的区域内的定积分，其边界被定义为定向的定向集，这种方法可以用来识别函数的边界值，从而进行求积分。

定积分是现代数学的一种重要概念，早在17世纪就提出来了，在很多研究领域都有重要的应用，例如在物理、经济学、生物统计学等诸多领域得到广泛的应用。

定积分知识点总结大一定积分知识点总结定积分是微积分中的重要概念，它在数学、物理等各个领域中具有广泛的应用。

在大学一年级的学习中，我们需要掌握定积分的基本性质、计算方法和应用等方面的知识。

本文将对定积分的相关知识点进行总结和介绍。

一、定积分的基本性质1. 定积分的定义：设函数f(x)在区间[a, b]上有界，将[a, b]划分成n个小区间，每个小区间的长度为Δx，任取xi*在第i个小区间中值，如果极限存在且与划分方式无关，那么该极限值称为函数f(x)在区间[a,b]上的定积分，记作∫(a到b)f(x)dx。

2. 定积分的几何意义：定积分表示曲线f(x)和x轴之间的有向面积。

3. 定积分的性质：a. 线性性质：∫(a到b)[k*f(x)+g(x)]dx = k*∫(a到b)f(x)dx + ∫(a 到b)g(x)dx，其中k为常数。

b. 区间可加性：∫(a到b)f(x)dx = ∫(a到c)f(x)dx + ∫(c到b)f(x)dx，对于[a, c, b]上的任意点c成立。

c. 保号性：若对于[a, b]上的任意点x，有f(x) ≥ 0，则∫(a到b)f(x)dx ≥ 0。

d. 平均值定理：若函数f(x)在区间[a, b]上连续，则存在ξ∈(a, b)，使得∫(a到b)f(x)dx = f(ξ)(b-a)。

e. 积分中值定理：若函数f(x)在区间[a, b]上连续且非负，则存在ξ∈(a, b)，使得∫(a到b)f(x)dx = f(ξ)(b-a)，其中ξ为[a, b]上的某点。

二、定积分的计算方法1. 利用基本积分表：根据不同的函数形式，可以利用基本积分表中给出的积分公式快速计算定积分。

2. 分部积分法：将不定积分中的积分符号拆分成被积分函数和微分函数两部分，并运用分部积分公式进行计算。

3. 换元积分法：通过变量代换，将被积函数转化为简化形式的积分，然后进行计算。

4. 几何意义法：利用定积分的几何意义，可以通过几何图形的面积或曲线的长度等来计算定积分。

定积分大一上知识点总结定积分是微积分中的一个重要概念，是在一定区间上求函数曲线下的面积。

本文将对定积分的概念、性质以及求解方法进行总结和介绍。

一、定积分的概念定积分可以看作是对无穷小的加和，用极限的思想进行定义。

对于函数f(x)在[a, b]上的定积分表示为：∫[a, b] f(x) dx其中∫表示积分符号，[a, b]表示积分的区间，f(x)表示被积函数，dx表示积分变量。

二、定积分的性质1. 线性性质：定积分具有线性性质，即∫[a, b] (af(x) + bg(x)) dx= a∫[a, b] f(x) dx + b∫[a, b] g(x) dx。

2. 区间可加性：如果函数f(x)在[a, b]和[b, c]上可积，则有∫[a, c] f(x) dx = ∫[a, b] f(x) dx + ∫[b, c] f(x) dx。

3. 零函数积分：对于任意常数c，有∫[a, b] c dx = c(b - a)。

三、定积分的求解方法1. 几何意义法：定积分的几何意义是函数曲线下的面积，可以通过几何方法进行求解。

将区间[a, b]划分成n个小区间，每个小区间的长度为Δx，选取小区间上的任意一点ξi，将函数在小区间上的面积近似为矩形的面积，即ΔS = f(ξi)Δx。

然后将这些矩形面积相加，当划分越来越细时，矩形面积的和趋近于定积分∫[a, b] f(x) dx。

2. 定积分的基本性质：定积分具有数学上的基本性质，可以通过这些性质来求解定积分。

例如，可以利用定积分的线性性质、区间可加性和零函数积分性质，将复杂的定积分化简为简单的定积分，并通过已知的积分表达式进行计算。

3. 换元法：对于一些复杂函数，可以通过换元法进行求解。

通过变量代换，将原定积分转化为新变量上的积分，从而简化计算难度。

常用的换元法有代换变量法和三角换元法。

4. 分部积分法：对于一些积分需要进行多次运算的情况，可以通过分部积分法进行求解。

用定积分定义求定积分定积分是微积分中的重要概念之一，它可以用来计算曲线下的面积、求解物理问题中的总量以及描述变化率等。

本文将通过用定积分定义来解释定积分的概念和应用。

定积分是微积分中的一个概念，它可以被看作是无穷小量的累加。

在数学中，定积分可以通过求和的方式来计算。

具体而言，定积分可以被定义为一个函数在一个区间上的无穷小划分之和的极限。

这个极限就是定积分的值。

为了更好地理解定积分的概念，让我们来考虑一个简单的例子。

假设我们有一个函数f(x)，它在区间[a, b]上连续。

我们想要计算f(x)在该区间上的定积分。

首先，我们将区间[a, b]划分成n个小区间，每个小区间的宽度为Δx。

然后，我们在每个小区间上选择一个点xi，并计算出f(xi)乘以Δx的值。

最后，将所有这些乘积相加，即可得到定积分的近似值。

然而，这个近似值并不是准确的定积分值，因为我们仅仅考虑了有限个小区间。

为了得到准确的定积分值，我们需要让这个小区间的数量趋近于无穷大。

这就是求极限的过程，也是定积分的定义。

用定积分定义求定积分的过程可以用以下公式表示：∫(a→b) f(x)dx = lim(n→∞) Σ[f(xi)Δx]其中，∫表示定积分的符号，a和b表示积分的上下限，f(x)表示被积函数，dx表示自变量的微小变化量，lim表示极限运算，Σ表示求和符号，xi表示每个小区间的中点，Δx表示小区间的宽度，n表示小区间的数量。

通过用定积分定义来求解定积分，我们可以计算曲线下的面积、求解物理问题中的总量以及描述变化率等。

定积分在物理学、经济学、工程学等领域中都有广泛的应用。

例如，在物理学中，我们可以使用定积分来计算物体的质量、速度、加速度以及动能等。

在经济学中，我们可以使用定积分来计算市场的总需求、总供给以及总收益等。

在工程学中，我们可以使用定积分来计算电路的电流、功率以及能量等。

定积分是微积分中的重要概念，它可以通过用定积分定义来计算。

定积分可以用来计算曲线下的面积、求解物理问题中的总量以及描述变化率等。

高数大一最全知识点总结高等数学作为一门重要的学科，对于大一学生来说是一门必修课程。

掌握高等数学的基本知识点，不仅对于日后的学习打下了坚实的基础，也有助于理解其他相关学科的内容。

本文将对高数大一学习中的各个知识点进行总结和归纳，帮助读者更好地理解和应用这些知识。

一、微分与导数1. 函数与极限- 一元函数与多元函数- 函数的极限定义- 常见函数的极限计算方法2. 导数与微分- 导数的定义与性质- 常见函数的导数计算方法- 微分的概念与应用3. 高级导数- 高阶导数的定义- 高阶导数的性质- 隐函数与参数方程的高阶导数计算二、积分与微分方程1. 不定积分与定积分- 不定积分的定义与性质- 常见函数的积分计算方法- 定积分的定义与性质- 积分中值定理及其应用2. 微分方程基础- 微分方程的概念- 一阶常微分方程的解法- 高阶常微分方程的解法3. 微分方程的应用- 物理问题中的微分方程- 生活中的微分方程应用- 模型问题中的微分方程建立与求解三、级数与数列1. 数列与极限- 数列极限的定义与性质- 常见数列极限计算方法- 无穷大与无穷小2. 常数项级数- 级数的概念与性质- 常数项级数的敛散性判定- 常数项级数的收敛性判定方法3. 幂级数- 幂级数的概念与性质- 幂级数的收敛区间与收敛半径的计算 - 幂级数的应用四、空间解析几何1. 三维空间中的点、直线、平面- 点的坐标表示- 直线的参数方程与一般方程- 平面的点法式与一般方程2. 直线与平面的位置关系- 直线与平面的交点- 直线与平面的夹角- 平面与平面的位置关系3. 空间曲线与曲面- 空间曲线的参数方程- 隐函数方程与参数方程的相互转化 - 曲面方程的一般形式与特殊形式五、多元函数与偏导数1. 多元函数的概念与性质- 多元函数的定义- 多元函数的极限与连续性判定- 多元函数的偏导数与全微分2. 偏导数的计算- 偏导数的定义与性质- 偏导数的计算方法与应用- 高阶偏导数的定义与计算3. 多元函数极值与条件极值- 多元函数的极值判定条件- 多元函数的最值计算- 有条件的极值问题总结：通过对高数大一知识点的总结，我们了解了微分与导数、积分与微分方程、级数与数列、空间解析几何以及多元函数与偏导数等重要内容。

大一高数笔记知识点归纳高等数学作为大一学生的重要课程之一，是培养学生数学思维和逻辑推理能力的基础。

为了更好地掌握高等数学，下面将对大一高数的一些重要知识点进行归纳总结。

一、函数与极限1. 函数的概念与性质：函数是一种特殊的映射关系，即将一个自变量的值映射到一个因变量的值上。

函数具有定义域、值域、奇偶性、周期性等性质。

2. 极限与连续：极限是研究函数变化趋势的重要工具。

若函数在某点的左右极限相等，则该点的极限存在。

连续是指函数在定义域内的每一个点都存在极限且极限值等于函数值。

3. 导数与微分：导数描述了函数在某一点的变化率，定义为函数在该点的极限。

微分是导数的几何意义，反映了函数在该点附近的线性近似。

4. 高阶导数与泰勒展开：函数的高阶导数可以用于研究函数的凹凸性、极值等性质。

泰勒展开是将函数在某一点展开成幂级数，用于逼近函数的近似计算。

二、微分学应用1. 函数的最值与最优化：通过求函数的导数，可以找出函数的极大值和极小值，并应用于实际问题中的最优化计算。

2. 曲线的凹凸性与拐点：利用函数的二阶导数可以判断函数图像的凹凸性和存在的拐点，对曲线进行形状分析。

3. 参数方程与极坐标方程：参数方程是一种描述曲线的方式，适用于复杂曲线的考察。

极坐标方程则用于描述与原点距离和极角的关系。

4. 微分方程与基本解法：微分方程是描述变量之间关系的方程，通过求解微分方程可以得到函数的解析表达式。

三、重要的积分方法1. 不定积分与定积分：不定积分是求导的逆运算，可以求出函数的原函数。

定积分是计算曲线下面积或求解定量问题的重要手段。

2. 牛顿-莱布尼茨公式与定积分的应用：牛顿-莱布尼茨公式将定积分与不定积分联系起来，用于求解曲线下面积等问题。

3. 抽象积分与换元法：抽象积分是一种推广的积分形式，通过适当的换元法可以将复杂积分化简为简单的形式。

4. 分部积分与定积分的应用：分部积分可以将复杂积分的求解转化为简单积分的相乘形式，适用于求解含有积分的方程。

高数中极限和定积分的关系在高等数学中，极限和定积分是两个非常重要且密切相关的概念。

下面我们来探讨一下二者之间的关系：一、极限与定积分的定义1. 极限极限是一种数学概念，它描述函数在某一点附近的行为。

也就是说，当自变量趋近于某个值时，函数的取值会越来越接近一个固定的值。

通常用极限符号 $\lim$ 来表示。

2. 定积分定积分是一种有限积分，它是对于一个给定的函数，从区间 $a$ 到$b$ 的积分值。

通常表示为 $\int^b_a f(x)dx$，其中 $f(x)$ 是要积分的函数，$a$ 和 $b$ 是积分区间。

二、极限和定积分之间的关系1. 基本思路极限和定积分虽然看上去没有什么关系，但它们之间其实存在着密切的联系。

基本思路是，我们可以通过极限的方法来描述定积分的值。

2. 区间划分为了方便对定积分的处理，我们通常会将积分区间 $[a, b]$ 划分成$n$ 个小区间。

每个小区间的长度为 $\Delta x=\frac{b-a}{n}$，我们用$x0,x1,...,x_{n-1}$ 来表示各个小区间的左端点。

3. 极限的应用现在假设我们有一个函数 $f(x)$，我们可以将它在小区间 $[x_{i-1},x_{i}]$ 内进行连续的近似。

我们将把每个小区间的面积相加，此时利用极限的思想就可以得出定积分的值：$$\int^b_a f(x)dx=\lim_{n\to \infty}\sum^{n-1}_{i=0}f(x_i)\Delta x$$也就是说，将黎曼和中的 $\Delta x$ 取极限，可以求得定积分的值。

三、总结通过上述的讨论可知，极限和定积分在二者定义和应用方面存在着密切的联系。

利用极限的思想，我们可以更好地理解定积分的概念和计算方法，也可以更加深刻地认识微积分在数学中的重要性。