图形的变换练习题

12、平移：要说清楚向什么 左 方向平移多少格。
上 右 B A D O C 逆时针
旋转：要说清楚绕什么点 下
顺时针
什么方向
旋转多少度。
13、看上图填一填。
（1）图形 A绕点O（逆时针）方向旋转（90 ）度得到图形B。
（2）图形 B绕点O逆时针方向旋转90度得到图形（ C ）。 顺时针 （3）图形 B绕点O（ ）旋转（ 180）度得到图形D。 逆时针 （4）图形 A绕点O（ 顺时针 ）旋转（ 90 ）度得到图形D。
3 （ 40％ 5 2 5
）填百分数
（
二成 ）填成数
（ 50% ）填百分数 （ 7折 ）填折扣
10、找规律填数：20％ 0.3
（ 六成 ）填成数
11、找规律填数：100％ （
（ 70％ ）填百分数
0.9 ）填小数
4 5
（ 六成 ）填成数
第三单元 图形的变换
三、考点3：起跑线
判断：
2、在短跑比赛中，运动员所在的起跑线的位置不一样，
（1）以直线MN为对称轴作图形A的轴对称图形，得到图形B。
（2）将图形B绕点O顺时针旋转90°，得到图形C。 （3）将图形C向右平移6格，得到图形D。 A
M
C
O
D
N
B
第三单元 图形的变换
二、考点2：比赛场次、找规律
1、有8人参加乒乓球比赛，如果每2个人之间比赛一场， 一共要赛（ 28 ）场。 2、某学校有7个班级参加篮球赛，如果每两个班级之间 都进行一场比赛，一共要赛（ 21 ）场。 3、一次体育比赛中，有10名运动员，如果每两个运动员 之间都要握一次手，一共握了（
①钟面上分钟和时针的转动 ③汽车车轮的滚动 ⑤滑滑梯 ②电梯的运动 ④国旗的升降 ⑥大风车

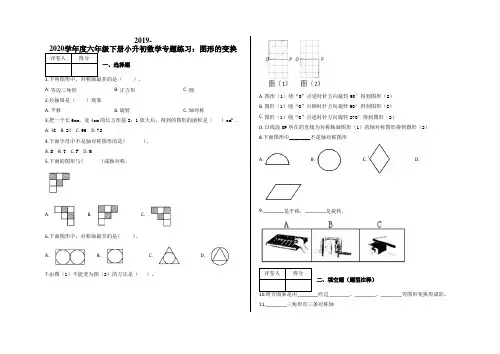
2019-一、选择题）。

A. 等边三角形B. 正方形C. 圆2.拉抽屉是（）现象A. 平移B. 旋转C. 轴对称3.把一个长6cm，宽4cm的长方形按2：1放大后，得到的图形的面积是（）cm2．A. 48B. 24C. 96D. 724.下面字母中不是轴对称图形的是( )。

A. DB. TC. FD. M5.下面的图形与( )成轴对称。

A. B. C.6.下面图形中，对称轴最多的是( )。

A. B. C. D.7.由图（1）不能变为图（2）的方法是（）。

A. 图形（1）绕“O”点逆时针方向旋转90°得到图形（2）B. 图形（1）绕“O”点顺时针方向旋转90°得到图形（2）C. 图形（1）绕“O”点逆时针方向旋转270°得到图形（2）D. 以线段OP所在的直线为对称轴画图形（1）的轴对称图形得到图形（2）8.下面图形中________不是轴对称图形A. B. C. D.9.________是平移，________是旋转．二、填空题（题型注释）经过________、________、________等图形变换形成的。

11.________三角形有三条对称轴12.拧开矿泉水的瓶盖是________现象。

13.看一看，辨一辨上面________是轴对称图形。

14.等腰三角形有________条对称轴，若它的一个底角是35°，则它的顶角是________度． 15.中有________条对称轴．16.一个图形的某条对称轴对称的图形和它的面积________。

17.再括号里填上平移或旋转。

三、解答题（题型注释）1厘米，请按要求画图形．）（1）把图①按2：1的比放大．（2）把图①绕B 点逆时针旋转90度．（3）在A 点南偏东45°方向画一个直径4厘米的圆．19.数学中的图形是完美的化身，是变化无穷的，如果把下面的两个图形各截一次，能拼成正方形吗？20.观察下面的轴对称图形，你发现了什么？四、判断题（_______）22.在推导圆的面积公式时，用到平移或旋转。

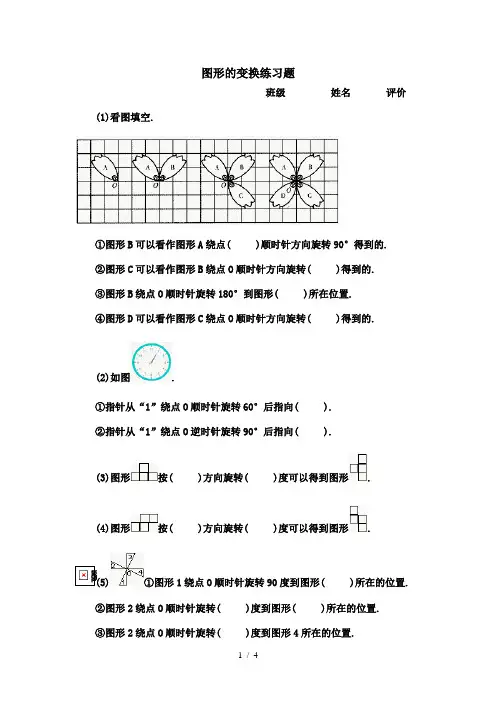
图形的变换练习题班级姓名评价(1)看图填空.①图形B可以看作图形A绕点( )顺时针方向旋转90°得到的.②图形C可以看作图形B绕点O顺时针方向旋转( )得到的.③图形B绕点O顺时针旋转180°到图形( )所在位置.④图形D可以看作图形C绕点O顺时针方向旋转( )得到的.(2)如图.①指针从“1”绕点O顺时针旋转60°后指向( ).②指针从“1”绕点O逆时针旋转90°后指向( ).(3)图形按( )方向旋转( )度可以得到图形.(4)图形按( )方向旋转( )度可以得到图形.(5)①图形1绕点O顺时针旋转90度到图形( )所在的位置.②图形2绕点O顺时针旋转( )度到图形( )所在的位置.③图形2绕点O顺时针旋转( )度到图形4所在的位置.二、判断.对的在题后的括号里画“√”，错的画“×”(7分)下列各题中图形旋转都是绕中心点进行的。

(1)图A向右平移五个格得到图B.( )(2)图A逆时针旋转90度，再向右平移五个格得到图B.( )(3)图B顺时针旋转90度，再向左平移五个格得到图C.( )(4)图B逆时针旋转90度，向下平移三个格，再向左平移五个格得到图C.( )(5)图C顺时针旋转90度，再向右平移八个格得到图D.( )(6)图B顺时针旋转180度，向下平移三个格，再向右平移三个格得到图D.( )(7)图A顺时针旋转90度，向下平移三个格，再向右平移八个格得到图D.( )三、选择.将代表正确答案的字母填在括号内(14分)(1)将顺时针旋转270度得到的图形是( ).A. B. C. D.(2)把下面的图A绕中心点顺时针旋转90度后再向下平移四个格得到图形是( ).(3)下面的图形中，( )不能由通过平移或旋转得到.A.B C. D.(4)将图形A绕点O逆时针旋转90度，得到图形B的是( ).A. B. C(5)左图中共有( )条线段.A、4B、5C、8D、10(6)体育课上，第一小组六名同学为了庆祝胜利，小组内每两名同学相互击掌一次，共击掌( )次.A、6B、8C、10D、15(7)下列现象中，不属于平移的是( ).A.乘直升电梯从一楼上到二楼B.钟表的指针嘀嗒嘀嗒地走C.火车在笔直的轨道上行驶D.汽车在平坦笔直的公路上行驶四、画一画.(20分)(1)画出三角形AOB绕O点逆时针旋转90°后得到的图形.(2)画出下图锤形图绕O点顺时针旋转90°后得到的图形.(3)画出绕O点顺时针旋转90°后的图形.(4)画出绕O点逆时针旋转90°后的图形.五、描述下图中，图A如何变换得到图B？图C如何变换得到图D？(7分)本节课的收获和缺失是：。

几何图形的变换练习题
1. 平移：
(1) 将正方形ABCD顺时针平移4个单位，得到新的正方形EFGH。

若A(-3,2)，求新的正方形的顶点坐标。

2. 旋转：
(1) 将三角形ABC顺时针旋转90°，得到新的三角形DEF。

已知
A(-1,2)，B(3,4)，C(2,1)，求新的三角形的顶点坐标。

3. 对称：
(1) 将矩形EFGH关于y轴进行对称，得到新的矩形IJKL。

已知
E(2,3)，F(5,3)，G(5,1)，H(2,1)，求新的矩形的顶点坐标。

(2) 将点P(3,4)关于x轴进行对称，得到新的点Q。

求点Q的坐标。

4. 缩放：
(1) 将正方形MNPQ按照原点为中心，缩小一半，得到新的正方形RSTU。

若M(2,2)，求新的正方形的顶点坐标。

5. 组合变换：
(1) 将三角形VWX顺时针旋转60°，然后再将旋转后的三角形关于
y轴进行对称，得到新的三角形YZT。

已知V(1,1)，W(4,3)，X(2,5)，
求新的三角形的顶点坐标。

以上为几何图形的变换练习题，通过练习可以加深对平移、旋转、
对称和缩放等变换操作的理解和掌握。

通过计算坐标，可以推算出新
图形的顶点坐标，从而绘制出变换后的图形。

练习题的难度逐步增加，建议先从简单的开始，逐步挑战更复杂的变换操作，提高对几何变换
的熟练度。

五年级数学下册《图形的变换》练习题一、下面的图案各是从哪张纸张上剪下来的？请连线。

二、画出图形的另一半，使它成为一个轴对称图形。

三、画出三角形aob绕o点顺时针旋转90度后的图形。

答案：一、下面的图案各是从哪张纸张上剪下来的？请连线。

二、画出图形的另一半，使它成为一个轴对称图形。

三、画出三角形aob绕o点顺时针旋转90度后的图形。

《图形的变换》第四稿【教材分析】“图形的旋转”是继对称、平移之后的又一种图形的基本变换，是义务教育阶段数学课程标准中图形变换的一个重要组成部分。

“图形的旋转”这节课的教学内容灵活丰富，符合四年级学生的年龄特点和已有的生活经验。

学习本课前，学生已经在三年级初步感受了生活中的平移与旋转现象，并能在方格纸上画出一个沿水平、垂直方向平移后的图形，本节课是在上述基础上的进一步发展，通过具体实例的展示，呈现学生在生活中随处可见的美丽图案，使学生运用变换的知识分析、欣赏、发现美，了解一个简单图形经过旋转制作成复杂图形的过程，进一步体会数学的文化价值，激发学生创造欲望，为后面设计简单图案做好铺垫，也为后续学习“图形的变换”奠定基础。

在生活中，有各种美丽的图案，其中有很多图案是由简单的图形经过平移或旋转得到的。

本节课所展示的正是简单图形经过旋转形成复杂图案的过程。

教材从“欣赏图案”入手，让学生观察这些图案的特点，然后将图案进行分解，逐步展示简单图形经过旋转后形成复杂图案的过程。

教材编排注重以下两点：1、在操作过程中，让学生体会图形变换的特点。

2、在图形的变换中，提倡不同的操作方法。

3、鼓励学生设计制作美丽的图案。

在教学时，我把旋转的三要素“中心点、方向、角度”作为重点来突破，在学生观察的基础上，鼓励学生动手操作，体验旋转的过程，以提高学生的感性认识。

教学中注重让学生“先想一想，再做一做，再想一想”，试图在操作的过程中，让学生体会图形变换的特点，发展学生的空间观念。

【学生分析】学生特点：求知欲高、模仿能力强，思维多依赖于具体直观形象。

五年级数学第一单元《图形的变换》一、在下面图形中，你还能画出其它对称轴吗？如果能，请画出来。

二、你知道方格纸上图形的位置关系吗？(1图形B 可以看作图形A 绕点顺时针方向旋转90°得到的。

(2图形C 可以看作图形B 绕点O 顺时针方向旋转得到的。

(3图形B 绕点O 顺时针旋转180°到图形所在位置。

(4图形D 可以看作图形C 绕点O 顺时针方向旋转得到的。

三、画出三角形AOB 绕O 点逆时针旋转180o 后的图形。

( 条对称轴 ( 条对称轴 ( 条对称轴四、如图五、画出图形的另一半，使它成为一个轴对称图形。

六、(1画出三角形AOB 绕O 点（2）绕O 点顺时针旋转90°顺时针旋转90度后的图形。

（3）绕O 点逆时针旋转90°一、这些现象哪些是“平移”现象，哪些是“旋转”现象：（1）张叔叔在笔直的公路上开车，方向盘的运动是（）现象。

（2）升国旗时，国旗的升降运动是（）现象。

（3）妈妈用拖布擦地，是（）现象。

（4）自行车的车轮转了一圈又一圈是（）现象。

二．请按照给出的对称轴画出第一个图形的对称图形，第二个图形请向上移动3格。

2、（1）图形1绕A 点（）旋转90。

到图形2。

（2）图形2绕A 点（）旋转90。

到图形3。

（3）图形4绕A 点顺时针旋转（）到图2。

（4）图形3绕A 点顺时针旋转（）到图1。

三．“动手操作”显身手。

11分（2+2+7）1．在下面的方格纸中任意设计一个轴对称图形，并画出它的对称轴。

2．画出平行四边形ABCD 绕D 点顺时针旋转900后的图形。

一、填空。

1、一个数的最小倍数减去它的最大因数，差是（）。

2、一个自然数比20小，它既是2的倍数，又有因数7，这个自然数是（）。

3、我是54的因数，又是9的倍数，同时我的因数有2和3。

（）4、我是50以内7的倍数，我的其中一个因数是4。

（）5、我是30的因数，又是2和5的倍数。

（）6、我是36的因数，也是2和3的倍数，而且比15小。

初中图形变换试题及答案一、选择题1. 以下哪个图形经过旋转后与原图形重合？A. 正方形B. 长方形C. 等边三角形D. 圆答案：D2. 一个图形经过轴对称变换后，以下哪个说法是正确的？A. 图形的形状和大小都发生了改变B. 图形的形状不变，大小发生了改变C. 图形的形状和大小都不变D. 图形的形状发生了改变，大小不变答案：C3. 在平移变换中，图形的位置会发生变化，而以下哪个属性不会改变？A. 形状B. 大小C. 颜色D. 以上所有答案：D二、填空题4. 如果一个图形绕着某一点旋转180度后与原图形重合，那么这个图形具有______对称性。

答案：中心5. 平移变换不改变图形的______和______。

答案：形状、大小三、解答题6. 给定一个等腰直角三角形ABC，其中∠C=90°，AC=BC=2cm。

请画出经过以下变换后的图形：(1) 将三角形ABC绕点C顺时针旋转90度；(2) 将旋转后的三角形沿AC边平移3cm。

答案：根据题目描述，首先画出等腰直角三角形ABC，然后进行旋转和平移变换，得到变换后的图形。

7. 已知一个矩形，长为4cm，宽为2cm。

请计算经过以下变换后的图形的周长：(1) 将矩形沿长边方向平移2cm；(2) 将平移后的矩形绕其中心点旋转180度。

答案：由于平移和旋转变换不改变图形的形状和大小，所以变换后的图形周长与原图形周长相同，即(4+2)×2=12cm。

四、综合题8. 给定一个正五边形，边长为3cm。

请回答以下问题：(1) 正五边形具有哪种对称性？(2) 如果将正五边形绕其中心点旋转72度，旋转后的图形与原图形的关系是什么？答案：(1) 正五边形具有轴对称性和中心对称性；(2) 旋转后的图形与原图形重合。

初二数学几何图形变换练习题在初中数学学习中，几何图形变换是一个重要的内容。

通过对图形进行平移、旋转、反射和放缩等操作，可以帮助我们加深对几何图形性质的理解。

下面将给出一些初二数学几何图形变换的练习题，希望能够帮助同学们巩固与拓展相关知识。

题目一：平移1. ABCD为一个平行四边形，EF是平行四边形的一条对角线。

（1）将平行四边形ABCD沿向量→→→→e向右平移3个单位得到平行四边形A1B1C1D1，连接DD1，证明A1D1∥EF。

（2）将平行四边形ABCD沿向量→→−→−→a向左平移4个单位得到平行四边形A2B2C2D2。

若A1A2的向量表示为→→−→−→b，则求向量→→−→−→b。

题目二：旋转2. 将正方形ABCD顺时针旋转90°得到正方形A1B1C1D1，连接CC1并延长，证明A1C1⊥CC1。

3. 将正方形ABCD顺时针旋转45°得到正方形A2B2C2D2，连接A2C2，若AC的长度为a，则求A2C2的长度。

题目三：反射4. 已知顶点是A(1,-3)的三角形ABC关于x轴反射得到三角形A1B1C1，连接AA1并延长，若直线AA1与x轴交于点D，求点D的坐标。

5. 直线y=x与直线y=2x关于直线y=-x反射，分别得到直线L1和L2。

若L1与L2的交点为P，则求P的坐标。

题目四：放缩6. 图中三角形ABC经过放缩得到三角形A1B1C1，若放缩比例为k，求A1B1 : BC的比值。

解答：题目一：平移1.（1）设向量→→→→AD=a，向量→→→→AC=b，由平移的性质知AA1=a+3，DD1=b+3。

根据平行四边形的性质，有AD=BC，AC=BD。

故A1D1∥EF得证。

（2）设向量→→−→−→a=〈x，y〉，则向量→→−→−→b=〈x-4，y〉。

根据平行四边形的性质，有AB=A1B1，AD=A1D1。

故向量→→−→−→a=AB-AD=〈x，y〉=A1B1-A1D1=向量→→−→−→b=〈-√2，0〉。

五年级数学下册数学变换专项练习题一、图形的旋转1. 将图形A绕顺时针旋转90度，得到图形B。

请画出图形B。

- 图形A：<img src="图形A.png" width="100">- 图形B：（请自行画出）2. 将图形C绕逆时针旋转180度，得到图形D。

请画出图形D。

- 图形C：<img src="图形C.png" width="100">- 图形D：（请自行画出）二、图形的翻转1. 图形E关于直线a对称，得到图形F。

请画出图形F。

- 图形E：<img src="图形E.png" width="100">- 图形F：（请自行画出）2. 图形G关于点b对称，得到图形H。

请画出图形H。

- 图形G：<img src="图形G.png" width="100">- 图形H：（请自行画出）三、图形的平移1. 图形I向左平移3个单位，得到图形J。

请画出图形J。

- 图形I：<img src="图形I.png" width="100">- 图形J：（请自行画出）2. 图形K向下平移4个单位，得到图形L。

请画出图形L。

- 图形K：<img src="图形K.png" width="100">- 图形L：（请自行画出）四、图形的缩放1. 图形M沿着中心点O缩小一半，得到图形N。

请画出图形N。

- 图形M：<img src="图形M.png" width="100">- 图形N：（请自行画出）2. 图形P沿着中心点O放大2倍，得到图形Q。

请画出图形Q。

- 图形P：<img src="图形P.png" width="100">- 图形Q：（请自行画出）以上是五年级数学下册数学变换专项练习题，请同学们根据题目要求进行练习，并在纸上进行作答。

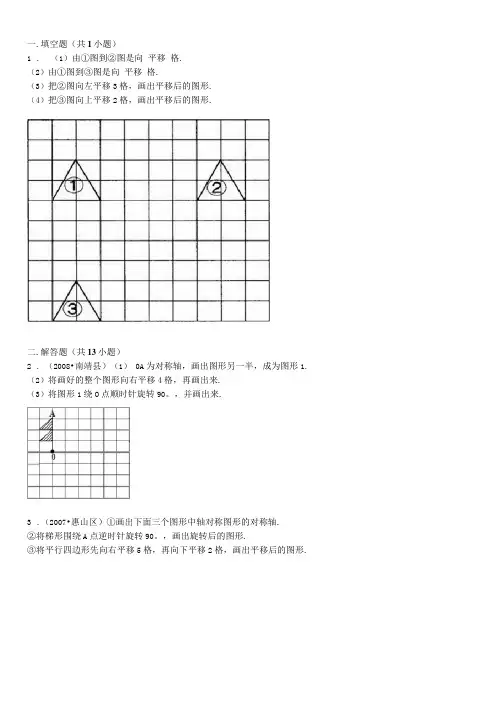
一.填空题（共1小题）1. （1）由①图到②图是向平移格.（2）由①图到③图是向平移格.（3）把②图向左平移3格，画出平移后的图形.（4）把③图向上平移2格，画出平移后的图形.二.解答题（共13小题）2. （2008•南靖县）（1） 0A为对称轴，画出图形另一半，成为图形1. （2）将画好的整个图形向右平移4格，再画出来.（3）将图形1绕O点顺时针旋转90。

，并画出来.3.（2007•惠山区）①画出下面三个图形中轴对称图形的对称轴.②将梯形围绕A点逆时针旋转90。

，画出旋转后的图形.③将平行四边形先向右平移5格，再向下平移2格，画出平移后的图形.4.（2009•兴国县模拟）（1）以0A为对称轴，画出图形另一半，成为图形A.（2）将画好的图形A向右平移4格，得到图形B.（3）将图形A绕O点顺时针旋转90。

，得到图形C.2格得到图形C,请在图中画出图形B和图形C.7.请画出先向右平移8格，再向下平移2格后得到的图形.8,按要求画一画.（1）在方格子中画出图①绕0点顺时针方向旋转90。

后的图形. （2）画出将图②向右平移7格，再向上平移3格后的图形. （3）画出图③的另一半，使它成为轴对称图形. 9 .按要求画图.（1）将图形A 向上平移5格，再向右平移7格，得到图形B. （2）以横虚线为对称轴，画出和图形A 对称的图形. （3）以竖虚线为对称轴，画出和图形C 对称的图形.1—— r 1--H L 」 1 —— . 」 一- j 一一 一 —— r 1 —— L 」 卜―- 一 Jn一一 —— r i i LT 1l_ J一———— 「一1 —111—— --H L 」——一- 一一 一—— —— .一一 一 —— r । । H-i 1L J LJ二1一一X一■ 1CJ L r 1__一—— -J.JL1_一 一 一」一一1 一J10 .先画出图形：（1）向下平移3小格后的图形（2）再画出图形①绕顶点A 逆时针旋转90度后的图形③.①12.在格子图中，把平行四边形先向右平移4格，再向下平移6格：把小房图绕A 点逆时针旋转90。

[必刷题]2024二年级数学下册图形变换专项专题训练（含答案）试题部分一、选择题：1. 下列哪个图形经过一次平移后，能与原来的图形重合？（）A. 正方形B. 长方形C. 三角形D. 椭圆形2. 将一个长方形向右平移3格，再向下平移2格，下列哪个选项表示这个长方形的新位置？（）A. (3, 2)B. (2, 3)C. (3, 2)D. (2, 3)3. 下列哪个图形经过旋转90度后，能与原来的图形重合？（）A. 正方形B. 长方形C. 三角形D. 半圆形4. 一个图形向右旋转90度，再向上平移2格，下列哪个选项表示这个图形的新位置？（）A. (2, 90)B. (90, 2)C. (2, 90)D. (90, 2)5. 下列哪个图形既是轴对称图形，也是中心对称图形？（）A. 正方形B. 长方形C. 三角形D. 梯形6. 一个图形沿着某条直线对折，两侧完全重合，这个图形是（）A. 轴对称图形B. 中心对称图形C. 平移图形D. 旋转图形7. 将一个正方形绕其中心点旋转180度，下列哪个选项表示这个正方形的新位置？（）A. (0, 0)B. (1, 1)C. (1, 1)D. (2, 2)8. 下列哪个图形经过旋转180度后，能与原来的图形重合？（）A. 等边三角形B. 等腰三角形C. 矩形D. 梯形9. 一个图形向上平移3格，再向左平移2格，下列哪个选项表示这个图形的新位置？（）A. (3, 2)B. (3, 2)C. (2, 3)D. (2, 3)10. 下列哪个图形不是轴对称图形？（）A. 正方形B. 长方形C. 圆形D. 梯形二、判断题：1. 旋转是将一个图形绕某一点转动一个角度的图形变换。

（）2. 平移是将一个图形上的所有点按照某个方向作相同距离的移动。

（）3. 所有的三角形都是轴对称图形。

（）4. 一个图形经过旋转后，其大小和形状都不会改变。

（）5. 中心对称图形的对称中心一定是图形上的一个点。

六年级数学上册《图形的变换》专项练习题及答案(人教版) 【学习目标】1.复习轴对称、平移、旋转、图形的放大与缩小等图形变换方式的特点。

2.根据变换方式的特点，按要求画图。

利用比例知识计算面积。

【学习过程】一、知识梳理（课本103页）观察下面的图片，你能发现哪些图形变换的现象？它们有什么特点？（）（）（）（）二、课堂练习1.下面图形各有几条对称轴？请画出前5个图形的所有对称轴。

（）条（）条（）条（）条（）条（）条2.看图填空。

（1）指针从“12”绕点A顺时针旋转（°）到“3”；（2）指针从“1”绕点A顺时针旋转（°）到“6”；（3）指针从“3”绕点A逆时针旋转30°到“（）”；（4）指针从“7”绕点A顺时针旋转（°）到“12”。

3.想一想，这些平面图形绕对称轴旋转一周，可以得到哪些立体图形？（）（）（）（）（）A4.判断。

（1）平行四边形是轴对称图形。

（）（2）把一个图形按3：1放大后，周长也扩大到原来的3倍。

（）（3）把一个长方形按4：1放大后，它的面积也扩大到原来的4倍。

（）(4) 右图中有两个等边三角形，小三角形的面积是大三角形的四分之一。

（）5.根据对称轴，画出另一半。

6.按要求旋转。

（1）绕点O按顺时针方向旋转90°（2）绕点O按逆时针方向旋转90°三、当堂检测1.画一画。

（1）小旗向左平移8格后的图形。

（2）小旗绕O点按顺时针方向旋转90°后的图形。

（3）小旗按2：1扩大后的图形。

2.把一个长12厘米、宽8厘米的长方形按1：4缩小后，得到的长方形的周长、面积各是多少？与原来的周长、面积是怎样变化的？参考答案解析【学习目标】1.复习轴对称、平移、旋转、图形的放大与缩小等图形变换方式的特点。

2.根据变换方式的特点，按要求画图。

利用比例知识计算面积。

【学习过程】一、知识梳理（课本103页）观察下面的图片，你能发现哪些图形变换的现象？它们有什么特点？（旋转）（平移）（对称）（放大）二、课堂练习1.下面图形各有几条对称轴？请画出前5个图形的所有对称轴。

图形的变换练习题一、选择题1. 下列哪种变换不是图形变换的基本类型？A. 平移B. 旋转B. 缩放D. 颜色变换2. 在进行图形的平移变换时，图形的哪个属性不会改变？A. 形状B. 面积C. 角度D. 颜色3. 旋转变换中，图形绕哪个点进行旋转？A. 任意点B. 原点C. 图形的中心点D. 旋转轴上的点4. 缩放变换中，图形的面积会如何变化？A. 保持不变B. 按比例增加C. 按比例减少D. 无法确定5. 以下哪个选项不是图形变换的属性？A. 变换前后图形的相似性B. 变换前后图形的对应点连线平行或共线C. 变换前后图形的对应角相等D. 变换前后图形的对应边颜色相同二、填空题6. 图形的平移变换是指图形上的每一点在平面上按照某个_________方向作相同距离的移动。

7. 旋转变换中，图形绕某一点旋转_________度，图形上的所有点都绕该点旋转相同的角度。

8. 缩放变换中，图形上的所有点都按照相同的比例因子向_________或远离中心点移动。

9. 图形的反射变换是指图形沿某一条直线翻转，这条直线称为_________。

10. 图形的相似变换是指图形按照相同的比例因子进行平移、旋转和缩放，使得变换后的图形与原图形_________。

三、简答题11. 简述图形的平移变换有哪些特点，并给出一个平移变换的例子。

12. 解释图形的旋转变换，并说明旋转中心和旋转角度对图形的影响。

13. 描述图形的缩放变换，并解释缩放因子对图形大小和形状的影响。

14. 什么是图形的反射变换？请说明反射轴的作用。

15. 什么是图形的相似变换？它与图形的缩放变换有何不同？四、计算题16. 给定一个正方形，边长为4cm，进行平移变换，移动距离为3cm，求平移后正方形的边长。

17. 一个圆形的半径为5cm，进行旋转变换90度，求旋转后圆形的半径。

18. 一个矩形的长为6cm，宽为4cm，进行缩放变换，缩放因子为1.5，求缩放后矩形的长和宽。

2024年数学图形变换基础练习题五年级下册（含答案）试题部分一、选择题：1. 在平面内，将一个图形上的所有点都向右平移3个单位，这种变换叫做（）。

A. 转动B. 反射C. 平移D. 旋转2. 下列图形中，不是轴对称图形的是（）。

A. 正方形B. 长方形C. 梯形D. 圆3. 下列哪个现象属于平移现象？（）A. 旋转的风扇B. 摇摆的钟摆C. 升降机的上下运动D. 自行车的车轮运动4. 把一个平行四边形绕着它的一个顶点旋转，能够得到的图形是（）。

A. 长方形B. 正方形C. 平行四边形D. 梯形5. 下列图形中，既是轴对称图形，又是中心对称图形的是（）。

A. 等边三角形B. 矩形C. 梯形D. 直角三角形6. 将一个正方形绕着它的中心旋转90度，得到的图形与原图形（）。

A. 重合B. 相似C. 全等D. 不确定7. 在平面直角坐标系中，点A(2,3)向右平移3个单位，再向上平移2个单位，得到的新坐标是（）。

A. (5,5)B. (5,3)C. (2,5)D. (3,5)8. 下列哪个图形可以通过旋转得到另一个图形？（）A. 等腰三角形和平行四边形B. 正方形和矩形C. 长方形和正方形D. 等边三角形和等腰梯形9. 一个图形沿着一条直线对折，两侧的图形完全重合，这样的图形叫做（）。

A. 平移图形B. 旋转图形C. 对称图形D. 相似图形10. 下列说法正确的是（）。

A. 平移不改变图形的大小和形状B. 旋转不改变图形的大小和形状C. 反射不改变图形的大小和形状D. 所有选项都正确二、判断题：1. 平移是将一个图形上的所有点都按照某个方向作相同距离的移动。

（）2. 旋转是将一个图形绕着某一点转动一个角度的图形变换。

（）3. 轴对称图形的对称轴一定是直线。

（）4. 平移和旋转都会改变图形的位置，但不会改变图形的大小和形状。

（）5. 所有的图形都有对称轴。

（）6. 一个图形沿某条直线对折，两侧的图形完全重合，这样的图形叫做轴对称图形。

图形变换练习题在几何学中，图形变换是研究如何通过一系列操作改变或转换图形的形状、大小和位置的方法。

通过练习和掌握图形变换技巧，可以帮助我们更好地理解和应用几何学的相关知识。

本文将为您提供一些有趣的图形变换练习题，帮助您巩固对图形变换的理解和应用能力。

一、平移平移是指将图形沿着某个方向上的直线移动一段固定的距离，并保持原始图形的形状和大小不变。

下面是一个练习题：练习题1：把一个正方形平移到坐标平面上的另外一个位置。

解答：我们可以先确定正方形的一个顶点和目标位置的对应顶点，然后根据两个顶点的坐标差值进行移动。

举个例子，假设正方形的一个顶点为A(2,3)，我们要将其平移到坐标平面上的点B(6,9)，那么只需要将正方形的每个顶点的坐标都分别增加(4,6)即可。

二、旋转旋转是指将图形绕某个中心点按照一定角度旋转，使得原始图形在平面上绕一定的路径做圆周运动。

下面是一个练习题：练习题2：将一个三角形绕原点逆时针旋转90度。

解答：对于一个三角形ABC，我们可以通过以下步骤进行旋转：1. 找到三角形的质心G，计算出它的坐标；2. 将三角形的每个顶点的坐标相对于质心进行平移，使得质心位于原点；3. 根据旋转矩阵的公式，将每个顶点绕原点逆时针旋转90度；4. 将旋转后的三角形恢复到原点附近，即将每个顶点的坐标相对于原来的质心进行平移。

三、缩放缩放是指通过增大或减小图形的各个部分之间的距离，改变图形的大小。

下面是一个练习题：练习题3：将一个矩形的长和宽分别缩放为原来的一半。

解答：假设矩形的长为L，宽为W，我们可以通过以下步骤进行缩放：1. 将矩形的每个顶点相对于矩形的中心进行平移，使得中心位于原点；2. 根据缩放因子为0.5，将每个顶点的坐标分别乘以0.5，即可得到缩放后的矩形的顶点坐标；3. 将缩放后的矩形恢复到原来的位置，即将每个顶点的坐标相对于原来的中心进行平移。

四、对称对称是指通过某个中心轴将图形中的每个点对应到另外一个点，使得图形关于中心轴具有对称性。

小升初数学《图形与变换》专题练习（含解析）一．选择题1．如图图形中，()是轴对称图形．A．B．C．D．2．（2019秋•中山区期末）下列图形中，对称轴条数最少的是()A．圆B．半圆C．等边三角形D．长方形3．（2019秋•黔东南州期末）下列图形对称轴最多的是()A．等边三角形B．半圆C．等腰梯形D．长方形4．（2019秋•宝鸡期末）下面图形中不是轴对称图形的是()A．平行四边形B．长方形C．等腰三角形D．扇形5．（2019•长沙）将一个长是5厘米、宽是3厘米的长方形按4:1放大，得到的图形面积是()平方厘米．A．15B．240C．60D．646．（2018•扬州）一个正方形的面积是100平方厘米，把它按1:2的比缩小．缩小后图形的面积是()平方厘米．A．50B．200C．25D．207．（2013•宜昌）下列图形中不可能通过将图形平移或旋转得到的是()A．B．C．D．8．（2012•台州）一个长方形的长是6厘米，宽是2厘米．以它的长为轴旋转一周所得到的圆柱体的体积是()A．75.36立方厘米B．150.72立方厘米C．56.52立方厘米D．226.08立方厘米二．填空题9．（2018秋•涿州市期末）汽车行驶时，车轮的运动是，电梯上升或下降的运动是．（填“平移”或“旋转”)10．（2018秋•沧州期末）风车的转动是现象，箱子在地面上被推动是现象．11．（2019秋•定西期中）平移后的图形与原图形相比较，只改变，不改变和．12．（2018秋•浦口区校级期末）把你们教室里的窗户打开，窗户的运动是；把你们教室里的门打开，门的运动是．13．（2018•阜宁县）一直角三角板的两条直角边分别为6厘米、8厘米，以8厘米长的直角边为轴旋转一圈（如图），将出现一个体，它的体积是立方厘米．14．（2014•慈溪市）如图，图2是图1按:放大后的图形；图1三角形面积是平方厘米．15．（2012•东城区）一个长方形以它的一条边为轴，旋转一周得到的旋转体是一个圆柱．．三．判断题16．（2019秋•无棣县期末）圆是轴对称图形，有无数条对称轴，每条对称轴都过圆心．（判断对错）17．（2019秋•龙州县期末）拧开水龙头时水龙头的运动是旋转．（判断对错）18．直线行进中的滑雪板的运动属于平移现象．（判断对错）19．（2017•南明区）同一钟面上，当时针旋转了30度，分针就旋转了360度．（判断对错）20．（2019•福田区）正方形、等腰梯形、三角形和圆都是轴对称图形．（判断对错）21．（2018•工业园区）长方形和正方形都有4条对称轴．．（判断对错）22．（2016•天津）一个长是10cm，宽是6cm的长方形按1:2缩小，得到图形的面积是原来面积的12．（判断对错）23．（2015•揭阳）以直角三角形任意一条直角边为轴旋转一周，可以形成一个圆柱．（判断对错）四．应用题24．（2019春•龙岗区期中）把一张长7厘米、宽5厘米的长方形卡片按3:1的比例放大后，得到的卡片的面积是多少平方厘米？25．小明在照镜子时发现，镜子中的钟面上时针与分针的位置是，那么这时的时间是26．将一个半径是3cm的圆按3:1的比例放大，放大后圆的周长是原来圆的几倍？放大后圆的面积是原来圆的几倍？27．下图中的三角形是从哪张对折后的纸上剪下来的？在()里填上序号．28．小明在电脑上把一张长方形图片按比例放大后如图，放大后的宽是多少厘米？五．操作题29．如图哪些图形能通过旋转与图形A重合？涂上你喜欢的颜色．30．如图所示的图案分别是从哪张纸上剪下来的？连一连．31．（2019秋•梁园区期中）如图，图形①经过怎样的运动可以得到图形②？32．（2018•无锡）按要求画一画．（1）把长方形按3:1的比放大，画出放大后的图形；（2）把梯形绕点O按逆时针旋转90 ，画出旋转后的图形；（3）画一个三角形和一个平行四边形，使它们的面积都是6平方厘米．33．（2017•兴化市）如图每格表示边长为1厘米的正方形，请按要求画出图形并填空．（1）按照2:1的比，画出直角三角形放大后的图形．（2）画出三角形ABC绕C点顺时针旋转90 后的图形，旋转后三角形A点的位置用数对表示为(，)34．如图是由三个小正方形组成的图形，请你用两种不同的方法分别在下面的两个图形中添上一个同样大小的小正方形，使它们成为轴对称图形．六．解答题35．（2019•杭州模拟）下列现象哪些是平移？在括号里画“△”．哪些是旋转？在括号里画“〇”．36．（2019春•长春月考）认真辨一辨，下面的物体运动，是平移的打“ ”，是旋转的画“〇”．37．（2019春•化州市校级月考）连线．38．（2019春•东莞市期中）下面各图形，绕轴旋转后得到的是哪个图形？连一连．39．（2019•岳阳模拟）把图中的平行四边形先按2:1的比放大，画出放大后的图形，再绕A 点顺时针旋转90 ，画出旋转后的图形．40．（2014•宁夏）按3:1画出下面的三角形放大后的图形．参考答案：一．选择题1．如图图形中，()是轴对称图形．A．B．C．D．【分析】依据轴对称图形的意义，即在平面内，如果一个图形沿一条直线对折，对折后的两部分都能完全重合，这条直线叫做对称轴，这样的图形叫做轴对称图形，据此即可进行解答．【解答】解：根据分析可得，是轴对称图形，其它选项都不是轴对称图形．故选：D．2．（2019秋•中山区期末）下列图形中，对称轴条数最少的是()A．圆B．半圆C．等边三角形D．长方形【分析】一个图形沿一条直线对折，直线两旁的部分能够完全重合，那么这个图形就是轴对称图形，这条直线就是这个图形的一条对称轴，由此即可确定这个图形的对称轴的条数及位置．【解答】解：圆有无数条对称轴，半圆有1条对称轴，等边三角形有3条对称轴，长方形有2条对称轴，所以半圆的对称轴的条数最少；故选：B．3．（2019秋•黔东南州期末）下列图形对称轴最多的是( ) A ．等边三角形B ．半圆C ．等腰梯形D ．长方形【分析】根据轴对称图形的定义：一个图形沿某条直线对折，直线两旁的部分能够完全重合，则这个图形就是轴对称图形，这条直线就是它的一条对称轴，据此分别确定出选项中各个图形中对称轴的条数，然后选择即可．【解答】解：等边三角形有3条对称轴，半圆有1条对称轴，等腰梯形有1条对称轴，长方形有2条对称轴； 故选：A ．4．（2019秋•宝鸡期末）下面图形中不是轴对称图形的是( ) A ．平行四边形B ．长方形C ．等腰三角形D ．扇形【分析】根据轴对称图形的意义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴；依次进行判断即可．【解答】解：根据轴对称图形的意义可知：长方形、等腰三角形和扇形都是轴对称图形，而平行四边形不是轴对称图形； 故选：A ．5．（2019•长沙）将一个长是5厘米、宽是3厘米的长方形按4:1放大，得到的图形面积是( )平方厘米． A ．15B ．240C ．60D ．64【分析】此题只要求出放大后的长和宽，根据“图上距离=实际距离⨯比例尺”可求出；然后根据“长方形的面积=长⨯宽”即可得出结论． 【解答】解：5420⨯=（厘米） 3412⨯=（厘米） 2012240⨯=（平方厘米）答：得到的图形面积是240平方厘米． 故选：B ．6．（2018•扬州）一个正方形的面积是100平方厘米，把它按1:2的比缩小．缩小后图形的面积是( )平方厘米． A ．50B ．200C ．25D ．20【分析】面积是100平方厘米的正方形的边长是10厘米，根据图形放大与缩小的意义，边长是10厘米的正方形按1:2缩小后，边长是1025÷=（厘米），根据正方形的面积计算公式“2S a =”即可求出它的面积．【解答】解：因为10厘米10⨯厘米100=平方厘米，所以面积是100平方厘米的正方形的边长是10厘米，1025÷=（厘米）⨯=（平方厘米）5525答：缩小后图形的面积是25平方厘米．故选：C．7．（2013•宜昌）下列图形中不可能通过将图形平移或旋转得到的是()A．B．C．D．【分析】平移只改变图形的位置，而不改变图形的形状和大小；旋转变化前后，对应线段、对应角分别相等，图形的大小、形状都不改变，据此解答即可．【解答】解：A、是由图形通过顺时针旋转90︒得到的图形；C、是由图形通过顺时针旋转180︒得到的图形；D、是由图形通过顺时针旋转270︒得到的图形．故选：B．8．（2012•台州）一个长方形的长是6厘米，宽是2厘米．以它的长为轴旋转一周所得到的圆柱体的体积是()A．75.36立方厘米B．150.72立方厘米C．56.52立方厘米D．226.08立方厘米【分析】将一个长为6厘米，宽是2厘米的长方形，以它的长为轴旋转一周所围成的圆柱体的底面半径是2厘米，高是6厘米；要求它们的体积，可利用圆柱的体积公式V SH=，列式解答即可．【解答】解：2⨯⨯，3.1426=⨯⨯，3.1446=（立方厘米）；75.36答：这个圆柱的体积是75.36立方厘米．故选：A．二．填空题9．（2018秋•涿州市期末）汽车行驶时，车轮的运动是旋转，电梯上升或下降的运动是．（填“平移”或“旋转”)【分析】旋转是物体运动时，每一个点离同一个点（可以在物体外）的距离不变的运动，称为绕这个点的转动，这个点称为物体的转动中心，旋转自然是转动的；推拉门窗是把整个门窗按一定的方向来回运动，根据图形平移的意义，在平面内，将一个图形沿某个方向移动一定的距离，这样的图形运动称为平移，依此根据平移与旋转定义判断即可．【解答】解：汽车行驶时，车轮的运动是旋转，电梯上升或下降的运动是平移；故答案为：旋转，平移．10．（2018秋•沧州期末）风车的转动是旋转现象，箱子在地面上被推动是现象．【分析】平移是物体运动时，物体上任意两点间，从一点到另一点的方向与距离都不变的运动；旋转是物体运动时，每一个点离同一个点（可以在物体外）的距离不变的运动，称为绕这个点的转动，这个点称为物体的转动中心．所以，它并不一定是绕某个轴的．根据平移与旋转定义判断即可．【解答】解：风车的转动是旋转现象，箱子在地面上被推动是平移现象；故答案为：旋转，平移．11．（2019秋•定西期中）平移后的图形与原图形相比较，只改变位置，不改变和．【分析】平移是把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同，但位置不同．【解答】解：平移后的图形与原图形相比较，只改变位置，不改变形状和大小；故答案为：位置，形状，大小．12．（2018秋•浦口区校级期末）把你们教室里的窗户打开，窗户的运动是平移；把你们教室里的门打开，门的运动是．【分析】根据平移图形的特征，如图两个图形的大小、形状、方向不变，只是位置的不同，这两个图形就是平移；根据旋转图形的特征，如图两个图形的大小、形状不变，只是方向不变，只是位置的不同，这样的两个图形就是旋转．【解答】解：把你们教室里的窗户打开，窗户的运动是平移；把你们教室里的门打开，门的运动是旋转．故答案为：平移，旋转．13．（2018•阜宁县）一直角三角板的两条直角边分别为6厘米、8厘米，以8厘米长的直角边为轴旋转一圈（如图），将出现一个圆锥体，它的体积是立方厘米．【分析】以8厘米的直角边为轴旋转一周所形成的图形是一个高为8厘米，底面半径为6厘米的圆锥体；根据圆锥的体积公式“213V r h π=”，即可求得它的体积． 【解答】解：以8厘米长的直角边为轴旋转一圈，将出现一个圆锥体； 圆锥的体积是：21 3.14683⨯⨯⨯ 1 3.143683=⨯⨯⨯ 301.44=（立方厘米）． 故答案为：圆锥，301.44．14．（2014•慈溪市）如图，图2是图1按 3 : 放大后的图形；图1三角形面积是 平方厘米．【分析】图2的底是6厘米，图1中的对应部分是2厘米，623÷=，也就是说图2是图1对应部分的3倍，因此，图2是由图1按3:1放大后的图形，由此用43÷求出图1三角形的高，然后根据三角形的面积公式12S ah =即可求出图1的面积． 【解答】解：623÷=，即图2是图1对应部分的3倍，因此，图2是由图1按3:1放大后的图形；4433÷=（厘米） 1442233⨯⨯=（平方厘米）． 故答案为：3，1；43． 15．（2012•东城区）一个长方形以它的一条边为轴，旋转一周得到的旋转体是一个圆柱． √ ．【分析】我们知道，点动成线，线动成面，面动成体，把一个长方形以它的一条边为轴旋转一周，所得到的图形是以为旋转轴的这条边为高，另一边为半径的一个圆柱．【解答】解：如图，一个长方形以它的一条边为轴，旋转一周得到的旋转体是一个圆柱；故答案为：√三．判断题16．（2019秋•无棣县期末）圆是轴对称图形，有无数条对称轴，每条对称轴都过圆心．√（判断对错）【分析】根据对称轴的含义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴；据此即可解答．【解答】解：根据轴对称图形的定义可知：圆是轴对称图形，它有无数条对称轴，因为圆的对称轴是直径所在的直线，又因为通过圆心、并且两端都在圆上的线段，叫做直径，所以圆的对称轴一定通过圆心，故原题说法正确；故答案为：√．17．（2019秋•龙州县期末）拧开水龙头时水龙头的运动是旋转．√（判断对错）【分析】把一个图形绕着某一点O转动一个角度的图形变换叫做旋转；据此解答即可．【解答】解：拧开水龙头时水龙头的运动是旋转是正确的．故答案为：√．18．直线行进中的滑雪板的运动属于平移现象．√（判断对错）【分析】根据平移的含义：平移是物体运动时，物体上任意两点间，从一点到另一点的方向与距离都不变的运动，据此解答即可．【解答】解：根据平移的意义可知：直线行进中的滑雪板的运动属于平移现象，所以本题说法正确；故答案为：√．19．（2017•南明区）同一钟面上，当时针旋转了30度，分针就旋转了360度．√（判断对错）【分析】钟面一周为360︒，共分12大格，每格为3601230÷=︒，当时针旋转了30度，是经历了1小时，所以分针正好旋转了一周，是360度，据此解答即可．【解答】解：同一钟面上，当时针旋转了30度，分针就旋转了360度，说法正确；故答案为：√．20．（2019•福田区）正方形、等腰梯形、三角形和圆都是轴对称图形．⨯（判断对错）【分析】依据轴对称图形的概念，即在平面内，如果一个图形沿一条直线折叠，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形，据此即可进行判断．【解答】解：因为正方形、等腰梯形和圆分别沿一条直线折叠，直线两旁的部分能够完全重合，则说正方形、等腰梯形和圆都是轴对称图形；但是除等腰三角形外的三角形沿一条直线折叠，直线两旁的部分不能够完全重合，则除等腰三角形外的三角形不是轴对称图形．故答案为：⨯．21．（2018•工业园区）长方形和正方形都有4条对称轴．⨯．（判断对错）【分析】根据轴对称图形的意义找出长方形和正方形的对称轴的条数，即可判断正误．【解答】解：长方形的对称轴有2条，正方形的对称轴有4条，所以原题说法错误．故答案为：⨯．22．（2016•天津）一个长是10cm，宽是6cm的长方形按1:2缩小，得到图形的面积是原来面积的12．⨯（判断对错）【分析】一个长是10cm，宽是6cm的长方形按1:2缩小，长是5cm，宽是3cm，根据长方形面积计算公式“S ab=”分别求出缩小后的面积、原来的面积，再用缩小后的面积除以原来的面积．【解答】解：1025(cm÷=，623()cm÷=(53)(106)⨯÷⨯1560=÷14=即得到图形的面积是原来面积的1 4原题的说法错误．故答案为：⨯．23．（2015•揭阳）以直角三角形任意一条直角边为轴旋转一周，可以形成一个圆柱．⨯（判断对错）【分析】根据直角三角形及圆锥的特征，直角三角形绕一直角边旋转一周形成一个以旋转直角边为高，另一直角边为底面半径的圆锥．【解答】解：以直角三角形任意一条直角边为轴旋转一周，可以形成一个圆锥．故答案为：⨯．四．应用题24．（2019春•龙岗区期中）把一张长7厘米、宽5厘米的长方形卡片按3:1的比例放大后，得到的卡片的面积是多少平方厘米？【分析】一个长7厘米、宽5厘米的长方形按3:1放大，即将这个长方形的长和宽同时扩大3倍，根据长方形的面积公式可知得到的图形的面积是：(73)(53)315⨯⨯⨯=（平方厘米）．【解答】解：(73)(53)⨯⨯⨯=⨯2115=（平方厘米）315答：得到的卡片的面积是315平方厘米．25．小明在照镜子时发现，镜子中的钟面上时针与分针的位置是，那么这时的时间是8:30【分析】根据镜面对称的性质，在平面镜中的像与现实中的事物恰好左右颠倒，且关于镜面对称，分析并作答．【解答】解：根据镜面对称的性质可知：小明在照镜子时发现，镜子中的钟面上时针与分针的位置是，那么这时的时间是8:30；故答案为：8:30．26．将一个半径是3cm的圆按3:1的比例放大，放大后圆的周长是原来圆的几倍？放大后圆的面积是原来圆的几倍？【分析】按32:1的比放大就是把原来的圆的半径扩大3倍，用33⨯求出扩大后的圆的半径，然后根据圆的周长公式与面积公式分别求出放大前和放大后圆的周长与面积，然后再进一步解答．【解答】解：339⨯=（厘米）(2 3.149)(2 3.143)⨯⨯÷⨯⨯=÷93=322⨯÷÷(3.149)(3.143)=÷8199=答：放大后圆的周长是原来圆的3倍，放大后圆的面积是原来圆的9倍．27．下图中的三角形是从哪张对折后的纸上剪下来的？在()里填上序号．【分析】根据轴对称图形的意义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形．因为①的对称轴在折痕，所以如果按①剪下来，得到的是等腰三角形，符合要求．【解答】解：根据轴对称图形可知，图中的三角形是①对折后的纸上剪下来的．故答案为：①．28．小明在电脑上把一张长方形图片按比例放大后如图，放大后的宽是多少厘米？【分析】原来长方形的长是3厘米，宽是2厘米．长放大后是18厘米，1836÷=，即小明是把原来的图形按6:1放大的，根据图形放大与缩小的意义，长放大到原来的6倍，宽也放大到原来的6倍．【解答】解：1836÷=⨯=2612()cm答：放大后的宽是12厘米．五．操作题29．如图哪些图形能通过旋转与图形A重合？涂上你喜欢的颜色．【分析】在平面内，将一个图形绕一点按某个方向转动一个角度，这样的运动叫作图形的旋转，旋转可以简单的理解为图形的转动．解答即可．【解答】解：三个图都能通过旋转得到A．30．如图所示的图案分别是从哪张纸上剪下来的？连一连．【分析】依据轴对称图形的概念，即在平面内，如果一个图形沿一条直线折叠，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形，这条直线就是其对称轴，据此解答即可．【解答】解：31．（2019秋•梁园区期中）如图，图形①经过怎样的运动可以得到图形②？【分析】据平移的意义“平移是指在同一平面内，将一个图形整体按照某个直线方向移动一定的距离，这样的图形运动叫作图形的平移运动，简称平移”，由此可知：把图①向下平移4格再向右平移5格即可得到图②；由此解答即可．【解答】解：根据平移的性质可知：把图①向下平移4格再向右平移5格即可得到图②．32．（2018•无锡）按要求画一画．（1）把长方形按3:1的比放大，画出放大后的图形；（2）把梯形绕点O按逆时针旋转90︒，画出旋转后的图形；（3）画一个三角形和一个平行四边形，使它们的面积都是6平方厘米．【分析】（1）根据图形放大与缩小的意义，把这个长形的长、宽均扩大到原来的3倍所得到的长方形就是原长方形按3:1放大后的图形．（2）根据旋转的特征，梯形绕点O逆时针旋转90︒，点O的位置不动，其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形．（3）根据平行四边形的面积计算公式“S ah=”只要画的平行四边形底、高之积为6即可，如可画底为3厘米，高为2厘米的平行四边形，其面积就是6平方厘米；根据三角形的面积计算公式“2=÷”，只要S ah画的三角形与平行四边形等底（或等高），高（或底）为平行四边形的2倍，其面积就与平行四边形面积相等．【解答】解：（1）把长方形按3:1的比放大，画出放大后的图形（图中红色部分）；（2）把梯形绕点O按逆时针旋转90︒，画出旋转后的图形（图中绿色部分）；（3）画一个三角形（图中黄色部分）和一个平行四边形（图中蓝色部分），使它们的面积都是6平方厘米．33．（2017•兴化市）如图每格表示边长为1厘米的正方形，请按要求画出图形并填空．（1）按照2:1的比，画出直角三角形放大后的图形．（2）画出三角形ABC绕C点顺时针旋转90︒后的图形，旋转后三角形A点的位置用数对表示为(9，)【分析】（1）根据图形放大与缩小的意义，把原直角三角形的两直角边均放大到原来的2倍，所得到的直角三角形就是原直角三角形按2:1放大后的图形（直角三角形两直角边即可确定其形状）．（2）根据旋转的特征，三角形ABC绕点C顺时针旋转90︒，点A的位置不动，其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形．根据用数对表示点的位置的方法，第一个数字表示列数，第二个数字表示行数及旋转后点A的位置即可用数对表示出点A的位置．【解答】解：（1）按照2:1的比，画出直角三角形放大后的图形（下图红色部分）:（2）画出三角形ABC绕C点顺时针旋转90︒后的图形（下图绿色部分），旋转后三角形A点的位置用数对表示为：(9,10)．故答案为：9，10．34．如图是由三个小正方形组成的图形，请你用两种不同的方法分别在下面的两个图形中添上一个同样大小的小正方形，使它们成为轴对称图形．【分析】根据轴对称与对称轴的定义，对称轴两侧的部分能够完全重合，由此即可求得答案．【解答】解：六．解答题35．（2019•杭州模拟）下列现象哪些是平移？在括号里画“△”．哪些是旋转？在括号里画“〇”．【分析】平移是物体运动时，物体上任意两点间，从一点到另一点的方向与距离都不变的运动；旋转是物体运动时，每一个点离同一个点（可以在物体外）的距离不变的运动，称为绕这个点的转动，这个点称为物体的转动中心．所以，它并不一定是绕某个轴的．根据平移与旋转定义判断即可．【解答】解：36．（2019春•长春月考）认真辨一辨，下面的物体运动，是平移的打“√”，是旋转的画“〇”．【分析】旋转就是围绕着一个中心转动，运动方向发生改变；平移就是直直地移动，移动过程中方向不发生改变．据此解答即可．【解答】解：故答案为：〇，√，〇，〇，√，√．37．（2019春•化州市校级月考）连线．【分析】根据各平面图形及立体图形的特征，进行连线即可．长方形绕长边旋转后是圆柱，半圆绕直径旋转后是球，三角形绕一条直角边旋转后是圆锥，直角梯形绕成直角的边（高)旋转后是圆台．【解答】解：根据各图形的特征连线如下：38．（2019春•东莞市期中）下面各图形，绕轴旋转后得到的是哪个图形？连一连．【分析】一个半圆旋转后会得到一个圆球；两个长方形旋转后会得到两个圆柱；一个梯形旋转后会得到一个圆台；一个三角形和一个正方形旋转后会得到一个圆柱和一个圆锥．【解答】解：连线如下：39．（2019•岳阳模拟）把图中的平行四边形先按2:1的比放大，画出放大后的图形，再绕A点顺时针旋转90︒，画出旋转后的图形．【分析】（1）按2:1的比画出平行四边形放大后的图形，先数出原平行四边形的底与高分别是3和2；则放大后底与高的长度分别是326⨯=；由此即可画出放大后的平行四边形1；⨯=、224（2）根据图形旋转的方法，先把与点A相连的两条边顺时针旋转90︒，再根据平行四边形的对边平行的性质，画出另外两条边，即可得出旋转后的平行四边形2．【解答】解：根据题干分析，可画图如下：40．（2014•宁夏）按3:1画出下面的三角形放大后的图形．。

精选资料欢迎下载
人教版小学数学五年级下册《图形变换》综合练习题
一、先观察右图，再填空。

（ 1）图 1 绕点“ O”逆时针旋转 900到达图（）的位置；
（ 2）图 1 绕点“ O”逆时针旋转 1800到达图（）的位置；
2（3）图 1绕点“ O”顺时针旋转（0）到达图 4的位置；3
（4）图 2绕点“ O”顺时针旋转（0）到达图 4的位置；
（5）图 2绕点“ O”顺时针旋转 900到达图（）的位置；1
O （6）图 4绕点“ O”逆时针旋转 900到达图（）的位置；4
二、画出图形的另一半，使它成为一个轴对称图形。

三、 (1)画出三角形 AOB 绕 O 点（2）绕O点顺时针旋转90°
顺时针旋转 90 度后的图形。

（3）绕 O 点逆时针旋转 90°（4）绕O点顺时针旋转90°。

精选资料欢迎下载
四、画出绕点“ O”顺时针旋转 90 度后的图形。

画出绕点“A”逆时针旋转 90 度后的图形。

O A
五、画出三角形 AOB 围绕 O 顺时针或逆时针旋转后的图形。

00
逆时针旋转 90顺时针旋转 90
A A
B
B
O O
六、填空题。

①号三角形绕 A 点按 ______时针方向旋转了 ______度。

②号梯形绕 B 点按 ______时针方向旋转了 ______度。

③号三角形绕 C 点按 ______时针方向旋转了 ______度。

④号平行四边行绕 D 点按 ______时针方向旋转了 ______度。