山西省太原五中2012-2013学年高二10月月考 数学理试题

山西省部分学校2024-2025学年高二上学期10月月考数学试题一、单选题1．已知直线l 经过A ，B 两点，则l 的倾斜角为（ ） A ．6π B ．3π C ．23π D ．56π 2．已知圆C 的方程是2242110x y x y ++--=，则圆心C 的坐标是（ ） A ．()2,1-B ．()2,1-C ．()4,2-D ．()4,2-3．在长方体1111ABCD A B C D -中，M 为棱1CC 的中点.若1,,AB a AD b AA c ===u u u r r u u u r r u u u r r ，则AM u u u u r等于（ ）A ．12a b c ++r r rB ．12a b c -+r r rC ．111222a b c ++r r rD ．111222a b c -+r r r4．两平行直线1l ：20x y -=，2l ：240x y -+=之间的距离为（ ）AB ．3C D ．5．曲线y =x 轴围成区域的面积为（ ） A ．4πB ．2πC ．πD ．π26．已知平面α的一个法向量(1,1,2)n =-r，(0,1,2)A 是平面α内一点，(2,1,4)P 是平面α外一点，则点P 到平面α的距离是（ ）A ．B ．CD ．37．在平面直角坐标系xOy 中，圆C 的方程为22430x y y +-+=，若直线1y kx =-上存在点P ，使以P 点为圆心，1为半径的圆与圆C 有公共点，则实数k 的取值范围是（ ）A ．11,,44⎛⎤⎡⎫-∞-⋃+∞ ⎪⎥⎢⎝⎦⎣⎭B ．,⎛⎫-∞⋃+∞ ⎪ ⎪⎝⎦⎣⎭C ．,⎛⎫-∞⋃+∞ ⎪ ⎪⎝⎭⎝⎭D ．11,,22⎛⎤⎡⎫-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭U8．在正三棱柱111ABC A B C -中，2AB =，1AA 2BC BO =u u u r u u u r，M 为棱11B C 上的动点，N为线段AM 上的动点，且MN MOMO MA=，则线段MN 长度的最小值为（ ）A ．2BC D二、多选题9．下列关于空间向量的命题中，是真命题的是（ ）A ．若三个非零向量能构成空间的一个基底，则它们一定不共面B ．若0a b ⋅>r r ，则a r ，b r 的夹角是锐角C ．不相等的两个空间向量的模可能相等D ．若a r，b r 是两个不共线的向量，且(,c a b λμλμ=+∈R r r r 且0)λμ⋅≠，则{},,a b c r r r 构成空间的一个基底10．已知直线1:30l ax y a +-=，直线2:2(1)60l x a y +--=，则（ ）A ．当3a =时，1l 与2l 的交点为(3,0)B ．直线1l 恒过点(3,0)C ．若12l l ⊥，则13a =D ．存在a ∈R ，使12l l ∥11．“太极图”是中国传统文化之一，其形状如对称的阴阳两鱼互抱在一起，也被称为“阴阳鱼太极图”.如图是放在平面直角坐标系中的“太极图”.整个图形是一个圆形2216x y +=，其中黑色阴影区域在y 轴右侧部分的边界为一个半圆.则下列命题正确的是（ ）A ．黑色阴影区域在y 轴右侧部分的边界所在圆的方程为()2224x y +-= B ．直线780x y -+=与白色部分有公共点C ．点(),P x y 是黑色阴影部分（包括黑白交界处）中一点，则3x y -的最大值为4D ．过点()3,1M 作互相垂直的直线1l 、2l ，其中1l 与圆2216x y +=交于点A 、C ，2l 与圆2216x y +=交于点B 、D ，则四边形ABCD 面积的最大值是22三、填空题12．若直线l 与直线122y x =-+垂直，且它在y 轴上的截距为4，则直线l 的方程为． 13．圆222:1O x y +=和圆()()222:4316C x y -+-=的公切线的方程为. 14．如图所示，在四棱锥P -ABCD 中，AB CD ∥，且==90BAP CDP ∠∠︒，若PA PD AB DC ===，=90APD ∠︒，则平面APB 与平面PBC 夹角的余弦值为．四、解答题15．已知直线:210l x y -+=与22:420C x y x y a +-++=e 交于A ，B 两点． (1)求线段AB 的垂直平分线的方程； (2)若AB 4=，求a 的值．16．如图所示的几何体是圆锥的一部分，其中PO 是圆锥的高，AB 是圆锥底面的一条直径，2PO =，1OA =，C 是»AB 的中点．(1)求直线BC 与PA 所成角的余弦值； (2)求直线PA 与平面PBC 所成角的正弦值．17．在平行四边形ABCD 中，()1,1A --，()1,3B ，()7,5D . (1)若圆E 过A ，B ，D 三点，求圆E 的方程； (2)过点C 作圆E 的切线，切点为M ，N ，求MN .18．如图，四边形ABCD 是直角梯形，//,,22,AB CD AB BC AB BC CD E ⊥===为BC 的中点，P 是平面ABCD 外一点，1,,PA PB PE BD M ==⊥是线段PB 上一点，三棱锥M BDE -的体积是19.(1)求证：PA ⊥平面ABCD ； (2)求二面角M DE A --的余弦值.19．已知圆C 的圆心在直线30x y -=上，与y 轴正半轴相切，且截直线:20l x y -=所得的弦长为4.(1)求圆C 的方程；(2)设点A 在圆C 上运动，点()5,1B -，M 为线段AB 上一点且满足3AM MB=，记点M 的轨迹为曲线E.①求曲线E的方程，并说明曲线E的形状；②在直线l上是否存在异于原点的定点T，使得对于E上任意一点P，PTPO为定值，若存在，求出所有满足条件的点T的坐标，若不存在，说明理由.。

山西省太原市第五中学校2024-2025学年九年级上学期10月月考数学试题一、单选题1．下列关于x 的方程一定是一元二次方程的是（ ） A ．20ax bx c ++= B ．2210x x +-= C ．212+=x xD ．220x x --=2．关于频率和概率的关系，下列说法正确的是（ ）. A ．频率等于概率B ．当实验次数很大时，频率稳定在概率附近C ．当实验次数很大时，概率稳定在频率附近D ．实验得到的频率与概率不可能相等3．以下列长度（同一单位）为长的四条线段中，不成比例的是（ ）A ．2，3，6，9B ．1，2，3，4C ．2，1，12，4D4．布袋中装有除颜色外没有其他区别的1个红球和2个白球，搅匀后从中摸出一个球，放回搅匀，再摸出第二个球，两次都摸出白球的概率是（ ） A ．49B ．29C ．23D ．135．如图，直线a 、b 、c 分别与直线m 、n 交于点A 、B 、C 、D 、E 、F ．已知直线a b c ∥∥，若2AB =，3BC =，则DEEF的值为（ ）A ．23B ．32C ．25D ．356．如图，在矩形ABCD 中，对角线AC ，BD 相交于点O ，点E ，F 分别是AO ，AD 的中点，连接EF ，若6AB cm =，8BC cm =，则EF 的长是（ ）A ．2.2cmB ．2.3cmC ．2.4cmD ．2.5cm7．为宣传“扫黑除恶”专项行动，社区准备制作一幅宣传版面，喷绘时为了美观，要在矩形图案四周外围增加一圈等宽的白边，已知图案的长为2米，宽为1米，图案面积占整幅宣传版面面积的90%，若设白边的宽为x 米，则根据题意可列出方程（ ）A ．90%×（2+x ）（1+x ）=2×1B ．90%×（2+2x ）（1+2x ）=2×1C ．90%×（2﹣2x ）（1﹣2x ）=2×1 D ．（2+2x ）（1+2x ）=2×1×90% 8．如图，将线段AB 绕它的中点O 逆时针旋转(0180)αα︒<<得到线段,,A B A B ''的对应点分别是点A '，B '，依次连接,,,AA A B BB B A ''''．则下列结论不一定．．．正确的是（ ）A ．90AAB '∠=︒ B ．对于任意α，四边形AA BB ''都是矩形C ．2AB BB ='D ．当90α=︒时，四边形AA BB ''是正方形9．用配方法解一元二次方程x 2﹣8x ﹣11=0时，下列变形正确的是（ ）A ．（x ﹣4）2=5B ．（x+4）2=5C ．（x ﹣4）2=27D ．（x+4）2=2710．如图，在菱形纸片ABCD 中，60A ∠=︒，点E 在BC 边上，将菱形纸片ABCD 沿DE 折叠，点C 对应点为点C '，且DC '是AB 的垂直平分线，则DEC ∠的大小为（ ）A．30︒B．45︒C．60︒D．75︒二、填空题11．如果35a bb-=，那么ab=．12．经过某十字路口的行人，可能直行，也可能左拐或右拐．假设这三种可能性相同，现有两人经过该路口，则恰好有一人直行，另一人左拐的概率为．13．如图，点E、F分别是正方形ABCD内部、外部一点，四边形ADFE与四边形BCFE均为菱形、则CBE∠的度数等于．14．为积极响应国家提出的“大众创业，万众创新”号召，某市加大了对“双创”工作的支持力度，据悉，2022年该市此项拨款为1.5亿元，2024年的拨款达到2.16亿元，这两年该市对“双创”工作专项拨款的平均增长率为．15．如图，在正方形ABCD中，4AB=，点E是BC边上一个动点（不与点B，C重合），将ABEV沿AE翻折到AB E'V，再将AB E'V沿AB'翻折得到AB E''V．当点E'恰好落在正方形ABCD的边所在的直线上时，线段BE的长度为．三、解答题16．用适当的方法解下列方程 (1)2221x x x =+- (2)()()325225x x x +=+17．小明在解方程2210x x --=时出现了错误，其解答过程如下： 221x x -=- （第一步）22111x x -+=-+ （第二步）2(1)0x -= （第三步） 121x x == （第四步）（1）小明解答过程是从第 步开始出错的，其错误原因是 ； （2）请写出此题正确的解答过程．18．如图，在ABC V 中，D 、E 、F 分别是AB 、AC 、BC 上的点，且DE BC ∥，EF AB ∥，:2:3AD DB =，20cm BC =，求BF 的长．19．太原是一座具有4700多年历史、2500年建城史的历史古都，系有“锦绣太原城”的美誉，在“我可爱的家乡”主题班会中，主持人准备了“晋祠园林”、“崇山大佛”、“龙山石窟”、“凌霄双塔”这四处景点的照片各一张，并将它们背面朝上放置（照片背面完全相同），甲同学从中随机抽取一张，不放回，乙再从剩下的照片中随机抽取一张，若要根据抽取的照片作相关景点介绍，求甲、乙两人中恰好有一人介绍“晋祠园林”的概率．（提示：可用照片序号列表或画树状图）20．如图，已知菱形ABCD 的对角线AC BD ，相交于点O ，点E 是菱形外一点，且DE AC CE BD ∥，∥，连接OE ．求证：OE CD =．21．某灯具制造厂新研发出一种节能护眼台灯，该台灯的成本价为30元/盏．试销一段时间后，发现按40元/盏的价格销售，每周可售出600盏；当每盏台灯售价在40元至60元之间时，每盏售价每上涨2元，每周的销售量将减少20盏． (1)若每盏台灯销售价为46元，求这周的销售利润；(2)如果要实现每周的销售利润10000元的目标，求每盏台灯的销售价格． 22．阅读下面的例题，回答问题：例：解方程：220x x --=令y x =，原方程化成220y y --= 解得122,1y y ==-（不合题意，舍去）2,2x x ∴=∴=±∴ 原方程的解是122,2x x ==-．请模仿上面的方法解方程：()21160x x ----= 23．综合与实践 问题情境：数学活动课上，老师要求同学们以矩形为背景探索几何图形运动变化中的数学结论．如图1，在矩形ABCD 中，点O 为对角线BD 的中点，连接CO ．点E 在AB 边上，且BE BO =，线段EO 的延长线交CD 于点F ．猜想证明：（1）“笃学”小组发现DF OC =，请你证明这一结论；操作探究：（2）“勤思”小组将图1中的BOE △绕B 点顺时针旋转（设点O ，E 的对应点分别为O E ''）在认真分析旋转到不同位置时的情形后，提出如下问题，请你解答：①如图2，当点O '落在AB 的延长线上时，连接CE '，判断四边形OBE C '的形状，并说明理由； ②若8,6AB AD ==，当线段O E ''所在直线与EF 所在直线垂直时，直接写出,A O '两点间的距离．。

太原五中2012—2013学年度第一学期月考(10月)高三地理一、选择题(本题有40个小题，每小题1分，共40 分。

每小题只有1个正确选项，不选、多选、错选均不得分。

答案写在后面的答题纸上)2012年6月16日18时37分我国在酒泉航天发射场用长征二F遥九火箭将搭载有景海鹏、刘旺和我国首位女航天员刘洋的神舟九号飞船送入太空运行轨道。

6月24日11时许，神舟九号飞船与天宫一号分离，12时38分神舟九号飞船在航天员刘旺的操作下与天宫一号顺利实现人工操纵交会对接，12时50分35秒完成人工对接锁紧成一体状态。

根据上述材料回答1～2题。

1．最可能干扰航天器与地面指挥系统通信联系的是（）A．云雾 B．太阳辐射 C．流星 D．太阳活动2．从神舟九号发射到成功实现人工对接的过程中，下列现象正确的是（）A．地中海地区气候温和多雨，河流水位保持着上涨态势B．南极洲的极昼范围逐渐扩大到南极圈附近C．北京地区白昼变化的特点是：昼渐长——昼最长——昼渐短D．天安门广场上的旗杆正午时影子逐渐变短小刚和小明同一天出生在我国的两个不同城市，下表是他们出生那天出生地的日出和日落时刻（北京时间）表。

据此回答3～4题。

为晨昏线，ANB为经线圈的一部分，其中，N为北极点，经线题。

7．下列判读：①AB为晨线②AB为昏线③AB线上各地此时正好日出④AB线上地方时为6时⑤AB线上各地此时的太阳高度为0°。

正确的是（）A．①④⑤ B．①③⑤ C．②③⑤ D．②③④我国某中学建了一座太阳历广场，广场中间是6米高的雕像柱。

一年中大多数日子，正午影子投影朝丙方向，且影长从不超过6米的外圈。

北京时间12：30是一天中雕像柱影子最短的时刻。

据此回答8～9题。

8.该学校可能位于（）A．黑龙江B．湖南C．云南D．广东9.下列说法正确的是（）A．从雕像柱可观测到北极星在丙柱方向附近B．春秋分日太阳从丙丁两柱之间升起C．夏至日，正午雕像柱影子朝向丙柱一侧3米的圈内D．一天中雕像柱的影子不会超过外圈板块构造学说是20世纪最重要的科学成果之一。

山西省太原五中2015届高三10月月考数学理第I 卷一、选择题：(本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一个选项是符合题目要求的.)1. 已知集合{1,16,4}A x =，2{1,}B x =，若B A ⊆，则x = （ ） A.0 B.4- C.0或4- D.0或4±2. 设命题:p 函数xy 1=在定义域上为减函数；命题:q ,(0,)a b ∃∈+∞,当1a b +=时,113a b +=，以下说法正确的是 （ ） A.p ∨q 为真 B.p ∧q 为真 C.p 真q 假D.p ，q 均假3. 函数⎪⎩⎪⎨⎧≤-->+-=)0(32)0(2ln )(22x x x x x x x x f 的零点个数为 （ ）A ．1 个B ．2个C ．3个D ．4个 4. 若2x a =，b =12log c x =，则“a b c >>”是“1x >”的 （ ）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分又不必要条件5. 函数2()sin ln(1)f x x x =⋅+的部分图像可能是 （ ）Ox O yx O yx.Ox .A B C D6. 已知函数⎩⎨⎧<+≥=4)2(42)(x x f x x f x ，则)3log 1(2+f 的值为 ( )A ．6B ．12C ．24D ．36 7. 已知()f x 是定义在(,)-∞+∞上的偶函数，且在区间(,0]-∞上是增函数，设12730.64(l o g ),(l o g ),(0.2)a f b f c f-===,则,,ab c 的大小关系是 ( ) A. c a b << B. c b a << C.b c a << D.a b c <<8. 已知函数()2014sin (01)(),log 1x x f x x x π⎧≤≤⎪=⎨>⎪⎩若c b a 、、互不相等，且)()()(c f b f a f ==，则c b a ++的取值范围是 ( ) A ．（1，2014） B ．（1，2015） C ．（2，2015） D ．[2，2015] 9. 若函数3()()log(01)x ax af x a a -=>≠且在区间1(,0)2-内单调递增，则a 的取值范围是 ( )A. 1[,1)4B. 3[,1)4C. 9[,)4+∞D. 9(,1)4- 10. 设()f x 是定义在R 上的奇函数，且(2)0f =,当0x >时,有'2()()xf x f x x -<0恒成立，则不等式2()0x f x >的解集为 ( )A. (2,0)(2,)-+∞B. (2,0)(0,2)-C. (,2)(2,)-∞-+∞ D. (,2)(0,2)-∞-11. 若(2)y f x =的图像关于直线2a x =和2bx =()b a >对称，则()f x 的一个周期为 ( )A.2a b + B. 2()b a - C. 2b a- D. 4()b a - 12．定义在R 上的函数)(x f y =的图象关于点)0,43(-成中心对称，对任意的实数x 都有)23()(+-=x f x f ，且1)1(=-f ，2)0(-=f ，则(1)(2)(3)f f f +++L(2014)f +的值为 ( )A ．2B ．1C ．－1D ．－2第Ⅱ卷二、填空题：(本大题共4小题，每小题5分，共20分，把答案填写在题中横线上.)13. 已知(2)x y f =的定义域为[－1，1]，则2(log )xy f =的定义域是_________.14. 已知函数161,1()ln ,1x x f x x x +≤⎧=⎨>⎩则方程()f x ax =恰有两个不同的实根时，实数a的取值范围是_______________.15. 已知()x f 为奇函数，当[]2,0∈x 时，x x x f 2)(2+-=；当()+∞∈,2x 时，42)(-=x x f ，若关于x的不等式)()(x f a x f >+有解，则a 的取值范围 为_____________________.16. 已知,m k Z ∈,且方程220mx kx -+=在(0,1)上有两个不同的实数根，则m k +的最小值为__________________.三、解答题:(本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤.) 17．（本题小满分10分）已知命题p ：函数2()log xf x =在(0，＋∞)上单调递增；命题q ：关于x 的方程3222log 0a x x ++=的解集只有一个子集．若q p ∨为真，q p ∧为假，求实数a 的取值范围．18.（本题小满分12分）已知函数||)(a x x f -=.（1）若m x f ≤)(的解集为}51|{≤≤-x x ，求实数m a ,的值;（2）当2=a 且0≥t 时，解关于x 的不等式)2()(t x f t x f +≥+.19.（本题小满12分）已知圆锥曲线⎩⎨⎧==θθsin 22cos 3y x (θ是参数)和定点A )33,0(,21,F F 是圆锥曲线的左、右焦点.(1)求经过点2F 且垂直于直线1AF 的直线l 的参数方程;(2)以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,求直线2AF 的极坐标方程. 20.（本题小满分12分）已知函数2()25(1)f x x ax a =-+>．（1）若函数()f x 的定义域和值域均为[1,]a ，求实数a 的值；（2）若()f x 在区间(],2-∞上是减函数，且对任意的[]12,1,1x x a ∈+，总有12()()4f x f x -≤，求实数a 的取值范围.21.（本题小满分12分）已知函数3)(+=mx x f ，m x x x g ++=2)(2. (1) 求证：函数)()(x g x f -必有零点；(2) 设函数1)()()(--=x g x f x G ，若)(x G 在]0,1[-上是减函数，求实数m 的取值范围． 22．（本小题满分12分） 设函数21()ln .2f x x ax bx =-- (1)当12a b ==时,求函数)(x f 的最大值; (2)令21()()2aF x f x ax bx x=+++(03x <≤)其图象上任意一点00(,)P x y 处切线的斜率21≤k 恒成立,求实数a 的取值范围;(3)当0a =,1b =-,方程22()mf x x =有唯一实数解,求正数m 的值.答案一、选择题：本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的.13. 14.116[,)e15. (2,0)(0,)-+∞ 16. 13三．解答题(本大题共6小题，共70分.) 17．（本题小满分10分）设命题p ：函数2()log ||f x x =在(0，＋∞)上单调递增；q ：关于x 的方程023log 22=++a x x 的解集只有一个子集．若“p∨q”为真，“p∧q”为假，求 实数a 的取值范围．17.解:当命题q 是真命题时，关于x 的方程023log 22=++ax x 无解，所以023log 44<-=∆a ,解得231<<a .或0a ≤或a=1. 由于q p ∨为真，则p 和q 中至少有一个为真；又由于q p ∧为假，则p 和q 中至少有一个为假，所以p 和q 中一真一假，当p 假q 真时，不存在符合条件的实数 a ；p 真q 假时，01a <<或23≥a ,综上所述，实数的取值范围是01a <<或23≥a18. （本题小满分12分）已知函数||)(a x x f -=.（1）若m x f ≤)(的解集为}51|{≤≤-x x ，求实数m a ,的值. （2）当2=a 且0≥t 时，解关于x 的不等式)2()(t x f t x f +≥+. 18.解：（Ⅰ）由|x ﹣a|≤m 得a ﹣m ≤x ≤a+m ，所以解之得为所求．（Ⅱ）当a=2时，f （x ）=|x ﹣2|，所以()(2)|22||2|f x t f x t x t x t +≥+⇒-+--≤ 当t=0时，不等式①恒成立，即x ∈R ； 当t ＞0时，不等式2222(2)x t t x x t <-⎧⇔⎨----≤⎩或22222(2)t x x t x t -≤<⎧⎨-+--≤⎩或222(2)x x t x t≥⎧⎨-+--≤⎩ 解得x ＜2﹣2t 或或x ∈ϕ，即；综上，当t=0时，原不等式的解集为R ， 当t ＞0时，原不等式的解集为．19.（本题小满12分）已知圆锥曲线⎩⎨⎧==θθsin 22cos 3y x (θ是参数)和定点A )33,0(,F 1,F 2是圆锥曲线的左、右焦点.(1)求经过点F 2且垂直于直线AF 1的直线l 的参数方程.(2)以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,求直线AF 2的极坐标方程.19.解：(1)圆锥曲线 ⎩⎨⎧==θθsin 22cos 3y x化为普通方程为18922=+y x ,所以)0,1(),0,1(21F F -, 则直线1AF 的斜率33=k , 于是经过点2F 且垂直于直线1AF 的直线l 的斜率k 1=-,直线l 的倾斜角是0120,所以直线l 的参数方程是⎪⎩⎪⎨⎧=+=0120sin 120cos 1t y t x (t 为参数), 即 为参数）t t y t x (23121⎪⎪⎩⎪⎪⎨⎧=+-=. (2)直线AF 2的斜率33-=k ,倾斜角是0150, 设P(ρ,θ)是直线AF 2上任一点, 则=, 030sin )150sin(=-θρ ,所以直线AF 2的极坐标方程为:1cos sin 3=+θρθρ. 21. （本题小满分12分）已知函数3)(+=mx x f ，m x x x g ++=2)(2. (1) 求证：函数)()(x g x f -必有零点；(2) 设函数1)()()(--=x g x f x G ，若|)(|x G 在]0,1[-上是减函数，求实数m 的取值范围． 20. （本题小满分12分）已知函数2()25(1)f x x ax a =-+>．（1）若函数()f x 的定义域和值域均为[1,]a ，求实数a 的值；（2）若()f x 在区间(],2-∞上是减函数，且对任意的[]12,1,1x x a ∈+，总有12()()4f x f x -≤，求实数a 的取值范围.解（1）2()25f x x ax =-+Q 在(,a]-∞上的减函数，∴2()25f x x ax =-+在[1,]a 上单调递减max ()(1)f x f a ==，min ()(a)1f x f ==∴a=2(2) ()(,2]f x -∞Q 在上是减函数,2a ∴≥()[1,a]f x ∴在上单调递减，在[a,a+1]上单调递增2min ()()5f x f a a ∴==-,{max ()max (1),(1)}f x f f a =+ 2(1)(1)62(6)(2)0f f a a a a a -+=---=-≥ max ()(1)62f x f a ∴==-1212,[1,1],()()4x x a f x f x ∈+-≤Q 对任意的总有 max min ()()4,f x f x ∴-≤≤≤即-1a 32,2a 3a ≥≤≤而故.21. (1) 证明：f(x)－g(x)＝(mx ＋3)－(x 2＋2x ＋m)＝－x 2＋(m －2)x ＋(3－m)．由Δ1＝(m －2)2＋4(3－m)＝m 2－8m ＋16＝(m －4)2≥0，知函数f(x)－g(x)必有零点．(2) 解：|G(x)|＝|－x 2＋(m －2)x ＋(2－m)|＝|x 2－(m －2)x ＋m －2|，Δ2＝(m －2)2－4(m －2)＝(m －2)(m －6)， ① 当Δ2≤0，即2≤m≤6时，|G(x)|＝x 2－(m －2)x ＋(m －2)，若|G(x)|在[－1，0]上是减函数，则m －22≥0，即m≥2，所以2≤m≤6时，符合条件．② 当Δ2＞0，即m ＜2或m ＞6时，若m ＜2，则m －22＜0，要使|G(x)|在[－1，0]上是减函数，则m －22≤－1且G(0)≤0，所以m≤0；若m ＞6，则m －22＞2，要使|G(x)|在[－1，0]上是减函数，则G(0)≥0，所以m ＞6.综上，m ≤0或m≥2. 22．（本小题满分12分） 设函数21()ln .2f x x ax bx =-- (1)当12a b ==时,求函数)(x f 的最大值; (2)令21()()2a F x f x ax bx x =+++(03x <≤)其图象上任意一点00(,)P x y 处切线的斜率k ≤21恒成立,求实数a 的取值范围;(3)当0a =,1b =-,方程22()mf x x =有唯一实数解,求正数m 的值. 22．解：(1)依题意,知()f x 的定义域为(0,)+∞, 当12a b ==时,211()ln 42f x x x x =--, 111(2)(1)()222x x f x x x x-+-'=--= 令()0f x '=,解得 1.(0)x x =>Q因为()0g x =有唯一解,所以2()0g x =,当01x <<时,()0f x '>,此时()f x 单调递增; 当1x >时,()0f x '<,此时()f x 单调递减. 所以()f x 的极大值为3(1)4f =-,此即为最大值 (2)()ln ,(0,3]aF x x x x =+∈,则有00201(),2x a k F x x -'==≤在0(0,3]x ∈上恒成立, ∴a ≥max 020)21(x x +-,]3,0(0∈x 当10=x 时,02021x x +-取得最大值21,所以a ≥21(3)因为方程2)(2x x mf =有唯一实数解,所以22ln 20x m x mx --=有唯一实数解,设2()2ln 2g x x m x mx =--,则2222().x mx mg x x--'=令()0g x '=,20x mx m --=因为0,0,m x >>所以10x =<(舍去),2x =当2(0,)x x ∈时,()0g x '<,()g x 在2(0,)x 上单调递减, 当2(,)x x ∈+∞时,()0g x '>,()g x 在2(,)x +∞上单调递增, 当2x x =时,2()0g x '=,()g x 取最小值2()g x则22()0()0g x g x =⎧⎨'=⎩ 即22222222ln 20x m x mx x mx m ⎧--=⎪⎨--=⎪⎩所以222ln 0,m x mx m +-=因为0,m >所以222ln 10()x x +-=* 设函数()2ln 1h x x x =+-,因为当0x >时,()h x 是增函数, 所以()0h x =至多有一解.∵0)1(=h ,∴方程(*)的解为21x =,1=,解得21=m .。

太 原 五 中2013—2014学年度第一学期月考(12月)高 二 数学（理）一．选择题(本题共10个小题，每小题4分，共40分；在每小题给出的四个选项中，有且只有一项是正确的)1．已知方程11222=-+-k y k x 的图象是双曲线，那么k 的取值范围是（ ）Ａ．k ＜１ Ｂ．k＞２ Ｃ．k ＜１或k ＞２ Ｄ．１＜k ＜２2、已知21,F F 是椭圆)0(12222>>=+b a by a x 的两个焦点，AB 是过1F 的弦，则2ABF ∆的周长是 ( )A.a 2B.a 4C.a 8D.b a 22+ 3、一动圆与圆221x y +=外切，同时与圆226910x y x +--=内切，则动圆 的圆心在（ ）A. 一个椭圆上B.一条抛物线上C.双曲线的一支上D. 一个圆上 4、抛物线y 2=4px （p ＞0）上一点M 到焦点的距离为a ，则M 到y 轴距离为 ( ) A.a - p B.a + p C.a －2pD.a+2p 5. 设椭圆12622=+y x 和双曲线1322=-y x 的公共焦点为21,F F ，P 是两曲线的一个公共点，则cos 21PF F ∠的值等于（ ）A.41 B.31 C.91 D.536. 设F 1、F 2为双曲线1422=-y x 的两个焦点，点P 在双曲线上满足∠F 1PF 2=90°，那么△F 1PF 2的面积是（ ）A ． 1 B.25C. 2D. 5 7. 椭圆()222210x y a a b+=＞b ＞的右焦点为F ，其右准线与x 轴的交点为A ，在椭圆上存在点P 满足线段AP 的垂直平分线过点F ，则椭圆离心率的取值范围是( )A. （0（0，121，1） D. [12，1）8. 已知抛物线y 2=2px （p>0）与双曲线 x 2a - y 2b =1（a>0,b>0）有相同的焦点F ，点A 是两曲线的一个交点，AF ⊥x 轴,若直线L 是双曲线的一条渐近线，则直线L 的倾斜角所在的区间可能为( )A. (0, π6 )B. ( π6 ,π4 )C. ( π4 ,π3 )D. ( π3 ,π2 )9. 抛物线22x y =上两点),(11y x A 、),(22y x B 关于直线mx y +=对称，且2121-=⋅x x ，则m 等于（ ）A ．23 B ．2 C ．25D ．310. 已知椭圆2222:1(0)x y C a b a b +=＞＞F 且斜率为(0)k k ＞的直线与C 相交于A B 、两点．若3AF FB =，则k =( )二．填空题（本题5个小题，共4⨯5=20分）11.已知抛物线y 2=2px(p>0)的准线与圆(x-3)2+ y 2= 16相切，则p 的值为 . 12.已知圆C:(x+1)2+ y 2=16及点A （1，0），Q 为圆C 上一点，AQ 的垂直平分线交C Q 于M则点M 的轨迹方程为 .13. 双曲线116922=-y x 的两个焦点为Ｆ１、Ｆ２，点P 在双曲线上，若ＰＦ１⊥ＰＦ２，则点P 到ｘ轴的距离为 ___________14. 已知椭圆C:x 22 + y 2 =1的两焦点为12,F F , 点00(,)P x y 满足2200012x y <+<,则|1PF |+ 2PF |的取值范围为____ ___ .15. 过双曲线()222210,0x y a b a b-=>>的左焦点且垂直于x 轴的直线与双曲线相交于M 、N两点，以MN 为直径的圆恰好过双曲线的右顶点，则双曲线的离心率等于______.三.解答题（本题4个小题，共4⨯10=40分）16. (10分) 在直角坐标系中，o 为坐标原点，如果一个椭圆经过点P(3, 2 ),且以点F(2,0)为它的一个焦点.（1）求此椭圆的标准方程；（2）在（1）中求过点F(2,0)的弦AB 的中点M 的轨迹方程. 17．已知抛物线y 2= - x 与直线y=k(x+1)交于A 、B 两点. (1) 求证：OA ⊥OB ；（2）当∆AOB 的面积等于10 时，求k 的值.18．已知双曲线2222:1(0,0)x y C a b a b -=>>3x =,(1)求双曲线C 的方程；(2)已知直线0x y m -+=与双曲线C 交于不同的两点A ，B ，且线段AB 的中点在以双曲线C 的实轴长为直径的圆上，求m 的值.19．（10分）在平面直角坐标系xOy 中，点B 与点A （-1,1）关于原点O 对称，P 是动点，且直线AP 与BP 的斜率之积等于13-.（1）求动点P 的轨迹方程；（2）设直线AP 和BP 分别与直线x=3交于点M,N ，问：是否存在点P 使得△PAB 与△PMN 的面积相等？若存在，求出点P 的坐标；若不存在，说明理由.太 原 五 中2013—2014学年度第一学期月考(12月)高二数学参考答案一．选择题CBAAB ADDAB二．填空题（本题5个小题，共4⨯5=20分）11. 2 ； 12. x 24 + y 23 =1 ；13. 165 ； 14. [ 2, 2 2 )；15. 2三.解答题（本题4个小题，共4⨯10=40分） 解：(1)设所求椭圆方程为：x 2a 2 + y2b2 =1,则有：22224921a b ab ìï=+ïïíï+=ïïî 解得：22128a b ìï=ïíï=ïî ， 故所求椭圆方程为：x 212 + y28 = 1----------5分；（2）设A(x 1,y 1)、B(x 2，y 2), M(x,y)则有：221222211281128x yx y ìïï+=ïïïíïïï+=ïïî当x 1≠x 2时， y 1-y 2x 1-x 2 = - 8(x 1+x 2)12(y 1+y 2) = - 23 ⋅ 2x 2y = - 23 ⋅ xy ;又因为k AB = k MF = y-0x-2 , 所以: - 23 ⋅ x y = y-0x-2 ,整理得：2x 2+3y 2-4x=0 ；当x 1=x 2时，中点M(2,0)满足条件总上可知：所求轨迹方程为：2x 2+3y 2-4x=0 -------10分 17.解：(1)由方程组2(1)y x y k x ìï=-ïíï=+ïî得：ky 2+y-k=0 ,令A （x 1,y 1）, B （x 2,y 2）, 由韦达定理得：y 1+ y 2 = - 1k , y 1y 2 = -1∴ OA OB = x 1x 2+ y 1y 2 = (-y 12)( -y 22)+ y 1y 2 = 1-1 = 0 ∴ OA ⊥OB , 即：OA ⊥OB ；--------------4分 （2）设直线与x 轴交于N 点，则N(-1,0) S ∆AOB = S ∆OAN + S ∆OBN = 12 ⎢ON ⎢y 1 + 12 ⎢ON ⎢y 2= 12⎢ON ⎢ y 1- y 2⎢ ∴ S ∆AOB = 12 ⨯1⨯(y 1+y 2)2-4y 1y 2 = 12(- 1k)2+4 = 10∴ k = ± 16 --------------------------------------------1018．解：(1) x 2- y22=1 ---------4分（2）以双曲线实轴长为直径的圆方程为：x 2+y 2= 1, 把y=x+m 代入双曲线方程得： x 2-2mx-m 2-2 = 0, 令A(x 1,y 1), B(x 2,y 2) ,AB 的中点M(x 0,y 0) 则有：221221244(2)022m m x x mx x m ìïD =--->ïïï+=íïïï=--ïî, x 0= x 1+x 22 = m , y 0= y 1+y 22 = x 1+x 22 + m = 2m , 代入圆方程x 2+y 2 = 1中得：m 2= 15 , 所以： m = ± 55.19．（1）解：因为点B 与A (1,1)-关于原点O 对称，所以点B 得坐标为(1,1)-. 设点P 的坐标为(,)x y 由题意得111113y y x x -+=-+- ，化简得：2234(1)x y x +=≠±.故动点P 的轨迹方程为：2234(1)x y x +=≠±-------------4分（2）解法一：设点P 的坐标为00(,)x y ，点M ，N 得坐标分别为(3,)M y ,(3,)N y .则直线AP 的方程为0011(1)1y y x x --=++，直线BP 的方程为0011(1)1y y x x ++=-- 令3x =得000431M y x y x +-=+，000231N y x y x -+=-.于是∆PMN 的面积，2000020||(3)1||(3)2|1|PMNM N x y x Sy y x x +-=--=- 又直线AB 的方程为0x y +=，||AB = 点P 到直线AB的距离d =.于是∆PAB 的面积 001||||2PABS AB d x y ==+ 当PABPMN SS =时，得20000020||(3)|||1|x y x x y x +-+=- 又00||0x y +≠，所以20(3)x -=20|1|x -，解得05|3x =. 因为220034x y +=，所以09y =±故存在点P 使得∆PAB 与∆PMN 的面积相等，此时点P的坐标为5(,3.---10分 解法二：若存在点P 使得PAB 与PMN 的面积相等，设点P 的坐标为00(,)x y则11||||sin ||||sin 22PA PB APB PM PN MPN ∠=∠. 因为sin sin APB MPN ∠=∠, 所以||||||||PA PN PM PB =，所以000|1||3||3||1|x x x x +-=-- 即 2200(3)|1|x x -=-，解得0x 53= 因为220034x y +=，所以0y =故存在点P S 使得PAB 与PMN 的面积相等，此时点P 的坐标为5(,3.。

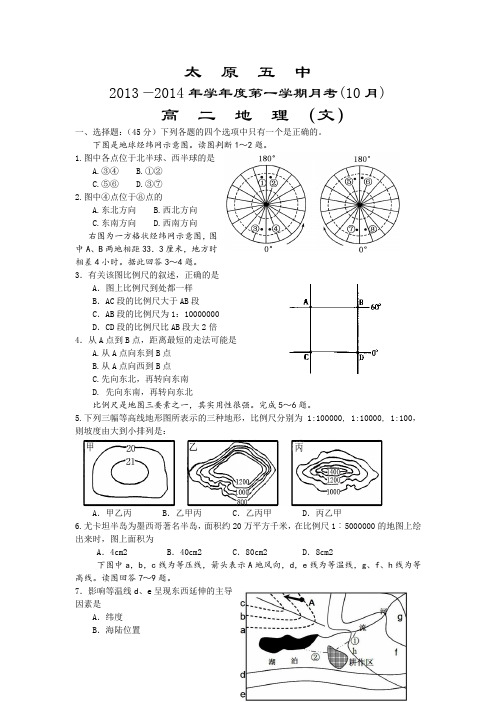
太原五中2013—2014年学年度第一学期月考(10月)高二地理（文）一、选择题：（45分）下列各题的四个选项中只有一个是正确的。

下图是地球经纬网示意图。

读图判断1～2题。

1.图中各点位于北半球、西半球的是A.③④B.①②C.⑤⑥D.③⑦2.图中④点位于⑧点的A.东北方向B.西北方向C.东南方向D.西南方向右图为一方格状经纬网示意图，图中A、B两地相距33．3厘米，地方时相差4小时。

据此回答3～4题。

3．有关该图比例尺的叙述，正确的是A．图上比例尺到处都一样B．AC段的比例尺大于AB段C．AB段的比例尺为1：10000000D．CD段的比例尺比AB段大2倍4．从A点到B点，距离最短的走法可能是A.从A点向东到B点B.从A点向西到B点C.先向东北，再转向东南D. 先向东南，再转向东北比例尺是地图三要素之一，其实用性很强。

完成5～6题。

5.下列三幅等高线地形图所表示的三种地形，比例尺分别为1:100000, 1:10000, 1:100，则坡度由大到小排列是：A．甲乙丙 B．乙甲丙 C．乙丙甲 D．丙乙甲6.尤卡坦半岛为墨西哥著名半岛，面积约20万平方千米，在比例尺1︰5000000的地图上绘出来时，图上面积为A．4cm2 B．40cm2 C．80cm2 D．8cm2下图中a，b，c线为等压线，箭头表示A地风向，d，e线为等温线，g、f、h线为等高线。

读图回答7～9题。

7．影响等温线d、e呈现东西延伸的主导因素是A．纬度B．海陆位置C．地形D．人类活动8．根据图中信息可以推断A．a<cB．从②引水灌溉比①有利C．d>eD．图中湖泊可能为咸水湖9．若此时A地多云，即将迎来的天气变化可能为A．晴朗、气温升高、气压降低B．晴朗、气温降低、气压升高C．阴雨、气温降低、气压升高D．阴雨、气温升高、气压降低读“某大陆沿南回归线地形剖面图示意图”，判断10～11题。

10．图中山脉A的成因是A．由美洲板块和太平洋板块张裂而形成B．由美洲板块和太平洋板块碰撞而形成C．由美洲板块和南极洲板块张裂面形成D．由美洲板块和南极洲板块碰撞而形成11．一轮船从E沿岸的港口出发前往印度的孟买，走最短航线须经A．巴拿马运河B．麦哲伦海峡C．好望角 D．苏伊士运河读下列经纬线示意图,回答12～13题。

山西大学附属中学2024～2025学年第一学期高二10月月考（总第二次）数学试题考试时间：120分钟 满分：150分一、选择题（本小题8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．若直线2:tan 5l x π=的倾斜角为α，则α=（ ）A ．0B ．25πC ．2πD ．不存在 2．已知向量(),2,1a x =− ，()2,4,2b =− ，若a b，则（ ） A ．1−B ．1C ．5−D ．53．已知直线1:2l y x a =−+与直线()22:22l y a x =−+，则“1a =−”是“12l l ”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件4．在空间四边形OABC 中，若E ，F 分别是AB ，BC 的中点，H 是EF 上的点，且13EH EF =，记OH xOA yOB zOC =++，则(),,x y z 等于（ ）A ．111,,326B ．111,,263C ．111,,362D ．111,,2365．如图，在圆锥SO 中，AB 是底面圆O 的直径，2AB SO ==，D ，E 分别为SO ，SB 的中点，点C 是底面圆周上一点（不同于A ，B ）且OC AB ⊥，则直线AD 与直线CE 所成角的余弦值为（ ）ABCD ．126．已知直线l 过点()2,3,1A ，且()1,1,1a =为其一个方向向量，则点()4,3,2P 到直线l 的距离为（ ）ABCD7．已知两点()1,5A −，()0,0B ，若直线:22l y kx k =−+与线段AB 有公共点，则k 的取值范围为（ ） A ．(][),11,−∞−+∞ B ．(][],10,1−∞− C ．[][)1,01,−+∞D ．[]1,1−8．已知点P 和非零实数λ，若两条不同的直线1l ，2l 均过点P ，且斜率之积为λ，则称直线1l ，2l 是一组“P λ共轭线对”，如直线1:2l y x =，21:2l y x =−是一组“1O −共轭线对”，其中O 是坐标原点．已知1l ，2l 是一组“3O −共轭线对”，则1l ，2l 的夹角的最小值为（ ） A ．6πB ．3πC ．4πD ．12π二、选择题（本小题3小题，每小题6分，共18分．在每小题给出的四个选项中，有多项符合题目要求的，全部选对的得6分，部分选对的得部分分，有选错的得0分．）9．下列说法中不正确的是（ ）A ．若直线的倾斜角越大，则直线的斜率就越大B ．若直线过点()1,2，且它的倾斜角为45°，则这条直线必过点()3,4C ．过()11,x y ，()22,x y 两点的直线的方程为112121y y x x y y x x −−=−− D ．直线2y kx =−在在y 轴上的截距为210．在空间直角坐标系Oxyz 中，点()0,0,0O ，()2,1,1A −−，()3,4,5B ，下列结论正确的有（ ） A．AB =B ．向量OA 与OB的夹角的余弦值为C ．点A 关于z 轴的对称点坐标为()2,1,1−−−D ．向量OA 在OB 上的投影向量为110OB −11．如图，在三棱锥P ABC −中，AB BC ==BA BC ⊥，2PAPB PC ===，O 为AC 的中点，点M 是棱BC 上一动点，则下列结论正确的是（ ）A ．三棱锥P ABC −1+B ．若M 为棱BC 的中点，则异面直线PM 与ABC ．若PC 与平面PAM 所成角的正弦值为12，则二面角M PA C −−D ．PM MA +的取值范围为4三、填空题（本题共3小题，每小题5分，共15分．）12．已知点P 在平面ABC 上，点O 是空间内任意一点，且()1322OP OA mOB OC m R =++∈，则m 的值为_______________．13．直线的一个方向向量为()1,3v=−，且经过点()0,2，则直线的一般式方程为_______________.14．在棱长为1的正方体1111ABCD A B C D −中，P 为棱1BB 上一点，且12B P PB =，Q 为正方形11BB C C内一动点（含边界），若1D Q =且1D Q 与平面1A PD 所成的角最大时，线段1AQ 的长度为_______________.四、解答题（本题共5小题，共77分．解答应写出文字说明，证明过程或演算步骤．）15．（本小题满分13分）已知ABC △的顶点坐标分别是()1,5A −，()2,1B −−，()4,3C ，M 为BC 边的中点． （1）求BC 边上的中线AM 的一般式方程； （2）求经过点C 且与直线AB 垂直的直线方程． 16．（本小题满分15分）已知()2,1,2a =−，()4,2,b x =− ，且a b ⊥．（1）求a b +；（2）求a 与a b +夹角的余弦值．17．（本小题满分15分）已知直线():120l kx y kk −++=∈R （1）若直线l 不经过第四象限，求k 的取值范围；（2）若直线l 交x 轴负半轴于点A ，交y 轴正半轴于点B ，O 为坐标原点，设AOB △的面积为S ，求S 的最小值及此时直线l 的方程． 18．（本小题满分17分）已知在四棱锥P ABCD −中，底面ABCD 是边长为4的正方形，PAD △是正三角形，点E ，F ，M ，O 分别是PC ，PD ，BC ，AD 的中点，PO ⊥平面ABCD ． （1）求证：EF PA ⊥；（2）求点B 到平面EFM 的距离；（3）在线段PA 上是否存在点N ，使得直线MN 与平面EFM PN 的长度；若不存在，说明理由．19．（本小题满分17分）已知Ω的正四面体ABCD ，设Ω的四个顶点到平面α的距离所构成的集合为M ，若M 中元素的个数为k ，则称α为Ω的k 阶等距平面，M 为Ω的k 阶等距集．（1）若α为Ω的1阶等距平面且1阶等距集为{}a ，求a 的所有可能值以及相应的α的个数；（2）已知β为Ω的4阶等距平面，且点A 与点B ，C ，D 分别位于β的两侧．是否存在β，使Ω的4阶等距集为{},2,3,4b b b b ，其中点A 到β的距离为b ？若存在，求平面BCD 与β夹角的余弦值；若不存在，说明理由．山西大学附中2024～2025学年第一学期高一（10月）月考（总第一次）数学评分细则一．选择题：1234567891011A DBAABCDABCBDABD三．填空题：本题共3小题，每小题4分，共12分。

山西省太原五中2013-2014学年高二下学期期中（生物）理试题试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，请将答案填写在答题卡上。

满分100分。

时间90分钟。

一、单项选择题：(本题共40分，每小题1分)1．下列关于植物组织培养的叙述中，错误的是A．培养基中添加蔗糖的目的是提供营养和调节渗透压B．培养中的生长素和细胞分裂素影响愈伤组织的生长和分化C．离体器官或组织的细胞都必须通过脱分化才能形成愈伤组织D．同一株绿色开花植物不同部位的细胞经培养获得的愈伤组织基因相同2．菊花的花粉经组织培养可发育成一株幼苗，这一过程不涉及下列哪一项A．有丝分裂、细胞分化、组织器官的形成B．呼吸作用、光合作用、相关激素的调控C．DNA的复制、转录、蛋白质的生物合成D．等位基因的分离、非等位基因的自由组合3．科学家将月季花的花药进行离体培养获得了许多完整幼小植株，下列说法正确的是A．细胞内染色体数量高度一致B．需要进一步鉴定和筛选C．彼此性状极其相似D．都是纯合体4.下列有关植物组织培养的叙述，正确的是A．愈伤组织是一团有特定结构和功能的薄壁细胞B．二倍体植株的花粉经脱分化与再分化后得到稳定遗传的植株C．用人工薄膜将胚状体、愈伤组织等分别包装可制成人工种子D．植物耐盐突变体可通过添加适量NaCl的培养基培养筛选而获得5．在采用鸡血为材料对DNA进行粗提取的实验中，若需进一步提取杂质较少的DNA，可以依据的原理是A．在物质的量浓度为0．14 mol／L的氯化钠溶液中DNA的溶解度最小B．DNA遇二苯胺在沸水浴的条件下会染成蓝色C．DNA不溶于酒精而细胞中的一些物质易溶于酒精D．质量浓度为0．1g／mL的柠檬酸钠溶液具有抗凝血作用6．蒸馏时要提高产品质量，应采取的措施是A．提高蒸馏温度，延长蒸馏时间 B．提高蒸馏温度，缩短蒸馏时间C．降低蒸馏温度，缩短蒸馏时间 D．严控蒸馏温度，延长蒸馏时间7．不同生物之间能进行转基因并能获得基因产物，其理论依据有①这些生物的基因结构都是相同的②组成这些生物的DNA分子都遵循碱基互补配对原则③这些生物在基因表达时共用一套遗传密码子④组成这些生物的DNA分子的空间结构和化学成分一致A.①②③B.②③④C.①③④D.①②④8．在基因工程中，作为基因运输工具的运载体，不是必须具备的条件有A．能够在宿主细胞中复制，并稳定地保存 B．具有多个限制酶切点C．必须是细菌的质粒或噬菌体 D．具有某些标记基因9．如右图，有关工具酶功能的叙述错误的是A．限制性内切酶可切断a处B．DNA聚合酶可连接a处C．解旋酶可使b处解开D．DNA连接酶可以连接c处10．下列关于基因文库的说法中，不正确的是A．某果蝇X染色体上的所有基因组成的文库是部分基因文库B．cDNA文库中的基因可以在不同物种间进行交流C．可以根据基因的碱基序列、基因的功能、基因在染色体上的位置、基因的转录产物mRNA，以及基因的表达产物蛋白质等特性来获取目的基因D．取果蝇某细胞中全部mRNA，通过反转录产生DNA片段为该果蝇的基因组文库11．基因工程中，不需进行碱基互补配对的步骤有A．人工合成目的基因B．目的基因与运载体相结合C．将目的基因导入受体细胞D．目的基因的检测与表达12．下图依次为四种限制酶BamHI, EcoRI, HindIII以及BglII的辨识序列，箭头表示每种限制酶的特定切割部位，其中哪两种限制酶所切割出来的DNA片段末端可以互补黏合A．BamHI和EcoRI, B．BamHI和HindIIIC．BamHI和Bgl II D．EcoRI,和HindIII13．蛋白质工程的基本流程是①蛋白质分子结构设计②DNA合成③预期蛋白质功能④据氨基酸序列推出脱氧核苷酸序列A.①②③④B.④②①③C.③①④②D.③④①②14．采用基因工程技术将人凝血因子基因导入山羊受精卵，培育出了转基因羊。

太原五中2015-2016学年度第二学期阶段性检测高 二 数 学(理)出题人、校对人：雷英俊 廉海栋（2016.5）一、选择题（每小题4分,共40分,每小题只有一个正确答案）1.已知随机变量X 服从二项分布，且E(X)＝2.4，D(X)＝1.44，则二项分布的参数n ，p 的值为( )A ．n ＝4，p ＝0.6B ．n ＝6，p ＝0.4C ．n ＝8，p ＝0.3D ．n ＝24，p ＝0.12.已知离散型随机变量X 等可能取值1,2,3，…，n ，若P(1≤X ≤3)＝15，则n 的值为( )A ．3B ．5C ．10D ．153.已知随机变量ξ服从正态分布N(2，σ2)．且P(ξ<4)＝0.8，则P(0<ξ<2)等于( )A ．0.6B ．0.4C ．0.3D ．0.24. 53()y x 展开式的第三项为10,则y 关于x 的函数图象大致为( )5.10件产品，其中3件是次品，任取2件，若ξ表示取到次品的个数，则E(ξ)等于( )A.35B.815C.1415D ．1 6.6把椅子摆成一排,3人随机就座,任何两人不相邻的坐法种数为A ．144B ．120C ．72D ．247.在所有的两位数中，个位数字大于十位数字的两位数共有( )个A ．50B ．45C ．36D ．358.如图，花坛内有5个花池，有5种不同颜色的花卉可供栽种，每个花池内只能种一种颜色的花卉，相邻两池的花色不同，则栽种方案的种数为( )A ．180B ．240C ．360D ．4209.将三颗骰子各掷一次，记事件A ＝“三个点数都不同”， B ＝“至少出现一个６点”，则条件概率()P A B ，()P B A 分别是（ ）A.6091，12 B.12，6091C.518，6091D.91216，12 10.从正方体六个面的对角线中任取两条作为一对，其中所成的角为60°的共有( )A ．24对B ．30对C ．48对D ．60对二、填空题（每小题分，共12分）11. 如果将甲、乙、丙3名志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在乙、丙的前面,则不同的安排方法共有 种 12. 三元一次方程x+y+z=13的非负整数解的个数有_____ 13. n ∈N *,0n C +31n C +…+(2n+1)nn C =_______14.设一次试验成功的概率为p ，进行100次独立重复试验，当p=______时成功的次数 的标准差最大为_______. 三、解答题（共48分） 15.（8分）已知()14142210721x a x a x a a x x ++++=+- .求（1）14210a a a a ++++ .（2）13531a a a a ++++16. (10分)(1)3人坐在有八个座位的一排上，若每人的左右两边都要有空位，则不同坐法的种数有多少种？(2)有5个人并排站成一排，如果甲必须在乙的右边，则不同的排法有多少种？(3)现有10个保送上大学的名额，分配给7所学校，每校至少有一个名额，问：名额分配的方法共有多少种？17.（10分）甲、乙两个篮球运动员互不影响地在同一位置投球，命中率分别为12与p ，且乙投球2次均未命中的概率为116． （Ⅰ）求乙投球的命中率p ；（Ⅱ）求甲投球2次，至少命中1次的概率；（Ⅲ）若甲、乙两人各投球2次，求两人共命中2次的概率．18.（10分）甲、乙两支排球队进行比赛，约定先胜3局者获得比赛的胜利，比赛随即结束．除第五局甲队获胜的概率是12外，其余每局比赛甲队获胜的概率都是23.假设各局比赛结果相互独立．(1)分别求甲队以3∶0, 3∶1, 3∶2胜利的概率；(2)若比赛结果为3∶0或3∶1，则胜利方得3分，对方得0分；若比赛结果为 3∶2，则胜利方得2分，对方得1分．求乙队得分X 的分布列及数学期望． 19.（10分）袋子A 和B 中装有若干个均匀的红球和白球，从A 中摸出一个红球的概率是31，从B 中摸出一个红球的概率为p ．(Ⅰ) 从A 中有放回地摸球，每次摸出一个，有3次摸到红球即停止． (i)求恰好摸5次停止的概率；(ii)记5次之内(含5次)摸到红球的次数为ξ，求随机变量ξ的分布列及数学期望E ξ． (Ⅱ) 若A 、B 两个袋子中的球数之比为1:2，将A 、B 中的球装在一起后，从中摸 出一个红球的概率是25，求p 的值．17.【答案】（Ⅰ）乙投球的命中率为4． （Ⅱ）甲投球2次至少命中1次的概率为34.（Ⅲ）甲、乙两人各投两次，共命中2次的概率为1132． 18.解析： (1)记“甲队以3∶0胜利”为事件A 1，“甲队以3∶1胜利”为事件A 2，“甲队以3∶2胜利”为事件A 3，由题意知，各局比赛结果相互独立， 故P (A 1)＝⎝⎛⎭⎫233＝827，P (A 2)＝C 23⎝⎛⎭⎫232⎝⎛⎭⎫1－23×23＝827，P (A 3)＝C 24⎝⎛⎭⎫232⎝⎛⎭⎫1－232×12＝427. 所以甲队以3∶0胜利、以3∶1胜利的概率都为827，以3∶2胜利的概率为427.(2)设“乙队以3∶2胜利”为事件A 4， 由题意知，各局比赛结果相互独立，所以P (A 4)＝C 24⎝⎛⎭⎫1－232⎝⎛⎭⎫232×⎝⎛⎭⎫1－12＝427. 由题意知，随机变量X 的所有可能的取值为0,1,2,3， 根据事件的互斥性得P (X ＝0)＝P (A 1＋A 2)＝P (A 1)＋P (A 2)＝1627.又P (X ＝1)＝P (A 3)＝427，P (X ＝2)＝P (A 4)＝427，P (X ＝3)＝1－P (X ＝0)－P (X ＝1)－P (X ＝2)＝327，故X 的分布列为X 0 1 2 3 P1627427427327所以E (X )＝0×1627＋1×427＋2×427＋3×327＝79.19.袋子A 和B 中装有若干个均匀的红球和白球，从A 中摸出一个红球的概率是31，从B中摸出一个红球的概率为（1）随机变量的分布列为 0123P其数学期望为（2）解析试题分析：解：（1）①恰好摸5次停止的概率为（2）②随机变量的可能取值为0，1，2，3.；；；所以，随机变量的分布列为0 1 2 3P故随机变量的数学期望为（10）（2）设袋子A中有m个球，则袋子B中有2m个球，由题意得，解得（14）。

太原五中2013—2014学年度第二学期期中高二化学（理）可能用到的相对原子质量：H 1 C 12 Cl 35.5 Cu 64 Zn 65第Ⅰ卷（客观题共40分）（每题2分，，共40分。

每题只有一个正确选项。

）1．以下表示氦原子结构的化学用语中，对电子运动状态描述最详尽的是A．He： B． C．1s2 D．2．铋（Bi）在医药方面有重要应用。

下列关于20983Bi和21083Bi的说法正确的是A．20983Bi和21083Bi都含有83个中子B．20983Bi和21083Bi互为同位素C．20983Bi和21083Bi的核外电子数不同D．20983Bi和21083Bi分别含有126和127个质子3．金属的下列性质和金属晶体结构无关的是A．良好的导电性 B．良好的延展性 C．反应中易失电子 D．良好的导热性4．关于硫原子核外电子的叙述错误的是A．排布在K、L、M三个电子层上 B．3p能级上有2个空轨道C．共有16种不同的运动状态 D．共有5种不同的能级5．下列事实与氢键有关的是A．水结成冰体积膨胀B．水加热到很高的温度都难以分解C．CH4、SiH4、GeH4、SnH4熔点随相对分子质量增大而升高D．HF、HCl、HBr、HI的热稳定性依次减弱6．具有下列电子排布式的原子中，半径最小的是A．ls22s22p63s23p3 B．1s22s22p3 C．1s22s22p2 D．1s22s22p63s23p4 7．下列各组中的两种固态物质熔化或升华时，克服的微粒间相互作用力属于同种类型的是A．碘和氯化钾 B．金刚石和冰晶石 C．二氧化硅和干冰 D．冰和冰醋酸8．下列物质中同时具有离子键、共价键和配位键的是A．H3O+ B．NaOH C．NH4Cl D．H2SO49．下列物质分子中，既含有极性键又含有非极性键的非极性分子是A．C2H4 B．Br2 C．Na2O2 D．CH3COOH10．下列有关分子中指定原子的杂化类型正确的是A．CH4分子中C原子：sp B．BF3中B原子：sp3C．C2H2中C原子：sp D．SiO2中Si原子：sp211．向盛有硫酸铜水溶液的试管里加入氨水，首先生成难溶物，继续添加氨水，难溶物溶解得到深蓝色的透明溶液。

2023~2024学年山西省高二10月联合考试数学（答案在最后）注意事项：1.答题前，考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3.考试结束后，将本试卷和答题卡一并交回。

4.本试卷主要考试内容：人教A 版选择性必修第一册第一章至第二章2.2。

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.在空间直角坐标系中，点()7,9,5A 关于xOy 平面对称的点的坐标为A.()7,9,5- B.()7,9,5- C.()7,9,5- D.()7,9,5---2.直线l 320y -+=的倾斜角为A.150︒B.120︒C.60︒D.30︒3.已知向量(),2,3a x = ，()3,4,3b =-- ，若()a b a +⊥，则x =A.4- B.4C.4-或1D.4或1-4.已知点()1,4A ，()3,2B -，则经过线段AB 的中点，且与直线290x y -+=平行的直线的方程为A.280x y --= B.20x y -=C.2100x y +-= D.250x y +-=5.若直线l ：0Ax By C ++=的倾斜角为α，则“0A B ⋅<”是“α不是钝角”的A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件6.已知点()1,2A ，(),B a b ，(),C c d ，若A 是直线1l ：10ax by ++=和2l ：10cx dy ++=的公共点，则直线BC 的方程为A.210x y +-= B.210x y ++=C.210x y +-= D.210x y ++=7.如图，将菱形纸片ABCD 沿对角线AC 折成直二面角，E ，F 分别为AD ，BC 的中点，O 是AC 的中点，23ABC π∠=，则折后平面OEF 与平面ABC 的夹角的余弦值为A.31111 B.1111 C.31313D.2178.正方体1111ABCD A B C D -的棱长为2，P 是空间内的动点，且1PB PD += ，则AP PB ⋅的最小值为A.1-B.1C.4-+D.4--二、选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.9.如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，底面ABCD 为矩形，E ，F 分别为PB ，PD 的中点，则A.BF 在AD 方向上的投影向是为12ADB.EF 在AD 方向上的投影向还为ADC.CE 在AB 方向上的投影向是为12AB-D.CF 在AB方向上的投影向是为AB- 10.经过点()6,3P -，且在两坐标轴上的截距相等的直线的方程可能为A.20x y += B.90x y --=C.30x y +-= D.2150x y --=11.直线1l ：y ax b =+与2l ：y bx a =+在同一平面直角坐标系内的位置可能是A. B. C. D.12.已知正方体1111ABCD A B C D-的棱长为2，P是正方体1111ABCD A B C D-所在空间内一点，下列结论正确的是A.若()1014AP AB ADλλ=+，则1B P PD+B.若()()101AP AB ADλλλ=+-，则平面1PAD截正方体1111ABCD A B C D-所得截面积的最大值为C.若112AP AD=，则三棱锥P ABC-的表面积为2D.若()101AP ADλλ=，则直线1C D与BP所成角的最小值为45︒三、填空题：本题共4小题，每小题5分，共20分.13.已知点()3,2,3A，()1,1,4B，()2,0,1C，则AB AC⋅=______.14.已知直线l：310x y+-=的倾斜角为α，则cosα=______.15.如图，已知二面角A EF D--的平面角大小为3π，四边形ABFE，EDCF均是边长为4的正方形，则BD=______.16.某公园的示意图为如图所示的六边形ABCDEF，其中AB AF⊥，AF BC∥，AB DE∥，BCD AFE∠∠=，且3tan4BCD∠=-，50CD EF==米，80BC DE==米.若计划在该公园内建一个有一条边在AB上的矩形娱乐健身区域，则该娱乐健身区域面积（单位：平方米）的最大值为______.四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17.（10分）已知直线l ：210ax y a -++=经过第一、二、四象限.（1）求a 的取值范围；（2）若直线1l ：()37230a x y +-+=与直线l 垂直，求a 的值.18.（12分）《九章算术》中将四个面都为直角三角形的四面体称为鳖臑.如图，在鳖臑P ABC -中，PA ⊥平面PBC ，BC ⊥平面PAB ，D 为PC 的中点，2BE EA =.（1）设PA a = ，PB b = ，BC c = ，用a ，b ，c表示DE ；（2）若1PA PB BC === ，求AC DE ⋅.19.（12分）已知直线l ：()()22150a x a y ++-+=.（1）证明无论a 为何值，直线l 经过定点P ，并求出点P 的坐标；（2）若斜率大于0，且经过（1）中点P 的直线与x 轴，y 轴分别交于A ，B 两点，O 为坐标原点，求OAB △面积的最小值.20.（12分）如图，在直四棱柱1111ABCD A B C D -中，底面ABCD 是菱形，且60BAD ∠=︒，E ，F ，G 分别为11B C ，AC ，1A C 的中点，12AA AB ==.（1）求直线1D F 与EG 所成角的余弦值；（2）求点1D 到平面EFG 的距离.21.（12分）已知ABC △的三个顶点是()1,1A ，()3,3B ，()2,8C .（1）过点B 的直线1l 与边AC 相交于点D ，若BCD △的面积是ABD △面积的3倍，求直线1l 的方程；（2）求BAC ∠的角平分线所在直线2l 的方程.22.（12分）如图，在四棱锥P ABCD -中，底面ABCD 是正方形，2AB =，5PA PD ==，E 为BC 的中点.（1）证明：AD PE ⊥.（2）若二面角P AD B --的平面角为23π，G 是线段PC 上的一个动点，求直线DG 与平面PAB 所成角的最大值.2023~2024学年山西省高二10月联合考试数学参考答案1.A 点()7,9,5A 关于xOy 平面对称的点的坐标为()7,9,5-.2.D设l 的倾斜角为α，则tan 3α=.因为0180α︒︒< ，所以30α=︒.3.C 因为()a b a +⊥ ，所以22133170a a b x x +⋅=++-= ，解得4x =-或1.4.B 线段AB 中点的坐标为()2,1，过点()2,1且与直线290x y -+=平行的直线的方程为20x y -=.5.A 若0A B ⋅<，则l 的斜率0AB->，则α不是钝角.若0α=︒或90α=︒，则0A B ⋅=.故“0A B ⋅<”是“α不是钝角”的充分不必要条件.6.B 由点()1,2A 在1l ：10ax by ++=上可知，210a b ++=，同理210c d ++=，故点(),B a b 与(),C c d 均满足方程210x y ++=，因此直线BC 的方程为210x y ++=.7.D以O 为原点，OB ，OC ，OD 所在的直线分别为x 轴、y 轴、z 轴，AB 为两个单位长度，建立如图所示的空间直角坐标系，则()0,0,1D，10,,22E ⎛⎫- ⎪ ⎪⎝⎭，1,,022F ⎛⎫ ⎪ ⎪⎝⎭，10,,22OE ⎛⎫=- ⎪ ⎪⎝⎭，1,22OF ⎛⎫= ⎪ ⎪⎝⎭.设平面OEF 的法向量为(),,n x y z = ，则0,0,n OE n OF ⎧⋅=⎪⎨⋅=⎪⎩得10,2210,22y z x y ⎧-+=⎪⎪⎨⎪+=⎪⎩，取1y =，则x =，z =，得平面OEF的一个法向量为(n =，易得平面ABC 的一个法向量为()0,0,1OD =，所以平面OEF 与平面ABC的夹角的余弦值为7n OD n OD⋅= .8.D 取1BD 的中点M ，连接PM （图略），则12PB PD PM +=，则12PB PD PM +==，即PM =，故动点P 的轨迹为以M为球心，.由正方体1111ABCD A B C D -的棱长为2，可知正方体1111ABCD A B C D -即动点P 的轨迹为正方体1111ABCD A B C D -的外接球.取AB 的中点N ，连接PN （图略），则()()()()2221AP PB PN NA PN NB PN NA PN NA NA PN PN ⋅=-+⋅+=-+⋅-=-=- .由题可知，MN =PN，255PN -+则2414PN ----+ 9.ACD 由图可知，BF 在AD 方向上的投影向量为12AD ，EF 在AD 方向上的投影向量为12AD ，CE在AB 方向上的投影向量为12AB -，CF 在AB 方向上的投影向量为AB - .故选ACD.10.AC 若直线在两坐标轴上的截距均为0，则直线的方程为20x y +=，A 正确.若直线在两坐标轴上的截距不为0，可设直线的方程为1x ya a+=，将()6,3P -代入方程得3a =，则直线的方程为30x y +-=，C 正确.11.BC对于A 选项，两条直线的斜率和截距均大于0，且其中一条直线的斜率和截距均大于另一条直线的斜率和截距，不符合题意，A 不正确.对于B 选项，当0ab <时，符合题意，B 正确.对于C 选项，当0,0a b =⎧⎨<⎩或0,a b <⎧⎨=⎩时，符合题意，C 正确.对于D 选项，其中一条直线斜率不存在，不符合题意，D 不正确.12.ABD 对于A 选项，在AB 上取点H （图略），使得14AH AB =，在CD 上取点K ，使得14DK DC = ，则由14AP AB AD λ=+ ，得AP AH AD λ-= ，即HP AD λ=，故P 是线段HK 上一点.将平面11HKC B 沿HK 展开至与平面AHKD 共面，此时113AB AH B H =+=，当1B ，P ，D 三点共线时，1B P PD +A 正确.对于B 选项，由()()101AP AB AD λλλ=+-，可知P 是线段BD 上一点.连接AC 并与BD 交于点Z （图略）.当P 与D 重合时，平面1PAD 与平面11ADD A 重合，不符合题意.当P 在线段DZ （不含点D ）上时，平面1PAD 截正方体1111ABCD A B C D -所得截面为三角形，且当P 与Z重合时，截面面积最大，最大值为当P 在线段BZ （不含点B ，Z ）上时，延长AP 并与BC 交于点W ，作1WR AD ∥并与1CC 交于点R ，则截面为等腰梯形1AWRD ，设BW x =，则1AW D R ==)2WR x =-.梯形1AWRD 的高h =，面积为()(14122x AD WR h -+⋅=<.当P 与B 重合时，截面为矩形11ABC D ，面积为.故平面1PAD 截正方体1111ABCD A B CD -所得截面积的最大值为，B 正确.对于C 选项，因为112AP AD =，所以P 为1AD 的中点，三棱锥P ABC -的表面积为1111222222222⨯⨯+⨯⨯⨯⨯+，C 不正确.对于D 选项，以1A 为坐标原点，建立如图所示的空间直角坐标系，则()12,2,0C ，()0,2,2D ，()2,0,2B ，()0,2,22P λλ-，则()12,0,2C D =- ，()2,2,2BP λλ=--，111cos ,C D BP C D BP C D BP ⋅==因为01λ，所以202，所以直线1C D 与BP 所成角的最小值为45︒，D 正确.13.2因为()3,2,3A ，()1,1,4B ，()2,0,1C ，所以()2,1,1AB =-- ，()1,2,2AC =--- ，2AB AC ⋅=.14.10-由题可知tan 3α=-，因为[)0,απ∈，所以cos 10α=-.15.因为BD BF FC CD=++ ，所以()22222222BD BF FC CDBF FC CD BF FC BF CD FC CD =++=+⋅+++⋅+⋅ .又二面角A EF D --的平面角大小为3π，四边形ABFE ，EDCF 均为边长为4的正方形，所以22216BF FC CD === ，14482BF FC ⎛⎫⋅=⨯⨯-=- ⎪⎝⎭，0BF CD FC CD ⋅=⋅= ，所以232BD =，则BD =.16.338003以AF 所在直线为x 轴，DE 所在直线为y 轴建立平面直角坐标系，娱乐健身区域为矩形PQMN .由题可知，直线EF 的方程为3304y x =-+，直线CD 的方程为31104y x =+.设3,304P a a ⎛⎫-+ ⎪⎝⎭，其中040a ，则3,1104Q a a ⎛⎫+ ⎪⎝⎭，3120,304N a ⎛⎫-+ ⎪⎝⎭，则3802PQ a =+，120PN a =-，四边形PQMN 的面积()23310033800801202233S PQ PN a a a ⎛⎫⎛⎫==+-=--+⎪⎝⎭⎝⎭.当1003a =时，S 取得最大值338003.17.解：（1）将直线l 的方程转化为21y ax a =++.因为l 经过第一、二、四象限，所以0,210,a a <⎧⎨+>⎩解得102a -<<，即a 的取值范围为1,02⎛⎫- ⎪⎝⎭（2）将直线1l 的方程转化为37322a y x +=+，因为1l l ⊥，所以()3712a a +=-解得2a =-或13a =-.又102a -<<，所以13a =-.18.解：（1）连接BD ，PE （图略）.DE PE PD PA AE PB BD=-=+--因为D 为PC 的中点，2BE EA = ，所以1111111,3332222AE AB PB PA BD BP BC PB BC==-=+=-+所以211211362362DE PA PB BC c =--=-- .（2）因为AC AP PB BC PA PB BC =++=-++，所以()211362AC DE PA PB BC PA PB ⎛⎫⋅=-++⋅-- ⎪⎝⎭222211572362663PA PB BC PA PB PA BC PB BC =---+⋅+⋅-⋅.因为PA ⊥平面PBC ，BC ⊥平面PAB ，所以PA PB ⊥，PA BC ⊥，PB BC ⊥.又1PA PB BC === ，所以22221157243626633PA PB BC PA PB PA BC PB BC ---+⋅+⋅-⋅=- ，即43AC DE ⋅=- .19.（1）证明：将直线l 的方程转化为()2250x y a x y ++-+=，令20, 250,x y x y +=⎧⎨-+=⎩，解得2,1,x y =-⎧⎨=⎩，故无论a 为何值，直线l 经过定点P ，且点P 的坐标为()2,1-.（2）解：依题意可设该直线的方程为()12y k x -=+，0k >令0y =，得12,0A k ⎛⎫-- ⎪⎝⎭，令0x =，得()0,21B k +，则OAB △的面积()1112112224222k S OA OB k k k k+==⋅⋅+=++ ，当且仅当12k =时，等号成立，故OAB △面积的最小值为4.20.解：（1）连接BD ，因为底面ABCD 是菱形，所以AC BD⊥因为F ，G 分别为AC ，1A C 的中点，所以1FG AA ∥，则FG ⊥平面ABCD .以F 为坐标原点，FA ，FB ，FG 所在直线分别为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系.由60BAD ∠=︒，12AA AB ==，得()0,0,0F ，()10,1,2D -，()0,0,1G，1,,222E ⎛⎫- ⎪ ⎪⎝⎭，则()10,1,2D F =-，1,,122GE ⎛⎫=- ⎪ ⎪⎝⎭.111122cos ,20D F GE D F GE D F GE-⋅==-，故直线1D F 与EG所成角的余弦值为20.（2）由（1）知()0,0,1FG = .设平面EFG 的法向量为()000,,m x y z =，则000010,220,x y z z ⎧-++=⎪⎨⎪=⎩令01x =，得()m =.点1D 到平面EFG 的距离为132D F m m⋅=.21.解：（1）设()00,D x y ，则()001,1AD x y =-- ，()002,8DC x y =--因为BCD △的面积是ABD △面积的3倍，所以3DC AD = 则()()0000231,831,x x y y -=-⎧⎪⎨-=-⎪⎩解得005,411,4x y ⎧=⎪⎪⎨⎪=⎪⎩故直线1l 的方程为()113433534y x --=--，即7180x y -+=.（2）显然，2l 的斜率存在且不为零，设2l 的方程为()11y k x -=-，则过点B 且与2l 垂直的直线l 的方程为()133y x k-=--.设点B 关于直线l 对称的点为()111,33B x x k ⎛⎫-- ⎪⎝⎭'，因为直线AC 的方程为760x y --=，所以()()1111173360,1333311,22x x kx x k k ⎧-+--=⎪⎪⎨+--⎪+⎛⎫-=-⎪⎪⎝⎭⎩整理得322320k k k --=.因为0k ≠，所以22320k k --=，解得2k =或12k =-.又70AC k =>，10AB k =>，所以0k >，故直线2l 的方程为()121y x -=-，即210x y --=.22.（1）证明：如图，取AD 的中点F ，连接PF ，EF .∵底面ABCD 是正方形，PA PD =，∴AD EF ⊥，AD PF ⊥，∵EF PF F = ，EF ，PF ⊂平面PE ，∴AD ⊥平面PEF 又∵PE ⊂平面PEF ，∴AD PE⊥（2）解：如图，由（1）可知，二面角P AD B --的平面角为PFE ∠，且23PFE π∠=，过点P 作PO 垂直于直线EF ，垂足为O .以O 为原点，OE ，OP 所在的直线分别为y 轴、z 轴，建立如图所示的空间直角坐标系.易得3PFO π∠=，2PF =，1OF =，PO =，则(P ，()1,1,0A ，()1,3,0B ，()1,3,0C -，()1,1,0D -，(1,1,PA = ，()0,2,0AB =，(1,DP =-，(1,3,PC =- 设平面PAB 的法向量为(),,n x y z = ，则0,0,n PA n AB ⎧⋅=⎪⎨⋅=⎪⎩得0,20,x y y ⎧+=⎪⎨=⎪⎩取1z =，则)n =设(),3,PG PC λλλ==- ，[]0,1λ∈，则()1,3DG DP PG λλ=+=--设直线DG 与平面PAB 所成的角为θ，则sin cos ,DG nDG n DG nθ--⋅===.令1t λ=-，则[]0,1t ∈，sin θ-==.当0t =时，sin 0θ=，0θ=；当0t≠时，sin θ==。

山西省高二数学上学期10月联合考试试题理（含解析）考生注意：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分．考试时间120分钟． 2．请将各题答案填写在答题卡上．3．本试卷主要考试内容：人教A 版立体几何、空间向量．第Ⅰ卷一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知空间向量()1,0,1=a ，()1,1,n =b ，且3⋅=a b ，则向量a 与b 的夹角为() A.π6B.π3C.π3或2π3D.π6或5π6【答案】A 【解析】 【分析】由数量积的坐标求法，可得n 的值，再利用向量的夹角公式即可求解. 【详解】∵13n ⋅=+=a b ，∴2n =，又2a =，()1,1,2=b ，∴cos ,22⋅===⨯a b a b a b．又[],0,π∈a b ，∴向量a 与b 的夹角为π6．【点睛】设向量()()111222,,,,,x y z x y z ==a b ， 则 112121221,cos x x y y z z ,x y ⋅⋅=++〈〉=+a b a b a b =a b..2.下列说法中正确的是() A. 圆锥的轴截面是等边三角形B. 用一个平面去截棱锥，一定会得到一个棱锥和一个棱台C. 将一个等腰梯形绕着它的较长的底边所在的直线旋转一周，所围成的几何体是由一个圆台和两个圆锥组合而成D. 有两个面平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行的几何【答案】D 【解析】 【分析】根据圆锥的结构特征即可判断A 选项；根据棱台的定义即可判断选项B;结合圆柱、圆锥、圆台的旋转特征，举出反例即可判断选项C ；由棱柱的定义即可判断选项D.【详解】圆锥的轴截面是两腰等于母线长的等腰三角形，A 错误；只有用一个平行于底面的平面去截棱锥，才能得到一个棱锥和一个棱台，B 错误；等腰梯形绕着它的较长的底边所在的直线旋转一周的几何体，是由一个圆柱和两个圆锥组合而成，故C 错误；由棱柱的定义得，有两个面平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱，故D 正确．【点睛】解决空间几何体结构特征问题的3个策略 (1)把握几何体的结构特征，提高空间想象力． (2)构建几何模型、变换模型中的线面关系． (3)通过反例对结构特征进行辨析．3.已知圆柱的轴截面为正方形，且圆柱的体积为54π，则该圆柱的侧面积为() A. 27π B. 36πC. 54πD. 81π【答案】B 【解析】 【分析】由圆柱的轴截面为正方形可知，底面圆直径与圆柱的高相等，根据圆柱的体积公式，可求得底面圆的半径，再由圆柱的侧面积公式即可求解.【详解】设圆柱的底面半径为r ．因为圆柱的轴截面为正方形，所以该圆柱的高为2r ．因为该圆柱的体积为54π，23π2π54πr h r ==，解得3r =，所以该圆柱的侧面积为2π236r r ⨯=π．【点睛】设圆柱的底面圆半径为r,高为h,则侧面积=2S rh π侧，体积2V Sh r h π==.4.如图，某四边形的斜二测直观图是上底为2，下底为4，高为1的等腰梯形，则原四边形的A. 4B. 2C. 6D. 62【答案】D 【解析】 【分析】根据题意可求出斜二测图形的面积，再结合原图的面积与斜二测图形面积的关系即可求解. 【详解】原图的面积是斜二测图形面积的22倍．该四边形的斜二测图形面积为()243211⨯+⨯=，故原图面积为32262⨯=． 【点睛】按照斜二测画法得到的平面图形的直观图，其面积与原图形的面积的关系：2S 直观图原图形．5.设α，β为两个不同的平面，m ，n 为两条不同的直线，则下列判断正确的是() A. 若n α⊥，m α⊥，则m n ⊥ B. 若αβ∥，m α⊥，则m β⊥ C. 若αβ⊥，l αβ=，m l ⊥，则m β⊥D. 若m n ，m α，则n α 【答案】B 【解析】 【分析】选项A 由线面垂直的性质定理可得；选项B ，由面面平行的定义找两组相交直线，结合线面垂直的判定定理即可证明；选项C,D ，找到反例即可.【详解】A 选项不正确，根据垂直于同一个平面的两个直线平行，可得m n ；B 选项正确，若αβ∥，则存在,,a b a b αα⊂⊂⋂，在平面β内存在',',''a a b b a b ⋂∥∥，由m α⊥，可得,','m a m b m a m b ⊥⊥⇒⊥⊥ ，由线面垂直的判定定理可得m β⊥；C 选项不正确，因为根据面面垂直的性质定理，需要加上“m 在平面α内或者平行于α”这个条件，才能判定m β⊥；D 选项不正确，直线n 可能在平面α上． 【点睛】解决平行、垂直关系基本问题的3个注意点(1)注意判定定理与性质定理中易忽视的条件，如线面平行的条件中线在面外易忽视． (2)结合题意构造或绘制图形，结合图形作出判断． (3)会举反例或用反证法推断命题是否正确．6.设1e ，2e ，3e 为空间的三个不同向量，如果112233λλλ++=0e e e 成立的等价条件为1230λλλ===，则称1e ，2e ，3e 线性无关，否则称它们线性相关．若()2,1,3=-a ，()1,0,2=b ，()1,1,m =-c 线性相关，则m =()A. 9B. 7C. 5D. 3【答案】A 【解析】 【分析】根据定义列出向量坐标的关系，即可求解.【详解】依题意，三个向量线性相关，则存在不全为0的实数x ，y ，z ，使得x y z ++=0a b c 成立．故20,0,320,x y z x z x y mz ++=⎧⎪-=⎨⎪-++=⎩由20,0x y z x z ++=⎧⎨-=⎩得x z =，3y z =-，代入320x y mz -++=，得()90m z -=，由于x ，y ，z 不全为0，故0z ≠，则9m =．【点睛】设向量()()111222,,,,,x y z x y z ==a b ,则()121212,,x x y y z z λμλμλμλμ+++a +b = .7.在三棱柱111ABC A B C -中，11111B ABCABC A B CV V --=()A.18B.12C. 13D.16【答案】C 【解析】 【分析】利用等体积转化法，则有1111B ABC C ABB V V --=，又1CC 平面1ABB ,所以点1,C C 到平面1ABB 的距离相等，故可得111111B ABC C ABB C ABB B ABC V V V V ----===，求解即可. 【详解】设三棱柱111ABC A B C -的高为h,因为1CC 平面11ABB A ，所以1111111111133B ABC C ABB C ABB B ABC ABCABC A B C V V V V h S V -----====⋅=． 故选：C【点睛】本题考查椎体体积，注意若直线a ∥平面α，则直线a 上的任一点到平面α的距离都相等的应用8.如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的体积为()A.23B.23C.323D.643【答案】C 【解析】 【分析】根据三视图的长度，可在棱长为4的正方体中还原几何体，进一步计算即可. 【详解】根据题意，得该几何体是如图所示的三棱锥A BCD -，1132444323A BCD V -=⨯⨯⨯⨯=．【点睛】求以三视图为背景的几何体的体积．应先根据三视图得到几何体的直观图，然后根据条件求解．9.把边长为2的正ABC ∆沿BC 边上的高线AD 折成直二面角，则点A 到BC 的距离是() A. 1 B.62C.142D.154【答案】C 【解析】 【分析】对比翻折前、翻折后，,,,AC BC CD BD 的长度都不变，得翻折后ABC △为等腰三角形，故求AO 的长度即可.【详解】如图，取BC 的中点O ，连接AO ，DO ．∵翻折前ABC △为正三角形，∴2,1AC AB CD BD ====． ∴AO BC ⊥，即AO 为点A 到BC 的距离.∵翻折前AD 为BC 边上的高，∴CD AD ⊥，BD AD ⊥， ∴BDC ∠即为二面角的平面角，即90BDC ∠=︒， ∴222BC CD BD =+=．∴22142BC AO AB ⎛⎫=-= ⎪⎝⎭． 【点睛】折叠问题中的平行与垂直关系的处理关键是结合图形弄清折叠前后变与不变的数量关系，尤其是隐含量的垂直关系.10.在四面体PABC 中，PC PA ⊥，PC PB ⊥，22AP BP AB PC ====，则四面体PABC 外接球的表面积是()A.17π12B.19π12C.19π3D.17π3【答案】C 【解析】 【分析】由△PAB 为等边三角形，且PC ⊥平面PAB 可知，OH PC ∥，即可找到球心所在的位置，列出等量关系即可求出半径.【详解】∵PC PA ⊥，PC PB ⊥，∴PC ⊥平面PAB ．设O 是外接球球心，半径为R ，H 是ABP △的中心，OH ⊥ 平面PAB ，则()222PC OH PH R -+=，222OH PH R += ,322323PH =⨯⨯=，所以1122OH PC == ,2221912R OH PH =+=，故四面体外接球的表面积是219π4π3S R ==．【点睛】“切”“接”问题处理的注意事项 (1)“切”的处理解决与球的内切问题主要是指球内切多面体与旋转体，解答时首先要找准切点，通过作截面来解决．如果内切的是多面体，则作截面时主要抓住多面体过球心的对角面来作． (2)“接”的处理把一个多面体的几个顶点放在球面上即为球的外接问题．解决这类问题的关键是抓住外接的特点，即球心到多面体的顶点的距离等于球的半径．11.已知三棱锥D ABC -的体积为3，且AB BC ⊥，AB =AD BC +=三棱锥D ABC - 的表面积为()A. 2+B. 2+C. 2+D.2+【答案】A 【解析】 【分析】三棱锥D ABC -以△ABC 为底面，则高AD ≤，即可得到2AD BC ⋅≥，再结合基本不等式即可得到AD,BC 的长，且AD 为三棱锥D ABC -的高，利用线面垂直的判定定理可得BC ⊥平面ABD ，即可得三棱锥D ABC -的四个面均为直角三角形，即可计算其表面积.【详解】因为11323D ABC AD AB BC V -⎛⎫⋅⋅≥=⎪⎝⎭，AB =，即2AD BC ⋅≥．因为AD BC =+≥=，当且仅当AD BC ==时，等号成立，此时2AC =，AD =，且AD ⊥平面ABC ，2BD =，易得BC ⊥平面ABD ，所以三棱锥D ABC-的表面积为ABCABDACDBCDSS SS+++=11112222222⨯⨯=+． 【点睛】根据几何体特征求表面积(1)求多面体的侧面积时，应对每一个侧面分别求解后再相加；求旋转体的侧面积时，一般要将旋转体展开为平面图形后再求面积．(2)对于组合体，要弄清它是由哪些简单几何体组成的，要注意“表面(和外界直接接触的面)”的定义，以确保不重复、不遗漏．12.如图,正方形ABCD 中,E F 、分别是AB BC 、的中点将,,ADE CDF BEF ∆分别沿DE DF EF 、、折起,使、、A B C 重合于点P .则下列结论正确的是（ ）A. PD EF ⊥B. 平面PDE PDF ⊥平面C. 二面角P EF D --的余弦值为13D. 点P 在平面DEF 上的投影是DEF ∆的外心 【答案】ABC 【解析】 【分析】对于A 选项，只需取EF 中点H ，证明EF ⊥平面PDH ；对于B 选项，知,,PE PF PD 三线两两垂直，可知正确；对于C 选项，通过余弦定理计算可判断；对于D 选项，由于PE PF PD =≠，可判断正误.【详解】对于A 选项，作出图形，取EF 中点H ，连接PH ，DH ，又原图知BEF ∆和DEF ∆为等腰三角形，故PH EF ⊥,DH EF ⊥，所以EF ⊥平面PDH ，所以PD EF ⊥，故A 正确；根据折起前后，可知,,PE PF PD 三线两两垂直，于是可证平面PDE PDF ⊥平面，故B 正确；根据A 选项可知 PHD ∠为二面角P EF D --的平面角，设正方形边长为2，因此1PE PF ==，22PH =，2322222DH =-=，222PD DF PF =-=，由余弦定理得：2221cos 23PH HD PD PHD PH HD +-∠==⋅，故C 正确；由于PE PF PD =≠，故点P 在平面DEF 上的投影不是DEF ∆的外心，即D 错误；故答案为ABC.【点睛】本题主要考查异面直线垂直，面面垂直，二面角的计算，投影等相关概念，综合性强，意在考查学生的分析能力，计算能力及空间想象能力，难度较大.第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分．将答案填在答题卡中的横线上． 13.在空间直角坐标系O xyz -中，点()5,3,1A -关于y 轴的对称点的坐标为______． 【答案】()5,3,1--- 【解析】 【分析】点A 关于y 轴的对称点,则纵坐标不变，其它坐标变为相反数即可. 【详解】点()5,3,1A -关于y 轴的对称点的坐标为()5,3,1---．【点睛】在空间直角坐标系中，点(),,P x y z 关于x 轴的对称点的坐标为(),,x y z --；关于y 轴的对称点的坐标为(),,x y z --；关于z 轴的对称点的坐标为(),,x y z --.14.如图，PA ⊥平面ABCD ，ABCD 为正方形，且PA AD =，E ，F 分别是线段PA ，CD 的中点，则异面直线EF 与BD 所成角的余弦值为______．3 【解析】 【分析】作BD 的平行线FG ,即可证明EFG （或其补角）就是异面直线EF 与BD 所成的角，计算出EF,EG,FG 的长度，在△EFG 中，利用余弦定理即可求解.【详解】如图，取BC 的中点G ，连接FG ，EG ，AG ,则BDFG ，通过异面直线所成角的性质可知EFG （或其补角）就是异面直线EF 与BD 所成的角． 设2AD =，则226EF EA AF =+=，同理可得6EG．又122FG BD ==，所以在EFG 中，2223cos 2EF FG EG EFG EF FG +-∠==⋅， 故异面直线EF 与BD 所成角的余弦值为3．【点睛】用平移法求异面直线所成角的3个步骤(1)一作：即据定义作平行线，作出异面直线所成的角； (2)二证：即证明作出的角是异面直线所成的角；(3)三求：解三角形，求出作出的角，如果求出的角是锐角或直角，则它就是要求的角，如果求出的角是钝角，则它的补角才是要求的角．15.在四棱锥P ABCD -中，底面ABCD 为正方形，PA ⊥底面ABCD ，且22PA =．E 为棱BC 上的动点，若PE DE +17，则PB =______． 【答案】3 【解析】 【分析】由,BC AB PA BC ⊥⊥,可得BC ⊥平面PAB ,则将PBC 沿棱BC 翻折至与底面ABCD 共面，点P '在AB 的延长线上，则问题转化为BC 上的动点E 到定点P '，D 的距离和的最小值，显然当三点共线时最小，即可计算求解.【详解】易证BC ⊥平面PAB ，则BC PB ⊥，将PBC 沿棱BC 翻折至与底面ABCD 共面，如图所示．设AB x =，则3PB x =，当P '，D ，E 三点共线时，PE DE +取得最小值，故()22417x x +=，解得1x =，则3PB =．【点睛】几何体中，最短路径问题通常将曲面展开，研究两点连线最短的问题，从而将曲面的最短路径问题转化为平面最短路径问题.16.在四面体PABC 中，PC PA ⊥，PC PB ⊥，22AP BP AB PC ====，则四面体PABC 外接球的表面积是_______．【答案】19π3【解析】 【分析】由△PAB 为等边三角形，且PC ⊥平面PAB 可知，OH PC ∥，即可找到球心所在的位置，列出等量关系即可求出半径.【详解】∵PC PA ⊥，PC PB ⊥，∴PC ⊥平面PAB ．设O 是外接球球心，H 是ABP △的中心，OH ⊥ 平面PAB ，则1122OH PC ==，322323PH =⨯⨯=，则22221912R OP OH PH ==+=，故四面体外接球的表面积是219π4π3S R ==．【点睛】“切”“接”问题处理的注意事项 (1)“切”的处理解决与球的内切问题主要是指球内切多面体与旋转体，解答时首先要找准切点，通过作截面来解决．如果内切的是多面体，则作截面时主要抓住多面体过球心的对角面来作． (2)“接”的处理把一个多面体的几个顶点放在球面上即为球的外接问题．解决这类问题的关键是抓住外接的特点，即球心到多面体的顶点的距离等于球的半径．三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤． 17.已知正方体1111ABCD A B C D -，O 是底ABCD 对角线的交点.求证：（1）1//C O 面11AB D ； （2）1A C ⊥面11AB D ．【答案】（1）证明见解析；（2）证明见解析. 【解析】 【分析】（1）取11AB D ∆ 的边11B D 的中线1AO ，由证四边形11AOC O 是平行四边形，得11//OC AO ，由线面平行的判定定理可得结论；（2）由1111111,D B AA D B AC ⊥⊥ 证得11D B ⊥面1A C ，可得面1A C ⊥ 面11AB D 【详解】(1)连结，设 连结，是正方体四边形11ACC A 是平行四边形 ． ,∴A1C1∥AC 且． 又分别是的中点，∴11C O //AO 且,四边形11AOC O 是平行四边形 ．11C O //AO ,1AO ⊂面，面11AB D ,∴1C O ∥面．（2）在正方体中，AA1⊥平面A1B1C1D1，11D B ⊂平面A1B1C1D1，111D B AA ⊥ ．在平面A1B1C1D1内，1111D B A C ⊥,1111AA A C A ⋂=，111A C A C ⊂面，11AA A C 面⊂,111D B A C ⊥面 ． 1111D B AB D ⊂面,面A1C⊥面AB1D1 ．点睛：处理直线、平面平行问题时应注意的事项(1)在推证线面平行时，一定要强调直线不在平面内，否则，会出现错误。

太原五中2013—2014学年度第一学期月考（10月）高二物理（理）选择题（每小题4分，共48分。

每个题有一个或几个选项是正确的，全选对的得 4 分，选不全的得 2 分，有选错的或不答的得 0 分，请将符合题意的选项填入答题栏内。

）1．关于电场，下列说法正确的是( )A．由E＝Fq知，若q减半，则该处电场强度为原来的2倍B．由E＝k Qr2知，E与Q成正比，而与r2成反比C．由E＝k Qr2知，在以Q为球心，以r为半径的球面上，各处场强均相同D．电场中某点场强方向就是该点所放电荷受到的静电力的方向2、处于静电平衡中的导体，内部场强处处为零的原因是( )A、外电场不能进入导体内部B、所有感应电荷在导体内部产生的合场强为零C、外电场和所有感应电荷的电场在导体内部叠加的结果为零D、以上解释都不正确3、设星球带负电，一带电粉尘悬浮在距星球表面1000 km的地方，又若将同样的带电粉尘带到距星球表面2000 km的地方相对于该星球无初速释放，则此带电粉尘( )A．向星球下落B．仍在原处悬浮C．推向太空D．无法判断4.如右图所示，匀强电场场强E＝100 V/m，A、B两点相距10 cm，A、B连线与电场线夹角为60°，则UBA的值为( )A．－10 V B．5 VC．－5 V D．－5 3 V5．两个完全相同的小金属球，它们的带电荷量之比为5∶1(皆可视为点电荷)，它们在相距一定距离时相互作用力为F1，如果让它们接触后再放回各自原来的位置上，此时相互作用力变为F2，则F1∶F2可能为( )A．5∶2 B．5∶4 C．5∶6 D．5∶96．如图所示，在平面直角坐标系中，有方向平行于坐标平面的匀强电场，其中坐标原点O 处的电势为0 V，点A处的电势为6 V, 点B处的电势为3 V, 则电场强度的大小为 ( ) A.200V/m B.2003C.100 V/mD. 1003 V/mo7．如图所示，在y 轴上关于O 点对称的A 、B 两点有等量同种点电荷＋Q ，在x 轴上C点有点电荷－Q 且CO ＝OD ，∠ADO ＝60°.下列判断正确的是( )A ．O 点电场强度为零B ．D 点电场强度为零C ．若将点电荷＋q 从O 移向C ，电势能增大D ．若将点电荷－q 从O 移向C ，电势能增大8、一水平放置的平行板电容器的两极板间距为d ，极板分别与电池两极相连，上极板中心有一小孔(小孔对电场的影响可忽略不计)．小孔正上方d2处的P 点有一带电粒子，该粒子从静止开始下落，经过小孔进入电容器，并在下极板处(未与极板接触)返回．若将下极板向上平移d3，则从P 点开始下落的相同粒子将( )A ．打到下极板上B ．在下极板处返回C ．在距上极板d2处返回D ．在距上极板25d 处返回9、如图所示，在平行板电容器A 、B 两板上加上如图所示的交变电压，开始时B 板电势比A 板高，这时两板中间原来静止的电子在电场力作用下开始运动，设A 、B 两板间的距离足够大，则下述说法中正确的是( ) ks5uA ．电子先向A 板运动，然后向B 板运动，再返回A 板做周期性来回运动 B ．电子一直向A 板运动C ．电子一直向B 板运动D ．电子先向B 板运动，然后向A 板运动，再返回B 板做周期性来回运动10.如图所示，平行板电容器两个极板为A 、B ，B 板接地，A 板带电荷量＋Q ，板间电场内有一固定点P .若将B 板固定，A 板下移一些，或者将A 板固定，B 板上移一些，在这两种情况下，以下说法正确的是( )A.A 板下移时，P 点的电场强度不变，P 点电势不变B.A 板下移时，P 点的电场强度不变，P 点电势升高C.B 板上移时，P 点的电场强度不变，P 点电势降低D.B 板上移时，P 点的电场强度减小，P 点电势降低11、如图所示，实线为电场线，虚线为等势面，相邻两等势面间的电势差相等．一个正电荷在等势面L 3处的动能为20 J ，运动到等势面L 1处时动能为零；现取L 2为零电势参考平面，则当此电荷的电势能为4 J 时，它的动能为(不计重力及空气阻力)( ) A ．16 J B ．10 J C ．6 J D ．4 J12、如图所示，质量为m 、电量为q 的带电微粒，以初速度V 0从A 点竖直向上射入水平方向、电场强度为E 的匀强电场中。

山西省太原五中2013-2014学年高二下学期期中（数学）理试题一．选择题(本题共10小题，每小题4分，共40分；在每小题给出的四个选项中，有且只有一项是正确的)1. 在一次运动会上有四项比赛的冠军在甲、乙、丙三人中产生，那么不同的夺冠情况共有（ ）种.A ．34A B.34 C.43 D.34C2. 复数ii 31315++-)(的值（ ）A.-16B.16C.41-D.i 4341- 3. 观察下列各式 ,,,,,1680772401734374977754321=====，则20147的末尾两位数是（ ）A ．01B ．43C ．49D ．07 4. 下列说法正确的有（ ）（1）用反证法证明：“三角形的内角中至少有一个不大于︒60”时的假设是“假设三角形的三个内角都不大于︒60；（2）分析法是从要证明的结论出发，逐步寻求使结论成立的充要条件； （3）用数学归纳法证明(1)(2)()213(21)n n n n n n +++=-····，从k 到1k +，左边需要增乘的代数式为2（2k+1）；（4）演绎推理是从特殊到一般的推理，其一般模式是三段论； A.0个 B.1个 C.2个 D.3个5. 已知函数1()(*)n f x x n N +=∈的图象与直线1x =交于点P ，若图象在点P 处的切线与x 轴交点的横坐标为n x ，则201320142201412014x x x log log log +++ 的值为（ ） A ．－1 B ．201312014log - C ．20132014log - D ．16. 将一颗骰子抛掷两次，所得向上点数分别为n m ,，则函数1323+-=nx mx y 在⎪⎪⎭⎫⎢⎣⎡∞+,22上为增函数的概率是（）A ．21 B ．125 C ．127D ．32 7. 函数32()393,f x x x x =--+若函数()()[2,5]g x f x m x =-∈-在上有3个零点，则m 的取值范围为（ ）A ．（-24,8）B ．（-24,1]C ．[1,8]D ．[1,8）8. )(21f '的取值范围是（ ）A ．[-2，2]B ．．2] D ．2] 9. 用数学归纳法证明1＋2＋3＋…＋n 2＝n 4＋n 22，则当n ＝k ＋1时左端应在n ＝k 的基础上加上( )．A ．k 2＋1 C. (k ＋1)4＋(k ＋1)22B ．(k ＋1)2 D ．(k 2＋1)＋(k 2＋2)＋(k 2＋3)＋…＋(k ＋1)210. 已知()f x 为R上的可导函数，且,x R ∀∈均有()f x f >′（x），则有（ ） A．20132013(2013)(0),(2013)(0)e f f f e f -<> B．20132013(2013)(0),(2013)(0)e f f f e f -<< C．20132013(2013)(0),(2013)(0)e f f f e f ->>D ．20132013(2013)(0),(2013)(0)ef f f e f -><二．填空题（本题5个小题，共4⨯5=20分） 11.定积分=+⎰-dx x x 112)sin (___________;12. 将甲乙丙丁四名同学分到两个不同的班，每班至少分到一名同学，且甲乙不能分到同一个班，则不同分法总数为 ；13. 设0<a ,若函数R x ax e y x∈+=,2有小于零的极值点，则实数a 的取值范围是 ；14. 若数列{}n a 满足1111,4nn n a a a +⎛⎫=+= ⎪⎝⎭，设21123444n n n S a a a a -=+++⋅⋅⋅+，()n N *∈，类比课本中推导等比数列前n 项和公式的方法，可求得54nn n S a -=____.15．已知函数y ＝f (x )在定义域⎝⎛⎭⎫－32，3上可导，其图象如图，记y ＝f (x )的导函数y ＝f ′(x )，则不等式xf ′(x )≤0的解集是________．三.解答题（本题4个小题，共40分）16. （8分）设复数z 的共轭复数为z ，已知i z i 3421+=+)(， （1）求复数z 及zz ；（2）求满足||||z z =-11的复数1z 对应的点的轨迹方程.17.(10分) 已知函数f (x )＝ax ＋b xe x，a ，b ∈R ，且a ＞0． （1）若a ＝2，b ＝1，求函数f (x )的极值；（2）设g (x )＝a (x －1)e x －f (x )．当a ＝1时，对任意x ∈(0，＋∞)，都有g (x )≥1成立，求b 的最大值；18. （10分） 已知数列{}n a 满足：189a =，1228(1)(21)(23)n n n a a n n ++=+++ （1）求2a 、3a ；（2）猜想{}n a 的通项公式，并用数学归纳法证明. (3) 求证: 121...4n a a a n +++>- （*n ∈N ）19 ．（12分）已知函数2()ln(1)f x ax x =++．（1）当14a =-时，求函数()f x 的单调区间；（2）当[0,)x ∈+∞时，不等式()f x x ≤恒成立，求实数a 的取值范围．（3）求证：134(1[1e (2+⋅⋅+<（其中*n ∈N ， e 是自然对数的底数）．太原五中2013—2014学年度第二学期期中高二数学答题纸（理）二、填空题（每小题4分共20分）11. ；12. ；13. ；14. ；15. .三．解答题（本题共4小题，共40分）16.（8分）17. （10分）18.（10分）19.（12分）太 原 五 中2013--2014学年度第二学期期中高二数学参考答案11.32； 12. 8 ； 13.021<<-a ； 14. n ； 15.[0,1]∪⎝⎛⎦⎤－32，－12 三．解答题（本题共4小题，共40分） 16.解：（1）i zz i z 54532+=+=;；(2).)(5122=+-y x 17. 解：解：（1）当a ＝2，b ＝1时，f (x )＝(2＋1x)e x ，定义域为(－∞，0)∪(0，＋∞)．所以f ′(x )＝(x ＋1)(2x －1)x 2e x．令f ′(x )＝0，得x 1＝－1，x 2＝12，列表x(－∞，－1)－1(－1，0)(0，12)12(12，＋∞)f ′(x ) +－ － 0f (x )↗极大值↘↘极小值↗由表知f (x )的极大值是f (－1)＝e －1，f (x )的极小值是f (12)＝4e ．（2）① 因为g (x )＝(ax －a )e x －f (x )＝(ax －bx －2a )e x ，当a ＝1时，g (x )＝(x －bx－2)e x ．因为g (x )≥1在x ∈（0，＋∞）上恒成立，所以b ≤x 2－2x －xe x 在x ∈（0，＋∞）上恒成立．记h (x )＝x 2－2x －xe x （x ＞0），则h ′(x )＝(x －1)(2e x ＋1)e x．当0＜x ＜1时，h ′(x )＜0，h (x )在（0，1）上是减函数； 当x ＞1时，h ′(x )＞0，h (x )在（1，＋∞）上是增函数． 所以h (x )min ＝h (1)＝－1－e －1．所以b 的最大值为－1－e －1．18. 解：（1）4948=,2524=32a a19. (1).当14a =-时，21()ln(1)4f x x x =-++ (1)x >- 11(1)(2)()212(1)x x f x x x x -+'=-+=-++，当(1,1)x ∈-时，()0f x '>； 当(1,)x ∈+∞时，()0f x '<.()f x ∴的单调增区间为(1,1)-，单调减区间为(1,)+∞。

2024—2025学年山西名校十月联合考试高二数学注意事项：1.答题前，考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上.2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上无效.3.考试结束后，将本试卷和答题卡一并交回.4.本试卷主要考试内容：人教A 版必修第一册、必修第二册、选择性必修第一册第一章至第二章2.4.一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知向量，.若，则（ ）A.4B. C.8D.2，将函数的图象向左平移个单位长度后得到函数的图象，则（ ）A. B. C. D.3，若直线：与直线：垂直，且直线：与直线：垂直，则（ ）A.1B. C.2D.4.若点在圆：的外部，则的取值范围为（ ）A. B.C. D.5.在山西的某个旅游景点内有刀削面、油炸糕、糖火烧、炕馍、莜面这5种传统小吃.某游客从中随机选择3种品尝，则该游客选择了油炸糕和莜面品尝的概率为（ ）A.B.C.D.6.我国古代数学名著《九章算术》中，将底面为直角三角形，且侧棱垂直于底面的棱柱称为堑堵.已知在堑堵中，，，，，分别是所在棱的中点，则下列3个直观图中满足的有（ ）()1,a m = ()2,8b m =-//a b m =4-8-()sin 9f x x =19()g x ()g x =()sin 91x +1sin 981x ⎛⎫+⎪⎝⎭1sin 99x ⎛⎫+⎪⎝⎭πsin 99x ⎛⎫+⎪⎝⎭1l 320ax y -+=2l 330ax y ++=3l 240a x y -+=4l ()20x a y ++=a =1-2-()2,2P C 2224380x y ax y a +++++=a 24,17⎛⎫-- ⎪⎝⎭()24,4,7⎛⎫-∞--+∞ ⎪⎝⎭()1,+∞()24,14,7⎛⎫--+∞ ⎪⎝⎭353102513111ABC A B C -π2ABC ∠=1AB BC AA ==D E F BF DE ⊥A.0个B.1个C.2个D.3个7.在四面体中，为的外心，底面，，，，则四面体外接球的表面积为（ ）A.B. C.D.8.已知，直线：，过点作的垂线，垂足为，则点到轴的距离的最小值为（ ）A. B. C. D.二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得分分，有选错的得0分.9.已知集合，，，则（）A. B. C. D.10.已知一组数据为1，，，3，4，，1，1，3，2，其中，则（ ）A.这组数据的中位数不可能为3B.当这组数据的众数为1时，C.当时，这组数据的方差为1.25D.当这组数据的平均数为2.2时，的最小值为11.已知四棱柱的底面是边长为6的菱形，平面，，，点满足，其中，则（ ）A.当为底面的中心时，B.当时，C.当时，长度的最大值为6ABCD E ABC △DE ⊥ABC 1AC =DE =1sin 4ABC ∠=ABCD 49π318π50π320π()1,3A -l ()()21210m x m y m +-++-=A l B B x 444+8-1,2M x x m m ⎧⎫==+∈⎨⎬⎩⎭Z 32,2N x x n n ⎧⎫==-∈⎨⎬⎩⎭Z ,2p P x x p ⎧⎫==∈⎨⎬⎩⎭Z N P⊆P M⊆N M⊆M N⊆x y x 05x y <<≤3x ≠340x y -+-=24x y +1671111ABCD A B C D -1AA ⊥ABCD 13AA =π3DAB ∠=P 1AP AB AD t AA λμ=++ [],,0,1t λμ∈P 1111A B C D 53t λμ++=1t λμ++=AP 1t λμ++=APD.当时，为定值三、填空题：本题共3小题，每小题5分，共15分.把答案填在答题卡中的横线上.12.若复数满足，则的虚部为______，______.13.已知在正四棱台中，，，，则异面直线与所成角的余弦值为______.14.已知函数.若不等式对任意恒成立，则的取值范围是______.四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.15.（13分）在中，角，，的对边分别为，，，已知.（1）若，求；（2）若，，求的面积.16.（15分）如图，在正六棱柱中，为的中点.设，，.（1）用，，表示向量，；（2）若，求的值.17.（15分）已知圆经过点，，.（1）求圆的标准方程；（2）若一条光线从点射向直线，经该直线反射后经过圆上的点，求该光线从点到点的路线长的最小值.18.（17分）如图，已知，，，四点均在直径为6的球的球面上，，，，221t λμλμ++==1A Pz ()2i 10z +⋅=z z =1111ABCD A B C D -()0,4,0AB = ()13,1,1CB =- ()112,0,0A D =-1DB 11A D ())3311log 4f x x x =-++()()()42320x x f f m f -+⋅+-<x ∈R m ABC △A B C a b c 2cos c b a B +=π2A =B a =1b =ABC △111111ABCDEF A B CDEF -M 1FF AB a = AF b = 1AA c =a b c DM 1BE2a c ==1DM BE ⋅ M ()1,3A ()2,4B ()3,3C M ()0,1D 40x y --=M E D E A O C P B 6AP =0AO OC ⋅= AH HO =，，直线与平面所成的角为，点在线段上运动.（1）证明：平面.（2）设平面与平面的夹角为，求的最大值.19.（17分）过点作斜率分别为，的直线，，若（），则称直线，是定积直线或定积直线.（1）已知直线：（），直线：，试问是否存在点，使得直线，是定积直线？请说明理由.（2）在中，为坐标原点，点与点均在第一象限，且点在二次函数的图象上.若直线与直线是定积直线，直线与直线是定积直线，直线与直线是定积直线，求点的坐标.（3）已知直线与是定积直线，设点到直线，的距离分别为，，求的取值范围.OK KC = PC AC =PO AOC π3D PC CP ⊥AOC BOC KHD θcos θ()00,A x y 1k 2k 1l 2l 12k k μ=0μ≠1l 2l ()A K μ()()00,xy K μa y kx =0k ≠b 13y x k=-A a b ()A K μOPM △O P M ()00,M x y 23y x =-OP OM ()()0,01K OP PM ()2P K -OM PM ()00,202x y K x ⎛⎫- ⎪⎝⎭P m n ()()2,44K --()0,0O m n 1d 2d 12d d2024—2025学年山西名校十月联合考试高二数学参考答案1. D 根据题意可得，解得.2. A 易得.3. B 由得.4. D 根据题意可得解得或.5. B 将刀削面、油炸糕、糖火烧、炕馍、莜面这5种传统小吃分别设为，，，，，根据题意可得该游客从中随机选择3种品尝的所有情况有，，，，，，，，，，共10种，其中该游客选择了油炸糕和莜面品尝的情况有3种，故所求概率为.6. C 设，以，，所在直线分别为轴，轴，轴建立空间直角坐标系（图略），则.在图①中，，，，则，，所以，满足；在图②中，，，，则，，所以，满足；在图③中，，，，则，，所以，不满足.7. C 设四面体的外接球为球，其半径为，外接圆的半径为.由正弦定理得，则.由，，得，解得，所以球的表面积为.82m m -=8m =-()()11sin 9sin 9199g x f x x x ⎛⎫⎛⎫=+=+=+ ⎪ ⎪⎝⎭⎝⎭()22330,20,a a a ⎧-=⎪⎨-+=⎪⎩1a =-()24448380,4164380,a a a a +++++>⎧⎨+-+>⎩2417a -<<-4a >A B C D E ()A,B,C ()A,B,D ()A,B,E ()A,C,D ()A,C,E ()A,D,E ()B,C,D ()B,C,E ()B,D,E ()C,D,E 3102AB =BA BC 1BB x y z ()0,0,0B ()1,0,2D ()0,1,0E ()1,1,0F ()1,1,0BF = ()1,1,2DE =--110BF DE ⋅=-+=BF DE ⊥()1,0,2D ()1,1,0E ()0,2,1F ()0,2,1BF = ()0,1,2DE =-220BF DE ⋅=-= BF DE ⊥()1,0,0D ()1,1,0E ()1,1,2F ()1,1,2BF = ()0,1,0DE =10BF DE ⋅=≠BF DE ⊥ABCD O r ABC △R 24sin ACR ABC==∠2CE R ==OC OD =OE CE ⊥)2222r r =+r =O 250π43r π=8. B 由，得.令解得即过定点，所以点在以为直径的圆上，其中圆心.因为圆心到轴的距离为4，所以点到轴的距离的最小值为.9. AC 由题意得，，所以，A ，C 正确，B，D 错误.10. BCD 当时，这组数据的中位数为3，A 错误.当这组数据的众数为1时，若，则这组数据的众数为3，这与这组数据的众数为1矛盾，所以，B 正确.当时，，，，，C 正确.当这组数据的平均数为2.2时，，则，当且仅当，即时，等号成立，D 正确.11. BCD 连接，.设与交于点，则.当为底面的中心时，.()()21210m x m y m +-++-=()2210m x y x y -++--=20,210,x y x y -+=⎧⎨--=⎩3,5,x y =⎧⎨=⎩l ()3,5C B AC M ()1,4M =M x B x 4-21,2m M x x m ⎧+⎫==∈⎨⎬⎩⎭Z ()4114341,,222n n k N x x n x x k ⎧⎫-+-⎧+⎫⎪⎪===∈==∈⎨⎬⎨⎬⎩⎭⎪⎪⎩⎭Z Z 221,2k x x k ⎧⨯+⎫==∈⎨⎬⎩⎭Z N M P ÞÞ3x ≥3x =3x ≠340x y -+-=3x =4y = 2.5x =()222150.55 1.5 1.2510s =⨯⨯+⨯=2 2.210157x y +=⨯-=()(241241281162887777y x x y x y x y x y ⎛⎫⎛⎫+=++=++≥+= ⎪ ⎪⎝⎭⎝⎭28y x x y =722y x ==11A C 11B D 11A C 11B D E 1111111112222A E AB A D AB AD =+=+P 1111A B C D 1111122AP AA A E AB AD AA =+=++因为，所以，，所以，A 错误.当时，点在平面内，则长度的最大值为6，长度的最小值即到平面的距离.设到平面的距离为，则，解得，B ，C 均正确.因为，所以在底面上，且，则，得，D 正确.12.；依题意得，则的虚部为，.依题意得，设异面直线与所成的角为，因为，所以14. 因为的定义域为，1AP AB AD t AA λμ=++ 12λμ==1t =2t λμ++=1t λμ++=P 1A BD AP AP A 1A BD A 1A BD h 11π1166sin 3632332h ⨯⨯⨯⨯⨯=⨯⨯h =221t λμλμ++==P 1111A B C D 1A P AB AD λμ=+()2222222123636A P AB AD AB AD λμλμλμλμ=++⋅=++= 16A P =2-()()()102i 102010i42i 2i 2i 2i 5z --====-++-z 2-z ==()1113,3,1DB DC CB AB CB =+=+= 1DB 11A D θπ0,2θ⎛⎤∈ ⎥⎝⎦111111111cos cos ,DB A D DB A D DB A D θ⋅====(),4-∞()f x R ())3311log 4f x x x-=--+-，所以为奇函数.因为函数在上单调递增，函数在上单调递增，所以在上单调递增.因为为奇函数，所以在上单调递增，因为，所以不等式即为，则.因为，所以，即.因为，当且仅当，即时，等号成立，所以，即的取值范围是.15.解：（1）因为，所以.因为，所以，则或（舍去），所以.因为，所以.（2）由（1）得.因为，解得所以，，，所以.故的面积为.16.解：（1）.)()3331311log 1log 44x x x f x =--+=-+-=-()f x 3114y x =-[)0,+∞)3log y x =+[)0,+∞()f x [)0,+∞()f x ()f x R ()()3232f f --=()()()42320xx ff m f -+⋅+-<()()()4232x x f f m f -+⋅<()4232x x f m -+⋅<()34311log 932f =-+=424xxm -+⋅<444222x x xx m +<=+4242x x +≥=422xx =1x =4m <m (),4-∞2cos c b a B +=sin sin 2sin cos C B A B +=()sin sin sin cos cos sin C A B A B A B =+=+()sin sin cos cos sin sin B A B A B A B =-=-B A B =-πB A B +-=2A B =π2A =π4B =2A B =sin sin a bA B=1sin B =cos B =π4B =π2A =π4C =1c b ==ABC △111122⨯⨯=()111222DM DE EF FM AB AB AF AA a b c =++=--++=--+ ()111122BE BA AF FE EE AB AF AB AF AA AF AA a c=+++=-++++=+=+（2）由题意易得，，则.17.解：（1）设圆的标准方程为（）.代入，，的坐标，得解得所以圆的标准方程为.（2）设点关于直线对称的点的坐标为，则解得即.由（1）可得圆的圆心为，半径，则该光线从点到点的路线长的最小值为.18.（1）证明：由题意可知为球的直径，所以，.又因为，所以，，所以平面，平面，所以，，所以平面.（2）解：如图，以为坐标原点，，所在直线分别为轴，轴建立空间直角坐标系.2π1cos 22232a b a b ⎛⎫⋅=⨯=⨯⨯-=- ⎪⎝⎭0a c ⋅= ()11222DM BE a b c b c⎛⎫⋅=--+⋅+ ⎪⎝⎭22221142242222a b a c b b c b c c a b a c b c=-⋅-⋅--⋅+⋅+=-⋅-⋅-+ ()2214222222=-⨯--⨯+⨯=M ()()222x a y b r -+-=0r >()1,3A ()2,4B ()3,3C ()()()()()()22222222213,24,33,a b r a b r a b r ⎧-+-=⎪⎪-+-=⎨⎪-+-=⎪⎩2,3,1,a b r =⎧⎪=⎨⎪=⎩M ()()22231x y -+-=()0,1D 40x y --=D '(),m n 111,0140,22n m m n -⎧⨯=-⎪⎪-⎨+⎪--=⎪⎩5,4,m n =⎧⎨=-⎩()5,4D '-M ()2,3M 1r =D E 11D M r '-=-=-AP B AC CP ⊥AO OP ⊥0AO OC ⋅=AO OC ⊥OC OP O = AO ⊥POC CP ⊂POC AO CP ⊥AO AC A = CP ⊥AOC O OA OC x y根据题意可得，，，则，所以，，，，，，则，，，设平面的法向量为，则取.设（），则.设平面的法向量为，则取.令，，，6AP =PC AC ==π3POC ∠=OC ==AO ==()A ()C )HK ⎛⎫⎪ ⎪⎝⎭(P B OB = ()OC = HK ⎛⎫= ⎪ ⎪⎝⎭BOC ()111,,m x y z =11110,0,m OB y z m OC ⎧⋅=+=⎪⎨⎪⋅==⎩ (m = ()CD CP λ==01λ≤≤KD KC CD ⎛⎫=+= ⎪ ⎪⎝⎭KHD ()222,,n x y z =22220,0,n HK y n KD y z ⎧⋅=+=⎪⎪⎨⎪⋅=+=⎪⎩ ),,1n =- cos cos ,m n m n m n θ⋅====31t λ=+[]1,4t ∈11,14t ⎡⎤∈⎢⎥⎣⎦则，当，即，时，.19.解：（1）由题意可得，由得故存在点，使得，是定积直线，且.（2）设直线的斜率为（），则直线的斜率为，直线的斜率为.依题意得，得，即或.直线的方程为，因为点在直线上，所以.因为点在第一象限，所以，解得或（舍去），，，所以直线的方程为，直线的方程为，由得即点的坐标为.（3）设直线：，直线：，其中，则，，当且仅当，即时，等号成立，所以，即，故的取值范围为.cos θ===123t =32t =16λ=cos θ1133k k ⎛⎫⋅-=- ⎪⎝⎭()0,1,3y kx k y x k ⎧=≠⎪⎨=-⎪⎩0,0,x y =⎧⎨=⎩()0,0A a b ()A K μ13μ=-OM λ0λ≠OP 1λPM 2λ-()2022x λλ⋅-=-2201x λ=01x λ=1-OM y x λ=()200,3M x x -OM 2003x x λ-=M 20031x x λ-==02x =2-12λ=()2,1M OP 12y x x λ==PM ()2213y x x λ=--+=-+2,3,y x y x =⎧⎨=-+⎩1,2,x y =⎧⎨=⎩P ()1,2m ()42y t x -=+n ()442y x t -=-+0t ≠12d d ===2216171725t t ++≥=2216t t=24t =08≤<1208d d ≤<12d d [)0,8。

太原五中2013—2014学年度第一学期月考（10月）高二历史(文)一、选择题（本大题25小题，共50分。

）1．《春秋》重灾异，孔子也曾说：“邦大旱，毋乃失诸刑与德乎？”又强调“获罪于天，无所祷也。

”但英国学者李约瑟却盛赞儒家思想基本是重理性的，反对任何迷信以至超自然的宗教。

这主要是因为A．孔子所说的天指的是自然规律 B．儒家讲究仁德倡导以民为本C．儒家重人事重入世而敬远鬼神 D．儒家对佛道等宗教坚决抵制2. “吾是以明仁义爱惠之不足用，而严刑重罚可以治国也。

”这派思想在当时的最大贡献是A．稳定了社会秩序 B．揭露了道学虚伪C．推动了中央集权 D．提高了法律地位3.孟子曰：“尽其心者，知其性也。

知其性，则知天矣。

存其心，养其性，所以事天也。

夭寿不二，修身以俟之。

”在修养论上与其最接近的是A.荀子B.庄子C.朱熹D.王阳明4.儒学籍孔子而立，又在中国几经变迁，一变为汉代经学，再变为宋明理学，三变为经世致用之学。

宋明理学发展相对与汉代经学最主要的变化是A．研究天人关系为核心内容 B．维护封建统治为己任C．认识自然发展规律为导向 D．伦理道德为核心内容5．社会发展决定了“宋型文化”的热情奔放、浅俗直白的一面。

这也直接刺激了明清两代的文化，使之呈现出社会风尚“导奢导淫”“好色”“好货”，价值观念上拜金逐利；文艺品味上重自由表达，“单纯以低级的平民趣味为依归”的特征。

下列文学艺术成就同属于这个文化序列的是A．宋词元杂剧世情小说 B．唐诗宋词风俗画C．草书文人画宗教画 D．楚辞神魔小说年画6.“好为惊世骇俗之论、务反宋儒道学之说。

……儒释从之者几千万人。

其学以解脱直截为宗，少年高旷豪举之士，多乐慕之。

后学如狂，不但儒教溃防，即释宗绳检，亦多所清弃。

”此人从哲学的根本问题入手反宋儒之道的言论是A.万物生于水B.万物皆生于两C.理在气中D.心外无理7.明清易代之际，清流名士要么顺应，要么抗争不成退而归隐，很少有人选择死节。

太原五中2014-2015学年度第一学期月考（10月）高 二 数 学第Ⅰ卷（选择题 共40分）一、选择题：(本大题共10小题，每小题4分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的)。

1. 1l ，2l ，3l 是空间三条不同的直线，则下列命题正确的是( )．A ．12l l ⊥，23l l ⊥13//l l ⇒B ．12l l ⊥，23//l l ⇒13l l ⊥C ．l 1∥l 2∥l 3⇒1l ，2l ，3l 共面D ．1l ，2l ，3l 共点⇒1l ，2l ，3l 共面 2.正六棱柱的底面边长为4,高为6,则它的外接球的表面积为（ ） A. 20π B. 25π C. 100π D. 200π3. 一个简单几何体的主视图，左视图如图所示，则其俯视图不可能为 ①长方形；②直角三角形；③圆；④椭圆,其中正确的是 A.①B.②C.③D.④4. 在二面角α-l -β的两个面α,β内,分别有直线a,b,它们与棱l 都不垂直,则( ) (A)当该二面角是直二面角时,可能a ∥b,也可能a ⊥b (B)当该二面角是直二面角时,可能a ∥b,但不可能a ⊥b (C)当该二面角不是直二面角时,可能a ∥b,但不可能a ⊥b (D)当该二面角不是直二面角时,不可能a ∥b,也不可能a ⊥b5.已知长方体的表面积是224cm ，过同一顶点的三条棱长之和是6cm ，则它的体对角线长是（ ）B. 4cmC.D. 6. 如图, 甲烷CH 4 的分子结构是: 碳原子位于正四面体的中心, 4个氢原子分别位于正四面体的四个顶点上. 设碳原子与4个氢原子连成的四条线段两两组成的角为θ, 则cos θ=( ) 0.A 41.B - 31.C - 21.D -7.已知球的半径为5，球面被互相垂直的两个平面所截，得到的两个圆的公共弦长为32，若其中一个圆的半径为32，则另一个圆的半径为（ ）A.3B.4C.10D.11 8.如图，正△ABC 的中线AF 与中位线DE 相交于G ，已知△A ′ED 是△AED 绕DE 旋转过程中的一个图形，下列命题中，错误．．的是( )DA ．动点A ′在平面ABC 上的射影在线段AF 上B ．恒有平面A ′GF ⊥平面BCEDC ．三棱锥A ′—FED 的体积有最大值 D ．异面直线A ′E 与BD 不可能垂直9.如图所示，正方体ABCD －A 1B 1C 1D 1中，E 、F 分别是正方形ADD 1A 1和ABCD 的中心，G 是CC 1的中点，设GF 、C 1E 与AB 所成的角分别是α、β，则α＋β等于A ．120°B ．60°C ．75°D ．90°10.已知在矩形ABCD 中，AB=22，BC=a,PA ⊥面ABCD ，若在BC 上存在点Q 满足PQ ⊥DQ ，则a 的最小值是A. 1B. 2C.22D.24第Ⅱ卷（非选择题 共60分）二、填空题（每小题4分，共20分）11. 等腰梯形ABCD ，上底1CD =，腰AD CB ==3AB =，以下底所在直线为x 轴，则由斜二测画法画出的直观图''''A B C D 的面积为_______12. 已知圆锥的全面积是底面积的3倍，那么该圆锥的侧面展开图扇形的圆心角的弧度数是__________ 13、如图，在正三棱柱ABC —A 1B 1C 1中，D 为棱AA 1的中点，若截面△BC 1D 是面积为6的直角三角形，则此三棱柱的体积为________．14.如图，在四面体ABCD 中，已知DA ⊥面ABC ，面ABD ⊥面BCD ，，四面体的三个面DAB 、DBC 、DCA 面积的平方和是8，则=∠AD B _________.15. 已知四棱锥S-ABCD 的底面是平行四边形，O SDAO SBC O SCDO SAB O V V V V ----++=__________三解答题：（本题共4小题，共40分）16.如图，在直三棱柱111ABC A B C -中，12CC AC BC ===，90ACB ∠=︒. （1） 下图给出了该直三棱柱三视图中的主视图，请据此画出它的左视图和俯视图； （2） 若P 是1AA 的中点，求异面直线PC 与BC 1 所成角的余弦值.A 1C BAB17.如图所示，直三棱柱ABC －A 1B 1C 1的侧棱长和底面边长都是a ，截面AB 1C 和截面A 1BC 1相交于DE ，求四面体B －B 1DE 的体积．18、斜三棱柱ABC－A1B1C1中，侧面ACC1A1⊥平面ABC，∠ACB＝90°.(1)求证：BC⊥AA1；(2)若M，N是棱BC上的两个三等分点，求证：A1N∥平面AB1M.（1）求证：平面ABC⊥平面APC（2）求直线PA与平面PBC所成角的正弦值；（3）若动点M在底面三角形ABC上，二面角M-PA-C的大小为。