高中数学试卷模板(密封线俱全8开)

试卷规范为了加强对制卷工作的领导和管理，统一试卷格式和要求，提出如下规范。

一、试卷版式要求1.试卷采用Word文件格式排版。

2.页面设置：8开版面，单页打印。

横向排列,左侧留密封线。

3.页边距：上2厘米，左2厘米，下2厘米，右2厘米4.行间距：行间距统一为1.5。

左侧装订，页眉1.5，页脚1.75。

5.正文字体和字号：宋体五号。

二、试卷头格式1.卷号：按A、B、C卷三套试卷。

2.考试时间：标注考试年月。

3.考试试卷名称：课程的全称。

4.考试范围：试卷内容覆盖教学内容的范围。

如全部或第1至8章。

5.考试形式：指开卷、闭卷或半开卷。

6.课程类别：按教学计划填写为必修、选修等。

7.学期：学期定义：20091表示2009年上半年，20092表示2009年下半年。

三、试卷内容1.题型排列：题型按从易到难的顺序排列。

2.题型名称：概括表明本大题题型3.题数及分值分配：紧接题型列出，标明（本大题共×小题，每小题×分，共×分）。

①某大题只一个小题，分值就标在题型后面。

格式为：（本大题共1题，共×分）②某大题有多个小题，且分值相等，格式为：（本大题共×小题，每小题×分，共×分）③某大题有多个小题，且分值不等，格式为：（本大题共×小题，共×分），每小题分值标在小题后。

4.指导语：是针对题型需要达到的目的，向应考者指明答题方式的语句。

答题指导语置于括号内，对本题解题提出具体要求。

无特殊要求的可以不列指导语。

5.试题题干：表达一道题内容的语言，其作用是使应考者明白试题是什么，要求做什么，试题题干一般由完整的语句组成，亦可由完整的段落或专业术语构成。

6.总题量：文科类为：40-50道之间；理科类为：35-45道之间。

7.注意：设计题型及试卷格式时，应考虑到学生答题的方便，考生直接在试卷上做题。

20 年月模拟考试
数学试题（卷）
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分钟。

第I卷（选择题共50分）
一、选择题（本大题共10小题，每小题5分，共50分，在
每小题给出的四个选项中，只有一项是最符合题目要求的。

）
（）A． B．
C． D．
2．
() A．B．
C．D．
3．
() A．B．
C．D．
4．
()
A. B. C. D.
5．
（）
A. B. C. D.
6．
（）
A. B. C. D.
7．()
A．B．C．D．
8．
（） A. B. C. D
9．
（）A．B．C．D．
10．
（）A．B． C．D．
第Ⅱ卷（非选择题共100分）
二、填空题（本大题共5小题，每小题5分，共25分，把
答案填在题中横线上）。

11．
12．
13.
14．
15.
三、解答题：（本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤。

）
16．（本小题满分12分）
17．（本小题满分12分）；
18．（本小题满分12分）( 19．（本小题满分13分）
20．（本小题满分13分）21．（本小题满分13分）。

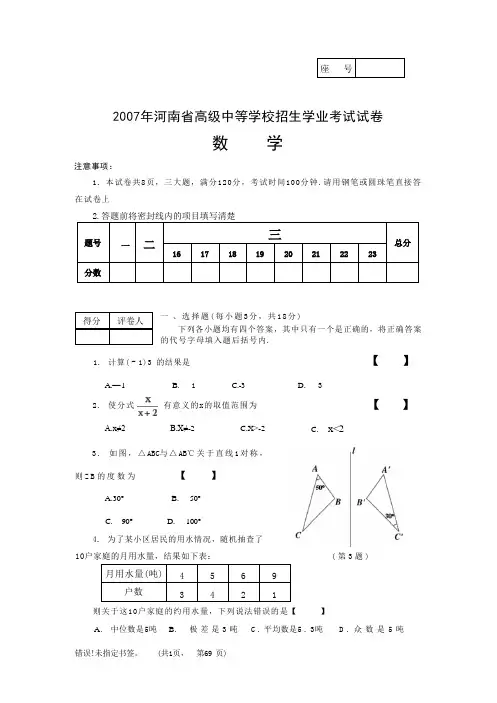
2007年河南省高级中等学校招生学业考试试卷数 学注意事项：1. 本试卷共8页，三大题，满分120分，考试时间100分钟.请用钢笔或圆珠笔直接答在试卷上下列各小题均有四个答案，其中只有一个是正确的，将正确答案的代号字母填入题后括号内.【 】A.— 1B. 1C.-3 2. 使分式有意义的x 的取值范围为A.x≠2B.X≠-2C.X>-23. 如图，△ABC 与△AB ℃关于直线1对称， 则 Z B 的 度 数 为 【 】A.30°B. 50°C. 90°D. 100°4. 为了某小区居民的用水情况，随机抽查了10户家庭的月用水量，结果如下表：D. 3【 】C. x<2( 第 3 题 )则关于这10户家庭的约用水量，下列说法错误的是【 】A. 中位数是5吨B. 极 差 是 3 吨 C . 平均数是5 . 3吨 D . 众 数 是 5 吨一 、选择题(每小题3分，共18分)1. 计算( - 1)3 的结果是得分 评卷人5. 由一些大小相同的小正方体组成的几何体的俯视图如图所示，其中正方形中的数字表 示在该位置上的小正方体的个数，那么，这个几何体的左视图是 【 】A. B. C. D. (第5题图)6. 二次函数y=ax²+x+a² - 1 的图像可能是 【 】A. B. C. D.7. 的相反数是 .8. 计算：(-2x²) · 3x ⁴=9. 写出一个经过点(1, — 1)的函数的表达式10. 如图， PA 、PB 切◎O 于点A 、B,点C 是◎O 上 一 点，且ZACB=65°,则ZP=.(第10题图) (第11题图)11. 如图，在直角梯形ABCD 中， AB//CD,ADICD,AB=1cm,AD=2cm,CD=4cm, 则BC= ·12. 已知x 为整数，且满足- √2≤x≤ √3,则x= .13. 将图①所示的正六边形进行分割得到图②,再将图②中最小的某一个正六边形按同样的方式进行分割得到图③,再将图③中最小的某一个正六边形按同样的方式进行分割， … ,则第n 个图形中共有 个正六边形.● ·0度 二、 填空题(每小题3分，共27分)得分评卷人14.将图，四边形OABC为菱形，点B、C在以点○为圆心的EF上，若OA=3,Z1=22,则扇形OEF的面积为 .15.如图，点P是ZAOB的角平分线上一点，过P作P C//OA交OB于点C .若ZAOB=60°,O C = 4 , 则点P 到O A 的距离P D 等于三、解答题(本大题共8个小题，满分75分)16 . (8分)(第15题图)17 . (9分)如图，点E 、F 、G分别是□ABCD 的边AB 、BC、CD 、DA 的中点.求证：△BEF丝△DGH .18. (9分)下图是2006年某省各类学校在校生数情况制作的扇形统计图和不完整的条形统计图.人数 ( 万人)得分评卷人得分评卷人已知2006年该省普通高校在校生为97.41万人，请根据统计图中提供的信息解答下列问题：(1)2006 年该省各类学校在校生总人数约多少万人? (精确到1万)(2)补全条形统计图；(3)请你写出一条合理化建议.19.(9分)张彬和王华两位同学为得到一张观看足球比赛的入场券，各自设计了一种方案：张彬：如图，设计了一个可以自由转动的转盘，随意转动转盘，当指针指向阴影区域时，张彬得到了入场券；否则，王华得到入场券；王华：将三个完全相同的小球分别标上数字1、2、3后，放入一个不透明的袋子中.从中随机取出一个小球，然后放回袋子；混合均匀后，再随机取出一个小球.若两次取出的小球上的数字之和为偶数，王华得到入场券；否则，张彬得到入场券.请你运用所学的概率知识，分析张彬和王华的设计方案对双方是否公平.20. (9分)如图，A BCD 是边长为1的正方形，其中D E 、EF 、FG 的圆心依次是点A 、B 、C .(1)求点D 沿三条圆弧运动到G 所经过的路线长； (2)判断直线GB 与DF 的位置关系，并说明理由 .(2)在你所画的等腰△ ABC 中设底边BC=5米，求腰上的高BE . 22. (10分)某商场用36万元购进A 、B 两种商品，销售完后共获利6万元，其进价和售价如下表：(注：获利=售价一进价)(1)该商场购进A 、B 两种商品各多少件?底边上的高AD=BC .(1)求tanB 和sinB 的值；21. (10分)请你画出一个以BC 为底边的等腰△ ABC,使(2)商场第二次以原进价购进A、B两种商品.购进B种商品的件数不变，而购进A种商品的件数是第一次的2倍，A种商品按原价出售，而B种商品打折销售.若两种商品销售完毕，要使第二次经营活动获利不少于81600元，B种商品最低售价为每件多少元?23 . (11分)如图，对称轴为直线的抛物线经过点A ( 6 , 0 ) 和B ( 0 , 4 ) .(1)求抛物线解析式及顶点坐标；(2)设点E(x,y)是抛物线上一动点，且位于第四象限，四边形OEAF是以OA为对角线的平行四边形，求四边形OEAF的面积S与x之间的函数关系式，并写出自变量x 的取值范围；(3)①当四边形OEAF的面积为24时，请判断OEAF是否为菱形?②是否存在点E,使四边形OEAF为正方形?若存在，求出点E的坐标；若不存在，请说明理由.2007年河南省实验区中考数学试题参考答案79例三、解答题16.解：方程两边同乘以(x+2)(x-2),得3x(x-2)+2(x+2)=3(x+2)(x-2)解之，得X= 4检验：当x=4时，(x+2)(x-2)=(4+2)(4-2)≠0所以，X=4是原方程的解.17. 证明：∵四边形ABCD 是平行四边形，·ZB= ZD,AB = CD,BC =AD.又∵E、F 、G 、H 分别是平行四边形ABCD 的四边中点， . · B E = DG,BF = DH. · △BEF 丝△DGH.18. 解：(1)2006年该省种类学校在校生总数为97 .41÷4 . 87%≈2000(万人) .(2)普通高中在校生人数约为2000×10 . 08%= 201 . 6(万人) . (没有计算，但图形正确者可给满分)(3)(答案不唯一 ，回答合理即可) .19. 解：张彬的设计方案：,,,所以，张彬的设计方案不公平.王华的设计方案：可能出现的的所有结果列表如下：第一次第二次1 2 31 2 3 42 3 4 53 4 5 65: P ( 王华得到入场券) = P ( 和为偶数) = 9 ,4P(张彬得到入场券)=P(和不是偶数)=9因头所以，王华的设计方案也不公平.20.解：(1)∵AD=1,ZDAE=90°,. D E 的长同理，EF的长所以，点D运动到点G所经过的路线长l=l+1z+l3=3π(2)直线GBLDF .理由如下：延长GB交DF于H.∵CD=CB,LDCF= ZBCG,CF = CG,·△FDC丝△GBC .·ZF =LG.又∵ZF+ ZFDC = 90°,LG + ZFDC = 90°,即ZGHD = 9 0 ,故G B L D F .21. 解：如图，正确画出图形.(1)∵A B=A C,A D工B C,A D=B C,·:AB=√ED²+AD⁷=√5BD即AD=2BD ..(2)作BELAC 于E .在Rt △BEC 中，又 ∵·故BE=2 √5(米).22. (1)设购进A 种商品X 件，B 种商品Y 件.根据题意，得化简，得解之，得答：该商场购进A 、B 两种商品分别为200件和120件. (2)由于A 商品购进400件，获利为(1380- 1200)×400 = 72000(元).从而B 商品售完获利应不少于81600-72000 = 9600(元).设B 商品每件售价为x 元，则120(x- 1000)≥9600. 解之，得x≥1080.所以，B 种商品最低售价为每件1080元.23. 解：(1)由抛物线的对称轴是,可设解析式为把A 、B 两点坐标代入上式，得解之，得故抛物线解析式为,顶点为.(2)∵点E(x y)在抛物线上，位于第四象限，且坐标适合:y<0,即-y>0,-y 表示点E 到OA 的距离.∵0A是口OEAF 的对角线，因为抛物线与X 轴的两个交点是(1,0)的(6,0),所以，自变量X 的取值范围是1<X<6.根据题意，当S = 24时，即化简，得 解之，得×=3,X2= 4. 故所求的点E 有两个，分别为El(3,-4),E2(4,—4).点E1(3,-4)满足OE = AE,所以□OEAF 是菱形；点E2(4,—4)不满足OE = AE,所以□OEAF 不是菱形.当OALEF,且OA=EF 时，口OEAF 是正方形，此时点E 的坐标只能是(3, 一 3) .而坐标为(3,-3)的点不在抛物线上，故不存在这样的点E,使□OEAF为正方形.(实验区)(濮阳市的中原油田、南阳市的南阳油田)2008年河南省高级中等学校招生统一考试试卷数 学注意事项：1、本试卷共8页，三大题，满分120分，考试时间100分钟。

考试时间：120分钟满分：150分一、选择题（本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

）1. 已知函数$f(x) = 2x^3 - 3x^2 + 1$，则$f'(x)$的零点为：A. $x = \frac{1}{2}$B. $x = 1$C. $x = \frac{3}{2}$D. $x = 2$2. 若$\sin A + \sin B = \sqrt{2}\sin(A + B)$，则$A + B$的值为：A. $\frac{\pi}{4}$B. $\frac{\pi}{2}$C. $\frac{3\pi}{4}$D. $\pi$3. 在平面直角坐标系中，点P的坐标为$(2, 3)$，点Q在直线$y = 2x - 1$上，且$|PQ| = 3$，则点Q的坐标为：A. $(1, 1)$B. $(1, 5)$C. $(5, 1)$D. $(5, 5)$4. 若$a, b, c$是等差数列，且$a + b + c = 9$，$ab + bc + ca = 27$，则$abc$的值为：A. $9$B. $27$C. $81$5. 若$y = \ln(x - 1) + \frac{1}{x - 1}$，则$y'$的值为：A. $\frac{1}{x^2 - 1}$B. $\frac{1}{(x - 1)^2}$C. $-\frac{1}{(x - 1)^2}$D. $\frac{1}{x^2 - 1}$6. 已知复数$z = a + bi$（$a, b \in \mathbb{R}$），若$|z - 1| = |z + 1|$，则$z$的取值范围是：A. $a = 0$B. $a = 1$C. $a = -1$D. $a = \pm 1$7. 在三角形ABC中，$a = 5, b = 6, c = 7$，则$\cos A$的值为：A. $\frac{1}{2}$B. $\frac{1}{3}$C. $\frac{2}{3}$D. $\frac{3}{4}$8. 若$a^2 + b^2 = 1$，则$\sqrt{a^2 + b^2 + 2ab\cos C}$的值为：A. $1$B. $\sqrt{2}$C. $2$D. $\sqrt{3}$9. 若函数$f(x) = ax^2 + bx + c$在$x = 1$处取得极值，则$a + b + c$的值为：A. $0$C. $-1$D. 不确定10. 若$y = \log_2(3x - 1)$，则$y'$的值为：A. $\frac{3}{2}$B. $\frac{1}{2}$C. $\frac{3}{2} \ln 2$D. $\frac{1}{2} \ln 2$二、填空题（本大题共5小题，每小题5分，共25分。

2016年河南省普通高中招生考试试卷数 学注意事项：1．本试卷共8页，三个大题，满分120分，考试时间100分钟，请用蓝、黑色水笔或圆珠笔直接答在试卷上．2．答卷前请将密封线内的项目填写清楚．题号 一 二 三总分 1～8 9～15 16 17 18 19 20 21 22 23分数一、选择题（每小题3分，共24分）下列各小题均有四个答案，其中只有一个是正确的，将正确答案的代号字母填入题后括号内．1．31-的相反数是（ ） （A ）31- （B ）31（C ）－3 （D ）32．某种细胞的直径是0.00000095米，将0.00000095用科学计数法表示为 （ ）A.9.5×10－7B. 9.5×10－8C.0.95×10－7D. 95×10－83. 下列几何体是由4个相同的小正方体搭成的，其中主视图和左视图相同的是（ ）4．下列计算正确的是 （ ） （A ）＝（B ）（－3）2＝6（C ）3a 4-2a 3= a 2（D ）（－a 3）2=a 55. 如图，过反比例函数y=（x> 0）的图象上一点A ，作AB ⊥x 轴于点B ，S △AOB =2，则k 的值为（ ）（A ）2 （B ）3 （C ）4 （D ）56. 如图，在ABC 中，∠ACB=90°，AC=8，AB=10. DE 垂直平分AC 交AB 于点E ，则DE 的长为（ ）（A）6 （B）5 （C）4 （D）37、下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差：甲乙丙丁平均数（cm）185 180 185 180方差 3.6 3.6 7.4 8.1根据表中数据，要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择（）A．甲 B．乙 C．丙 D．丁8．如图，已知菱形OABC的顶点O(0,0)，B(2,2)，若菱形绕点O逆时针旋转，每秒旋转45°，则第60秒时，菱形的对角线交点D的坐标为（）(A)(1，-1) (B)(-1，-1) (C)(√2，0) (D)(0，√2)二、填空题（每小题3分，共21分）9．计算：（－2）0－＝ .10．如图，在□ABCD中，BE⊥AB交对角线AC于点E，若∠1=20°，则∠2的度数是 .11．关于x的一元二次方程x2+3x-k=0有两个不相等的实数根.则k的取值范围＝ .12．在“阳光体育”活动时间，班主任将全班同学随机分成了四组进行活动，该班小明和小亮同学被分在同一组的概率是 .13．已知A（0，3），B（2，3）抛物线y=-x2+bx+c上两点，则该抛物线的顶点坐标是 .14．如图，在扇形AOB中，∠AOB=90°，以点A为圆心，OA的长为半径作交于点C.若OA=2，则阴影部分的面积为______.15．如图，已知AD∥BC，AB⊥BC,AB=3,点E为射线BC上的一个动点，连接AE，将△ABE 沿AE 折叠，点B 落在点B'处，过点B'作AD 的垂线，分别交AD 、BC 于点M 、N,当点B'为线段MN 的三等份点时，BE 的长为 .三、解答题（本大题共8个小题，满分75分）16．（8分）先化简，再求值：)121()1(222++-÷-+x x x x x x ，其中x 的值从不等式组的整数解中选取。

数 学（理工类）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至2页，第Ⅱ卷3至10页。

满分150分。

考试时间120分钟。

考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷注意事项：1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号，不能答在试卷上。

3．本试卷共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一个是符合题目要求的。

参考公式：一、选择题：（１）设全集R U =，集合{}0>=x x M ，{}x x x N ≥=2，，则下列关系中正确的是A.M N M ∈B.M N M ⊆C.R N M =D.=N M C U )(φ（２）复数ii i 21)1)(2(2--+的值是A. 2B. -1C. i 2D.i 2-（３）某小组有4名男生，5名女生，从中选派5人参加竞赛，要求有女生且女生人数少于男生人数的选派方法种数有A. 40B. 45C. 105D. 110 （４）已知,a b 为两条不同的直线,,,αβγ为三个不同的平面，在下列四个命题中，①,,//a b a b αα⊥⊥则; ②,,//a a αβαβ⊥⊥则 ③,,//γαγβαβ⊥⊥则; ④,,//a a ααββ⊥⊥则真命题是A ,①④B ,①②C ,③④D ,②③（５）已知1F 、2F 是双曲线)0,0(12222>>=-b a by a x 的两个焦点，M 为双曲线上的点，若21MF MF ⊥，︒=∠6012F MF ，则双曲线的离心率为A ．13-B ．26C ．13+D ．213+（６）“2a =”是“6()x a -的展开式的第三项是604x ”的 条件。

A.充分不必要B. 必要不充分C. 充要D.既不充分也不必要（７）已知平面上三点A 、B 、C 满足3||=,4||=BC ,5||=，+∙BC ABCA BC ∙AB CA ∙+的值等于A. 25B. 24C.-25D. -24（８）球面上有三点A 、B 、C ，任意两点之间的球面距离都等于球大圆周长的四分之一，且过这三点的截面圆的面积为4π，则此球的体积为A. B. C. D. （９）直线)1(1:-=-x k y l 和圆0222=-+y y x 的关系是A .相离B .相切或相交C .相交D .相切（10）过点（-1，0）作曲线12++=x x y 的切线，其中一条切线为A.022=++y xB. 033=+-y xC. 01=++y xD. 01=+-y x （11）如图，ABCD 为矩形，AB=3，BC=1，EF//BC 且AE=2EB ，G 为BC 中点，K 为△ADF 的外心。

一、选择题（本大题共25小题，每小题4分，共100分）1. 若函数f(x) = x^2 - 3x + 2在区间[1, 2]上单调递增，则实数a的取值范围是（）A. a < 1B. a ≥ 1C. a < 2D. a ≥ 22. 已知向量a = (2, 3)，向量b = (-1, 2)，则向量a与向量b的点积是（）A. 1B. -1C. 7D. -73. 若等差数列{an}的公差d > 0，且首项a1 = 3，则第10项a10与第5项a5的和为（）A. 18B. 21C. 24D. 274. 在平面直角坐标系中，点A(2, 3)，点B(5, 1)在直线y = kx + b上，则直线AB的斜率k和截距b分别是（）A. k = -2，b = 7B. k = 2，b = 7C. k = -2，b = -7D. k = 2，b = -75. 若复数z满足|z - 3i| = 5，则复数z的实部取值范围是（）A. -2 ≤ Re(z) ≤ 2B. -5 ≤ Re(z) ≤ 5C. -5 ≤ Re(z) ≤ 2D. -2 ≤ Re(z) ≤ 56. 函数y = log2(x - 1)的图像与直线y = x相交于点P，则点P的坐标是（）A. (2, 1)B. (3, 2)C. (4, 3)D. (5, 4)7. 在△ABC中，∠A = 60°，∠B = 45°，则sinC的值为（）A. √3/2B. 1/2C. √2/2D. 18. 若函数f(x) = |x - 2| + |x + 1|在区间[-1, 2]上的最小值为4，则实数x的取值范围是（）A. -1 ≤ x ≤ 2B. -1 < x < 2C. -1 ≤ x < 2D. -1 < x ≤ 29. 若等比数列{an}的公比q > 0，且首项a1 = 2，则第5项a5与第3项a3的积为（）A. 16B. 32C. 64D. 12810. 在平面直角坐标系中，点P(1, 2)关于直线y = x的对称点为Q，则点Q的坐标是（）A. (2, 1)B. (1, 2)C. (2, 2)D. (1, 1)11. 若函数y = x^3 - 6x^2 + 9x - 1在区间[0, 2]上有极值点，则实数a的取值范围是（）A. a < 0B. a > 0C. a ≤ 0D. a ≥ 012. 在△ABC中，∠A = 30°，∠B = 75°，则sinC的值为（）A. √3/2B. 1/2C. √2/2D. 113. 若函数y = 2^x在区间[0, 1]上单调递增，则函数y = log2(x + 1)在区间[-1, 0]上（）A. 单调递增B. 单调递减C. 有极值点D. 不是单调函数14. 在平面直角坐标系中，点A(1, 2)，点B(4, 5)在直线y = kx + b上，则直线AB的斜率k和截距b分别是（）A. k = 1，b = 1B. k = 1，b = 3C. k = -1，b = 1D. k = -1，b = 315. 若复数z满足|z - 3i| = 5，则复数z的虚部取值范围是（）A. -2 ≤ Im(z) ≤ 2B. -5 ≤ Im(z) ≤ 5C. -5 ≤ Im(z) ≤ 2D. -2 ≤ Im(z) ≤ 516. 函数y = log2(x - 1)的图像与直线y = x相交于点P，则点P的坐标是（）A. (2, 1)B. (3, 2)C. (4, 3)D. (5, 4)17. 在△ABC中，∠A = 60°，∠B = 45°，则cosC的值为（）A. √3/2B. 1/2C. √2/2D. 118. 若函数y = |x - 2| + |x + 1|在区间[-1, 2]上的最大值为5，则实数x的取值范围是（）A. -1 ≤ x ≤ 2B. -1 < x < 2C. -1 ≤ x < 2D. -1 < x ≤ 219. 若等比数列{an}的公比q > 0，且首项a1 = 2，则第5项a5与第3项a3的积为（）A. 16B. 32C. 64D. 12820. 在平面直角坐标系中，点P(1, 2)关于直线y = x的对称点为Q，则点Q的坐标是（）A. (2, 1)B. (1, 2)C. (2, 2)D. (1, 1)21. 若函数y = x^3 - 6x^2 + 9x - 1在区间[0, 2]上有极值点，则实数a的取值范围是（）A. a < 0B. a > 0C. a ≤ 0D. a ≥ 022. 在△ABC中，∠A = 30°，∠B = 75°，则cosC的值为（）A. √3/2B. 1/2C. √2/2D. 123. 若函数y = log2(x + 1)在区间[-1, 0]上单调递增，则函数y = 2^x在区间[0, 1]上（）A. 单调递增B. 单调递减C. 有极值点D. 不是单调函数24. 在平面直角坐标系中，点A(1, 2)，点B(4, 5)在直线y = kx + b上，则直线AB的斜率k和截距b分别是（）A. k = 1，b = 1B. k = 1，b = 3C. k = -1，b = 1D. k = -1，b = 325. 若复数z满足|z - 3i| = 5，则复数z的实部取值范围是（）A. -2 ≤ Re(z) ≤ 2B. -5 ≤ Re(z) ≤ 5C. -5 ≤ Re(z) ≤ 2D. -2 ≤ Re(z) ≤ 5二、填空题（本大题共10小题，每小题5分，共50分）26. 已知函数f(x) = 2x - 3，若f(2) = 1，则x的值为______。

如何使用Word2003制作试卷密封线、装订线、模板2012-08-20 20:07:44 来源：评论：0点击：135一、设置页面试卷通常使用B4纸、横向、分两栏印刷，因此在制作之前，先要设置页面。

启动Word 2003（其他版本操作相似），新建一空白文...一、设置页面试卷通常使用B4纸、横向、分两栏印刷，因此在制作之前，先要设置页面。

启动Word 2003（其他版本操作相似），新建一空白文档。

执行“文件→页面设置”命令，打开“页面设置”对话框，切换到“纸张”标签下，设置纸张大小为B4纸；再切换到“页边距”标签下，设置好边距，并选中“横向”方向（图1）。

全部设置完成后，确定返回。

二、制作密封线正规的试卷上都有密封线，我们可以用文本框来制作。

执行“视图→页眉和页脚”命令，进入“页眉和页脚”编辑状态。

然后执行“插入→文本框竖排”命令，再在文档中拖拉出一个文本框（图2），并仿照图2的样式输入字符及下划线。

将光标定在文本框中，执行“格式→文字方向”命令，打开“文字方向&—文本框”对话框（图3），选中“右边”一种文字方向样式，确定返回。

将文本框定位到页面左边页边距外侧，并根据页面的大小调整好文本框的大小及字符位置等。

将鼠标移至文本框边缘处成“梅花状”时，双击鼠标，打开“设置文本框格式”对话框，在“颜色与线条”标签中，将“线条”设置为“无颜色线条”，确定返回。

最后单击“页眉和页脚”工具栏上的“关闭”按钮返回文档编辑状态，密封线制作完成（局部效果如图4）。

小提示：添加了页眉后，页眉处出现了一条横线，影响试卷的制作，我们可以用下面的方法将其清除：在页眉处双击鼠标，再次进入“页眉和页脚”编辑状态，执行“格式→边框和底纹”命令，打开“边框和底纹”对话框，在“边框”标签下，选中“无”边框样式，然后将其“应用于”“段落”，确定返回即可。

用Word制作试卷模版的方法和技巧[日期：2012-02-22] 来源：作者：[字体：大中小] 【摘要】介绍了用Word2000编排一张试卷模版的方法和技巧。

2016年河南省普通高中招生考试试卷数学注意事项：1．本试卷共8页，三个大题，满分120分，考试时间100分钟，请用蓝、黑色水笔或圆珠笔直接答在试卷上．2．答卷前请将密封线内的项目填写清楚．题号一二三总分1～8 9～15 16 17 18 19 20 21 22 23分数一、选择题（每小题3分，共24分）下列各小题均有四个答案，其中只有一个是正确的，将正确答案的代号字母填入题后括号内．1．的相反数是（）（A）（B）（C）－3 （D）32．某种细胞的直径是0.00000095米，将0.00000095用科学计数法表示为（）A.9.5×10－7B. 9.5×10－8C.0.95×10－7D. 95×10－83. 下列几何体是由4个相同的小正方体搭成的，其中主视图和左视图相同的是（）4．下列计算正确的是（）（A）＝（B）（－3）2＝6（C）3a4-2a3 = a2（D）（－a3）2=a55. 如图，过反比例函数y=（x> 0）的图象上一点A，作AB⊥x轴于点B，S△AOB=2，则k的值为（）（A）2 （B）3 （C）4 （D）56. 如图，在ABC中，∠ACB=90°，AC=8，AB=10. DE垂直平分AC交AB于点E，则DE的长为（）（A）6 （B）5 （C）4 （D）37、下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差：甲乙丙丁平均数（cm）185 180 185 180方差 3.6 3.6 7.4 8.1根据表中数据，要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择（）A．甲 B．乙 C．丙 D．丁8．如图，已知菱形OABC的顶点O(0,0)，B(2,2)，若菱形绕点O逆时针旋转，每秒旋转45°，则第60秒时，菱形的对角线交点D的坐标为（）(A)(1，-1) (B)(-1，-1) (C)(√2，0) (D)(0，√2)二、填空题（每小题3分，共21分）9．计算：（－2）0－＝ .10．如图，在□ABCD中，BE⊥AB交对角线AC于点E，若∠1=20°，则∠2的度数是 .11．关于x的一元二次方程x2+3x-k=0有两个不相等的实数根.则k的取值范围＝ .12．在“阳光体育”活动时间，班主任将全班同学随机分成了四组进行活动，该班小明和小亮同学被分在同一组的概率是 .13．已知A（0，3），B（2，3）抛物线y=-x2+bx+c上两点，则该抛物线的顶点坐标是 .14．如图，在扇形AOB中，∠AOB=90°，以点A为圆心，OA的长为半径作交于点C.若OA=2，则阴影部分的面积为______.15．如图，已知AD∥BC，AB⊥BC,AB=3,点E为射线BC上的一个动点，连接AE，将△ABE沿AE折叠，点B落在点B'处，过点B'作AD的垂线，分别交AD、BC于点M、N,当点B'为线段MN的三等份点时，BE的长为 .三、解答题（本大题共8个小题，满分75分）16．（8分）先化简，再求值：，其中x的值从不等式组的整数解中选取。

本文部分内容来自网络整理，本司不为其真实性负责，如有异议或侵权请及时联系，本司将立即删除！== 本文为word格式，下载后可方便编辑和修改！ ==8开试卷模板篇一：八开试卷模板试题第1页（共4页）试题第2页（共4页）试题第3页（共4页）试题第4页（共4页）篇二：8开高考试卷模板※※※※※※※※※※※※※※ ※※※※※※※ ※※※※※※※※※※※※※※ ※※※※※※※·●···装——订···● ··· ······校名··············密·班级密··················姓名—···················封考号封··········· ······ ··（··密—····封··线·· ···内·· ··线·不线··要··答····题·· ··）—·· ····●···装——订· ··●···※※※※※※※※※※※※※※※※※※※※※ ※※※※※※※※※※※※※※ ※※※※※※※201X年秋学期中学数学一年级上册测试题 (一)●···············●· ············································································································ ···········································································································●···············●封（密封线内不要答题密封）线线篇三：8开试卷模板※※※※※※※※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※●· ··装——订···● ··· ······校名···············密·班级密·················姓名—····················封··考号封················ ·· ··（··密—··封····线·· ··内·· ··线不线··要····答····题··）—··· ·●···· ··装——订· ··●···※※※※※※※※※※※※※※※※※※※※※ ※※※※※※※※※※※※※※ ※※※※※※※七年级数学《平面直角坐标系》练习题(考试时间∶90分钟满分∶100分)一、选择题（4分×6=24分） 1．点A（?3,4）所在象限为（）A、第一象限B、第二象限C、第三象限D、第四象限 2．点B（?3,0）在（）上A、在x轴的正半轴上B、在x轴的负半轴上C、在y轴的正半轴上D、在y轴的负半轴上3．点C在x轴上方，y轴左侧，距离x轴2个单位长度，距离y轴3个单位长度，则点C的坐标为（） A 、（2,3） B、（?2,?3）C、（?3,2） D、（3,?2） 4．若点P（x,y）的坐标满足xy=0，则点P 的位置是（）。