正弦稳态响应的一般求解方法

正弦稳态电路的分析1.复数法分析：a. 复数电压和电流表示：将正弦波电流和电压表示为复数形式，即I = Im * exp(jωt)，V = Vm * exp(jωt)，其中Im和Vm为幅值，ω为角频率，j为虚数单位。

b.使用欧姆定律和基尔霍夫定律来建立复数表达式。

c.找到电路中的频域参数，如电阻、电感和电容等，并使用复数法计算电路中的电流和电压。

d.计算电源电压和电流的相位差，这会决定电路中的功率因数。

2.相量法分析：a.相量表示：将电路中的电流和电压表示为相量形式，即以幅值和相位角表示，例如I=Im∠θ，V=Vm∠θ。

b.使用欧姆定律和基尔霍夫定律来建立相量表达式。

c.对电路中的频域参数应用相量法，计算电路中的电流和电压。

d.计算电源电压和电流的相位差，以确定电路中的功率因数。

无论是复数法还是相量法，分析正弦稳态电路的关键是计算电路中的电流和电压的幅值和相位。

在计算过程中，需要使用复数代数、欧姆定律、基尔霍夫定律以及频域的电路参数等相关知识。

在实际应用中，正弦稳态电路的分析主要包括以下几个方面：1.交流电路中的电阻：电阻对交流电流的影响与直流电路相同，即按欧姆定律计算。

复数法计算时，电流和电压与频率无关，可以直接使用欧姆定律计算。

2.交流电路中的电感：电感器对交流电流的响应取决于电流的频率。

复数法计算电感电压和电流时，需要将频率变量引入到电感的阻抗中。

3.交流电路中的电容：电容器对交流电压的响应取决于电压的频率。

复数法计算电容电压和电流时，需要将频率变量引入到电容的阻抗中。

4.交流电路中的复数阻抗：电路中的电感、电容和电阻组成复数阻抗。

复数阻抗可以用来计算电路中的电流和电压。

根据欧姆定律和基尔霍夫定律，可以建立复数电流和电压之间的关系。

5.交流电路中的功率因数：功率因数是电路中有功功率与视在功率之比。

在分析正弦稳态电路时，可以计算电路中电源电压和电流的相位差，从而确定功率因数。

总结起来，正弦稳态电路的分析步骤包括选择复数法或相量法、建立复数或相量表达式、计算电流和电压的幅值和相位、计算功率因数等。

第九章正弦稳态电路的分析本章内容1．阻抗和导纳的概念2．阻抗的串并联及电路的相量图3．正弦稳态电路的分析4．瞬时功率、有功功率、无功功率、视在功率、复功率及最大输出功率5．串联和并联谐振本章重点：正弦量的向量正表示; 正弦电路中的阻抗和导纳;正弦电路的分析串联谐振的谐振条件及特征; 并联谐振的谐振条件及特征本章重点：正弦电路参数的分析及最大功率输出的分析§9-1 阻抗和导纳阻抗和导纳是正弦电流电路分析的重要内容一、阻抗在无源的线性网络中，端口的电压相量与电流相量的比值定义为该一端口的阻抗（复阻抗），用Z表示。

式中：•U=U∠ϕu•I=I∠ϕI阻抗的模：Z= U/I，阻抗角：ϕZ= ϕu-ϕi 阻抗的代数式： Z=R+jX式中：R—电阻 X—电抗1．若网络N 0内只含单一元件，则单一元件的复阻抗（1）电阻的复阻抗：Z R =R（2）电感的复阻抗：Z L =ωj L=jX L X L =ωL —感抗 （3）电容的复阻抗：Z C =cj ω1=c jω1-=jX C X C =cω1-—容抗 2．若网络N 0内为RLC 串联，则阻抗为（1）阻抗：Z=•U /•I = R+ωj L+cj ω1=R+j(ωL-Cω1)=R+jx=Z ϕ∠Z可见：阻抗Z 的实部为电阻R （R=Z cos ϕZ ），阻抗Z 的虚部为电抗X （X= R=Z sin ϕZ ），三者构成阻抗三角形 （2） 阻抗的模：Z =22)(C L X X R -+=22X R +=U/I （3）阻抗角：ϕZ =arctanR X X C L -=RX=ϕu -ϕi X 〉0 ωL>C ω1电路呈电感性 X<0 ωL<Cω1电路呈电容性X=0 电路呈电阻性一、 导纳：复阻抗的倒数定义为复导纳（电流相量与对应端口的电流相量的比值），用Y 表示 Y=Z 1=••UI =)(u i U Iϕϕ-∠=Y Y ϕ∠导纳的模： Y =U I导纳角： Y ϕ=u i ϕϕ- 导纳的代数式： Y=G+JB式中：G —电导 B —电纳1．若网络N 0内只含单一元件，则单一元件的复阻抗 （1） 电阻的复导纳：Y R =G=1/R （2） 电感的复导纳：Y L =Lj ω1=L jω1- =jB L B L =Lω1-—感纳 （3）电容的复导纳：Z C ==ωj C =jB C B C =ωC —容纳2．若网络N 0内为RLC 并联，则导纳为(1)导纳Y=••UI基尔霍夫电流定律的相量形式：∑•I =0•I =•I R +•I L +•I C =⎥⎦⎤⎢⎣⎡-+)1(1L C j R ωω•U =G+j(B C +B L )•UY=R 1+L j ω1+ωj C=R1+)1(L C j ωω-=G+jB可见：导纳Y 的实部为电导G （G=Y cos ϕY ），导纳Y 的虚部为电纳B （B= Y sin ϕY ），三者构成导纳三角形 （2）导纳的模：Y =22)(L C B B G -+=22B G +=I/U （3）阻抗角：ϕY =arctanG B B L C -=GB=ϕi -ϕu B 〉0 ωC>L ω1电路呈电容性 B<0 ωC<Lω1电路呈电感性B=0 电路呈电阻性二、阻抗和导纳相互转换（自学）§9-2 阻抗（导纳）串联和并联阻抗的串并联与电阻的串并联的计算规则相同，只是要把电阻换成阻抗。

第9章 正弦稳态电路的频率响应9.1 网络函数【网络函数（传递函数）】 网络函数又称为传递函数。

图9-1-1所示正弦稳态下的线性时不变电路，只有一个激励()E j ω 和一个响应()R j ω ，称为单输入――单输出网络，网络函数()H j ω定义为def()()()Rj H j E j ωωω= 由于激励()Ej ω 和响应()R j ω 均可以是端口电压或电流，且可以位于不同端口，也可以位于同一个端口，因此，网络函数有6种类型。

网络函数取决于电路的结构，参数和激励的角频率。

图9-1-1 单输入――单输出网络【频率响应】 正弦稳态电路的响应随激励角频率的变化规律，称为电路的频率响应。

网络函数()H j ω能反映线性时不变电路的频率响应，通常将()H j ω写成极坐标形式，即()()()H j H j j ωωϕω=∠【幅频特性】 ()H j ω表征响应的幅值随激励角频率的变化规律，称为幅频响应，亦称幅频特性。

【相频特性】 ()j ϕω表征响应的相角随激励角频率的变化规律，称为相频响应，亦称相频特性。

【例9-1-1】 试确定图9-1-2所示电路的电流增益()()()o s Ij H j I j ωωω= 。

sI0.5Fo图9-1-2 例9-1-1 图解 由分流关系可得42(1)12420.5s sj I I j I j jωωωω+==++- 因此()(1)arctan 22osI H j j I ωωω==+=9.2 谐振电路的频率响应【谐振】 至少包含一个电感和一个电容元件的无源一端口网络，当其端口等效阻抗（或导纳）呈现纯电阻性时，称电路发出了谐振，或电路工作在揩振状态。

【谐振电路】 谐振电路对信号频率具有选择性，广泛应用于通信系统中。

最简单的揩振电路为RLC 串联谐振电路和RLC 并联揩振电路。

9.2.1 RLC 串联揩振电路【RLC 串联谐振角频率】 图9-2-1所示为RLC 串联电路。

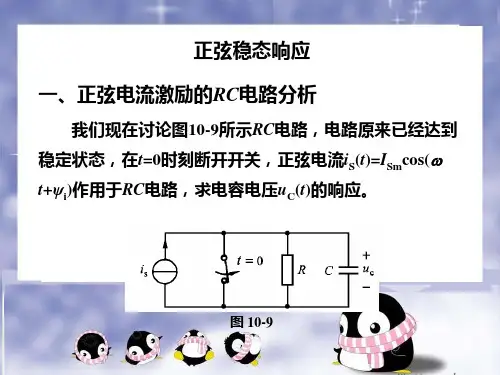
正弦电路三要素法求解正弦电路是交流电路的一种重要形式，其特点是电流和电压的大小和方向都随时间变化。

在正弦电路中，可以使用三要素法来求解相关的参数，包括初始值、稳态值、时间常数、阻尼系数和相位差。

1.初始值初始值是指在时间t=0时的电路参数值。

在正弦电路中，初始值通常表示为I0（电流的初始值）和U0（电压的初始值）。

这些初始值可以根据电路的元件参数和连接方式进行计算。

2.稳态值稳态值是指在时间t趋于无穷大时的电路参数值。

在正弦电路中，稳态值表示为I∞（电流的稳态值）和U∞（电压的稳态值）。

当电路达到稳态时，所有动态元件的变量都将停止变化，此时的电流和电压值即为稳态值。

3.时间常数时间常数是描述电路动态特性的一个参数，它决定了电路达到稳态值所需的时间。

在正弦电路中，时间常数可以通过元件参数计算得出，它表示为R/L（电阻与电感的比值）。

时间常数越小，电路达到稳态所需的时间就越短。

4.阻尼系数阻尼系数是指在正弦电路中，用来描述电流或电压幅值衰减快慢程度的参数。

阻尼系数越大，幅值的衰减速度就越快。

在正弦电路中，阻尼系数可以通过元件参数计算得出，它表示为1/（R^2*C），其中C是电容器的电容量。

5.相位差相位差是指在正弦电路中，两个同频率的正弦量之间的相位差。

相位差可以通过计算两个同频率正弦量之间的相位角差来得到。

相位差的大小和方向可以影响正弦电路的性能和输出。

通过使用三要素法，我们可以求解正弦电路的相关参数，包括初始值、稳态值、时间常数、阻尼系数和相位差。

这些参数对于理解和分析正弦电路的性能具有重要的意义。