数值分析3-插值方法
- 格式:ppt
- 大小:1.84 MB
- 文档页数:16
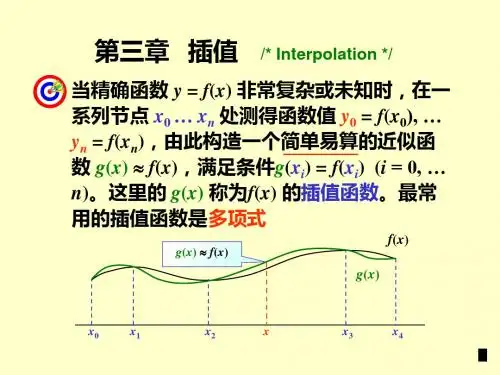


数值分析插值法插值法是数值分析中的一种方法,用于通过已知数据点的函数值来估计介于这些数据点之间的未知函数值。
插值法在科学计算、数据处理、图像处理等领域中得到广泛应用。
插值法的基本思想是通过已知数据点构造一个函数,使得该函数逼近未知函数,并在已知数据点处与未知函数值相等。
插值法的关键是选择适当的插值函数,以保证估计值在插值区间内具有良好的近似性质。
常用的插值法有拉格朗日插值法、牛顿插值法和埃尔米特插值法等。
以下将分别介绍这些插值法的原理及步骤:1. 拉格朗日插值法:拉格朗日插值法通过构造一个多项式函数来逼近未知函数。
假设已知n+1个数据点(x0, y0), (x1, y1), ..., (xn, yn),其中x0, x1, ..., xn为给定的节点,y0, y1, ..., yn为对应的函数值。
拉格朗日插值多项式的一般形式为:L(x) = y0 * l0(x) + y1 * l1(x) + ... + yn * ln(x)其中l0(x), l1(x), ..., ln(x)为拉格朗日基函数,定义为:li(x) = (x - x0)(x - x1)...(x - xi-1)(x - xi+1)...(x - xn) / (xi - x0)(xi - x1)...(xi - xi-1)(xi - xi+1)...(xi - xn)拉格朗日插值法的步骤为:a. 计算基函数li(xi)的值。
b.构造插值多项式L(x)。
c.计算L(x)在需要估计的插值点上的函数值f(x)。
2.牛顿插值法:牛顿插值法通过构造一个差商表来逼近未知函数。
差商表的第一列为已知数据点的函数值,第二列为相邻数据点的差商,第三列为相邻差商的差商,以此类推。
最终,根据差商表中的数值,构造一个差商表与未知函数值相等的多项式函数。
牛顿插值法的步骤为:a.计算差商表的第一列。
b.计算差商表的其他列,直至最后一列。
c.根据差商表构造插值多项式N(x)。

数值分析中的插值理论及应用数值分析是一门研究数学运算方法在计算机上实现的学科。
在数值分析中,插值是一种常用的数值近似方法,用于估计或预测在给定数据点之间的未知数值。
本文将介绍插值理论的基本概念和常见方法,并探讨其在实际应用中的作用和意义。
一、插值理论的概念插值是指通过已知数据点之间的数值关系,计算得出新的数据点的数值。
在数值分析中,插值主要用于以下两个方面:1. 数据重建:在给定的数据点上,通过插值方法得到相应函数的近似曲线。
这样可以对已知数据进行补充和估计,使数据更加完整。
2. 函数逼近:在某个区间内,通过数据点之间的插值方法得到一个与原函数相似的函数,以便分析和处理。
二、常见的插值方法以下是数值分析中常见的几种插值方法:1. 线性插值:线性插值是最简单的插值方法之一,其思想是通过已知数据点的连线来估计新数据点的数值。
线性插值适用于数据点之间变化较为平缓的情况。
2. 拉格朗日插值:拉格朗日插值是一种多项式插值方法,通过已知数据点和一个构造的拉格朗日多项式,计算新数据点的数值。
拉格朗日插值适用于任意数据分布的情况。
3. 牛顿插值:牛顿插值是一种基于差商的插值方法,通过已知数据点和一个构造的牛顿插值多项式,计算新数据点的数值。
牛顿插值适用于数据点较为密集的情况。
4. 样条插值:样条插值是一种光滑插值方法,通过已知数据点和一个构造的光滑曲线,计算新数据点的数值。
样条插值适用于数据点较为离散和分段光滑的情况。
三、插值方法的应用插值方法在各个领域都有广泛的应用,以下是一些典型的应用场景:1. 数学建模:在数学建模中,常常需要通过已知数据点进行函数逼近和数值预测。
插值方法可以用来构建逼近函数和预测模型,为建模提供支持。
2. 图像处理:在图像处理中,插值方法可以用于图像的放大、缩小和重建。
通过已知像素点之间的插值,可以获得新的像素点的数值,从而改变图像的大小和清晰度。
3. 数据分析:在大数据分析中,常常需要对缺失数据进行估计和填补。




数值分析中的插值算法及其应用数值分析是研究解决数学问题的数值方法的一门学科。
其中,插值算法是数值分析中重要的方法之一。
插值是指在给定一些数据点的情况下,用一些方法建立一个函数,该函数可以在给定区间内的任何一点上计算出函数值。
插值方法有很多种,其中比较常用的有拉格朗日插值法、牛顿插值法和埃尔米特插值法。
1. 拉格朗日插值法拉格朗日插值法是一种将一个多项式函数p(x)与一系列已知数据点相联系的方法。
假设给定n个数据点(x1, y1), (x2, y2), ..., (xn, yn),其中x1 < x2 < ... < xn,那么可以构造一个次数小于等于n-1的多项式函数p(x)满足p(xi) = yi,i=1,2,...,n。
设p(x)的表达式为:p(x) = Σyi li(x)其中,li(x)为拉格朗日基函数。
每个基函数都满足:li(xi) = 1, li(xj) = 0, j≠i基函数的表达式为:li(x) = Π[j≠i] (x - xj) / (xi - xj)利用拉格朗日插值法,可以在给定数据点的情况下,快速计算函数在其他点上的值。
2. 牛顿插值法牛顿插值法是一种利用差商的方法建立插值多项式的方法。
相比于拉格朗日插值法,牛顿插值法更注重于递推计算。
给定n个数据点(x1, y1), (x2, y2), ..., (xn, yn),牛顿插值法可以建立一个关于x的n次多项式。
首先,定义一个差商:f[xi] = yif[xi, xi+1, ..., xj] = (f[xi+1, ..., xj] - f[xi, ..., xj-1]) / (xj - xi)差商f[xi, xi+1, ..., xj]是由区间(xi, xj)内的函数值f(xi), f(xi+1), ..., f(xj)所计算得到的。
定义一个新的多项式qk(x),其中:qk(x) = f[x0, x1, ..., xk] + (x - xk) qk-1(x)其中q0(x) = f[x0]。



数值分析中常用的插值方法在数值计算中,许多问题都可以用插值方法来近似求解,比如曲线拟合、函数逼近和图像重建等。
插值方法是指在已知数据点的情况下,通过一些数值计算技巧,在每个数据点处构造一个多项式函数,使得该函数在每个数据点处都能通过数据点。
在数据点之间计算函数值时,就可以使用这个多项式函数进行估算。
接下来,我们就来详细介绍一些常见的插值方法。
一、拉格朗日插值法拉格朗日插值法是一个经典的插值方法,它的思想是通过给定的数据点,构造一个经过这些点的多项式函数进行逼近。
具体来讲,拉格朗日插值法会首先构造一个基函数,该函数满足只在其对应的数据点处等于1,其余的数据点处等于0。
然后,根据基函数和数据点,构造一个多项式函数,使得该函数在每个数据点处都能通过数据点。
最终得到的多项式函数就是插值函数。
优点:简单易懂,使用较为广泛。
缺点:多项式次数较高时造成的误差会较大,且在数据点密集的区域可以出现龙格现象,使得插值函数在某些区间内呈现大幅度振荡。
二、牛顿插值法牛顿插值法是一种递推式的插值方法,它通过利用已知的数据点和前面已经计算出来的差商,得到一个逐步逼近的插值函数。
具体来讲,牛顿插值法会先将已知的数据点连成一条曲线,然后逐个向这条曲线添加新的数据点,每次添加一个新的数据点后,将差商计算出来并加入到之前的差商序列中,最终得到一个多项式函数,它在每个数据点处都能通过数据点。
牛顿插值法的优缺点与拉格朗日插值法相似,但是由于牛顿插值法是递推式的,可以方便的添加新的数据点,因此在数据点多变的情况下,牛顿插值法具有很大的优势。
三、分段插值法分段插值法是一种将插值区间划分为多个子区间的插值方法,在每个子区间内使用插值方法进行插值,然后将所有子区间内的插值函数拼接起来,得到最终的插值函数。
分段插值法主要分为两种:线性分段插值和三次样条插值。
1.线性分段插值线性分段插值的思路很简单,即在每个数据点处构造两条直线,在数据点之间的区间内使用一条直线作为插值函数。
数值分析中的插值方法应用数值分析是一门研究数值计算方法和计算机求解数学问题的学科。
在实际问题中,我们经常需要根据有限的数据估计和预测未知数值,而插值方法就是一种常用的数值计算技术,用来构造未知数据点的函数表达式。
本文将介绍数值分析中的插值方法及其应用。
一、线性插值方法1. 线性插值原理线性插值是一种简单而常用的插值方法,它假设函数在给定的两个数据点之间是线性的。
根据两个已知数据点(x0, y0)和(x1, y1),可以通过以下公式求得在这两个点之间插值的函数表达式:y = y0 + (x - x0) * (y1 - y0) / (x1 - x0)2. 线性插值应用场景线性插值方法适用于对连续函数进行近似估计的场景。
例如,在传感器数据处理中,由于数据采样的时间间隔有限,我们需要通过线性插值方法来估计中间时刻的数据值,以获得更精确的测量结果。
二、拉格朗日插值方法1. 拉格朗日插值原理拉格朗日插值是一种基于多项式的插值方法,它通过构造一个满足已知数据点的多项式函数来进行插值。
给定n个数据点,拉格朗日插值多项式的表达式如下:P(x) = Σ yi * li(x),i=0 to n其中,yi是第i个数据点的函数值,li(x)是拉格朗日基函数,计算公式为:li(x) = Π (x - xj) / (xi - xj),j ≠ i2. 拉格朗日插值应用场景拉格朗日插值方法适用于对离散数据进行高次多项式逼近的场景。
例如,在数据拟合中,我们可利用拉格朗日插值方法构造出一个多项式函数,以逼近已知数据点所代表的曲线,从而进行数据的预测和估计。
三、牛顿插值方法1. 牛顿插值原理牛顿插值是一种利用差商的插值方法,它通过构造一个满足已知数据点的插值多项式来进行插值。
给定n个数据点,牛顿插值多项式的表达式如下:P(x) = f[x0] + Σ f[x0, ..., xi] * Π (x - xj),i=0 to n-1其中,f[x0, ..., xi]是差商,计算公式为:f[x0, ..., xi] = (f[x1, ..., xi] - f[x0, ..., xi-1]) / (xi - x0)2. 牛顿插值应用场景牛顿插值方法适用于对具有大量数据点的函数进行插值和逼近的场景。
数值分析插值法数值分析是数学的一个分支,用于研究如何使用数值方法来近似和解决数学问题。
插值是数值分析的一个重要概念,它涉及到如何通过已知数据点的信息来估计未知数据点的值。
在本文中,我们将着重讨论插值法。
插值法是一种基于已知数据点的函数值,通过建立适当的插值函数来估计未知数据点的函数值的方法。
插值问题的目标是找到一个函数f(x),使得f(x_i)=y_i(i=0,1,2,...,n),其中x_i是已知的数据点,y_i是相应的函数值,n是已知数据点的数量。
然后,通过插值函数可以近似估计任意一个未知数据点的函数值。
常见的插值方法包括拉格朗日插值、牛顿插值和埃尔米特插值等。
下面我们将逐一介绍这些插值方法。
拉格朗日插值是一种利用拉格朗日多项式进行插值的方法。
拉格朗日多项式是一个多项式函数,满足通过已知数据点的函数值。
具体地说,设给定的已知数据点为(x_i,y_i),我们需要找到一个多项式P(x)=y,使得P(x_i)=y_i。
拉格朗日插值多项式的形式如下:P(x)=Σ(y_i*l_i(x))其中l_i(x)是拉格朗日基函数,它定义为:l_i(x)=Π((x-x_j)/(x_i-x_j))(j≠i)牛顿插值是另一种常用的插值方法。
它通过使用差商来递归地计算插值多项式。
差商是一个递归定义的函数,用于计算多项式的系数。
设给定的已知数据点为(x_i,y_i),我们需要找到一个多项式P(x)=y,使得P(x_i)=y_i。
牛顿插值多项式的形式如下:P(x)=y_0+(x-x_0)*f[x_0,x_1]+(x-x_0)*(x-x_1)*f[x_0,x_1,x_2]+...其中,f[x_i,x_j,...,x_k]是差商的定义,它可以通过递归公式计算得到:f[x_i,x_j,...,x_k]=(f[x_j,...,x_k]-f[x_i,...,x_{k-1}])/(x_k-x_i)埃尔米特插值是一种利用已知数据点及其导数信息进行插值的方法。
数值分析中的插值方法在数值分析中,插值是一种通过在已知数据点之间估计未知数据点的方法。
它是一种常见的数据处理技术,用于填补数据间的空白,揭示数据间的关联性,或者建立数据模型。
在本文中,我们将讨论数值分析中的几种常见的插值方法。
一、拉格朗日插值拉格朗日插值是一种基于多项式的插值方法。
假设有n个离散数据点,我们想要在这些点之间插值得到未知数据点的值。
拉格朗日插值可以通过构建一个n次多项式来实现。
例如,给定三个数据点(x0, y0),(x1, y1),(x2, y2),我们可以假定插值多项式为:P(x) = y0 * L0(x) + y1 * L1(x) + y2 * L2(x)其中,L0(x),L1(x),L2(x)是拉格朗日插值多项式的基函数,由以下公式得到:L0(x) = (x - x1) * (x - x2) / ((x0 - x1) * (x0 - x2))L1(x) = (x - x0) * (x - x2) / ((x1 - x0) * (x1 - x2))L2(x) = (x - x0) * (x - x1) / ((x2 - x0) * (x2 - x1))利用这些基函数,我们可以得到插值多项式P(x),从而计算出未知点的值。
二、牛顿插值牛顿插值是另一种常见的插值方法,也是基于多项式的。
与拉格朗日插值不同的是,牛顿插值使用了差商的概念来构建插值多项式。
差商是一种表示数据间差异的指标,它可以用于计算插值多项式的系数。
对于n个数据点,差商可以由以下递归公式计算得到:f[x0] = f(x0)f[x0, x1] = (f[x1] - f[x0]) / (x1 - x0)f[x0, x1, ..., xn] = (f[x1, x2, ..., xn] - f[x0, x1, ..., xn-1]) / (xn - x0)基于差商,我们可以得到牛顿插值多项式的表达式:P(x) = f[x0] + f[x0, x1] * (x - x0) + f[x0, x1, x2] * (x - x0) * (x - x1) + ...利用牛顿插值,我们可以通过已知数据点构建插值多项式,进而估计未知点的值。
数值分析-插值法我们能得到⼀个函数f在区间[a,b]上某些点的值或者这些点上的⾼阶导数我们就能通过插值法去得到⼀个函数g,g与f是⾮常相近的⼀般来说g分为三类,⼀类是n次多项式 a n*x n +a n-1*x n-1 + .......+a0,⼀类是三⾓多项式,最后⼀类是分段n次多项式多项式插值这个可以说是最简单的插值了对于a n*x n +a n-1*x n-1 + .......+a0,我们有n+1个未知数,我只需要知道n+1个点的函数值就可以解出这n+1个未知数将解出的值带⼊即可优点:简单粗暴缺点:要解n+1个⽅程,时间复杂度较⾼,n不好确定,若n过⼤,容易过拟合,若n过⼩,容易⽋拟合拉格朗⽇插值先说⼀阶多项式我们有两点式f(x) = y k*(x k+1 - x) / (x k-x k+1) + y k+1*(x-x k) / (x k+1 - x k)此两点式可以看做∂ * y k + (1-∂) * y k+1那么⾃然的在x=x k的时候 ∂=0 在x=x k+1的时候∂=1这⾥的∂其实是与x相关的⼀阶多项式再说⼆阶多项式对于⼀个⼆次函数,我们有三个点(x k-1,y k-1) ,(x k,y k) ,(x k+1,y k+1)我们有l k-1,l k,l k+1f(x) = l k-1*y k-1 + l k*y k + l k+1*y k+1其中l是与x相关的⼆次多项式我们可以把l当作基函数这样的话就有x = x k-1 时l k-1 = 1, l k=0, l k+1 = 0x = x k时 l k-1 = 0, l k=1, l k+1 = 0x = x k+1时l k-1 = 0, l k=0, l k+1 = 1那么这个插值基函数是很好求的因为每个插值函数都有两个零点对于l k-1来说有零点x k,x k+1那么lk-1就可以表⽰为l k-1 = A*(x-x k)*(x-x k+1)因为x=xk-1时l k-1 = 1所以A = 1 / ((x k-1 - x k)* (x k-1 - x k+1) )那么同理l k和l k+1也能求出来了那我们得到⼆阶的拉格朗⽇插值多项式现在将⼆阶推⼴到n阶得到n接的拉格朗⽇插值多项式余项:R n(x) = f(x) - L n(x) R n(x)表⽰n次拉格朗⽇多项式的插值余项R n(x) = f n+1(e)/(n+1)! * w n+1(x) e属于[a,b]且依赖与x w n+1(x) = (x-x0)(x-x1).......(x-x n)优点:算法较为简单缺点:⽆法处理动态增加节点的情况⽜顿插值还是先从⼀阶到⼆阶进⾏说明我先得到了⼀阶差值多项式P1(x),P1(x) 满⾜过点(x1, f(x1)), (x2,f(x2))假设现在有第三个点(x3,f(x3))我们要通过这个点去得到⼆阶差值多项式P2(x) 使得P2(x)过这三个点可以设P2(x) = P1(x) + a2*(x-x0)*(x-x1)通过第三个点解出a2就⾏了推⼴到多阶那么可以得到P n(x) = a0 + a1(x-x0) + a2(x-x0)(x-x1) + a3(x-x0)(x-x1)(x-x2) + ......求这个插值多项式的值可以通过递推⼀步⼀步的求这样就实现了动态增删可以看到计算a k需要计算(k-1)2次,那么⽜顿插值法就是⼀个快速的计算⽅法均差⼀阶均差 f[x0, x k] = ( f(x k) - f(x0) ) / (x k - x0)⼆阶均差 f[x0, x1, x2] = (f[x0, x2] -f[x0, x1] ) / (x2 - x1)可以看到⼀阶均差就是简单的求斜率⼆阶均差就是对⼀阶均差求斜率那么k阶均差就是f[x0, x1,,,,,,x k] = (f[x0,,,,,x k-2, x k] -f[x0, ,,,,,,,x k-2,x k-1] ) / (x k - x k-1)f[x0, x1,,,,,,x k] = f n(ε) / n!均差的性质k阶均差可表⽰为f(x0),f(x1), f(x2),,,,,,,,, f(x k)的线性组合⽜顿插值中的a就是均差,可以从⼀阶开始推,然后使⽤数学归纳法证明那么⽜顿插值多项式就是:在计算f[x0,x1,,,,,,,,,,x n]时,⼀般使⽤均差表均差表的计算⽅式为a[i,j] = ( a[i-1][j] - a[i-1][j-1] ) / (末尾的x - 最开始的x)误差:误差为最后⼀阶的均差 * w(x)优点:可动态增删节点缺点:⽆法处理要求导数相同的情况埃尔⽶特插值法实验报告⼀个点,多个导数:⽜顿插值中的均差在xi->x0时其实分别是i阶导数,这样就是我们熟悉的泰勒多项式此时的插值函数就是泰勒多项式两个点,⼀个导数我们有三个条件,也就是说我们能求出三次插值多项式这时我们先写出过这两个点的⽜顿插值多项式在这个多项式的基础上我们再加上⼀个三次项搞定,可以观察到,这三个项数其实可以算是正交的,因为当x=x1或者x=x2时最后⼀项是0满⾜条件的两个点,两个导数这也是题⽬所要求的情况因为有两个导数,所以⽜顿插值法⽆法解决,这⾥只能使⽤基函数⽅法设插值函数为H(x), 点与导数分别为(x1,y1,m1),(x2,y2,m2)H(x)满⾜:H(x1) =y1, H(x2) = y2, H(x1)’ = m1,H(x2)=m2H(x) = a1*x1 + a2*x2 + b1*m1 + b2*m2其中 a1, a2, b1, b2均为三层插值多项式X=x1时 a1(x1) = 1,a2(x1) = 0, b1(x1) = 0,b2(x1) = 0,a1’(x1) = 1,a2’(x1) = 0X=x2时 a1(x2) = 0,a2(x2) = 1, b1(x2) = 0,b2(x2) = 0,a1’(x2) = 1,a2’(x2) = 0X=x1时 b1’(x1) = 1,b2’(x1) = 0X=x2时b1’(x1) = 0,b2’(x1) = 1然后⽤了⼀个很巧妙的⽅法设基函数,解出来值和就是这样⼦的R3(x) = 1/4! * (x-x k)2(x-x k+1)2*f4(ε)两个点,两个导数2直接使⽤泰勒多项式,并把将余项改为未知数,使⽤多余的⼀个条件去求余项的值例如:求次数⼩于等于3的多项式P(x),使满⾜条件P(x0)=f(x0),P'(x0)=f'(x0),P"(x0)=f"(x0),P(x1)=f(x1)。