设计中心对称图形高品质版
- 格式:ppt
- 大小:797.00 KB
- 文档页数:23

23.2.2中心对称图形【教学目标】 一、知识与技能让学生经历观察、探究、发现、讨论、阅读的过程,学习中心对称图形的定义和性质。
二、过程与方法1.通过学生动手、合作和讨论,培养学生的参与意识,加强学生的合作与交流精神。
2.同时使学生积累一定的审美体验。
三、情感态度与价值观激发学生学习数学的兴趣,使学生更加喜欢数学。
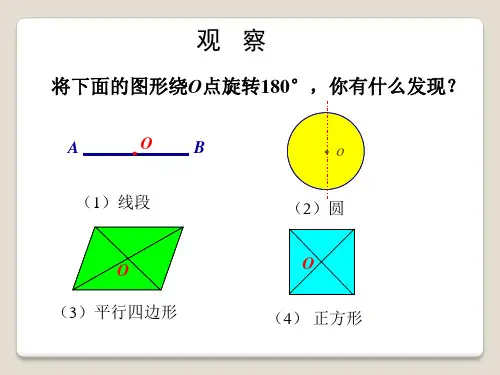
四、教学重难点教学重点:理解中心对称图形的定义及其性质教学难点:理解中心对称图形的定义,会判断哪些图形是中心对称图形 【教学过程】 一、情景导入同学们,让我们用数学的眼光去欣赏这些图片,用所学的数学知识去描述它们二、新授过程 1.动手试一试,想一想图1图3图5图2图4下面这些图形通过怎样的变换可以与原来的图形重合?2、观察与发现(中心对称图形的有关概念)如果一个图形绕一个点_________后,能和_________ ,那么这个图形叫做_________;这个点叫做它的_________互相重合的点叫做_________. 如图(见课件)中_________是中心对称图形,对称中心是_________,点A的对称点是______,点D的对称点是______。
3、请欣赏下列图形4、生活中,你还见过哪些中心对称图形?请举例说明.5、问题:判断下列图形是否是中心对称图形?如果是,那么对称中心在哪里?(见课件)6、练习,a选择题:(1)下列图形中即是轴对称图形又是中心对称图形的是()A 角B 等边三角形C 线段D平行四边形(2)下列多边形中,是中心对称图形而不是轴对称图形的是()A平行四边形B矩形C菱形D正方形b小魔术:小明先拿出图(1)所示的四张纸牌,然后背着大家将其中某一张旋转了180°,得到图(2)。
问小明旋转的是哪一张?(见课件)三、探索1、我们已经知道,平行四边形是中心对称图形,根据你的思考,你能验证平行四边形的哪些性质?你能进而总结中心对称图形的性质吗?(见课件)2、中心对称图形的性质:对称点的连线经过_________并且被对称中心_________3、(看谁算得快)如图,有一组数排列成方阵,试计算这组数的和。
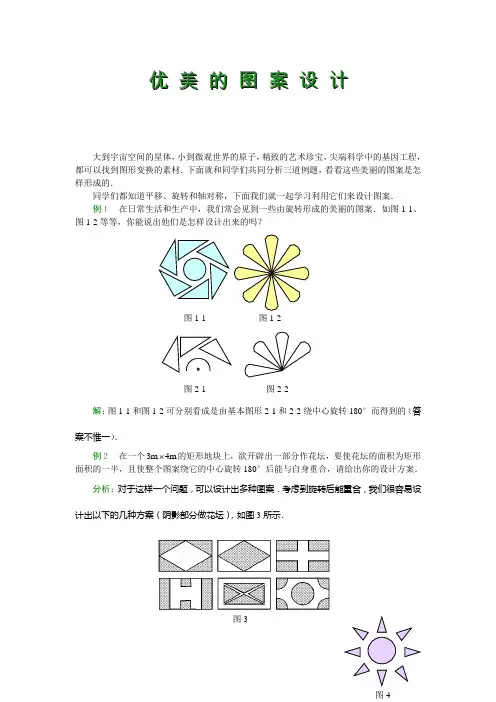
优 美 的 图 案 设 计大到宇宙空间的星体,小到微观世界的原子,精致的艺术珍宝,尖端科学中的基因工程,都可以找到图形变换的素材.下面就和同学们共同分析三道例题,看看这些美丽的图案是怎样形成的.同学们都知道平移、旋转和轴对称,下面我们就一起学习利用它们来设计图案. 例1 在日常生活和生产中,我们常会见到一些由旋转形成的美丽的图案.如图1-1、 图1-2等等,你能说出他们是怎样设计出来的吗?解:图1-1和图1-2可分别看成是由基本图形2-1和2-2绕中心旋转180°而得到的(答案不惟一).例2 在一个3m 4m 的矩形地块上,欲开辟出一部分作花坛,要使花坛的面积为矩形面积的一半,且使整个图案绕它的中心旋转180°后能与自身重合,请给出你的设计方案. 分析:对于这样一个问题,可以设计出多种图案.考虑到旋转后能重合,我们很容易设计出以下的几种方案(阴影部分做花坛),如图3所示.图3图1-1 图1-2 图2-1 图2-2 图4例3请同学们分析下面图4中的图案能不能由旋转形成?如果能,旋转中心在哪里?它绕旋转中心最少旋转多少度后能与自身重合?分析:仔细观察图4可以发现,它可以由旋转得到,它的旋转中心是圆的圆心.图案由两部分组成,一是圆,一是三角形,这一图形旋转多少度后能与自身重合,显然取决于图形中的三角形的个数.图中共有八个完全相同的三角形,它们均匀的分布在圆的周围,正好把整个圆周平分成了八等份.这样,只要此图形绕其圆心旋转136045⨯︒=︒就能与自身重合.8探索:请同学们自己分析图5中的各个图形,指出旋转中心在哪里?它绕旋转中心最少旋转多少度能与自身重合?如果让你来设计下面的图案,你会设计吗?与同学交流你的设计方法.有条件的同学,不妨用电脑操作一下,体验用电脑设计图案的乐趣.图5。