材料力学习题册答案-第1章 绪论1
- 格式:pdf
- 大小:372.60 KB
- 文档页数:12

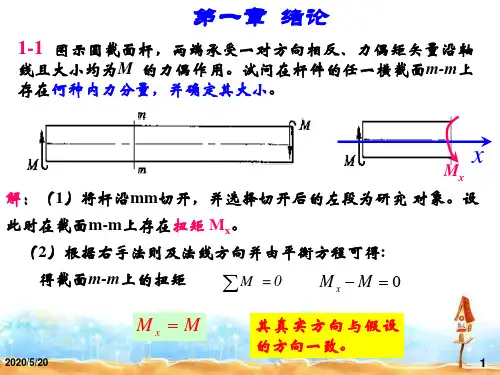
材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆,两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量,并确定其大小。
解:从横截面m-m将杆切开,横截面上存在沿轴线的内力偶矩分量M x,即扭矩,其大小等于M。
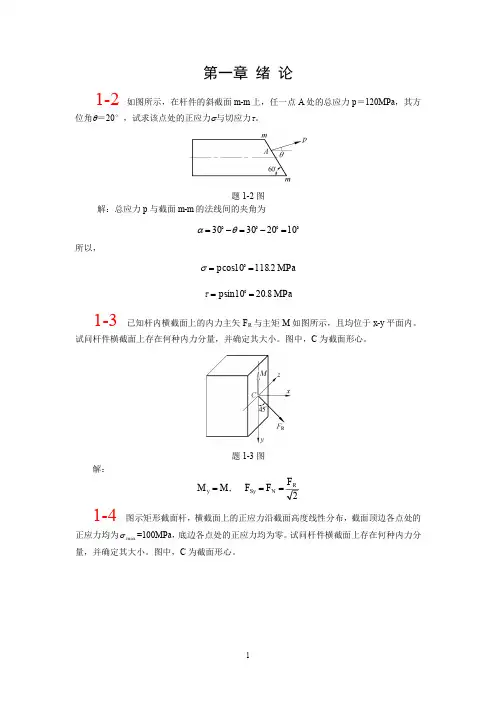
1-2 如图所示,在杆件的斜截面m-m上,任一点A处的应力p=120 MPa,其方位角θ=20°,试求该点处的正应力σ与切应力τ。
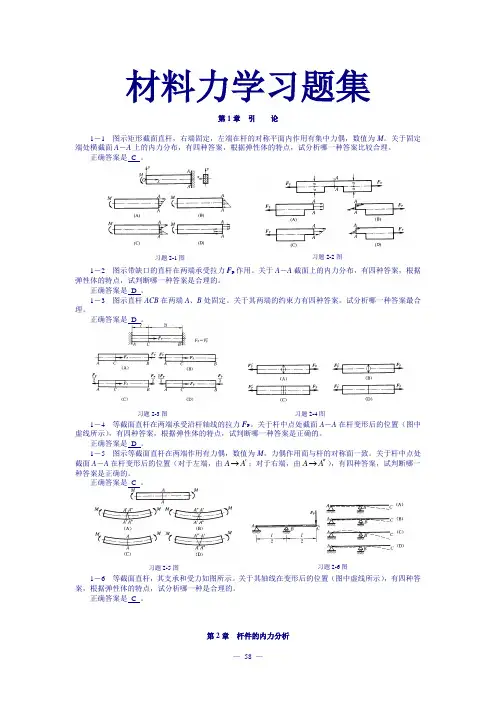
解:应力p与斜截面m-m的法线的夹角α=10°,故σ=p cosα=120×cos10°=118.2MPaτ=p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆,横截面上的正应力沿截面高度线性分布,截面顶边各点处的正应力均为σmax=100 MPa,底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量,并确定其大小。
图中之C点为截面形心。
解:将横截面上的正应力向截面形心C简化,得一合力和一合力偶,其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解:第二章轴向拉压应力2-1试计算图示各杆的轴力,并指出其最大值。
解:(a) F N AB=F, F N BC=0, F N,max=F(b) F N AB=F, F N BC=-F, F N,max=F(c) F N AB=-2 kN, F N2BC=1 kN, F N CD=3 kN, F N,max=3 kN(d) F N AB=1 kN, F N BC=-1 kN, F N,max=1 kN2-2 图示阶梯形截面杆AC,承受轴向载荷F1=200 kN与F2=100 kN,AB段的直径d1=40 mm。
习题2-1图 习题2-2图习题2-3图 习题2-4图 习题2-5图 习题2-6图 材料力学习题集第1章 引 论1-1 图示矩形截面直杆,右端固定,左端在杆的对称平面内作用有集中力偶,数值为M 。
关于固定端处横截面A -A 上的内力分布,有四种答案,根据弹性体的特点,试分析哪一种答案比较合理。
正确答案是 C 。
1-2 图示带缺口的直杆在两端承受拉力F P 作用。
关于A -A 截面上的内力分布,有四种答案,根据弹性体的特点,试判断哪一种答案是合理的。
正确答案是 D 。
1-3 图示直杆ACB 在两端A 、B 处固定。
关于其两端的约束力有四种答案。
试分析哪一种答案最合理。
正确答案是 D 。
1-4 等截面直杆在两端承受沿杆轴线的拉力F P 。
关于杆中点处截面A -A 在杆变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试判断哪一种答案是正确的。
正确答案是 D 。
1-5 图示等截面直杆在两端作用有力偶,数值为M ,力偶作用面与杆的对称面一致。
关于杆中点处截面A -A 在杆变形后的位置(对于左端,由A A '→;对于右端,由A A ''→),有四种答案,试判断哪一种答案是正确的。
正确答案是 C 。
1-6 等截面直杆,其支承和受力如图所示。
关于其轴线在变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试分析哪一种是合理的。
正确答案是 C 。
第2章 杆件的内力分析习题2-1图习题2-2图习题2-3图习题2-4图2-1 平衡微分方程中的正负号由哪些因素所确定?简支梁受力及Ox 坐标取向如图所示。
试分析下列平衡微分方程中哪一个是正确的。
(A d Q F d M(B (C (D 2-2 对于图示承受均布载荷q 的简支梁,其弯矩图凸凹性与哪些因素相关?试判断下列四种答案中。
2-3 已知梁的剪力图以及a 、e 截面上的弯矩M a 和M e ,如图所示。
为确定b M 、M ,现有下列四种答案,试分析哪一种 (A (B (C (D 之间剪力图的面积,以此类推。

第一章 绪论一、是非判断题1.1 材料力学的研究方法与理论力学的研究方法完全相同。
( × ) 1.2 内力只作用在杆件截面的形心处。
( × ) 1.3 杆件某截面上的内力是该截面上应力的代数和。
( × ) 1.4 确定截面内力的截面法,适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。
( ∨ ) 1.5 根据各向同性假设,可认为材料的弹性常数在各方向都相同。
( ∨ ) 1.6 根据均匀性假设,可认为构件的弹性常数在各点处都相同。
( ∨ ) 1.7 同一截面上正应力σ与切应力τ必相互垂直。
( ∨ ) 1.8 同一截面上各点的正应力σ必定大小相等,方向相同。
( × ) 1.9 同一截面上各点的切应力τ必相互平行。
( × ) 1.10 应变分为正应变ε和切应变γ。
( ∨ ) 1.11 应变为无量纲量。
( ∨ ) 1.12 若物体各部分均无变形,则物体内各点的应变均为零。
( ∨ ) 1.13 若物体内各点的应变均为零,则物体无位移。
( × ) 1.14 平衡状态弹性体的任意部分的内力都与外力保持平衡。
( ∨ ) 1.15 题1.15图所示结构中,AD 杆发生的变形为弯曲与压缩的组合变形。
( ∨ )1.16 题1.16图所示结构中,AB 杆将发生弯曲与压缩的组合变形。
( × )二、填空题1.1 材料力学主要研究 受力后发生的以及由此产生1.2 拉伸或压缩的受力特征是 ,变形特征是 。
B题1.15图题1.16图外力的合力作用线通过杆轴线 杆件1.3 剪切的受力特征是 ,变形特征是 。
1.4 扭转的受力特征是 ,变形特征是 。
1.5 弯曲的受力特征是 ,变形特征是 。
1.6 组合受力与变形是指 。
1.7 构件的承载能力包括 , 和 三个方面。
1.8 所谓 ,是指材料或构件抵抗破坏的能力。

材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆,两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量,并确定其大小。
解:从横截面m-m将杆切开,横截面上存在沿轴线的内力偶矩分量M x,即扭矩,其大小等于M。
1-2 如图所示,在杆件的斜截面m-m上,任一点A处的应力p=120 MPa,其方位角θ=20°,试求该点处的正应力σ与切应力τ。
解:应力p与斜截面m-m的法线的夹角α=10°,故σ=p cosα=120×cos10°=118.2MPaτ=p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆,横截面上的正应力沿截面高度线性分布,截面顶边各点处的正应力均为σmax=100 MPa,底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量,并确定其大小。
图中之C点为截面形心。
解:将横截面上的正应力向截面形心C简化,得一合力和一合力偶,其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解:第二章轴向拉压应力2-1试计算图示各杆的轴力,并指出其最大值。
解:(a) F N AB=F, F N BC=0, F N,max=F(b) F N AB=F, F N BC=-F, F N,max=F(c) F N AB=-2 kN, F N2BC=1 kN, F N CD=3 kN, F N,max=3 kN(d) F N AB=1 kN, F N BC=-1 kN, F N,max=1 kN2-2 图示阶梯形截面杆AC,承受轴向载荷F1=200 kN与F2=100 kN,AB段的直径d1=40 mm。
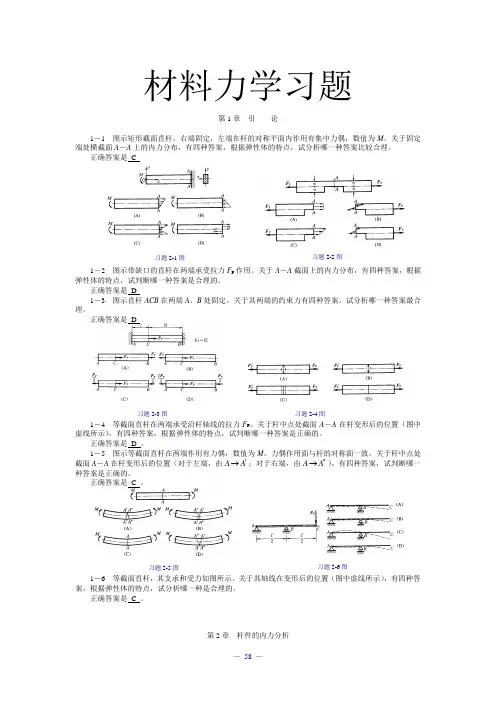
习题2-1图 习题2-2图习题2-3图 习题2-4图 习题2-5图 习题2-6图 材料力学习题第1章 引 论1-1 图示矩形截面直杆,右端固定,左端在杆的对称平面内作用有集中力偶,数值为M 。
关于固定端处横截面A -A 上的内力分布,有四种答案,根据弹性体的特点,试分析哪一种答案比较合理。
正确答案是 C1-2 图示带缺口的直杆在两端承受拉力F P 作用。
关于A -A 截面上的内力分布,有四种答案,根据弹性体的特点,试判断哪一种答案是合理的。
正确答案是 D1-3 图示直杆ACB 在两端A 、B 处固定。
关于其两端的约束力有四种答案。
试分析哪一种答案最合理。
正确答案是 D1-4 等截面直杆在两端承受沿杆轴线的拉力F P 。
关于杆中点处截面A -A 在杆变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试判断哪一种答案是正确的。
正确答案是 D 。
1-5 图示等截面直杆在两端作用有力偶,数值为M ,力偶作用面与杆的对称面一致。
关于杆中点处截面A -A 在杆变形后的位置(对于左端,由A A '→;对于右端,由A A ''→),有四种答案,试判断哪一种答案是正确的。
正确答案是 C 。
1-6 等截面直杆,其支承和受力如图所示。
关于其轴线在变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试分析哪一种是合理的。
正确答案是 C 。
第2章 杆件的内力分析习题2-1图习题2-2图习题2-3图习题2-4图2-1 平衡微分方程中的正负号由哪些因素所确定?简支梁受力及Ox 坐标取向如图所示。
试分析下列平衡微分方程中哪一个是正确的。
(A d Q F d M(B (C (D 2-2 对于图示承受均布载荷q 的简支梁,其弯矩图凸凹性与哪些因素相关?试判断下列四种答案中。
2-3 已知梁的剪力图以及a 、e 截面上的弯矩M a 和M e ,如图所示。
为确定b M 、M ,现有下列四种答案,试分析哪一种 (A (B (C (D 之间剪力图的面积,以此类推。

第一章绪论一、是非判断题1.1资料力学的研究方法与理论力学的研究方法完整相同。
(×) 1.2内力只作用在杆件截面的形心处。
(×) 1.3杆件某截面上的内力是该截面上应力的代数和。
(×) 1.4确立截面内力的截面法,合用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或随意截面的广泛状况。
(∨) 1.5依据各向同性假定,可以为资料的弹性常数在各方向都相同。
(∨) 1.6依据均匀性假定,可以为构件的弹性常数在各点处都相同。
(∨) 1.7同一截面上正应力σ与切应力τ必互相垂直。
(∨) 1.8同一截面上各点的正应力σ必然大小相等,方向相同。
(×) 1.9同一截面上各点的切应力τ必互相平行。
(×)1.10应变分为正应变ε和切应变γ。
(∨)1.11应变为无量纲量。
(∨) 1.12若物体各部分均无变形,则物体内各点的应变均为零。
(∨) 1.13若物体内各点的应变均为零,则物体无位移。
(×) 1.14均衡状态弹性体的随意部分的内力都与外力保持均衡。
(∨) 1.15题 1.15 图所示构造中, AD 杆发生的变形为曲折与压缩的组合变形。
(∨) 1.16题 1.16 图所示构造中, AB 杆将发生曲折与压缩的组合变形。
(×)FFA A CBBCD D题 1.15 图题 1.16 图二、填空题1.1资料力学主要研究杆件受力后发生的变形,以及由此产生的应力,应变。
1.2拉伸或压缩的受力特色是外力的协力作用线经过杆轴线,变形特色是。
1沿杆轴线伸长或缩短1.3剪切的受力特色是受一平等值,反向,作用线距离很近的力的作用,变形特色是沿剪切面发生相对错动。
1.4扭转的受力特征是外力偶作用面垂直杆轴线,变形特色是随意二横截面发生绕杆轴线的相对转动。
1.5曲折的受力特色是外力作用线垂直杆轴线,外力偶作用面经过杆轴线,变形特征是梁轴线由直线变为曲线。
1.6组合受力与变形是指包含两种或两种以上基本变形的组合。

第一章 绪论一、是非判断题1.1 材料力学的研究方法与理论力学的研究方法完全相同。
( × ) 1.2 力只作用在杆件截面的形心处。
( × ) 1.3 杆件某截面上的力是该截面上应力的代数和。
( × ) 1.4 确定截面力的截面法,适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。
( ∨ ) 1.5 根据各向同性假设,可认为材料的弹性常数在各方向都相同。
( ∨ ) 1.6 根据均匀性假设,可认为构件的弹性常数在各点处都相同。
( ∨ ) 1.7 同一截面上正应力σ与切应力τ必相互垂直。
( ∨ ) 1.8 同一截面上各点的正应力σ必定大小相等,方向相同。
( × ) 1.9 同一截面上各点的切应力τ必相互平行。
( × ) 1.10 应变分为正应变ε和切应变γ。
( ∨ ) 1.11 应变为无量纲量。
( ∨ ) 1.12 若物体各部分均无变形,则物体各点的应变均为零。
( ∨ ) 1.13 若物体各点的应变均为零,则物体无位移。
( × ) 1.14 平衡状态弹性体的任意部分的力都与外力保持平衡。
( ∨ ) 1.15 题1.15图所示结构中,AD 杆发生的变形为弯曲与压缩的组合变形。
( ∨ )1.16 题1.16图所示结构中,AB 杆将发生弯曲与压缩的组合变形。
( × )二、填空题1.1 材料力学主要研究 受力后发生的以及由此产生1.2 拉伸或压缩的受力特征是 ,变形特征是 。
1.3 剪切的受力特征是 ,变形特征B题1.15图题1.16图外力的合力作用线通过杆轴线 杆件 沿杆轴线伸长或缩短 受一对等值,反向,作用线距离很近的力的作用 沿剪切面发生相对错动是 。
1.4 扭转的受力特征是 ,变形特征是 。
1.5 弯曲的受力特征是 ,变形特征是 。
1.6 组合受力与变形是指 。
1.7 构件的承载能力包括 , 和 三个方面。

题型:问答题1.1对图1.2a所示钻床,试求n−n截面上的内力。
答案:见习题答案。
解析:采用截面法。
难度:容易能力:知识运用用途:作业,考试,自测知识点:第一章绪论题型:问答题1.2试求图示结构m−m和n−n两截面上的内力,并指出AB和BC两杆的变形属于哪一类基本变形。
答案:见习题答案。
解析:采用截面法。
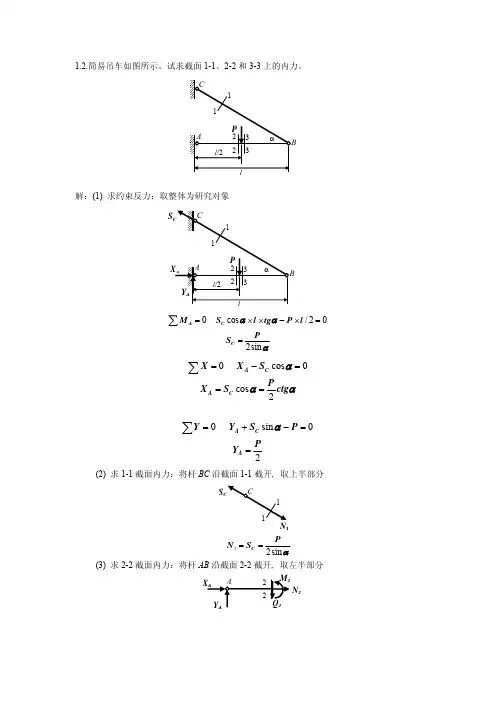
难度:一般能力:知识运用用途:作业,考试,自测知识点:第一章绪论题型:问答题1.3在图示简易吊车的横梁上,力F可以左右移动。
试求截面1−1和2−2上的内力及其最大值。
答案:见习题答案。
解析:利用平衡方程求支座约束力,利用截面法求指定截面上的内力。
难度:一般能力:知识运用用途:作业,考试,自测知识点:第一章绪论题型:问答题1.4图示拉伸试样上A、B两点的距离l称为标距。
受拉力作用后,用引伸计量出两点距离的增量为Δl=5×10−2 mm。
若l的原长为100 mm,试求A与B两点间的平均线应变εm。
答案:见习题答案。
解析:利用线应变的定义。
难度:容易能力:知识运用用途:作业,考试,自测知识点:第一章绪论题型:问答题1.5图示三角形薄板因受外力作用而变形,角点B垂直向上的位移为0.03 mm,但AB和BC仍保持为直线。
试求沿OB的平均线应变,并求薄板在B点处的切应变。
答案:见习题答案。
解析:利用线应变和切应变的定义。
难度:一般能力:知识运用用途:作业,考试,自测知识点:第一章绪论题型:问答题1.6图示圆形薄板的半径为R,变形后R的增量为ΔR。
若R=80 mm,ΔR=3×10−3 mm,答案:见习题答案。
解析:利用线应变的定义。
难度:一般能力:知识运用用途:作业,考试,自测知识点:第一章绪论题型:问答题1.7取出某变形体在A点的微元体如图中实线所示,变形后的微元体如图中虚线所示。
试求A点的切应变。
答案:见习题答案。
解析:利用切应变的定义。
难度:容易能力:知识运用用途:作业,考试,自测知识点:第一章绪论题型:问答题1.8图示正方形薄板,边长为a AB的平均线应变。
材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆,两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量,并确定其大小。
解:从横截面m-m将杆切开,横截面上存在沿轴线的内力偶矩分量M x,即扭矩,其大小等于M。
1-2 如图所示,在杆件的斜截面m-m上,任一点A处的应力p=120 MPa,其方位角θ=20°,试求该点处的正应力ζ与切应力η。
解:应力p与斜截面m-m的法线的夹角α=10°,故ζ=p cosα=120×cos10°=118.2MPaη=p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆,横截面上的正应力沿截面高度线性分布,截面顶边各点处的正应力均为ζmax=100 MPa,底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量,并确定其大小。
图中之C点为截面形心。
解:将横截面上的正应力向截面形心C简化,得一合力和一合力偶,其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解:第二章轴向拉压应力2-1试计算图示各杆的轴力,并指出其最大值。
解:(a) F N AB=F, F N BC=0, F N,max=F(b) F N AB=F, F N BC=-F, F N,max=F(c) F N AB=-2 kN, F N2BC=1 kN, F N CD=3 kN, F N,max=3 kN(d) F N AB=1 kN, F N BC=-1 kN, F N,max=1 kN2-2 图示阶梯形截面杆AC,承受轴向载荷F1=200 kN与F2=100 kN,AB段的直径d1=40 mm。
材料⼒学习题册答案练习1绪论及基本概念1-1 是⾮题(1)材料⼒学是研究构件承载能⼒的⼀门学科。
(是)(2)可变形固体的变形必须满⾜⼏何相容条件,即变形后的固体既不可以引起“空隙”,也不产⽣“挤⼊”现象。
(是)(3)构件在载荷作⽤下发⽣的变形,包括构件尺⼨的改变和形状的改变。
(是)(4)应⼒是内⼒分布集度。
(是)(5)材料⼒学主要研究构件弹性范围内的⼩变形问题。
(是)(6)若物体产⽣位移,则必定同时产⽣变形。
(⾮)(7)各向同性假设认为,材料沿各个⽅向具有相同的变形。
(F)(8)均匀性假设认为,材料内部各点的⼒学性质是相同的。
(是)(9)根据连续性假设,杆件截⾯上的内⼒是连续分布的,分布内⼒系的合⼒必定是⼀个⼒。
(⾮)(10)因为构件是变形固体,在研究构件的平衡时,应按变形后的尺⼨进⾏计算。
(⾮)1-2 填空题(1)根据材料的主要性质对材料作如下三个基本假设:连续性假设、均匀性假设、各向同性假设。
(2)⼯程中的强度,是指构件抵抗破坏的能⼒;刚度,是指构件抵抗变形的能⼒。
(3)保证构件正常或安全⼯作的基本要求包括强度,刚度,和稳定性三个⽅⾯。
(4)图⽰构件中,杆1发⽣拉伸变形,杆2发⽣压缩变形,杆3发⽣弯曲变形。
(5)认为固体在其整个⼏何空间内⽆间隙地充满了物质,这样的假设称为连续性假设。
根据这⼀假设构件的应⼒,应变和位移就可以⽤坐标的连续函数来表⽰。
(6)图⽰结构中,杆1发⽣弯曲变形,构件2发⽣剪切变形,杆件3发⽣弯曲与轴向压缩组合。
变形。
(7)解除外⼒后,能完全消失的变形称为弹性变形,不能消失⽽残余的的那部分变形称为塑性变形。
(8)根据⼩变形条件,可以认为构件的变形远⼩于其原始尺⼨。
1-3 选择题(1)材料⼒学中对构件的受⼒和变形等问题可⽤连续函数来描述;通过试件所测得的材料的⼒学性能,可⽤于构件内部的任何部位。
这是因为对可变形固体采⽤了( A )假设。
(A)连续均匀性;(B)各向同性;(C)⼩变形;(D)平⾯。
材料力学 分析与思考题集第一章 绪论和基本概念一、选择题1.关于确定截面内力的截面法的适用范围,有下列四种说法:【D.适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普通情况。
2.关于下列结论的正确性:【C 1.同一截面上正应力τσ与剪应力必须相互垂直3.同一截面上各点的剪应力必相互平行。
】3.下列结论中那个是正确的:【B.若物体各点均无位移,则该物体必定无变形】4.根据各向同性假设,可认为构件的下列量中的某一种量在各方向都相同:【B 材料的弹性常数】5.根据均匀性假设,可认为构件的下列量中的某个量在各点处都相同:【C 材料的弹性常数】6.关于下列结论:【C 1.应变分为线应变ε和切应变γ 2.应变为无量纲量 3.若物体的各部分均无变形,则物体内各点的应变均为零】7.单元体受力后,变形如图虚线所示,则切应变γ为【B 2α】二、填空题1.根据材料的主要性能作如下三个基本假设 连续性假设 , 均匀性假设 和 各向同性假设 。
2.构件的承载能力包括强度、刚度和稳定性三个方面。
3.图示结构中,杆1发生轴向拉伸变形,杆2发生轴向压缩变形,杆3发生弯曲变形。
4.图示为构件内A 点处取出的单元体,构件受力后单元体的位置为虚线表示,则称dx du /为A 点沿x 方向的线应变,dy dv /为【A 点沿y 方向的线应变】,)(21a a +为【A 在xy 平面内的角应变】。
5.认为固体在其整个几何空间内无间隙地充满了物质,这样的假设称为连续性假设。
根据这一假设,构件的应力、应变和位移就可以用坐标的连续性函数来表示。
6.在拉(压)杆斜截面上某点处分布内力集度称为应力(或全应力),它沿着截面法线方向的分量称为正应力,而沿截面切线方向的分量称为切应力。
第二章 杆件的内力分析一、选择题1.单位宽度的薄壁圆环受力如图所示,p 为径向压强,其n-n 截面上的内力N F 有四个答案:【B 2/pD 】2.梁的内力符号与坐标系的关系是:【B 剪力、弯矩符号与坐标系无关】3.梁的受载情况对于中央截面为反对称(如图)。
第一张绪论一、选择题1.根据均匀性假设,可认为构件的(C)在各处相同。
A. 应力B. 应变C. 材料的弹性系数D. 位移2. 构件的强度是指(C),刚度是指(A),稳定性是指(B)。
A. 在外力作用下构件抵抗变形的能力B. 在外力作用下构件保持原有平衡状态的能力C. 在外力作用下构件抵抗强度破坏的能力3. 单元体变形后的形状如下图虚线所示,则A点剪应变依次为图(a)(A),图(b)(C),图(c)(B)。
(a) (b) (c)A. 0B. 2rC. rD. 1.5r4. 下列结论中(C)是正确的。
A. 内力是应力的代数和;B. 应力是内力的平均值;C. 应力是内力的集度;D. 内力必大于应力;5. 两根截面面积相等但截面形状和材料不同的拉杆受到同样大小的轴向拉力,它们的应力是否相等(B)。
A. 不相等;B. 相等;C. 不能确定;二、填空题1.材料力学对变形固体的基本假设是连续性假设,均匀性假设,各向同性假设。
2.材料力学的任务是满足强度,刚度,稳定性的要求下,为设计经济安全的构件提供必要的理论基础和计算方法。
3.外力按其作用的分布方式可以分为表面力和体积力,按载荷随时间的变化情况可以分为静载荷和动载荷。
4.度量一点变形过程的两个基本量是应变ε和切应变γ。
三、判断题1. 因为构件是变形固体,在研究构件平衡时,应按构件变性后的尺寸进行计算。
(×)2. 外力就是构件所承受的载荷。
(×)3. 用截面法求内力时,可以保留截开后构件任意一部分进行平衡计算。
(√)4. 应力是横截面上的平均力。
(×)5. 杆件的基本变形只是拉(压)、剪、扭和弯四种,如果还有另一种变形,必定是这四种变形的某种组合。
(×)6. 材料力学只限于研究等截面杆。
(×)四、计算题1.图示三角形薄板因受外力作用而变形,角点B垂直向上的位移为0.03mm,但AB和BC仍保持为直线。
试求沿OB的平均应变,并求AB、BC两边在B点的角度改变。