下载文档原格式
物理复习学习计划物理学习计划第一周：力学星期一：运动学✔️看完《大学物理》力学部分的运动学章节，复习基本运动学公式。
✔️做练习题，巩固对运动学的理解。
星期二：牛顿定律✔️学习牛顿三定律，了解牛顿运动定律的应用。
✔️做相关题目，加深对牛顿定律的理解。
星期三：动力学✔️学习动力学相关知识，了解动力学的公式和应用。
✔️做练习题，掌握动力学的解题方法。
星期四：能量和动量✔️学习能量和动量的基本概念，了解它们在力学中的作用。
✔️做相关练习题，加深对能量和动量的理解。
星期五：作业✔️完成本周所学知识的作业。
✔️复习本周所学内容，做相关复习题。
第二周：热学星期一：热力学第一定律✔️学习热力学第一定律的内容和应用。
✔️做相关练习题，加深对热力学第一定律的理解。
星期二：热力学第二定律✔️学习热力学第二定律的内容，了解热力学第二定律的应用。
✔️做相关练习题，掌握热力学第二定律的解题方法。
星期三：理想气体定律✔️学习理想气体定律的概念，了解理想气体定律的公式和应用。
✔️做相关练习题，加深对理想气体定律的理解。
星期四：热力学循环✔️学习热力学循环的基本概念，了解各种热力学循环的特点。
✔️做相关练习题，掌握热力学循环的解题方法。
星期五：作业✔️完成本周所学知识的作业。
✔️复习本周所学内容，做相关复习题。
第三周：电学星期一：电场✔️学习电场的基本概念，了解电场的性质和计算方法。
✔️做相关练习题，加深对电场的理解。
星期二：电势✔️学习电势的概念，了解电势的计算方法和应用。
✔️做相关练习题，掌握电势的解题方法。
星期三：电流和电阻✔️学习电流和电阻的基本概念，了解电流和电阻的计算方法。
✔️做相关练习题，加深对电流和电阻的理解。
星期四：电路✔️学习电路的基本概念，了解串联和并联电路的特点。
✔️做相关练习题，掌握电路的解题方法。
星期五：作业✔️完成本周所学知识的作业。
✔️复习本周所学内容，做相关复习题。
第四周：光学星期一：几何光学✔️学习几何光学的基本原理，了解光的折射和反射规律。
大学物理电磁学知识点电磁学是物理学中一个重要的分支，涵盖了电荷、电场、磁场、电磁波等内容。
在大学物理学课程中，电磁学知识点是必不可少的。
本文将探讨一些关键的电磁学知识点，帮助读者更好地了解这一领域。
首先，我们来谈谈电荷和电场。
电荷是电磁学的基本概念，分为正电荷和负电荷。
在物体中，正负电荷相互吸引，相同电荷相互排斥。
电场是由电荷产生的力场，它描述了电荷对周围空间的影响。
对于一个点电荷Q来说，其周围的电场强度E与距离r成反比，符合库仑定律E=kQ/r^2，其中k是一个常数。
接下来，我们将探讨电场的另一个重要概念-电势。
电势是描述电场状态的一种物理量，它反映了单位正电荷在电场中所具有的能量。
在电势的概念中，我们引入了电势能和电势差。
电势能是指电荷在电场中所具有的能量，而电势差是指在单位正电荷移动时所做的功。
而物体的导体性质也与电磁学紧密相关。
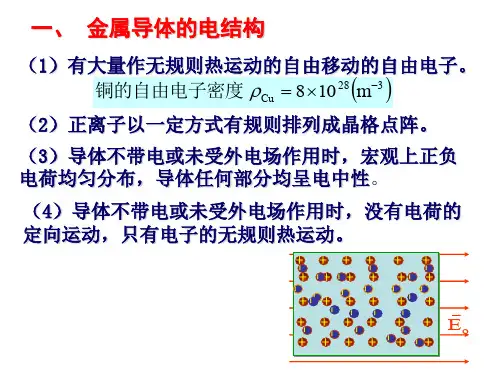
导体是一种能够传导电流的材料，其内部的自由电子可以自由移动。
导体中的电荷分布是非常均匀的，所以电场在导体内外表面垂直分布。
此外，导体内的电场强度为零，这是由于导体内部的电荷分布所决定的。
当我们讨论电磁学时，不得不提磁场。
磁场是由磁荷和电流产生的。
磁荷是一种假想的磁性单极子，而电流则是电荷的流动。
磁场可以通过磁感应强度B来描述，它是反映物体对磁场的响应的一个物理量。
磁感应强度的单位是特斯拉(T)，在磁场中的物体将受到一个磁力的作用。
当电荷和磁场相互作用时，将产生电磁感应现象。
法拉第电磁感应定律描述了电磁感应的规律。
当一个闭合线圈中的磁感应强度发生变化时，线圈中将会产生感应电动势。
这一定律也是电磁感应中电磁场与电荷之间相互转化的基础。
最后，我们来谈一谈电磁波。
电磁波是一种电场和磁场相互关联扩展传播的现象。
电磁波有许多不同的频率和波长，包括射频、微波、红外线、可见光、紫外线、X射线和γ射线。
这些电磁波在现代通信、医疗、无线电和电视等领域中都有着广泛的应用。
以上是一些大学物理电磁学的基本知识点。
电磁学部分总结 静电场部分第一部分：静电场的基本性质和规律电场是物质的一种存在形态，它同实物一样也具有能量、动量、质量等属性。
静电场的物质特性的外在表现是：(1)电场对位于其中的任何带电体都有电场力的作用(2)带电体在电场中运动,电场力要作功——电场具有能量1、描述静电场性质的基本物理量是场强和电势，掌握定义及二者间的关系。
电场强度 电势2、反映静电场基本性质的两条定理是高斯定理和环路定理要掌握各个定理的内容，所揭示的静电场的性质，明确定理中各个物理量的含义及影响各个量的因素。
重点是高斯定理的理解和应用。
3、应用(1)、电场强度的计算a)、由点电荷场强公式 及场强叠加原理 计算场强q FE =⎰∞⋅==aa ar d E q W U 0∑⎰⎰=⋅=ΦiSe qS d E 01ε ⎰=⋅0r d E L 02041r rq E πε=iiE E ∑=一、离散分布的点电荷系的场强二、连续分布带电体的场强其中，重点掌握电荷呈线分布的带电体问题b)、由静电场中的高斯 定理计算场源分布具有高度对称性的带电体的场强分布一般诸如球对称分布、轴对称分布和面对称分布，步骤及例题详见课堂笔记。
还有可能结合电势的计算一起进行。
c)、由场强和电势梯度之间的关系来计算场强（适用于电势容易计算或电势分布已知的情形），掌握作业及课堂练习的类型即可。
（2）、电通量的计算2041i ii i i i r r q E E πε∑=∑=⎰⎰π==0204d r rq E d E εUgradU E -∇=-=)(k zU j y U i x U ∂∂+∂∂+∂∂-=a)、均匀电场中S 与电场强度方向垂直b)、均匀电场，S 法线方向与电场强度方向成q 角c)、由高斯定理求某些电通量（3）、电势的计算a)、场强积分法（定义法）——根据已知的场强分布，按定义计算b)、电势叠加法——已知电荷分布，由点电荷电势公式，利用电势叠加原理计算第二部分：静电场中的导体和电介质 一、导体的静电平衡状态和条件导体内部和表面都没有电荷作宏观定向运动的状态称为静电平衡状态。
【课后习题】 第12章 一、填空题1、两个大小完全相同的带电金属小球，电量分别为2q 和－1q ，已知它们相距为r 时作用力为F ，则将它们放在相距3r 位置同时其电量均减半，相互作用力大小为____1/36________F 。
2、电场强度可以叙述为电场中某一点上单位正电荷所受的_____电场力___________；电场中某一点的电势可以叙述为：单位正电荷在该点所具有的__电势能_________。
3、真空环境中正电荷q 均匀地分布在半径为R 的细圆环上，在环环心O 处电场强度为____0________，环心的电势为__R q o πε4/_________。
4、高斯定理表明磁场是 无源 场,而静电场是有源场。
任意高斯面上的静电场强度通量积分结果仅仅取决于该高斯面内全部电荷的代数和。
现有图1-1所示的三个闭合曲面S 1、S 2、S 3，通过这些高斯面的电场强度通量计算结果分别为：⎰⎰⋅=Φ11S SE d ,⎰⎰⋅=Φ22S SE d ,⎰⎰⋅=Φ33S SE d ，则Φ1=___o q ε/_______;Φ2+Φ3=___o q ε/-_______。
5、静电场的场线只能相交于___电荷或无穷远________。
6、两个平行的无限大均匀带电平面，其电荷面密度分别如图所示，则A 、B 、C 三个区域的电场强度大小分别为：E A =_o εσ/4________；E B =_o εσ/________；E C =__o εσ/4_______。
7、由一根绝缘细线围成的边长为l 的正方形线框，使它均匀带电，其电荷线密度为λ，则在正方形中心处的电场强度的大小E ＝____0____________．8、初速度为零的正电荷在电场力的作用下,总是从__高____电势处向_低____电势处运动。
9、静电场中场强环流为零，这表明静电力是__保守力_________。
10、如图所示，在电荷为q 的点电荷的静电场中，将一电荷为q 0的试验电荷从a 点经任意路径移动到b 点，外力所作的功 W ＝___⎪⎪⎭⎫ ⎝⎛-120114r r Qq πε___________．11、真空中有一半径为R 的均匀带电半园环，带电量为Q ，设无穷远处为电势零点，则圆心O 处的电势为___RQ 04πε_________；若将一带电量为q 的点电荷从无穷远处移到O 点，电场力所作的功为__RqQ 04πε__________。
大学物理综合复习（二）引言概述：在大学物理学习的过程中，及时进行复习是非常重要的。
本文将提供大学物理综合复习的第二部分，涵盖了五个大点，每个大点下有五到九个小点。
通过对这些内容的复习，相信能够帮助读者更好地理解和掌握大学物理的知识。
正文内容：一、电磁场的特性1. 电场和磁场的基本概念2. 高斯定律和安培定律的应用3. 电场和磁场的叠加原理4. 静电场和静磁场的能量5. 电磁场的辐射和波动二、电磁波和光学1. 电磁波的产生和传播2. 光的波动特性和光的衍射3. 光的干涉和光的偏振4. 光的反射和光的折射5. 光的多普勒效应和光的色散三、物质的性质与热学1. 固体、液体和气体的性质2. 热力学第一定律和第二定律的应用3. 物质的相变和理想气体定律4. 热传导、热对流和热辐射5. 热力学循环和热机效率四、原子与分子物理1. 原子和原子核的结构2. 元素周期表和化学键的形成3. 分子光谱学和原子光谱学4. 原子核的衰变和核反应5. 原子与分子的量子力学描述五、相对论和量子力学1. 相对论的基本原理和伽利略变换2. 狭义相对论和洛伦兹变换3. 质能关系和相对论力学4. 微观粒子的波粒二象性和不确定性原理5. 量子力学的基本原理和薛定谔方程总结：通过对大学物理综合复习的第二部分的学习，我们重新回顾了电磁场的特性、电磁波和光学、物质的性质与热学、原子与分子物理以及相对论和量子力学等重要知识点。
这些内容构成了大学物理学习的基础，理解和掌握这些知识有助于提高我们对物理学的理解和应用能力。
建议读者在复习过程中注重理论与实践结合，进行大量的例题和习题练习，以加深对知识点的理解和应用能力的提升。
大学物理（2）期末复习试题库第四篇 电磁学一、判断题1.关系H B μ=对所有各向同性线性介质都成立。
（ ）2.静电场中任何两条电力线不相交，说明静电场中每一点的场强是唯一的。
（ ）3.导体内部处处没有未被抵消的静电荷，静电荷只分布在导体的表面上。
（ ）4.电源电动势的方向是自正极经电源内部到负极的方向。
（ ）5.自感系数只依赖线圈本身的形状、大小及介质的磁导率而与电流无关。
（ ）6.恒定磁场中定理∑⎰=⋅I l d H 成立。
（ ）7.关系E D ε=对所有各向同性电介质都成立。
（ ）8. 0ε∑⎰⎰=⋅q s d E 对任意电场均成立。
（ ） 9.可以把电子的自旋运动和宏观物体的自转运动相类比。
（ ）10.无论是在稳恒磁场还是非稳恒磁场中安培环路定理∑⎰=⋅i LI l d H 都成立。
（ ）11.导体静电平衡的条件是导体内部场强处处为零。
（ ）12.有人把⎰⎰=⋅0S B d 称为磁场高斯定理,它只对恒定磁场成立，在变化磁场中⎰⎰≠⋅0S B d 。
（ ）13.由电容计算公式ab U q C =，理解为当0=q 时电容0=C 。
（ ）14.洛伦兹力不能改变运动电荷速度的大小，只能改变速度的方向。
（ ）15.任何导体内部场强都处处为零。
（ ）16.由安培环路定理∑⎰=⋅I l d H 可知，H 仅与传导电流有关。
（ ）17. 自感系数为L 的载流线圈磁场能量的公式221LI W =只适用于无限长密绕螺线管。
（ ）18．当一个带电导体达到静电平衡时, 表面上电荷密度较大处电势较高。
（ ）19.高斯定理⎰⎰=⋅VS dV d ρS D ,只对静电场成立，对变化的电场不成立。
（ ） 20．在电场中，电场强度为零的点，电势不一定为零。
（ ）21.稳恒电流磁场的磁场强度H 仅与传导电流有关 。
（ ）22.当一个带电导体达到静电平衡时, 导体内任一点与其表面上任一点的电势差等于零。
（ ）23.有人把0=⋅⎰Sd S B 称为磁高斯定理,它只对恒定磁场成立，在变化的磁场中该式不成立。
1、 半径为R ，带电量为Q 的金属导体球，其外表面处的电场强度大小为多少？电势为多少？导体
球内距离球心r （r<R ）处的电势为多少?
2、 半径为R 的无限长直圆柱体内均匀带电，电荷体密度为ρ，求：（1）圆柱体内、外的电场强度分
布；（2）轴线上一点到离轴距离为2R 处的电势差。
3、 一球形电容器内、外半径分别为R 1和R 2，电势差为U 且恒定，求：（1）电容器极板所带电量；
（2）电容器所储存的能量。
推广：半径R 的金属球带电量为Q ,则该球的电势V =多少？电容C =多少？
R C R
Q V 004;4πεπε==
4、 用不带电的细塑料弯成半径为R 的圆弧，两端之间空隙为d （d<<R ），电量为q 的正电荷均匀分
布在圆弧棒上，则圆弧的圆心处的电场强度大小是多少？方向是什么?
5、 半径为R 的金属球球心与点电荷q 2相距为d ，金属球带电q 1，则金属球球心O 处的电场强度大
小为多少？电势为多少？金属球表面上任意一点P 处的电势为多少 ?
6、半径为R 的无限长直圆柱体内均匀带电，电荷线密度为λ，求：（1）圆柱体内、外的电场强度的分布；（2）轴线上一点到离轴距离为2R 处的电势差。
7、 真空中有一无限大均匀带电平面，带电电荷密度为σ ，现将一点电荷q 0从a 点移到b 点，电场
力做功是多少？从c 点移到a 点，电场力做功是多少？设ab=2l ，bc=l 。
8、 真空中有一带电量为q 的空心导体球壳，内外半径分别为R 1，R 2，P 1，P 2分别为球壳内、外的
一点，对应的半径分别为r 1，r 2。
则P 1点处的电场强度为多少？P 2点的电势为多少？P 1点处的电场能量密度为多少？
9、一均匀带电的细棒，长为L ，带电量为q ，在其延长线上有两点P 、Q ，距细棒中心O 点的距离分别为a 和b ，求P 、Q 两点之间的电势差。
10、球心为O 点，内、外半径分别为R 1、R 2的均匀带电球壳，其电荷体密度为ρ，求空间的电场强度分布。
（设球壳的相对介电常数为1）
σ q 0 b 题7图
P 2
8图
题9图
11、半径R ，电荷面密度为σ的均匀带电半球面在球心处的电势为多少？球心处的电场强度方向为设什么？把一个点电荷q 从无穷远移到球心O 点时电场力作功为多少？
12、半径为R 的导体薄球壳带电量Q ，在球心处O 点放一个点电荷q ，求：(1)
壳内A 点(r A )和壳外B(r B )点间的电热差U AB ；(2)在薄球壳外的电场中贮存的电
场能；
13、一均匀带电的细棒，长为L ，带电量为q ，在其延长线上有一点P ，距细棒中心O 点为a ，求P 点的电场强度。
14、电荷密度为ρ、半径为R 的匀电球体，在体内离球心r 1（r 1<R ）处的场强值E 1为多少？球外离
球心r 2（r 2>R ）处的电势U 2为多少？
15、球形电容器两金属薄壳的半径分别为R A 、R B （R A <R B ）,分别带电量＋Q 、－Q ；求：（1）两壳间电场强度分布E （r ）；（2）两壳的电势差U AB ；（3）该电容器的电容C ；（4）电场的能量W 。
16、长为l 、电荷线密度为λ的匀电线段，求其延长线上p 点的场强和电势。
（尺寸如图所示）
17、高斯定理描述了静电场的什么性质；环流定理描述了静电场的什么性
质。
18、如图所示，电荷线密度为λ的长直线电荷，A 点处的场强值为
多少？若将正电荷q 0从A 点沿ACB 路径移到B 点，电场力做功A ＝ 多少？
19、半径为R 的金属球带电量＋Q ，则该球的电势和电容值分别为U ＝多少？C ＝多少？
20、有一圆柱形电容器，内、外薄圆筒的半径分别为R A 、R B ，长为h ；内、外筒上单位长度所带电量分别为λ、－λ；求：（1）两筒间场强分布E (r)和电势差U AB ；（2）该电容器的电容C 和电场能W 。
21、一无限长均匀带电直线，电荷线密度为λ，则离直线距离为r 处电场强度大小为多少？距直线距离为a r 和b r （b r ＞a r ）的两点间的电势差=-b a U U 多少？
22、半径为R ， 带电量为Q 的金属导体球， 导体球面外靠近其外表面处的电场强度的大小为多少？
导体球内距球心r （r<R ）处的电势为多少？导体球外距球心r （r ＞R ）处的电场能量体密度为多少？
23、一无限长均匀带电圆柱，体电荷密度为ρ，截面半径为R 用高斯定理求出柱内外电场强度分布。
24、一无限长均匀带电圆柱，体电荷密度为ρ，截面半径为R 。
（1）用高斯定理求出柱内外电场强度分布;(2)以轴线为势能零点，求出圆柱外的电势分布。
25、两块面积相同且S=200cm 2导体平板正对放置，间距d=2.00mm ，A 板带电C Q A 8100.2-⨯=，B 板接地，略去边缘效应。
求：（1）各板面电荷分布；（2）系统的电容。
26、如右图所示，在厚度为d 的无限大平板层内，均匀地分布着正电荷，体电荷密度为ρ，则d
x <处的电场强度大小为多少？
0=x 的a 点与d x 2=的b 点的电势差
=-b a U U 为多少？
27、长为L ，内外半径分别为a 、b 的圆柱形电容器， 带电量为Q ，则距对称轴距离为r （a<r<b ）处的电场强度的大小为多少？两极板的电势差为多少？该电容器的电容为多少？
28、如右图，一个细的带电塑料圆环，半径为R ，所带线电荷密度λ和
θ有θλλsin 0=的关系。
求圆心处的电场强度的大小和方向。
29、半径为1R 的导体球外套有一个与它同心的内、外半径分别为2R 和
3R 导体球壳，当内球带电量为Q 时，求：（1）场强分布；（2）这个系统储存了多少电场能？
30、电量为+q 的匀电细杆,弯成半径为R ，缺口间距为a 的圆形，如图，若a<<R ，则圆心处电场强度值是多少？方向指向是什么？
31、球形空气电容器内外球面A ，B 的半径分别为R 1和R 2，带电量为Q ,求:(1)两板间的场强E 和电压V AB ；(2)电容器的电容C ；(3)电场能量W 。
32、半径为R ，电荷体密度为ρ的均匀带电长直圆柱体，内部一点A (离轴的距离为
r A ),外部一
点B (离轴的距离为r B ).试求:(1)A ，B 两点的电场强度值E A ，E B ； (2)A ，B 两点的电势差V AB 。
a
题30图。
