空间统计学模拟方法在城市重金属污染分析中的应用
- 格式:pdf
- 大小:1.66 MB
- 文档页数:5

空间统计模型在环境科学中的应用在环境科学中,空间统计模型是一种重要的分析工具,它通过整合空间变异性和统计方法,对环境现象进行建模和预测。
本文将探讨空间统计模型在环境科学中的应用,并介绍其优势和局限性。
一、空间统计模型的基本原理空间统计模型是基于空间自相关性的理论基础而建立的。
在环境科学中,许多环境现象具有空间依赖性,即相邻区域之间存在相关性。
空间统计模型通过量化和分析这种空间相关性,可以揭示环境现象的内在规律。
二、环境污染物分布预测空间统计模型在环境科学中的一个重要应用是污染物分布的预测。
通过收集现场采集的环境数据,如空气质量监测点的浓度数据,借助空间统计模型可以推断其他地点的污染物浓度水平。
这对于环境管理和决策具有重要意义,可以帮助制定更精确的环境保护措施和监管政策。
三、生态系统模拟和保护生态系统是环境科学研究的重要对象,而空间统计模型在生态系统的模拟和保护中也有广泛应用。
通过分析生态环境的空间变异性,可以对生态系统的植被分布、物种多样性、生物量等进行模拟和预测。
这有助于科学合理地进行生态环境管理和保护,保护濒危物种和生态系统的完整性。
四、土地利用规划空间统计模型在土地利用规划中也发挥着重要作用。
通过分析现有的土地利用数据和空间统计模型,可以预测未来土地利用的趋势和变化,为城市规划和农业发展提供科学依据。
同时,空间统计模型还可以评估土地利用决策对环境的影响,帮助制定可持续的土地利用策略。
五、空气质量评估与管理空气质量是环境科学中一项重要的研究内容,而空间统计模型在空气质量评估与管理中具有广泛应用。
通过对空气污染物的测量数据进行分析和建模,可以揭示污染物的时空分布规律,帮助监管部门制定针对性的空气质量改善和治理策略。
六、空间统计模型的优势和局限性空间统计模型具有许多优势,如能够考虑空间相关性、能够利用有限的样本数据进行预测等。
然而,空间统计模型也存在一些局限性,如需要大量的数据支持、计算复杂度高等。

空间统计方法在环境科学研究中的应用在当今的环境科学研究领域,空间统计方法正发挥着日益重要的作用。
这些方法为我们理解和解决环境问题提供了全新的视角和有力的工具。
环境现象往往具有明显的空间特征。
例如,污染物的分布在地理空间上并非均匀,而是受到多种因素的影响,呈现出特定的模式。
空间统计方法能够帮助我们捕捉和分析这些空间模式,从而更深入地理解环境过程。
一种常见的空间统计方法是克里金插值法。
它基于已知的采样点数据,对未采样区域进行预测和估值。
比如说,在研究土壤污染时,我们可能只在有限的地点采集了土壤样本并测定了污染物浓度。
通过克里金插值,就能够估计整个研究区域内污染物浓度的分布情况。
这对于评估污染的范围和程度,制定相应的治理策略非常有帮助。
热点分析也是空间统计中的重要手段。
它可以识别出数据中的高值或低值聚集区域,也就是所谓的“热点”和“冷点”。
以空气质量监测为例,通过热点分析,我们能够迅速发现空气质量较差的区域,进而聚焦于这些重点区域采取更有针对性的减排措施。
空间自相关分析在环境科学中同样不可或缺。
它用于研究某一变量在空间上是否存在自相关性。
比如,如果相邻地区的水质指标具有较强的相似性,那么就表明存在空间正自相关;反之,如果相邻地区的水质差异较大,则可能存在空间负自相关。
了解这种空间自相关性,有助于我们揭示环境现象背后的驱动因素和传播机制。
在生态环境研究中,空间统计方法可以用于评估生物多样性的空间格局。
比如,通过分析不同物种在地理空间上的分布情况,我们能够了解它们的栖息地偏好,以及人类活动对其生存空间的影响。
这对于制定生物保护策略、划定自然保护区等具有重要的指导意义。
在气候变化研究方面,空间统计方法也大有用武之地。
例如,研究气温、降水等气候要素的空间变化趋势,以及极端气候事件的空间分布规律。
这有助于我们更好地理解气候变化的区域差异,制定适应和减缓气候变化的策略。
然而,空间统计方法在环境科学研究中的应用也并非一帆风顺。


关于城市表层土壤重金属污染的数学模型分析摘要本文以某城区为例,建立了分析土壤重金属的空间分布及各种重金属污染的主要原因的数学模型,并求出了地质环境演变模式。
首先,运用Surfer8.0软件中的克里格(Kriging)插值模块对土壤重金属浓度进行空间数据插值并应用单项污染指数法对各重金属元素的污染情况进行估计,得到了各元素在不同功能区的分布特征及各功能区的污染程度。
然后,利用多元统计分析中的因子分析法对8种元素进行相关性分析及主成分提取,得到该区域内重金属污染的主要原因是工业污染、交通污染和生活污染。
最后,在前面分析结果的基础上,通过收集该地区历年来土壤中重金属的分布数据,建立土壤重金属含量的动态变化模型:QT=Q0K?T+QK-Z,运用该模型可以描述该城区地质环境的演变模式。
关键词土壤重金属;空间分布;污染源位置;克里格插值;因子分析;地质演变模式中图分类号TN914 文献标识码 A 文章编号1673-9671-(2012)071-0188-02随着城市经济的快速发展和城市人口的不断增加,人类活动对城市环境质量的影响日显突出。
对城市土壤地质环境异常的查证,以及如何应用查证获得的海量数据资料开展城市环境质量评价,研究人类活动影响下城市地质环境的演变模式,日益成为人们关注的焦点。
按照功能划分,城区一般可分为生活区、工业区、山区、主干道路区及公园绿地区等。
现对某城市城区土壤地质环境进行调查,为此,将所考察的城区划分为间距1公里左右的网格子区域,按照每平方公里1个采样点对表层土(0~10厘米深度)进行取样、编号,并用GPS记录采样点的位置。
由于在地表各重金属浓度的分布是相互影响的,并且受多种因素的多重影响,因此,我们应用因子分析法来研究重金属污染的主要原因。
地质环境是指由岩石圈、水圈和大气圈组成的环境系统。
各种元素在土壤中都是处于一个动态的循环过程。
一是土壤本身含有一定的量,即土壤背景值,这一值是自然形成的;二是元素的输入是多途径、多层次的,如工业、生活污染等;三是输入的元素会有一部分随着河流冲刷、地表侵蚀、植物吸收等因素流失。

统计学在环境污染评估中的应用在当今日益严重的环境污染问题下,人们对于环境质量的评估和监测变得尤为重要。
统计学作为一门研究数据处理和分析的学科,可以在环境污染评估中发挥重要作用。
本文将探讨统计学在环境污染评估中的应用,并分析其重要性和优势。
一、样本调查与数据收集环境污染评估需要对环境污染的源头和影响范围进行调查和研究。
在样本调查和数据收集过程中,统计学可以提供有效的方法和工具。
首先,统计学可以通过随机抽样的方式,保证样本的代表性和可靠性。
其次,统计学可以对环境样本进行测量和监测,并将数据进行结构化和整理,以便后续的分析研究。
二、数据分析与模型建立在收集到环境污染数据后,统计学可以提供数据分析和模型建立的方法。
通过统计学的方法,可以对环境数据进行处理和分析,提取其中的规律和趋势。
例如,可以通过回归分析的方法,建立环境污染指标与污染源之间的关系模型,方便进一步的研究和控制。
三、空间分析与地理信息系统在环境污染评估中,空间分析和地理信息系统(GIS)的应用也尤为重要。
统计学可以结合空间统计学的方法,对环境样本的空间分布进行分析和研究。
通过将环境数据与地理位置信息相结合,可以更加准确地评估环境污染的程度和范围。
四、风险评估与决策支持环境污染评估的一个重要目标是对环境风险进行评估和管理。
统计学可以通过概率与统计模型,对环境风险进行定量评估。
同时,统计学还可以为决策制定者提供科学的决策支持,帮助其制定出针对环境污染问题的有效措施和政策。
总结起来,统计学在环境污染评估中的应用十分广泛,可以通过样本调查与数据收集,数据分析与模型建立,空间分析与地理信息系统以及风险评估与决策支持等方面,为环境保护和污染治理提供重要的帮助和支持。
因此,进一步发展和推广统计学在环境污染评估中的应用,将对于实现可持续发展和构建美丽中国具有重要意义。
(字数:449字)。
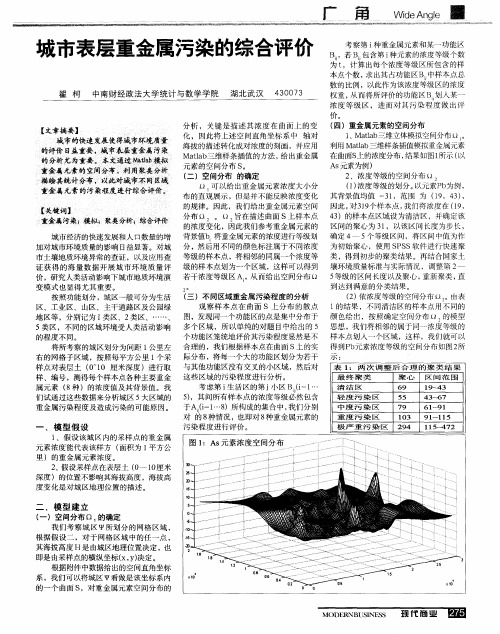
城市表层土壤重金属污染的空间分布特征分析摘要:分析了某城市城区表层土壤中的As、Cd 等8种重金属在生活区、工业区、山区、主干道路区及公园绿地区的含量水平,得出了不同区域重金属的污染程度;运用污染负荷指数法对影响土壤各重金属主要因子进行分析,确定不同区域重金属污染的主要特征;建立重金属污染物的传播模型,运用Kriging插值法对重金属含量进行最优无偏估计插值,对重金属污染的空间分布进行分析,揭示了城市表层土壤中重金属含量的空间分布特征。
关键词:城市城区;表层土壤;重金属污染;空间分布特征随着城市经济的快速发展和城市人口的不断增加,大量工业“三废”、城市生活垃圾和污泥等污染物的排放与不恰当处置使重金属在土壤中不断积累,加重了土壤重金属的污染负荷,导致我国城市表层土壤的重金属污染日趋严重。
而城市土壤重金属污染是能有效反映城市环境污染状况的重要指标之一。
因此,对城市土壤环境异常的查证并应用查证数据开展城市环境质量评价、研究人类活动影响城市土壤环境的演变模式日益成为人们关注的焦点。
1 数据来源与研究方法以某城市城区为研究区,将其划分为间距1 km左右的网格子区域,按照每平方公里1个采样点对表层土壤(0~10 cm土层)进行取样、编号,并用GPS 记录采样点的位置。
应用专门仪器测试分析,获得了每个样本所含的多种重金属元素的浓度数据。
另外,按照2 km的间距在那些远离人群及工业活动的自然区取样,将分析数据作为该城区表层土壤中重金属元素的背景值。
研究以2011年高教社杯全国大学生数学建模竞赛A题[1]所列的数据为数据来源,文献[1]列出了采样点的位置、海拔高度及其所属功能区的信息、8种主要重金属元素在采样点处的浓度和8种主要重金属元素的背景值。
按照功能划分,现代城市整个城区一般可分为生活区、工业区、山区、主干道路区及公园绿地区等,分别记为1类区、2类区、3类区、4类区、5类区,不同的区域环境受人类活动影响的程度不同。
统计分析在环境污染监测中的应用在当今社会,环境污染问题日益严峻,对人类的生存和发展构成了巨大威胁。
为了有效地保护环境,我们需要对环境污染进行监测和评估。
而统计分析作为一种强大的工具,在环境污染监测中发挥着至关重要的作用。
统计分析可以帮助我们收集、整理和分析大量的环境监测数据。
这些数据可能来自于各种监测站点、不同的时间段和多种污染物指标。
通过对这些数据的汇总和分类,我们能够清晰地了解环境污染的整体状况和变化趋势。
比如说,在空气质量监测中,我们会收集到诸如二氧化硫、氮氧化物、可吸入颗粒物等污染物的浓度数据。
利用统计分析方法,我们可以计算出这些污染物的平均值、中位数、标准差等统计指标。
平均值能够反映出一段时间内污染物浓度的总体水平;中位数则可以更好地体现数据的中间值,避免极端值的影响;标准差则能告诉我们数据的离散程度,即污染物浓度的波动情况。
统计分析还能帮助我们发现环境污染中的异常值和数据的分布特征。
异常值可能是由于监测设备故障、突发的环境污染事件或者其他特殊原因导致的。
通过识别这些异常值,我们可以及时对监测数据进行核实和修正,确保数据的准确性和可靠性。
对于数据的分布特征,常见的有正态分布、偏态分布等。
了解数据的分布形态有助于我们选择合适的统计方法和模型进行分析。
例如,如果数据呈正态分布,我们可以使用基于正态分布假设的统计检验方法;如果数据呈偏态分布,可能需要进行数据转换或者选择非参数统计方法。
在环境污染监测中,时间序列分析是一种常用的统计方法。
它可以用于分析污染物浓度随时间的变化规律。
通过建立时间序列模型,我们能够预测未来一段时间内污染物的浓度水平,为环境管理部门制定相应的政策和措施提供科学依据。
例如,对于某个地区的河流水质监测数据,我们可以构建时间序列模型来预测未来几个月内化学需氧量(COD)和氨氮等指标的变化情况。
如果预测结果显示水质有恶化的趋势,相关部门就可以提前采取措施,如加强污水处理、限制污染源排放等,以防止环境污染进一步加剧。
统计学方法在环境污染分析中的应用研究近年来,随着环境污染问题的日益突出,人们对于环境污染的影响以及对策的需求也越来越迫切。
在环境污染分析中,统计学方法作为一种强大的工具,被广泛应用于数据处理与分析、模型建立与预测等方面。
本文将以统计学方法在环境污染分析中的应用为主题,探讨其在污染源解析、风险评估和环境监测预警等方面的应用。
一、污染源解析环境污染常常由多个源头引起,而准确识别和解析各个源头的贡献程度对于采取相应的治理措施至关重要。
统计学方法在污染源解析中发挥了重要作用。
通过采集环境样本数据,并利用统计学方法对其进行模型建立和优化,可以准确推断出污染源的排放量和排放成分。
例如,利用多元统计分析方法,可以对不同区域或不同时间段的大气中某些污染物的浓度数据进行聚类,从而识别出不同的污染源。
二、风险评估环境污染对人类健康和生态系统造成的风险不容忽视。
统计学方法可以帮助我们对环境污染的风险进行评估和预测。
例如,在土壤中发现某种有毒物质时,可以利用统计学方法分析其浓度分布和空间变异性,从而评估周围环境的污染程度和可能的风险。
同时,还可以利用统计学方法建立风险模型,通过对环境因素与疾病发生的关联性进行统计分析,预测某一地区的疾病发生率。
三、环境监测预警及时监测环境的污染状况并进行预警,对于采取有效的防控措施至关重要。
统计学方法为环境监测预警提供了有效的手段。
例如,利用时间序列分析方法,可以对水质、大气等环境因素进行实时监测和预测,从而及时发现异常情况。
同时,还可以结合统计学方法和地理信息系统(GIS),对环境监测数据进行空间分析和建模,实现对整个区域的环境状况和趋势的综合评估。
综上所述,统计学方法在环境污染分析中的应用研究具有重要的意义。
它为我们提供了科学的数据处理和分析手段,帮助我们更好地认识和应对环境污染问题。
然而,也需要注意统计学方法在环境污染分析中的局限性和不确定性。
在使用统计学方法时,应注意数据的质量和可靠性,并综合考虑其他因素,以获得更准确、综合的分析结果。
统计方法在环境污染监测中的应用研究在当今社会,环境污染问题日益严峻,对人类的健康和生态平衡构成了严重威胁。
为了有效地监测和评估环境污染状况,统计方法发挥着至关重要的作用。
本文将详细探讨统计方法在环境污染监测中的应用,包括数据收集与处理、污染趋势分析、污染源识别以及环境质量评估等方面。
一、数据收集与处理准确可靠的数据是环境污染监测的基础。
统计方法在数据收集和处理过程中起着关键作用。
首先,通过合理设计抽样方案,可以确保采集到具有代表性的数据。
例如,在监测大气污染时,可以采用分层抽样的方法,根据不同的地理位置、气象条件和污染源分布来确定采样点,以提高数据的代表性和准确性。
在数据处理方面,统计方法可以用于去除异常值和噪声。
异常值可能是由于测量误差、仪器故障或特殊的环境事件导致的。
通过统计检验,如格拉布斯检验或狄克逊检验,可以识别并剔除这些异常值,从而提高数据的质量。
此外,还可以运用数据平滑技术,如移动平均法或指数平滑法,来减少数据的波动,更清晰地反映出数据的趋势。
二、污染趋势分析了解环境污染的变化趋势对于制定有效的环保政策和措施至关重要。
统计方法中的时间序列分析是研究污染趋势的有力工具。
例如,通过建立自回归移动平均(ARMA)模型或季节性自回归移动平均(SARIMA)模型,可以对长期的环境监测数据进行拟合和预测,从而揭示污染指标随时间的变化规律。
此外,趋势分析还可以帮助我们判断环保措施的效果。
如果在采取某项环保措施后,污染指标呈现出下降的趋势,且这种趋势在统计学上具有显著性,那么就可以认为该措施是有效的。
相反,如果污染趋势没有明显改变甚至恶化,就需要对措施进行调整和改进。
三、污染源识别确定环境污染的来源是治理污染的关键。
统计方法可以通过相关性分析、主成分分析和因子分析等手段来识别污染源。
相关性分析可以用于研究不同污染物之间的关系。
如果两种污染物之间存在显著的正相关,那么它们很可能来自相同的污染源。
主成分分析和因子分析则可以将多个相关的污染指标归结为几个综合的主成分或因子,从而揭示潜在的污染源类型。
生态环境 2008, 17(6): 1898-1902 Ecology and Environment E-mail: editor@基金项目:建设部研究开发项目(06-K9-8)作者简介:孙英君(1976年生),女,副教授,博士,主要研究方向为空间信息分析技术在城市建设中的应用。
E-mail:qingdaosyj@ 收稿日期:2008-06-11空间统计学模拟方法在城市重金属污染分析中的应用孙英君,丁宁,蔡菲,孟飞山东建筑大学土木学院,山东 济南 250014摘要:城市土壤重金属污染是城市化后噬待解决的一个重要问题。
传统的土壤重金属污染分析方法——克里格方法,通过满足未采样点局部方差最小而获得土壤污染状况预测结果,算法本身会给估值结果带来光滑作用,并只能提供未采样点的局部不确定性。
文章提出利用空间统计学的模拟方法,对土壤重金属污染状况进行研究,通过获取多幅模拟结果之间的差异来揭示研究区域土壤重金属污染的整体空间分布形态。
文章以上海某区域6种重金属(Cu 、Pb 、Cd 、Cr 、Hg 和As)为研究对象,利用空间统计学模拟方法对其空间分布予以研究,给出每种重金属空间分布模拟结果。
最后,文章以研究区域土壤环境背景上限值为标准,给出研究区域不同土壤重金属空间分布相应级别的不确定性分析结果。
关键词:模拟;地统计学;空间变异;重金属;不确定性中图分类号:X14 文献标识码:A 文章编号:1672-2175(2008)05-1898-05城市的土壤环境质量与人类健康息息相关,随着城市化进程的迅速发展,城市土壤重金属污染日趋引起人们的关注。
研究者将汞、镉、铅、铬、砷、锌、铜、镍合称为重金属环境污染元素,尤其是铅、镉、汞、铜及其复合污染最为突出,其中镉、汞、铅等重金属是城市和工业发展过程中产生的典型的“污染元素”,给区域土壤资源的保护、利用与管理带来了严峻挑战[1]。
据报道,中国受镉、砷、铬、铅等重金属污染的耕地面积近2000万hm 2,约占总耕地面积的1/5。
土壤重金属污染导致严重的经济损失,如中国每年就因重金属污染而减产粮食1000多万t ,另外被重金属污染的粮食每年也多达1200万t ,合计经济损失至少200亿元[2]。
同时,土壤重金属污染也会导致重金属在植物体中积累,并通过食物链富集到人体和动物体中,危害人畜健康,引发癌症和其他疾病等。
其次,土壤受到重金属污染会导致大气污染、地表水污染,地下水污染等生态环境问题。
因此开展土壤重金属空间结构特征的研究,特别是模拟土壤重金属的全局空间分布形态,定量化评价土壤重金属污染程度,及时有效地采取防护、修复措施,对减少城市重金属污染,提高人们的生活质量具有重要的意义。
1 土壤重金属空间结构及分布特征研究现状已有一些研究者对城市重金属污染状况进行分析:Hu 等利用地统计学对北京市大兴区土壤重金属含量的空间分布特征进行了研究[3];郑袁明、陈同斌等利用地统计技术对北京市近郊区土壤Ni 的空间结构及分布特征进行了研究[4];钟晓兰等以江苏省太仓市为例,运用地统计技术研究了长江三角洲地区土壤重金属污染的空间变异特征[5];郑海龙等利用地统计学普通克里格插值方法对上海梅山刚体集团附近的土壤重金属空间变异进行研究[6];李亮亮等通过克里格插值对葫芦岛市连山区、龙港区土壤重金属汞、铬、镍的空间分布进行单因子评价[7]。
Pilar Burgos 等运用Kriging 方法对Seville , Spain 地区的土壤修复前后重金属、微量元素的变化进行了分析[8];M. Biasioli 等利用地统计方法及GIS 技术对大型城市发展对土壤重金属的影响加以分析[9]。
Li 等利用克里格方法,结合GIS 技术对香港九龙6种重金属元素(Cd 、Cr 、Cu 、Ni 、Pb 和Zn )的空间分布加以研究,并通过热点探测的方法进行污染源的求解[10]。
黄勇等对地统计学在土壤重金属研究中的应用做了综述及其展望[11]。
总结起来,在土壤重金属空间结构及分布特征研究上,研究人员较多地基于GIS 技术与空间(地)统计学克里格系列插值方法对城市重金属污染状况进行分析:利用GIS 技术进行研究区域及其采样数据、空间分布插值结果的可视化表达;利用空间统计学的变异函数对采样数据的空间异质性予以分析,并通过理论变异函数的不同因子、系数来寻求异质性产生的原因(影响因子),最后给出克里格算法插值得到的某重金属空间分布结果。
2 存在的问题及解决方法经过克里格插值得到的重金属空间分布结果不能够反映研究区域的真实状况,特别是当研究者孙英君等:空间统计学模拟方法在城市重金属污染分析中的应用 1899的目标是发现研究区域的全局分布态势或进行热点探测时。
因为克里格算法本身具有一定的平滑作用:即将极大值估计偏小,极小值估计偏大,因此插值后的结果趋于平缓[12]。
但在某些问题的解决中,人们需要的恰恰是被克里格方法平滑掉的极值,例如在污染分析中,研究者主要是通过污染金属所表现的极值来发现污染源。
此外,克里格方法只能为未采样点提供唯一的“最优”估计值,且仅仅能够提供该点估值的局部不确定性。
土壤重金属污染的全局模拟预测及其空间不确定性分析可通过空间统计学的系列模拟方法加以解决。
在此,本文选择序列高斯模拟方法进行研究区域土壤重金属空间分布的模拟预测。
该方法通过随机扰动因子,获得不同搜索路径,从而在某一具体点位预测时采用不同的已知采样点及已模拟点估值结果,最后得到相同概率的多个不同模拟结果。
这些模拟结果与已知采样点的空间结构(变异函数或直方图分布)一致,但对某个单一的未采样点而言,不同轮次的模拟结果会有所差异,也正是这种差异,体现了模拟结果的空间不确定性问题。
3 应用实例本文以上海某试验区域为研究对象,采用梅花多点取样方法共获取240个样品。
土壤样品经风干、过100目筛后,Hg和As用王水水浴加热消解,其他重金属用HNO3-HClO4-HF消化法制样,土壤中全量Cu、Zn、Pb、Cr采用X荧光法,全量Hg、As采用原子荧光法。
全量Cd采用原子吸收石墨炉法。
重金属的分析测定中,均加入国家标准土壤标样(GSS-1)进行分析质量控制,分析结果符合质量控制要求。
3.1 土壤重金属空间结构分析研究区域土壤重金属空间结构分析如下表1所示,有关半方差函数模型选取及参数交互验证等可以参考文献[13]。
从表1可以看出,研究区域内6种重金属元素的变程大小顺序为:Cd> Cr> As> Pb> Hg> Cu。
其中Cd、Cr、As的变程较大,分别为11.54 km、11.0 km、7.0 km,反映了区域因素对Cd和Cr的影响较大,而植物吸收、施肥等小尺度因素对它们的影响较小;其余重金属的变程范围为0.81~1.73 km,说明它们受到污水灌溉、施肥等随机因素的影响较大,导致了它们在一个较小的距离范围内存在相关关系。
表1中块金值C0与基台值C0+C1之比是反映区域化变量空间异质性程度的重要指标,该比值用以反映空间变异影响因素中区域因素(自然因素)和非区域因素(人为因素)的作用[12]。
从表1可以看出Cu、Pb、Cr、As的7种重金属元素的块金常数/基台值均大于0.25小于0.75,属于中等空间相关。
而Hg和Cd的块金常数/基台值大于0.75,反映了受随机因子影响较大,外源污染物对表层土壤Hg 和Cd含量的贡献较大。
3.2 土壤重金属空间分布模拟6种土壤重金属空间分布模拟均在GS+(v.9)软件环境下完成,下图1所示均是取自1000次模拟结果的平均值。
为识别土壤重金属空间分布的整体态势,作者对每一类重金属选择10个以上取值区间成图。
同时,本文选取研究区所在城市1987年土壤重金属背景值上限值(按95%置信限)为判断标准,分别是:Cu 40.6 mg/kg、Pb 36.1 mg/kg、Cd 0.293 mg/kg、Cr 99.5 mg/kg、Hg 0.259 mg/kg、As 14.2 mg/kg[14]。
对比各重金属标准值,可以看出,研究区域西北区域铜要素严重超标,此外Cr、Pb元素也存在较明显超标斑块,其余三种重金属超过标准值的斑点相对较少。
而从研究区域而言,西北、中南偏下部位是受各种重金属污染较为严重的区域。
3.3 土壤重金属空间分布模拟不确定性分析如“3.2”所述,文章选取研究区域所在城市1987年土壤重金属背景值上限值为阈值,对取得的土壤重金属空间分布模拟结果进行不确定性分析,分别给出每一种金属超出阈值的概率分布图。
由图2可以看出,在Cd、Cr、Cu三幅图上,均出现了概率较高的紫色区域,而这些区域比较集中在图幅的西北角及其中南偏下部位,与3.2中的分析取得一致结果。
特别是Cu,在整幅图面上,只有少部分区域超标的概率小于50%,预示了铜要素在该研究区域的严重污染。
其他三中重金属元素,As、Hg及Pb,存在特定斑点区域超标,几率在60%上(红色系以上色彩表示),但大部分研究区域污染程度较轻。
4 总结以上研究,由于资料所限,作者并没有将分析结果与研究区域的自然、社会状况相关联,如污染区域是否与研究区域的厂矿企业分布一致等。
但从上文分析可以看出,经过1000次高斯序列模拟,其表1 研究区域土壤重金属的半方差函数模型Table 1 The semi-variogram models of heavy metals in the studied soilsHeavymetalModel Nugget/C0 Sill/(C0+C1) Range/km C0/(C0+C1) Hg Gaussian 0.006 0.007 1.54 0.860 Cu Spherical 152.450 361.660 0.81 0.422 Pb Exponential 39.829 65.294 1.73 0.609 Cd Gaussian 0.037 0.047 11.54 0.785 Cr Gaussian 189.120 307.570 11.0 0.614 As Gaussian 2.331 3.496 7.0 0.6661900 生态环境 第17卷第5期(2008年9月)结果已相对稳定,能够揭示研究区域整体空间分布形态。
特别是结合研究区域土壤重金属背景值对模拟结果进行不确定性分析,不仅对模拟结果做了有效的印证,同时还发现一些在模拟结果中没突现出来,而发生几率又相对较高的污染斑点(如重金属Cd )。
将二者结合起来,可以对重金属污染区域进行评价区划,为决策部门对土壤的整治与修复提供科学的依据。
参考文献:[1] 刘勋鑫,王翠红,廖超林, 等. 土壤重金属特性空间变异性方法研究[J]. 农业网络信息,2007,6:106-108.Liu Xunxin, Wang Cuihong, Liao Chaolin, et al. The research on the methods of heavy metal spacial variation in soil [J]. Agriculture net-work information, 2007,6:106-108.[2] 隋红建,吴璇,崔岩山. 土壤重金属迁移模拟研究的现状与展望[J].农业工程学报,2006,22(6): 197-200.Sui HongJian, Wu Xuan, Cui Yanshan. Modeling heavy metal move-ment in soil: review and further study directions [J]. Transactions of the CSAE, 2006,22(6): 197 - 200.[3] Hu Kelin ,Zhang Fengrong ,Li Hong, et al. Spatial patterns of soilheavy metals in urban-rural transition zone of Beijing[J]. Pedosphere ,2006,6: 690-698.[4] 郑袁明,陈同斌,陈煌, 等. 北京市近郊区土壤镍的空间结构及分布特征[J]. 地理学报,2003,3:470 - 476.Zheng Yuanming, Chen Tongbin, Chen Huang, et al. The spatial structure and distribution of Ni Contents in soils of suburbs of Bei-jing[J]. Acta geographica sinica, 2003,3:470 - 476.[5] 钟晓兰,周生路,李江涛, 等. 长江三角洲地区土壤重金属污染的空间变异特征:以江苏省太仓市为例[J]. 土壤学报,2007,1:33-40. Zhong Xiaolan, Zhou Shenglu, Li Jiangtao, et al. Spatial variability of soil heavy metals contamination in the yangtze river delta —a case图1 研究区重金属空间分布模拟结果 Fig. 1 The spatial distribution of heavy metalsCrCuHgPbCdAs孙英君等:空间统计学模拟方法在城市重金属污染分析中的应用 1901study of taicang city in jiangsu province[J]. Acta pedologica sinica, 2007,1:33 - 40.[6] 郑海龙,陈杰,邓文靖, 等. 城市边缘带土壤重金属空间变异及其污染评价[J]. 土壤学报,2006,1:39 - 45.Zheng Hailong, Chen Jie, Deng Wenjing, et al. Spatial analysis and pollution assessment of soil heavy metals in the steel industry areas of nanjing periurban zone [J]. Acta pedologica sinica, 2006,1:39 - 45. [7] 李亮亮,张大庚,王延松, 等. 葫芦岛市连山区、龙港区土壤重金属汞、铬及镍的空间分布及其污染评价[J]. 土壤通报,2006,6:1207 - 1211.Li Liangliang, Zhang Dageng, Wang Yansong, et al. Spatial distribu-tion contamination evaluation of Hg, Cr and Ni in soil of Lianshan and Longgang districts, Huludao city [J]. Chinese Journal of Soil Science, 2006,6:1207 - 1211.[8] BURGOS P, MADEJO´N E, PE´REZ-DE-MORA A, et al. Spatialvariability of the chemical characteristics of a trace-element-contami-nated soil before and after remedi-ation[J]. Geoderma, 2006, 130: 157-175.[9] BIASIOLIA M ,BARBERIS R ,AJMONE-MARSAN F. The influenceof a large city on some soil properties and metals content[J]. Science of the Total Environment ,2006,356: 154-164.[10] XIANGDONG LI ,SIULAN LEE ,SZECHUNG WONG, et la. Thestudy of metal contamination in urban soils of Hong Kong using a GIS-based approach [J]. Environmental Pollution ,2004,129:113-124. [11] 黄勇,郭庆荣,任海, 等. 地统计学在土壤重金属研究中的应用及展望[J]. 生态环境,2004, 13(4): 681-684.Huang Yong, Guo Qingrong, Ren Hai, et al. Application and perspec-tive of geostatistics in the study on soil heavy metals[J]. Ecology and图2 土壤重金属空间分布不确定性预测结果 Fig. 2 The Probability Map of heavy metalsProb. of AsProb. of CdProb. of HgProb. of PbProb. of CuProb. of Cr1902 生态环境第17卷第5期(2008年9月)Environment, 2004, 13(4): 681-684.[12] Goovaerts P. Geostatistics in Soil Science: State-of-the-Art and Per-spectives [J]. Geoderma,2002,89:1 - 45.[13] 徐建华. 现代地理学中的数学方法[M]. 北京: 高等教育出版社,2002: 105 - 115.Xu Jianhua. Mathematical methods in contemporary geography[M].Beijing: Higher Education Press, 2002: 105 - 115.[14] 王云,汪雅谷,罗海林, 等. 上海市土壤环境背景值[M]. 北京:中国环境科学出社,1992: 37 - 57.Wang Yun, Wang Yagu, Luo Hailin, et al. The background values of soil elements in Shanghai[M]. Beijing: Chinese Environment Science Press, 1992: 37 - 57.The application of spatial statistics simulation in the study of heavy metalcontamination of urban soilsSun Yingjun, Ding Ning, Cai Fei, Meng FeiCollege of Civil Engineering; Shandong Jianzhu UniversityAbstract: The pollution of surface soils caused by heavy metals was a focus problem appeared in the process of urbanization. In-stead of the acquisition of the smoothed and “best” estimation of unsampled points,the paper paid much attention to describe the detail of contamination and assess the spatial uncertainty about unsampled values. The simulation method in Geostatistics was ap-plied to the study of heavy metal contamination. Based on the statistics (histogram, Variogram) of sampled points,the simulation method can generate a set of equally-probable realizations. They represented the different situation of contamination possibly, which was particularly helpful for uncertainty assessment. The case study was from an Urban-Rural transition zone of Shanghai,China. Six kinds of heavy metals (Cu, Pb, Cd, Cr, Hg and As) in agricultural surface soils were analyzed in the paper. Based on the sequential simulation methods, the author got the different realizations of the six kinds of heavy metals respectively. At last,the author drew the conclusion that Cu,Cd and Cr were the dominant elements that influenced soil quality in the study area. Meanwhile,the author gave the uncertainty map of the six heave metals with the standards values of background as the threthold.Key words: simulation; geostatistics; spatial variability; heavy metals; uncertainty。