三角形中位线的推论

三角形中位线定理及推论一、中位线定理中位线是指连接三角形一个顶点与对边中点的线段。

三角形中位线定理是指在一个三角形中，三条中位线交于一点，且这个交点与三个顶点的距离相等。

我们先来证明中位线交于一点这一结论。

假设ABC为一个三角形，AD是BC中点连线，BE是AC中点连线，CF 是AB中点连线。

我们可以得到△ADC和△BCD是全等三角形。

根据全等三角形的性质，我们可以得到∠ADC=∠CBD，∠ACD=∠BCD，且AD=BD。

同理，我们可以得到△AEB和△CEB是全等三角形，∠AEB=∠CEB，∠ABE=∠CBE，且AE=BE。

因为∠ADC=∠CBD，∠ACD=∠BCD，所以∠ADC+∠ACD=∠CBD+∠BCD，即∠ADC+∠ACD=180°。

同理，∠AEB+∠ABE=180°。

我们可以得到∠ADC+∠ACD+∠AEB+∠ABE=∠ADC+∠ACD+∠AEB+∠ABE+∠BCD+∠CBE。

而∠ADC+∠ACD+∠AEB+∠ABE+∠BCD+∠CBE=360°。

所以∠ADC+∠ACD+∠AEB+∠ABE+∠BCD+∠CBE=360°。

而∠ADC+∠ACD+∠AEB+∠ABE=360°。

所以∠BCD+∠CBE=0°。

由于∠BCD+∠CBE=0°，所以∠BCD=0°，∠CBE=0°。

因此，BD和CE是平行线。

根据平行线的性质，我们可以得到三角形BDF和三角形CEG是全等三角形，∠BFD=∠CGE，∠BDF=∠CEG，且BD=CE。

所以，我们可以得到BF=CG。

因此，在三角形ABC中，三条中位线AD、BE、CF交于一点G，且这个交点与三个顶点的距离相等。

二、中位线推论1. 三角形中位线推论一：中位线长度在一个三角形中，连接一个顶点与对边中点的中位线的长度等于对边的一半。

假设ABC为一个三角形，AD是BC中点连线。

我们已经证明了AD和BC是平行线，且AD=BD。

三角形的中位线与三角形的中线有什么不同？
学过教科书上关于三角形的中位线的知识后，我们可以推出，判定一条线段是三角形的中位线的方法有以下3种：
1.定义：连结三角形两边中点的线段叫做三角形的中位线。

2.判定定理：经过三角形一边中点的直线，如果平行于另一边，那么这条直线位于三角形内的部分是这个三角形的中位线。

3.判定定理：端点位于三角形两边上的线段，如果平行于第三边，且等于第三边的一半，那么这两条线段是这个三角形的中位线。

由此可知：三角形的中位线平分这个三角形的两条边，平行于第三边，且等于第三边的一半，但不经过这个三角形的任何顶点；而三角形的中线只平分这个三角形的一条边，不平行于这个三角形的任何边，但经过与它所平分的边相对的顶点。

三角形的中位线是两两相交；而在将来我们可以证明，三角形的中线相交于一点，这一点把三条中线都分成2比1两段，被称为三角形的重心，它在物理学中用处很大。

三角形中位线定理及推论一、三角形中位线定理三角形中位线定理是指在任意三角形中，连接一个顶点与对边中点的线段称为中位线，三条中位线交于一点，且该点与三个顶点的距离相等。

具体表述为：三角形三条中位线的交点与三个顶点的距离相等。

以三角形ABC为例，连接顶点A与边BC的中点D，顶点B与边AC 的中点E，顶点C与边AB的中点F，根据中位线定理可知，中位线AD、BE和CF三条线段交于一点G，并且AG=BG=CG。

中位线定理的证明可以通过向量法或平面几何法进行，这里我们选择平面几何法证明。

证明思路如下：1. 连接顶点A与边BC的中点D，假设点G是中位线AD与中位线BE 的交点；2. 连接顶点B与边AC的中点E；3. 通过顶点C以平行于边AB的直线与中位线AD交于点H；4. 由平行线的性质可知，AH=CH；5. 进一步，由三角形的对应边成比例可得：AH/AD=CH/CF；6. 由于AH=CH，所以AD=CF；7. 同样地，由中位线定理可得：BE=CF；8. 综上所述，AD=BE=CF，即证明了中位线定理。

二、三角形中位线推论基于中位线定理，我们可以得出一些有关三角形的推论。

1. 三角形中位线长度关系推论根据中位线定理，三角形三条中位线的交点与三个顶点的距离相等，即AG=BG=CG。

由此可得，中位线上的点距离顶点的距离是相等的。

进一步推论，三角形中位线的长度满足以下关系：AG=2GD，BG=2GE，CG=2GF。

2. 三角形中位线与三角形面积推论由三角形中位线定理可知，三条中位线交于一点G。

以G为顶点，三边中点分别为D、E、F，连接DG、EG和FG。

我们可以发现，连接G与三角形顶点的线段将三角形分成了六个小三角形，而这些小三角形的面积相等。

因此，我们可以推论得到：三角形中位线所分割的三个小三角形的面积相等。

3. 三角形中位线与三角形高度推论在三角形中，如果我们将中位线作为底边，那么与之对应的高度就是顶点到底边中点的距离。

三角形的中线与中位线在几何学中，三角形是最基本的图形之一，而其中线和中位线则是与三角形密切相关的概念。

本文将重点探讨三角形的中线与中位线，并阐述它们在三角形属性研究和实际应用中的重要性。

一、中线的概念首先，我们来介绍三角形的中线。

中线是连接三角形的一个顶点与对边中点的直线段。

对于任意三角形ABC，连接顶点A与对边BC的中点M的线段AM就是该三角形的中线。

中线有以下两个重要性质：1. 中线的长度相等：在任意三角形中，连接一个顶点与对边中点的线段的长度相等。

即AM = BM = CM。

2. 中线互相平分：在任意三角形中，中线互相平分。

即AM与BM 的长度相等，BM与CM的长度相等，CM与AM的长度相等。

二、中位线的概念接下来，我们来介绍三角形的中位线。

中位线是连接三角形的两个顶点的中点与对边中点的直线段。

对于任意三角形ABC，连接顶点A 与对边BC中点M以及连接顶点B与对边AC中点N的线段AM和BN就是该三角形的中位线。

中位线有以下两个重要性质：1. 中位线长度：在任意三角形中，连接一个顶点与对边中点的线段的长度等于对边的一半。

即AM = 0.5 BC，BN = 0.5 AC。

2. 中位线交点：在任意三角形中，三条中位线的交点被称为三角形的重心G，也就是三角形的质心。

重心G将每条中位线都平分成两段，其中一段的长度是另一段的两倍。

三、中线和中位线的应用中线和中位线是研究三角形属性时经常使用的重要工具。

它们有多种应用，如下所示：1. 确定三角形的重心：通过连接三角形的顶点和对边中点，可以确定三角形的重心G。

重心G在三角形内部，对于一些三角形问题的解决具有重要作用。

2. 判断三角形的形状：根据中线和中位线互相平分的性质，可以判断三角形的形状。

例如，如果三角形的三条中位线相等，则该三角形是等边三角形；如果三角形的中线相等，则该三角形是等腰三角形。

3. 解决三角形的证明问题：在三角形的证明中，利用中线和中位线的性质可以简化问题的证明过程。

三角形的中线与中位线在解析几何中，三角形是一个基础而重要的概念，而其中线和中位线则是三角形中的两个重要线段。

本文将介绍三角形的中线和中位线，并探讨它们的性质和应用。

一、中线的定义和性质中线是连接三角形两个顶点与对应边中点的线段。

在任意三角形ABC中，连结A与BC的中点D，B与AC的中点E，C与AB的中点F，则线段DE称为三角形ABC的中线。

中线有以下几个重要性质：1. 中线长度相等在任意三角形中，三条中线的长度是相等的。

这一性质可以用中位线定理进行证明。

假设DE为中线，在三角形ABC中，连接EF和FD，由中位线定理可知，EF和FD分别是AC和AB的中位线，所以EF=FD=1/2AC=1/2AB，因此DE与EF长度相等。

2. 中线互相平分在任意三角形中，三条中线相互平分。

换句话说，三条中线的交点是三角形的重心。

设三条中线相交于点G，则可以证明GD:GA=GE:GB=GF:GC=1:2。

3. 中线与对应边平行在任意三角形中，中线与对应边是平行的。

即DE∥AB，EF∥BC，FD∥AC。

这一性质可以通过向量法进行证明，利用向量的平行性质和中点的定义可以推导出这一结论。

二、中位线的定义和性质中位线是连接三角形的两个边中点的线段。

在任意三角形ABC中，连结AB的中点D，AC的中点E，BC的中点F，则线段DE称为三角形ABC的中位线。

中位线有以下几个重要性质：1. 中位线长度相等在任意三角形中，三条中位线的长度是相等的。

由于中位线连接对边的中点，而对边的长度相等，所以中位线的长度也相等。

2. 中位线与对边平行在任意三角形中，中位线与对边是平行的。

即DE∥BC，DF∥AC，EF∥AB。

这一性质同样可以通过利用向量法进行证明。

3. 中位线与中线交点在任意三角形中，三条中位线的交点是三角形的重心。

与中线类似，重心是三角形内部的一个特殊点，可以用中位线的交点来确定。

重心具有平分中线和平分面积的性质，是三角形的一个重要参考点。

三角中位线定理的应用中位线的性质：平行与第三边，并且等于第三边的一半。

三角形有三条中位线，最终将三角形分成四个全等三角形。

能够造出三个平行四边形，其中平行四边形的周长恰好等于三角形长两边之和。

中位线与第三边上的中线互相平分。

利用的是平行四边形的对角线互相平分。

三角形的中位线围成的三角形跟原三角形形状一样，周长是原来的一半，面积是原来的1/4，中位线的应用测距，中位线的定义，经过三角形两边中点的连线。

中线指的是一顶点与对边中点的连线。

中线性质，中线将三角形分成面积相等的两部分（等底同高面积相等）知识要点：三角形的中位线平行于三角形第三边，并且等于第三边的一半.1.三角形三条中位线围成的三角形与原三角形在某些数量上的关系（形状一样/相似）⑴.周长关系三角形的三条中位线围成的三角形的周长是原三角形的周长的一半.⑵.三角形的三条中位线围成的三角形的面积是原三角形的面积的41.2.中点四边顺次连结四边形四边中点所构成的四边形，我们把它简称为中点四边形.中点四边形的特殊性主要是看原四边形的对角线的特征，分为下面几种情况：任意四边形的中点四边形是平行四边形。

对角线相等的四边形的中点四边形是菱形；对角线垂直的四边形的中点四边形的是矩形；对角线既相等又垂直的四边形的中点四边形是正方形。

中位线与第三边上的中线互相平分。

利用的是平行四边形的对角线互相平分。

1、已知△ABC 的周长为1，连结△ABC 的三边中点构成第二个三角形， 再连结第二个三角形的三边中点构成第三个三角形，依此类推，第2010个三角形的周长是（）2、如图所示，已知四边形ABCD ，R ，P 分别是DC ，BC 上的点，E ，F 分别是AP ，RP 的中点，当点P 在BC 上从点B 向点C 移动而点R 不动时，那么下列结论成立的是（）A ．线段EF 的长逐渐增大B ．线段EF 的长逐渐减少C ．线段EF 的长不变D ．线段EF 的长不能确定3、如图ABC 中，EF 为三角形的中位线，AD 是BC 边上的中点，点O 为EF 和AD 的交点.求证：EF 和AD 互相平分.4、如图，在四边形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点．四边形EGFH 是平行四边形吗？请证明你的结论．5、如图，在四边形ABCD 中，E 、F 、G 、H 分别是AB 、CD 、AC 、BD 的中点．四边形EGFH 是平行四边形吗？请证明你的结论．6、如图，在四边形ABCD中，点P是对角线BD的中点，点E，F分别是AB，CD的中点，AD＝BC，（1）∠PEF＝35°，则∠PFE的度数．（2）∠CBD=20°，∠ADB=100°，则∠PFE的度数．7、已知：如图，在四边形ABCD中，对角线AC、BD相交于O，且AC＝BD，E、F分别是AB、CD的中点，E、F分别交BD、AC于点G、H．求证：（1）OG＝OH．（2）∠ONM＝∠OMN.8、如图，在四边形ABCD中，已知AB＝CD，点E，F分别为AD，BC的中点，延长BA，CD，分别交射线FE于P，Q两点．求证：∠P＝∠CQF..９、点M为△ABC的边BC的中点，AB＝12，AC＝18，BD⊥AD于点D，连DM.(1)如图1，若AD为∠BAC的平分线，则MD＝；（1）DM∥AC；DM＝21（AC﹣AB）．(2)如图2，若AD为∠BAC的外角平分线，则MD＝．．【变式】如图，在Rt△ABC中，∠ACB＝90°，D为△ABC外一点，使∠DAC＝∠BAC，E为BD的中点．若∠ABC＝60°，则∠ACE＝.１０、如图，△ABC的中线BD、CE相交于点O，F、G分别是OB、OC的中点，线段EF与DG之间有什么关系？为什么？１１、如图，点E F G H、、、分别是CD BC AB DA、、、的中点.求证：四边形EFGH是平行四边形１２、如图，已知在□ABCD中，EF∥BC,分别交AB CD、于E F、两点，DE AF、交于M,CE BF、交于N．求证:1MN AB2=.１３、已知：E为ABCD的边DC的延长线上的一点，且CE DC=,连结AE分别交BC BD、于F G、，对角线AC BD、交于点O.求证：AB2OF=。

梯形、三角形中位线一、梯形、三角形中位线在证明平行、线段相等及线段的倍、半问题中起了重要的作用，对此我们应给予足够的重视。

二、知识要点：1.平行线等分线段定理：如果一组平行线在一条直线上截得的线段相等，那么在其它直线上截得的线段也相等。

推论1：经过梯形一腰的中点与底平行的直线必平分另一腰。

推论2：经过三角形一边中点与另一边平行的直线必平分第三边。

2.三角形中位线：（1）定义：连结三角形两边中点的线段叫做三角形的中位线。

（2）三角形中位线定理：三角形中位线平行于第三边，并且等于它的一半。

3.梯形中位线：（1）定义：连结梯形两腰中点的线段叫做梯形中位线。

（2）梯形中位线定理：梯形中位线平行于两底，并且等于两底和的一半。

三、例题例1.如图，△ABC中，D是AB中点，E是AC上的点，且3AE=2AC，CD、BE交于O点。

求证：OE=BE。

分析：已知D是AB中点，遇到中点我们应当考虑到可能要用中位线，有中位线就可以得到线段的一半，同样可能再得到线段的一半，从而可以得到某线段的；又已知3AE=2AC，得AE=AC，如果取AE中点F，连结DF就可得到△ABE的一条中位线。

证明：取AE中点F，连结DF，∵D是AB中点，∴DF是△ABE的中位线∴ DF= BE且DF//BE（三角形中位线定理）∵ 3AE=2AC，∴ AE= AC∴ AF=FE=EC= AC在△CFD中，∵ EF=EC且DF//BE即OE//DF，∴ CO=DO（过三角形一边中点，与另一边平行的直线，必平分第三边）∴ OE是△CDF的中位线∴ OE= DF∴ OE= BE。

说明：本题我们做了一条中位线，使得在两个三角形中可使用中位线定理。

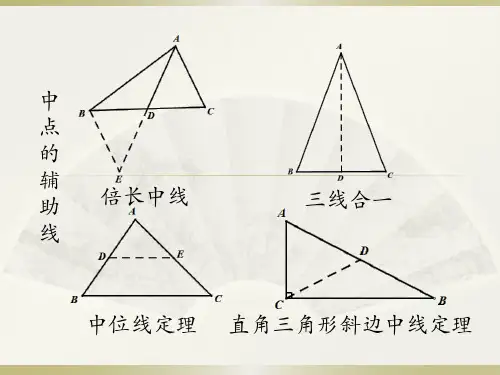
遇中点，作中位线是常见的辅助线。

例2如图，在梯形ABCD中AD//BC，E、F分别是AB、CD的中点，EF分别与BD、AC相交于M、N。

且AD=20cm，BC=36cm。

求MN的长。

分析：因为EF是中位线，所以EF//AD//BC，EF= (AD+BC)如果能求出EM和NF的长，就可以求出MN的长。

三角形的中位线与中心三角形是几何学中最基本的图形之一，它有很多重要的性质和特点。

本文将着重讨论三角形的中位线及其与三角形中心的关系。

一、中位线的定义所谓中位线，是指三角形内任意两个顶点之间的连线中点所组成的线段。

对于任意三角形ABC，连接顶点A和B的中点M₁，连接顶点B和C的中点M₂，连接顶点C和A的中点M₃所组成的线段M₁M₂M₃即为三角形的中位线。

二、中位线的性质1. 中位线互相平行在任意三角形中，三条中位线互相平行，即M₁M₂ // M₂M₃ //M₃M₁。

2. 中位线长度相等三角形三条中位线的长度相等，即M₁M₂ = M₂M₃ = M₃M₁。

3. 中位线交于一点三条中位线交于同一点G，这个交点G被称为三角形的重心。

重心是三角形的内心，也是重心到三角形三个顶点的距离之和最小的点。

三、三角形中位线与重心的关系重心是三角形的中位线的交点，也是三角形的一个特殊点。

1. 重心到顶点的距离重心到三角形三个顶点的距离之比为2:1。

即AG = 2GM₁，BG =2GM₂，CG = 2GM₃。

2. 重心的位置重心将每条中位线分成两个部分，即AG = GM₁，BG = GM₂，CG = GM₃。

3. 重心的作用重心是三角形内部重要的几何中心之一，具有以下作用：- 重心所在的中位线可以将三角形分成面积相等的两部分。

- 当三角形悬挂在任意一条中位线上时，重心处于该中位线的中点。

- 重心是三角形内切圆的圆心。

四、应用实例1. 设计建筑在建筑设计中，重心的概念被广泛运用。

由于重心的位置对于建筑物的平衡性和稳定性具有重要影响，建筑师需要在设计过程中考虑到重心的位置，以确保建筑物能够安全地承受外部的压力和重力。

2. 交通规划在交通规划中，重心也是一个重要的考虑因素。

交通规划师通过分析城市不同区域的人口、就业机会和基础设施等因素，可以确定城市的重心位置，从而优化交通网络的设计，提高交通效率。

3. 科学研究三角形的中位线和重心不仅仅在几何学中有重要的应用，它们在其他学科中也扮演着重要的角色。