2014高考数学(文)二轮专题升级训练:专题5 第1讲 空间几何体]
- 格式:doc
- 大小:335.50 KB
- 文档页数:5

阶段检测卷(五)一、填空题(每小题5分,共70分)1.一支田径运动队有男运动员56人,女运动员42人;现用分层抽样的方法抽取若干人,若抽取的男运动员有8人,则抽取的女运动员有________人. 解析 设抽取的女运动员有x 人,则856=x42,解得x =6. 答案 62.(2011·江苏卷)某老师从星期一到星期五收到的信件数分别为10,6,8,5,6,则该组数据的方差s 2=________.解析 由题意得该组数据的平均数为x =15(10+6+8+5+6)=7,所以方差为s 2=15[32+(-1)2+12+(-2)2+(-1)2]=3.2.答案 3.23.(2011·江苏卷)从1,2,3,4这四个数中一次随机地取两个数,则其中一个数是另一个数的两倍的概率是________.解析 从中取出两个数共有{1,2},{1,3},{1,4},{2,3},{2,4},{3,4}6种情况.其中一个数是另一个数的两倍的情况共有{1,2},{2,4}2种,∴p =26=13. 答案 134.(2010·江苏卷)盒子里共有大小相同的3只白球,1只黑球.若从中随机摸出两只球,则它们颜色相同的概率是________.解析 四个球取出两球有6种等可能基本事件:(黑,白1),(黑,白2),(黑,白3),(白1,白2),(白1,白3),(白2,白3).两只球颜色相同有3种:(白1,白2),(白1,白3),(白2,白3). 所以所求概率为P =36=12. 答案 125.(2013·南通调研)已知正四棱锥的底面边长是6,高为7,这个正四棱锥的侧面积是________.解析由于四棱锥的斜高h=(7)2+32=4,故其侧面积S=12×4×6×4=48.答案486.某校开展“爱我海西、爱我家乡”摄影比赛,9位评委为参赛作品A给出的分数如茎叶图所示.记分员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是________解析当x≥4时,89+89+92+93+92+91+947=6407≠91,∴x<4,∴89+89+92+93+92+91+x+907=91,∴x=1.答案 17.(2012·辽宁卷改编)在长为12 cm的线段AB上任取一点C.现作一矩形,邻边长分别等于线段AC,CB的长,则该矩形面积大于20 cm2的概率为________.解析设线段AC的长为x cm,则线段CB的长为(12-x)cm,那么矩形的面积为x(12-x)cm2,由x(12-x)>20,解得2<x<10.又0<x<12,所以该矩形面积大于20 cm2的概率为2 3.答案2 38.(2013·辽宁卷改编)某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100].若低于60分的人数是15,则该班的学生人数是________.解析由频率分布直方图,低于60分的频率为(0.01+0.005)×20=0.3.所以该班学生人数150.3=50.答案509.(2012·南通模拟)给出如下10个数据:63,65,67,69,66,64,66,64,65,68.根据这些数据制作频率分布直方图,其中[64.5,66.5)这组所对应的矩形的高为________.解析落在区间[64.5,66.5)的数据依次为65,66,66,65,共4个,则矩形的高等于频率组距=41066.5-64.5=15.答案1 510.(2012·淮阴、海门、天一中学联考)在圆x2+y2=4所围成的区域内随机取一个点P(x,y),则|x|+|y|≤2的概率为________.解析|x|+|y|≤2表示的图形是正方形及其内部,用正方形的面积除以圆x2+y2=4的面积易得概率为2π.答案2π11.如图,正方体ABCD-A1B1C1D1中,AB=2,点E为AD 的中点,点F在CD上,若EF∥平面AB1C,则线段EF 的长度等于________.解析∵EF∥平面AB1C,EF⊂平面ABCD,平面ABCD∩平面AB1C=AC,∴EF∥AC,又∵E是AD的中点,∴F是CD的中点,即EF是△ACD的中位线,∴EF=12AC=12×22= 2.答案 212.从个位数与十位数之和为奇数的两位数中任取一个,其个位数为0的概率是________.解析①个位数为1,3,5,7,9时,十位数为2,4,6,8;个位数为0,2,4,6,8时,十位数为1,3,5,7,9,共45个.②个位数为0时,十位数为1,3,5,7,9,共5个,个位数为0的概率是545=19.答案 1913.已知P 是△ABC 所在平面内一点, PB →+PC →+2P A →=0,现将一粒黄豆随机撒在△ABC 内,则黄豆落在△PBC 内的概率是________.解析 取边BC 上的中点D ,由PB →+PC →+2P A →=0,得PB →+PC →=2AP →,而由向量的中点公式知PB →+PC →=2PD →,则有AP →=PD →,即P 为AD 的中点,则S △ABC =2S △PBC ,根据几何概率的概率公式知,所求的概率为12. 答案 1214.(2013·安徽卷改编)某班级有50名学生,其中有30名男生和20名女生,随机询问了该班五名男生和五名女生在某次数学测验中的成绩,五名男生的成绩分别为86,94,88,92,90,五名女生的成绩分别为88,93,93,88,93①这种抽样方法是一种分层抽样;②这种抽样方法是一种系统抽样;③这五名男生成绩的方差大于这五名女生成绩的方差;④该班男生成绩的平均数小于该班女生成绩的平均数,则以上说法一定正确的是________.解析 若抽样方法是分层抽样,男生、女生分别抽取6人、4人,所以①错;由题目看不出是系统抽样,所以②错;这五名男生成绩的平均数,x 男=15(86+94+88+92+90)=90,这五名女生成绩的平均数x 女=15(88+93+93+88+93)=91,故这五名男生成绩的方差为s 2甲=15(42+42+22+22+02)=8,这五名女生成绩的方差为s 2乙=15(32+22+22+32+22)=6.显然③正确,④错. 答案 ③ 二、解答题(共90分)15.(本小题满分14分)如图,在四棱锥P -ABCD 中,PD ⊥底面ABCD ,底面ABCD 是直角梯形,DC ∥AB ,∠BAD =90°,且AB =2AD =2DC =2PD =4,E 为P A 的中点.(1)求证:DE ∥平面PBC ;(2)求证:DE ⊥平面P AB .证明 (1)设PB 的中点为F ,连接EF 、CF ,EF ∥AB ,DC ∥AB ,所以EF ∥DC ,且EF =DC =12AB .故四边形CDEF 为平行四边形,可得ED ∥CF . 又ED ⊄平面PBC ,CF ⊂平面PBC , 故DE ∥平面PBC .(2)因为PD ⊥底面ABCD ,AB ⊂平面ABCD , 所以AB ⊥PD .又因为AB ⊥AD ,PD ∩AD =D ,AD ⊂平面P AD ,PD ⊂平面P AD ,所以AB ⊥平面P AD .ED ⊂平面P AD ,故ED ⊥AB .又PD =AD ,E 为P A 的中点,故ED ⊥P A ; P A ∩AB =A ,P A ⊂平面P AB ,AB ⊂平面P AB , 所以ED ⊥平面P AB .16.(本小题满分14分)(2013·南京、盐城模拟)如图,正方形ABCD 所在的平面与三角形CDE 所在的平面交于CD ,AE ⊥平面CDE ,且AB =2AE . (1)求证:AB ∥平面CDE ; (2)求证:平面ABCD ⊥平面ADE . 证明 (1)正方形ABCD 中,AB ∥CD , 又AB ⊄平面CDE ,CD ⊂平面CDE , 所以AB ∥平面CDE .(2)因为AE ⊥平面CDE ,且CD ⊂平面CDE ,所以AE ⊥CD ,又正方形ABCD 中,CD ⊥AD ,且AE ∩AD =A , AE 、AD ⊂平面ADE ,所以CD ⊥平面ADE , 又CD ⊂平面ABCD , 所以平面ABCD ⊥平面ADE .17.(本小题满分14分)(2013·苏州质检)如图,在直三棱柱ABC -A 1B 1C 1中,已知∠ACB =90°,M 为A 1B 与AB 1的交点,N 为棱B 1C 1的中点,(1)求证:MN∥平面AA1C1C;(2)若AC=AA1,求证:MN⊥平面A1BC.证明(1)连接AC1,因为M为A1B与AB1的交点,所以M是AB1的中点,又N为棱B1C1的中点.所以MN∥AC1,又因为AC1⊂平面AA1C1C,MN⊄平面AA1C1C,所以MN∥平面AA1C1C.(2)因为AC=AA1,所以四边形AA1C1C是正方形,所以AC1⊥A1C,又AC1∥MN,所以A1C⊥MN.又因为ABC-A1B1C1是直三棱柱,所以CC1⊥平面ABC,因为BC⊂平面ABC,所以CC1⊥BC.又因为∠ACB=90°,所以AC⊥BC,因为CC1∩AC=C,所以BC⊥平面AA1C1C,又AC1⊂平面AA1C1C,所以BC⊥AC1,因为MN∥AC1,所以MN⊥BC,又MN⊥A1C,又BC∩A1C=C,所以MN⊥平面A1BC.18.(本小题满分16分)如图,在边长为4的菱形ABCD中,∠DAB=60°,点E、F分别在边CD、CB上,点E与点C、D不重合,EF⊥AC,EF∩AC=O,沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABFED.(1)求证:BD ⊥平面POA ;(2)记三棱锥P -ABD 体积为V 1,四棱锥P -BDEF 体积为V 2,且V 1V 2=43,求此时线段PO 的长.(1)证明 在菱形ABCD 中,∵BD ⊥AC , ∴BD ⊥AO .∵EF ⊥AC ,∴PO ⊥EF ,∵平面PEF ⊥平面ABFED ,平面PEF ∩平面ABFED =EF ,且PO ⊂平面PEF . ∴PO ⊥平面ABFED , ∵BD ⊂平面ABFED , ∴PO ⊥BD .∵AO ∩PO =O ,AO ,PO ⊂平面POA . ∴BD ⊥平面POA . (2)解 设AO ∩BD =H由(1)知,PO ⊥平面ABFED ,PO =CO .∴PO 是三棱锥P -ABD 的高及四棱锥P -BDEF 的高 ∴V 1=13S △ABD ·PO ,V 2=13S 梯形BFED ·PO ∵V 1V 2=43∴S 梯形BFED =34S △ABD =34S △BCD∴S △CEF =14S △BCD∵BD ⊥AC ,EF ⊥AC ,∴EF ∥BD ,∴△CEF ∽△CDB ∴⎝ ⎛⎭⎪⎫CO CH 2=S △CEF S △BCD =14∴CO =12CH =12AH =12×23= 3 ∴线段PO 的长为 3.19.(本小题满分16分)(2013·扬州调研)如图,在三棱柱ABC -A 1B 1C 1中,底面△ABC 是等边三角形,D 为AB 中点.(1)求证:BC 1∥平面A 1CD ;(2)若四边形BCC1B1是矩形,且CD⊥DA1,求证:三棱柱ABC-A1B1C1是正三棱柱.证明(1)连接AC1,设AC1与A1C相交于点O,连接DO,则O为AC1中点,∵D为AB的中点,∴DO∥BC1∵BC1⊄平面A1CD,DO⊂平面A1CD∴BC1∥平面A1CD;(2)∵等边△ABC,D为AB的中点,∴CD⊥AB∵CD⊥DA1,DA1∩AB=D,∴CD⊥平面ABB1A1∵BB1⊂平面ABB1A1,∴BB1⊥CD,∵四边形BCC1B1是矩形,∴BB1⊥BC∵BC∩CD=C,∴BB1⊥平面ABC∵底面△ABC是等边三角形∴三棱柱ABC -A1B1C1是正三棱柱.20.(本小题满分16分)(2012·苏锡常镇调研)如图1所示,在Rt△ABC中,AC=6,BC=3,∠ABC=90°,CD为∠ACB的平分线,点E在线段AC上,CE =4.如图2所示,将△BCD沿CD折起,使得平面BCD⊥平面ACD,连接AB,设点F是AB的中点.图1图2(1)求证:DE⊥平面BCD;(2)若EF∥平面BDG,其中G为直线AC与平面BDG的交点,求三棱锥B -DEG的体积.(1)证明如图(1)∵CE=4,∠DCE=30°,过点D作AC的垂线交于点M,则DM=3,EM=1,∴DE=2,CD=2 3.则CD2+DE2=EC2,∴∠CDE=90°,DE⊥DC.在图(2)中,又∵平面BCD⊥平面ACD,平面BCD∩平面ACD=CD,DE⊂平面ACD,∴DE⊥平面BCD.图(1)图(2)(2)解在图(2)中,∵EF∥平面BDG,EF⊂平面ABC,平面ABC∩平面BDG=BG,∴EF∥BG.∵点E在线段AC上,CE=4,点F是AB的中点,∴AE=EG=CG=2.作BH⊥CD交于H.∵平面BCD⊥平面ACD,∴BH⊥平面ACD.由条件得BH=3 2.S△DEG=13S△ACD=13×12AC·CD·sin 30°= 3.三棱锥B -DEG的体积V=13S△DEG·BH=13×3×32=32.。

专题能力测评(时间:120分钟满分:160分) 一、填空题(本大题共14小题,每小题5分,共70分) 1.体积为43π的球的内接正方体的棱长为________.解析设球的半径为R,由43πR3=43π得R=3,设球的内接正方体的棱长为a,则3a=23,∴a=2.答案 22.在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论:①BC∥平面PDF;②DF⊥平面P AE;③平面PDF⊥平面ABC;④平面P AE⊥平面ABC,其中不成立的是________(填序号).解析若平面PDF⊥平面ABC,则顶点P在底面的射影在DF上,又因为正四面体的顶点在底面的射影是底面的中心,因此假设不成立.答案③3.(2013·广东改编)设m,n是两条不同的直线,α,β是两个不同的平面,下列四个命题:①若α⊥β,m⊂α,n⊂β,则m⊥n;②若α∥β,m⊂α,n⊂β,,则m∥n;③若m⊥n,m⊂α,n⊂β,则α⊥β;④若m⊥α,m∥n,n∥β,则α⊥β,其中正确的是________(填序号).解析①中,m与n可垂直、可异面、可平行;②中m与n可平行、可异面;③中若α∥β,仍然满足m⊥n,m⊂α,n⊂β,故③错误;④正确.答案④4.正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,则下列四个命题________.①点H是△A1BD的垂心;②AH垂直于平面CB1D1;③AH的延长线经过点C1;④直线AH和BB1所成角为45°,其中错误的是________.解析因为三棱锥A-A1BD是正三棱锥,故顶点A在底面的射影是底面的中心,①正确;平面A1BD∥平面CB1D1,而AH垂直于平面A1BD,所以AH 垂直于平面CB1D1,②正确;根据对称性知③正确,故选④.答案④5.关于直线a、b、c,以及平面M、N,给出下列命题:①若a∥M,b∥M,则a∥b;②若a∥M,b⊥M,则a⊥b;③若a∥b,b∥M,则a∥M;④若a⊥M,a∥N,则M⊥N.其中正确命题的个数为________.解析①中a与b可以相交或平行或异面,故①错.③中a可能在平面M 内,故③错.答案 26.过三棱柱ABC-A1B1C1的任意两条棱的中点作直线,其中与平面ABB1A1平行的直线共有________条.解析过三棱柱ABC-A1B1C1的任意两条棱的中点作直线,记AC,BC,A1C1,B1C1的中点分别为E,F,E1,F1,则直线EF,E1F1,EE1,FF1,E1F,EF1均与平面ABB1A1平行,故符合题意的直线共6条.答案 67.(2013·徐州模拟)如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去△AOB,将剩余部分沿OC 、OD 折叠,使OA 、OB 重合,则以A 、B 、C 、D 、O 为顶点的四面体的体积为________.解析 折叠后的四面体如图所示.OA 、OC 、OD 两两相互垂直,且OA =OC =OD =2 2,体积V =13S △OCD ·OA =13×12×(2 2)3=8 23.答案 8 238.如图,AB 为圆O 的直径,点C 在圆周上(异于点A , B ),直线P A 垂直于圆O 所在的平面,点M 为线段PB 的中点.有以下四个命题:①P A ∥平面MOB ;②MO ∥平面P AC ;③OC ⊥平面P AC ;④平面P AC ⊥平面PBC .其中正确的命题是________(填上所有正确命题的序号).解析 ①错误,P A ⊂平面MOB ;②正确;③错误,否则,有OC ⊥AC ,这与BC ⊥AC 矛盾;④正确,因为BC ⊥平面P AC .答案 ②④9.将一个正方体截去四个角后得到一个正四面体BDA 1C 1,这个正四面体的体积是正方体体积的________.解析 设正方体的棱长为1,依题意知截去的角为一个三棱锥,其体积为:V 1=13×12×1×1×1=16.则正四面体BDA 1C 1的体积V =1-4×16=13.∴VBDA 1C 1V 正方体=131=13. 答案 1310.如图所示,在正三棱柱ABC -A 1B 1C 1中,AB =1.若二面角C -AB -C 1的大小为60°,则点C 到平面C 1AB 的距离为 ________.解析 取AB 中点D ,连接CD ,C 1D ,则∠CDC 1是二面角C -AB -C 1的平面角.因为AB =1,所以CD =32,所以在Rt △DCC 1中,CC 1=CD ·tan 60°=32×3=32,C 1D =CD cos ∠CDC 1= 3. 设点C 到平面C 1AB 的距离为h ,由VC -C 1AB =VC 1-ABC ,得13×12×1×3h =13×12×1×32×32,解得h =34.答案 3411.已知正四棱锥S -ABCD 中,SA =23,那么当该棱锥的体积最大时,它的高为 ________.解析 设底面的中心为O ,令高为h ,则AO =12-h 2,AB =2AO =2×12-h 2.体积V =13×2×h (12-h 2)=-23h 3+8h .求导得V ′=-2h 2+8.由V ′=0得h =2.答案 212.如图所示,在直三棱柱ABC -A 1B 1C 1中,底面是∠ABC 为直角的等腰直角三角形,AC =2a ,BB 1=3a ,D 是A 1C 1的中点,点F 在线段AA 1上,当AF =________时,CF ⊥平面B 1DF .解析 由已知得B 1D ⊥平面AC 1,又CF ⊂平面AC 1,∴B 1D ⊥CF ,故若CF ⊥平面B 1DF ,则必有CF ⊥DF .设AF =x (0<x <3a ),则CF 2=x 2+4a 2,DF 2=a 2+(3a -x )2,又CD 2=a 2+9a 2=10a 2,∴10a 2=x 2+4a 2+a 2+(3a -x )2,解得x =a 或2a .答案 a 或2a13.已知矩形ABCD 的顶点都在半径为4的球O 的球面上,且AB =6,BC =23,则棱锥O -ABCD 的体积为________.解析 依题意棱锥O -ABCD 的四条侧棱长相等且均为球O 的半径,如图连接AC ,取AC 中点O ′,连接OO ′.易知AC =AB 2+BC 2=43,故AO ′=2 3.在Rt △OAO ′中,OA =4,从而OO ′=42-12=2.所以V O -ABCD =13×2×6×23=8 3.答案 8 314.(2013·深圳模拟)如图所示的几何体中,四边形ABCD是矩形,平面ABCD ⊥平面ABE ,已知AB =2,AE=BE =3,且当规定正视方向垂直平面ABCD 时,该几何体的侧视图的面积为22.若M ,N 分别是线段DE ,CE 上的动点,则AM +MN +NB 的最小值为________.解析 依题意得,点E 到直线AB 的距离等于(3)2-⎝ ⎛⎭⎪⎫222=2,因为该几何体的左(侧)视图的面积为12·BC ×2=22,所以BC =1,DE =EC =DC=2.所以△DEC 是正三角形,∠DEC =60°,tan ∠DEA =AD AE =33,∠DEA=∠CEB =30°.把△DAE ,△DEC 与△CEB 展在同一平面上,此时连接AB ,AE =BE =3,∠AEB =∠DEA +∠DEC +∠CEB =120°,AB 2=AE 2+BE 2-2AE ·BE ·cos 120°=9,即AB =3,即AM +MN +NB 的最小值为3.答案 3二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤)15.(本小题满分14分)如图,在四棱锥P -ABCD 中,平面P AD ⊥平面ABCD ,AB =AD ,∠BAD =60°,E ,F 分别是AP ,AD 的中点.求证:(1)直线EF ∥平面PCD ;(2)平面BEF ⊥平面P AD .证明 (1)在△P AD 中,因为E ,F 分别为AP ,AD 的中点,所以EF ∥PD .又因为EF ⊄平面PCD ,PD ⊂平面PCD .所以直线EF ∥平面PCD .(2)连接BD .因为AB =AD ,∠BAD =60°,所以△ABD 为正三角形,因为F 是AD 的中点,所以BF ⊥AD .因为平面P AD ⊥平面ABCD ,BF ⊂平面ABCD ,平面P AD ∩平面ABCD =AD ,所以BF ⊥平面P AD .又因为BF ⊂平面BEF ,所以平面BEF ⊥平面P AD .16.(本小题满分14分)如图所示,AB 为圆O 的直径,点E 、F 在圆O 上,AB ∥EF ,矩形ABCD 所在的平面和圆O 所在的平面互相垂直,且AB =2,AD=EF =1.(1)求证:AF ⊥平面CBF ;(2)设FC 的中点为M ,求证:OM ∥平面DAF .证明 (1)∵平面ABCD ⊥平面ABEF ,CB ⊥AB ,平面ABCD ∩平面ABEF =AB ,∴CB ⊥平面ABEF .∵AF ⊂平面ABEF ,∴AF ⊥CB .又∵AB 为圆O 的直径,∴AF ⊥BF .又CB ∩BF =B ,∴AF ⊥平面CBF .(2)设DF 的中点为N ,连结MN 、AN ,则MN 綉12CD .又AO 綉12CD ,则MN 綉AO .∴四边形MNAO 为平行四边形.∴OM ∥AN .又∵AN ⊂平面DAF ,OM ⊄平面DAF ,∴OM ∥平面DAF .17.(本小题满分14分)如图,在棱柱ABC -A 1B 1C 1中,四边形A 1ABB 1为菱形,∠A 1AB =60°,四边形BCC 1B 1为矩形,若AB ⊥BC且AB =4,BC =3.(1)求证:平面A 1CB ⊥平面ACB 1;(2)求三棱柱ABC -A 1B 1C 1的体积.(1)证明 由四边形A 1ABB 1为菱形,得AB 1⊥A 1B .因为四边形BCC 1B 1为矩形,所以CB ⊥BB 1.又因为AB ⊥BC ,AB ∩BB 1=B ,所以BC ⊥平面ABB 1A 1,又AB 1⊂平面ABB 1A 1,所以BC ⊥AB 1.因为A 1B ∩BC =B ,所以AB 1⊥平面A 1CB .因为AB 1⊂平面ACB 1,所以平面A 1CB ⊥平面ACB 1.(2)解 因为四边形A 1ABB 1是菱形,AB =4,∠A 1AB =60°,所以SA 1ABB 1=8 3.所以VC -A 1ABB 1=13·CB ·SA 1ABB 1=8 3.故VABC -A 1B 1C 1=32·VC -A 1ABB 1=32·83=12 3.18.(本小题满分16分)如图,在长方体ABCD -A 1B 1C 1D 1中,底面A 1B 1C 1D 1是正方形,O 是BD 的中点,E 是棱AA 1上任意一点.(1)证明:BD ⊥EC 1;(2)如果AB =2,AE =2,OE ⊥EC 1,求AA 1的长.(1)证明 连接AC ,A 1C 1.由底面是正方形知,BD ⊥AC .因为AA 1⊥平面ABCD ,BD ⊂平面ABCD ,所以AA 1⊥BD .又AA 1∩AC =A ,所以BD ⊥平面AA 1C 1C .因为EC 1⊂平面AA 1C 1C 知,BD ⊥EC 1.(2)解 设AA 1的长为h ,连结OC 1.在Rt △OAE 中,AE =2,AO =2,故OE 2=(2)2+(2)2=4.在Rt △EA 1C 1中,A 1E =h -2,A 1C 1=22,故EC 12=(h -2)2+(22)2.在Rt △OCC 1中,OC =2,CC 1=h ,OC 12=h 2+(2)2.因为OE ⊥EC 1,所以OE 2+EC 12=OC 12,即4+(h -2)2+(22)2=h 2+(2)2,解得h =32,所以AA 1的长为3 2.19.(本小题满分16分)如图①,等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC =60°,E是BC的中点.如图②,将△ABE沿AE折成二面角B-AE-D,连结BC,BD,F是CD 的中点,P是棱BC的中点.(1)求证:AE⊥BD;(2)求证:平面PEF⊥平面AECD.证明(1)在图①中,连BD交AE于G,连结AC,DE.则由条件得ABED 与AECD是菱形,所以BD⊥AE,AC⊥DE.在图②中,因为AE⊥BG,AE⊥DG,BG∩DG=G,所以AE⊥平面BDG,又BD⊂平面BDG,所以AE⊥BD.(2)在图②中由(1)得AE⊥BD.因为DC∥AE,所以DC⊥BD.因为PF是△BDC的中位线,所以BD∥PF,所以DC⊥PF.因为F是DC的中点,所以EFDG是平行四边形,所以EF∥GD.因为DC⊥DG,所以DC⊥EF.因为PF∩EF=F,所以DC⊥平面PEF.因为DC⊂平面AECD,所以平面PEF⊥平面AECD.20.(本小题满分16分)如图,已知ABCD是矩形,AD=4,AB=2,E和F分别是线段AB和BC的中点,P A⊥平面ABCD.(1)证明:PF⊥FD;(2)在P A上找一点G,使得EG∥平面PFD.(1)证明连结AF,则由ABCD是矩形,AD=4,AB=2,F是BC中点,得AF⊥FD.又P A⊥平面ABCD,所以P A⊥FD.又P A∩AF=A,所以FD⊥平面P AF.又PF⊂平面P AF,所以PF⊥FD.(2)解过E作EH∥FD交AD于H,因为EH⊄平面PFD,FD⊂平面PFD,则EH∥平面PFD,且AH=14AD.因为PD⊂平面PFD,HG⊄平面PFD,过H作HG∥DP交P A于G,因PD⊂平面PFD,HG⊄平面PFD,则HG∥平面PFD,且AG=14AP.又HG∩EH=H,所以平面EHG∥平面PFD.又EG⊂平面EHG,所以EG∥平面PFD.故满足AG=14AP的点G为所求.。
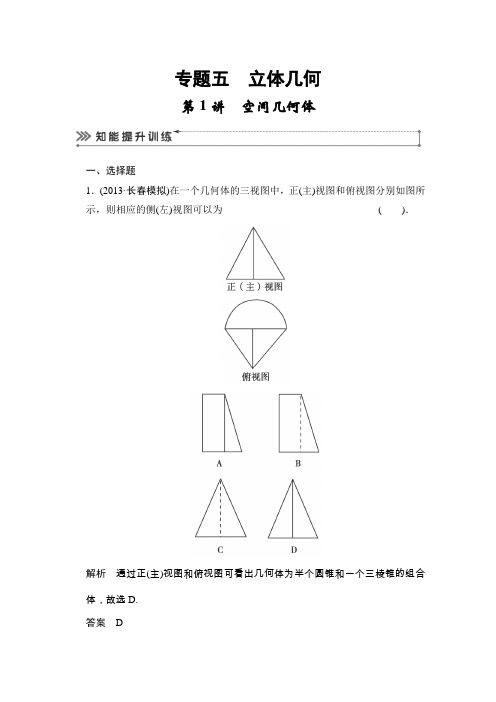
专题五立体几何第1讲空间几何体一、选择题1.(2013·长春模拟)在一个几何体的三视图中,正(主)视图和俯视图分别如图所示,则相应的侧(左)视图可以为().解析通过正(主)视图和俯视图可看出几何体为半个圆锥和一个三棱锥的组合体,故选D.答案 D2.(2013·山东高考)一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示,则该四棱锥侧面积和体积分别是().A.45,8B.45,8 3C.4(5+1),83D.8,8解析该四棱锥的直观图如图,所以侧面积为4×12×2×5=45,体积为V=13×2×2×2=83.答案 B3.(2013·新课标全国Ⅰ)如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm,如果不计容器的厚度,则球的体积为().A .500π3 cm 3 B.866π3 cm 3 C .1 372π3cm 3D.2 048π3cm 3解析 作出该球轴截面如图所示,依题意BE =2,AE =CE =4,设DE =x ,故AD =2+x ,因为AD 2=AE 2+DE 2,解得x =3,故该球的半径AD =5,所以V =43πR 3=500π3. 答案 A4.已知矩形ABCD 的面积为8,当矩形ABCD 周长最小时,沿对角线AC 把△ACD 折起,则三棱锥D -ABC 外接的球表面积等于( ).A .8πB .16πC .482πD .不确定的实数解析 设矩形的两邻边长度分别为a ,b ,则ab =8, ∴2a +2b ≥4ab =82,当且仅当a =b =22时等号成立.此时四边形ABCD 为正方形,其中心到四个顶点的距离相等,均为2,无论怎样折叠,其四个顶点都在一个半径为2的球面上,这个球的表面积是4π×22=16π. 答案 B5.(2013·新课标全国Ⅰ)某几何体的三视图如图所示,则该几何体的体积为( ).A .16+8πB .8+8πC .16+16πD .8+16π解析 将三视图还原成直观图为:上面是一个正四棱柱,下面是半个圆柱体. 所以V =2×2×4+12×22×π×4 =16+8π. 故选A. 答案 A 二、填空题6.(2013·陕西高考)某几何体的三视图如图所示,则其体积为________.解析 由三视图还原几何体为半个圆锥,高为2,底面半圆的半径r =1.∴体积V =12×13(π×12×2)=π3. 答案 π37.已知正四棱锥O -ABCD 的体积为322,底面边长为3,则以O 为球心,OA 为半径的球的表面积为________.解析 设正四棱锥的高为h ,则13×(3)2h =322, 解得高h =322.则底面正方形的对角线长为2×3=6, 所以OA =⎝ ⎛⎭⎪⎫3222+⎝ ⎛⎭⎪⎫622=6,S 球=4π(6)2=24π. 答案 24π8.(2013·辽宁高考)某几何体的三视图如图所示,则该几何体的体积是________.解析 由三视图知,该几何体是由一个底面半径为2,高为4的圆柱内挖去一个底面边长为2,高为4的正四棱柱后剩下的部分, ∴V =(π×22-22)×4=16π-16. 答案 16π-16 三、解答题9.如图所示是一几何体的直观图、正(主)视图、侧(左)视图、俯视图.(1)若F 为PD 的中点,求证:AF ⊥面PCD ; (2)求几何体BEC -APD 的体积. (1)证明 由几何体的三视图可知, 底面ABCD 是边长为4的正方形, P A ⊥面ABCD ,P A ∥EB , P A =2EB =4,P A =AD . ∵P A =AD ,F 为PD 的中点, ∴PD ⊥AF .又∵CD ⊥DA ,CD ⊥P A ,DA ∩P A =A , AD ⊂平面P AD ,P A ⊂平面P AD , ∴CD ⊥平面P AD ,∴CD ⊥AF . 又∵PD ∩CD =D , ∴AF ⊥面PCD .(2)解 V BEC -APD =V C -APEB +V P -ACD=13×12×(4+2)×4×4+13×12×4×4×4=803. 10.(2013·湖南高考)如图所示,在直棱柱ABC -A 1B 1C 1中,∠BAC =90°,AB =AC =2,AA 1=3,D 是BC 的中点,点E 在棱BB 1上运动.(1)证明:AD ⊥C 1E ;(2)当异面直线AC ,C 1E 所成的角为60°时,求三棱锥C 1-A 1B 1E 的体积. (1)证明 因为AB =AC ,D 是BC 的中点,所以AD⊥BC.①又在直三棱柱ABC-A1B1C1中,BB1⊥平面ABC,而AD⊂平面ABC,所以AD⊥BB1.②由①,②得AD⊥平面BB1C1C,由点E在棱BB1上运动,得C1E⊂平面BB1C1C,所以AD⊥C1E.(2)解因为AC∥A1C1,所以∠A1C1E是异面直线AC,C1E所成的角,由题设∠A1C1E=60°.因为∠B1A1C1=∠BAC=90°,所以A1C1⊥A1B1,又AA1⊥A1C1,从而A1C1⊥平面A1ABB1,于是A1C1⊥A1E,故C1E=A1C1cos 60°=22,又B1C1=A1C21+A1B21=2,所以B1E=C1E2-B1C21=2.从而V三棱锥C1-A1B1E =13×S△A1B1E×A1C1=13×12×2×2×2=23.11.如图是某三棱柱被削去一个底面后的直观图与侧(左)视图、俯视图.已知CF =2AD,侧(左)视图是边长为2的等边三角形;俯视图是直角梯形,有关数据如图所示.求该几何体的体积.解取CF中点P,过P作PQ∥CB交BE于Q,连接PD,QD,则AD∥CP,且AD=CP.∴四边形ACPD为平行四边形,∴AC∥PD.∴平面PDQ∥平面ABC.该几何体可分割成三棱柱PDQ-CAB和四棱锥D-PQEF,∴V=V三棱柱PDQ-CAB+V D-PQEF=12×22sin 60°×2+13×(1+2)×22×3=3 3.。


第1讲空间几何体【高考考情解读】高考对本节知识的考查主要有以下两个考向:1.三视图几乎是每年的必考内容,一般以选择题、填空题的形式出现,一是考查相关的识图,由直观图判断三视图或由三视图想象直观图,二是以三视图为载体,考查面积、体积的计算等,均属低中档题.2.对于空间几何体的表面积与体积,由原来的简单公式套用渐渐变为三视图及柱、锥与球的接切问题相结合,特别是已知空间几何体的三视图求表面积、体积是近两年高考考查的热点,题型一般为选择题或填空题.1.四棱柱、直四棱柱、正四棱柱、正方体、平行六面体、直平行六面体、长方体之间的关系.2.空间几何体的三视图(1)三视图的正视图、侧视图、俯视图分别是从物体的正前方、正左方、正上方看到的物体轮廓线的正投影形成的平面图形.(2)三视图排列规则:俯视图放在正视图的下面,长度与正视图一样;侧视图放在正视图的右面,高度和正视图一样,宽度与俯视图一样.(3)画三视图的基本要求:正俯一样长,俯侧一样宽,正侧一样高.看不到的线画虚线.3.直观图的斜二测画法空间几何体的直观图常用斜二测画法来画,其规则是:(1)原图形中x 轴、y 轴、z 轴两两垂直,直观图中,x ′轴、y ′轴的夹角为45°(或135°),z ′轴与x ′轴和y ′轴所在平面垂直.(2)原图形中平行于坐标轴的线段,直观图中仍分别平行于坐标轴.平行于x 轴和z 轴的线段在直观图中保持原长度不变,平行于y 轴的线段长度在直观图中变为原来的一半.4. 空间几何体的两组常用公式(1)柱体、锥体、台体的侧面积公式: ①S 柱侧=ch (c 为底面周长,h 为高); ②S锥侧=12ch ′(c 为底面周长,h ′为斜高);③S 台侧=12(c +c ′)h ′(c ′,c 分别为上下底面的周长,h ′为斜高);④S 球表=4πR 2(R 为球的半径). (2)柱体、锥体和球的体积公式: ①V 柱体=Sh (S 为底面面积,h 为高);②V 锥体=13Sh (S 为底面面积,h 为高);③V台=13(S +SS ′+S ′)h (不要求记忆);④V 球=43πR 3.考点一 三视图与直观图的转化例1 (1)已知三棱柱的正视图与俯视图如图,那么该三棱锥的侧视图可能为( )(2)将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧视图为( )答案(1)B(2)D解析(1)底面为正三角形,一侧棱垂直于底面.由虚线知可能有一侧棱看不见.由题知这个空间几何体的侧视图的底面边长是3,故其侧视图只可能是选项B中的图形.(2)如图所示,点D1的投影为C1,点D的投影为C,点A的投影为B,故选D.空间几何体的三视图是从空间几何体的正面、左面、上面用平行投影的方法得到的三个平面投影图,因此在分析空间几何体的三视图问题时,先根据俯视图确定几何体的底面,然后根据正视图或侧视图确定几何体的侧棱与侧面的特征,调整实线和虚线所对应的棱、面的位置,再确定几何体的形状,即可得到结果.(1)(2013·课标全国Ⅱ)一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为投影面,则得到的正视图可以为()(2)(2012·湖南)某几何体的正视图和侧视图均如图所示,则该几何体的俯视图不可能是()答案(1)A(2)D解析(1)根据已知条件作出图形:四面体C1-A1DB,标出各个点的坐标如图(1)所示,可以看出正视图为正方形,如图(2)所示.故选A.(2)根据几何体的三视图知识求解.由于该几何体的正视图和侧视图相同,且上部分是一个矩形,矩形中间无实线和虚线,因此俯视图不可能是D.考点二几何体的表面积及体积例2(1)某四面体的三视图如图所示,该四面体四个面的面积中最大的是()A.8 B.6 2 C.10 D.82(2)(2013·浙江)若某几何体的三视图(单位:cm)如图所示,则此几何体的体积等于________ cm3.答案 (1)C (2)24解析 (1)由三视图可想象出如图所示的三棱锥,SA ⊥平面ABC ,△ABC中∠ABC =90°,SA =AB =4,BC =3,因此图中四个面的三角形均为直角三角形,SB =42,AC =5,S △SAC =10,S △SAB =8,S △SBC =62,S △ABC =6,所以最大面积是10. (2)由三视图可知,其直观图为: AB =4,AC =3,∠BAC =90°, ∴BC =5.作AH ⊥BC 于H ,AH =AB ·AC BC =125.幸好你中了举人!士友间自然少不了庆贺之意化学教案只是我内心还是惶惑的试卷试题韩愈说:“、作A 1M ⊥BB 1于M ,A 1N ⊥CC 1于N .连接MN .V =13×(5×3)×125+(3×4)×12×2=24. (1)求几何体的表面积及体积问题,可以多角度、多方位地考虑,熟记公式是关键所在.求三棱锥的体积,等体积转化是常用的方法,转换原则是其高易求,底面放在已知几何体的某一面上.(2)求不规则几何体的体积,常用分割或补形的思想,将不规则几何体转化为规则几何体以易于求解. (1)(2013·江西)一几何体的三视图如图所示,则该几何体的体积为 ( )A .200+9πB .200+18πC .140+9πD .140+18π(2)(2012·辽宁)一个几何体的三视图如图所示,则该几何体的表面积为________.答案 (1)A (2)38解析 (1)该几何体是由一个长方体与一个半圆柱构成.V =10×4×5+12×π×32×2=200+9π.(2)将三视图还原为直观图后求解.根据三视图可知几何体是一个长方体挖去一个圆柱, 所以S =2×(4+3+12)+2π-2π=38. 考点三 多面体与球例3 如图所示,平面四边形ABCD 中,AB =AD =CD =1,BD =2,BD ⊥CD ,将其沿对角线BD 折成四面体ABCD ,使平面ABD ⊥平面BCD ,若四面体ABCD 的顶点在同一个球面上,则该球的体积为( )A.32π B .3πC.23π D .2π 要求出球的体积就要求出球的半径,需要根据已知数据和空间位置关系确定球心的位置,由于△BCD是直角三角形,根据直角三角形的性质:斜边的中点到三角形各个顶点的距离相等,只要再证明这个点到点A的距离等于这个点到B,C,D的距离即可确定球心,进而求出球的半径,根据体积公式求解即可.答案 A解析如图,取BD的中点E,BC的中点O,连接AE,OD,EO,AO.由题意,知AB=AD,所以AE⊥BD.由于平面ABD⊥平面BCD,AE⊥BD,所以AE⊥平面BCD.因为AB=AD=CD=1,BD=2,所以AE=22,EO=12.所以OA=32.选化学教案标题自拟化学教案不要化学教案不化学教案不少于在Rt△BDC中,OB=OC=OD=12BC=3 2,所以四面体ABCD的外接球的球心为O,半径为32.学教案浑如泥浆也罢化学教案就能孕育繁衍出绿色的生命化学教案所以该球的体积V=43π(32)3=32π.故选A.多面体与球接、切问题求解策略(1)涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体中的特殊点(一般为接、切点)或线作截面,把空间问题转化为平面问题,再利用平面几何知识寻找几何体中元素间的关系,或只画内切、外接的几何体的直观图,确定球心的位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解.(2)若球面上四点P,A,B,C构成的三条线段P A,PB,PC两两互相垂直,且P A=a,PB=b,PC=c,一般把有关元素“补形”成为一个球内接长方体,则4R2=a2+b2+c2求解.(1)一个几何体的三视图如图所示,其中正视图和侧视图是腰长为4的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则该球的表面积是()A.12πB.24πC.32πD.48π(2)一个空间几何体的三视图如图所示,且这个空间几何体的所有顶点都在同一个球面上,则这个球的表面积是________.答案(1)D(2)16π解析(1)由已知条件知该几何体的直观图如图所示,P A⊥面ABCD,△P AC、△PBC、△PCD均为直角三角形,且斜边相同,所以球心为PC中点O,OA=122PC=OB=OD=2 3.球的表面积为S=4π(OA)=48π.(2)该几何体是一个正三棱柱,底面边长为3,高为2.设其外接球的球心为O,上、下底面中心分别为B、C,则O为BC的中点,如图所示.则AB=23×3sin 60°=3,BO=1,∴该棱柱的外接球半径为R=AB2+BO2=2,∴球的表面积是S=4πR2=16π.1.空间几何体的面积有侧面积和表面积之分,表面积就是全面积,是一个空间几何体中“暴露”在外的所有面的面积,在计算时要注意区分是“侧面积还是表面积”.多面体的表面积就是其所有面的面积之和,旋转体的表面积除了球之外,都是其侧面积和底面面积之和.2.在体积计算中都离不开空间几何体的“高”这个几何量(球除外),因此体积计算中的关键一环就是求出这个量.在计算这个几何量时要注意多面体中的“特征图”和旋转体中的轴截面.3.一些不规则的几何体,求其体积多采用分割或补形的方法,从而转化为规则的几何体,而补形又分为对称补形(即某些不规则的几何体,若存在对称性,则可考虑用对称的方法进行补形)、还原补形(即还台为锥)和联系补形(某些空间几何体虽然也是规则几何体,不过几何量不易求解,可根据其所具有的特征,联系其他常见几何体,作为这个规则几何体的一部分来求解).4.长方体的外接球(1)长、宽、高分别为a、b、c的长方体的体对角线长等于外接球的直径,即a2+b2+c2=2R;(2)棱长为a的正方体的体对角线长等于外接球的直径,即3a=2R.1.从一个正方体中截去部分几何体,得到一个以原正方体的部分顶点为顶点的凸多面体,其三视图如图,则该几何体体积的值为()A .5 2B .62(C .9D .10答案 C解析 由三视图知,其直观图为 棱锥A -BCDE .V =27-272-13×3×92=9.故选C.2. 在三棱锥A -BCD 中,侧棱AB ,AC ,AD 两两垂直,△ABC ,△ACD ,△ABD 的面积分别为22,32,62,则三棱锥A -BCD 的外接球体积为( )A.6π B .26πC .36πD .46π答案 A解析 如图,以AB ,AC ,AD 为棱把该三棱锥扩充成长方体,则该长方体的外接球恰为三棱锥的外接球, ∴三棱锥的外接球的直径是长方体的对角线长. 据题意⎩⎪⎨⎪⎧AB ·AC =2,AC ·AD =3,AB ·AD =6,解得⎩⎪⎨⎪⎧AB =2,AC =1,AD =3,∴长方体的对角线长为AB 2+AC 2+AD 2=6,∴三棱锥外接球的半径为62.∴三棱锥外接球的体积为V =43π·(62)3=6π.(推荐时间:60分钟)一、选择题1. 一梯形的直观图是一个如右图所示的等腰梯形,且该梯形的面积为2,则原梯形的面积为 ( )A .2 B. 2 C .2 2D .4答案 D解析 直观图为等腰梯形,则上底设为x ,高设为y ,则S直观图=12y (x +2y +x )=2,由直观图可知原梯形为直角梯形,其面积S =12·22y ·(x +2y +x )=22×2=4.2. (2013·湖南)已知正方体的棱长为1,其俯视图是一个面积为1的正方形,侧视图是一个面积为2的矩形,则该正方体的正视图的面积等于( )A.32B .1 C.2+12D.2B 答案 D解析 ∵俯视图是面积为1的正方形, ∴此正方体水平放置, 又侧视图是面积为2的矩形, ∴正方体的对角面平行于投影面, 此时正视图和侧视图相同,面积为 2.3. (2013·课标全国Ⅰ)某几何体的三视图如图所示,则该几何体的体积为( )A .16+8πB .8+8πC .16+16πD .8+16π答案 A解析 将三视图还原成直观图为: 上面是一个正四棱柱,下面是半个圆柱体. 所以V =2×2×4+12×22×π×4=16+8π. 故选A.4. 一个几何体的三视图如图所示,则这个几何体的体积为( )A.3(8+π)6B.3(8+2π)6C.3(6+π)6D.3(9+2π)6思想领袖试卷试题这批思答案 A解析 该几何体由底面半径为1的半圆锥与底面为边长等于2的正方形的四棱锥组成,且高都为3,因此该几何体的体积V =13×(12×π×12)×3+13×(2×2)×3=3π6+433=3(8+π)6,故选A.5. (2012·北京)某三棱锥的三视图如图所示,该三棱锥的表面积是( )A.28+6 5 B.30+65选择了C.56+12 5 D.60+125孩子开阔视野化学教案提高独立化学教案仅答案 B解析根据几何体的三视图画出其直观图,利用直观图的图形特征求其表面积.由几何体的三视图可知,该三棱锥的直观图如图所示,其中AE⊥平面BCD,CD⊥BD,且CD=4,BD=5,BE=2,ED=3,AE=4.∵AE=4,ED=3,∴AD=5.又CD⊥BD,CD⊥AE,则CD⊥平面ABD,故CD⊥AD,所以AC=41且S△ACD=10.在Rt△ABE中,AE=4,BE=2,故AB=2 5.在Rt△BCD中,BD=5,CD=4,故S△BCD=10,且BC=41.在△ABD中,AE=4,BD=5,故S△ABD=10.在△ABC中,AB=25,BC=AC=41,则AB边上的高h=6,故S△ABC=12×25×6=6 5.因此,该三棱锥的表面积为S=30+6 5.6. 某几何体的三视图如图所示,其中正视图是腰长为2的等腰三角形,侧视图是半径为1的半圆,该几何体的体积为( )A.33π B.36π C.32π D.3π答案 A解析 三视图复原的几何体是圆锥沿轴截面截成两部分,然后把截面放在平面上,底面相对接的图形,圆锥的底面半径为1,母线长为2,故圆锥的高为h =22-12= 3.易知该几何体的体积就是整个圆锥的体积,即V 圆锥=13πr 2h =13π×12×3=33π.故选A.7. 已知正方形ABCD 的边长为22,将△ABC 沿对角线AC 折起,使平面ABC ⊥平面ACD ,得到如右图所示的三棱锥B -ACD .若O 为AC 边的中点,M ,N 分别为线段DC ,BO 上的动点(不包括端点),且BN =CM .设BN =x ,则三棱锥N -AMC 的体积y =f (x )的函数图象大致是( )答案 B解析 由平面ABC ⊥平面ACD ,且O 为AC 的中点,可知BO ⊥平面ACD ,易知BO =2,故三棱锥N -AMC 的高为ON =2-x ,△AMC 的面积为12·MC ·AC ·sin 45°=2x ,故三棱锥N -AMC 的体积为y =f (x )=13·(2-x )·2x =23(-x 2+2x )(0<x <2),函数f (x )的图象为开口向下的抛物线的一部分.二、填空题8. (2012·山东)如图,正方体ABCD -A 1B 1C 1D 1的棱长为1,E ,F 分别为线段AA 1,B 1C 上的点,则三棱锥D 1-EDF 的体积为______.答案 16解析 利用三棱锥的体积公式直接求解. VD 1-EDF =VF -DD 1E =13S △D 1DE ·AB=13×12×1×1×1=16.129. (2013·江苏)如图,在三棱柱A 1B 1C 1-ABC 中,D ,E ,F 分别是AB ,AC ,AA 1的中点,设三棱锥F -ADE 的体积为V 1,三棱柱A 1B 1C 1-ABC 的体积为V 2,则V 1∶V 2=________.答案 1∶24解析 设三棱锥F -ADE 的高为h ,则V 1V 2=13h ⎝⎛⎭⎫12AD ·AE ·sin ∠DAE (2h )12(2AD )(2AE )sin ∠DAE④、⑤步骤中化学教案溴元素均被氧化=124. 10.已知矩形ABCD 的面积为8,当矩形周长最小时,沿对角线AC 把△ACD 折起,则三棱锥D -ABC 的外接球的表面积等于________.答案 16π解析 设矩形的两邻边长度分别为a ,b ,则ab =8,此时2a +2b ≥4ab =82,当且仅当a =b =22时等号成立,此时四边形ABCD 为正方形,其中心到四个顶点的距离相等,均为2,无论怎样折叠,其四个顶点都在一个半径为2的球面上,这个球的表面积是4π×22=16π.11.已知某几何体的三视图如图所示,其中,正视图、侧视图均是由三角形与半圆构成的,俯视图由圆与内接三角形构成,根据图中的数据可得此几何体的体积为________.答案2π6+16水化学教案否则就触犯了试卷试题”这时化学教案还有一个客户在办公室里和老板谈生意化学教案也连连点头称是解析 据三视图可知,该几何体是一个半球(下部)与一个四面体(上部)的组合体,其直观图如图所示,其中BA ,BC ,BP 两两垂直,且BA =BC =BP =1,∴(半)球的直径长为AC =2,∴该几何体的体积为V =V半球+V P -ABC=12×43π(AC 2)3+13×12×BA ·BC ·PB =2π6+16.化学教案风云往来不定化学教案古木、奇藤、修三、解答题12.(2013·福建)如图,在四棱锥P —ABCD 中,PD ⊥平面ABCD ,AB ∥DC ,AB ⊥AD ,BC =5,DC =3,AD =4,∠P AD =60°.(1)当正视方向与向量AD →的方向相同时,画出四棱锥P —ABCD 的正视图(要求标出尺寸,并写出演算过程);(2)若M 为P A 的中点,求证:DM ∥平面PBC ; (3)求三棱锥D —PBC 的体积.(1)解 在梯形ABCD 中,过点C 作CE ⊥AB ,垂足为E . 由已知得,四边形ADCE 为矩形,AE =CD =3, 在Rt △BEC 中,由BC =5,CE =4,依据勾股定理得 BE =3,从而AB =6.又由PD ⊥平面ABCD 得,PD ⊥AD ,从而在Rt △PDA 中,由AD =4,∠P AD =60°,得PD =4 3. 正视图如图所示:(2)证明 取PB 中点N ,连接MN ,CN . 在△P AB 中,∵M 是 P A 的中点, ∴MN ∥AB ,MN =12AB =3,又CD ∥AB ,CD =3, ∴MN ∥CD ,MN =CD , ∴四边形MNCD 为平行四边形, ∴DM ∥CN .又DM ⊄平面PBC ,CN ⊂平面PBC , ∴DM ∥平面PBC .(3)解 V D —PBC =V P —DBC =13S △DBC ·PD ,又S △DBC =6,PD =43, 所以V D —PBC =8 3.13.如图,在Rt △ABC 中,AB =BC =4,点E 在线段AB 上.过点E 作EF ∥BC 交AC 于点F ,将△AEF 沿EF 折起到△PEF 的位置(点A 与P 重合),使得∠PEB =30°.(1)求证:EF ⊥PB ;(2)试问:当点E 在何处时,四棱锥P —EFCB 的侧面PEB 的面积最大?并求此时四棱锥P —EFCB 的体积.(1)证明 ∵EF ∥BC 且BC ⊥AB ,∴EF ⊥AB ,即EF ⊥BE ,EF ⊥PE .又BE ∩PE =E , ∴EF ⊥平面PBE ,∴EF ⊥PB . (2)解 设BE =x ,PE =y ,则x +y =4.∴S △PEB =12BE ·PE ·sin ∠PEB =14xy ≤14⎝ ⎛⎭⎪⎫x +y 22=1.当且仅当x =y =2时,S △PEB 的面积最大. 此时,BE =PE =2. 由(1)知EF ⊥平面PBE , ∴平面PBE ⊥平面EFCB ,在平面PBE 中,作PO ⊥BE 于O ,则PO ⊥平面EFCB . 即PO 为四棱锥P —EFCB 的高.又PO =PE ·sin 30°=2×12=1.S EFCB =12(2+4)×2=6.∴V P —BCFE =13×6×1=2.。
专题升级训练空间几何体(时间:60分钟满分:100分)一、选择题(本大题共6小题,每小题6分,共36分)1.一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是( )A.球B.三棱锥C.正方体D.圆柱2.用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个正方形,则原来的图形是( )3.(2013·四川,文2)一个几何体的三视图如图所示,则该几何体可以是( )A.棱柱B.棱台C.圆柱D.圆台4.若正四棱锥的正(主)视图和俯视图如图所示,则该几何体的表面积是( )A.4B.4+4C.8D.4+45.如下图是某几何体的三视图,其中正(主)视图是腰长为2的等腰三角形,侧(左)视图是半径为1的半圆,则该几何体的体积是( )A.πB.C.πD.6.若一个螺栓的底面是正六边形,它的正(主)视图和俯视图如图所示,则它的体积是( )A.27+12πB.9+12πC.27+3πD.54+3π二、填空题(本大题共3小题,每小题6分,共18分)7.把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1∶4,母线长是10cm,则圆锥的母线长为cm.8.一个正三棱柱的侧棱长和底面边长相等,体积为2,它的三视图中的俯视图如图所示,侧(左)视图是一个矩形,则这个矩形的面积是.9.如图,直三棱柱ABC-A1B1C1中,AB=1,BC=2,AC=,AA1=3,M为线段BB1上的一动点,则当AM+MC1最小时,△AMC1的面积为.三、解答题(本大题共3小题,共46分.解答应写出必要的文字说明、证明过程或演算步骤)10.(本小题满分15分)如图,已知某几何体的三视图如下(单位:cm).(1)画出这个几何体的直观图(不要求写画法);(2)求这个几何体的表面积及体积.11.(本小题满分15分)(2013·安徽,文18)如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°.已知PB=PD=2,PA=.(1)证明:PC⊥BD;(2)若E为PA的中点,求三棱锥P-BCE的体积.12.(本小题满分16分)如图,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD是边长为2的等边三角形,且与底面ABCD垂直,E为PA的中点.(1)求证:DE∥平面PBC;(2)求三棱锥A-PBC的体积.##一、选择题(本大题共6小题,每小题6分,共36分)1.D解析:因为球的三视图均为圆;正方体的三视图均可以为正方形,所以排除A,C.而三条侧棱两两垂直且相等的正三棱锥的三视图可以为全等的直角三角形,排除B.因为圆柱的正(主)视图与侧(左)视图均是矩形,俯视图为圆,故选D.2.A解析:由直观图可知,在直观图中多边形为正方形,对角线长为,所以原图形为平行四边形,位于y轴上的对角线长为2,故选A.3.D解析:从俯视图可看出该几何体上下底面为半径不等的圆,正(主)视图与侧(左)视图为等腰梯形,故此几何体为圆台.4.B5.D6.C解析:该螺栓是由一个正六棱柱和一个圆柱组合而成的,V总=V正六棱柱+V圆柱=×32×6×2+π×12×3=27+3π.二、填空题(本大题共3小题,每小题6分,共18分)7. 解析:作出圆锥的轴截面如图,设SA=y,O'A'=x,利用平行线截线段成比例,得SA'∶SA=O'A'∶OA,即(y-10)∶y=x∶4x,解得y=.所以圆锥的母线长为.8.2 解析:如图,设底面边长为a,则侧棱长也为a,由题意得a2·a=2,故a3=8,a=2.侧(左)视图与矩形DCC1D1相同,a·a=2.9. 解析:将直三棱柱沿侧棱A1A剪开,得平面图形如图所示,A'C1为定长,当A,M,C1共线时AM+MC1最短,此时AM=,MC1=2.又在原图形中AC1=,易知∠AMC1=120°,∴×2×sin 120°=.三、解答题(本大题共3小题,共46分.解答应写出必要的文字说明、证明过程或演算步骤)10.解:(1)这个几何体的直观图如图所示.(2)这个几何体可看成是正方体AC1及直三棱柱B1C1Q-A1D1P的组合体.由PA1=PD1=,A1D1=AD=2,可得PA1⊥PD1.故所求几何体的表面积S=5×22+2×2×+2××()2=22+4(cm2).所求几何体的体积V=23+×()2×2=10(cm3).11.解:(1)证明:连接AC,交BD于O点,连接PO.因为底面ABCD是菱形,所以AC⊥BD,BO=DO.由PB=PD知,PO⊥BD.再由PO∩AC=O知,BD⊥面APC,因此BD⊥PC.(2)解:因为E是PA的中点,所以.由PB=PD=AB=AD=2知,△ABD≌△PBD.因为∠BAD=60°,所以PO=AO=,AC=2,BO=1.又PA=,PO2+AO2=PA2,即PO⊥AC,故S△APC=PO·AC=3.由(1)知,BO⊥面APC,因此··BO·S△APC=.12. 解:(1)证明:如图,取AB的中点F,连接DF,EF.在直角梯形ABCD中,CD∥AB,且AB=4,CD=2,所以BF CD.所以四边形BCDF为平行四边形.所以DF∥BC.在△PAB中,PE=EA,AF=FB,所以EF∥PB.又因为DF∩EF=F,PB∩BC=B,所以平面DEF∥平面PBC.因为DE⊂平面DEF,所以DE∥平面PBC.(2)解:取AD的中点O,连接PO.在△PAD中,PA=PD=AD=2,所以PO⊥AD,PO=.又因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,所以PO⊥平面ABCD.在直角梯形ABCD中,CD∥AB,且AB=4,AD=2,AB⊥AD,所以S△ABC=×AB×AD=×4×2=4.故三棱锥A-PBC的体积V A-PBC=V P-ABC=×S△ABC×PO=×4×.。
1.(2013·长春调研)一个简单几何体的正(主)视图、俯视图如图所示,则其侧(左)视图不可能是()A.正方形B.圆C.等腰三角形D.直角梯形解析:选D 当几何体是一个长方体,其中一个侧面为正方形时,A可能;当几何体是一个横放的圆柱时,B可能;当几何体是横放的三棱柱时,C可能;只有D不可能.2.(2013·陕西检测)如图是由若干个相同的小立方体组成的几何体的俯视图,其中小立方体中的数学表示相应位置的小立方体的个数,则该几何体的侧(左)视图为()解析:选C 由俯视图知侧(左)视图从左到右能看到的小立方体的个数分别为2,3,1。
3.(2013·湖南高考)已知正方体的棱长为1,其俯视图是一个面积为1的正方形,侧(左)视图是一个面积为错误!的矩形,则该正方体的正(主)视图的面积等于()A.错误!B.1C。
错误!D。
错误!解析:选D 由已知,正方体的正(主)视图与侧(左)视图都是长为2,宽为1的矩形,所以正(主)视图的面积等于侧(左)视图的面积等于2。
4.(2013·洛阳模拟)如图是某几何体的三视图,则该几何体的体积为( )A.64+32π B.64+64πC.256+64π D.256+128π解析:选C 依题意,该几何体是一个正四棱柱及一个圆柱的组合体,其中正四棱柱的底面边长是8,侧棱长是4,圆柱的底面半径是4,高是4,因此所求几何体的体积等于π×42×4+82×4=256+64π.5.(2013·东城检测)一个几何体的三视图如图所示,则该几何体的表面积为()A.75+2错误!B.75+4错误!C.48+4错误!D.48+2错误!解析:选B 由三视图可知该几何体是一个四棱柱.两个底面的面积之和为2×错误!×3=27,四个侧面的面积之和为(3+4+5+错误!)×4=48+4错误!,故表面积为75+4错误!。
1.(角度新)用若干个体积为1的正方体搭成一个几何体,其正(主)
视图、侧(左)视图都是如图所示的图形,则这个几何体的最大体积是
( )
A .9
B .11
C .13
D .15
2.(交汇新)一个几何体的三视图如图所示,其中正(主)视图是一
个正三角形,则这个几何体的外接球的表面积为( )
A .8π3
B . 16π3
C .43π
D .23π
[历 炼]
1.解析:由正(主)视图、侧(左)视图可知,几何体的体积最大时,底层有9个小正方体,上面有2个,共11个,最大体积为11,故选
B .
答案:B
2.解析:根据三视图还原几何体得到一个如图所示的三棱锥D -ABC ,其中平面ADC ⊥平面ABC ,△ADC 为等边三角形.
取AC 的中点为E ,连接DE ,BE ,则有DE ⊥AC ,所以DE ⊥平面
ABC ,所以DE ⊥EB.由图中数据知AE =EC =EB =1,DE =3,AD =2.设此三棱锥的外接球的球心为O ,则它落在高线DE 上,连接OA ,则有AO 2=AE 2+OE 2=1+OE 2,AO =DO =DE -OE =3-OE ,所以AO =23,故球O 的半径为23
,故所求几何体的外接球的表面积S =4π×⎝ ⎛⎭
⎪⎫232=163π,故选B . 答案:B。
2014届高考数学第一章空间几何体复习提升训练新人教A版必修2一、选择题1、一个几何体的三视图如图所示,则该几何体的体积为()A.12 B.11 C. D.2、设底部为三角形的直棱柱的体积为V,那么其表面积最小时,底面边长为()A.B.C.D.3、(2013某某二中第4次月考)一个棱锥的三视图如图(尺寸的长度单位为m),则该棱锥的全面积是(单位:m2).()A.B.C.D.4、有一个几何体的三视图及其尺寸如下(单位:cm),则该几何体的表面积及体积分别为()A.24πcm 2,12πcm3B.15πcm 2,12πcm3C.24πcm 2,36πcm3D.以上都不正确5、如图是某一几何体的三视图,则这个几何体的体积为()A.4 B.8 C.16 D.206、如图直三棱柱ABC﹣A1B1C1的体积为V,点P、Q分别在侧棱AA1和CC1上,AP=C1Q,则四棱锥B﹣APQC的体积为()A.B.C.D.7、一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是()A.B.C.D.8、长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是() A.25πB.50πC.125πD.都不对9、棱长都是1的三棱锥的表面积为()A.B.C.D.10、(2013琼海4月模拟)在正方体中,,分别是,的中点,则下列判断错误的是A.与垂直 B.与垂直C.与平行 D.与平行11、过球面上三点A、B、C的截面和球心的距离是球半径的一半,且AB=6,BC=8,AC=10,则球的表面积是()A.B.C.D.12、如图,是正三棱锥且侧棱长为,两侧棱的夹角为,分别是上的动点,则三角形的周长的最小值为().. ..13、在一个几何体的三视图中,正视图与俯视图如右图所示,则相应的侧视图可以为()14、如图,正三棱锥P﹣ABC的侧棱长为a,两侧棱PA、PC的夹角为30°,E、F分别是PA、PC上的动点,则△BEF的周长的最小值是()A.B.C.D.15、用单位立方块搭一个几何体,使它的主视图和俯视图如图所示,则它的体积的最小值与最大值分别为()A.9与13 B.7与10 C.10与16 D.10与1516、如右图所示,一个空间几何体的主视图和左视图都是边长为的正方形,俯视图是一个直径为的圆,那么这个几何体的表面积为()A.B.C.D.17、把1、3、6、10、15、21、…这些数叫做三角形数,这是因为这些数目的点子可以排成一个正三角形(如下图),试求第七个三角形数是( )A.27 B.28 C.29 D.3018、(2013某某二模)若空间几何体的三视图如图所示,则该几何体体积为A.B.C.D.819、(2013下某某期中)一个简单几何体的主视图,左视图如图所示,则其俯视图不可能为( ) .A.长方形B.直角三角形C.圆D.椭圆参考答案一、选择题1、A2、考点:平均值不等式;棱柱、棱锥、棱台的侧面积和表面积;棱柱、棱锥、棱台的体积.专题:计算题.分析:设底边边长为a,高为h,利用体积公式V=Sh= a2×h,得出 h=,再根据表面积公式得S=+a2,最后利用基本不等式求出它的最大值及等号成立的条件即得.解答:解:设底边边长为a,高为h,则V=Sh= a2×h,∴h=,表面积为S=3ah+a2=+a2=++a2≥3=定值,等号成立的条件,即a=,故选C.点评:本小题主要考查棱柱、棱锥、棱台、棱柱、棱锥、棱台的侧面积和表面积、基本不等式等基础知识,考查运算求解能力,考查转化思想.属于基础题.3、考点:由三视图求面积、体积.专题:计算题;图表型.分析:由三视图可以看出,此几何体是一个侧面与底面垂直的三棱锥,垂直于底面的侧面是一个高为2,底连长也为2的等腰直角三角形,底面与垂直于底面的侧面全等,此两面的面积易求,另两个与底面不垂直的侧面是全等的,可由顶点在底面上的射影作出此两侧面底边的高,将垂足与顶点连接,此线即为侧面三角形的高线,求出侧高与底面的连长,用三角形面积公式求出此两侧面的面积,将四个面的面积加起来即可解答:解:由三视图可以看出,此几何体是一个侧面与底面垂直且底面与垂直于底面的侧面全等的三棱锥由图中数据知此两面皆为等腰直角三角形,高为2,底面连长为2,故它们的面积皆为=2,由顶点在底面的投影向另两侧面的底边作高,由等面积法可以算出,此二高线的长度长度相等,为,将垂足与顶点连接起来即得此两侧面的斜高,由勾股定理可以算出,此斜高为2,同理可求出侧面底边长为,可求得此两侧面的面积皆为=,故此三棱锥的全面积为2+2++=,故选A.点评:本题考点是由三视图求几何体的面积、体积,考查对三视图的理解与应用,主要考查对三视图与实物图之间的关系,用三视图中的数据还原出实物图的数据,再根据相关的公式求表面积与体积,本题求的是三棱锥的全面积,做本题时要注意本题中的规律应用,即四个侧面两两相等,注意到这一点,可以大大降低运算量.三视图的投影规则是主视、俯视长对正;主视、左视高平齐,左视、俯视宽相等.4、考点:由三视图求面积、体积.专题:空间位置关系与距离.分析:由已知中的三视图及其尺寸,我们易判断这个几何体是圆锥,且底面直径为6,圆锥的母线长为5,代入圆锥的表面积和体积公式,我们易得结论.解答:解:由三视图可得该几何体为圆锥,且底面直径为6,即底面半径为r=3,圆锥的母线长l=5,则圆锥的底面积S底面=π•r2=9π侧面积S侧面=π•r•l=15π,故几何体的表面积S=9π+15π=24πcm2,又由圆锥的高h==4,故V=•S底面•h=12πcm3.故选A.点评:本题考查的知识点是由三视图求面积和体积,根据三视图判断几何体的底面半径和母线长是解答本题的关键.5、考点:由三视图求面积、体积.专题:计算题.由三视图可知,几何体是三棱锥,底面三角形一边长为6,对应的高为2,几何体高为4,按照锥体体积公式求解即可.解答:解:由三视图可知,几何体一三棱锥,底面三角形一边长为6,对应的高为2,几何体高为4底面积S=×6×2=6,所以V=Sh=×6×4=8故选B点评:本题是基础题,考查三视图与直观图的关系,几何体的体积计算,考查计算能力,空间想象能力.6、考点:组合几何体的面积、体积问题.专题:计算题.分析:把问题给理想化,认为三棱柱是正三棱柱,设底面边长a和侧棱长h均为1,P、Q分别为侧棱AA′,CC′上的中点求出底面面积高,即可求出四棱锥B﹣APQC的体积.解答:解:不妨设三棱柱是正三棱柱,设底面边长a和侧棱长h均为1则V=S ABC•h=•1•1••1=认为P、Q分别为侧棱AA′,CC′上的中点则V B﹣APQC=S APQC•=(其中表示的是三角形ABC边AC上的高)所以V B﹣APQC=V点评:本题考查几何体的体积,考查计算能力,特殊化法,在解题中有独到效果,本题还可以再特殊点,四棱锥变为三棱锥解答更好.7、考点:棱柱、棱锥、棱台的侧面积和表面积;旋转体(圆柱、圆锥、圆台).专题:计算题.分析:设圆柱底面积半径为r,求出圆柱的高,然后求圆柱的全面积与侧面积的比.解答:解:设圆柱底面积半径为r,则高为2πr,全面积:侧面积=[(2πr)2+2πr2]:(2πr)2=.故选A.点评:本题考查圆柱的侧面积、表面积,考查计算能力,是基础题.8、考点:球的体积和表面积;球内接多面体.专题:计算题.分析:由题意长方体的外接球的直径就是长方体的对角线,求出长方体的对角线,就是求出球的直径,然后求出球的表面积.解答:解:因为长方体的一个顶点上的三条棱长分别是3,4,5,且它的8个顶点都在同一个球面上,所以长方体的对角线就是确定直径,长方体的对角线为:,所以球的半径为:,所以这个球的表面积是:=50π.故选B.点评:本题是基础题,考查球的内接多面体的有关知识,球的表面积的求法,注意球的直径与长方体的对角线的转化是本题的解答的关键,考查计算能力,空间想象能力.9、考点:棱柱、棱锥、棱台的侧面积和表面积.专题:计算题.分析:棱长都是1的三棱锥,四个面是全等的正三角形,求出一个面积即可求得结果.解答:解:因为四个面是全等的正三角形,则.故选A点评:本题考查棱锥的面积,是基础题.10、D11、D14、考点:棱锥的结构特征.专题:空间位置关系与距离.分析:画出三棱锥的沿PA展开的侧面展开图,直接求得的△BEF的周长的最小值AA1.解答:解:三棱锥的侧面展开图,如图,△BEF的周长的最小值为BB1,由于题设知∠BPB1=90°,正三棱锥P﹣ABC的侧棱长为a所以BB1=a,故选A.点评:本题考查棱锥的结构特征、棱锥的侧面展开图,是基础题.15、考点:由三视图求面积、体积.专题:由于主视图第一列为3层,故俯视图中第一列至少有一个是3层的,其余可是1~3层,同时可分析第2列和第三列,进而得到答案.解答:解:由主视图第1,2,3列高分别为3,2,1则该几何体体积的最大值为:3+3+3+2+2+2+1=16体积的最小为:3+1+1+2+1+1+1=10故选:C点评:本题考查的知识点是由三视图求体积,其中根据主视图的层数,分析俯视图中每一列的最高层数是解答的关键.16、C17、B18、C19、C。
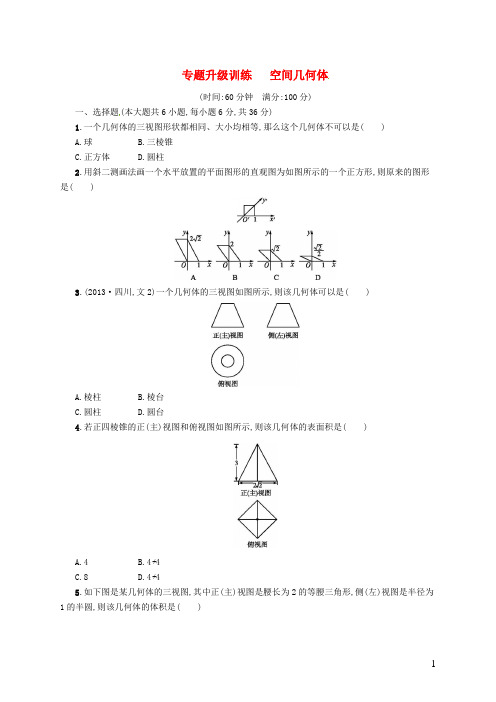
专题升级训练空间几何体
(时间:60分钟满分:100分)
一、选择题 (本大题共6小题,每小题6分,共36分)
1.一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是()
A.球
B.三棱锥
C.正方体
D.圆柱
2.用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个正方形,则原来的图形是()
3.(2013·四川,文2)一个几何体的三视图如图所示,则该几何体可以是()
A.棱柱
B.棱台
C.圆柱
D.圆台
4.若正四棱锥的正(主)视图和俯视图如图所示,则该几何体的表面积是()
A.4
B.4+4
C.8
D.4+4
5.如下图是某几何体的三视图,其中正(主)视图是腰长为2的等腰三角形,侧(左)视图是半径为1的半圆,则该几何体的体积是()
A.π
B.
C.π
D.
6.若一个螺栓的底面是正六边形,它的正(主)视图和俯视图如图所示,则它的体积是()
A.27+12π
B.9+12π
C.27+3π
D.54+3π
二、填空题(本大题共3小题,每小题6分,共18分)
7.把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1∶4,母线长是10cm,则圆锥的母线长为cm.
8.一个正三棱柱的侧棱长和底面边长相等,体积为2,它的三视图中的俯视图如图所示,侧(左)视图是一个矩形,则这个矩形的面积是.
9.如图,直三棱柱ABC-A1B1C1中,AB=1,BC=2,AC=,AA1=3,M为线段BB1上的一动点,则当AM+MC1最小时,△AMC1的面积为.
三、解答题(本大题共3小题,共46分.解答应写出必要的文字说明、证明过程或演算步骤)
10.(本小题满分15分)如图,已知某几何体的三视图如下(单位:cm).
(1)画出这个几何体的直观图(不要求写画法);
(2)求这个几何体的表面积及体积.
11.(本小题满分15分)(2013·安徽,文18)如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°.已知PB=PD=2,PA=.
(1)证明:PC⊥BD;
(2)若E为PA的中点,求三棱锥P-BCE的体积.
12.(本小题满分16分)如图,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中AD⊥AB,CD ∥AB,AB=4,CD=2,侧面PAD是边长为2的等边三角形,且与底面ABCD垂直,E为PA的中点.
(1)求证:DE∥平面PBC;
(2)求三棱锥A-PBC的体积.
##
一、选择题(本大题共6小题,每小题6分,共36分)
1.D解析:因为球的三视图均为圆;正方体的三视图均可以为正方形,所以排除A,C.而三条侧棱两两垂直且相等的正三棱锥的三视图可以为全等的直角三角形,排除B.因为圆柱的正(主)视图与侧(左)视图均是矩形,俯视图为圆,故选D.
2.A解析:由直观图可知,在直观图中多边形为正方形,对角线长为,所以原图形为平行四边形,位于y轴上的对角线长为2,故选A.
3.D解析:从俯视图可看出该几何体上下底面为半径不等的圆,正(主)视图与侧(左)视图为等腰梯形,故此几何体为圆台.
4.B
5.D
6.C解析:该螺栓是由一个正六棱柱和一个圆柱组合而成的,
V总=V正六棱柱+V圆柱=×32×6×2+π×12×3=27+3π.
二、填空题(本大题共3小题,每小题6分,共18分)
7.解析:作出圆锥的轴截面如图,设SA=y,O'A'=x,利用平行线截线段成比例,得SA'∶
SA=O'A'∶OA,即(y-10)∶y=x∶4x,解得y=.
所以圆锥的母线长为.
8.2解析:如图,设底面边长为a,则侧棱长也为a,由题意得a2·a=2,故a3=8,a=2.
侧(左)视图与矩形DCC1D1相同,a·a=2.
9.解析:将直三棱柱沿侧棱A1A剪开,得平面图形如图所示,A'C1为定长,当A,M,C1共线时AM+MC1最短,此时AM=,MC1=2.
又在原图形中AC1=,易知∠AMC1=120°,∴×2×sin 120°=.
三、解答题(本大题共3小题,共46分.解答应写出必要的文字说明、证明过程或演算步骤)
10.解:(1)这个几何体的直观图如图所示.
(2)这个几何体可看成是正方体AC1及直三棱柱B1C1Q-A1D1P的组合体.
由PA1=PD1=,A1D1=AD=2,
可得PA1⊥PD1.
故所求几何体的表面积S=5×22+2×2×+2××()2=22+4(cm2).
所求几何体的体积V=23+×()2×2=10(cm3).
11.解:(1)证明:连接AC,交BD于O点,连接PO.因为底面ABCD是菱形,所以AC⊥
BD,BO=DO.由PB=PD知,PO⊥BD.再由PO∩AC=O知,BD⊥面APC,因此BD⊥PC.
(2)解:因为E是PA的中点,所以.
由PB=PD=AB=AD=2知,△ABD≌△PBD.
因为∠BAD=60°,所以PO=AO=,AC=2,BO=1.
又PA=,PO2+AO2=PA2,即PO⊥AC,故S△APC=PO·AC=3.
由(1)知,BO⊥面APC,
因此··BO·S△APC=.
12. 解:(1)证明:如图,取AB的中点F,连接DF,EF.
在直角梯形ABCD中,CD∥AB,且AB=4,CD=2,
所以BF CD.
所以四边形BCDF为平行四边形.
所以DF∥BC.
在△PAB中,PE=EA,AF=FB,
所以EF∥PB.
又因为DF∩EF=F,PB∩BC=B,
所以平面DEF∥平面PBC.
因为DE⊂平面DEF,
所以DE∥平面PBC.
(2)解:取AD的中点O,连接PO.
在△PAD中,PA=PD=AD=2,
所以PO⊥AD,PO=.
又因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,所以PO⊥平面ABCD.
在直角梯形ABCD中,CD∥AB,且AB=4,AD=2,AB⊥AD,所以S△ABC=×AB×AD=×4×2=4.故三棱锥A-PBC的体积V A-PBC=V P-ABC=×S△ABC×PO=×4×.。