八年级上轴对称及最短路线问题分析

课题学习《最短路径问题》说课稿各位领导、专家、同仁们大家好：今天我说课的的内容是：人教八年级上册第13章第四节课题学习最短路径问题。

下面我将从：教材分析、学情分析、教学目标、教学重难点、教法、学法、教学手段、教学过程、板书设计、反思十个方面展开我的说课。

一、教材分析：本节课的内容是在学习了轴对称图形及两点之间线段最短知识的基础上学习的最短路径问题。

同时为我们今后解决坐标系下线段和最短的问题打下基础。

所以本节课的学习既是对前面所学知识的应用又为今后学习新知识做了铺垫，起到了呈上起下的作用。

二、学情分析1、已有的知识与能力：八年级学生已经学习了“两点之间线段最短”“垂线段最短”这些关于距离最短问题的解决依据。

也初步接触了逻辑推理证明的方法。

2、未接触的知识能力：由于八年级学生首次遇到线段和最小，所以无从下手，另外证明两条线段和最小时要选取另外一点，学生想不到、不会用，所以利用轴对称将最短路径问题转化为线段和最小问题，逻辑推理证明所求距离最短是本节课的难点。

3.综合能力方面：八年级学生这一阶段的学生思维能力发展较快,自我意识增强,有较强的求知欲和表现欲,在情感方面他们能进行自我教育。

经过一年多新课程理念的熏陶及实践,学生已有了初步的自主学习、合作探究的能力,但部分学生存在不自信,羞于表现等思想顾虑,但又希望能得到他人的肯定。

因此我的教学目标分了三层,照顾不同程度的学生。

在教学活动中尽量让他们参与到活动中来,减少他们的恐惧感,通过学生间的合作学习,降低他们的学习难度,使各层次的学生都有所收获,使他们体验到成功的喜悦。

通过以上教材与学情分析我制定了本节课教学目标：三、教学目标：1、知识与能力目标：（1）能利用轴对称解决简单的最短路径问题。

（2）能将实际问题中的“地点”、“河”抽象为数学中的“点”、“直线”，把实际问题抽象为数学问题。

2、过程与方法目标：（1）使学生经历提出问题——合作探究——动手操作——组间对比——理论证明——解决问题的过程。

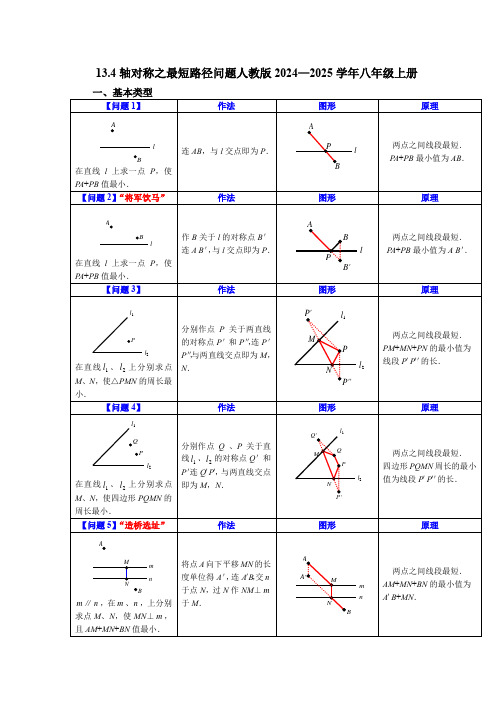
13.4轴对称之最短路径问题人教版2024—2025学年八年级上册二、例题讲解例1.如图，C为线段BD上一动点，分别过点B、D作AB⊥BD，ED⊥BD，连接AC、EC，已知线段AB＝4，DE＝2，BD＝8，设CD＝x．（1）用含x的代数式表示AC+CE的长；（2）请问点C满足什么条件时，AC+CE最小？最小为多少？（3）根据（2）中的规律和结论，请构图求代数式的最小值．变式1.如图，C为线段BD上一动点，分别过点B，D作AB⊥BD，ED⊥BD，连结AC，EC，已知AB＝5，DE＝1，BD＝8．（1）请问点C什么位置时AC+CE的值最小？最小值为多少？（2）设BC＝x，则AC+CE可表示为，请直接写出的最小值为．例2.如图，直线l是一条河，P，Q是两个村庄，欲在l上的某处修建一个水泵站，向P，Q两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则所需管道最短的是（）A．B．C．D．变式1.如图，在⊥ABC中，BA＝BC，BD平分⊥ABC，交AC于点D，点M、N 分别为BD、BC上的动点，若BC＝10，⊥ABC的面积为40，则CM+MN的最小值为．变式2.如图，等腰三角形ABC的底边BC长为8，面积是24，腰AC的垂直平分线EF分别交AC，AB于E，F点，若点D为BC边的中点，点M为线段EF 上一动点，则⊥CDM的周长的最小值为（）A．7B．8C．9D．10变式3.如图，在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，OA=3，OB=4，D为边OB的中点．（1）点D的坐标为；（2）若E为边OA上的一个动点，当⊥CDE的周长最小时，求点E的坐标．例3.如图，⊥AOB内一点P，P1，P2分别是P关于OA、OB的对称点，P1P2交OA于点M，交OB于点N．若⊥PMN的周长是6cm，则P1P2的长为（）A．6cm B．5cm C．4cm D．3cm变式1.已知点P在⊥MON内．如图1，点P关于射线OM的对称点是G，点P 关于射线ON的对称点是H，连接OG、OH、OP．（1）若⊥MON＝50°，求⊥GOH的度数；（2）如图2，若OP＝6，当⊥P AB的周长最小值为6时，求⊥MON的度数．变式2.如图，⊥MON＝45°，P为⊥MON内一点，A为OM上一点，B为ON上一点，当⊥P AB的周长取最小值时，⊥APB的度数为（）A．45°B．90°C．100°D．135°变式3.如图，⊥AOB＝30°，P是⊥AOB内的一个定点，OP＝12cm，C，D分别是OA，OB上的动点，连接CP，DP，CD，则⊥CPD周长的最小值为．变式4.如图，在五边形中，⊥BAE＝140°，⊥B＝⊥E＝90°，在边BC，DE上分别找一点M，N，连接AM，AN，MN，则当⊥AMN的周长最小时，求⊥AMN+⊥ANM 的值是（）A．100°B．140°C．120°D．80°例4.如图，在⊥ABC中，AB＝AC，⊥A＝90°，点D，E是边AB上的两个定点，点M，N分别是边AC，BC上的两个动点．当四边形DEMN的周长最小时，⊥DNM+⊥EMN的大小是（）A．45°B．90°C．75°D．135°变式1.如图，在平面直角坐标系中，已知点A（0，1），B（4，0），C（m+2，2），D（m，2），当四边形ABCD的周长最小时，m的值是（）A．B．C．1D．变式2.如图，在四边形ABCD中，⊥B＝90°，AB⊥CD，BC＝3，DC＝4，点E 在BC上，且BE＝1，F，G为边AB上的两个动点，且FG＝1，则四边形DGFE 的周长的最小值为．例5.如图，⊥AOB＝20°，点M、N分别是边OA、OB上的定点，点P、Q分别是边OB、OA上的动点，记⊥MPQ＝α，⊥PQN＝β，当MP+PQ+QN最小时，则β﹣α的值为（）A．10°B．20°C．40°D．60°变式1.如图，∠AOB＝20°，M，N分别为OA，OB上的点，OM＝ON＝3，P，Q分别为OA，OB上的动点，求MQ+PQ+PN的最小值。

13.4课题学习最短路径问题课标要求掌握基本事实：两点Z间，线段最短。

理解线段垂直平分线的概念，探索并证明线段垂直平分线性质定理：线段垂直平分线上的点到线段两端距离相等；反Z,到线段两端距离相等的点在线段的垂直平分线上。

教材分析本节课是在已经学习了轴对称图形性质的基础上进一步学习“经过直线上一点，在直线同侧两点之1'可路径最短问题”的解决方案。

为后续平面几何线段之和最短一类问题奠基。

学情分析1.学生己经学习了已经掌握轴对称的性质以及“两点之间，线段最短”、三角形三边不等公理，这为学习最短路径问题做好了知识和能力上的准备。

2.学生已经具备了一定的学习能力及作图能力，所以本节课屮，主要采用学生自主学习、合作探究的方式，教师引导让每位学生都参与探究。

课时目标1.能利用轴对称解决简单的最短路径问题；2•体会图形的变化在解决最值问题中的作用；3.能通过逻辑推理证明所求距离最短，感悟转化思想；4.体验数学活动中的探索与创新、感受数学的严谨性.教学重卢直线线上一点，到同侧两点距离之和最短问题利用作轴对称将直线线上一点，到同侧两点距离之和最短问题转化为“两点之间，线段最短”问题.教学难点利用作轴对称将直线线上一点，到同侧两点距离之和最短问题转化为“两点之间，线段最短”问题. 提炼的课题利用作轴对称将直线线上一点，到同侧两点距离之和最短问题转化为“两点之间，线段最短”问题.教学过程教学环节教学内容及师生活动设计意图媒体选择分析1 •情境引入引入新课PPT1-4：通过创设情景，•引导学生思考，激发学生学习兴趣。

1出示问题：相传，古希腊亚历山大里亚城里有一位久负盛名的学者，名叫海伦.有一天，一位将军专程拜访海伦，求教一个百思不得其解的问题：从图中的A地出发，到一条笔直的河边1饮马，然后到B 地.到河边什么地方饮马可使他所走的路线全程最短？2、倾听学生对上面问题的回答，揭示课题3、引入新课。

从小故事出发，引发学生思考问题的兴趣；激励自主学习探索直线线上一点，到同侧两点距离之和最短问题.类型：t+w作用：b使用：3、b时间：3回顾“两点之间，线段最短”，思考故事中存在的数学问题。

与轴对称相关的线段之和最短问题在中考复习课中，有一种题型我们不可避免地要帮学生复习，即求：某种情节下的最短距离、最短路线；以何种情况下由3点围成的三角形、由4点围成的四边形的周长最小，等等。

试题虽然花样翻新，但其实质还是一样的。

当这类题目呈现在学生面前时，学生的感觉往往是一个字——难，不善于做这类题。

现以“用轴对称知识解决最值问题”的题组为例，通过几个强有力的数学模型，例说相关中考试题的解决方法，供老师们参考。

一、基本模型【数学模型1】：已知一条直线l与这条直线同侧的两点A、B，如图（1），在直线上找出一点P，使得这点与已知两点的距离和PA+PB最短。

作为题组的“基石”，中考复习时，我们重在让学生明白相关的解题策略。

如何解决线段的和的最短的问题？我们需要寻求和其中一条线段长度相等的线段，充分利用轴对称的有关性质，从而将线段的和最短转化为线段最短的问题。

让学生记住这个模型，并理解其中相关的数学原理，从而利用这个基本模型，轻松解决“最短”问题，这才是我们的最终目的。

二、变式模型通过基本问题结构的局部灵活重组，或者结论的拓展延伸，或者与其他问题的有机组合，加深学生对相关知识的理解，同时强化策略及思想等高层次的能力。

拓展延伸型问题也可以通过设问方式的改变，丰富问题设计的立意及内涵。

【数学模型2】：已知两条平行直线l1，l2及位于这两条直线上的两点A、B（线段AB与直线l1，l2不垂直），如图（3），分别在这两条直线上找出两点N、M，使得路径A-M-N-B最短。

解决方法：如图（3），分别作出A、B两点关于直线l2，l1的对称点A′、B′，连接 A′B′，分别交直线l2，l1于点M、N，有轴对称的有关性质，则路径A-M-N-B的长度就是线段A B′的长度，最短。

对比图（4），折线A-M-N-B的长度不是最短。

从一条定直线上的一个动点到分布在两条直线上的两个动点，孤立地看，变量增多（AM、MN、NB），问题较模型1复杂。

第十三章轴对称---最短路径问题
一、学习目标
能用轴对称解决简单的最短路径问题，体会图形的变化在最值问题中的作用二、知识精讲
知识点1：两点之间，线段最短。

归纳：在解决最短路径问题时，通常利用轴对称、平移等变化把已知问题转化为容易解决的问题，从而作出最短路径的选择。

【例1】
1.如下图:
由A地到B地有三条路供选择，你会选择，
理由是：
2.请画出点A关于直线L的对称点。

A．
_______________________ L
3.已知线段AB，请在平面内找一点P，使PA+PB的值最小。

A___________________B
【例2】如图，牧马人从A地出发，到一条笔直的河边L饮马，然后到B地，牧马人到河边的什么地方饮马，可使所走的路径最短？
A．
．B
____________________________
想一想：如图所示，如果A、B处于小河的两侧，你能找到使所走路径最短的点么？
A．
____________________________
．B
【例3】如图，牧马人从A地出发，先到草地边某一处牧马，再到河边饮马，然后回到B处，请画出最短路径。

【例4】如图，A和B两地在一条河的两岸，现在要在小河上造一座桥MN。

桥造在何处可使从A到B的路径AMNB最短？（假设河的两岸是平行的直线，桥要与河垂直）请你根据作法画出图形并给出理由。

·A
a
b
·B
【题组训练】：
1.如图，点P在∠AOB的内部，点M，N分别是点P关于直线OA，OB的对称点，线段MN交OA，OB与点E,F，若△PEF的周长是20cm，求MN的长。

初二数学上册：利用轴对称求解最短路径问题一、知识重点1、最短路径问题(1)求直线异侧的两点与直线上一点所连线段的和最小的问题，只要连接这两点，与直线的交点即为所求．(2)求直线同侧的两点与直线上一点所连线段的和最小的问题，只要找到其中一个点关于这条直线的对称点，连接对称点与另一个点，则与该直线的交点即为所求．2、运用轴对称解决距离最短问题运用轴对称及两点之间线段最短的性质，将所求线段之和转化为一条线段的长，是解决距离之和最小问题的基本思路，不论题目如何变化，运用时要抓住直线同旁有两点，这两点到直线上某点的距离和最小这个核心，所有作法都相同．3、利用平移确定最短路径选址解决连接河两岸的两个点的最短路径问题时，可以通过平移河岸的方法使河的宽度变为零，转化为求直线异侧的两点到直线上一点所连线段的和最小的问题．二、经典例子解析【例一】有两棵树位置如图，树脚分别为A，B.地上有一只昆虫沿A—B的路径在地面上爬行．小树顶D处一只小鸟想飞下来抓住小虫后，再飞到大树的树顶C处，问小鸟飞至AB之间何处时，飞行距离最短，在图中画出该点的位置．解：如图，作D关于AB的对称点D′，连接CD′交AB于点E，则点E就是所求的点．【例二】如图所示，点A，B分别是直线l异侧的两个点，在l上找一个点C，使CA＋CB最短，这时点C是直线l与AB的交点解：如图，【例三】如图所示，点A，B分别是直线l同侧的两个点，在l上找一个点C，使CA＋CB最短。

解：先作点B关于直线l的对称点B′，则点C是直线l与AB′的交点．为了证明点C的位置即为所求，我们不妨在直线上另外任取一点C′，连接AC′，BC′，B′C′，证明AC＋CB＜AC′＋C′B.如下：证明：由作图可知，点B和B′关于直线l对称，所以直线l是线段BB′的垂直平分线．因为点C与C′在直线l上，所以BC＝B′C，BC′＝B′C′.在△AB′C′中，AB′＜AC′＋B′C′，所以AC＋B′C＜AC′＋B′C′，所以AC＋BC＜AC′＋C′B【例四】在图中直线l上找到一点M，使它到A，B两点的距离和最小解：如图，作点B关于直线l的对称点B′；连接AB′交直线l于点M.则点M即为所求的点．【例五】如图，小河边有两个村庄A，B，要在河边建一自来水厂向A 村与B村供水。

轴对称最短路线问题原理
一、问题描述
轴对称最短路线问题，即求平面上两点间沿轴对称线走的最短距离。

二、问题解法
1. 构造对称轴
首先需要找到两点的对称轴，对称轴的构造方法有多种，常用的有以
下两种：
（1）连接两点，垂直平分线即为对称轴。

（2）以两点为圆心，以它们之间的距离为半径，画两个圆；两圆的交
点就是对称轴。

2. 沿对称轴转换
对称轴将平面分为两个对称部分，假设起点在对称轴左侧（或右侧），求出终点在对称轴右侧（或左侧）的最短距离，即为要求的轴对称最
短路线。

3. 求最短距离
最短距离可以使用最短路算法（如 Dijkstra 算法、Bellman-Ford 算法等）来计算。

三、应用领域
轴对称最短路线问题常见于自动化生产线、机器人运动等领域，在这
些领域中，机器人需要在不碰撞的情况下从一个点到达另一个点，同
时保证走的路径最短。

该问题的解决方法可以为机器人运动路径规划
提供参考。

13.4课题学习：最短路径问题夯实基础篇一、单选题：1．直线L是一条河，P，Q是两个村庄．欲在L上的某处修建一个水泵站，向P，Q两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则所需管道最短的是（）．A．B．C．D．【答案】D【知识点】轴对称的应用-最短距离问题【解析】【解答】作点P关于直线L的对称点P′，连接QP′交直线L于M．根据两点之间，线段最短，可知选项D铺设的管道，则所需管道最短．故选D．【分析】利用对称的性质，通过等线段代换，将所求路线长转化为两定点之间的距离．2．如图，点M，N在直线l的同侧，小东同学想通过作图在直线l上确定一点Q，使MQ与QN的和最小，那么下面的操作正确的是（）A．B．C．D．【答案】C【知识点】轴对称的应用-最短距离问题【解析】【解答】作点M关于直线l的对称点M′，再连接M′N交l于点Q，则MQ+NQ=M′Q+NQ=M′N，由“两点之间，线段最短”，可知点Q即为所求.故答案为：C【分析】先作点M关于l的对称点M′，连接M′N交l于点Q，即可.3．如图，在等腰△AB C中，AB=AC=6，∠ACB=75°，AD⊥BC于D，点M、N分别是线段AB，AD上的动点，则MN+BN的最小值是（）C．4.5D．6A．3B．【答案】A【知识点】角平分线的性质；等腰三角形的性质；含30°角的直角三角形；轴对称的应用-最短距离问题【解析】【解答】解：如图，作BH⊥AC，垂足为H，交AD于M′点，过M′点作M′N′⊥AB，垂足为N′，则BM′+M′N′为所求的最小值．∵AB=AC，AD⊥BC于D，∴∠ABC=∠C，AD是∠BAC 的平分线，∴M′H=M′N′，∴BH是点B到直线AC的最短距离（垂线段最短），∵∠ABC=∠C，∠ACB=75°，∴∠BAC=30°，∵BH⊥AC，∴BH=12AB=3．故答案为：A【分析】根据等腰三角形的三线合一，得到AD是∠BAC的平分线，由角平分线的性质可知，角平分线上的点到角两边的距离相等，得到BH是点B到直线AC的最短距离，再由三角形内角和定理得到∠BAC=30°，根据在直角三角形中，30度角所对的边是斜边的一半，求出MN+BN的最小值.4．如图：△AB C中， ACB=90°，AC=BC，AB=4，点E在BC上，且BE=2，点P在 ABC 的平分线BD上运动，则PE+PC的长度最小值为（）A．1B．2C．3D．4【答案】B【知识点】三角形的角平分线、中线和高；轴对称的应用-最短距离问题【解析】【解答】作点E关于BD的对称点E'，连接E'C，如下图：∵BD是∠ABC的平分线，∴通过作图知，BP垂直平分EE'，∴PE'=PE∴此时PE+PC=PE'+PC=E'C，PE+PC的长度最小，∵点E、点E'关于BD的对称，∴BE'=BE=2，又∵AB=4，∴点E'是A B中点，CE'是中线.∵△AB C中，∠ACB=90°，AC=BC，∴△ABC是等腰直角三角形，∠ABC=45 ，∴CE'又是底边AB的高，∴△BE'C也是等腰直角三角形，∴E'C=2，即：PE+PC的长度最小值为2.故选B.【分析】此题考查最短路径问题，利用轴对称，作点E关于BD的对称点E'，连接E'C，可知此时PE+PC的长度最小，PE+PC=PE'+PC=E'C.再根据作图和等腰直角三角形性质求出E'C的长即可.5．如图，在锐角△AB C中，AB＝AC＝10，S△ABC＝25，∠BAC的平分线交BC于点D，点M，N分别是AD和AB上的动点，则BM＋MN的最小值是（）A．4B．245C．5D．6【答案】C【知识点】等腰三角形的性质；轴对称的应用-最短距离问题【解析】【解答】解：如图，∵AD 是∠BAC 的平分线，AB =AC ，∴点B 关于AD 的对称点为点C ，过点C 作CN ⊥AB 于N 交AD 于M ，由轴对称确定最短路线问题，点M 即为使BM ＋MN 最小的点，CN ＝BM ＋MN ，∵AB ＝10，S △ABC ＝25，∴12×10•CN ＝25，解得CN ＝5，即BM ＋MN 的最小值是5.故答案为：C.【分析】根据AD 是∠BAC 的平分线，AB =AC 可得出确定出点B 关于AD 的对称点为点C ，根据垂线段最短，过点C 作CN ⊥AB 于N 交AD 于M ，根据轴对称确定最短路线问题，点M 即为使BM ＋MN 最小的点，CN ＝BM ＋MN ，利用三角形的面积求出CN ，从而得解.6．如图，等边ABC 中，D 为A C 中点，点P 、Q 分别为AB 、AD 上的点，4BP AQ ，3QD ，在BD 上有一动点E ，则PE QE 的最小值为（）A ．7B ．8C ．10D ．12【答案】C【知识点】等边三角形的判定与性质；轴对称的应用-最短距离问题【解析】【解答】解：如图，ABC ∵是等边三角形，BA BC ，∵D 为A C 中点，∴BD AC ，∵4AQ ，3QD ，7AD DC AQ QD ，作点Q 关于BD 的对称点Q '，连接PQ '交BD 于E ，连接QE ，此时PE +QE 的值最小，最小值PE +QE =PE +EQ '=PQ '，4AQ ∵，7AD DC ，3QD DQ ，4CQ BP ，10AP AQ ，60A ∵，APQ 是等边三角形，10PQ PA ，∴PE +QE 的最小值为10.故答案为：C.【分析】作点Q关于BD的对称点Q'，连接PQ'交BD于E，连接QE，此时PE+QE 的值最小，最小值PE+QE=PE+EQ'=PQ'，进而判断△APQ'是等边三角形，即可解决问题.7．如图，等腰三角形ABC的底边BC长为3，面积是18，腰AC的垂直平分线EF分别交AC，AB边于E，F点.若点D为BC边的中点，点M为线段EF上一动点，则△CDM 周长的最小值为（）A．7.5B．8.5C．10.5D．13.5【答案】D【知识点】三角形的面积；线段垂直平分线的性质；等腰三角形的性质；轴对称的应用-最短距离问题【解析】【解答】解：如图，连接AM、AD∵EF垂直平分线段AC∴CM=AM∴CM+MD=AM+MD≥AD即当A、M、D三点在一直线上且与AD重合时，CM+MD取得最小值，且最小值为线段AD的长∵△CMD的周长=CM+MD+CD=AM+MD+AD∴△CMD的周长的最小值为AD+CD ∵D为BC的中点，AB=AC∴1 1.52CD BC，AD⊥BC∴13182ABCS AD∴AD=12∴AD+CD=12+1.5=13.5即△CDM周长的最小值为13.5故答案为：D.【分析】连接AM、AD，由线段垂直平分线的性质可得CM=AM，当A、M、D三点在一直线上且与AD重合时，CM+MD取得最小值，且最小值为线段AD的长；根据等腰三角形三线合一的性质可得1 1.52CD BC，AD⊥BC，利用△ABC的面积可求出AD的长，从而求出此时△CDM的周长即可.二、填空题：8．如图的4×4的正方形网格中，有A，B，C，D四点，直线a上求一点P，使PA+PB 最短，则点P应选点（C或D）.【答案】C【知识点】轴对称的应用-最短距离问题【解析】【解答】解：如图，点A ′是点A 关于直线a 的对称点，连接A ′B ，则A ′B 与直线a 的交点，即为点P ，此时PA +PB 最短，∵A ′B 与直线a 交于点C ，∴点P 应选C 点.故答案为：C.【分析】点A ′是点A 关于直线a 的对称点，连接A ′B ，则A ′B 与直线a 的交点，即为点P ，此时PA +PB 最短，据此即得结论.9．如图，在ABC 中，3,4,,AB AC AB AC EF 垂直平分BC ，点P 为直线EF 上一动点，则ABP 周长的最小值是．【答案】7【知识点】轴对称的应用-最短距离问题【解析】【解答】解：∵EF 垂直平分BC ，∴B ，C 关于直线EF 对称．设AC 交EF 于点D ，∴当P 和D 重合时，AP BP 的值最小，最小值等于AC 的长，∴ABP 周长的最小值是437 ．【分析】根据题意知点B关于直线EF的对称点为点C，故当点P与点D重合时，AP+BP 的最小值，求出AC长度即可得到结论．中，AB=4，AC=6，BC=7，EF垂直平分BC，点P为直线EF上10．如图，在ABC的任一点，则ABP周长的最小值是.【答案】10【知识点】轴对称的应用-最短距离问题【解析】【解答】解：如图，连接PC，∵，4AB，AB PA PB PA PB的周长为4ABP要使ABP的周长最小，则需PA PB的值最小，∵垂直平分BC，EF，PC PBPA PB PA PC ，由两点之间线段最短可知，当点,,A P C 共线，即点P 在AC 边上时，PA PC 取得最小值，最小值为AC ，即PA PB 的最小值为6AC ，则ABP 周长的最小值是4610 .故答案为：10.【分析】如图，连接PC ，先把ABP 的周长表示出来为4+PA +PB ，接着根据垂直平分线性质得到PB =PC ，故只需PA +PC 最小△ABP 周长才最小，由两点之间线段最短得出P 点在AC 上时最小，此时PA +PC =AC =6，从而即可得出答案.11．如图，在△AB C 中，AB ＝AC ＝10，BC ＝12，AD ＝8，AD 是∠BAC 的平分线.若P ，Q 分别是AD 和AC 上的动点，则PC +PQ 的最小值是.【答案】9.6【知识点】三角形的面积；等腰三角形的性质；轴对称的应用-最短距离问题【解析】【解答】解：∵AB ＝AC ，AD 是∠BAC 的平分线，∴AD 垂直平分BC ，∴BP ＝CP .过点B 作BQ ⊥AC 于点Q ，BQ 交AD 于点P ，则此时PC +PQ 取最小值，最小值为BQ 的长，如图所示.∵S△ABC12BC•AD12AC•BQ，∴BQ12810BC ADAC9.6.故答案为：9.6.【分析】根据等腰三角形的三线合一得出AD垂直平分BC，根据垂直平分线上的点到线段两个端点的距离相等得出BP＝CP，过点B作BQ⊥AC于点Q，BQ交AD于点P，则此时PC+PQ取最小值，最小值为BQ的长，然后根据三角形的面积法，得出BC•AD =AC•BQ，根据等积式即可求出BQ的长.三、作图题：12．有一个养鱼专业户，在如图所示地形的两个池塘里养鱼，他每天早上要从住处P分别前往两个池塘投放鱼食，试问他怎样走才能以最短距离回到住地?(请用尺规作图，保留作图痕迹，不写做法)【答案】解：答图如图所示，该养鱼专业户若要以最短距离回到住地，则他所走路线是：，P M N P.或P N M P【知识点】轴对称的应用-最短距离问题【解析】【分析】分别作P点关于AB，AC的对称点，连接这两个对称点交AB于点M，交AC于点N，该养鱼专业户若要以最短距离回到住地，则他所走路线是：，或P N M P.P M N P13．如图，P和Q为△ABC边AB与AC上两点，在BC边上求作一点M， 使△PQM的周长最小。

利用轴对称求最短距离问题基本题引入:如图（1），要在公路道a上修建一个加油站，有Ａ，Ｂ两人要去加油站加油。

加油站修在公路道的什么地方，可使两人到加油站的总路程最短？你可以在a上找几个点试一试,能发现什么规律?·B ·A·B·Aa·B·Aa·A′图1M·A′MNa 图2图3思路分析：如图2，我们可以把公路a近似看成一条直线，问题就是要在a上找一点M，使AM与BM的和最小。

设A′是A的对称点，本问题也就是要使A′M与BM的和最小。

在连接A′B的线中，线段A′B最短。

因此，线段A′B与直线a的交点C的位置即为所求。

如图3，为了证明点C的位置即为所求，我们不妨在直线a上另外任取一点N，连接AN、BN、A′N。

因为直线a是A，A′的对称轴，点M,N在a上，所以AM= A′M,AN= A′N。

∴AM+BM= A′M+BM= A′B在△A′BN中，∵A′B＜A′N+BN∴AM+BM＜AN+BN即AM+BM最小。

点评：经过复习学生恍然大悟、面露微笑，不一会不少学生就利用轴对称知识将上一道中考题解决了。

思路如下：②∵BC＝9（定值），∴△PBC的周长最小，就是PB＋PC最小.由题意可知，点C关于直线DE的对称点是点A，显然当P、A、B三点共线时PB＋PA最小.此时DP＝DE，PB＋PA＝AB.由∠ADF＝∠FAE，∠DFA＝∠ACB＝90°，得△DAF∽△ABC.EF∥BC，1159AB＝，EF＝.∴AF∶BC＝AD∶AB，即6∶9＝AD∶15.∴AD＝10.Rt△ADF22292525中，AD＝10，AF＝6，∴DF＝8.∴DE＝DF＋FE＝8＋＝.∴当x＝时，△PBC的周长222得AE＝BE＝最小， y值略。

数学新课程标准告诉我们：教师要充分关注学生的学习过程，遵循学生认知规律，合理组织教学内容，建立科学的训练系统。

使学生不仅获得数学基础知识、基本技能，更要获得数学思想和观念，形成良好的数学思维品质。

初二数学中，轴对称是一个重要的几何概念，而在轴对称的基础上，寻找最短路线是一个有趣的数学问题。

本文将围绕初二数学中的轴对称和最短路线展开讨论，探究十二种不同情形下的最短路线问题。

1. 轴对称轴对称是初中数学中的基础概念之一，它指的是一个图形相对于某条直线对称。

在平面几何中，轴对称是一种非常常见的对称现象，例如正方形、矩形、圆形等图形都具有轴对称性质。

学生在初中数学学习中，通过理解和掌握轴对称的概念和特点，可以更好地理解图形的性质和变化。

2. 最短路线最短路线是数学中的一个经典问题，它可以运用在不同的领域和场景中，例如交通运输、网络规划、资源分配等。

在初中数学中，最短路线问题可以通过几何知识和数学推理进行解决，帮助学生培养逻辑思维和问题解决能力。

3. 十二种情形接下来我们将具体讨论初二数学中关于轴对称最短路线的十二种情形：1) 单个点关于坐标轴的对称；2) 直线段关于某一轴的对称；3) 圆关于圆心的对称；4) 长方形关于中心横纵轴的对称；5) 正方形关于对角线的对称；6) 三角形关于三条中线的对称；7) 五边形关于中心轴的对称；8) 六边形关于中心轴的对称；9) 人字形关于中心轴的对称；10) 对称图形的最短路线为直线；11) 非对称图形的最短路线为折线；12) 非对称图形的最短路线为曲线。

通过逐一分析这十二种情形，我们可以发现不同对称图形的最短路线具有不同的特点和规律。

例如对于对称图形，其最短路线往往为直线，而对于非对称图形，其最短路线则可能为折线或曲线。

通过解决这十二种情形下的最短路线问题，学生可以锻炼几何推理和数学建模能力，培养对数学问题的思考和解决能力。

总结回顾通过对初二数学中轴对称最短路线的十二种情形进行探讨，我们不仅加深了对轴对称和最短路线的理解，还培养了数学建模和问题解决能力。

在学习数学的过程中，我们不仅要注重理论知识的掌握，更要注重数学方法和思维能力的培养，这样才能更好地应用数学知识解决现实生活中的问题。