平行线的判定与性质综合运用习题课

平行线的判定与性质的综合应用专题练习平行线的判定与性质的综合运用专题一、推理填空题1.已知：如图，DE∥BC，∠ADE＝∠XXX，将说明∠1＝∠2成立的理由填写完整。

解：因为DE∥BC，所以∠ADE=∠XXX。

又因为DE∥BC，所以DB∥EF。

由平行线性质可知，∠1=∠ADE=∠XXX∠2.2.已知：如图所示，∠1＝∠2，∠A＝∠3.求证：XXX。

证明：因为∠1＝∠2，所以XXX。

又因为∠A＝∠3，所以AC∥BD。

由平行线性质可知，AC∥DE。

3.已知：如图，∠XXX∠ADC，BF、DE分别平分∠ABC 与∠ADC，且∠1＝∠3.求证：AB∥DC。

证明：因为∠XXX∠ADC，所以∠XXX∠ADC。

又因为BF、DE分别平分∠ABC与∠ADC，所以∠1=∠ABC，∠3=∠ADC。

由∠1＝∠3可得，∠2=∠ADC。

由平行线性质可知，AB∥DC。

二、证明题4.如图，AB∥CD，AE交CD于点C，DE⊥AE，垂足为E，∠A=37º，求∠D的度数。

证明：因为AB∥CD，所以∠A+∠D=180º。

又因为DE⊥AE，所以∠ADE=90º。

由∠A=37º可得，∠ADE=53º。

由三角形内角和定理可得，∠D=80º。

5.如图，已知AB∥CD，∠1=100°，∠2=120°，求∠α的度数。

证明：因为AB∥CD，所以∠1+∠α+∠2=180º。

由∠1=100º，∠2=120º可得，∠α= -40º。

由于∠α是角度，所以∠α=320º。

6.如图，XXX，AE平分∠BAD，求证：XXX与AE相交于F，∠XXX∠EAF。

证明：因为XXX，所以∠BAD=∠ACD。

又因为AE平分∠BAD，所以∠XXX∠DAF。

由相邻角的性质可得，∠EAF+∠DAF=∠BAD=∠ACD。

又因为CD与AE相交于F，所以∠CFE+∠EAF+∠ACD=180º。

平行线的判定及性质一、【基础知识精讲】1、平行线的判定（1）平行公理：经过直线外一点，有且只有一条直线与已知直线平行. （2）平行公理的推论：平行于同一条直线的两条直线. （3）在同一平面内，垂直于同一条直线的两条直线. （4）同位角相等，两直线平行. （5）内错角相等，两直线平行.（6）同旁内角互补，两直线平行.3、平行线的性质（1）两直线平行，同位角相等. （2）两直线平行，内错角相等.（3）两直线平行，同旁内角互补.二、【例题精讲】专题一：余角、补角、对顶角与三线八角例题1：∠A的余角与∠A的补角互为补角，那么2∠A是（）A．直角 B.锐角 C.钝角 D.以上三种都有可能【活学活用1】如图2-79中，下列判断正确的是（）A.4对同位角，2对内错角，4对同旁内角B.4对同位角，2对内错角，2对同旁内角C.6对同位角，4对内错角，4对同旁内角D.6对同位角，4对内错角，2对同旁内角【活学活用2】如图2-82，下列说法中错误的是( )A.∠3和∠5是同位角B.∠4和∠5是同旁内角C.∠2和∠4是对顶角D.∠1和∠2是同位角【活学活用3】如图,直线AB与CD交于点O,OE⊥AB于O,图中∠1与∠2的关系是（）A.对顶角B.互余C.互补D相等例题2：如果两个角的两边分别平行，而其中一个角比另一个角的4倍少30°，那么这两个角分别是_______.【活学活用4】如图，∠AOC +∠DOE +∠BOF = .专题二：平行线的判定例题3：如图，已知∠EFB+∠ADC=180°，且∠1=∠2，试说明DG ∥AB.1 2A BCDF E G【活学活用】1、长方体的每一对棱相互平行，那么这样的平行棱共有 ( )A ．9对B ．16对 C.18对 D ．以上答案都不对2、已知:如图2-96,DE ⊥AO 于E,BO ⊥AO,FC ⊥AB 于C ，∠1=∠2,求证：DO ⊥AB.3、如图2-97,已知：∠1=∠2=，∠3=∠4，∠5=∠6.求证:AD ∥BC.4、如图2—101，若要能使AB ∥ED ，∠B 、∠C 、∠D 应满足什么条件?ABCDOE F5、同一平面内有四条直线a 、b 、c 、d ，若a ∥b ，a ⊥c ，b ⊥d ，则c 、d 的位置关系为（ ） A.互相垂直 B ．互相平行 C.相交 D ．没有确定关系专题三：平行线的性质1、如图，110,ABC ACB BO ∠+∠=、CO 分别平分ABC ∠和,ACB EF ∠过点O 与BC 平行，则BOC ∠= . 2、如图，AB //CD ，BC //DE ，则∠B+∠D = .3、如图，直线AB 与CD 相交于点O ，OB 平分∠DOE .若60DOE ∠=，则∠AOC 的度数是 .4、 如图，175,2120,375∠=∠=∠=，则4∠= .13 425、如图，//AB CD ，直线EF 分别交AB 、CD 于E 、F ，ED 平分BEF ∠，若172∠=，则2∠= .【例题讲解】例1：如图，已知：AD ∥BC, ∠AEF=∠B,求证：AD ∥EF 。

平行线的判定与性质的综合应用专题练习编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（平行线的判定与性质的综合应用专题练习）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为平行线的判定与性质的综合应用专题练习的全部内容。

1D FCBA2E平行线的判定与性质的综合运用 专题一、推理填空题1．已知：如图，DE∥BC ，∠ADE ＝∠EFC ，将说明∠1＝∠2成立的理由填写完整。

解：∵ DE∥BC （ )∴∠ADE ＝_______( ) ∵∠ADE ＝∠EFC （ ）∴_______＝_______ ( ）∴DB∥EF （ ) ∴∠1＝∠2（ ）2。

已知:如图所示，∠1＝∠2，∠A ＝∠3。

求证:AC∥DE 证明：∵∠1＝∠2（ ）∴AB∥＿＿＿＿（ ） ∴∠A ＝∠4( ） 又∵∠A ＝∠3（ ）∴∠3=＿＿＿＿（ ）∴AC∥DE( ）3。

已知：如图，∠ABC ＝∠ADC ，BF 、DE 分别平分∠ABC 与∠ADC ．且∠1＝∠3．求证：AB∥DC ．证明：∵∠ABC ＝∠ADC ，( ）又∵BF 、DE 分别平分∠ABC 与∠ADC ，( ）∴∠______＝∠______．( ) ∵∠1＝∠3，( ） ∴∠2＝∠______．(等量代换）∴______∥______．（ ）二、证明题4。

如图,AB ∥CD ,AE 交CD 于点C ，DE ⊥AE ,垂足为E ，∠A =37º，求∠D 的度数．5.如图,已知AB∥CD,∠1=100°，∠2=120°，求∠α的度数。

.2121ADC ABC ∠=∠∴.212,211ADC ABC ∠=∠∠=∠∴4321ABCEDα21F E DCBA6．如图,,平分，与相交于，。

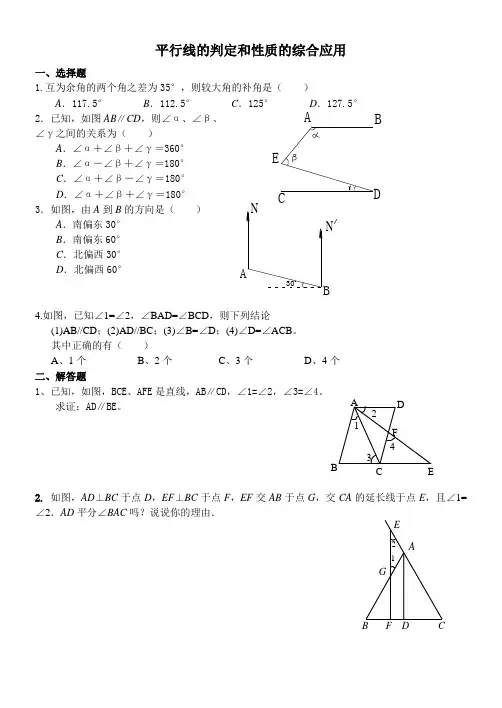
平行线的判定和性质的综合应用2. 如图，AD ⊥BC 于点D ，EF ⊥BC 于点F ，EF 交AB 于点G ，交CA 的延长线于点E ，且∠1=∠2．AD 平分∠BAC 吗？说说你的理由．C E 1 2 AB CD F G E3. 如图，若AB ∥CD ，∠1=∠2，则∠E =∠F ，为什么？4、如图，将纸片△ABC 沿DE 折叠，点A 落在点A ′处，已知∠1+∠2=100°，求 ∠A 的度数．5、如图，直线AC ∥BD ，连结AB ，直线AC ，BD 及线段AB 把平面分成①、②、③、④四个部分，规定：线上各点不属于任何部分，当动点P 落在某个部分时，连结P A ，PB ，构成∠P AC ，∠APB ，∠PBD 三个角．（提示：有公共端点的两条重合的射线所组成的角是0°．） （1）当动点P 落在第①部分时，试说明：∠APB =∠P AC +∠PBD ．（2）当动点P 落在第②部分时，∠APB =∠P AC +∠PBD 是否成立？（3）当动点P 落在第③部分时，请全面探究∠P AC ，∠APB ，∠PBD 之间的关系，并写出动点P 的具体位置和相应的结论， 选择其中一种结论加以说明．1 2 A B C D EF ADB C 1 2A E一、能力提升1. 如图，已知∠ABC +∠ACB =110°，BO 、CO 分别是∠ABC 和∠ACB 的平分线，EF 过O 与BC平行，则∠BOC = ．2. 如图，把一个长方形纸片沿EF 折叠后，点D ，C 分别落在D ′，C ′的位置．若∠EFB ＝65°，则∠AED ′的度数为 ．3. 如图，将三角尺的直角顶点放在直尺的一边上，130250∠=∠=°，°，则3∠= ．4.如图,已知∠1+∠2=180°,∠A=∠C,AD 平分∠BDF.求证:BC 平分∠DBE.B12FDECA5、如图，已知∠ABD 和∠BDC 的平分线交于E ，BE 交CD 于点F ，∠1 +∠2 = 90°． 求证：（1）AB ∥CD ； （2）∠2 +∠3 = 90°．6、如图，已知AB ∥CD ，∠BAE =30°，∠DCE =60°，EF 、EG 三等分∠AEC ． （1）求∠AEF 的度数； （2）求证：EF ∥AB ． EG DCF A B12 3 ED B C′F CD ′ A 第1题图 第2题图 第3题图 C1 2 3 AB DF E7.如图，已知AB ∥CD ，∠ABE 和∠CDE 的平分线相交于F ，∠E = 140º，求∠BFD 的度数．8.如图所示，A 1B ∥A n C ,求∠A 1+∠A 2+……∠A n -1+∠A n 度数．（1）在图1中，当A 1B ∥A 2C 时，∠A 1+∠A 2= ．（2）在图2中，当A 1B ∥A 3C 时，∠A 1+∠A 2+∠A 3= ． （3）在图3中，当A 1B ∥A 4C 时，∠A 1+∠A 2+∠A 3+∠A 4= ．（4）由上述结果，可以总结得到:当A 1B ∥A n C 时，∠A 1+∠A 2+……∠A n -1+∠A n = ．9.如图,已知射线CB ∥OA,∠C=∠OAB=100°,E 、F 在CB 上,且满足∠FOB=∠AOB,OE 平分∠COF. (1)求∠EOB 的度数.(2)若平行移动AB,那么∠OBC:∠OFC 的值是否随之发生变化?若变化,•找出变化规律;若不变,求出这个比值.(3)在平行移动AB 的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.BOF E C AA AB C1 2A A A3B C1 23A A ABCA1432 A AABCAn1nA 42410.平面内的两条直线有相交和平行两种位置关系.（1）AB //CD ．如图a ，点P 在AB 、CD 外部时，由AB ∥CD ，有∠B =∠BOD ，又因∠BOD 是△POD 的外角，故∠BOD =∠BPD +∠D ，得∠BPD =∠B -∠D ．如图b ，将点P 移到AB 、CD 内部，以上结论是否成立？，若不成立，则∠BPD 、∠B 、∠D 之间有何数量关系？请证明你的结论； （2）在图b 中，将直线AB 绕点B 逆时针方向旋转一定角度交直线CD 于点Q ，如图c ，则 ∠BPD ﹑∠B ﹑∠D ﹑∠BQD 之间有何数量关系？（3）根据（2）的结论求图d 中∠A +∠B +∠C +∠D +∠E +∠F 的度数．图aO图b图c图d。

平行线的性质与判定综合题本页仅作为文档页封面，使用时可以删除This document is for reference only-rar21year.March直线平行的条件和性质1．三线八角两条直线被第三条直线所截形成八个角，它们构成了同位角、内错角与同旁内角。

如图，直线a ，b 被直线所截（1）∠1与∠5在截线的同侧，同在被截直线a ，b 的上方，叫做（位置相同）（2）∠5与∠3在截线的两旁（交错），在被截直线a ，b 之间（内），叫做（位置在内且交错）（3）∠5与∠4在截线的同侧，在被截直线a ，b 之间（内），叫做。

（4）三线八角也可以成模型中看出。

同位角是“F ”型；内错角是“Z ”型；同旁内角是“U ”型。

2.平行线的性质（1）两直线平行， 相等； （2）两直线平行， 相等； （3）两直线平行， 互补。

3.平行线的判定（1） 相等，两直线平行； （2） 相等，两直线平行； （3） 互补，两直线平行。

l l l l a bl1、了解同位角、内错角、同旁内角的概念，会找同位角、内错角、同旁内角2、会用同位角、内错角、同旁内角之间的数量关系来说明两直线平行3、能理解并区分平行线的性质和平行线的条件4、熟练地运用平行线的判定和性质正确的进行分析推理和计算5、综合应用判定、性质进行推理证明题型一：平行线的性质与判定的综合例1. 已知：如图，AD⊥BC于D，EG⊥BC与G，∠E＝∠3，试问：AD是∠BAC 的平分线吗？若是，请说明理由。

解：是，理由如下：∵AD⊥BC，EG⊥BC（已知）∴∠4＝∠5＝90°（）∴AD∥EG（）∴∠1＝∠E（）∠2＝∠3（）∵∠E＝∠3（已知）∴＝（）∴AD是∠BAC的平分线（）练习1. 如图，已知AD⊥BC，EF⊥BC，垂足分别为D、F，∠2+∠3＝180°，试说明：∠GDC＝∠B．请补充说明过程，并在括号内填上相应的理由．解：∵AD⊥BC，EF⊥BC（已知）∴∠ADB＝∠EFB＝90°，∴EF∥AD（），∴+∠2＝180°（）．又∵∠2+∠3＝180°（已知），∴∠1＝∠3（），∴AB∥（），∴∠GDC＝∠B（）．例2. 如图，已知CF⊥AB于F，ED⊥AB于D，∠1=∠2，试说明：FG如图，△ABC中，点E在边BA上，AD⊥BC，EF⊥BC，垂足分别是D. F，∠1=∠2.(1)DG与BA平行吗为什么(2)若∠B=51∘,∠C=54∘，求∠CGD的度数。