玻璃折射率的测量方法

测量玻璃的折射率实验分析与总结折射率测量是国际上用来鉴定玻璃质量的常见方法之一。

该实验用来分析和总结玻璃材料折射率，是国外及国内标准检测中必不可少的重要实验过程。

本报告对折射率测量过程的技术原理进行了全面总结。

折射率测量是总结玻璃材料的折射率的标准化过程。

其原理是入射到玻璃材料表面上的光束会产生折射率，即便是入射到玻璃材料表面时，折射率也不能完全保持同样。

由于玻璃材料折射率的不同，会导致玻璃材料的光学特性发生变化，这就是玻璃材料折射率的重要性所在。

因此，玻璃材料的折射率测量是衡量其物理性能的基本指标。

测量玻璃材料折射率的步骤如下：首先，设定合适的实验条件，如发生临界角的光束的入射角度、实验室的温度和湿度等;其次，测量折射率是需要对玻璃材料进行样品剥离，层层递进，清楚测量表征材料表面形态，材料物理性质，如厚度、宽度、变形率、折射率等；再次，实验室要根据样品的特性，制定合适的实验方案，通过实验设备，测定玻璃材料折射率；最后，对实验结果进行分析和总结，给出玻璃材料的折射率等物理性质值，以及相应的特性曲线。

实验原理的总结，便是测量玻璃材料折射率的主要步骤。

要测量玻璃材料的折射率，除了有一定的实验技术外，还需要专业的实验设备，比如データ取得装置，折射角度计，光学准直器，测量系统等。

如果在实验过程中全程控制角度偏差，实验仪器湿度等参数，可以提高实验精确度、可信度，以期达到理想的折射测量结果。

折射率是玻璃材料最基础的物理性质，用于测量玻璃材料的折射率，可以满足国内外标准的检测要求，是企业生产玻璃材料的重要依据。

本报告对测量玻璃材料折射率实验分析与总结。

测量玻璃折射率的方法简介玻璃折射率是指光线从空气中射入玻璃时，光线的传播方向发生弯曲的程度。

测量玻璃折射率是一个重要的实验技术，在材料科学、光学领域以及工业应用中具有重要的意义。

本文将介绍一些常用的测量玻璃折射率的方法。

相关理论知识在测量玻璃折射率之前，我们需要了解一些相关的理论知识。

折射定律折射定律是光线通过两种介质的界面时，入射角、折射角和两种介质的折射率之间的关系。

根据折射定律可以得出以下公式：sini sinr =n2 n1其中，n1和n2分别为两种介质的折射率，i为入射角，r为折射角。

光程差光程差指光线在两个不同介质中传播时所经过的路径长度之差。

对于任意一段光程差Δx，可以表示为：Δx=n⋅d其中，n为介质的折射率，d为光线从入射介质到达出射介质的厚度。

测量方法下面将介绍几种常用的测量玻璃折射率的方法。

斯涅尔法原理斯涅尔法是利用折射定律测量玻璃折射率的一种方法。

当光线从空气射入玻璃时，根据折射定律可以得到以下公式：n=sini sinr若设玻璃板的厚度为d，入射角为i，在玻璃板内光线传播的距离为L，则可以得到光程差Δx为：Δx=nd=iL通过测量光程差Δx和厚度d，再根据入射角i的变化，可以得到多个光程差Δx和对应的入射角i。

从而可以描绘出折射率与入射角之间的关系曲线，进而得到玻璃的折射率。

测量步骤1.准备一块厚度已知的玻璃样品。

2.设计一套斯涅尔测量装置，包括光源、准直器、分光仪、望远镜等。

3.将光源射入准直器，并通过分光仪准直出来的光线。

4.将准直后的光线照射到玻璃样品上，通过调节望远镜观察到出射光线的角度。

5.测量不同入射角下的光程差Δx和对应的入射角i。

6.根据公式Δx=nd=iL计算出折射率n。

干涉法原理干涉法是利用光的干涉现象测量玻璃折射率的方法。

当光线从空气射入玻璃时，由于光在不同折射率的介质中传播时速度不同，会产生光程差。

当光线从玻璃中出射后，再次进入空气，也会产生光程差。

测量玻璃折射率的方法一、引言玻璃折射率是指光线从真空中进入玻璃后的折射程度，是材料物理学中的重要参数。

测量玻璃折射率的方法有很多种，本文将介绍两种常用的方法：菲涅尔反射法和自制单臂反射法。

二、菲涅尔反射法1. 原理菲涅尔反射法是利用光在两种介质交界面上发生反射时产生的相位差来测量折射率的方法。

当光线从真空中垂直入射到玻璃表面时，一部分光会被反射回来，另一部分光会穿过玻璃向下传播。

根据菲涅尔公式可以计算出反射光和透射光之间的相位差，从而求得玻璃的折射率。

2. 实验步骤（1）准备实验材料：平板玻璃、激光器、半透镜、平面镜、白纸等。

（2）将激光器置于离平板玻璃较远处，调整激光束使其垂直入射到玻璃表面上。

（3）在反射光线和透射光线的交界处放置一个半透镜，调整其位置使反射光和透射光的路径重合。

（4）在反射光线的路径上放置一个平面镜，将反射光线引出来，并将其投影到白纸上。

（5）测量反射角和入射角，并根据菲涅尔公式计算出折射率。

三、自制单臂反射法1. 原理自制单臂反射法是利用单臂反射仪测量玻璃折射率的方法。

该方法相对于菲涅尔反射法来说更加简便易行，同时也具有较高的精度。

单臂反射仪由一束激光器、一个准直器、一个半透镜和一个平板玻璃组成。

当激光束垂直入射到玻璃表面时，在半透镜和准直器的作用下，激光束被分成两束，并以相同的角度倾斜入射到玻璃表面上。

其中一束激光经过全内反射后返回原路，另一束激光则穿过玻璃向下传播。

通过测量反射光和透射光的角度，可以计算出玻璃的折射率。

2. 实验步骤（1）准备实验材料：平板玻璃、激光器、准直器、半透镜等。

（2）将激光器置于离平板玻璃较远处，调整激光束使其垂直入射到玻璃表面上。

（3）在反射光线和透射光线的交界处放置一个半透镜，调整其位置使反射光和透射光的路径重合。

（4）在透射光线的路径上放置一个准直器，将其调整到与反射光线平行，并且两条线之间距离相等。

（5）测量反射角和入射角，并根据单臂反射仪原理计算出折射率。

测量玻璃折射率实验报告详解标题：测量玻璃折射率实验报告详解摘要：本篇实验报告旨在详细介绍测量玻璃折射率的实验步骤、原理和结果分析。

通过实验，我们能够理解光的折射现象，并利用相关的测量方法确定不同种类玻璃的折射率。

本报告由文章生成AI撰写，内容丰富且有价值。

引言：玻璃是一种常用的材料，具有广泛的应用领域。

了解玻璃的折射率对光学器件的设计和工程实践非常重要。

本实验旨在通过测量玻璃的折射率来探究其光学特性。

实验将详细介绍使用角度测量法和光程差测量法两种方法来测量玻璃折射率的步骤和原理，并给出实验结果的分析和总结。

通过本实验的学习，我们将更深入地了解折射率的概念和测量方法。

实验步骤：1. 实验前准备：1.1 准备所需材料：光源、玻璃样品、测角仪等。

1.2 搭建实验装置并调整光源和测角仪的位置。

2. 角度测量法：2.1 将测角仪固定在光源和玻璃样品之间的适当位置。

2.2 调整测角仪，使其指向光源发出的光线。

2.3 将玻璃样品固定在测角仪上，并记录其表面与入射光线的夹角。

2.4 旋转测角仪，找到透射光线的夹角并记录。

3. 光程差测量法：3.1 将玻璃样品放置在一隔板上，使其与光源成一定夹角。

3.2 通过光程差装置，测量入射光线和透射光线的光程差。

3.3 根据光程差和样品厚度计算折射率。

结果和讨论：通过角度测量法和光程差测量法，我们得到了一系列玻璃样品的折射率数据。

根据实验数据，我们可以得出以下结论：1. 不同种类玻璃的折射率各不相同，这与其化学成分和微观结构有关。

2. 在相同条件下，角度测量法和光程差测量法得到的折射率数据具有一致性。

总结：本实验通过测量玻璃折射率，详细介绍了角度测量法和光程差测量法两种常用的测量方法。

通过实验，我们深入理解了折射率的概念和测量原理。

同时，我们发现不同种类的玻璃具有不同的折射率，这与其微观结构和化学成分有关。

在以后的实践中，我们可以根据实验数据选择合适的玻璃材料，并合理设计光学器件。

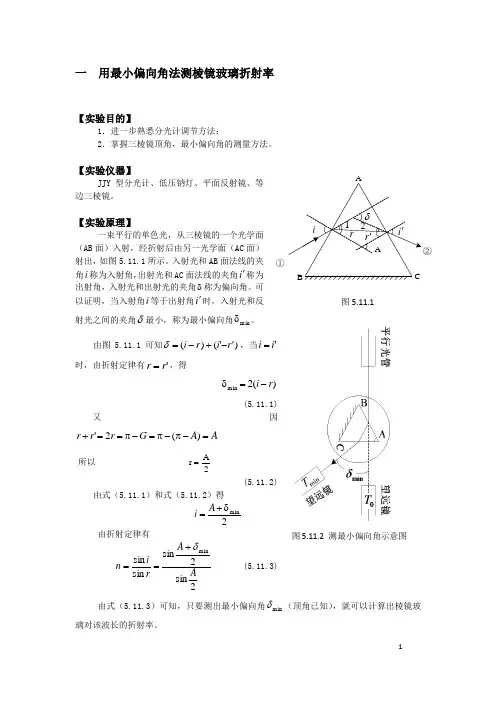
一 用最小偏向角法测棱镜玻璃折射率【实验目的】1．进一步熟悉分光计调节方法；2．掌握三棱镜顶角，最小偏向角的测量方法。

【实验仪器】JJY 型分光计、低压钠灯、平面反射镜、等边三棱镜。

【实验原理】一束平行的单色光，从三棱镜的一个光学面（AB 面）入射，经折射后由另一光学面（AC 面）射出，如图5.11.1所示。

入射光和AB 面法线的夹角i 称为入射角，出射光和AC 面法线的夹角i '称为出射角，入射光和出射光的夹角δ称为偏向角。

可以证明，当入射角i 等于出射角i '时，入射光和反射光之间的夹角δ最小，称为最小偏向角m in δ。

由图5.11.1可知)''()(r i r i -+-=δ，当'i i =时，由折射定律有'r r =，得)(2min r i -=δ(5.11.1)又因A A G r r r =-π-π=-π==+)(2'所以 =r 2A(5.11.2)由式（5.11.1）和式（5.11.2）得2minδ+=A i 由折射定律有2sin2sinsin sin minA A rin δ+==(5.11.3) 由式（5.11.3）可知，只要测出最小偏向角min δ（顶角已知），就可以计算出棱镜玻璃对该波长的折射率。

图5.11.2 测最小偏向角示意图①②图5.11.1【实验内容】1．正确调整分光计，使其满足实验要求（参阅§3.9） 2．测定玻璃三棱镜对钠光黄光的最小偏向角如图5.11.2所示，旋载物台，使一光学面AC 与平行光管入射方向基本上垂直。

当一束钠黄单色光从平行光管发出平行光射向三棱镜AB 光学面，经过三棱镜AC 光学面折射出来，望远镜从毛面BC 底边出发，沿着逆时针旋转，会看到清晰的狭缝像，说明找到折射光路。

此时转动小平台连同棱镜，观察狭缝像运动状态，如果向右移动，偏向角δ变小。

再转小平台狭缝像会走到一定位置转折，使δ偏大，此转折点即为该光谱线的最小偏向角位置，把望远镜对准这个转折点，记录下来，为m in T 、min 'T 。

课程论文题目：对玻璃折射率测定方法的探究班级：2010级物理学本科班姓名：学号：指导老师：对玻璃折射率测定方法的探究摘要：通过不同的方法测定玻璃的折射率，在对实验现象观察的同时，比较不同的方法之间的区别，并将实验结果与真实值比较。

关键词：玻璃，分光计，顶角，偏向角，折射率。

引言：运用钠灯灯光或激光照射玻璃，通过观察折射或反射光的性质来确定玻璃的折射率。

实验方法：（一） 最小偏向角法：1. 实验仪器与用具：分光计，玻璃三棱镜，钠灯。

2. 实验原理：（1）将待测的光学玻璃制成三棱镜，可用最小偏向角法测其折射率n ．测量原理见图1，光线α代表一束单色平行光，以入射角i 1投射到棱镜的AB 面上，经棱镜两次折射后以i 4角从另一面AC 射出来，成为光线t .经棱镜两次折射，光线传播方向总的变化可用入射光线α和出射光线t 延长线的夹角δ来表示，δ称为偏向角．由图1可知δ＝(i 1－i 2)＋(i 4－i 3)＝i 1＋i 4－A ．此式表明，对于给定棱镜,其顶角A 和折射率n 已定，则偏向角δ随入射角i 1而变，δ是i 1的函数.（2）用微商计算可以证明，当i 1＝i 4或i 2＝i 3时，即入射光线a 和出射光线t 对称地“站在”棱镜两旁时，偏向角有最小值，称为最小偏向角，用δm 表示.此时，有i 2＝A /2， i 1＝(A ＋δm )/2，故22mA A n sinsinδ+=。

用分光计测出棱镜的顶角A 和最小偏向角δm ,由上式可求得棱镜的折射率n ． 3.实验内容： 3.1棱镜角的测定图1置光源于准直管的狭缝前，将待测棱镜的折射棱对准准直管，由准直管射出的平行光束被棱镜的两个折射面分成两部分。

在棱镜的另外两侧分别找到狭缝像与竖直叉丝重合，分别记录此时分光计的读数''1212,,,V V V V ，望远镜的两位置所对应的游标读数之差为棱镜角A 的两倍。

3.2最小偏向角的测定（1）将待测棱镜放置在棱镜台上，转动望远镜使能清楚地看见钠光经棱镜折射后形成的黄色谱线。

实验报告测量玻璃折射率一、引言折射率是光线通过介质时发生折射的程度，是介质的一个重要光学性质。

本实验旨在通过测量玻璃的折射率，探究不同光线在不同介质中的传播规律，加深对光学的理解。

二、实验原理1.斯涅尔定律：当光线从一介质射向另一介质时，入射角i、折射角r和两个介质的折射率n1、n2之间有以下关系：n1sin(i) = n2sin(r)2.光程差：光线从空气进入玻璃，两束光线的光程差为：光程差δ=n1*BC+n2*AC3.中心黑环法测量：在测量折射率时，可以利用中心黑环法来测量不同颜色光线通过玻璃的光程差。

对称位置上可以形成环状的圆环，在灯光中观察两个相对的黑环，通过计算得到半径差，再根据光程差的公式计算出折射率。

三、实验步骤1.准备实验仪器：透镜架、白炽灯、屏，挠性导光管；2.将挠性导光管固定在透镜架上，使其与光轴平行；3.调节挠性导光管与透镜之间的距离，使挠性导光管上的圆环清晰可见；4.使用滤光片筛选出不同的颜色光线，使其通过挠性导光管到达透镜；5.观察两个相对的黑环，调节屏与透镜的距离，使黑环清晰；6.记下黑环对应的半径差，再测量出透镜与屏的距离AC和透镜与源之间的距离BC；7.记录各组数据，并计算出不同颜色光线对应的折射率。

四、实验数据颜色光线黑环半径差 R（mm）透镜到屏的距离 AC (mm)透镜到源的距离 BC (mm) 平均折射率 n红色7.8 189 1051.52黄色10.5 191 1041.61蓝色15.3 195 1091.69五、误差分析1.仪器本身存在一定的测量误差，如液晶模式准直器的度盘划度不精确等。

2.实验操作的误差，如对两个黑环的边缘判断不准确等。

3.折射率的实验值与参考值可能存在一定偏差。

六、结论通过本次实验，我们测量了不同颜色光线通过玻璃时的折射率，并得到如下结论：1.不同颜色光线的折射率不同，红光拥有较小的折射率，黄光次之，蓝光最大。

2.实验测量的折射率值与理论值存在一定误差，这可能是由于实验仪器的精度以及操作误差等因素导致的。

玻璃的折射率测量实验方法与数据处理折射率是衡量光在介质中传播速度变化的指标，也是评估材料光学性质的重要参数之一。

在材料科学和光学研究中，准确测量折射率对于理解光与物质相互作用的机理至关重要。

本文将介绍玻璃的折射率测量实验方法与数据处理。

一、实验方法1. 原理说明玻璃的折射率可以通过测量入射光线在空气与玻璃之间的折射角和折射光线在玻璃与空气之间的折射角，利用斯涅尔定律计算得出。

对于一束从空气垂直入射到玻璃表面的光线，其入射角为i，折射角为r。

根据斯涅尔定律，有折射定律的表达式：n1*sin(i) = n2*sin(r)。

其中，n1为空气的折射率（近似为1），n2为玻璃的折射率。

2. 实验装置为了测量玻璃的折射率，我们需要以下实验装置：- 一束光源- 一个可转动的望远镜和刻度盘- 一块平面玻璃样品- 一个角度测量装置3. 实验步骤（1）将光源对准玻璃表面，使光线垂直入射。

（2）通过调节望远镜和刻度盘的角度，将望远镜准确对准折射光线的方向。

（3）记录入射角和折射角的数值。

（4）重复实验多次，取平均值以提高测量结果的准确性。

二、数据处理为了得到准确的玻璃折射率，我们需要对实验数据进行处理。

1. 数据处理方法（1）计算入射角的正弦值sin(i)和折射角的正弦值sin(r)。

（2）利用斯涅尔定律的公式，根据测得的sin(i)和sin(r)计算折射率n2：n2 = n1 * sin(i) / sin(r)。

2. 典型数据示例为了更好地理解数据处理方法，我们给出一个典型的数据示例。

假设我们测量的入射角为30°，折射角为20°。

代入斯涅尔定律的公式中，可以得到玻璃的折射率。

n2 = 1 * sin(30°) / sin(20°) ≈ 1.5三、结果与讨论通过实验方法和数据处理，我们得到了玻璃的折射率。

玻璃的折射率值通常与材料类型和成分有关。

不同类型的玻璃具有不同的折射率，而且随着光的波长变化，折射率也会有所不同。

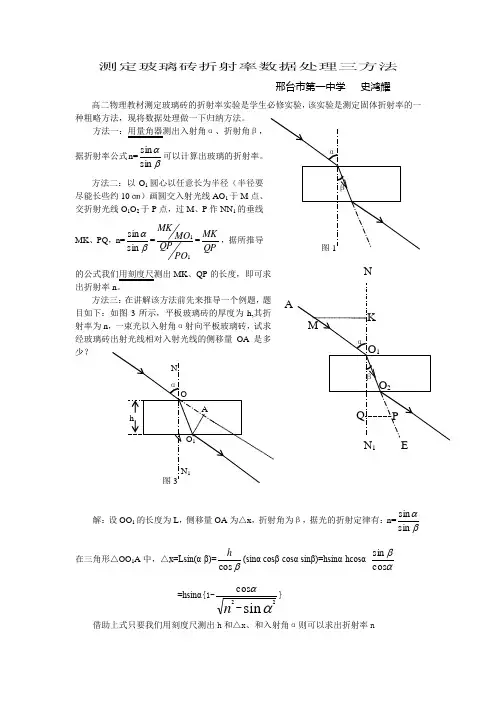
测定玻璃砖折射率数据处理三方法 邢台市第一中学 史鸿耀 高二物理教材测定玻璃砖的折射率实验是学生必修实验，该实验是测定固体折射率的一种粗略方法，现将数据处理做一下归纳方法。

方法一：用量角器测出入射角α、折射角β，
据折射率公式n=βαsin sin 可以计算出玻璃的折射率。

方法二：以O 1圆心以任意长为半径（半径要
尽能长些约10㎝）画圆交入射光线AO 1于M 点、
交折射光线O 1O 2于P 点，过M 、P 作NN 1的垂线MK 、PQ ，n=βαsin sin =1
1PO QP MO MK =QP MK ，据所推导的公式我们用刻度尺测出MK 、QP 的长度，即可求
出折射率n 。

方法三：在讲解该方法前先来推导一个例题，题
目如下：如图3所示，平板玻璃砖的厚度为h,其折
射率为n ，一束光以入射角α射向平板玻璃砖，试求
经玻璃砖出射光线相对入射光线的侧移量OA 是多
少？
解：设OO 1的长度为L ，侧移量OA 为△x ，折射角为β，据光的折射定律有：n=β
α
sin sin 在三角形△OO 1A 中，△x=Lsin(α-β)=βcos h (sinα cosβ-cosα sinβ)=hsinα-hcosα α
βcos sin =hsinα{1-ααsin 2
2cos -n } 借助上式只要我们用刻度尺测出h 和△x 、和入射角α则可以求出折射率n
小结：三种方法可以在一次数据处理中使用，开阔了学生的眼界，也起到验证作用。

N
1。

实验：测定玻璃的折射率1．实验原理：用插针法找出与入射光线AO对应的出射光线O′B，确定出O′点，画出折射光线OO′，然后测量出角θ1和θ2，代入公式计算玻璃的折射率．2．实验器材：白纸、图钉、大头针、直尺、铅笔、量角器、平木板、长方形玻璃砖．3．实验过程：(1)铺白纸、画线．①如图所示，将白纸用图钉按在平木板上，先在白纸上画出一条直线aa′作为界面，过aa′上的一点O画出界面的法线MN，并画一条线段AO作为入射光线．②把玻璃砖平放在白纸上，使它的长边跟aa′对齐，画出玻璃砖的另一条长边bb′.(2)插针与测量．①在线段AO上竖直地插上两枚大头针P1、P2，透过玻璃砖观察大头针P1、P2的像，调整视线的方向，直到P1的像被P2挡住，再在观察的这一侧依次插两枚大头针P3、P4，使P3挡住P1、P2的像，P4挡住P1、P2的像及P3，记下P3、P4的位置．②移去玻璃砖，连接P3、P4并延长交bb′于O′，连接OO′即为折射光线，入射角θ1＝∠AOM，折射角θ2＝∠O′ON.③用量角器测出入射角和折射角，查出它们的正弦值，将数据填入表格中．④改变入射角θ1，重复实验步骤，列表记录相关测量数据．4．数据处理：计算每次的折射率n，求出平均值n.5．注意事项(1)玻璃砖应选用厚度、宽度较大的．(2)大头针要插得竖直，且间隔要大些．(3)入射角不宜过大或过小，一般在15°～75°之间．(4)玻璃砖的折射面要画准，不能用玻璃砖界面代替直尺画界线．(5)实验过程中，玻璃砖和白纸的相对位置不能改变．1．用三棱镜做测定玻璃折射率的实验，先在白纸上放好三棱镜，在棱镜的一侧插入两枚大头针P1和P2，然后在棱镜的另一侧观察，调整视线使P1的像被P2的像挡住，接着在眼睛所在的一侧插两枚大头针P3、P4，使P3挡住P1、P2的像，P4挡住P3和P1、P2的像，在纸上标出的大头针位置和三棱镜轮廓如图所示．(1)在图上画出所需的光路．(2)为了测出棱镜玻璃的折射率，需要测量的量是__________，在图上标出它们．(3)计算折射率的公式是__________________．解析：(1)如图所示，画出通过P 1、P 2的入射光线，交AC 面于O ，画出通过P 3、P 4的出射光线交AB 面于O ′，则光线OO ′就是入射光线P 1P 2在三棱镜中的折射光线．(2)在所画的图上注明入射角θ1和折射角θ2，并画出虚线部分，用量角器量出θ1和θ2(或用直尺测出线段EF 、OE 、GH 、OG 的长度)．(3)根据折射率的定义可知n ＝sin θ1sin θ2⎝⎛ 或因为sin θ1＝EF OE ， sin θ2＝GH OG ，则n ＝EF OE GH OG ＝⎭⎫EF ·OG OE ·GH . 答案：(1)见解析 (2)θ1和θ2(或线段EF 、OE 、GH 、OG 的长度) (3)n ＝sin θ1sin θ2⎝⎛⎭⎫或n ＝EF ·OG OE ·GH 2．在“测定玻璃的折射率”的实验中，某同学经正确的操作，插好了4枚大头针P 1、P 2和P 3、P 4，如图所示．(1)在坐标线上画出完整的光路图，并标出入射角θ1和折射角θ2.(2)对你画出的光路图进行测量，求出该玻璃的折射率n ＝________(结果保留2位有效数字)．解析：(1)过P 1、P 2作直线与玻璃砖长表面交于O 点，过O 点作长表面的垂线EF ，即为过O 点的法线；过P 3、P 4作直线与玻璃砖短表面交于O ′点，过O ′点作短表面的垂线MN ，即为过O ′点的法线；连接O 、O ′两点；从P 1到P 4在三段线段上依次标出方向．如图所示．(2)根据图可知sin θ1＝222＋22＝22 sin θ2＝112＋1.752＝465 根据折射率公式得n ＝sin θ1sin θ2＝22465＝1308＝1.4 答案：(1)见解析 (2)1.43．(2016·福建晋江联考)在“测定玻璃折射率”的实验中，如图所示为所插四枚大头针的位置，aa ′为事先确定好的玻璃砖的其中一平行边，bb ′为准确操作时应画出的玻璃砖的另一平行边．(1)如果在实验过程中不小心将玻璃砖向上平移了一些，bb ′移到图中虚线①位置，而在作光路图时aa ′不变，则所测得的折射率将________(填“偏大”“偏小”或“不变”)；(2)若所使用的玻璃砖的bb ′边与aa ′不平行(如图虚线②所示)，其他操作无误，则所测得的折射率将________(填“偏大”“偏小”或“不变”)．解析：(1)如果在实验过程中不小心将玻璃砖向上平移了一些，bb ′移到图中虚线①位置，而在作光路图时aa ′不变，作出光路图如图所示，测量得到的入射角没有变化，而折射角偏小，根据折射率公式n＝sin i sin r可知，所测得的折射率将偏大．(2)测折射率时，只要操作正确，与玻璃砖形状无关．所以若所使用的玻璃砖的bb′边与aa′不平行，其他操作无误，则所测得的折射率将不变．答案：(1)偏大(2)不变课时规范训练[基础巩固题组]1．(多选)已知介质对某单色光的临界角为θ，则()A．该介质对此单色光的折射率为1 sin θB．此单色光在该介质中传播速度为c sin θ(c为真空中光速) C．此单色光在该介质中的波长是真空中波长的sin θ倍D．此单色光在该介质中的频率是真空中的1 sin θ解析：选ABC.介质对该单色光的临界角为θ，它的折射率n＝1sin θ，A正确；此单色光在介质中的传播速度v＝cn＝c sin θ，B正确；波长λ＝vf＝c sin θc/λ0＝λ0sin θ，C正确；光的频率是由光源决定的，与介质无关，D错误．2．如图，一束光经玻璃三棱镜折射后分为两束单色光a、b，波长分别为λa、λb，该玻璃对单色光a、b的折射率分别为n a、n b，则()A．λa＜λb，n a＞n bB．λa＞λb，n a＜n bC．λa＜λb，n a＜n bD．λa＞λb，n a＞n b解析：选B.由题图可知，在入射角相同的情况下，光线a的偏折程度小于光线b的偏折程度，因此光线a的折射率小于光线b的折射率，故选项A、D错误；由于折射率越大频率越高，因此光线a的频率小于光线b的频率，由c＝λν可知光线a的波长大于光线b的波长，选项B正确．3．某同学通过实验测定半圆形玻璃砖的折射率n.如图甲所示，O是圆心，MN是法线，AO、BO分别表示某次测量时光线在空气和玻璃砖中的传播路径．该同学测得多组入射角i 和折射角r，作出sin i－sin r图象如图乙所示．则()。

玻璃折射率测定
简介
玻璃折射率（也称为折射系数）是指光线从真空或空气中进入玻璃时的折射程度。

准确测定玻璃折射率对于材料科学和光学应用至关重要。

本文档介绍了一种常用的测定玻璃折射率的实验方法。

实验步骤
1. 准备材料和设备：
- 玻璃样品
- 光源（例如激光器或白光源）
- 精密角度测量仪器
- 直尺和标尺
2. 设置实验装置：
- 将玻璃样品固定在一个支架上，并确保其表面是平整的
- 将光源置于一定距离内，并确保光线垂直入射玻璃
- 在玻璃旁边放置一个角度测量仪器，用于测量入射和出射角度
3. 测量入射和出射角度：
- 将角度测量仪器的指针对准光线的入射和出射点，并记录两者的角度
4. 进行计算：
- 根据测得的入射和出射角度，使用折射率的定义公式计算玻璃的折射率
- 重复以上步骤多次，取平均值以提高准确性
5. 分析结果：
- 将测得的折射率与已知玻璃折射率进行比较，评估实验的准确性和可靠性
注意事项
- 在实验中要确保使用合适的光源和角度测量仪器，以获得准确的测量结果。

- 实验过程中要小心操作，避免损坏玻璃样品或设备。

- 测量过程中要尽量避免外界因素的干扰，如空气湿度和环境温度的变化。

结论
测定玻璃折射率是一项重要的实验，通过使用适当的材料和设备，结合准确的测量方法，可以得出较为准确的结果。

这些实验结果对于光学应用和材料科学具有重要的参考价值。

第96讲 测量玻璃折射率的四种方法与四种实验题型1．（2022•河北）如图，一个半径为R 的玻璃球，O 点为球心。

球面内侧单色点光源S 发出的一束光在A 点射出，出射光线AB 与球直径SC 平行，θ＝30°，光在真空中的传播速度为c 。

求：（ⅰ）玻璃的折射率；（ⅱ）从S 发出的光线经多次全反射回到S 点的最短时间。

【解答】解：（i ）设光线SA 对应的折射角为α，如图1所示；根据几何关系可得，入射角等于θ＝30°，折射角：α＝2θ＝2×30°＝60° 根据折射定律可得：n =sinαsinθ=sin60°sin30°=√3；（ii ）光线沿SA 方向射出时，经过两次反射回到S 点，但不是全反射；要发生全反射，设临界角为C ，则有：sinC =1n =√3√2 所以C ＜45°所以至少经过3次全反射才能够回到S ，如图2所示，这样回到S 的时间最短。

根据运动学公式可得： t =4√2R v=4√6Rc 答：（i ）玻璃的折射率为√3；（ii ）从S 发出的光线经3次全反射回到S 点的最短时间为4√6Rc。

2．（2021•浙江）小明同学在做“测定玻璃的折射率”实验时，发现只有3枚大头针，他把大头针A 、B 、C 插在如图所示位置，并测出了玻璃的折射率。

请在画出光路图，标出入射角i和折射角r，并写出折射率n的计算式。

【解答】解：光路图如图所示：根据折射定律可知：n=sini sinr答：光路图及入射角i和折射角r的标注如上图所示；折射率n的计算式为n=sini sinr。

3．（2021•乙卷）用插针法测量上、下表面平行的玻璃砖的折射率。

实验中用A、B两个大头针确定入射光路，C、D两个大头针确定出射光路，O和O′分别是入射点和出射点。

如图（a）所示。

测得玻璃砖厚度为h＝15.0mm；A到过O点的法线OM的距离AM＝10.0mm，M到玻璃砖的距离MO＝20.0mm，O′到OM的距离为s＝5.0mm。