第三章,湍流模拟

第三章，湍流模型第一节， 前言湍流流动模型很多，但大致可以归纳为以下三类：第一类是湍流输运系数模型，是Boussinesq 于1877年针对二维流动提出的，将速度脉动的二阶关联量表示成平均速度梯度与湍流粘性系数的乘积。

即：2121x u u u t ∂∂=''-μρ 3－1 推广到三维问题，若用笛卡儿张量表示，即有：ij ijj i t j i k x u xu u u δρμρ32-⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=''- 3－2 模型的任务就是给出计算湍流粘性系数t μ的方法。

根据建立模型所需要的微分方程的数目，可以分为零方程模型（代数方程模型），单方程模型和双方程模型。

第二类是抛弃了湍流输运系数的概念，直接建立湍流应力和其它二阶关联量的输运方程。

第三类是大涡模拟。

前两类是以湍流的统计结构为基础，对所有涡旋进行统计平均。

大涡模拟把湍流分成大尺度湍流和小尺度湍流，通过求解三维经过修正的Navier-Stokes 方程，得到大涡旋的运动特性，而对小涡旋运动还采用上述的模型。

实际求解中，选用什么模型要根据具体问题的特点来决定。

选择的一般原则是精度要高，应用简单，节省计算时间，同时也具有通用性。

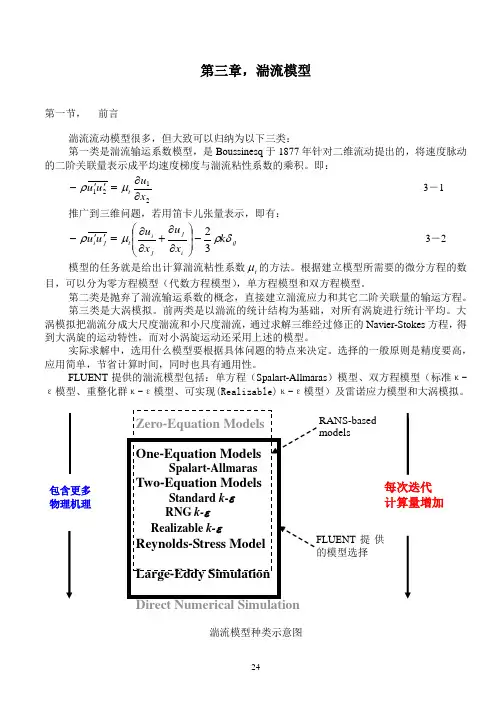
FLUENT 提供的湍流模型包括：单方程（Spalart-Allmaras ）模型、双方程模型（标准κ-ε模型、重整化群κ-ε模型、可实现(Realizable)κ-ε模型）及雷诺应力模型和大涡模拟。

湍流模型种类示意图包含更多 物理机理每次迭代 计算量增加提供RANS-based models第二节，平均量输运方程雷诺平均就是把Navier-Stokes 方程中的瞬时变量分解成平均量和脉动量两部分。

对于速度，有：i i i u u u '+= 3－3其中，i u 和i u '分别是平均速度和脉动速度（i=1,2,3）类似地，对于压力等其它标量，我们也有：φφφ'+= 3－4 其中，φ表示标量，如压力、能量、组分浓度等。

第三章 湍流模型第一节 前言湍流流动模型很多，但大致可以归纳为以下三类：第一类是湍流输运系数模型，是Boussinesq 于1877年针对二维流动提出的，将速度脉动的二阶关联量表示成平均速度梯度与湍流粘性系数的乘积。

即：2121x u u u t ∂∂=''-μρ 3－1 推广到三维问题，若用笛卡儿张量表示，即有：ij ijj i t j i k x u xu u u δρμρ32-⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=''- 3－2 模型的任务就是给出计算湍流粘性系数t μ的方法。

根据建立模型所需要的微分方程的数目，可以分为零方程模型（代数方程模型），单方程模型和双方程模型。

第二类是抛弃了湍流输运系数的概念，直接建立湍流应力和其它二阶关联量的输运方程。

第三类是大涡模拟。

前两类是以湍流的统计结构为基础，对所有涡旋进行统计平均。

大涡模拟把湍流分成大尺度湍流和小尺度湍流，通过求解三维经过修正的Navier-Stokes 方程，得到大涡旋的运动特性，而对小涡旋运动还采用上述的模型。

实际求解中，选用什么模型要根据具体问题的特点来决定。

选择的一般原则是精度要高，应用简单，节省计算时间，同时也具有通用性。

FLUENT 提供的湍流模型包括：单方程（Spalart-Allmaras ）模型、双方程模型（标准κ-ε模型、重整化群κ-ε模型、可实现(Realizable)κ-ε模型）及雷诺应力模型和大涡模拟。

湍流模型种类示意图Direct Numerical Simulation包含更多 物理机理每次迭代 计算量增加提的模型选RANS-based models第二节 平均量输运方程雷诺平均就是把Navier-Stokes 方程中的瞬时变量分解成平均量和脉动量两部分。

对于速度，有：i i i u u u '+= 3－3其中，i u 和i u '分别是平均速度和脉动速度（i=1,2,3）类似地，对于压力等其它标量，我们也有：φφφ'+= 3－4 其中，φ表示标量，如压力、能量、组分浓度等。

湍流模型理论§3.1 引言自然界中的实际流动绝大部分是三维的湍流流动，如河流，血液流动等。

湍流是流体粘性运动最复杂的形式，湍流流动的核心特征是其在物理上近乎于无穷多的尺度和数学上强烈的非线性，这使得人们无论是通过理论分析、实验研究还是计算机模拟来彻底认识湍流都非常困难。

回顾计算流体力学的发展，特别是活跃的80年代，不仅提出和发展了一大批高精度、高分辨率的计算格式，从主控方程看相当成功地解决了Euler方程的数值模拟，可以说Euler方程数值模拟方法的精度已接近于它有效使用范围的极限；同时还发展了一大批有效的网格生成技术及相应的软件，具体实现了工程计算所需要的复杂外形的计算网格；且随着计算机的发展，无论从计算时间还是从计算费用考虑，Euler方程都已能适用于各种实践所需。

在此基础上，80年代还进行了求解可压缩雷诺平均方程及其三维定态粘流流动的模拟。

90年代又开始一个非定常粘流流场模拟的新局面，这里所说的粘流流场具有高雷诺数、非定常、不稳定、剧烈分离流动的特点，显然需要继续探求更高精度的计算方法和更实用可靠的网格生成技术。

但更为重要的关键性的决策将是，研究湍流机理，建立相应的模式，并进行适当的模拟仍是解决湍流问题的重要途径。

要反映湍流流场的真实情况，目前数值模拟主要有三种方法：1.平均N-S方程的求解，2.大涡模拟（LES），3.直接数值模拟（DNS）。

但是由于叶轮机械内部结构的复杂性以及目前计算机运算速度较慢，大涡模拟和直接数值模拟还很少用于叶轮机械内部湍流场的计算，更多的是通过求解平均N-S方程来进行数值模拟。

因为平均N-S方程的不封闭性，人们引入了湍流模型来封闭方程组，所以模拟结果的好坏很大程度上取决于湍流模型的准确度。

自70年代以来，湍流模型的研究发展迅速，建立了一系列的零方程、一方程、两方程模型和二阶矩模型，已经能够十分成功的模拟边界层和剪切层流动。

但是，对于复杂的工业流动，比如航空发动机中的压气机动静叶相互干扰问题，大曲率绕流，激波与边界层相互干扰，流动分离，高速旋转以及其他一些原因，常常会改变湍流的结构，使那些能够预测简单流动的湍流模型失效，所以完善现有湍流模型和寻找新的湍流模型在实际工作中显得尤为重要。

第三章内燃机缸内流动高等内燃机学北京理工大学内燃机缸内流动⏹四缸内湍流流动的数学模型⏹1雷诺方程与湍流粘性系数⏹2湍流粘性系数方程⏹3单方成模型——湍能的k方程模型⏹4双方成模型——k-ε模型⏹5雷诺应力模型⏹6代数应力模型⏹7非粘性涡粘度模型，等湍流是一种连续介质的流动形态动力学的基本方程雷诺应力雷诺方程增加了脉动速度相关矩：它是一个二阶张量。

反映的是雷诺应力对动量输运功能与粘性应力类似。

参照牛顿内摩擦定律，湍流研究方法——基于现象湍流模拟方法分类由分子运动论：μ=1/3*ρυℓ其中：υ—分子热运动的均方根速度；ℓ—平均自由行程。

仿照上述关系式：μt=Cμρυtℓt其中：υt 、ℓt—湍流涡团的某一速度尺度和长度尺度。

2湍流粘性系数方程υt—通常取为表征湍流脉动强弱的湍流度u’,由于u’正比于湍能k的平方根，故上式可表示为：μt=Cμρk1/2ℓt(1)混合长度理论—普朗特Prandtl （1925）ℓt 视为与分子自由程相似的涡团自由程——混合长度ℓm 。

表示湍流涡团在随机运动中能保持自由前进而不与其它涡团相撞的距离（并不符合物理真实），并认为速度尺度：υt =ℓm |∂U/∂y| μt ≡C μρυt ℓt ~ρℓm 2|∂U/∂y|——人为定义 雷诺应力：τij =μt ∂U/∂y=ρℓm 2|∂U/∂y|∂U/∂y 如何确定混合长度ℓm ？一般需要根据具体问题做出假定。

对于沿光滑壁面的湍流，普朗特提出，混合长度与壁面距离成正比（壁面湍流），即：比例系数由试验定。

ℓm =ky(1)混合长度理论——应用混合长度理论是最早的湍流理论之一。

由于简单，在工程上应用广泛。

但该理论来自于分子运动相比拟，两者机理完全不同，理论上根据不足。

如：∂U/∂y=0，则μ=0，t也不合理。

混合长度理论在内燃机缸内湍流计算中应用不多。

在多维模型发展的较早阶段曾用它计算内燃机中的气体燃料射流与空气的混合。

采用了二维形式的混合长度公式：=αρ|∂U/∂x+∂V/∂z|（Δx）2μt相当于将网格间距Δx取为混合长度。

第三章，湍流模型第一节， 前言湍流流动模型很多，但大致可以归纳为以下三类：第一类是湍流输运系数模型，是Boussinesq 于1877年针对二维流动提出的，将速度脉动的二阶关联量表示成平均速度梯度与湍流粘性系数的乘积。

即：2121x u u u t ∂∂=''-μρ 3－1 推广到三维问题，若用笛卡儿张量表示，即有：ij ijj i t j i k x u xu u u δρμρ32-⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=''- 3－2 模型的任务就是给出计算湍流粘性系数t μ的方法。

根据建立模型所需要的微分方程的数目，可以分为零方程模型（代数方程模型），单方程模型和双方程模型。

第二类是抛弃了湍流输运系数的概念，直接建立湍流应力和其它二阶关联量的输运方程。

第三类是大涡模拟。

前两类是以湍流的统计结构为基础，对所有涡旋进行统计平均。

大涡模拟把湍流分成大尺度湍流和小尺度湍流，通过求解三维经过修正的Navier-Stokes 方程，得到大涡旋的运动特性，而对小涡旋运动还采用上述的模型。

实际求解中，选用什么模型要根据具体问题的特点来决定。

选择的一般原则是精度要高，应用简单，节省计算时间，同时也具有通用性。

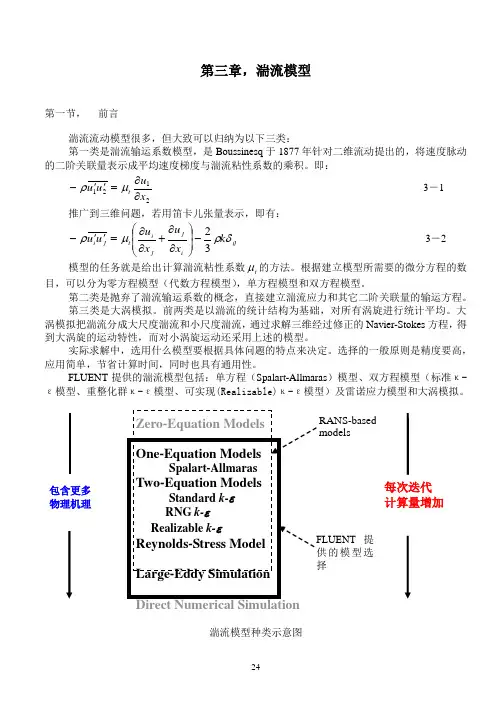
FLUENT 提供的湍流模型包括：单方程（Spalart-Allmaras ）模型、双方程模型（标准κ-ε模型、重整化群κ-ε模型、可实现(Realizable)κ-ε模型）及雷诺应力模型和大涡模拟。

湍流模型种类示意图包含更多 物理机理每次迭代 计算量增加提的模型选RANS-based models第二节，平均量输运方程雷诺平均就是把Navier-Stokes 方程中的瞬时变量分解成平均量和脉动量两部分。

对于速度，有：i i i u u u '+= 3－3其中，i u 和i u '分别是平均速度和脉动速度（i=1,2,3）类似地，对于压力等其它标量，我们也有：φφφ'+= 3－4 其中，φ表示标量，如压力、能量、组分浓度等。

空气动力学中的湍流模拟与优化湍流模拟与优化在空气动力学研究中扮演着重要的角色。

湍流是一种复杂的气体或流体运动形态，其产生源于速度分布的不稳定性。

而在空气动力学中，湍流的存在不仅会增加空气阻力，还会对飞行器的稳定性和控制性能产生重要影响。

因此，优化湍流模拟的方法对于提高飞行器性能至关重要。

在湍流模拟中，最常用的方法是使用计算流体力学（CFD）软件。

CFD软件通过求解流场的连续性方程和Navier-Stokes方程，可以模拟流体在各种条件下的运动。

然而，湍流模拟的计算量巨大，需要大量的计算资源和时间。

为了提高模拟效率和精度，研究人员不断探索新的算法和优化方法。

一种常用的优化方法是粗网格模拟结合壁面函数。

在湍流模拟中，通常使用网格划分技术将连续的流场离散成有限个小单元。

然而，细网格模拟往往过于耗时，而粗网格模拟则无法准确捕捉湍流的细节。

为了权衡模拟效率和精度，研究人员提出了粗网格模拟结合壁面函数的方法。

该方法通过在壁面附近引入特殊的边界条件来修正湍流模拟的误差，从而在保证模拟效率的同时提高模拟精度。

另一个优化湍流模拟的方法是使用湍流模型。

湍流模型是对湍流现象的统计描述，能够在减少计算量的同时保持较高的模拟精度。

目前，最常用的湍流模型是雷诺平均Navier-Stokes方程（RANS）模型。

RANS模型通过将流场变量分解为平均分量和脉动分量，并假设脉动分量服从某种统计规律，从而简化湍流模拟的计算。

此外，还有基于大涡模拟（LES）的湍流模型，它通过直接模拟大尺度湍流结构，忽略小尺度湍流结构的影响，从而减少计算量。

除了优化湍流模拟方法，研究人员还在探索湍流优化的方法。

湍流优化是通过改变流场的结构和特性，来减少湍流对飞行器的负面影响。

其中一种常用的湍流优化方法是使用被动流控技术。

被动流控技术通过在飞行器表面引入特殊的几何形状或纹理，可以改变流场的湍流特性，从而减少湍流阻力和噪声。

此外，还有主动流控技术，它通过在飞行器表面布置特殊的传感器和执行机构，来实时感知和调控湍流的运动，从而减少湍流产生和传播。

第三章 湍流模型第一节 前言湍流流动模型很多，但大致可以归纳为以下三类：第一类是湍流输运系数模型，是Boussinesq 于1877年针对二维流动提出的，将速度脉动的二阶关联量表示成平均速度梯度与湍流粘性系数的乘积。

即：2121x u u u t ∂∂=''-μρ 3－1 推广到三维问题，若用笛卡儿张量（笛卡尔坐标系）表示，即有：ij i j j i t j i k x u x u u u δρμρ32-⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=''- 3－2 ij δ为DELT 函数，一般i=j 时为1，否则为0.模型的任务就是给出计算湍流粘性系数t μ的方法。

根据建立模型所需要的微分方程的数目，可以分为零方程模型（代数方程模型），单方程模型和双方程模型。

（模拟大空间建筑空气流动）μt=0.038 74ρvl （模拟通风空调室内的空气流动）比例系数由直接数值模拟的结果拟合而得，其中：v 为当地时均速度，l 为当地距壁面最近的距离。

第二类是抛弃了湍流输运系数的概念，直接建立湍流应力和其它二阶关联量的输运方程。

第三类是大涡模拟。

前两类是以湍流的统计结构为基础，对所有涡旋进行统计平均。

大涡模拟把湍流分成大尺度湍流和小尺度湍流，通过求解三维经过修正的Navier-Stokes 方程，得到大涡旋的运动特性，而对小涡旋运动还采用上述的模型。

实际求解中，选用什么模型要根据具体问题的特点来决定。

选择的一般原则是精度要高，应用简单，节省计算时间，同时也具有通用性。

参见：湍流模型的选择资料。

FLUENT 提供的湍流模型包括：单方程（Spalart-Allmaras ）模型、双方程模型（标准κ-ε模型、重整化群κ-ε模型、可实现(Realizable)κ-ε模型）及雷诺应力模型和大涡模拟。

湍流模型种类示意图大涡模拟启动需要用命令：(rpsetvar 'les-2d? #t)Direct Numerical Simulation包含更多物理机理 每次迭代计算量增加 提的模型选RANS-based models第二节 平均量输运方程输运过程的粘滞系数、扩散系数和热传导率，故称为输运方程雷诺平均就是把Navier-Stokes 方程中的瞬时变量分解成平均量和脉动量两部分。

流体流动中的湍流模拟计算引言湍流是一种复杂的流体流动形态，其特点是流速和压力具有随机的瞬时和空间变化。

湍流的研究对于很多工程领域都具有重要意义，如飞行器设计、能源开发、天气预报等。

然而，湍流的数学模型十分复杂，难以直接求解。

因此，湍流的模拟计算成为一种重要的研究方法。

湍流模拟计算通过数值方法来模拟和预测湍流流动的行为。

目前主要有两种湍流模拟计算方法：直接数值模拟（DNS）和雷诺平均纳维-斯托克斯方程（RANS）模拟。

直接数值模拟（DNS）直接数值模拟是一种基于纳维-斯托克斯方程的数值模拟方法，它通过对流体流动中的连续性方程和动量方程进行离散化处理，得到一组离散的方程组，并使用数值方法进行求解。

直接数值模拟的核心思想是将流体流动中的每个小尺度的涡旋都考虑进去，从而能够准确地描述湍流的演化过程。

直接数值模拟的优点是能够提供非常精确的湍流解，并且不需要对湍流进行统计平均。

然而，由于湍流中涡旋尺度非常小而且非常多，所以直接数值模拟对计算资源的要求非常高，通常只能用于小规模的流动问题。

雷诺平均纳维-斯托克斯方程（RANS）模拟雷诺平均纳维-斯托克斯方程模拟是一种更为常用的湍流模拟方法。

该方法基于雷诺分解理论，将流体流动分解为平均流动和脉动流动两部分。

平均流动部分可以通过求解平均纳维-斯托克斯方程来得到，而脉动流动则通过引入湍流模型来描述。

湍流模型是湍流计算的关键。

目前常用的湍流模型有雷诺应力模型、k-ε模型、k-ω模型等。

这些模型通过对湍流的统计特性进行建模，来模拟湍流中的能量转换和动量传输过程。

虽然湍流模型相对于直接数值模拟来说计算代价较低，但由于模型本身的限制，其模拟结果通常无法捕捉到湍流的全部信息。

湍流模拟计算的应用湍流模拟计算在多个工程领域有着广泛的应用。

航空航天领域在航空航天领域，湍流模拟计算可以用来预测飞机翼面的湍流分布，优化气动外形设计，减小飞机的阻力和气动噪声。

此外，湍流模拟计算还可以用于预测飞机在起飞和着陆过程中的湍流扰动，从而提高飞机的稳定性和安全性。

湍流模拟与计算机模拟方法湍流是自然界中普遍存在的一种现象，它广泛存在于大气、海洋、河流、湖泊等自然环境中。

湍流的产生是由于流体运动中各种因素的不规则性，它会对自然界的物理、化学、生物等过程产生影响，同时也对工程建设、交通运输等方面带来影响。

因此，对湍流进行模拟和计算具有重要的意义。

湍流模拟是通过数学模型和计算机模拟方法对湍流进行预测和分析的过程，通过模拟可以更好地理解和研究湍流的规律性，从而为工程建设和科学研究提供指导和支持。

湍流模拟方法湍流模拟主要包括实验模拟和计算机模拟两种方法。

实验模拟是通过建立实验室模型，对湍流进行直接观测和测量，从而获得湍流的物理参数和特征。

计算机模拟是通过计算流体力学（CFD）等模型对湍流进行数字模拟，从而获得湍流的流场、速度、压力等物理参数和特征。

实验模拟在实验模拟中，主要采用的是流体力学实验技术，通过设计实验设备和实验场地，模拟湍流流动的物理环境，并通过数学方法对湍流进行测量和分析。

实验模拟方法具有直观性和真实性的优点，能够直接观察和测量湍流的物理特征，同时也可以用于验证计算机模拟方法的可靠性。

计算机模拟计算机模拟是通过数值计算和计算流体力学模型对湍流进行精细计算，从而获得湍流的流场、速度、压力等物理参数和特征。

计算机模拟方法具有高效性和精确性的优点，能够对湍流的细节和复杂性进行深入的分析和研究。

在计算机模拟中，目前常用的是基于雷诺平均N-S方程的湍流模型。

该模型通过将流场分解为平均流和湍流流动两部分，利用一定的近似方法，将湍流的影响作为一种粘度效应加入到平均流中，从而模拟湍流流动的效应。

该模型具有较高的准确性和广泛的适用范围，已经成为目前计算机模拟中最常用的湍流模拟方法之一。

湍流模拟应用湍流模拟在涉及到流体运动的许多工程领域中有着广泛的应用。

例如在能源、空气动力学、航空航天、水利、海洋、土建工程、自动化控制、医学等领域中，湍流模拟都有着重要的应用价值。

其中，为了提高燃烧效率和减少污染物排放，在能源工程中湍流模拟应用尤为重要。

机械流体力学中的湍流模拟与优化方法机械流体力学是研究流体力学与机械工程的交叉学科，主要研究流体在机械设备中的力学行为。

在机械流体力学中，湍流是一个非常重要的现象。

湍流是指流体在运动中产生的混乱、不规则的流动状态，具有突变、扩散、涡旋等特点。

湍流往往是由于流体的运动速度大、涡量强、流动过程不稳定等因素导致的。

湍流的出现会增加流体力学系统的阻力，降低效率，甚至影响设备的安全和稳定运行。

因此，研究湍流的形成机理、预测湍流的行为以及优化湍流对于机械流体力学领域具有重要的意义。

湍流模拟是研究湍流行为最常用的方法之一。

湍流模拟通过数学建模与计算机仿真的方法，对湍流的流动过程进行模拟与预测。

在湍流模拟中，常用的方法有直接数值模拟(Direct Numerical Simulation, DNS)、大涡模拟(Large Eddy Simulation, LES)和雷诺平均纳维-斯托克斯方程(RANS)模拟等。

其中，DNS模拟是最为直接和精确的湍流模拟方法之一，可以在计算中精确解决湍流运动的所有尺度。

然而，由于湍流的尺度范围很大，包含着从毫米到千米的尺度，因此DNS模拟需要处理的自由度很高，对计算资源要求很大，不适用于大规模的工程计算。

而对于工程应用而言，LES模拟是一种较为合适的湍流模拟方法。

LES模拟采用了大涡模拟 (Large Eddy Simulation)的思想，通过将湍流中的大尺度涡旋直接模拟，而将小尺度的湍流在计算中进行模型化处理。

这样既解决了湍流中大尺度特征的建模问题，也减小了计算量。

LES模拟在许多领域中得到了广泛的应用，如风力发电机的空气动力学设计、飞行器的气动特性研究等。

除了湍流模拟，湍流优化也是机械流体力学中的重要研究内容之一。

湍流优化旨在通过改变流动结构、优化控制参数等方式，减小湍流对设备性能的负面影响，提高工程系统的效率。

湍流优化方法可以通过数值模拟和实验研究相结合的方式进行，如基于数值模拟得到的湍流特征进行优化设计，或者通过实验观测湍流改善的效果。

第三章湍流模型湍流模型第一节前言湍流流动模型很多，但大致可以归纳为以下三类：第一类是湍流输运系数模型，是Boussinesq于1877年针对二维流动提出的，将速度脉动的二阶关联量表示成平均速度梯度与湍流粘性系数的乘积。

即：3－1 推广到三维问题，若用笛卡儿张量（笛卡尔坐标系）表示，即有：3－2 为DELT函数，一般i=j时为1，否则为0. 模型的任务就是给出计算湍流粘性系数的方法。

根据建立模型所需要的微分方程的数目，可以分为零方程模型（代数方程模型），单方程模型和双方程模型。

（模拟大空间建筑空气流动）μt=0.038 74ρvl （模拟通风空调室内的空气流动）比例系数由直接数值模拟的结果拟合而得，其中：v为当地时均速度，l为当地距壁面最近的距离。

第二类是抛弃了湍流输运系数的概念，直接建立湍流应力和其它二阶关联量的输运方程。

第三类是大涡模拟。

前两类是以湍流的统计结构为基础，对所有涡旋进行统计平均。

大涡模拟把湍流分成大尺度湍流和小尺度湍流，通过求解三维经过修正的Navier-Stokes方程，得到大涡旋的运动特性，而对小涡旋运动还采用上述的模型。

实际求解中，选用什么模型要根据具体问题的特点来决定。

选择的一般原则是精度要高，应用简单，节省计算时间，同时也具有通用性。

参见：湍流模型的选择资料。

FLUENT提供的湍流模型包括：单方程（Spalart-Allmaras）模型、双方程模型（标准κ-ε模型、重整化群κ-ε模型、可实现(Realizable)κ-ε模型）及雷诺应力模型和大涡模拟。

Zero-Equation Models One-Equation Models Spalart-Allmaras Two-Equation Models Standard k-e RNG k-e Realizable k-e Reynolds-Stress Model Large-Eddy Simulation Direct Numerical Simulation 包含更多物理机理每次迭代计算量增加FLUENT提供的模型选择RANS-based models 湍流模型种类示意图大涡模拟启动需要用命令：(rpsetvar ＇les-2d? #t) 第二节平均量输运方程输运过程的粘滞系数、扩散系数和热传导率，故称为输运方程雷诺平均就是把Navier-Stokes方程中的瞬时变量分解成平均量和脉动量两部分。

3
层流区
过渡区
湍湍流某特定点的实测速度
实测风速
惯性子区
耗散区
湍流运动可以看作是能量由低频脉动向高频脉动过渡，并最终被流体粘性所耗散的过程。

4.3 湍流的数值模拟方法简介
14
•大涡模拟方法(LES):用瞬时湍流控制方程直接模拟湍流中的大尺度涡，不直接模拟小尺度涡，而小涡
•Reynolds平均法(RANS):不直接求解瞬时的N-S方程，而是想办法求解时均化的Reynolds方程。

湍动粘度湍动能
湍动粘度是空间坐标的函数，取决于流动状态，而不是物理参数，下标t表示湍流流动。

湍动粘度可以表示成湍动能和湍流耗散率的函数：
在该湍流模型中，湍动能和湍流耗散率是两个基本未知量，可以列出相应的输运方程。

壁面区3个子层的划分与相应的速度
求解壁面区流动的两种途径所对应的计算网格
42
☆LES方法控制方程中，滤波后的N-S方程与RANS 程在形式上类似，区别在于这里的变量是滤波后的值，仍是瞬时值，而非是均值。

同时湍流应力的表达。