霍尔效应数据处理表格

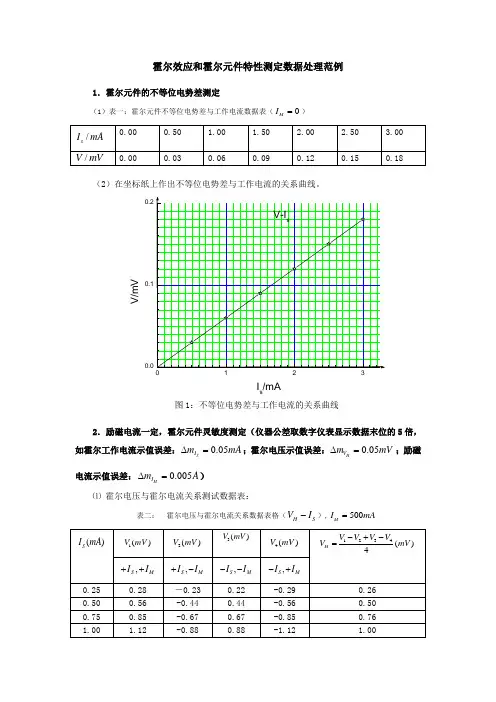
霍尔效应和霍尔元件特性测定数据处理范例1．霍尔元件的不等位电势差测定（1）表一：霍尔元件不等位电势差与工作电流数据表（0MI =）（2）在坐标纸上作出不等位电势差与工作电流的关系曲线。

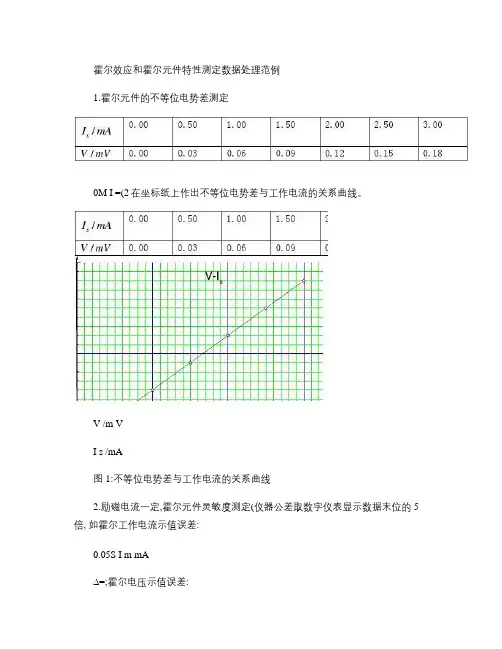
V /m VI s /mA图1：不等位电势差与工作电流的关系曲线2．励磁电流一定，霍尔元件灵敏度测定（仪器公差取数字仪表显示数据末位的5倍，如霍尔工作电流示值误差：0.05S I m mA ∆=；霍尔电压示值误差：0.05H V m mV ∆=；励磁电流示值误差：0.005M I m A ∆=）⑴ 霍尔电压与霍尔电流关系测试数据表：表二： 霍尔电压与霍尔电流关系数据表格（HS V I -）,500M I mA =⑵ 利用逐差法计算霍尔元件灵敏度及其不确定度（0.683p =）。

H HH S S V V KI B I B∆==∆⋅ a ）利用逐差法计算H V ∆的平均值及不确定度估算（该部分逐差法计算可用数据处理软件的逐差法进行计算）7182931041151261.750.26 1.49, 2.010.50 1.51,2.260.76 1.50, 2.51 1.00 1.51,2.76 1.26 1.50, 3.01 1.50 1.51H H H H H H H H H H H H V V mV V V mV V V mV V V mV V V mV V V mV-=-=-=-=-=-=-=-=-=-=-=-= 1.50H V mV ∆=某次测量的标准偏差：0.0082H V S mV ∆=，平均值的标准偏差：0.0033HV S mV ∆=肖维涅系数6 1.73n c c ==， 1.730.00820.014186H n V c S mV ∆*=*= 根据肖维涅准则（坏值条件：*i HH H n V V V c S ∆∆-∆>）检验无坏值出现。

H V ∆不确定度估算：1.110.00330.0037HA vp V u t S mV ∆==⨯=, （0.683p =）0.029B pu k mV ∆=== （0.683p =） 0.029H V u mV ∆===0.0290.01931.50H H V V Hu E V ∆∆===∆ b ）S I ∆的不确定度估算（该部分计算也可用数据处理软件的逐差法进行计算）1.50S I mA ∆=0.029S pu k mA I ∆=== （0.683p =） 0.0290.01931.50S S I I Su E I ===∆ （0.683p =） c ）磁感应强度B 及其不确定度的计算螺线管参数：线圈匝数N=1800匝，有效长度2L ＝181mm ，等效半径R ＝21mm18002181N n L mm== ()()01/21/2222201/21/2222201/222721/22232222410/18000.50020.02100.09056.08710M M Mu nI x L x L B R x L R x L u N I L L L R L R L u N I R L N A AmTπ--⎛⎫+- ⎪=- ⎪⎡⎤⎡⎤ ⎪+++-⎣⎦⎣⎦⎝⎭⎛⎫- ⎪=- ⎪⨯⎡⎤⎡⎤++⎣⎦⎣⎦⎝⎭=⎡⎤⨯+⎣⎦⨯⨯⨯=⎡⎤⨯+⎣⎦=⨯0.0029M I pu k A ∆=== （0.683p =） 0.00290.00580.500M M I B I Mu E E I ==== （0.683p =）d ）霍尔元件灵敏度的计算31.50164/1.50 6.08710H H H S S V V mVK mV mA T mA TI B I B -∆====⋅⨯⨯∆100%100% 2.7%H K E ===0.0271645/H H K K H u E K mV mA T =⨯=⨯=⋅所以霍尔元件的灵敏度为：()1645/H K mV mA T =±⋅,(0.683p =) 2.7%H K E =3．霍尔工作电流一定，励磁电流与霍尔电压关系测试⑴ 表三：霍尔电压与励磁电流关系测试数据表格(H M V I -)，3s I mA =⑵ 用坐标纸绘制H M V I -关系曲线.0100200300400500123V H /m VI M /mA图2：H M V I -关系曲线（H M V I -关系曲线，横坐标每格10mA ，纵坐标每格0.1mV ）⑶ 用图解法确定霍尔元件的灵敏度及不确定度（0.683p =）。

TH-H型霍尔效应实验组合仪霍尔效应及其应用置于磁场中的载流体，如果电流方向与磁场垂直，则在垂直于电流和磁场的方向会产生一附加的横向电场，这个现象是霍普斯金大学研究生霍尔于1879年发现的，后被称为霍尔效应。

随着半导体物理学的迅速发展，霍尔系数和电导率的测量已成为研究半导体材料的主要方法之一。

通过实验测量半导体材料的霍尔系数和电导率可以判断材料的导电类型、载流子浓度、载流子迁移率等主要参数。

若能测量霍尔系数和电导率随温度变化的关系，还可以求出半导体材料的杂质电离能和材料的禁带宽度。

如今，霍尔效应不但是测定半导体材料电学参数的主要手段，而且随着电子技术的发展，利用该效应制成的霍尔器件，由于结构简单、频率响应宽（高达10GHz）、寿命长、可靠性高等优点，已广泛用于非电量测量、自动控制和信息处理等方面。

在工业生产要求自动检测和控制的今天，作为敏感元件之一的霍尔器件，将有更广阔的应用前景。

了解这一富有实用性的实验，对日后的工作将有益处。

一、实验目的1．了解霍尔效应实验原理以及有关霍尔元件对材料要求的知识。

2．学习用“对称测量法”消除副效应的影响，测量并绘制试样的V H－I S和V H－I M曲线。

TH-H 型霍尔效应实验组合仪3．确定试样的导电类型、载流子浓度以及迁移率。

二、实验原理霍尔效应从本质上讲是运动的带电粒子在磁场中受洛仑兹力作用而引起的偏转。

当带电粒子（电子或空穴）被约束在固体材料中，这种偏转就导致在垂直电流和磁场的方向上产生正负电荷的聚积，从而形成附加的横向电场，即霍尔电场。

对于图（1）（a ）所示的N 型半导体试样，若在X 方向的电极D 、E 上通以电流Is ，在Z 方向加磁场B ，试样中载流子（电子）将受洛仑兹力： （1）其中e 为载流子（电子）电量， 为载流子在电流方向上的平均定向漂移速率，B 为磁感应强度。

B v g e F VTH-H 型霍尔效应实验组合仪（N型） 0 (Y)E （P型）0 (Y)E H H (X)、B（Z） Is <>（a ） （b ）图(1) 样品示意图无论载流子是正电荷还是负电荷，F g 的方向均沿Y 方向，在此力的作用下，载流子发生便移，则在Y 方向即试样A 、A ´电极两侧就开始聚积异号电荷而在试样A 、A ´两侧产生一个电位差V H ，形成相应的附加电场E —霍尔电场，相应的电压V H 称为霍尔电压，电极A 、A ´称为霍尔电极。

TH-H型霍尔效应实验组合仪霍尔效应及其应用置于磁场中的载流体，如果电流方向与磁场垂直，则在垂直于电流和磁场的方向会产生一附加的横向电场，这个现象是霍普斯金大学研究生霍尔于1879年収现的，后被称为霍尔效应。

随着半导体物理学的迅速収展，霍尔系数和电导率的测量已成为研究半导体材料的主要方法之一。

通过实验测量半导体材料的霍尔系数和电导率可以判断材料的导电类型、载流子浓度、载流子迁移率等主要参数。

若能测量霍尔系数和电导率随温度变化的关系，还可以求出半导体材料的杂质电离能和材料的禁带宽度。

如今，霍尔效应不但是测定半导体材料电学参数的主要手段，而且随着电子技术的収展，利用该效应制成的霍尔器件，由于结构简单、频率响应宽（高达10GHz）、寿命长、可靠性高等优点，已广泛用于非电量测量、自动控制和信息处理等方面。

在工业生产要求自动检测和控制的今天，作为敏感元件之一的霍尔器件，将有更广阔的应用前景。

了解这一富有实用性的实验，对日后的工作将有益处。

一、实验目的1．了解霍尔效应实验原理以及有关霍尔元件对材料要求的知识。

2．学习用“对称测量法”消除副效应的影响，测量幵绘制试样的V H－I S和V H－I M曲线。

3．确定试样的导电类型、载流子浓度以及迁移率。

二、实验原理TH-H 型霍尔效应实验组合仪霍尔效应从本质上讲是运动的带电粒子在磁场中受洛仑兹力作用而引起的偏转。

当带电粒子（电子或空穴）被约束在固体材料中，这种偏转就导致在垂直电流和磁场的方向上产生正负电荷的聚积，从而形成附加的横向电场，即霍尔电场。

对于图（1）（a ）所示的N 型半导体试样，若在X 方向的电极D 、E 上通以电流Is ，在Z 方向加磁场B ，试样中载流子（电子）将受洛仑兹力： （1）其中e 为载流子（电子）电量， 为载流子在电流方向上的平均定向漂移速率，B 为磁感应强度。

（a ） （b ）图(1) 样品示意图B vge F VTH-H 型霍尔效应实验组合仪（N型） 0 (Y)E （P型）0 (Y)E H H(X)、B（Z） Is <>无论载流子是正电荷还是负电荷，F g 的方向均沿Y 方向，在此力的作用下，载流子収生便移，则在Y 方向即试样A 、A ´电极两侧就开始聚积异号电荷而在试样A 、A ´两侧产生一个电位差V H ，形成相应的附加电场E —霍尔电场，相应的电压V H 称为霍尔电压，电极A 、A ´称为霍尔电极。

霍尔效应和霍尔元件特性测定数据处理范例1．霍尔元件的不等位电势差测定（1）表一：霍尔元件不等位电势差与工作电流数据表（0MI =）（2）在坐标纸上作出不等位电势差与工作电流的关系曲线。

V /m VI s /mA图1：不等位电势差与工作电流的关系曲线2．励磁电流一定，霍尔元件灵敏度测定（仪器公差取数字仪表显示数据末位的5倍，如霍尔工作电流示值误差：0.05S I m mA ∆=；霍尔电压示值误差：0.05H V m mV ∆=；励磁电流示值误差：0.005M I m A ∆=）⑴ 霍尔电压与霍尔电流关系测试数据表：表二： 霍尔电压与霍尔电流关系数据表格（HS V I -）,500M I mA =⑵ 利用逐差法计算霍尔元件灵敏度及其不确定度（0.683p =）。

H HH S S V V KI B I B∆==∆⋅ a ）利用逐差法计算H V ∆的平均值及不确定度估算（该部分逐差法计算可用数据处理软件的逐差法进行计算）7182931041151261.750.26 1.49, 2.010.50 1.51,2.260.76 1.50, 2.51 1.00 1.51,2.76 1.26 1.50, 3.01 1.50 1.51H H H H H H H H H H H H V V mV V V mV V V mV V V mV V V mV V V mV-=-=-=-=-=-=-=-=-=-=-=-= 1.50H V mV ∆=某次测量的标准偏差：0.0082H V S mV ∆=，平均值的标准偏差：0.0033HV S mV ∆=肖维涅系数6 1.73n c c ==， 1.730.00820.014186H n V c S mV ∆*=*= 根据肖维涅准则（坏值条件：*i HH H n V V V c S ∆∆-∆>）检验无坏值出现。

H V ∆不确定度估算：1.110.00330.0037HA vp V u t S mV ∆==⨯=, （0.683p =）0.029B pu k mV ∆=== （0.683p =） 0.029H V u mV ∆===0.0290.01931.50H H V V Hu E V ∆∆===∆ b ）S I ∆的不确定度估算（该部分计算也可用数据处理软件的逐差法进行计算）1.50S I mA ∆=0.029S pu k mA I ∆=== （0.683p =） 0.0290.01931.50S S I I Su E I ===∆ （0.683p =） c ）磁感应强度B 及其不确定度的计算螺线管参数：线圈匝数N=1800匝，有效长度2L ＝181mm ，等效半径R ＝21mm18002181N n L mm== ()()01/21/2222201/21/2222201/222721/22232222410/18000.50020.02100.09056.08710M M Mu nI x L x L B R x L R x L u N I L L L R L R L u N I R L N A AmTπ--⎛⎫+- ⎪=- ⎪⎡⎤⎡⎤ ⎪+++-⎣⎦⎣⎦⎝⎭⎛⎫- ⎪=- ⎪⨯⎡⎤⎡⎤++⎣⎦⎣⎦⎝⎭=⎡⎤⨯+⎣⎦⨯⨯⨯=⎡⎤⨯+⎣⎦=⨯0.0029M I pu k A ∆=== （0.683p =） 0.00290.00580.500M M I B I Mu E E I ==== （0.683p =）d ）霍尔元件灵敏度的计算31.50164/1.50 6.08710H H H S S V V mVK mV mA T mA TI B I B -∆====⋅⨯⨯∆100%100% 2.7%H K E ===0.0271645/H H K K H u E K mV mA T =⨯=⨯=⋅所以霍尔元件的灵敏度为：()1645/H K mV mA T =±⋅,(0.683p =) 2.7%H K E =3．霍尔工作电流一定，励磁电流与霍尔电压关系测试⑴ 表三：霍尔电压与励磁电流关系测试数据表格(H M V I -)，3s I mA =⑵ 用坐标纸绘制H M V I -关系曲线.0100200300400500123V H /m VI M /mA图2：H M V I -关系曲线（H M V I -关系曲线，横坐标每格10mA ，纵坐标每格0.1mV ）⑶ 用图解法确定霍尔元件的灵敏度及不确定度（0.683p =）。