测量中的坐标系及其

测量中的常用坐标系及坐标转换概述在测量领域中，常用的坐标系包括直角坐标系、极坐标系和球坐标系。

不同的坐标系适用于不同的测量任务和数据处理需求，而坐标转换则是将不同坐标系下的测量数据相互转换的方法。

本文将对常用坐标系及坐标转换进行概述。

1.直角坐标系直角坐标系是最常见的坐标系之一，通常用于描述二维或三维空间中的点的位置。

在二维直角坐标系中，一个点的位置可以由两个坐标值(x,y)表示。

而在三维直角坐标系中，一个点的位置可以由三个坐标值(x,y,z)表示。

直角坐标系中的坐标轴是相互垂直的，可以方便地描述点的位置和进行测量。

2.极坐标系极坐标系是另一种常用的坐标系，通常用于描述平面上的点的位置。

极坐标系由一个极径和一个极角组成。

极径表示点到原点的距离，极角表示点与正x轴的夹角。

在极坐标系中，一个点的位置可以由(r,θ)表示。

极坐标系在一些特定情况下对测量任务更加方便，例如描述圆形或对称物体的位置。

3.球坐标系球坐标系用于描述三维空间中的点的位置。

球坐标系由一个极径、一个极角和一个方位角组成。

极径表示点到原点的距离，极角表示点与正z轴的夹角，方位角表示点在xy平面上的投影与正x轴的夹角。

在球坐标系中，一个点的位置可以由(r, θ, φ)表示。

球坐标系在描述球体或对称物体的位置时非常有用。

在测量中，常常需要在不同的坐标系之间进行转换以满足不同的需求。

以下是常见的坐标转换方法：1.直角坐标系到极坐标系的转换从直角坐标系到极坐标系的转换可以通过以下公式实现：极径 r = sqrt(x^2 + y^2)极角θ = atan2(y, x)其中，sqrt表示平方根，atan2表示求反正切值。

2.极坐标系到直角坐标系的转换从极坐标系到直角坐标系的转换可以通过以下公式实现：x = r * cos(θ)y = r * sin(θ)3.直角坐标系到球坐标系的转换从直角坐标系到球坐标系的转换可以通过以下公式实现：极径 r = sqrt(x^2 + y^2 + z^2)极角θ = acos(z / r)方位角φ = atan2(y, x)4.球坐标系到直角坐标系的转换从球坐标系到直角坐标系的转换可以通过以下公式实现：x = r * sin(θ) * cos(φ)y = r * sin(θ) * sin(φ)z = r * cos(θ)需要注意的是，在进行坐标转换时，要确保所使用的公式和单位系统是一致的，否则会导致转换结果错误。

测绘技术中的测绘坐标系介绍导语：在测绘技术中，测绘坐标系是一个重要的概念。

它是测量和记录地理位置信息的基础，并用于地图制作、地理信息系统和其他应用领域。

本文将介绍测绘坐标系的概念、类型以及其在实际应用中的重要性。

一、测绘坐标系的概念测绘坐标系是一种数学工具，用于描述和表示地球表面上的任意点的位置。

它是将地球表面上的点与数学坐标系统相对应的一种方法。

通过确定测绘坐标系，我们可以将实际地理位置与抽象的坐标值相对应，从而方便进行地图绘制和空间数据分析。

二、测绘坐标系的类型1. 地理坐标系地理坐标系是最常用的一种测绘坐标系，它使用经度和纬度来精确定义地球上任意点的位置。

经度表示东西方向，纬度表示南北方向。

地球上的每个点都可以通过经度和纬度唯一确定。

地理坐标系通常用于全球定位系统（GPS）等应用中。

2. 平面坐标系平面坐标系是在地理坐标系基础上建立的，它将地球表面划分为多个局部的平面区域，方便在较小区域内进行测量和绘图。

常见的平面坐标系有国家坐标系和投影坐标系。

国家坐标系通常由各国测绘机构制定，用于全国范围内的测量和测绘。

投影坐标系是将三维地理坐标投影到二维平面上的一种方法，常用于地图制作。

三、测绘坐标系在实际应用中的重要性1. 地图绘制测绘坐标系是绘制地图的基础。

通过确定合适的坐标系，地图制作者可以准确地将实际地理位置转换为坐标值，并在地图上标注。

这样，人们就可以通过地图找到特定位置、导航、规划路线等。

2. 地理信息系统（GIS）分析地理信息系统是一种用于存储、管理、分析和展示地理数据的工具。

在GIS中，测绘坐标系是确保不同数据源之间可以进行空间关联和分析的基础。

通过将不同数据源的坐标统一到同一坐标系下，GIS可以进行地图叠加、空间查询、缓冲区分析等功能，为各行各业的决策提供支持。

3. 工程测量在工程测量中，测绘坐标系被广泛应用。

通过在工程现场测量点的坐标，并与工程设计图纸中的坐标进行对比，可以确定土地边界、地形图、蓝图等信息。

测量常用的坐标系有几种各有何特点在测量学中，常用的坐标系是对于空间中的点或物体进行准确位置描述的一种方法。

不同的坐标系适用于不同的应用场景，并具有各自独特的特点和优势。

本文将介绍常用的几种坐标系及其特点。

直角坐标系直角坐标系，也称为笛卡尔坐标系，是最为常见和基础的坐标系之一。

它采用了三个相互垂直的轴：x轴、y轴和z轴，分别代表横向、纵向和垂直方向。

这三个轴在原点交叉，形成一个三维坐标系。

直角坐标系适用于描述几何形状和计算物体的几何特性，如位置、距离、角度等。

通过表示物体在三个轴上的坐标，可以精确地确定物体的位置。

直角坐标系的优点是简单直观，容易理解和使用。

它的单位长度在各个轴上是相等的，便于进行几何计算和测量分析。

同时，直角坐标系也可以通过转换操作变成其他坐标系，如柱坐标系和球坐标系，进一步扩展了其应用范围。

柱坐标系柱坐标系是由一个平面和一个与该平面垂直的轴构成的坐标系。

它采用了两个独立变量和一个垂直轴，分别表示点在平面上的极径、极角和沿轴线方向的距离。

柱坐标系常用于描述圆锥体、圆柱体和旋转对称的物体。

柱坐标系的特点是可以直观地描述物体在平面上的位置关系和角度信息。

同时，由于柱坐标系中的极角和极径比直角坐标系中的角度和距离更直观，因此在某些场景下更易于进行几何计算和图形表达。

但是，柱坐标系在描述三维物体时会有一些不足，例如无法直接表示物体的高度和垂直位移。

球坐标系球坐标系是由一个球面和一个从球心到球面上某点的直线段构成的坐标系。

它采用了一个独立变量的角度和两个独立变量的距离，分别表示点在球面上的极角、方位角和距离。

球坐标系常用于描述球体、天体物理学中的天体运动和导航系统中的位置定位。

球坐标系的特点是可以直观地表示物体在球面上的位置和方向。

它具有对称性，便于处理球对称的问题。

球坐标系还适用于描述天体的运动和测量导航系统中的位置，如全球定位系统（GPS）。

极坐标系极坐标系是由一个平面和一个从该平面到某点的线段（极线）构成的坐标系。

工程测量的坐标系引言在工程测量中，坐标系是一个重要的概念。

坐标系是用来描述和确定空间中各个点的位置关系的一种数学模型。

在实际的工程测量中，我们常常需要确定各个测量点的位置，以便进行相关的计算和分析。

本文将介绍工程测量中常用的坐标系的概念和相关知识。

二维坐标系工程测量中最常用的坐标系之一是二维直角坐标系，也称为笛卡尔坐标系。

二维直角坐标系由两条相互垂直的坐标轴组成，通常用x和y表示。

其中，x轴称为横轴，y轴称为纵轴。

坐标系的原点是两个坐标轴的交点。

在二维坐标系中，每个点都可以用一个有序数对(x, y)来表示，其中x表示横坐标，y表示纵坐标。

通过测量某个点在横轴和纵轴上的投影长度，我们可以确定这个点的坐标。

这种坐标系常常用于工程测量中的平面布置和计算。

三维坐标系除了二维坐标系，工程测量中也经常使用三维坐标系。

三维坐标系由三个相互垂直的坐标轴组成，通常用x、y和z表示。

其中，x轴和y轴与二维坐标系的横轴和纵轴类似，z轴则表示垂直于二维平面的轴。

在三维坐标系中，每个点可以用一个有序数对(x, y, z)来表示，其中x、y、z分别表示点在x轴、y轴、z轴上的坐标。

通过测量某个点在三个坐标轴上的投影长度，我们可以确定这个点的坐标。

三维坐标系常常用于工程测量中的空间布置和计算。

大地坐标系除了直角坐标系，工程测量中还使用一种特殊的坐标系，即大地坐标系。

大地坐标系是以地球表面为参考平面的坐标系。

在大地坐标系中，一个点的位置可以用经度、纬度和高程来表示。

经度是指一个点在东西方向上的位置，通常用度来表示。

经度的0度点被定义为通过英国伦敦的经线。

纬度是指一个点在南北方向上的位置，同样用度来表示。

纬度的0度点被定义为通过赤道的纬线。

在大地坐标系中，我们还可以用高程来衡量一个点的高度。

高程表示一个点与参考水平面之间的垂直距离。

大地坐标系在工程测量中广泛应用于地理测量、导航定位和地图制作等领域。

它能够准确描述地球表面上不同点的位置关系，为工程测量提供了重要的参考框架。

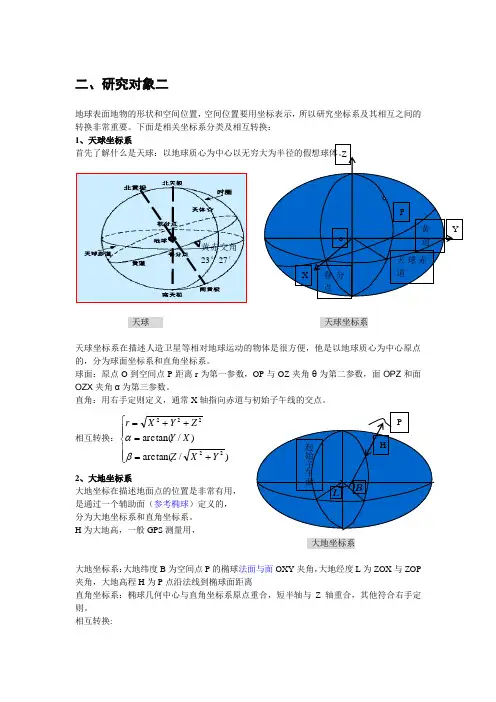
二、研究对象二地球表面地物的形状和空间位置，空间位置要用坐标表示，所以研究坐标系及其相互之间的转换非常重要。

下面是相关坐标系分类及相互转换： 1、天球坐标系首先了解什么是天球：以地球质心为中心以无穷大为半径的假想球体。

天球 天球坐标系天球坐标系在描述人造卫星等相对地球运动的物体是很方便，他是以地球质心为中心原点的，分为球面坐标系和直角坐标系。

球面：原点O 到空间点P 距离r 为第一参数，OP 与OZ 夹角θ为第二参数，面OPZ 和面OZX 夹角α为第三参数。

直角：用右手定则定义，通常X 轴指向赤道与初始子午线的交点。

相互转换：⎪⎪⎩⎪⎪⎨⎧+==++=)/arctan()/arctan(22222Y X Z X Y Z Y X r βα 2、大地坐标系大地坐标在描述地面点的位置是非常有用， 是通过一个辅助面（参考椭球）定义的， 分为大地坐标系和直角坐标系。

H 为大地高，一般GPS 测量用，大地坐标系大地坐标系：大地纬度B 为空间点P 的椭球法面与面OXY 夹角，大地经度L 为ZOX 与ZOP 夹角，大地高程H 为P 点沿法线到椭球面距离直角坐标系：椭球几何中心与直角坐标系原点重合，短半轴与Z 轴重合，其他符合右手定则。

相互转换:黄赤交角23°27′X YZ oP春分点黄道 天球赤道 起始子午面L B PH[]⎪⎩⎪⎨⎧+=+=-=+-=L B H N X L B H N Y B e a N B H e N Z cos cos )(sin cos )(e ,2sin 21/ sin )21(为第一扁率卯酉全曲率半径，其中3、惯性坐标系（CIS ）与协议天球坐标系① 惯性坐标系（CIS ）:在空间不动或做匀速直线运动的坐标系.② 协议天球坐标系：以某一约定时刻t0作为参考历元，把该时刻对应的瞬时自转轴经岁差和章动改正后作为Z 轴，以对应的春分点为X 轴的指向点，以XOZ 的垂直方向为Y 轴方向建立的天球坐标系。

测量常用的五种坐标系
1)像平面坐标系以像主点O为原点建立起来的右手直角坐标
系O-XY
2)像空间坐标系:以摄影中心S为坐标原点,平面坐标坐标
X,Y与像平面坐标系中X,Y轴平行,Z轴与摄影光束轴重合,建立的
空间右手直角坐标系S-xyz
3)像空间辅助坐标系:由于每张像片的像空间坐标系都不同,
所以需要建立一个统一的坐标系,用S-XYZ表示,坐标原点仍然取
摄影中心S,有下列三种情况:(1)取X,Y,Z平行于地面摄影测量坐标
系D-XYZ,这样同一像点a在像空间坐标系中坐标是X,Y,Z=-f,在
像空间辅助坐标系中坐标是X,Y,Z(2)以每条航带的第一张像片的像
空间坐标系作为像空间辅助坐标系(3)是以每个像片对的左像片摄影中心为坐标原点,摄影基线为X轴,以X轴和摄影光束形成的XZ平面,过原点作垂直于XZ平面(左核面)的Y轴构成右手直角坐标系.
4)地面测量坐标系:指高斯克吕6和3带投影下的平面直角坐标系和定义在某一高程基准面的高程,形成的空间左手直角坐标系
T-X t Y T Z T。

5)地面摄影测量坐标系:坐标原点在测区的某一地面点上,X
轴大致与航向一致的水平方向,Y轴垂直于X轴,Z轴沿铅垂方向,构成右手直角坐标系D-XYZ。

测量中常用的坐标系统[来源：本站 | 作者：原创 | 日期：2010年11月26日 | 浏览168次] 字体:[大中小] 1) 球面坐标系统天文地理坐标系：以大地水准面为基准，以铅垂线为基准线，地面点在基准面上投影位置由天文经度（λ）和天文纬度（φ）确定。

大地坐标系：以参考椭球体面为基准面，以法线为基准线。

地面点在椭球面上投影点的位置用大地经度L、大地纬度B表示。

2)空间直角坐标系：以参考椭球体的中心为坐标原点，指向地球北极的方向为Z轴，首子午面与赤道的交线为X轴，Y轴垂直于xoz平面。

WGS-84坐标系（世界大地坐标系）：采用WGS-84椭球，其坐标原点在地心，Z轴指向BIH1984.0定义的协议地球极(CTP)方向，X轴指向BIH1984.0的零子午面和CTP赤道的交点，Y轴与Z、X轴构成右手坐标系。

也称全球地心坐标系。

GPS卫星定位系统得到的地面点坐标就是WGS-84坐标。

3)高斯平面直角坐标系地图投影：将球面上图形、数据按一定的数学法则转到平面上的方法。

X= F 1 (L，B) 或 X= F 1 (x, y, z)Y= F 2 (L，B) Y= F 2 (x, y, z) 地图投影分类：按变形性质分为：等角投影、等积投影和任意投影。

其中，等角投影保持角度不变，投影后任意一点各方向的长度比不变，从而在有限范围内使得投影平面上图形与椭球上保持相似。

因此，等角投影也成为正形投影。

高斯投影：等角横切椭圆柱投影，又称高斯—克吕格投影。

a) 高斯投影的特点：中央子午线的投影为一条直线，且投影之后的长度无变形；其余子午线的投影均为凹向中央子午线的曲线，且以中央子午线为对称轴，离对称轴越远，其长度变形也就越大；赤道的投影为直线，其余纬线的投影为凸向赤道的曲线，并以赤道为对称轴；经纬线投影后仍保持相互正交的关系，即投影后无角度变形；中央子午线和赤道的投影相互垂直。

b) 分带法：为保证投影精度，限定投影的区域的方法——按经度分带。

测绘技术中常见的坐标系介绍导语：在测绘技术中，坐标系是一个非常重要的概念，它能够准确描述和定位地理信息。

本文将介绍测绘技术中常见的坐标系，包括地理坐标系、平面坐标系和投影坐标系，并讨论它们的应用和特点。

一、地理坐标系地理坐标系是用来表示地球上某一点位置的坐标系。

它的基本单位是度，可以精确到小数点后的位置。

地理坐标系一般使用经度和纬度来表示地球上的点，经度表示东西方向上的位置，纬度表示南北方向上的位置。

地理坐标系的一个重要特点是它能够保持地球表面真实的地理形状和地理距离。

这是因为地理坐标系是基于地球表面的椭球体模型来定义的，所以在测量和计算时能够考虑地球的曲率和形变。

地理坐标系在地理信息系统（GIS）中得到广泛应用。

通过使用地理坐标系，我们可以准确地描述和分析地球上的各种地理信息，如地图、空间数据和遥感图像。

二、平面坐标系在实际的测绘和地图制作中，为了方便表示和计算，通常会将地理坐标系投影到一个平面上，形成平面坐标系。

平面坐标系可以将地球上的三维点投影到一个二维坐标系中，使其落在平面上。

常见的平面坐标系有UTM坐标系、高斯-克吕格坐标系等。

这些平面坐标系使用不同的投影方法来将地理坐标转换为平面坐标。

平面坐标系的一个重要特点是它可以忽略地球的曲率和形变，从而简化测量和计算。

但是由于投影过程中会引入一定的误差，所以在大范围地图制作中需要考虑投影误差的修正。

三、投影坐标系投影坐标系是基于平面坐标系的一种特殊表示方法。

它使用一组坐标轴来表示地图上的点，并通过投影方法将地图上的点与地理坐标进行对应。

投影坐标系通常使用笛卡尔坐标系的形式，以米或英尺为单位。

它在地图制作和测绘工程中广泛应用，能够准确表示和测量实际地图上的位置和距离。

不同的地区和国家使用不同的投影坐标系，如横轴墨卡托投影、兰伯特投影等。

这些投影坐标系在保证地图形状的同时，还能控制地图上的形变和比例尺。

投影坐标系在工程测绘、地图制作、导航和地图分析中都有重要应用。

测量中常用的坐标系一、坐标系类型1、大地坐标系定义：大地测量中以参考椭球面（不准确）为基准面建立起来的坐标系。

一定的参考椭球和一定的大地原点上的大地起算数据，确定了一定的坐标系。

通常用参考椭球参数和大地原点上的起算数据作为一个参心大地坐标系建成的标志。

大地坐标（地理坐标）：将某点投影到椭球面上的位置用大地经度L和大地纬度B表示，（ B ， L）统称为大地坐标。

大地高H：某点沿投影方向到基准面（参考椭球面）的距离。

在大地坐标系中，某点的位置用（B ， L，H）来表示。

2、空间直角坐标系定义：以椭球体中心为原点，起始子午面与赤道面交线为X 轴，在赤道面上与X轴正交的方向为Y轴，椭球体的旋转轴为Z轴。

在空间直角坐标系中，某点的位置用（X，Y，Z）来表示。

3、平面直角坐标系在小区域进行测量工作若采用大地坐标来表示地面点位置是不方便的，通常采用平面直角坐标系。

测量工作以x轴为纵轴，以y轴为横轴投影坐标：为了建立各种比例尺地形图的控制及工程测量控制，一般应将椭球面上各点的大地坐标按照一定的规律投影到平面上，并以相应的平面直角坐标表示。

4、地方独立坐标系基于限制变形、方便、实用和科学的目的，在许多城市和工程测量中，常常会建立适合本地区的地方独立坐标系，建立地方独立坐标系，实际上就是通过一些参数来确定地方参考椭球与投影面。

二、国家大地坐标系1.1954年北京坐标系（BJ54旧）坐标原点：前苏联的普尔科沃。

参考椭球：克拉索夫斯基椭球。

平差方法：分区分期局部平差。

存在问题：（1）椭球参数有较大误差。

（2）参考椭球面与我国大地水准面存在着自西向东明显的系统性倾斜。

（3）几何大地测量和物理大地测量应用的参考面不统一。

（4）定向不明确。

2.1980年国家大地坐标系（GDZ80）坐标原点：陕西省泾阳县永乐镇。

参考椭球：1975年国际椭球。

平差方法：天文大地网整体平差。

特点：（1）采用1975年国际椭球。

（2）参心大地坐标系是在1954年北京坐标系基础上建立起来的。

测量常用的坐标系有哪些各有何特点坐标系是用来描述和定位空间中物体位置的一种方式。

在测量领域，常用的坐标系有直角坐标系、极坐标系和球坐标系。

每种坐标系都有其独特的特点和适用场景。

直角坐标系直角坐标系是最常见和最简单的坐标系。

它由两个相互垂直的轴组成，通常表示为X轴和Y轴。

在直角坐标系中，每个点的位置由其在X轴和Y轴上的坐标表示。

X轴和Y轴的交点称为原点，用(0,0)表示。

特点： 1. 简单直观：直角坐标系以直线和直角为基础，易于理解和使用。

2.坐标计算方便：通过简单的几何关系，可以通过坐标计算两个点之间的距离和角度。

3. 适用于平面测量：直角坐标系主要用于平面测量，如地图绘制、建筑布局等。

4. 不适用于曲面测量：直角坐标系无法准确描述曲面上的点的位置，因此在某些测量场景下不适用。

极坐标系极坐标系使用角度和距离来描述点的位置。

它以一个固定点为极点，以一条规定方向为极轴。

极坐标系中，点的位置由极径（距离）和极角（与极轴的夹角）来表示。

特点： 1. 独特的表示方式：相比直角坐标系，极坐标系通过角度和距离的组合来表示点的位置，具有其独特的表达方式。

2. 适用于圆形测量：极坐标系在测量圆形或呈放射状分布的物体时很有优势，如计算轮胎的直径、孔洞的位置等。

3.不适用于直线测量：极坐标系不适用于描述直线上的点的位置，精准度较低。

4.笛卡尔坐标的转换：极坐标系可以与直角坐标系进行转换，相互之间可以转化表达点的位置。

球坐标系球坐标系是一种用于描述三维空间中点的位置的坐标系。

它由两个角度和一个距离组成。

球坐标系的极点位于球心，其中一个角度是与一个确认的轴之间的角度，其他则是与这个确定的轴之间的角度。

特点： 1. 适用于球面测量：球坐标系特别适用于描述球面上物体的位置，如天体测量、机器人定位等。

2. 三维空间表达能力强：球坐标系不仅可以表示平面上的点，还可以表示三维空间中的点的位置。

3. 计算复杂度较高：由于球坐标系需要通过角度和距离来表示点的位置，所以计算复杂度较高，不够直观简单。

测量坐标系有哪几种各有什么特点在测量和工程领域中，坐标系是一种重要的工具，用于描述和定位物体或位置。

不同类型的测量任务需要使用不同的坐标系来满足特定的要求。

在本文中，将介绍常见的测量坐标系以及它们各自的特点。

1. 直角坐标系直角坐标系，也称为笛卡尔坐标系，是最常见和常用的坐标系之一。

它由两条互相垂直的直线（通常称为水平轴和垂直轴）构成。

这两条直线的交点被定义为原点。

直角坐标系可以用来描述一个平面内的点的位置。

特点：•简单直观：直角坐标系简单易懂，容易理解和使用。

•精确度高：通过坐标数值的精确表示，可以实现高精度的测量和定位。

•适应性广：直角坐标系适用于描述平面内的点的位置和测量，可以应用于各种不同的工程和科学领域。

2. 极坐标系极坐标系是一种使用角度和距离来描述点位置的坐标系。

它由一个固定点（称为极点）和一根从极点出发的射线（称为极轴）构成。

点的位置通过角度和距离来确定。

特点：•简洁表示：极坐标系通过极角和极径来描述点的位置，更加简洁明了。

•适用于特定情况：极坐标系适用于对对称性物体或旋转对称性物体的测量和描述。

•存在坐标歧义：由于存在极角的周期性，同一个点可能有多个不同的表示方式。

3. 三维坐标系三维坐标系是在直角坐标系的基础上发展而来的一种扩展。

它在二维坐标系的基础上增加了垂直于平面的第三个轴，形成一个立体空间坐标系。

特点：•表达空间位置：三维坐标系可以描述物体或点在三维空间中的位置，具有更丰富的信息。

•适应性广：三维坐标系广泛应用于地理测量、计算机图形学、机器人导航等领域。

•数据量大：相对于二维坐标系，三维坐标系需要更多的数据来描述点的位置。

4. 地理坐标系地理坐标系是一种用于描述地球上地理位置的坐标系，也称为大地坐标系。

地理坐标系通常使用经度和纬度来表示位置。

特点：•地球参考：地理坐标系基于地球参考椭球（如WGS84）来描述地球表面的位置。

•全球通用：地理坐标系被广泛应用于地理信息系统、导航系统和地图制作等各个领域。

测量中常用的坐标系有哪几种各有什么特点在测量领域中，常常需要用到坐标系来描述和定位物体的位置。

坐标系既可以是二维的，也可以是三维的。

不同类型的坐标系在测量应用中具有不同的特点和用途。

本文将介绍测量中常用的几种坐标系，并分别阐述它们的特点。

1.笛卡尔坐标系笛卡尔坐标系是最常见和最基本的坐标系之一。

它由数学家笛卡尔于17世纪提出，并广泛应用于几何学和物理学。

笛卡尔坐标系是一个二维平面坐标系，由两条垂直相交的直线（称为x轴和y轴）组成。

通过指定相对原点的位置和单位长度，可以用数值对来表示平面上的任意点。

笛卡尔坐标系的特点是简单直观，易于理解和计算，适用于大多数测量场景。

2.极坐标系极坐标系是另一种常用的二维坐标系统，它以极径和极角来表示点的位置。

极径是从原点到点的距离，表示点的径向位置；极角是从参考方向到线段的角度，表示点的方位角。

极坐标系适用于描述圆心对称的物体，如雷达扫描、天文观测等领域。

与笛卡尔坐标系相比，极坐标系在计算某些物理量时更加方便，但在表示复杂的几何形状时不如笛卡尔坐标系直观。

3.球坐标系球坐标系是一种三维坐标系统，由球心、极径、极角和方位角四个参数来描述点的位置。

球心是坐标系的原点，极径是从球心到点的距离，极角是从某个参考方向到线段的角度，方位角是从参考平面到线段的角度。

球坐标系在天文学、地理学、飞行控制等领域有广泛应用。

与笛卡尔坐标系和极坐标系相比，球坐标系能够更好地描述球对称的物体和场景，并在某些测量任务中具备较高的效率。

4.笛卡尔-直角坐标系笛卡尔-直角坐标系是笛卡尔坐标系的一种推广，用于描述三维空间中的点的位置。

它由三条相互垂直的坐标轴（称为x轴、y轴和z轴）组成，形成一个立方体。

通过指定相对原点的位置和单位长度，可以用数值对来表示三维空间中的任意点。

笛卡尔-直角坐标系在工程测量、地理测量、建筑设计等领域广泛使用。

它具有直观、精确和便于计算的特点，能够准确描述和定位三维物体。

测量中常用的坐标系在测量领域中，坐标系是非常重要的概念。

坐标系有助于描述和测量物体或位置在空间中的相对位置和方向关系。

在测量中常用的坐标系主要有直角坐标系、极坐标系和地理坐标系。

直角坐标系直角坐标系是最常见的坐标系之一，也称为笛卡尔坐标系。

它由两条垂直于彼此的直线（通常为x轴和y轴）组成，这两条直线的交点作为坐标原点。

直角坐标系常用于测量平面上的位置。

在直角坐标系中，每个点可以用一对有序实数(x,y)来表示，其中x表示点到y轴的有向距离，y表示点到x轴的有向距离。

例如，点A在直角坐标系中的坐标为(3,4)，表示点A在x轴上的距离为3，而在y轴上的距离为4。

直角坐标系的优点是易于使用和计算，而且可以方便地进行几何运算和数据处理。

因此，直角坐标系被广泛应用于测量、工程学和其他科学领域中。

极坐标系极坐标系是另一种常用的坐标系，它与直角坐标系有所不同。

极坐标系是通过点到原点的距离和点与正向x轴的角度来描述点的位置。

在极坐标系中，坐标由一个有序实数对(r,θ)表示，其中r表示点到原点的距离，θ表示点与正向x轴的夹角。

与直角坐标系相比，极坐标系更适用于描述圆形、旋转和对称的物体。

极坐标系在测量中的应用广泛，特别适用于天文学、物理学和工程领域中的极坐标测量。

地理坐标系地理坐标系是一种用于描述地球表面上位置的坐标系。

地理坐标系是基于经度和纬度的，它可以提供地球上任何一个点的准确位置。

地理坐标系的经度以子午线为基准，纬度以赤道为基准。

经度是从本初子午线（通常是格林威治子午线）起算的角度，表示东西方向；纬度是从赤道起算的角度，表示南北方向。

地理坐标系在地理信息系统（GIS）和导航系统中广泛使用，如谷歌地图和GPS。

地理坐标系的应用使得人们可以准确地定位地球上的任何一个点，方便了地理和测量工作。

小结测量中使用的坐标系包括直角坐标系、极坐标系和地理坐标系。

直角坐标系适用于测量平面上的位置，极坐标系适用于描述圆形和旋转对称物体的位置，地理坐标系可用于描述地球上点的位置。

测量中的常用坐标系及坐标转换概述1.引言在测量与空间信息处理中，坐标系是非常重要的概念。

通过坐标系，可以将现实世界中的点、线、面等空间要素进行数学建模和描述。

常用的坐标系包括笛卡尔坐标系、极坐标系、球坐标系等。

坐标系之间的转换是测量与空间信息处理中常用的操作。

2.笛卡尔坐标系笛卡尔坐标系是最常见的坐标系，由三个互相垂直的坐标轴构成。

在二维情况下，有两个坐标轴分别表示横坐标和纵坐标；在三维情况下，有三个坐标轴分别表示横坐标、纵坐标和高度坐标。

笛卡尔坐标系广泛应用于地理信息系统、测绘工程、建筑设计等领域。

3.极坐标系极坐标系由极径和极角两个坐标轴构成。

极径表示点到坐标原点的距离，极角表示点在平面上相对于一个基准线的角度。

极坐标系常用于极坐标测量仪器中，如激光扫描仪，雷达等。

极坐标系优点之一是可以简化角度变化的描述，适用于自然界中的很多环境和场景。

4.球坐标系球坐标系由球半径、极角和方位角三个坐标轴构成。

球半径表示点到坐标原点的距离，极角表示点距离球心的水平角度，方位角表示点在水平面上相对于一个基准线的角度。

球坐标系常用于天文学、地理学等领域，描述地球表面上各个点的位置。

5.坐标转换在实际测量中，经常需要在不同的坐标系之间进行转换，以实现测量数据的互通。

常见的坐标转换包括坐标系之间的旋转、平移和缩放等操作。

下面以笛卡尔坐标系和极坐标系为例，介绍一下坐标转换的基本原理。

-笛卡尔坐标系到极坐标系的转换：假设有一个点在笛卡尔坐标系中的坐标为(x,y)，则可以通过以下公式将其转换为极坐标系中的坐标(r,θ)：r=√(x²+y²)θ = arctan(y/x)-极坐标系到笛卡尔坐标系的转换：假设有一个点在极坐标系中的坐标为(r,θ)，则可以通过以下公式将其转换为笛卡尔坐标系中的坐标(x,y)：x = r * cos(θ)y = r * sin(θ)在实际测量中，常常需要进行坐标系之间的转换，比如将地理坐标转换为笛卡尔坐标，或者将局部坐标系转换为全球坐标系等。