数字信号处理1-5章习题课
- 格式:ppt
- 大小:1.20 MB
- 文档页数:33

第五章习题与上机题5.1 已知序列12()(),0 1 , ()()()nx n a u n a x n u n u n N =<<=--,分别求它们的自相关函数,并证明二者都是偶对称的实序列。
解:111()()()()()nn mx n n r m x n x n m a u n au n m ∞∞-=-∞=-∞=-=-∑∑当0m ≥时,122()1mmnx n ma r m aaa∞-===-∑ 当0m <时,122()1m mnx n a r m aaa -∞-===-∑ 所以,12()1mx ar m a =-2 ()()()()N x n u n u n N R n =--=22210121()()()()()1,0 =1,00, =()(1)x NN n n N mn N n m N r m x n x n m Rn R n m N m N m N m m Nm N m R m N ∞∞=-∞=-∞--=-=-=-=-⎧=--<<⎪⎪⎪⎪=-≤<⎨⎪⎪⎪⎪⎩-+-∑∑∑∑其他从1()x r m 和2()x r m 的表达式可以看出二者都是偶对称的实序列。
5.2 设()e()nTx n u n -=,T 为采样间隔。
求()x n 的自相关函数()x r m 。
解:解:()()()()e()e ()nTn m T x n n r m x n x n m u n u n m ∞∞---=-∞=-∞=-=-∑∑用5.1题计算1()x r m 的相同方法可得2e()1e m Tx Tr m --=-5.3 已知12()sin(2)sin(2)s s x n A f nT B f nT ππ=+,其中12,,,A B f f 均为常数。
求()x n 的自相关函数()x r m 。
解:解:()x n 可表为)()()(n v n u n x +=的形式,其中)2sin()(11s nT f A n u π=,=)(n v 22sin(2)s A f nT π,)(),(n v n u 的周期分别为 s T f N 111=,sT f N 221=,()x n 的周期N 则是21,N N 的最小公倍数。


数字信号处理 重点习题(1-5章)第一章5.设系统分别用下面的差分方程描述, x(n)与y(n)分别表示系统输入和输出, 判断系统是否是线性非时变的。
(6)y(n)=x(n2)(7)y(n)= (8)y(n)=x(n)sin(ωn)6.给定下述系统的差分方程, 试判定系统是否是因果稳定系统, 并说明理由。
(3) y(n)= x(k) (5) y(n)=e x(n)13.有一连续信号x a(t)=cos(2πft+),式中,f =20 Hz,=π/2。
(1)求出x a(t)的周期;(2)用采样间隔T=0.02 s对x a(t)进行采样,试写出采样信号 的表达式;(3) 画出对应 的时域离散信号(序列)x(n)的波形, 并求出x(n)的周期。
14. 已知滑动平均滤波器的差分方程为(1)求出该滤波器的单位脉冲响应;(2)如果输入信号波形如题14图所示,试求出y(n)并画出它的波形。
第二章3.线性时不变系统的频率响应(频率响应函数)H(e jω)=|H(e jω)|e jθ(ω), 如果单位脉冲响应h(n)为实序列,试证明输入x(n)=A cos(ω0n+)的稳态响应为10.若序列h(n)是实因果序列, 其傅里叶变换的实部如下式:H R(e jω)=1+cosω,求序列h(n)及其傅里叶变换H(e jω)。
18.已知,分别求:(1) 收敛域0.5<|z|<2对应的原序列x(n);(2)收敛域|z|>2对应的原序列x(n)。
24.已知线性因果网络用下面差分方程描述: y(n)=0.9y(n-1)+x(n)+0.9x(n-1),(1)求网络的系统函数H(z)及单位脉冲响应h(n);(2) 写出网络频率响应函数H(e jω)的表达式, 并定性画出其幅频特性曲线; (3) 设输入x(n)=e jω0n, 求输出y(n)。
28.若序列h(n)是因果序列, 其傅里叶变换的实部如下式:,求序列h(n)及其傅里叶变换H(e jω).29.若序列h(n)是因果序列, h(0)=1, 其傅里叶变换的虚部为,求序列h(n)及其傅里叶变换H(e jω)。




一、填空题1.某根据表中信号对应规律填写表格2.已知序列x (n )={5,-1, 2, -3,0,3 },则x((n-2))8 = 。
3. 已知序列x (n )={5,10, 2, -3,6,3, -2, -10}, 0≤ n ≤7,其8点DFT 为X (k ),(0≤ k ≤ 7), 计算下列各数值(a) X (0), (b) X (4), (c) 70()k X k =∑, (d)7280()kk X k W =∑ 4.已知序列x (n )={5,-1,0,-8},0≤ n ≤3。
y (n )={ 2,-3,-2,4,1},0≤ n ≤4。
线性卷积y (n ) = x (n ) * h (n )= , 圆周卷积w (n ) = x (n )⑥h (n )= 。
5. 已知实序列x(n)的4点DFT 的前3个值是0.25, 0.125-j0.301, 3,则最后一个值X(3)= 。
二、分析计算题6.有一信号)5sin(22cos )(t t t x ππ+=经过理想抽样系统,抽样频率为s Ω,抽样后信号经过LPF 恢复,其中 ⎩⎨⎧≤Ω=Ωother j Ha 03||1)(π问:1))(t x 的奈奎斯特率为多少?2)若s rad s/6π=Ω,抽样后信号的数字角频率为多少?抽样信号经过LPF 后哪种频率成分无失真,画出LPF 输出信号的幅度谱。
7.用微处理器对实序列作谱分析,要求频谱分辨率50F Hz ≤,信号最高频率为1kHz ,试确定以下各参数: (1)最小记录时间minp T ;(2)最大抽样间隔max T ;(3)最少抽样点数min N ;(4)在频带宽度不变的情况下,若将频率分辨率提高一倍,则F 和N 各为多少?8.利用顺序输入、倒序输出的基2 DIF-FFT 算法分析一个长度为N 点的序列x (n )的DFT X (k ),回答下列问题:(1)说明N 所需满足的条件,并说明如果N不满足的话, 该如何处理? (2)如果N=256,算法中共有多少级蝶形?第3级中有多少个蝶形?确定第3级蝶形中不同的权系数r N W 。

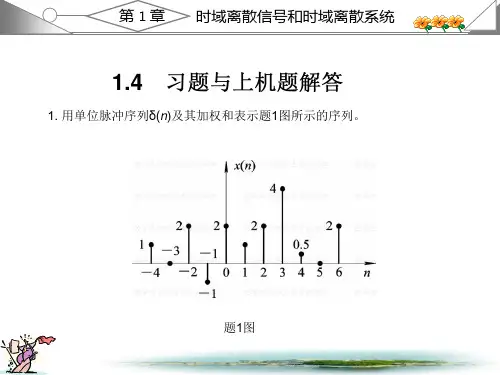
数字信号处理课后答案教材第一章习题解答1.用单位脉冲序列()nδ及其加权和表示题1图所示的序列。
解:2.给定信号:25,41 ()6,040,n nx n n+-≤≤-⎧⎪=≤≤⎨⎪⎩其它(1)画出()x n序列的波形,标上各序列的值;(2)试用延迟单位脉冲序列及其加权和表示()x n序列;(3)令1()2(2)x n x n=-,试画出1()x n波形;(4)令2()2(2)x n x n=+,试画出2()x n波形;(5)令3()2(2)x n x n=-,试画出3()x n波形。
解:(1)x(n)的波形如题2解图(一)所示。
(2)(3)1()x n的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4)2()x n的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画3()x n时,先画x(-n)的波形,然后再右移2位,3()x n波形如题2解图(四)所示。
3.判断下面的序列是否是周期的,若是周期的,确定其周期。
(1)3()cos()78x n A n ππ=-,A 是常数;(2)1()8()j n x n e π-=。
解:(1)3214,73w w ππ==,这是有理数,因此是周期序列,周期是T=14;(2)12,168w wππ==,这是无理数,因此是非周期序列。
5.设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
(1)()()2(1)3(2)y n x n x n x n =+-+-; (3)0()()y n x n n =-,0n 为整常数; (5)2()()y n x n =; (7)0()()nm y n x m ==∑。
解:(1)令:输入为0()x n n -,输出为'000'0000()()2(1)3(2)()()2(1)3(2)()y n x n n x n n x n n y n n x n n x n n x n n y n =-+--+---=-+--+--=故该系统是时不变系统。

第一章 离散时间信号与系统2.任意序列x(n)与δ(n)线性卷积都等于序列本身x(n),与δ(n-n 0)卷积x(n- n 0),所以(1)结果为h(n) (3)结果h(n-2) (2(4)3 .已知 10,)1()(<<--=-a n u a n h n,通过直接计算卷积和的办法,试确定单位抽样响应为 )(n h 的线性移不变系统的阶跃响应。
4. 判断下列每个序列是否是周期性的,若是周期性的,试确定其周期:)6()( )( )n 313si n()( )()873cos()( )(ππππ-==-=n j e n x c A n x b n A n x a分析:序列为)cos()(0ψω+=n A n x 或)sin()(0ψω+=n A n x 时,不一定是周期序列,nmm m n n y n - - -∞ = - ⋅ = = ≥ ∑ 2 31 2 5 . 0 ) ( 01当 3 4n m nm m n n y n 2 2 5 . 0 ) ( 1⋅ = = - ≤ ∑ -∞ = - 当 aa a n y n a a an y n n h n x n y a n u a n h n u n x m m nnm mn -==->-==-≤=<<--==∑∑--∞=---∞=--1)(11)(1)(*)()(10,)1()()()(:1时当时当解①当=0/2ωπ整数,则周期为0/2ωπ;②;为为互素的整数)则周期、(有理数当 , 2 0Q Q P QP =ωπ ③当=0/2ωπ无理数 ,则)(n x 不是周期序列。
解:(1)0142/3πω=,周期为14 (2)062/13πω=,周期为6 (2)02/12πωπ=,不是周期的 7.(1)[][]12121212()()()()()()[()()]()()()()[()][()]T x n g n x n T ax n bx n g n ax n bx n g n ax n g n bx n aT x n bT x n =+=+=⨯+⨯=+所以是线性的T[x(n-m)]=g(n)x(n-m) y(n-m)=g(n-m)x(n-m) 两者不相等,所以是移变的y(n)=g(n)x(n) y 和x 括号内相等,所以是因果的。

数字信号处理课后答案 高西全、丁美玉版1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。
解:()(4)2(2)(1)2()(1)2(2)4(3)0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号:25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它〔1〕画出()x n 序列的波形,标上各序列的值;〔2〕试用延迟单位脉冲序列及其加权和表示()x n 序列; 〔3〕令1()2(2)x n x n =-,试画出1()x n 波形; 〔4〕令2()2(2)x n x n =+,试画出2()x n 波形; 〔5〕令3()2(2)x n x n =-,试画出3()x n 波形。
解:〔1〕x(n)的波形如题2解图〔一〕所示。
〔2〕()3(4)(3)(2)3(1)6()6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-〔3〕1()x n 的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图〔二〕所示。
〔4〕2()x n 的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图〔三〕所示。
〔5〕画3()x n 时,先画x(-n)的波形,然后再右移2位,3()x n 波形如题2解图〔四〕所示。
3. 判断下面的序列是否是周期的,假设是周期的,确定其周期。
〔1〕3()cos()78x n A n ππ=-,A 是常数;〔2〕1()8()j n x n e π-=。
解:〔1〕3214,73w w ππ==,这是有理数,因此是周期序列,周期是T=14; 〔2〕12,168w wππ==,这是无理数,因此是非周期序列。
5. 设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
【最新整理,下载后即可编辑】习题一 (离散信号与系统)1.1周期序列,最小周期长度为5。
1.2 (1) 周期序列,最小周期长度为14。
(2) 周期序列,最小周期长度为56。
1.5()()()()()()()11s a s s s a n s s a s n X j x t p t X j ΩP j Ω2n τn τj sin j Ωjn e X 2n π2n n τj Sa X j jn e 2T 2πττ∞=-∞∞=-∞Ω==*⎡⎤⎣⎦ΩΩ⎛⎫-=-Ω ⎪⎝⎭ΩΩ⎛⎫-=Ω-Ω ⎪⎝⎭∑∑ 1.6 (1) )(ωj e kX (2) )(0ωωj n j e X e (3) )(21)(2122ωωj j e X e X -+ (4) )(2ωj e X1.7 (1) 0n z -(2) 5.0||,5.0111>--z z (3) 5.0||,5.0111<--z z (4)0||,5.01)5.0(11101>----z z z1.8 (1) 0,)11()(211>--=---z zz z z X N(2) a z az az z X >-=--,)1()(211 (3) a z az z a az z X >-+=---,)1()(311211.91.10 (1))1(2)(1----+n u n u n (2))1(24)()5.0(6--⋅--n u n u n n (3))()sin sin cos 1(cos 000n u n n ωωωω++(4) )()()(1n u a a a n a n ---+-δ 1.11(1))(1z c X - (2) )(2z X (3))()1(21z X z -+ (4)-+<<x x R z R z X /1/1),/1(1.12 (1) 1,11<-ab ab(2) 1 (3)00n a n1.13 (1) 该系统不是线性系统;该系统是时不变系统。
第一章数字信号处理概述简答题:1.在A/D变换之前和D/A变换之后都要让信号通过一个低通滤波器,它们分别起什么作用?答:在A/D变化之前为了限制信号的最高频率,使其满足当采样频率一定时,采样频率应大于等于信号最高频率2倍的条件。
此滤波器亦称为“抗混叠”滤波器.在D/A变换之后为了滤除高频延拓谱,以便把抽样保持的阶梯形输出波平滑化,故又称之为“平滑”滤波器.判断说明题:2.模拟信号也可以与数字信号一样在计算机上进行数字信号处理,自己要增加一道采样的工序就可以了。
( )答:错.需要增加采样和量化两道工序。
3.一个模拟信号处理系统总可以转换成功能相同的数字系统,然后基于数字信号处理理论,对信号进行等效的数字处理.( ) 答:受采样频率、有限字长效应的约束,与模拟信号处理系统完全等效的数字系统未必一定能找到。
因此数字信号处理系统的分析方法是先对抽样信号及系统进行分析,再考虑幅度量化及实现过程中有限字长所造成的影响。
故离散时间信号和系统理论是数字信号处理的理论基础.第二章 离散时间信号与系统分析基础一、连续时间信号取样与取样定理计算题:1.过滤限带的模拟数据时,常采用数字滤波器,如图所示,图中T 表示采样周期(假设T 足够小,足以防止混叠效应),把从)()(t y t x 到的整个系统等效为一个模拟滤波器.(a ) 如果kHz rad n h 101,8)(=π截止于,求整个系统的截止频率. (b)对于kHz T 201=,重复(a )的计算.解 (a )因为当0)(8=≥ωπωj e H rad 时,在数 — 模变换中)(1)(1)(Tj X Tj X Te Y a a j ωω=Ω=所以)(n h 得截止频率8πω=c 对应于模拟信号的角频率c Ω为8π=ΩT c因此 Hz Tf c c 6251612==Ω=π 由于最后一级的低通滤波器的截止频率为Tπ,因此对T8π没有影响,故整个系统的截止频率由)(ωj e H 决定,是625Hz 。
数字信号处理习题集数字信号处理习题集第⼀章习题1、已知⼀个5点有限长序列,如图所⽰,h (n )=R 5(n )。
(1)⽤写出的()n δ()x n 函数表达式;(2)求线性卷积*。
()y n =()x n ()hn 2、已知x (n )=(2n +1)[u (n +2)-u (n -4)],画出x (n )的波形,并画出x (-n )和x (2n )的波形。
3、判断信号是否为周期信号,若是求它的周期。
3()sin 73x n n ππ??=+4、判断下列系统是否为线性的,时不变的,因果的,稳定的?(1),(2)2()(3)y n x n =-0()()cos()y n x n n ω=5、已知连续信号。
()2sin(2),3002a x t ft f Hz ππ=+=(1)求信号的周期。
()a x t (2)⽤采样间隔T=0.001s 对进⾏采样,写出采样信号的表达式。
()a x t ?()a xt (3)写出对应于的时域离散信号的表达式,并求周期。
?()a xt ()x n 6、画出模拟信号数字处理的框图,并说明其中滤波器的作⽤。
第⼆章习题1、求下列序列的傅⽴叶变换。
(1),(2)11()333nx n n ??=-≤ ?[]2()()()n x n a u n u n N =--2、已知理想低通滤波器的频率响应函数为:为整数,000(),0j n j e H e n ωωωωωωπ-?≤≤?=? <≤??cc 求所对应的单位脉冲响应h (n )。
3、已知理想⾼通滤波器的频率响应函数为:,求所对应0()1j H e ωωωωωπ≤≤=<≤??cc 的单位脉冲响应h (n )。
4、已知周期信号的周期为5,主值区间的函数值=,求该周期信号的()(1)n n δδ+-离散傅⾥叶级数和傅⾥叶变换.5、已知信号的傅⽴叶变换为,求下列信号的傅⽴叶变换。
()x n ()j X e ω(1)(2)(3)x n -*()x n -6、已知实因果信号如图所⽰,求和。