《离散数学》-教案.doc
- 格式:doc
- 大小:748.01 KB
- 文档页数:27

《离散》公开课教案
离散公开课教案
一、教学目标
- 了解离散数学的基本概念和应用领域。
- 掌握离散数学中常用的逻辑、集合论和图论等基础知识。
- 培养学生的逻辑思维和问题解决能力。
二、教学内容
1. 离散数学简介
- 离散数学的定义和作用
- 离散数学在计算机科学、信息技术等领域的应用
2. 逻辑与命题
- 逻辑与命题的基本概念
- 命题的逻辑运算(与、或、非)
- 命题的真值表和推理规则
3. 集合论
- 集合的定义和表示方法
- 集合的基本运算(交、并、差、补)
- 集合的性质和特征
4. 图论
- 图的基本概念和术语
- 图的表示方法(邻接矩阵、邻接表)
- 常见的图算法(深度优先搜索、广度优先搜索)
三、教学方法
1. 授课讲解:通过讲解离散数学的基本概念和原理,帮助学生建立起相关知识框架。
2. 例题演示:通过解析一些典型的例题,引导学生掌握离散数学的基本方法和技巧。
3. 小组讨论:组织学生进行小组讨论,让学生在合作中研究、思考和解决问题。
4. 实践应用:通过实际问题的应用,让学生将离散数学的知识应用到实际情境中去。
四、教学评价
1. 每节课结束后进行小测验,检查学生对当堂课程的掌握情况。
2. 课堂参与度:评估学生在讨论和实践环节中的积极参与度。
3. 作业完成情况:评估学生对作业内容的完成情况和质量。
五、参考资料
1. 《离散数学导论》
2. 《离散数学(第2版)》
3. 《离散数学及其应用》
注:以上教案仅供参考,具体教学内容和方法可根据实际情况
进行调整。

离散数学教案一、教案引言离散数学作为计算机科学及相关领域的基础学科,对培养学生的逻辑思维能力和问题解决能力具有重要作用。
本教案旨在介绍离散数学课程的重点内容和教学方法,以帮助教师在教学中实现教学目标,提高学生的学习成效。
二、教学目标1. 了解离散数学的基本概念和方法,包括集合论、逻辑推理、图论等内容;2. 掌握离散数学的基本技能,包括集合的运算、证明方法、图的遍历等;3. 发展学生的逻辑思维和问题解决能力,培养学生的数学建模能力;4. 提高学生的团队合作和沟通能力,培养学生的创新意识。
三、教学内容1. 集合论1.1 集合与元素1.2 集合的运算1.3 集合的关系1.4 集合的应用2. 逻辑与证明2.1 命题与命题联结词2.2 命题的真值与命题的合取、析取、蕴含、等价关系2.3 命题逻辑的推理定律2.4 命题与谓词的等价关系2.5 谓词逻辑的推理定律3. 图论3.1 图的概念与性质3.2 图的表示方法3.3 图的遍历算法3.4 图的连通性与最小生成树3.5 图的应用四、教学方法1. 概念讲解与例题演练相结合:通过简洁清晰的讲解,引导学生理解离散数学的基本概念和方法,并通过大量的例题演练巩固学生的知识掌握能力。
2. 问题引导与探究学习:引导学生通过解决实际问题来理解和应用离散数学的原理和方法,培养学生的问题解决能力和数学建模能力。
3. 团队合作与讨论学习:组织学生进行小组活动,鼓励学生在团队合作中分享思路、互相讨论、共同解决问题,培养学生的合作意识和沟通能力。
4. 案例分析与实践应用:选取具体的案例,让学生将离散数学的知识应用于实际问题中,提升学生的学习兴趣和创新意识。
五、教学评估与反馈1. 课堂练习:通过课堂练习,检验学生对离散数学知识的掌握情况,及时发现和纠正学生的错误和不足。
2. 作业评定:通过布置作业并进行评定,评估学生对离散数学知识和方法的应用能力和问题解决能力。
3. 课后讨论与反馈:鼓励学生课后进行小组讨论,并提供及时的反馈和指导,加深学生对重点内容的理解和掌握程度。


《离散数学》教学大纲一、课程的性质和任务课程性质:离散数学是现代数学的一个重要分支,是计算机科学中基础理论的核心课程,是与信息网络及多媒体技术专业的一门必修课。
主要任务:使学生掌握离散数学的基本理论、基本知识;培养学生的抽象思维和慎密概括的能力。
二、课时分配序号课题教学时数小计讲课习题课及单元测验—-命题逻辑2102谓词逻辑12102三集合862四关系12102五图论20182六机动4总计685410三、课程教学内容第一章命题逻辑理解命题与命题公式概念;掌握命题联结词概念及真值表;会求命题公式真值表;掌握等价重言式和蕴含重言式;理解对偶与对偶原理;掌握命题演算的揄规则和证明方法;会求命题公式的标准形式。
重点:命题与命题公式概念;命题联结词;重言式;对偶;命题演算的推理规则和证明方法;命题公式的标准形式。
难点:重言式;命题演算的推理规则和证明方法;命题公式的标准形式。
第二章谓词逻辑掌握个体、谓词与命题函数概念;掌握量词概念;理解谓词公式概念,能进行自然语言与符号语言间的翻译;掌握谓词演算的推理理论和推理方法。
重点:个体、谓词与命题函数;量词;谓词公式与翻译;谓词演算。
难点:谓词演算。
第三章集合掌握集合基本概念;掌握集合的运算与运算定律;掌握集合对称美;理解集合的划分与覆盖;理解容斥原理,会利用容斥原理解决实际问题。
重点:集合基本概念;集合的运算与运算定律;对称差;容斥原理的应用。
特点:幕集;对称差;集合的划分与覆盖;容斥原理的应用。
第四章关系掌握序偶与笛卡尔积概念;掌握关系,关系矩阵和关系图;掌握关系的;掌握关系的性质;掌握关系的闭包运算;理解等价关系与等价类;理解偏序概念,会作哈斯图。
重点:序偶与笛卡尔积;关系;关系的运算;关系的性质;关系的闭包运算; 等价关系,偏序及哈斯图。
难点:关系概念;关系的运算、性质、闭包运算;偏序及哈斯图。
第五章图论理解图的基本概念;理解路与圈和连通性;了解图的矩阵表示;理解有向图与可达性矩阵;了解欧拉图与哈密尔顿图;掌握树的概念;掌握根树及其应用;了解平面图概念,掌握欧拉公式。

3.1集合的基本概念一.、教学目的.1.了解集合的含义、元素与集合的“属于”关系,能用自然语言、图形语言、集合语言描述不同的具体问题;2.理解集合之间包含与相等的含义,能识别给定集合的子集,在具体情境中了解全集与空集的含义;3.了解幂集的含义,并能计算一个集合的幂集.二、教学重难点:1.重点(1):集合中的元素具有的性质(2)理解两集合的包含关系及计算幂集.2.难点:理解集合相等的含义以及理解符号∈与的区别和联系。
三、教学方法:讲授法及描绘讲述法。
四、教学安排:2课时。
五、教学过程:一、元素与集合1.集合:一些可以确定的可分辨的事物构成的整体。
(集合是一个不能精确定义的基本概念.一般来说,把具有共同性质的一些东西,汇集成一整体,就形成了一个集合)。
简单数集:自然数集合(包括0)—N整数集—Z有理数集—Q实数集—R复数集—C2.元素:如果一个特定的事物属于这个集合,则称为这个集合的元素。
给出一个集合的方法:(1)列出集合的所有元素,元素之间用逗号隔开,并把它们用花括号括起来,例如:A={a,b,c,d}(2)用谓词概括该集合中元素的属性,如B={x︳x∈Z∧3<x≤6}3.集合中元素的特征:(1)确定性。
对于一个具体的集合来说,气元素是确定的,即一个元素或者在此集合中或者不在此集合中,两者必居其一且仅居其一(2)互异性。
集合中的元素彼此互不相同,没有重复的元素。
例如:集合{1,3,4}={1,3,4,4}(3)无序性。
集合中的元素是无序的。
例如:集合{1,2,3}={3,1,2}(4)抽象性。
集合中的元素是抽象的,甚至可以【是集合,也就是说一个集合可以作为另一个集合的元素。
例如:A={a,{b,c},d,{{d}}},其中a∈A,{b,c}∈A,d∈A,{{d}}∈A,但b A,{d} A4.练习例:判断下列说法是否正确,并说明理由。
(1)著名科学家组成一个集合(×)——“著名科学家”没有明确标准(2)数轴上到原点的距离大于1的点的全体组成一个集合(√)——数轴上任意一点到原点的距离要么等于1或小于1,要么大于1,所以是正确的(3)1,3/2,6/4,︱1/2︱,0.5 这些数组成的集合有5个元素(×)→因为3/2=6/4,︱-1/2︱=0.5由显异性知,这个集合只有3个元素。

第一章集合论一、教学内容及要求授课学时:2教学内容1.1 集合的基本概念集合的概念及其表示;集合与集合之间的包含、真包含和相等关系的定义,数学描述及判定和证明方法;空集、全集和幂集三个特殊集合的定义、性质以及幂集的计算算法。
1.2 集合的运算集合运算的定义、性质及证明1.3 无限集可数集合和不可数集合的概念。
1.4 与集合相关的应用与集合相关的简单应用实例。
基本要求1)能正确地用枚举法或叙述法表示一个集合,会画文氏图。
2)能判定元素与集合的属于关系。
3)能利用集合与集合关系的判定与证明方法证明两个集合之间的包含、相等、和真包含的关系。
4)能熟练计算集合之间的并、交、差、补运算,掌握集合运算的定律;5)能熟练地计算P(A)。
6)理解集合的归纳法表示。
7)理解集合的对称差运算。
8)了解集合的递归指定法表示。
9)了解无限集的基本概念。
10)了解集合的简单应用。
能力培养通过课堂讲解和课后实践作业,培养学生的抽象思维和问题解决能力。
二、教学重点、难点及解决办法教学重点:集合的概念及集合间关系的证明;集合的表示方法:列举法、描述法和文氏图;集合运算及定律和幂集P(A)的计算。
教学难点:从集合与元素两个角度去分析集合;集合与集合关系的证明和无限集基数的理解。
解决办法:1)在教学过程中,为了加强学生对一个集合“双重身份”的理解,可以通过实例教学法,让学生具体体会一个集合的“双重身份”带来的问题及解决办法;2)对于新概念—幂集,让学生编程实现求一个集合的幂集,从而加深对幂集的理解。
初步建立学生的发散思维能力以及实际动手编写程序的能力。
三、教学设计从集合伦论的创始人康托尔到集合论的最终完备,让学生明白科学研究的道路是坎坷的,但为全人类做出自己的贡献是有价值和意义的,从而要树立为科学献身的精神和爱国主义情怀。
从集合的定义入手,结合高中阶段对集合的认识,指出当时定义存在的不足,提出新的定义方法;重点介绍大学阶段学习集合的主要意义和内容,关注重点概念的理解;介绍属于关系与包含关系之间的区别与联系,特别是一个集合“双重身份”的理解;强调集合的基本运算,特别是幂集的计算;集合与集合包含、真包含和相等关系的数学描述及相应的证明方法。

离散数学教案一、教学目标通过本节课的学习,学生能够:1. 理解离散数学的基本概念和基础知识;2. 掌握离散数学中常用的逻辑、集合和函数等概念及其应用;3. 能够运用离散数学的方法解决实际问题。
二、教学内容1. 离散数学的概述- 离散数学的定义和特点- 离散数学在计算机科学、信息技术等领域的应用2. 逻辑与证明- 命题逻辑的基本概念- 命题逻辑的运算与推理规则- 数理逻辑的基本概念- 数理逻辑的运算与推理规则- 证明方法与常用证明技巧3. 集合与图论- 集合的基本概念- 集合的运算与关系- 图的基本概念和性质- 图的表示方法与应用4. 函数与关系- 函数的定义与性质- 函数的运算与特性- 逆函数与复合函数- 关系与关系矩阵5. 组合数学- 排列与组合的基本概念- 排列与组合的计算方法- 组合数学在密码学和编码中的应用三、教学过程1. 教师引入通过引入一个实际问题,介绍离散数学在解决问题中的重要性和应用场景。
2. 知识讲解依次讲解离散数学的概述、逻辑与证明、集合与图论、函数与关系以及组合数学等知识点,结合具体例子进行说明和展示,引导学生理解和掌握相关概念和方法。
3. 思维拓展训练给学生提供一些离散数学相关的思维拓展训练题,鼓励学生独立思考和解决问题,培养其离散数学思维能力。
4. 实践应用结合实际案例,让学生运用所学的离散数学知识,分析和解决实际问题,锻炼学生的应用能力和实践能力。
5. 总结归纳教师对本节课的内容进行总结和归纳,提醒学生重点和难点,巩固学生对离散数学的理解和掌握。
四、教学资源1. 教材:离散数学教材、相关参考书2. 多媒体教具:电脑、投影仪3. 练习题:离散数学练习题集五、教学评价1. 完成课堂练习和作业,检验学生对于离散数学知识的掌握情况;2. 参与思维拓展训练和实践应用活动,评估学生的思维能力和应用能力;3. 课堂表现和课后反馈,了解学生对于教学内容的理解和反馈,及时调整教学方法和策略。


离散数学教案一、教学目标通过本节课的学习,学生将能够:1. 了解离散数学的基本概念和重要性;2. 掌握离散数学中的基本运算规则;3. 理解离散数学在计算机科学和信息技术中的应用。
二、教学内容1. 离散数学的基本概念a. 离散数学的定义和特点b. 与连续数学的区别与联系2. 离散数学中的基本运算规则a. 集合的定义和运算b. 逻辑运算c. 排列与组合3. 离散数学的应用a. 离散数学在计算机科学中的重要性和应用领域b. 离散数学在信息技术中的应用案例分析三、教学过程1. 导入在课堂开始前,通过提问或引入一些相关问题的方式,引起学生的兴趣和思考离散数学的应用场景。
2. 概念介绍和讲解逐步介绍离散数学的定义、离散数学与连续数学的区别,以及离散数学在计算机科学和信息技术中的重要性。
3. 基本运算规则的学习通过示例和练习,教授集合的定义、集合的运算、逻辑运算、排列与组合等基本运算规则,并着重强调它们在离散数学中的应用。
4. 应用案例分析结合实际案例,对离散数学在计算机科学和信息技术中的应用进行分析和讨论。
可以使用图表、演示等形式,提高学生对离散数学应用的理解和实际运用能力。
5. 总结与扩展对本节课的内容进行总结,强调离散数学在计算机科学和信息技术中的重要性,并提供相关扩展资料供学生深入学习和研究。
四、教学评价1. 课堂参与度:观察学生在课堂上的积极参与程度,包括问题回答和举手提问等。
2. 练习和作业:布置相关的练习和作业,检验学生对离散数学的理解和应用能力。
3. 学习笔记:鼓励学生做好课堂笔记,评价学生对离散数学知识的整理和梳理能力。
五、教学资源1. PowerPoint演示文稿:包含离散数学的基本概念、基本运算规则和应用案例。
2. 练习和作业册:提供相关练习和作业,让学生巩固所学知识。
注意:以上教案仅为示例,具体的教学流程和内容可根据实际情况进行调整和修改。
祝您教学顺利!。

《离散数学(一)》教学教案第一部分课程总论一、课程简介课程名称:离散数学英文名称:Discrete Mathematics离散数学:离散数学是现代数学的一个重要分支,是计算机科学的核心课程。
以研究离散量的结构和相互间的关系为主要目标,其研究对象是有限个或无限个元素。
离散数学与计算机科学中的数据结构、操作系统、编译理论、算法分析、逻辑设计、系统结构、容错诊断、机器定理证明等课程紧密相关。
是一门重要的基础课程。
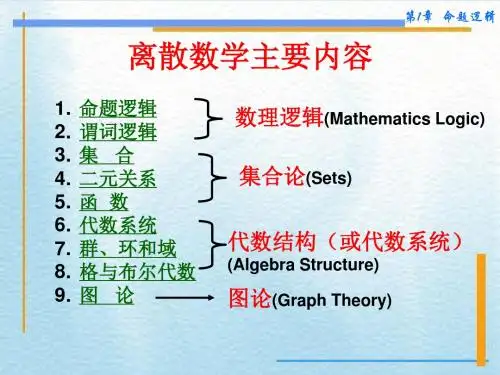
教学内容:数理逻辑、集合论、代数结构与布尔代数、图论和在计算机中的应用共五部分。
其中第五部分不做考试要求,不占计划内学时,可在第三学期安排讲座课讲授。
教学要求:通过该课程的学习,培养和锻炼抽象思维和缜密概括的能力,为专业基础课和专业课的学习打下坚实的理论基础。
授课总学时:4学时/周 16周=64学时二、适用对象本课程教学教案主要针对计算机科学与技术本科专业三、学习要领概念(正确):必须掌握好离散数学中大量的概念判断(准确):根据概念对事物的属性进行判断推理(可靠):根据多个判断推出一个新的判断四、离散数学与计算机的关系第一部分数理逻辑计算机是数理逻辑和电子学相结合的产物第二部分集合论集合:一种重要的数据结构关系:关系数据库的理论基础函数:所有计算机语言中不可缺少的一部分第三部分代数系统计算机编码和纠错码理论数字逻辑设计基础计算机使用的各种运算第四部分图论数据结构、操作系统、编译原理、计算机网络原理的基础五、教材及主要参考书教材:左孝凌、李为鑑、刘永才,离散数学,上海科学技术出版社,1982年9月第1版。
参考书:[1] 王元元、张桂芸,离散数学导论,科学出版社,2002[2] Kenneth H.Rosen Discrete Mathematics and Its Applications ( Fourth Edition), 机械工业出版社(华章),2001[3] 王元元、张桂芸,计算机科学中的离散结构,机械工业出版社,2004[4] Bernard Kolman , Robert C. Busby, Sharon Ross, Discrete Mathematical Structures (Fourth Edition), 高等教育出版社,2001[5] 孙吉贵杨凤杰欧阳丹彤李占山,离散数学,高等教育出版社,2002[6] 马振华,离散数学导引,清华大学出版社,1993[7] 王树禾,离散数学引论,中国科技大学出版社,2001[8] Andrew Simpon 著冯速译离散数学导学机械工业出版社2005第二部分课程内容与要求《离散数学》为计算机科学与技术专业的一门重要基础理论课。
《离散数学》教案课目:第一章命题逻辑教师:熊建英学时: 12课时Ⅰ教学提要一、教学对象(人数)学生:信息安全专业本科二年级学生50人二、教学目标(任务)各小结中知识点掌握程度(* 理解;** 基本掌握;***熟练掌握)三、教学要求(一)学生:着重知识点的学习,积极思考,参与提问。
(二)教官:严格纪律,严密组织、保持良好教学秩序,确保教学效果。
四、教官分工主讲教师1名:负责教案编写,课堂的组织教学,教学总结编写。
五、本章重点1、利用联接词构造复合命题公式2、真值表的构建3、等值演算4、复合命题公式转化为主析取范式、主合取范式的方法5、推理证明六、本章难点1、利用命题公式演算、真值表进行等值判断和公式类型判断2、利用命题公式演算、真值表转化主析取范式、主合取范式3、将现实背景下的条件约束构造为命题公式七、教学方法采用课堂教授,主要使用多媒体课件,部分内容及例题用黑板解释。
八、课时分配1.1 命题及联接词2课时;1.2 命题公式及其赋值2课时;1.3 等值式2课时;1.4 析取范式与合取范式2课时;1.5 推理理论与消解法2课时;1.6 命题逻辑应用案例2课时;九、场地器材多媒体教室十、参考书目1、杨圣洪、张英杰、陈义明:《离散数学》,科学出版社,2011年。
2、屈婉玲、耿素云、张立昂:《离散数学》,高等教育出版社,2008年。
3、屈婉玲、耿素云、张立昂:《离散数学学习指导与习题解析》,高等教育出版社,2008年。
Ⅱ教学进程1.1 命题及联接词(2课时)一、教学内容1、命题的概念表示与分类2、五种基本的联接词的逻辑关系3、复合命题的符号化4、复合命题的真值判断二、课程时间安排1、首先介绍本课程的性质,任务和教学安排,对学生明确提出教学上的要求(10分钟)2、介绍离散数学学科的发展历史(20分钟)3、命题与真值、命题的分类、简单命题符号化(15分钟)4、联结词与复合命题(35分钟)5、本次课小结(10分钟)三、教学实施(一)创设意境、导入课程(10分钟)目的体会离散数学理论在现实生活中的应用、是计算机专业多门核心课程的基础,让学生明白“离散数学”课程作用和意义。
离散数学教案教案标题:离散数学教案教学目标:1. 理解离散数学的基本概念和原理。
2. 掌握离散数学中的集合论、逻辑、图论等基础知识。
3. 培养学生的抽象思维和逻辑推理能力。
4. 培养学生的问题解决能力和数学建模能力。
教学内容:1. 集合论:a. 集合的定义和表示法。
b. 集合的运算:交集、并集、差集、补集。
c. 集合的基本性质和定理。
d. 集合的应用:排列组合、概率等。
2. 逻辑:a. 命题逻辑的基本概念和符号表示。
b. 命题逻辑的运算:与、或、非、蕴含、等价。
c. 命题逻辑的基本定理和推理规则。
d. 命题逻辑的应用:谓词逻辑、命题公式的简化等。
3. 图论:a. 图的基本概念和术语:顶点、边、路径、连通性等。
b. 图的表示方法:邻接矩阵、邻接表等。
c. 图的遍历算法:深度优先搜索、广度优先搜索。
d. 图的应用:最短路径问题、最小生成树等。
教学步骤:1. 导入引入:通过一个生活中的例子引出离散数学的重要性和应用领域。
2. 知识讲解:依次介绍集合论、逻辑和图论的基本概念、原理和应用。
3. 案例分析:通过具体案例分析,让学生理解离散数学在实际问题中的应用。
4. 练习与讨论:提供一些练习题和问题,让学生运用所学知识进行解答和讨论。
5. 总结归纳:对本节课所学内容进行总结,并强调重点和难点。
6. 拓展延伸:引导学生进一步探索离散数学的相关领域和应用。
教学资源:1. 教科书:提供相关章节的教材和练习题。
2. 多媒体教具:使用投影仪或电子白板展示相关图表和示意图。
3. 计算机软件:使用图论相关的计算机软件进行实践操作和模拟实验。
评估方法:1. 课堂练习:通过课堂练习题评估学生对基本概念和原理的理解程度。
2. 作业评估:布置相关作业,评估学生的问题解决能力和数学建模能力。
3. 课堂参与:评估学生在课堂讨论和案例分析中的积极参与程度。
教学反馈与调整:1. 收集学生的反馈意见和问题,及时解答疑惑。
2. 根据学生的学习情况和理解程度,调整教学进度和教学方法。
离散数学教案教案:离散数学概论教学目标:1.使学生了解离散数学的基本概念和方法。
2.培养学生的逻辑思维和数学推理能力。
3.帮助学生将离散数学的知识应用到实际问题中。
教学内容:1.真值逻辑与命题逻辑2.集合论与其运算3.二元关系与其属性4.递归与归纳5.图论与树论基础6.组合数学与概率论教学重难点:1.对学生来说,最难的可能是理解集合论和命题逻辑的基本概念和运算规则。
2.理解递归和归纳的思想和方法。
3.运用图论和树论的基础概念解决实际问题。
教学过程:第一课时:真值逻辑与命题逻辑(60分钟)1.真值表与命题的逻辑运算(10分钟)-介绍命题逻辑的基本概念和真值表的作用。
-教授真值表的构建方法和命题的逻辑运算规则。
2.命题逻辑的推理法则(20分钟)-介绍命题逻辑的推理法则,如合取范式、析取范式、蕴含式等。
-给出一些例子,帮助学生理解和应用这些推理法则。
3.应用实例:判断命题的真假(30分钟)-提供一些具体的例子,让学生通过构建真值表来判断命题的真假。
-引导学生思考如何通过命题逻辑的推理法则来判断复杂命题的真假。
第二课时:集合论与其运算(60分钟)1.集合的基本概念(10分钟)-介绍集合的定义和表示方法。
-引导学生通过例子理解集合的基本概念。
2.集合的运算(20分钟)-教授集合的运算,包括交集、并集、差集和补集。
-给出一些具体的例子,让学生通过集合运算来解决问题。
3.应用实例:集合的应用问题(30分钟)-提供一些实际问题,让学生通过集合的运算来解决。
-引导学生思考如何应用集合论解决实际问题。
第三课时:二元关系与其属性(60分钟)1.二元关系的定义(10分钟)-介绍二元关系的基本概念和定义。
-引导学生通过例子了解二元关系的特点。
2.二元关系的性质(20分钟)-教授二元关系的自反性、对称性和传递性等基本性质。
-给出一些具体的例子,让学生判断二元关系的性质。
3.应用实例:二元关系的应用问题(30分钟)-提供一些实际问题,让学生通过二元关系解决。